WĘDRÓWKI PO 

GRAFACH

• Obchody Eulera

• Cykle Hamiltona

 

 

U źródeł teorii grafów

• 1736: Euler odwiedza Królewiec 

(Königsberg, Kaliningrad).

• Rozwiązuje zagadkę 7 mostów.

• Uogólnia problem i też go 

rozwiązuje, otrzymując  1. 
twierdzenie teorii grafów

.

 

 

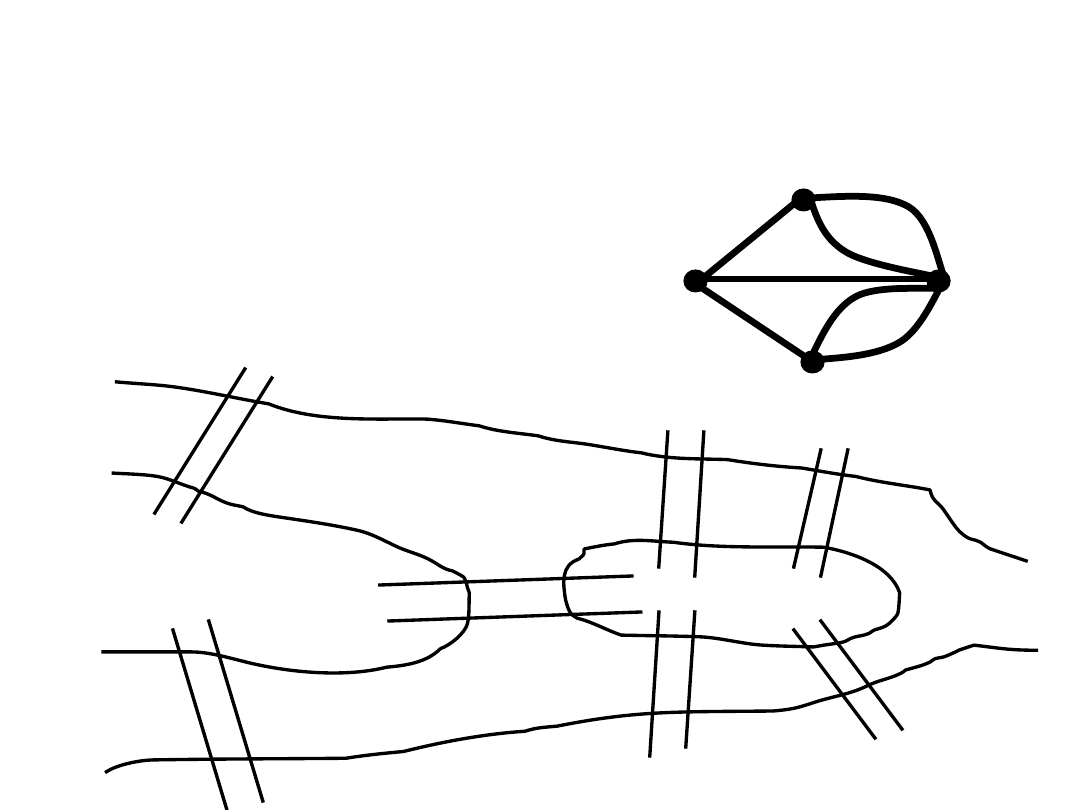
Mosty Królewieckie

A

B

C

D

A

C

B

D

 

 

Spacery i obchody

• Dla danego 

multigrafu

 G, ciąg    

W=v_0e_0v_1e_1...v_{k-1}e_{k-1}v_k  nazywamy

 

spacerem

, gdy e_i=v_iv_{i+1} jest krawędzią w 

G  dla każdego i<k. 

• W (Na ?) spacerze wierzchołki i krawędzie mogą 

się powtarzać

.

• Spacer jest 

zamknięty

, gdy  v_0=v_k.   

• Zamknięty spacer zawierający każdą krawędź 

dokładnie raz (dokładniej: tyle razy, ile wynosi jej 

krotność)  nazywamy 

obchodem Eulera

, a 

spójny

 

multigraf, dla którego istnieje obchód Eulera – 

grafem Eulera.            

 

 

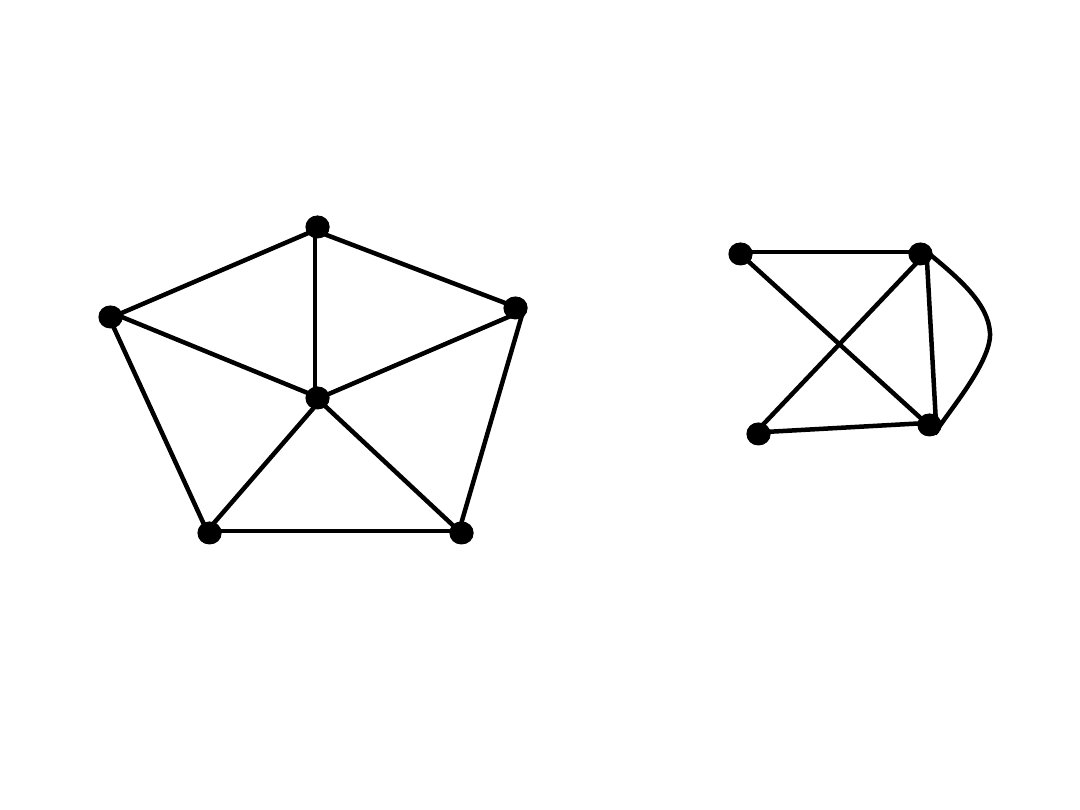
Ilustracja

a

b

c

d

e

f

a-b-c-f-b-a-e -- spacer

a-b-c-b-f-a – spacer zamknięty

a

b

c

d

a-b-d-c-b-c-a – 
obchód Eulera

 

 

Tw. Eulera

Tw (Euler, 1736)

. Spójny graf G jest grafem Eulera 

wgdy wszystkie stopnie wierzchołków są 
parzyste.

Dowód

 :  oczywiste

   

Rozważmy najdłuższy spacer W w G 

zawierający każdą krawędź nie więcej niż raz.

  W musi być zamknięty 

(dlaczego?).

  

Jeśli W nie jest obchodem Eulera, to istnieje 

krawędź e poza W, ale incydentna z W.

  

Wtedy jednak W można wydłużyć – sprzeczność

. 

 

 

Wniosek

Lemat

.

 Jeśli wszystkie stopnie wierzchołków w G 

są parzyste, to krawędzie w G można 
zorientować (skierować, ,,ostrzałkować”) tak, 
by do każdego wierzchołka wchodziło tyle samo 
strzałek co wychodziło.

Dowód: 

W każdej składowej znajdźmy obchód 

Eulera i zorientujmy krawędzie wzdłuż niego. 

Uwaga:

 Adaptacja pierwotnego dowodu tego 

lematu pozwala na indukcyjny dowód Tw. 
Eulera.

 

 

Zwiedzamy muzeum

• Zwiedzamy muzeum będące 

labiryntem korytarzy, w którym 
obrazy wiszą po obu stronach.

• Cel: przejść każdy korytarz 2 razy 

i wrócić do wyjścia.

 

 

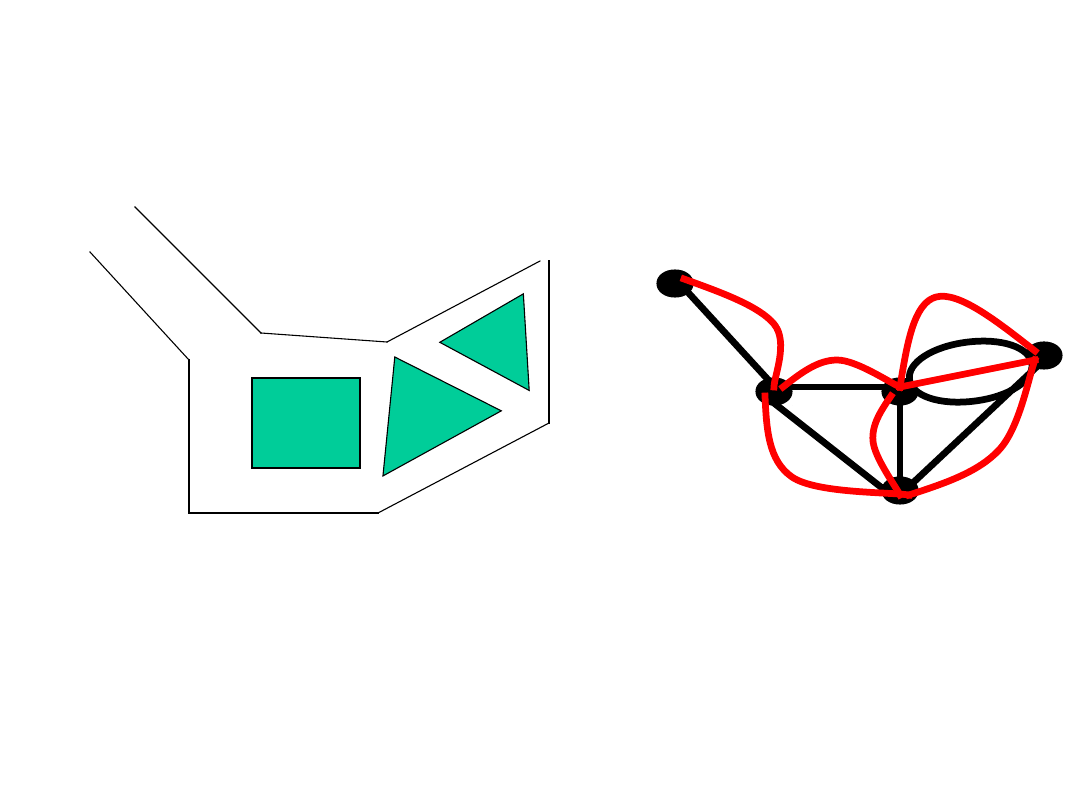
PLAN MUZEUM

a

b

c

d

e

a

b

c

d

e

Konkluzja:

 

KAŻDE

 muzeum da się tak przejść!

 

 

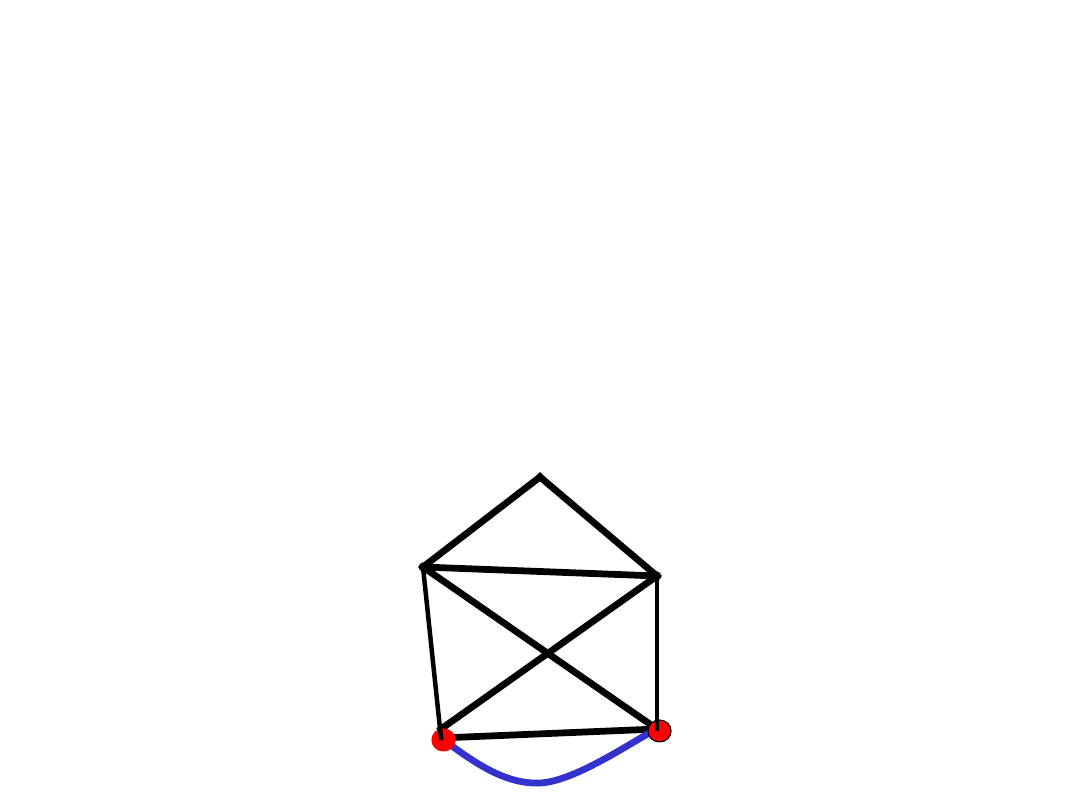
Rysowanie bez odrywania

Czy dany rysunek można narysować 

bez odrywania ołówka od papieru i 

bez powtarzania linii?

 

 

Trasa Eulera

• Spacer zawierający każdą krawędź 

dokładnie raz nazywamy 

trasą Eulera.

Wniosek.

 Spójny graf G ma trasę Eulera 

wgdy wszystkie stopnie wierzchołków 

są parzyste, oprócz co najwyżej dwóch.

Dowód:  

Jeśli trzeba, dodajmy krawędź, 

by powstał graf Eulera. Z obchodu 

Eulera usuńmy dodaną krawędź. 

 

 

Więcej nieparzystych

Wniosek.

 Jeśli multigraf G ma 2k nieparzystych 

stopni wierzchołków, to E(G) można pokryć przy 
pomocy k (krawędziowo rozłącznych) spacerów, 
w których żadna krawędź się nie powtarza.

Dowód:  

Dodajmy do G k krawędzi łączących 

parami wierzchołki nieparzyste. Nowy multigraf 
jest grafem Eulera i ma obchód Eulera W.

   Usuwając z W dodane krawędzie, dzielimy go na 

k spacerów o żądanej własności.  

 

 

Problem Chińskiego 

Listonosza

• Obchodem listonosza

 nazywamy 

zamknięty spacer przechodzący 
przez każdą krawędź 

co najmniej

 

raz.

• Problem (Guan 1960, Edmonds 

1965):

 Znaleźć najkrótszy obchód 

listonosza w spójnym multigrafie.

 

 

Rozwiązanie

• Niech G ma 2k nieparzystych 

stopni.

• Niech H będzie najmniejszym (co 

do liczby krawędzi) podgrafem 
rozpiętym w G, który ma te same 
nieparzyste wierzchołki co G.

 

Problem 1: 

Jak efektywnie wyznaczyć 

H

 

?    

(ćwiczenia)

  

 

 

Rozwiązanie – c.d.

• Dublując krawędzie  H w G 

otrzymamy graf Eulera G+H.

• Obchód Eulera W w G+H 

wyznacza obchód listonosza w G.

Problem 2: 

Wykazać, że

 

W jest 

najkrótszym obchodem listonosza 
w G? 

(ćwiczenia)

 

 

A

B

C

D

E

F

G

H

I

J

 

 

A

B

C

D

E

F

G

H

I

J

 

 

Ilustracja

 

 

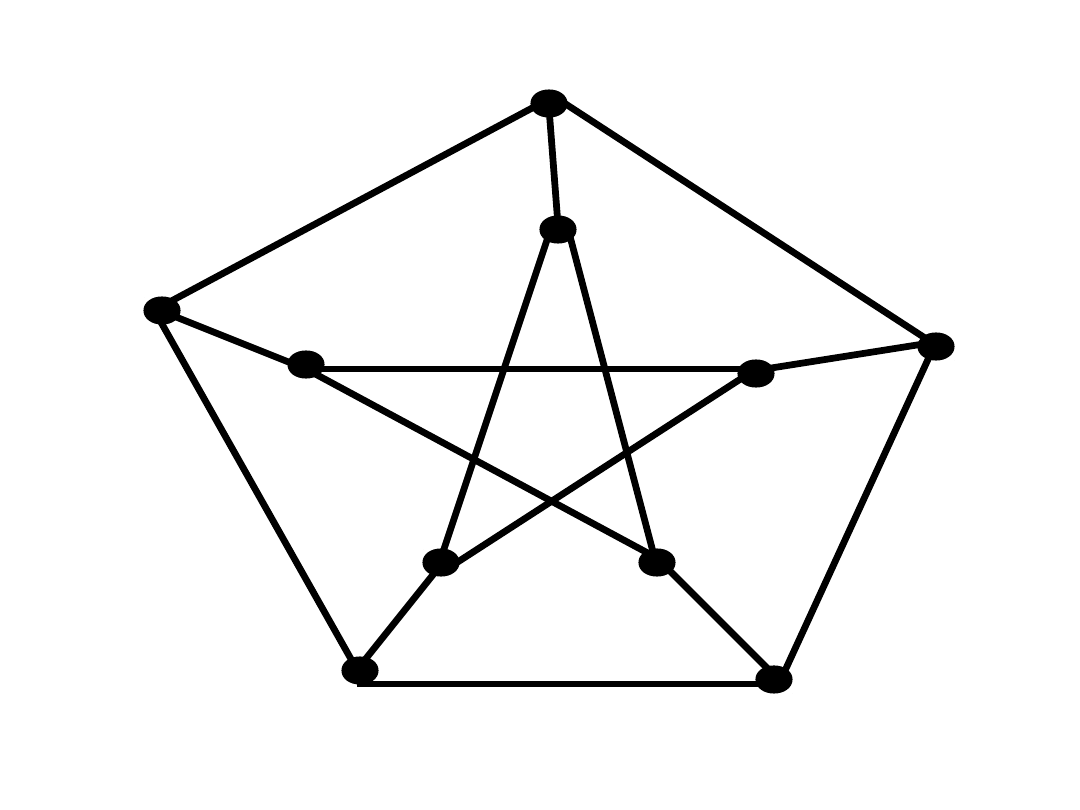
Zabawka Hamiltona

• Sir William Hamilton (1859):

• Przejść 

bez powtórzeń

 wszystkie 

wierzchołki dwunastościanu i wrócić do 
punktu wyjścia, poruszając się wzdłuż 
krawędzi.

 

 

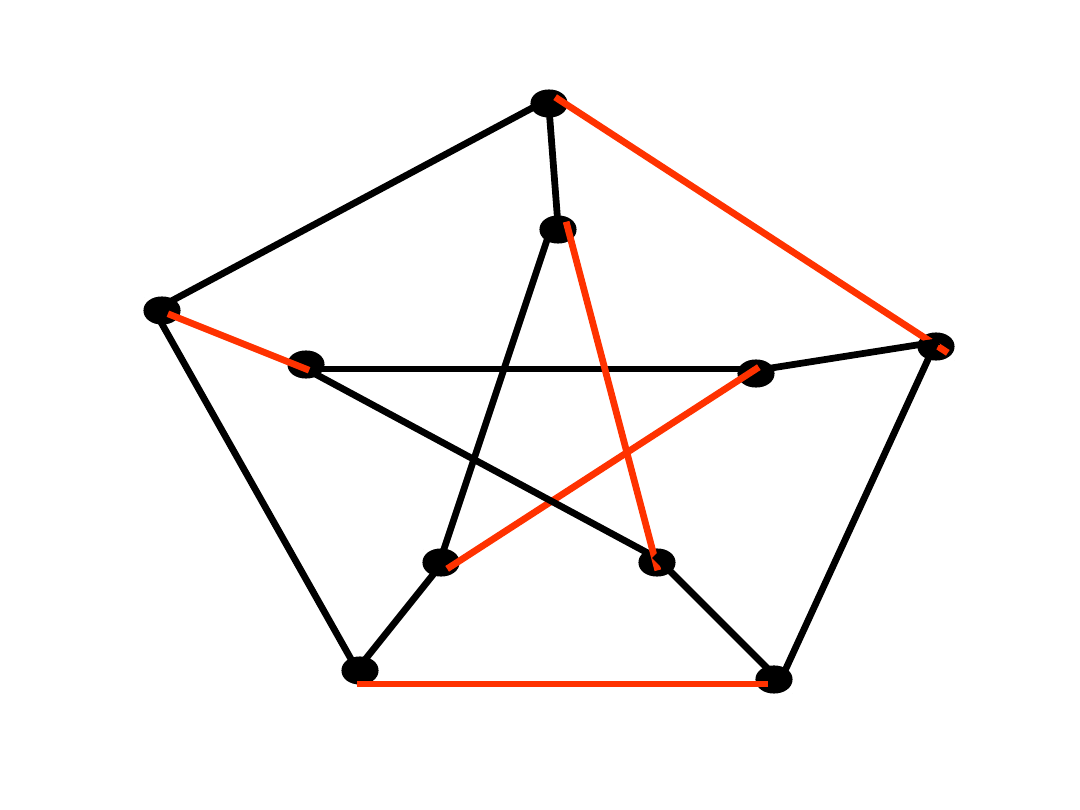
Cykl Hamiltona

• Cyklem Hamiltona

 w grafie G 

nazywamy rozpięty podgraf grafu G, 
który jest cyklem.

• Graf posiadający cykl Hamiltona 

nazywamy 

hamiltonowskim 

lub

 

Hamiltona.

• Ścieżką Hamiltona 

w grafie G 

nazywamy rozpięty podgraf grafu G, 
który jest ścieżką.

 

 

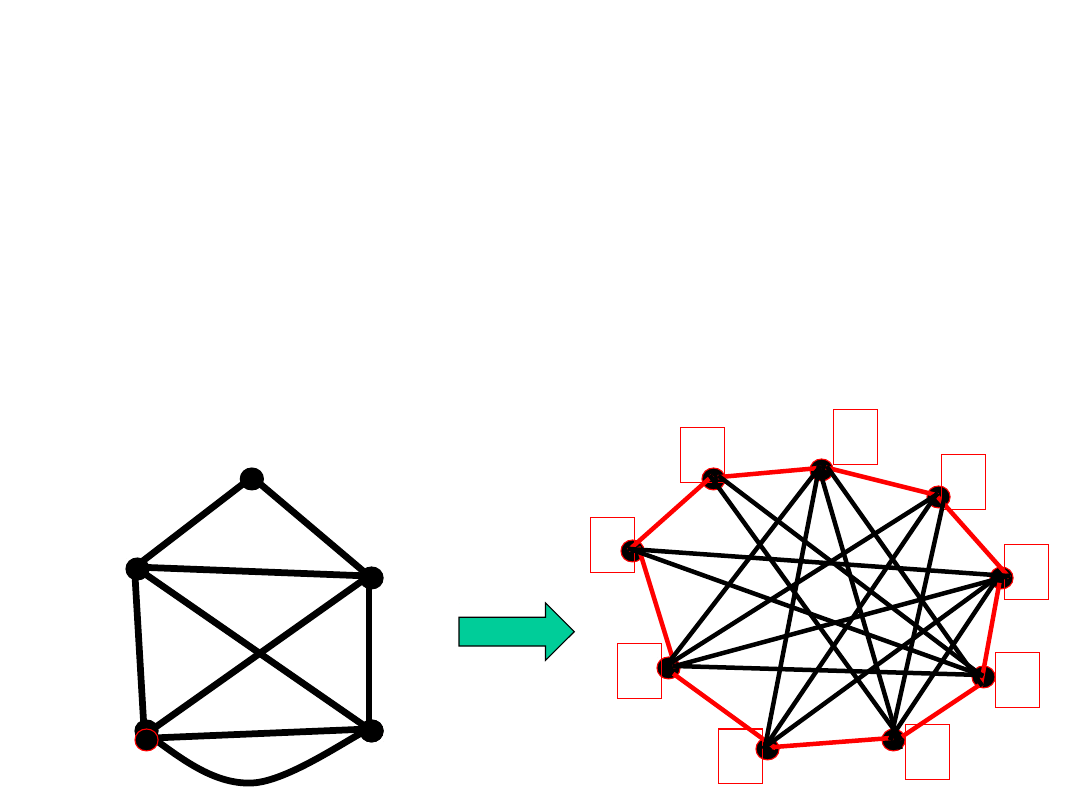
Euler vs. Hamilton

• Obchód (trasa) Eulera w grafie G 

jest cyklem (ścieżką) Hamiltona w 

grafie krawędziowym L(G).

1

2

3

4

5

6

7

8

9

1

2

3

4

5

6

7

8

9

 

 

Ale...

• Nie każdy graf jest grafem 

krawędziowym, np. K_{1,3}.

• Problem rozstrzygnięcia czy graf jest 

hamiltonowski jest 

NP-zupełny

.

• Problemy rozstrzygnięcia czy graf 

jest eulerowski oraz czy graf jest 
grafem krawędziowym są w 

klasie P

.

 

 

Warunek konieczny

Fakt 1.

 Jeśli istnieje w G zbiór 

wierzchołków S taki, że G-S ma 
więcej niż |S| składowych spójności, 
to G 

nie

 jest hamiltonowski.

Dowód: 

Jeśli usunąć z cyklu k 

wierzchołków, to rozpadnie się on 
na co najwyżej k składowych, więc 
to samo jest prawdą dla grafu 
hamiltonowskiego

. 

 

 

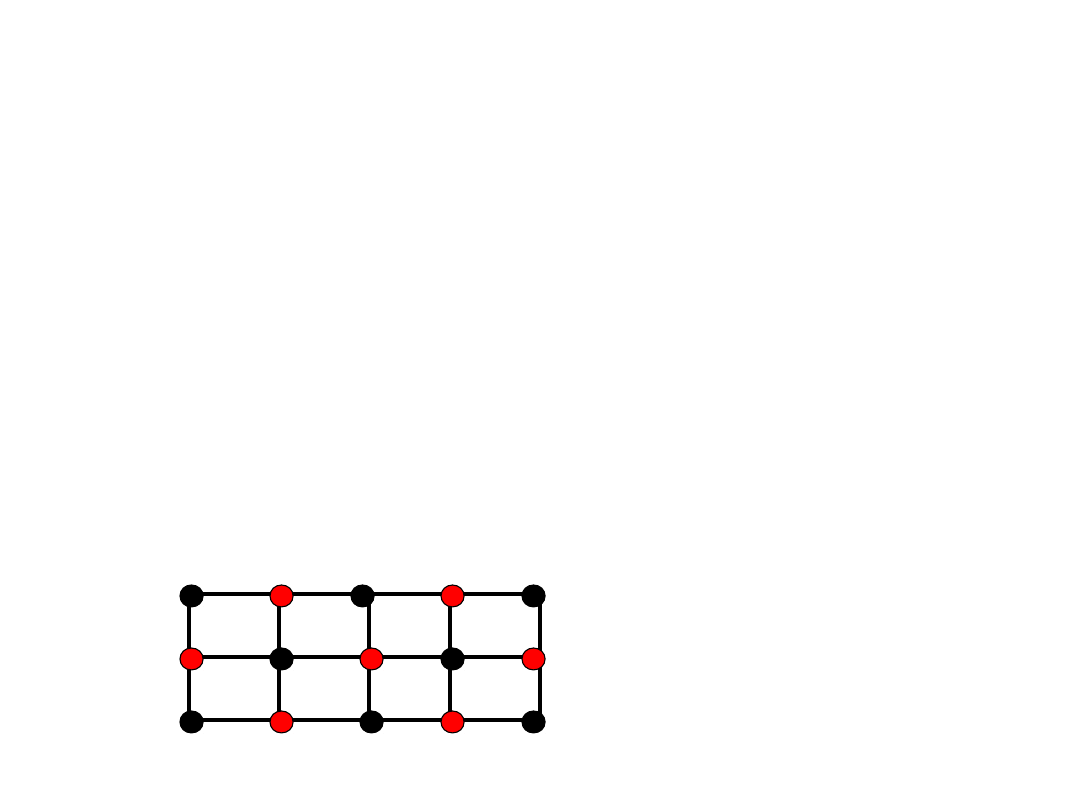
Wnioski

1. 

Graf Hamiltona musi być 2-spójny.

 

2. 

Dwudzielny graf Hamiltona musi 

mieć równy dwupodział, a więc musi 
mieć parzysta liczbę wierzchołków.

NIE!!!

 

 

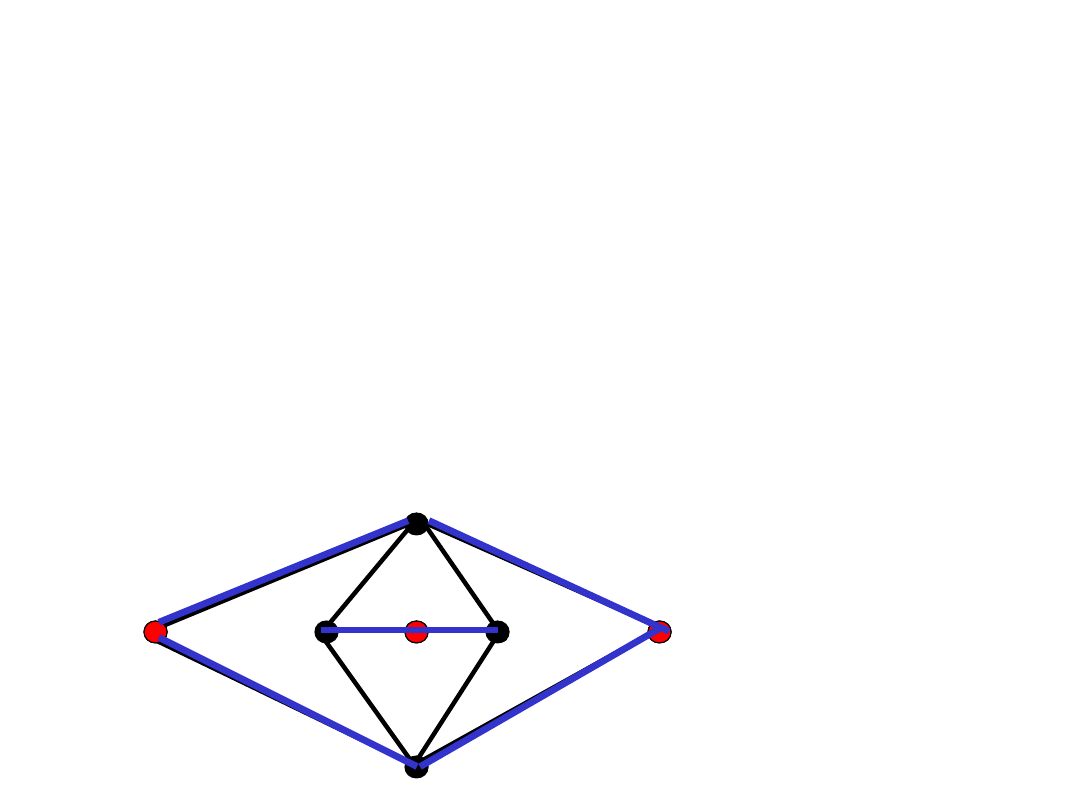
Inny warunek konieczny

Fakt 2.

 Jeśli G  jest hamiltonowski, to 

podgraf złożony z krawędzi incydentnych 
z wierzchołkami 

stopnia dwa

 w G musi 

być sumą ścieżek lub cyklem Hamiltona. 

NIE!!!

 

 

Tw. Diraca 

• Jak duże δ(G) gwarantuje cykl Hamiltona?

Tw.(Dirac 1952).

 Jeśli |V(G)|=n>2 i δ(G) ≥ 

n/2, to G jest hamiltonowski.

Dowód: 

• Przy powyższych założeniach G jest spójny.

• Rozważmy najdłuższą ścieżkę P w G.

• Jej końce, u i v, mają wszystkich sąsiadów 

w zbiorze V(P).

 

 

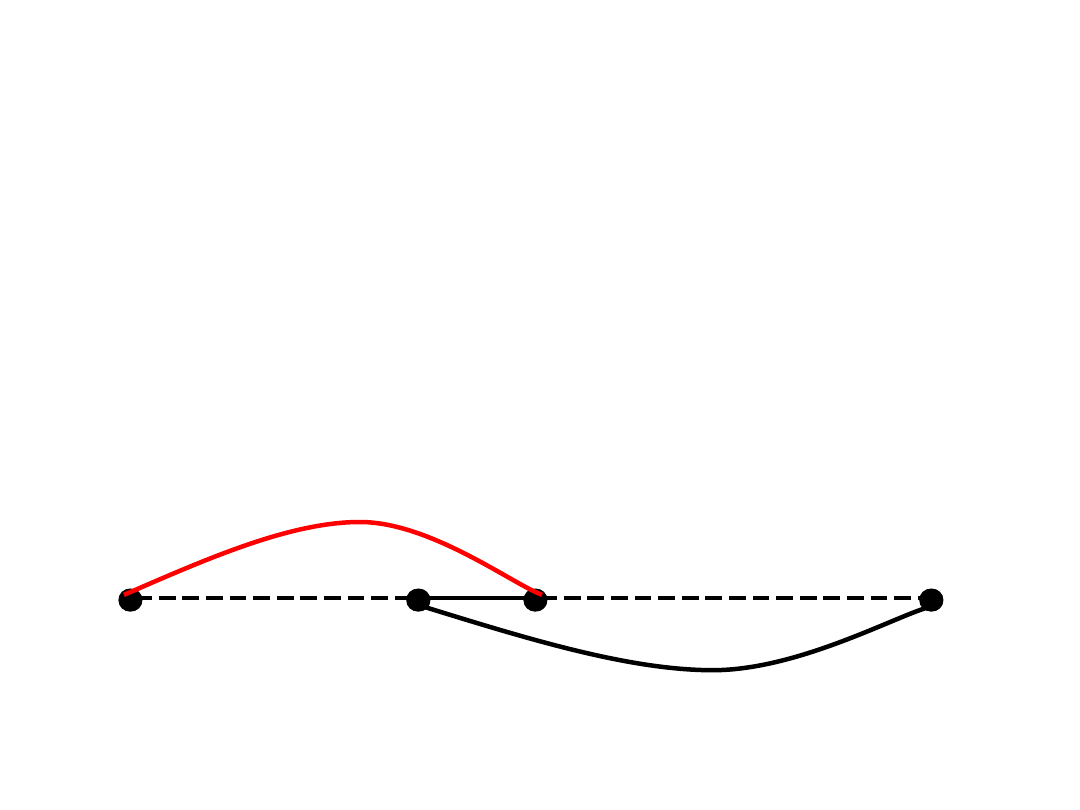
Dowód Tw. Diraca – c.d.

• Niech R będzie zbiorem wierzchołków 

położonych na P bezpośrednio ,,na 
prawo” od sąsiadów v. Precyzyjniej

:

}

1

)

,'

(

)

,

(

),

(

'

,'

:

)

(

{













u

w

d

u

w

d

G

E

v

w

w

P

V

w

R

P

P

u

v

w’

w













)

(

2

/

|

)

(

|

,

2

/

|

|

u

N

R

n

u

N

n

R

 

 

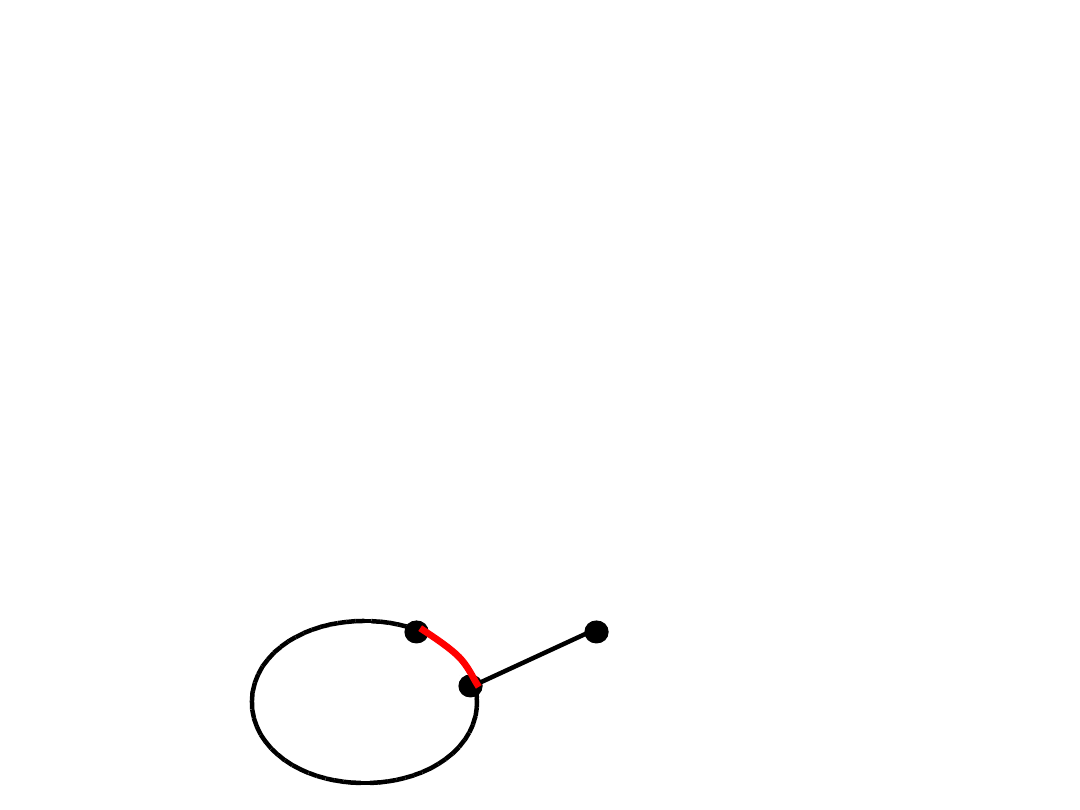
Dowód Tw. Diraca – 

dokończenie

• Zatem w G istnieje cykl C taki, że 

V(C)=V(P).

• Jeśli C nie jest cyklem Hamiltona, to na 

podstawie spójności grafu G, musi istnieć 
krawędź o dokładnie jednym końcu w V(C). 

• To jednak oznacza, że w G jest ścieżka 

dłuższa niż P – sprzeczność.



C

 

 

Tw. Ore

Tw.(Ore 1960).

 Jeśli |V(G)|=n>2 i 

dla każdej pary 

nie

sąsiednich 

wierzchołków u i v, 

to G jest hamiltonowski.

,

)

(

)

(

n

v

d

u

d

G

G





Dowód: 

Taki sam jak dowód Tw. Diraca.

 

 

Tw. Chvátala-Erdősa

• Jeśli κ(G)>k i |V(G)|>2k, to G ma cykl 

długości większej niż 2k 

(ćw.)

• Jeśli α(G)<k i |V(G)|>3k, to G ma cykl 

długości większej niż n/k  

(ćw.)

Tw. (Chvátal, Erdős, 1972) 

Jeśli |V(G)|>2 i

),

(

)

(

G

G







to G jest hamiltonowski.

 

 

Dowód

• Niech κ(G)=k.

 

• Niech C będzie najdłuższym cyklem.

• Przypuśćmy, że istnieje wierzchołek v poza C.

• Z Tw. Mengera, istnieje co najmniej min{k,|

V(C)|} rozłącznych (z wyjątkiem v) V(C)-{v} 

ścieżek. 

(

ćw.)

• Ich końce w V(C) nie mogą być sąsiednie na C.

 

• Zatem tych ścieżek jest co najmniej k ≤ |V(C)|/2. 

• Następcy ich końców na cyklu (zgodnie z 

ruchem wskazówek zegara) tworzą wraz z v 

zbiór niezależny mocy co najmniej k+1 – 

sprzeczność

.

 

 

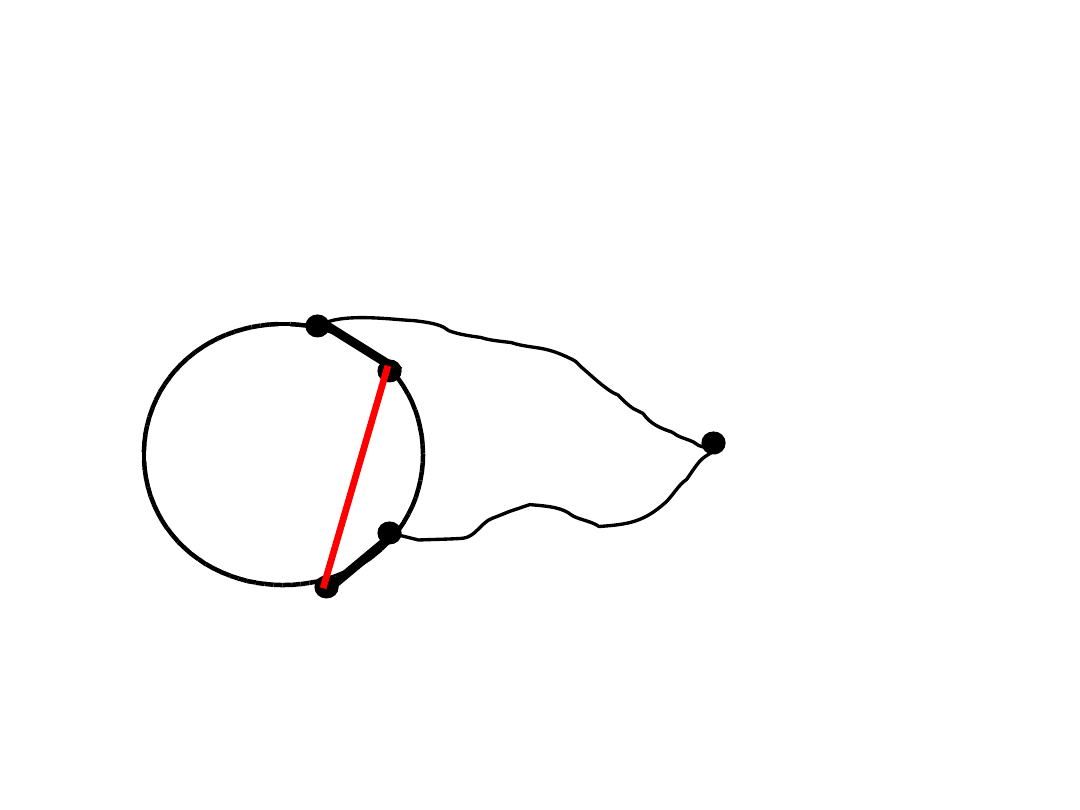
Ilustracja

C

v

P_1

P_2

u_1

u_2

w_2

w_1

Cykl w_1-w_2-...-u_1-P_1-v-P_2-u_2-...-w_1 jest dłuższy niż C.