KOLOROWANIE MAP

Grafy dualne do płaskich

• Dany jest 2-spójny graf płaski G.

• Wybierzmy po jednym wierzchołku v*(S) z

wnętrza każdej ściany S.

• Jeśli brzegi ścian S i S’ mają wspólną

krawędź e, to połączmy v*(S) i v*(S’)

krawędzią e* (krzywą Jordana

przechodzącą przez e).

• Otrzymujemy (multi)graf płaski G*, dualny

do G, gdzie

• n*=l, m*=m, l*=n

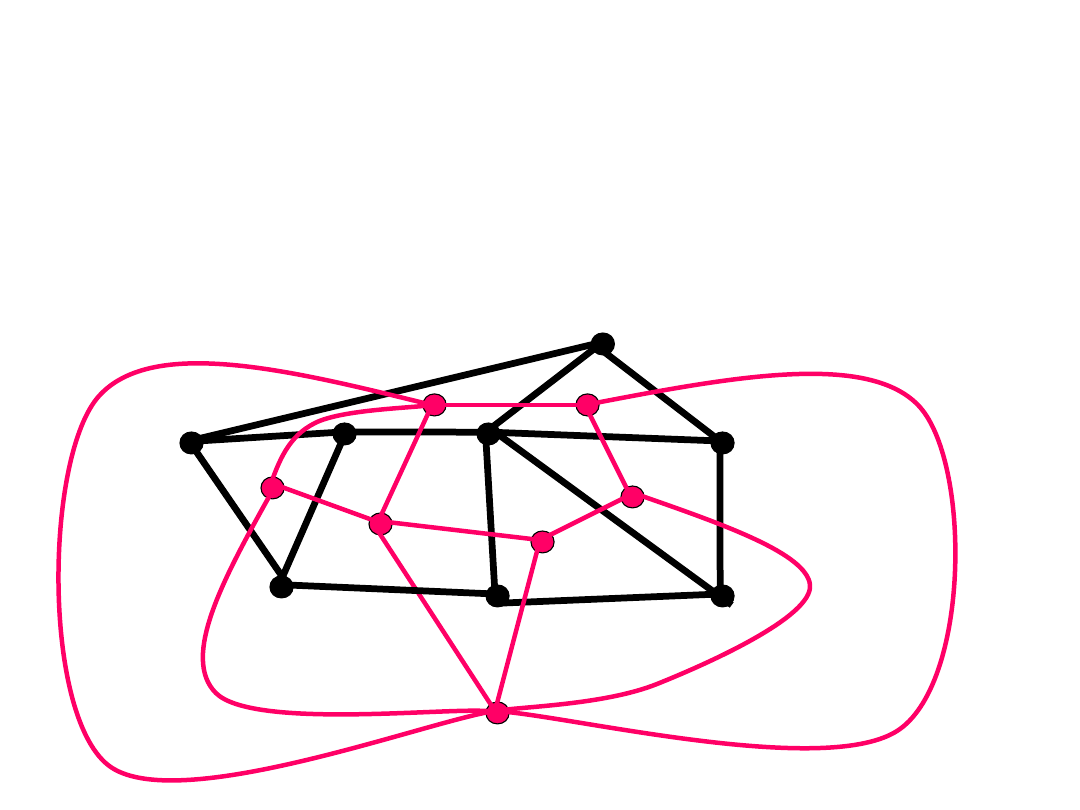
Ilustracja

G i

G*

e

e*

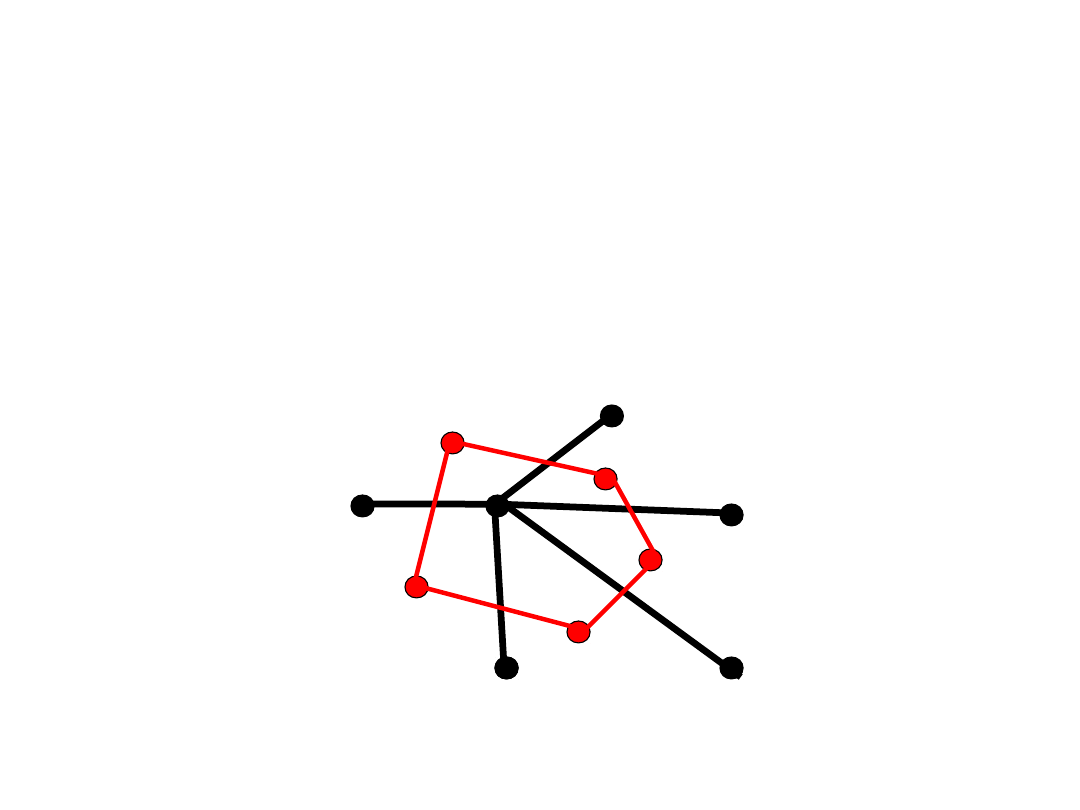
Ściany  wierzchołki

• Każda ściana grafu G staje się

wierzchołkiem grafu G*.

• I odwrotnie:

G**=G

Kolorowanie map

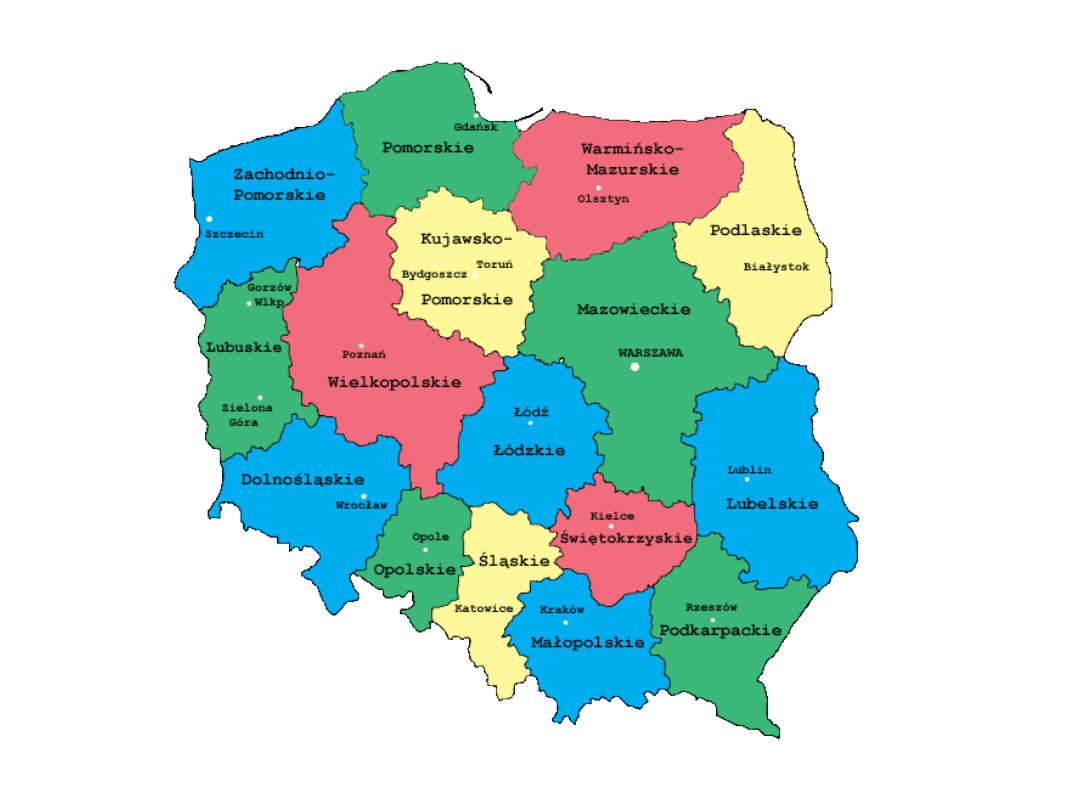
Mapy a grafy planarne

• Mapa

to zbiór ścian 2-spójnego grafu

płaskiego o δ(G)>2 (ścianę zewnętrzną
można traktować jako tło/ramę mapy).

• Kolorowanie mapy

to kolorowanie

(właściwe) wierzchołków grafu
dualnego.

• Są mapy, które wymagają aż 4 kolorów.

Hipoteza 4 kolorów -

historia

H4K:

KAŻDĄ

mapę można pomalować 4

kolorami!

•

Hipoteza z roku 1852 (de Morgan, bracia
Guthrie)

•

Dwa błędne dowody w XIX wieku (Kempe,
Tait)

•

Dowód komputerowy ogłoszony w 1976,
zweryfikowany w 1989 (Appel, Haken, Koch)
i 1997 (Robertson, Sanders, Seymour,
Thomas)

6 kolorów wystarczy!

Jeśli G jest planarny, to e(G)<3v(G), więc δ(G)<6.
Zatem

1

)

(

max

)

(







H

G

G

H





6

)

(



G



Algorytm zachłanny:

Heawood: 5 kolorów

wystarczy!

Tw. o 5 kolorach (Heawood, 1890)

Każdy

graf planarny jest 5-kolorowalny.

Dowód:

(nie wprost, oparty na korekcie

błędnego dowodu Kempe)

Niech G będzie grafem płaskim o χ(G)=6

i minimalnej liczbie wierzchołków.

Niech wierzchołek x ma stopień 5.
G-x jest 5-kolorowalny.

Dowód – c.d.

• Pomalujmy G-x 5 kolorami i spójrzmy na

sąsiadów x: x_1,...,x_5 ponumerowanych

cyklicznie wokół x.

• Można przyjąć, że x_i ma kolor i, i=1,...,5

• Niech H(i,j) –podgraf indukowany przez kolory i

i j.

• Gdyby x_1 i x_3 były w różnych składowych

H(1,3), to zamieniając kolory w jednej z nich

mielibyśmy tylko 4 kolory wokół x.

• Zatem x_1 i x_3 są połączone ścieżką, podobnie

x_2 i x_4 – sprzeczność z płaskością G.

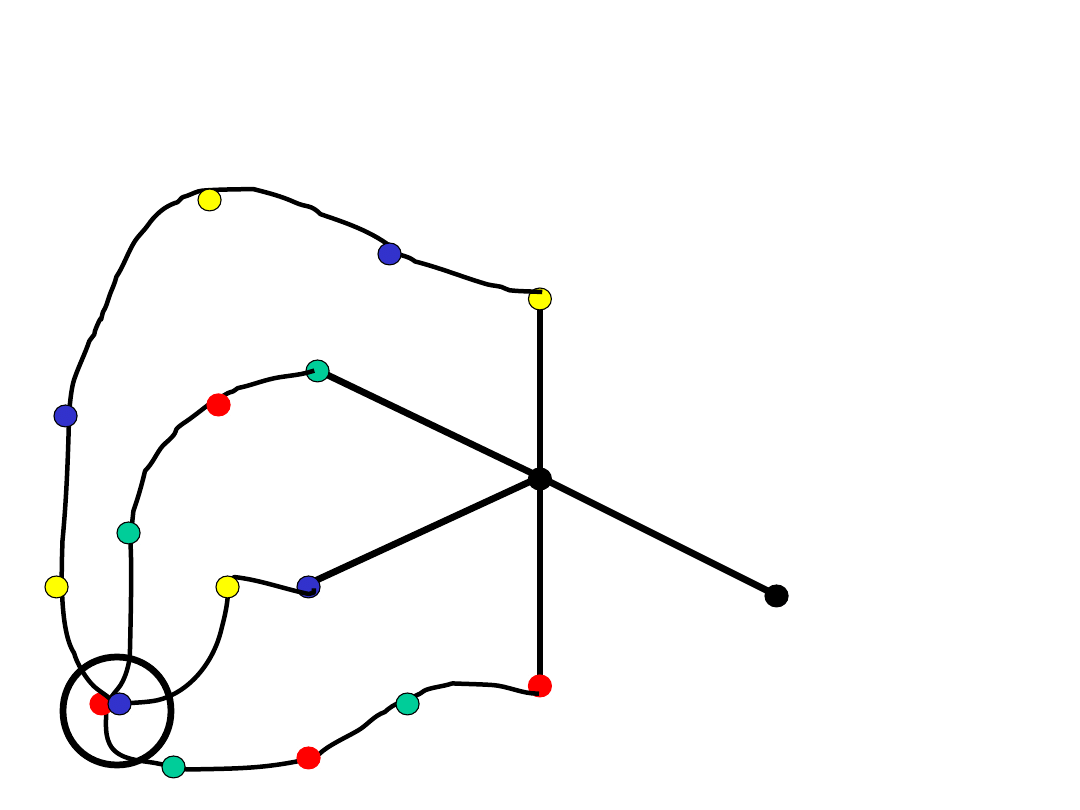
Ilustracja

?

x

x_1

x_3

x_2

x_4

x_5

Błąd Kempe

• Analogiczne przekolorowanie nie

działa, jeśli zamiast 5 różnych
kolorów, wystepują 4, (w tym
jeden dwa razy).

• Zauważył to dopiero Heawood.

Appel, Haken, Koch: idea

Idea dowodu Heawooda/Kempe:

1. Minimalny graf 6-kolorowalny G

nie może zawierać wierzchołka x

stopnia 5,

bo 5-kolorowanie G-x

można by rozszerzyć na G.

2. Każdy graf planarny zawiera taki

wierzchołek.

Konfiguracje

• Konfiguracja jest

redukowalna

, gdy żaden

minimalny 5-chromatyczny graf płaski jej nie

zawiera.

• Zbiór konfiguracji jest

nieunikniony

, gdy każda

triangulacja

zawiera przynajmniej jedną z nich.

• Appel i Haken znaleźli

nieunikniony

zbiór

złożony z 1482 konfiguracji i wraz z Kochem,

przy pomocy komputerów, sprawdzili, że

wszystkie one są

redukowalne

.

• To dowodzi H4K

(dlaczego?).

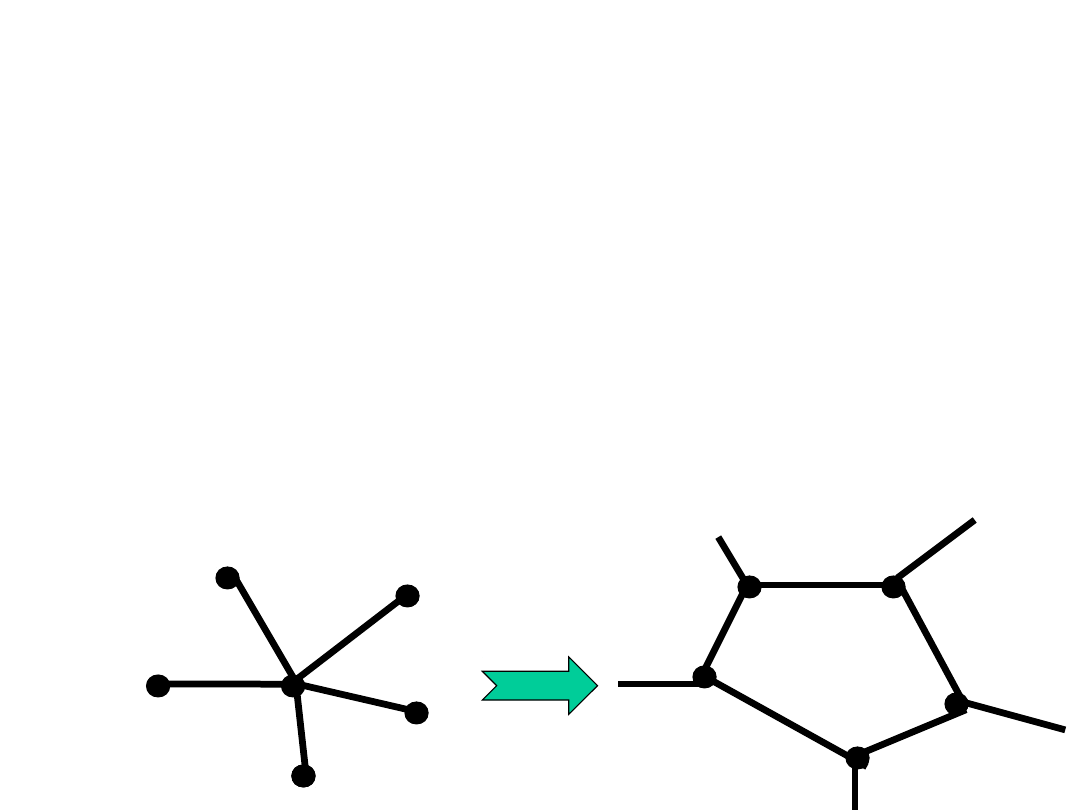
Redukcja do map 3-

regularnych

Fakt 1.

H4K jest prawdziwa wgdy każda 3-

regularna mapa jest 4-kolorowalna.

Dowód:

Weźmy mapę G (2-spójna, δ(G)>2).

Zastąpmy każdy wierzchołek stopnia >3

nowym krajem:

Pierwsza próba Taita 1880

Fakt 2.

H4K jest prawdziwa wgdy

każdy 3-regularny i 2-spójny

graf planarny ma indeks

chromatyczny 3.

(Tait sądził, że potrafi udowodnić

druga część tej równoważności.)

Dowód:



Pomalujmy ściany G elementami grupy

Kleina: c_0=(0,0), c_1=(1,0), c_2=(0,1),
c_3=(1,1) z dodawaniem mod 2.

Każdej krawędzi przypiszmy kolor będący

sumą kolorów ścian, które rozdziela.

Ta suma nigdy nie będzie równa c_0

.

Dla 3 różnych indeksów i,j,k z {0,1,2,3}
sumy c_i+c_j,c_i+c_k,c_j+c_k są parami

różne

. 

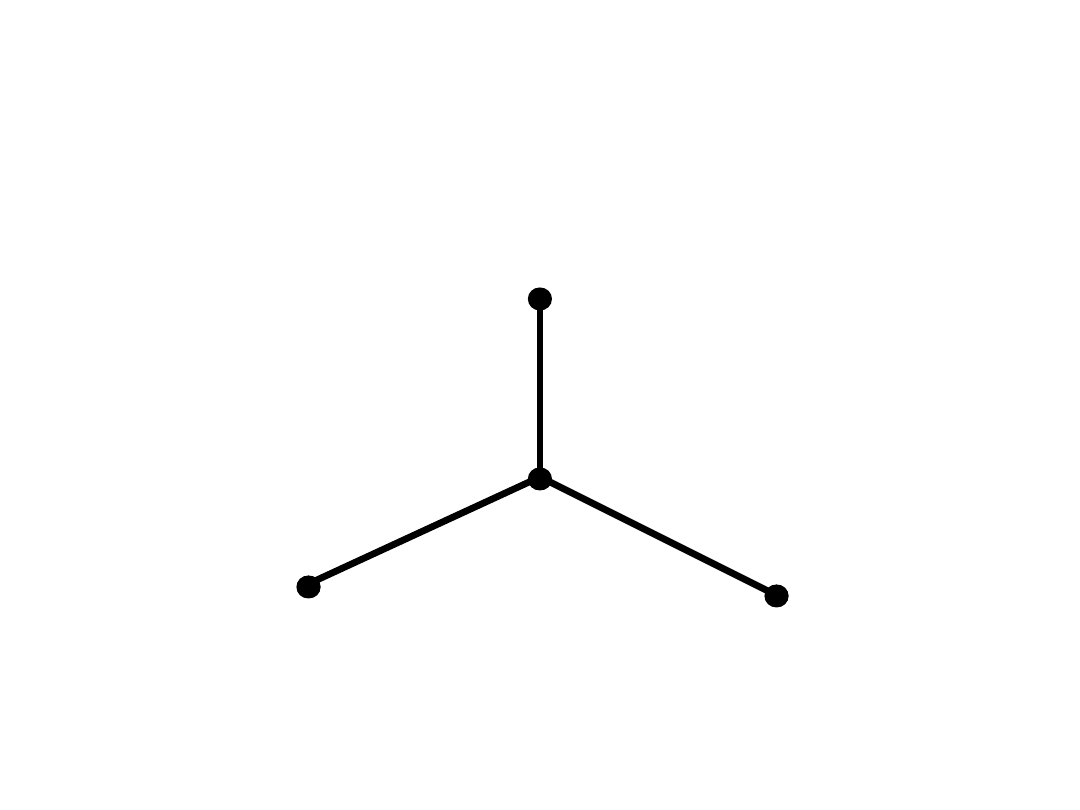
Ilustracja

c_i

c_j

c_k

c_i+c_k

c_i+c_j

c_j+c_k

Dowód 

• Malujemy krawędzie G niezerowymi

elementami grupy Kleina.

• Jeśli C jest krzywą zamkniętą omijającą

wierzchołki G, to suma kolorów krawędzi,

które przecina wynosi c_0=(0,0).

(ćw)

• Dowolną ścianę S_0 malujemy kolorem c_0.

• Do pozostałych ścian prowadzimy krzywe z

S_0 i nadajemy im kolory równe sumom

kolorów przecinanych krawędzi.

• Ta definicja jest poprawna a kolorowanie

właściwe

(ćw).



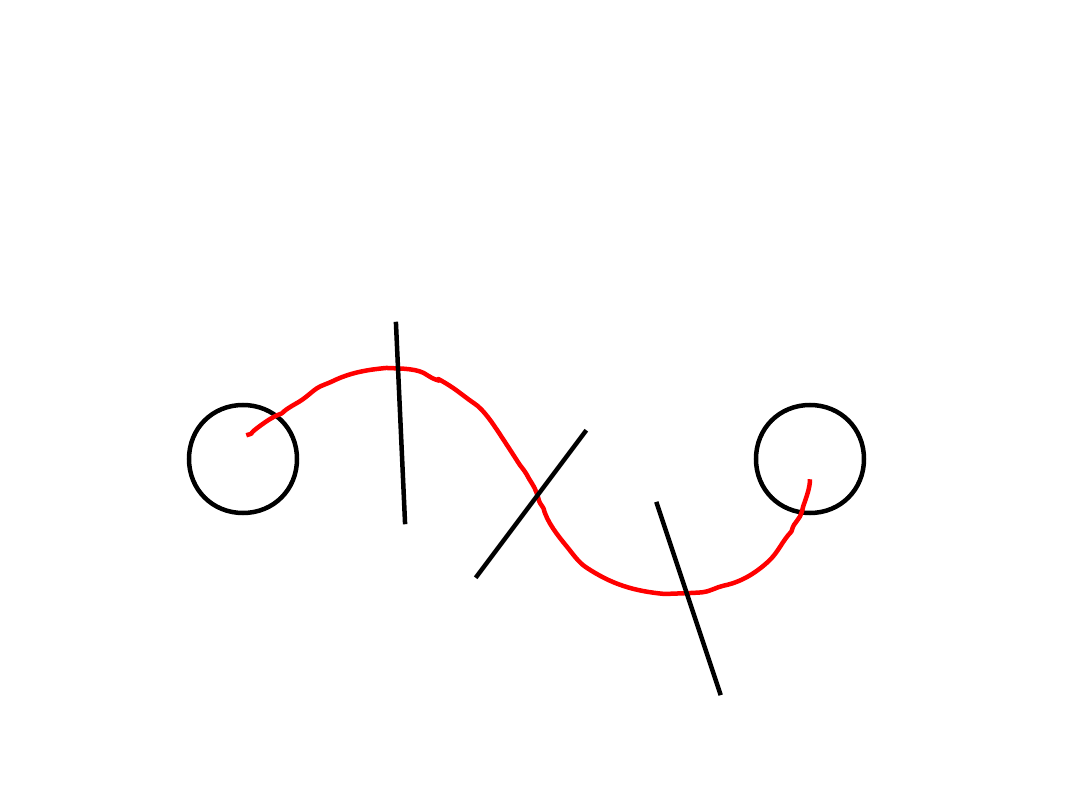
Ilustracja

S_0

c_0

S

Druga próba Taita 1880

• Mapę hamiltonowską

można pomalować 4

kolorami. Dowód bezpośredni

(ćw)

lub

korzystając z dowodu Faktu 2, bowiem

• 3-regularny

graf hamiltonowski

ma indeks

chromatyczny 3.

Hipoteza Taita (1890).

Każdy 3-spójny, 3-

regularny graf planarny jest hamiltonowski.

• Z niej wynikałaby H4K, bo wystarczy

ograniczyć się do map 3-regularnych (Fakt

1) oraz 3-spójnych (bez dowodu).

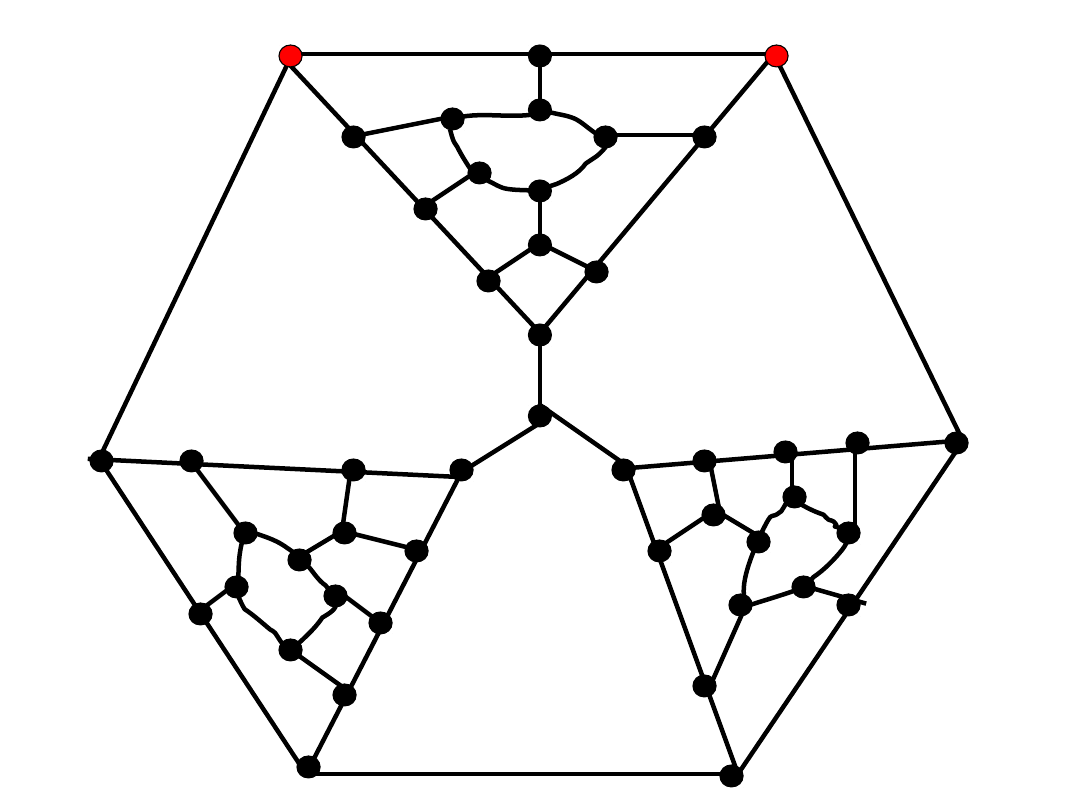
• Niestety...

kontrprzykład Tutte’a (1946).