
Wykład nr 2a
Metody komputerowe w
inżynierii materiałowej
Dr inż. Maciej Sułowski
A2, pok. 54H
Tel.:26-27
sulek@agh.edu.pl

Wykład nr 2a
Metody rozwiązywania układów
równań liniowych
• Metody rozwiązywania układów równań
linowych można podzielić na:
– metody dokładne
• metoda dla macierzy jednoprzekątniowej
• metoda dla macierzy trójkątnej
• metoda eliminacji Gaussa
• metoda Thomasa
– metody iteracyjne
• metoda iteracji prostej
• metoda Gaussa – Seidla
• metoda nadrelaksacji

Wykład nr 2a
Metody rozwiązywania układów
równań liniowych
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
...
..........
..........
...
...
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
B
A
X
B
X
A
*
*
1
Układ n-równań liniowych zawierających n–niewiadomych
można zapisać w postaci macierzowej
n
n
nn
n
n
n
n
b
b
b
B
x
x
x
X
a
a
a
a
a
a
a
a
a
A
...
...
...
...
...
...
...
...
...
2
1
2
1
2
1
2
22
21
1
12
11
Układ ma jedno rozwiązanie,gdy jest oznaczony (macierz
główna A układu równań jest osobliwa (det A ≠0)

Wykład nr 2a
Metody rozwiązywania układów
równań liniowych
n
n
nn
n
n
n
n
b
x
a
b
x
a
x
a
b
x
a
x
a
x
a
.....
..........
..........
..........
..........
...
...
2
2
2
22
1
1
2
12
1
11
nn
n
n
a
b
x
n
i
a
n
n
i
a
x
a
b
x
ii
ii
n
i
s
s
is
i
i
...,
,
2
,
1
,
0
1
...,
,
2
,
1
*
1
Trójkątny układ równań
Rozwiązanie
n
n
nn
b
x
a
b
x
a
b
x
a
..
..........
..........
..........
2
2
22
1
1
11
Układ równań z
elementami niezerowymi
na przekątnej głównej
0
...,
,
2
,
1
ii
ii
i
i
a
n
i
a
b
x
Rozwiązanie

Wykład nr 2a
Metody rozwiązywania układów
równań liniowych
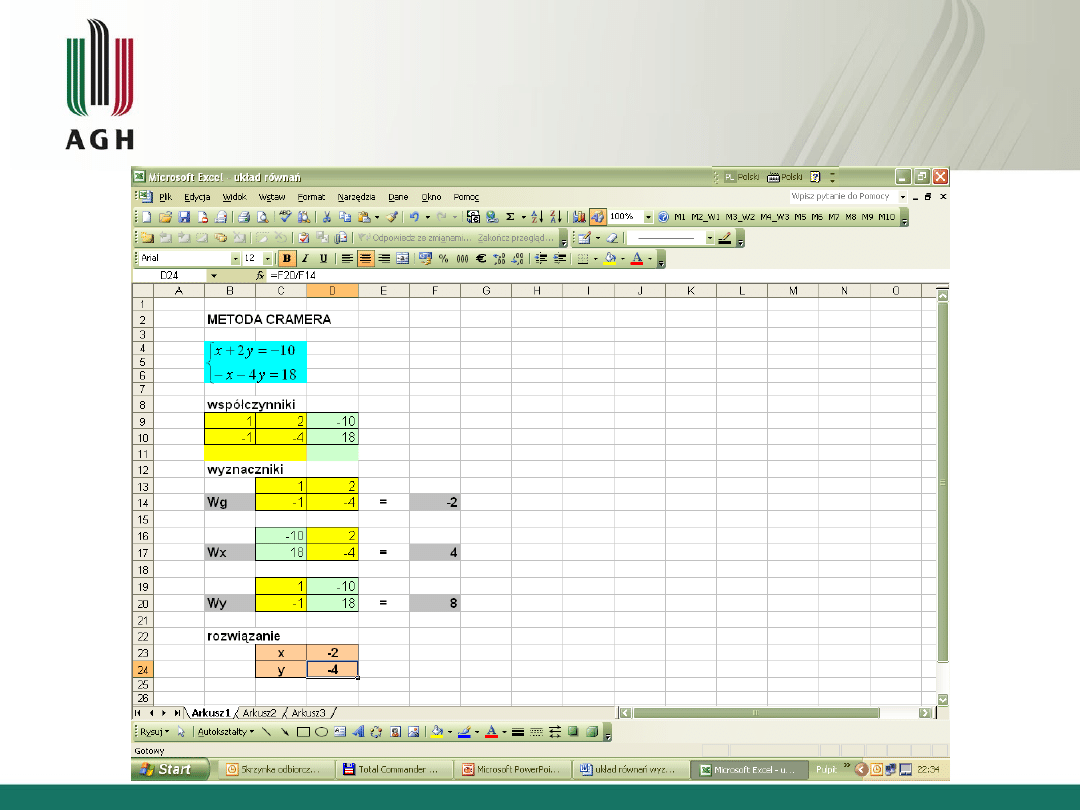
• Przykład rozwiązania trójkątnego układu
równań
• Przykład rozwiązania układu 2 równań
liniowych o 2 niewiadomych – metoda
Cramera

Wykład nr 2a
Zastosowanie macierzy do
rozwiązywania układów równań
Wykład nr 2a
Zastosowanie macierzy do
rozwiązywania układów równań
Wykład nr 2a
Zastosowanie macierzy do
rozwiązywania układów równań
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
...
..........
..........
...
...
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
Układ równań liniowych
zapisujemy w postaci macierzy C, w której macierz główną A
uzupełnia się dodatkową kolumną zawierającą wektor wyrazów
wolnych B, czyli:
1
,
2
1
1
,
2
2
22
21
1
,
1
1
12
11
1
,
2
1
1
,
2
2
22
21
1
,
1
1
12
11
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
n
n
nn
n
n
n
n
n
n
n
n
nn
n
n
n
n
n
n
c
c
c
c
c
c
c
c
c
c
c
c
b
a
a
a
b
a
a
a
b
a
a
a
C
n pierwszych kolumn
– elementy macierzy A,
kolumna n+1 – elementy
wektora B

Wykład nr 2a
Zastosowanie macierzy do
rozwiązywania układów równań
• Wariant podstawowy metody eliminacji Gaussa
polega na przekształceniu macierzy C w taki
sposób, aby otrzymać równoważny układ równań,
w którym n pierwszych kolumn macierzy C
tworzyło macierz trójkątną.
• Rozwiązanie układu równań metodą
przedstawioną wcześniej

Wykład nr 2a
Zastosowanie macierzy do
rozwiązywania układów równań
• W kroku pierwszym odejmujemy pierwsze równanie
pomnożone przez c
i1
/c
11
od i-tego równania (i=2, 3,…, n)
• Po przekształceniach otrzymujemy układ równań (a w
konsekwencji macierz C przekształconą do C
1
:
)
1
(
1
,
)
1
(
3
)
1
(
3
2
)
1
(
2
)
1
(
1
,
3
)
1
(
3
3
)
1
(
33
2
)
1
(
32
)
1
(
1
,
2
)
1
(
2
3
)
1
(
23
2
)
1
(
22
1
,
1
1
3
13
2
12
1
11
...
....
..........
..........
..........
..........
..........
..........
...
...
...
n
n
n
nn
n
n
n
n
n
n
n
n
n
n
n
c
x
c
x
c
x
c
c
x
c
x
c
x
c
c
x
c
x
c
x
c
c
x
c
x
c
x
c
x
c
1
,...,
3
,
2
;
,...,
3
,
2
;
...
0
...
...
...
...
...
...
...
0
...
0
...
1
11
1
)
1
(
)
1
(
1
,
)
1
(
)
1
(
3
)
1
(
2
)
1
(
1
,
3
)
1
(
32
)
1
(
33
)
1
(
32
)
1
(
1
,
2
)
1
(
2
)
1
(
23
)
1
(
22
1
,
1
1
13
12
11
1
n
j
n
i
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
C
j
i
ij
ij
n
n
nn
n
n
n
n
n
n
n

Wykład nr 2a
Zastosowanie macierzy do
rozwiązywania układów równań
• W kroku drugim odejmujemy drugie równanie pomnożone
przez c
i2(1)
/c
22(1)
od i-tego równania (i= 3, 4, …, n)
• Po przekształceniach otrzymujemy układ równań (a w
konsekwencji macierz C przekształconą do C
2
:
)
2
(
1
,
)
2
(
3
)
2
(
3
)
2
(
1
,
3
)
2
(
3
3
)
2
(
33
)
1
(
1
,
2
)
1
(
2
3
)
1
(
23
2
)
1
(
22
1
,
1
1
3
13
2
12
1
11
...
....
..........
..........
..........
..........
..........
..........
...
...
...
n
n
n
nn
n
n
n
n
n
n
n
n
n
n
c
x
c
x
c
c
x
c
x
c
c
x
c
x
c
x
c
c
x
c
x
c
x
c
x
c
1
,...,
4
,
3
;
,...,
4
,
3
;
...
0
0
...
...
...
...
...
...
...
0
0
...
0
0
...
)
1
(
2
)
1
(
22
)
1
(
2
)
1
(
)
2
(
)
2
(
1
,
)
2
(
)
2
(
3
)
2
(
1
,
3
)
2
(
32
)
2
(
33
)
1
(
1
,
2
)
1
(
2
)
1
(
23
1
,
1
1
13
12
11
2
n
j
n
i
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
C
j
i
ij
ij
n
n
nn
n
n
n
n
n
n
Wykład nr 2a
Zastosowanie macierzy do
rozwiązywania układów równań
• Po wykonaniu n kroków dochodzimy do trójkątnego
układu równań, któremu odpowiada
przekształcona macierz C
n-1
:
)
1
(
1
,
)
1
(
)
2
(
1
,
3
)
2
(
3
3
)
2
(
33
)
1
(
1
,
2
)
1
(
2
3
)
1
(
23
2
)
1
(
22
1
,
1
1
3
13
2
12
1
11
....
..........
..........
..........
..........
..........
..........
...
...
...
n
n
n
n
n
nn
n
n
n
n
n
n
n
n
n
c
x
c
c
x
c
x
c
c
x
c
x
c
x
c
c
x
c
x
c
x
c
x
c
)
1
(
1
,
)
1
(
)
2
(
1
,
3
)
2
(
32
)
2
(
33
)
1
(
1
,
2
)
1
(
2
)
1
(
23
1
,
1
1
13
12
11
1
...
0
0
0
...
...
...
...
...
...
...
0
0
...
0
0
...
n
n
n
n
nn
n
n
n
n
n
n
c
c
c
c
c
c
c
c
c
c
c
c
c
C
|A|
|B|

Wykład nr 2a
Zastosowanie macierzy do
rozwiązywania układów równań
• Przejście od układu równań liniowych do układu
trójkątnego jest więc realizowane wg
następującego wzoru iteracyjnego:
1
,...,
2
,
1
;
,...,
2
,
1
1
,...,
2
,
1
)
1
(
)
1
(
)
1
(
)
1
(
)
(
n
s
s
j
c
c
c
c
c
n
s
s
i
n
s
s
sj
s
ss
s
is
s
ij
s
ij

Wykład nr 2a
Zastosowanie macierzy do
rozwiązywania układów równań
• Przykład rozwiązania układu równań metodą
eliminacji Gaussa

Wykład nr 2a
Zastosowanie macierzy do
rozwiązywania układów równań
Układ postaci:
n
n
n
n
n
n
n
n
n
d
d
d
d
d
x
x
x
x
x
b
a
c
b
a
c
b
a
c
b
a
c
b
1
3
2
1
1
3
2
1
1
1
1
3
3
3
2
2
2
1
1
...
...
*
0
0
0
0
0
0
0
0
0
...
...
...
...
...
...
...
0
0
0
0
0
0
0
0
0
0
0
0
0
n
i
c
a
d
x
c
x
b
x
a
n
i
i
i
i
i
i
i
,...,
2
,
1
,
0
,
0
;
1
1
1
1
1
1
1
i
i
i
i
i
i
i
i
x
x
x
x
Można zapisać w postaci równoważnej jako [1]:
Rozwiązanie układu ma postać [2]:

Wykład nr 2a
Zastosowanie macierzy do
rozwiązywania układów równań
i
i
i
i
i
i
i
i
i
i
i
i
b
a
a
d
b
a
c
1
1
1
n
n
n
n
n
n
n
n
i
i
b
a
a
d
x
i
b
d
b
c
1
1
1
1
1
1
)
1
(
Po podstawieniu [2] do [1] otrzymujemy:
Z danych w równaniu [1] wyznaczamy wartości
początkowe (i=1) oraz wartość ostatniej niewiadomej
(i=n)
Kolejne niewiadome oblicza się z równania [2] dla
i= n-1, n-2, …, 1

Wykład nr 2a
Zastosowanie macierzy do
rozwiązywania układów równań
• Przykład rozwiązania układu równań metodą
Thomasa

Wykład nr 2a
Metody rozwiązywania układów
równań liniowych - podsumowanie
n
n
nn
n
n
n
n
b
x
a
b
x
a
x
a
b
x
a
x
a
x
a
.....
..........
..........
..........
..........
...
...
2
2
2
22
1
1
2
12
1
11
nn
n
n
a
b
x
n
i
a
n
n
i
a
x
a
b
x
ii
ii
n
i
s
s
is
i
i
...,
,
2
,
1
,
0
1
...,
,
2
,
1
*
1
Trójkątny układ równań
Rozwiązanie
n
n
nn
b
x
a
b
x
a
b
x
a
..
..........
..........
..........
2
2
22
1
1
11
Układ równań z
elementami niezerowymi
na przekątnej głównej
0
...,
,
2
,
1
ii
ii
i
i
a
n
i
a
b
x
Rozwiązanie

Wykład nr 2a
Metody rozwiązywania układów
równań liniowych - podsumowanie
Metoda eliminacji Gaussa
Rozwiązanie
Wzory Cramera
Wg
Wn
x
Wg
W
x
Wg
W
x
n
det
det
det
2
det
det
1
det
2
1
Rozwiązanie
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
...
..........
..........
...
...
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
1
,...,
2
,
1
;
,...,
2
,
1
1
,...,
2
,
1
)
1
(
)
1
(
)
1
(
)
1
(
)
(
n
s
s
j
c
c
c
c
c
n
s
s
i
n
s
s
sj
s
ss
s
is
s
ij
s
ij
)
2
(
1
,
)
2
(
3
)
2
(
3
)
2
(
1
,
3
)
2
(
3
3
)
2
(
33
)
1
(
1
,
2
)
1
(
2
3
)
1
(
23
2
)
1
(
22
1
,
1
1
3
13
2
12
1
11
...
....
..........
..........
..........
..........
..........
..........
...
...
...
n
n
n
nn
n
n
n
n
n
n
n
n
n
n
c
x
c
x
c
c
x
c
x
c
c
x
c
x
c
x
c
c
x
c
x
c
x
c
x
c

Wykład nr 2a
Metody rozwiązywania układów
równań liniowych - podsumowanie
Metoda
Thomasa
Rozwiązanie
n
n
n
n
n
n
n
n
n
d
d
d
d
d
x
x
x
x
x
b
a
c
b
a
c
b
a
c
b
a
c
b
1
3
2
1
1
3
2
1
1
1
1
3
3
3
2
2
2
1
1
...
...
*
0
0
0
0
0
0
0
0
0
...
...
...
...
...
...
...
0
0
0
0
0
0
0
0
0
0
0
0
0
)
1
,...,
2
,
1
(
)
(
)
,...,
3
,
2
(
)
1
(
1
1
1
1
1
1
1
1
1
1
1
1
n
n
i
x
x
n
i
b
a
a
d
x
n
i
b
a
a
d
b
a
c
i
b
d
b
c
i
i
i
i
n
n
n
n
n
n
n
n
i
i
i
i
i
i
i
i
i
i
i
i
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
Wyszukiwarka
Podobne podstrony:
Metody komputerowe w inzynierii materiałowej 6
Metody komputerowe w inzynierii materiałowej 8
ćwiczenie nr 2, Ćwiczenie nr 2 - Metody komputerowe w Inżynierii Materiałowej
Metody komputerowe w inzynierii materiałowej 2
Metody komputerowe w inzynierii materiałowej 10
Metody komputerowe w inzynierii materiałowej 9
Metody komputerowe w inzynierii materiałowej 6
2008 Metody komputerowe dla inzynierow 20 D 2008 1 8 22 18 59id 26588 ppt
2008 Metody komputerowe dla inzynierow 18 D 2008 1 8 22 16 21id 26586 ppt
METODY KOMPUTEROWE W MECHANICE 2
inzynieryjna, Geodezja, Geodezja Inżynieryjna, materialy
Zagadnienia do kolokwium zaliczeniowego 2013-2014, Inżynieria materiałowa pwr, Inżynieria chemiczna
więcej podobnych podstron