Wykład 5

Algorytmy

 

 

Przed programem jest 

algorytm

Jeżeli  mamy  do  wykonania  jakieś 
zadanie, 

budujemy 

sposób, 

przepis  realizacji

  tego  za-dania. 

Taki  przepis  to 

algorytm

.  Dopiero 

po zapisaniu w konkretnym języku 
programo-wania  algorytm  staje 
się 

programem

.  Słowo  „algorytm” 

pochodzi  od  nazwiska  matema-
tyka  Muhammada  ibn  Musy  al-
Chwarizmie-go  (IXw.)  -  jeden  z 
jego  traktatów  nadał  też  nazwę 
dziedzinie znanej jako „algebra”.

 

 

Który algorytm jest 

„dobry”?

Do  danego  celu  prowadzi  zwykle 
więcej  niż  jedna  droga.  Jak  więc 
oceniać 

alternatywne 

sposoby 

rozwiązania problemu?

Podstawowe  parametry  algorytmu 
to  jego 

złożoność  czasowa

  i 

złożoność 

pamięciowa

. 

Oprócz 

tego 

przy 

algorytmach 

działających  na  liczbach  trzeba 
pamiętać 

o 

stabilności 

nu-

merycznej

.

 

 

Który algorytm jest 

„dobry”?

Złożoność  czasowa

  mówi,  ile 

kroków obli-czeniowych i ile czasu 
wymaga  zakończenie  algorytmu 
dla  danej  porcji  danych. 

Często 

nie jest funkcją liniową!

Złożoność  pamięciowa

  mówi,  jaką 

maksy-malnie  część  danych  i 
wyników  pośrednich  trzeba  w 
ramach 

danego 

algorytmu 

przecho-wywać 

w 

pamięci 

operacyjnej. 

Również 

i 

ten 

parametr często nie zachowuje się 
liniowo.

 

 

Przykład złożoności 

czasowej

Na 

przyjęciu 

dyplomatycznym 

bawi  się  N  ambasadorów.  Ich 
uściski rąk są rejestro-wane przez 
fotografa 

po  kolei

.  Ile  czasu 

zajmie taka sesja zdjęciowa?

Algorytm:

  Ambasador  1  podaje 

rękę amba-sadorom 2, 3, 4... aż do 
N.  Ambasador  2  po-daje  rękę 
ambasadorom 3,4,...,N. W ten spo-
sób  dochodzimy  do  ambasadorów 
N-1  i  N,  którzy  jako  ostatni 
wymieniają uścisk.

Złożoność 

czasowa: 

N(N-1)/2 

jednostek

 

 

Stabilność numeryczna

Określa  ona 

wrażliwość

  wyniku 

końcowego na 

błędy zaokrągleń

 w 

trakcie 

obliczeń 

oraz 

na 

dokładność 

danych początkowych

.

Przykłady: 

Komputer 

wykonuje 

operacje 

liczbowe 

ze 

skończoną 

precyzją.  Może  się  okazać,  że  wynik 
działania  10  000  000  000  +  1  to  dalej 
10 000 000 000.

Podobnie,  realizacja  dzielenia  jako 
mnożenie  przez  odwrotność  jest  mało 
stabilna numerycznie dla ar-gumentów 
bliskich zeru.

 

 

Schematy blokowe

Służą  one  do  zapisu  algorytmu  w 
obrazowy 

sposób 

podając 

kierunek 

procesu 

obliczeń. 

Najważniejsze używane symbole:

BLOK 
DECYZYJNY

ODCZYT LUB 
ZAPIS 
DANYCH

START, 
STOP

PROCES 
(CZYNNOŚ
Ć)

 

 

 

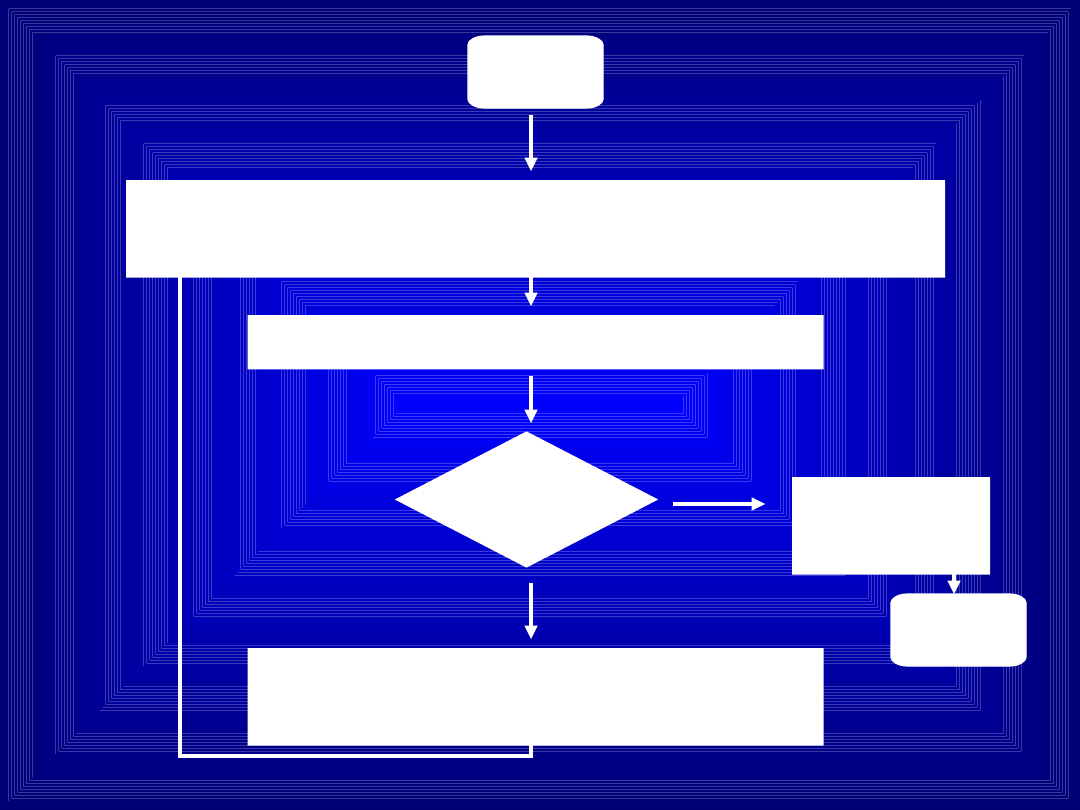
START

Wprowadź liczby X i Y. Wyzeruj licznik 

L (L := 0)

Odejmij Y od X (X := X - Y)

x<0 ?

Zwiększ licznik L o 1 (L := 

L + 1)

NIE

TAK

Wypisz 

L

STOP

 

 

 

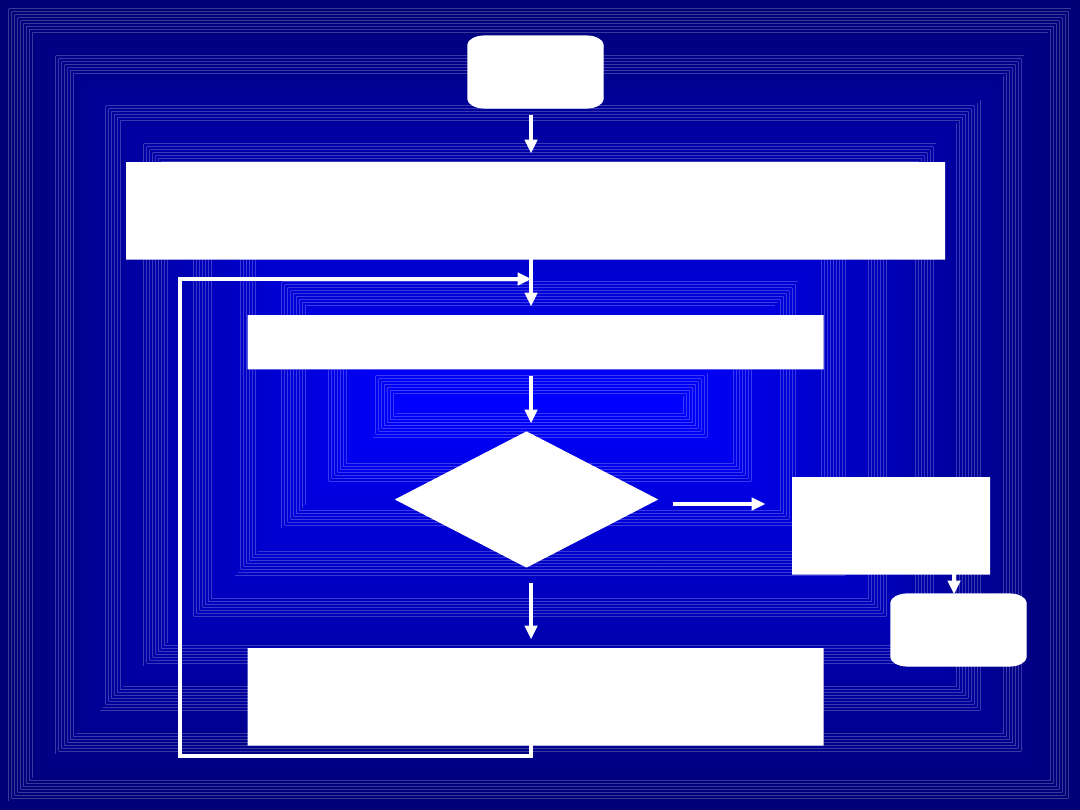
START

Wprowadź liczbę naturalną X.

Ustal zmienną W na X (W := X)

Zmniejsz X o 1 (X := X - 1)

X=0 ?

Pomnóż W przez X (W := W 

* X)

NIE

TAK

Wypisz 

W

STOP

 

 

 

START

Wprowadź liczbę naturalną X.

Ustal zmienną W na 1 (W := 1)

Wypisz 

W

STOP

Zmniejsz X o 1 (X := X - 1)

Pomnóż W przez X (W := W 

* X)

Wykonaj X razy:

 

 

 

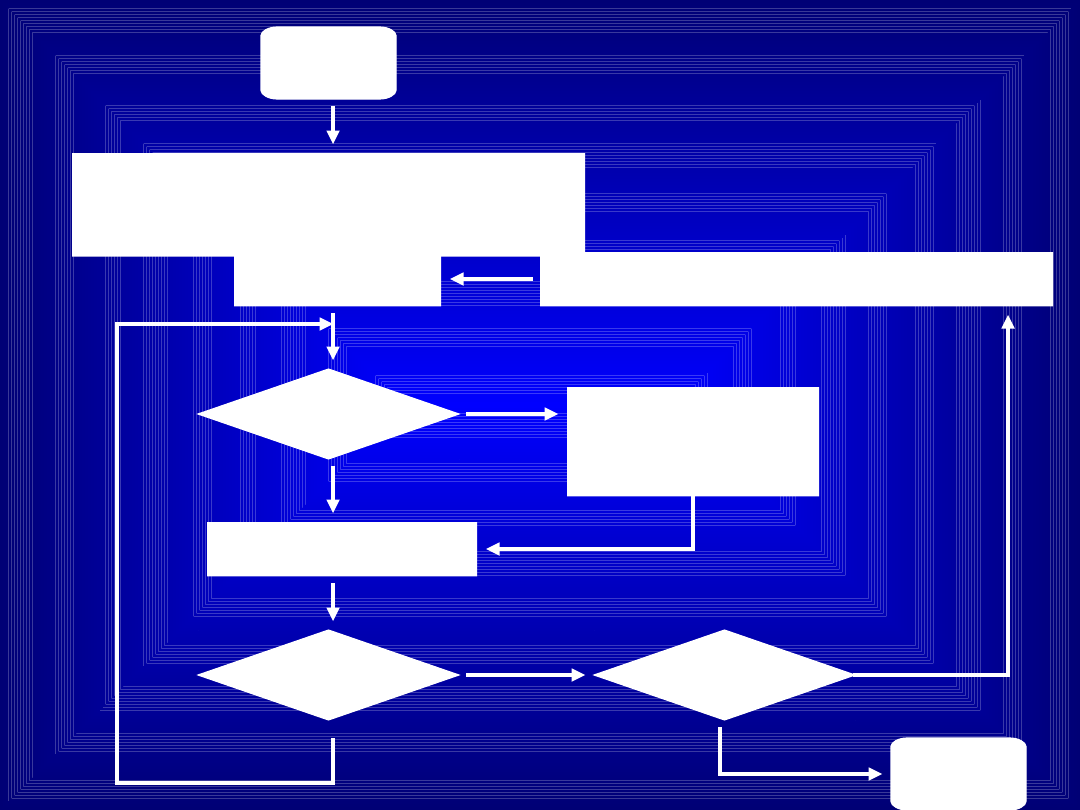
START

Wczytaj zbiór N danych, 

{x

i

}

i := 1

X

i 

> X

i+1

 ?

i := i + 1

NIE

TAK

Zamień X

i

 i 

X

i+1

 

STOP

i = N ?

NIE

Były zamiany ?

NIE

TAK

TAK

Zeruj licznik zamian

Algorytm

sortowania 

bąbelkowego

 

 

 

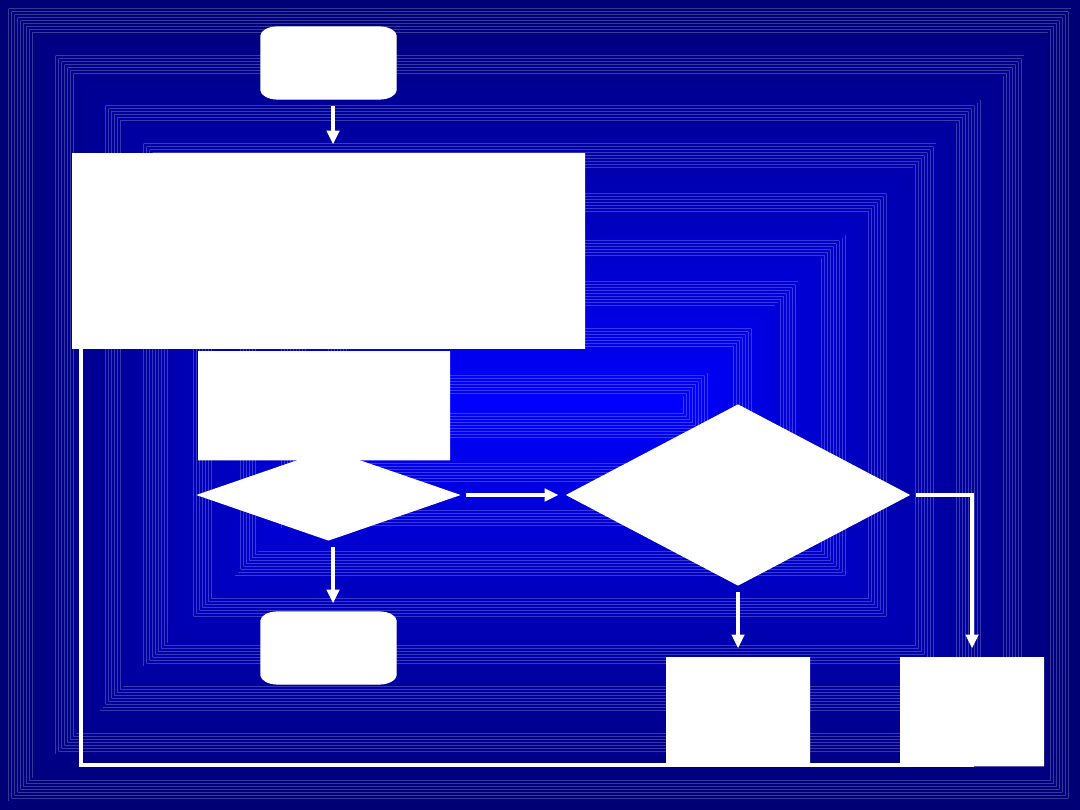
START

Dana funkcja f(x) oraz 

x

1

 i x

2

f(x

1

) i f(x

2

) są różnych 

znaków

f(x

3

) = 0 ?

x

2

 := 

x

3

NIE

TAK

x

3

 := (x

1

 + 

x

2

)/2 

STOP

f(x

1

) i f(x

3

) 

mają różne 

znaki ?

NIE

TAK

Algorytm 

poszukiwania

miejsca zerowego 

funkcji

metodą bisekcji

x

1

 := 

x

3

 

 

Obliczanie wartości 

wielomianu

Sprawdźmy 

złożoność 

obliczeniową operacji wyznaczenia 
wartości wielomianu W(x).

Niech 

W(x)  =  7x

4

  +  3x

3

  +  2x

2

  -3x 

+5

Klasycznie używamy zwykłego zapisu:

W(x)  =  7

*

x

*

x

*

x

*

x 

+

  3

*

x

*

x

*

x 

+

  2

*

x

*

x 

- 

3

*

x 

+ 

5

Użyto 

dziesięciu

  mnożeń, 

czterech

 

dodawań

W  ogólności  obliczenie  W(x)  tym 
algorytmem  wymaga 

n

  dodawań  oraz 

n(n+1)/2

 

mnożeń, 

gdzie 

n

 

jest 

stopniem wielomianu.

 

 

Obliczanie wartości 

wielomianu

Znaczącą 

redukcję 

kosztów 

obliczeń daje 

algorytm Hornera

.

Wystarczy inaczej zapisać wielomian:

W(x) = ( ( ( 7 

*

 x 

+

 3 ) 

*

 x 

+

 2 ) 

*

 x 

-

 3 ) 

*

 x 

+

 5

Użyto 

czterech

 

mnożeń, 

czterech

 

dodawań

W ogólności algorytm Hornera wymaga 

n

  mnożeń  oraz 

n

  dodawań.  Nie  ma 

zysku na dodawaniach, ale dla mnożeń 
zredukowaliśmy  koszt  metody  z 

O(n

2

)

 

do 

O(n)

.

 

 

Własność „STOP”

Czy  możemy  przewidzieć,  że  dany 
program  się  za-trzyma,  czyli  czy  ma 
własność „STOP”?

Nie  można

  sporządzić  schematu,  który 

zbada 

własność 

„STOP” 

każdego 

pomyślanego algorytmu!

Schemat  taki  musiałby  bowiem  umieć 
sprawdzić 

także 

poniższy 

krótki 

algorytm...

1)    Sprawdź,  czy  ten  algorytm  ma 
własność 

STOP

2) 

Jeśli 

TAK, 

to 

wpadnij 

w 

nieskończoną 

pętlę

3)  A jeśli nie, to ZAKOŃCZ

 

 

„Cudowne algorytmy”

Omówione 

uprzednio 

sortowanie 

bąbelkowe  jest  bardzo  powolne.  Dziś 
znamy  znacznie  szybsze  algorytmy 
stosowane np. w bazach danych.

Innym słynnym algorytmem jest 

Szybka 

Transfor-macja  Fouriera  (FFT,  Fast 
Fourier  Transform)

  powstała  w  latach 

60.  XX  w.  Redukuje  ona  czas  obliczeń 
transformacji  Fouriera  z 

O(n

2

)

  do 

O(nlogn)

Wiele  metod  chemii  obliczeniowej 
posiada  złożoność  obliczeniową  rzędu 

O(n

4

)

  i  gorszą.  Nieustannie  pro-jektuje 

się  algorytmy  jak  najbardziej  zbliżone 
do 

skalowania liniowego

, 

O(n)

.