ELEMENTARNE

ELEMENTARNE

ZAGADNIENIA KWANTOWE

ZAGADNIENIA KWANTOWE



W stanach stacjonarnych (gdy potencjał nie zależy od czasu) funkcja

falowa układu spełnia równanie Schrödingera niezależne od czasu (jest
to równanie własne operatora energii):

t

E

ω

}),

({q

e

t)

},

ψ({q

i

t

iω

-

i







,

E

H







ˆ







E

)

z

,

y

,

x

(

V

Δ

2m

2







ˆ

ˆ

ˆ

ˆ



})

({

i

q







funkcja falowa zależna od położeń i
pędów

Pełna funkcja falowa zależy ponadto od czasu:

Ponieważ

E

jest energią całkowitą, a

V

– potencjalną, to

E-V

ma

sens energii kinetycznej. W fizyce klasycznej jest ona zawsze
nieujemna.

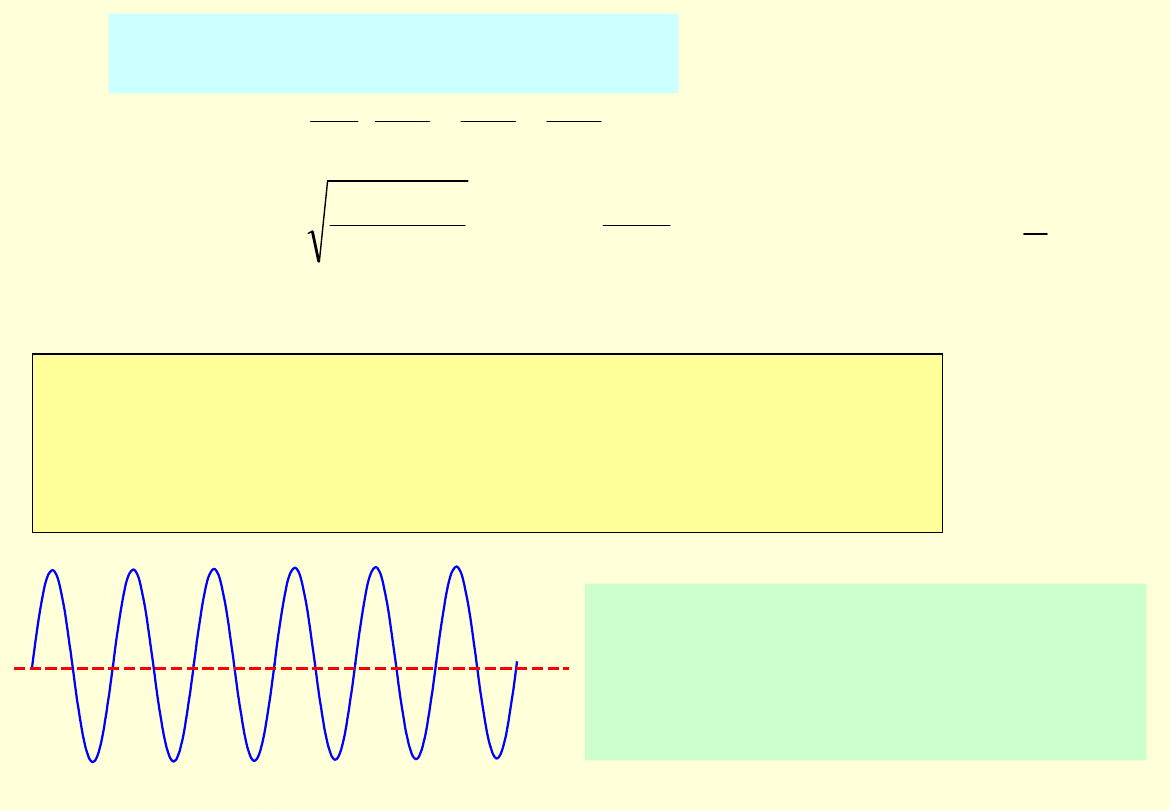
Przykład 1.

Cząstka swobodna,

V

=const.

V

2m

k

E

V)

-

2m(E

k

,

e

)

r

(

E

V

)

z

y

x

(

2m

const,

V

2

2

2

r

k

i

0

2

2

2

2

2

2

2













































,



























t)/

E

-

r

p

i(

0

t)

-

r

k

i(

0

e

e

t)

,

r

ψ(























p

k

k

p



 ,

W przypadku jednowymiarowym:



t)/

E

-

x

i(p

0

t)

-

i(k

0

ik

0

x

e

e

t)

ψ(x,

e

















x

x

,

Energia cząstki swobodnej (w
przestrzeni nieograniczonej) może
przyjmować dowolne wartości
dodatnie

E >V

– widmo energii

jest ciągłe.

x

-ik

x

ik

Be

Ae 





Rozwiązanie
ogólne:

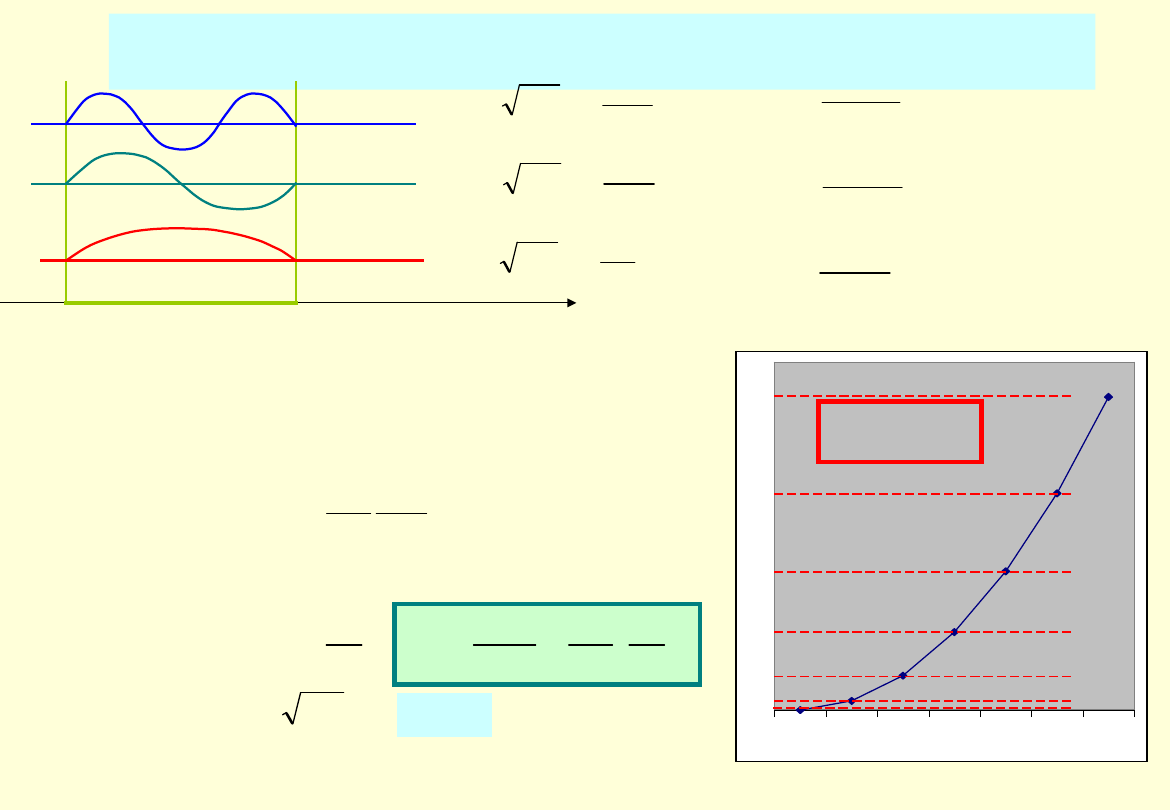
Przykład 2.

Cząstka w jednowymiarowej, nieskończonej studni

potencjału.

0
a

x

a

x

lub

0

x

dla

V(x)

a

x

0

dla

0,

V(x)















0

,

































1

2

2

2

2

n

n

2

2

2

E

2/a

C

1,2,3...,

n

)

a

nπ

(

2m

2m

k

E

,

a

nπ

k

Csinkx,

(x)

a

x

lub

0

x

dla

0

,

E

x

2m

:

a

x

0

Dla















a

πx

sin

2/a

a

x

2π

sin

2/a

a

x

3π

sin

2/a

1

2

3













2

2

1

2

2

2

2

2

3

2ma

E

2ma

E

2ma

E

2

2

2

4

9



















1

2

3

4

5

6

7

n

E

ne

rg

ia

E

n

~ n

2

Ograniczenie obszaru dostępnego dla cząstki powoduje, że
energia jest skwantowana (widmo energii jest dyskretne).

Najniższa energia E

1

jest większa od zera. Oznacza to, że

cząstka nie może znaleźć się w stanie całkowitego
spoczynku.

Układ może zmienić stan wyłącznie wtedy, gdy
dostarczona zostanie do niego (lub oddana przez układ)
ściśle określona porcja energii.

Wnioski

Wnioski

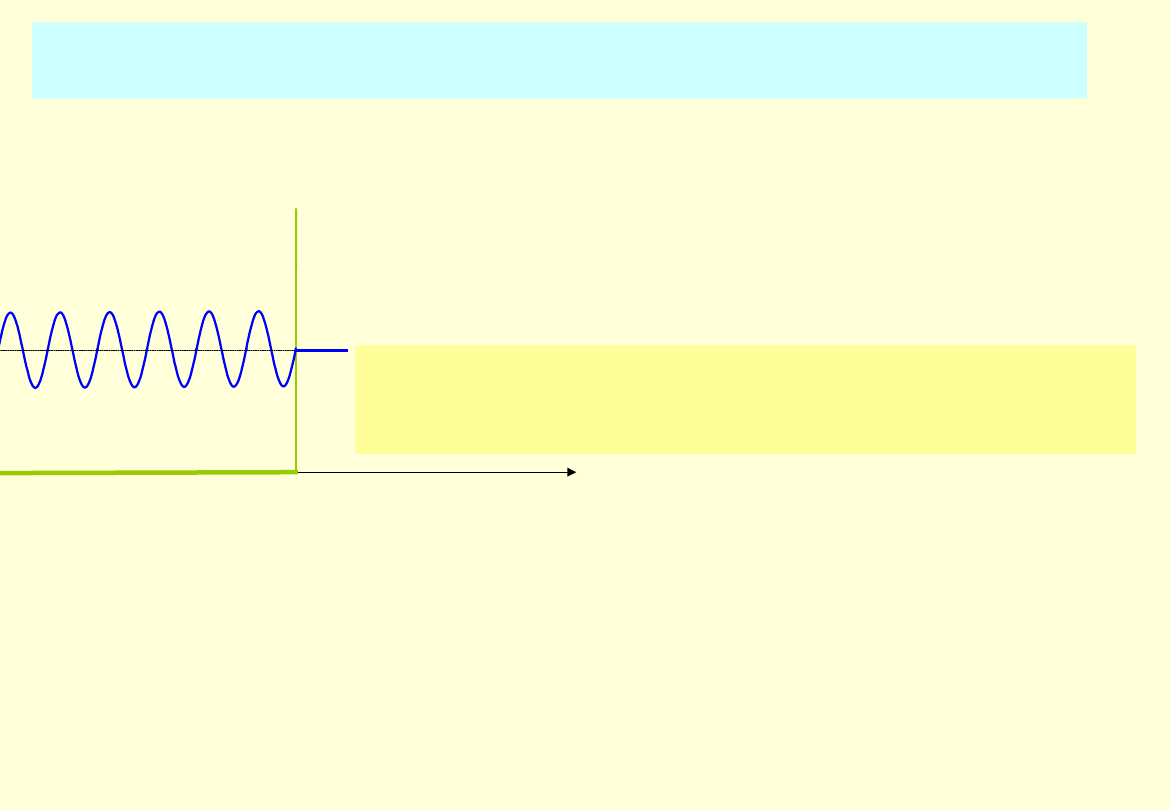
Przykład 3.

Cząstka padająca na nieskończenie wysoką barierę

potencjału
W fizyce klasycznej współrzędna siły jest równa pochodnej energii
potencjalnej ze znakiem (-). W punktach „skoku” potencjału działają siły
skierowane w stronę malejącego potencjału.

a

x

W fizyce kwantowej, podobnie, jak w fizyce klasycznej,
cząstka nie może wniknąć do obszaru o nieskończonym
potencjale.

2Csin(kx)

0

:

a

x

Be

Ae

:

a

x

-ikx

ikx

























0

)

0

(

a

x

,

V

a

x

0,

V











Warunek „zszycia” funkcji w punkcie
x=a:

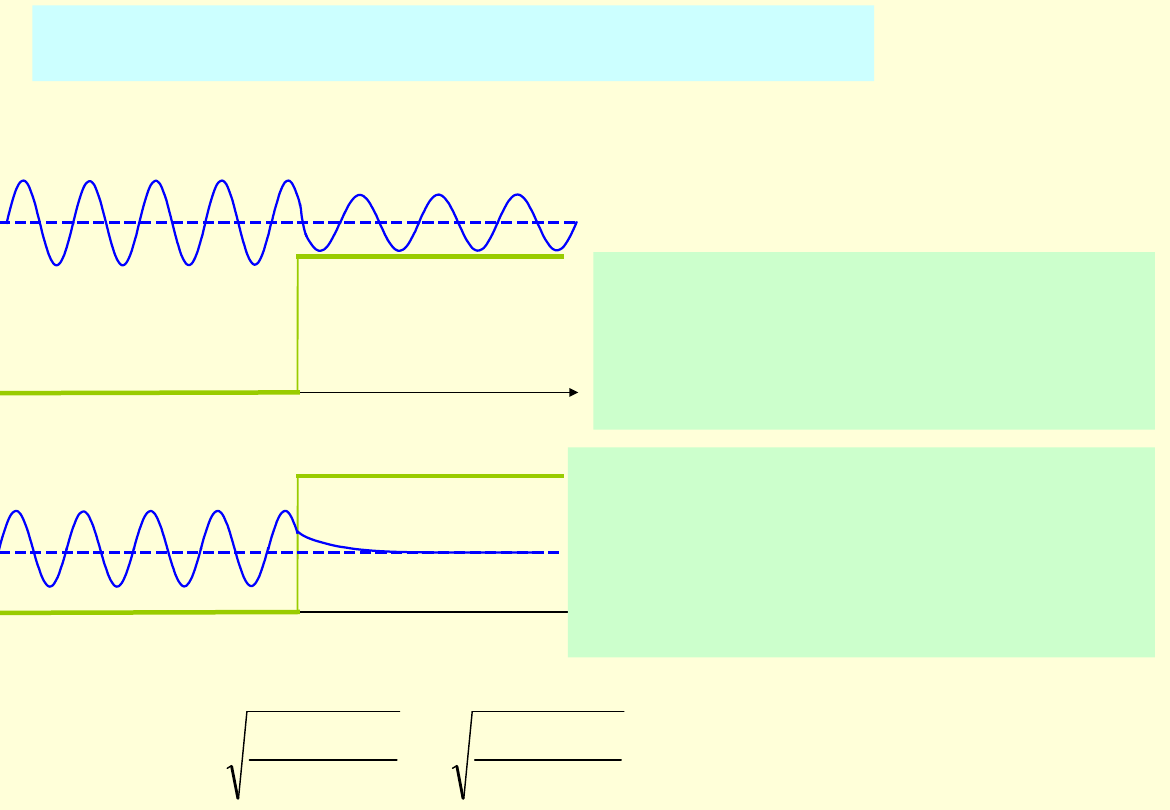
Przykład 4.

Cząstka padająca na skończoną barierę

potencjału

W rzeczywistych układach bariery potencjału są skończone i mają charakter
ciągły.

0

x

V

V

0,

x

0

V

0













Gdy E>V

0

,

cząstka nadbiegająca z lewej

strony częściowo odbija się od bariery.
Po przejściu przez barierę cząstka ma
mniejszą amplitudę, mniejszą energię i
pęd.

x

k

-

1

2

0

2

0

x

-iκ

x

iκ

0

1

Be

,

ik

E)

-

2m(V

i

)

V

-

2m(E

κ

,

Be

Ae

0,

V

E

























Gdy E<V

0,

cząstka nadbiegająca z lewej

strony, częściowo odbija się od bariery.
Istnieje niezerowa, zanikająca wraz z
odległością, funkcja falowa w obszarze,
gdzie energia całkowita jest mniejsza od
energii potencjalnej.

x

x

0

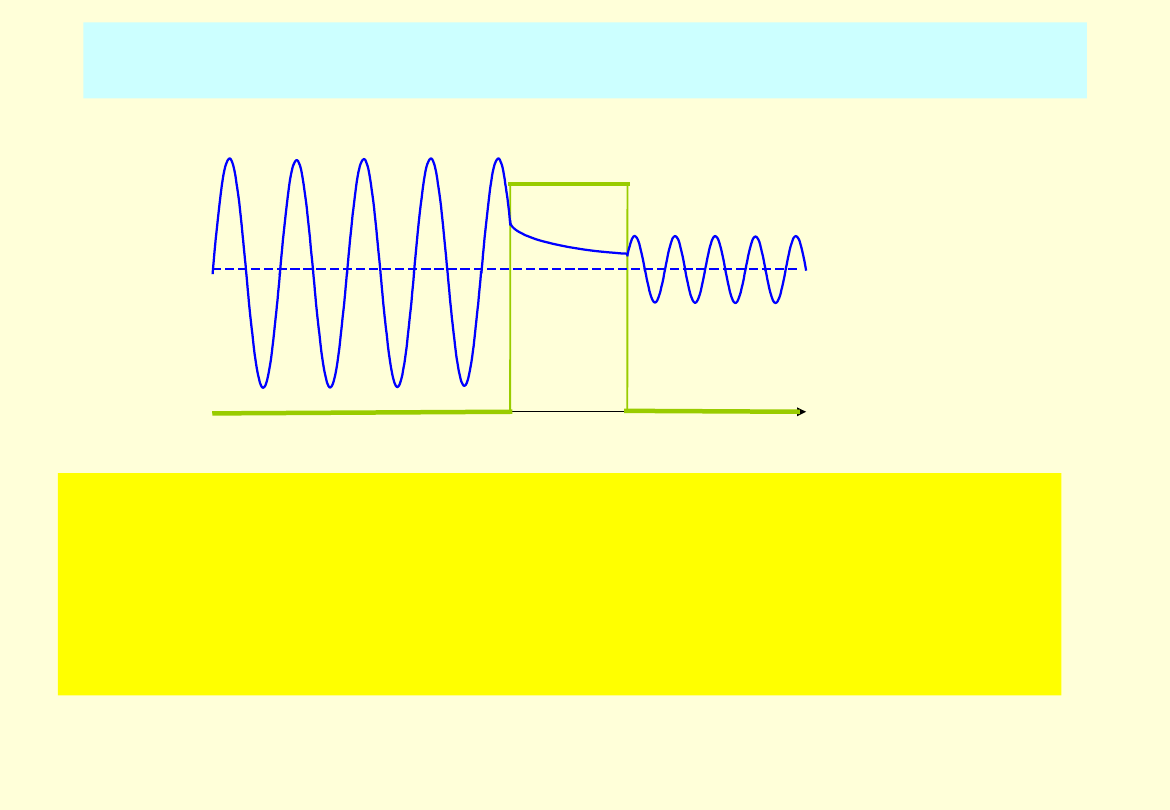
Przykład 5.

Cząstka padająca na skończoną, ograniczoną

przestrzennie barierę potencjału.

Występuje niezerowe prawdopodobieństwo przejścia cząstki
przez barierę, pomimo, że jej energia całkowita jest mniejsza,
niż energia potencjalna.

Zjawisko to nazywamy

efektem

tunelowym

(lub zjawiskiem

tunelowym). Jest to zjawisko kwantowe, nie dające się wyjaśnić
w ramach fizyki klasycznej.

W wyniku efektu tunelowego cząstki przenikają przez obszary, w
których energia całkowita jest mniejsza, niż energia potencjalna.

Przykłady występowania efektu

tunelowego



Synteza jądrowa

(łączenie jąder wodoru – protonów) będąca

źródłem energii Słońca zachodzi w dużym stopniu dzięki zjawisku
tunelowemu. Zjawisko to umożliwia pokonanie bariery odpychania
kulombowskiego jąder atomów w temperaturze niższej, niż
wynikałoby to z praw termodynamiki. Efekt tunelowy stwarza również
nadzieje na obniżenie temperatury fuzji jądrowej przeprowadzanej w
sposób kontrolowany.



Dzięki zjawisku tunelowemu następuje

emisja cząstek α

w procesie

rozpadu promieniotwórczego masywnych jąder atomowych.



Na zjawisku tunelowym oparte jest funkcjonowanie wielu
półprzewodnikowych elementów elektronicznych (np.

dioda

tunelowa

) oraz urządzeń (np.

skanningowy mikroskop

tunelowy

).

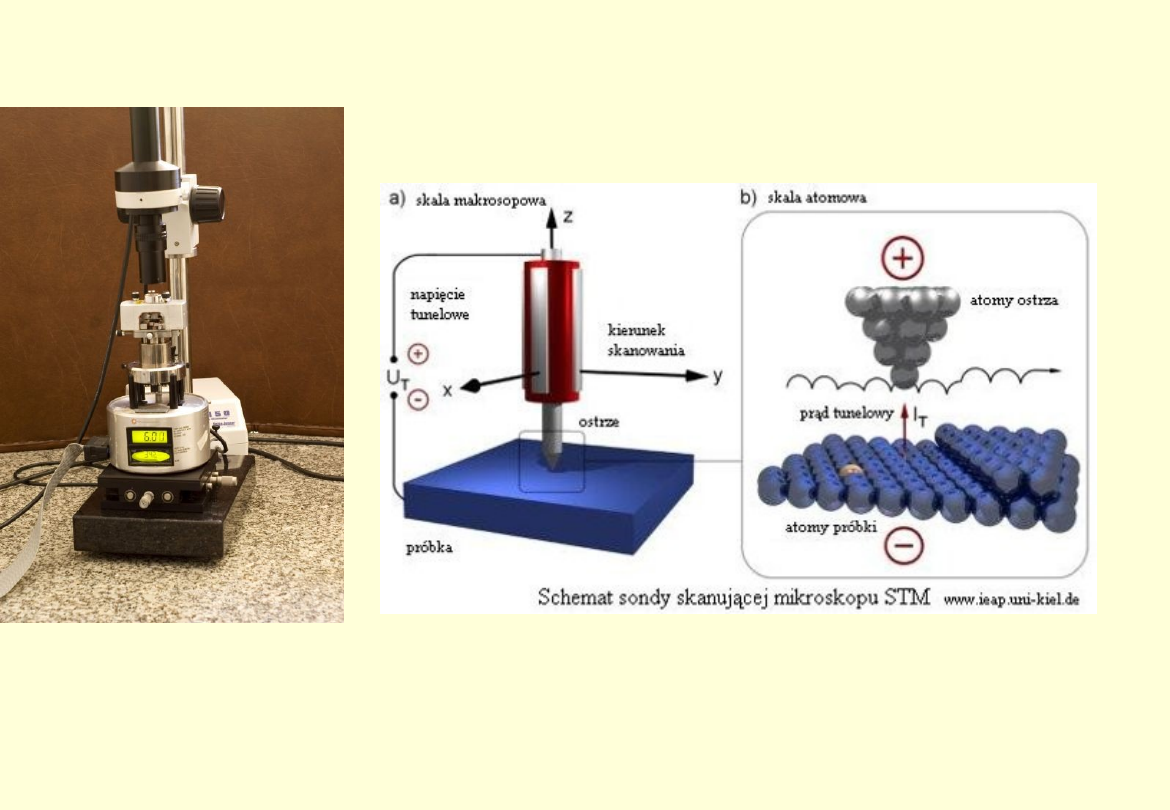
Mikroskop skanningowy

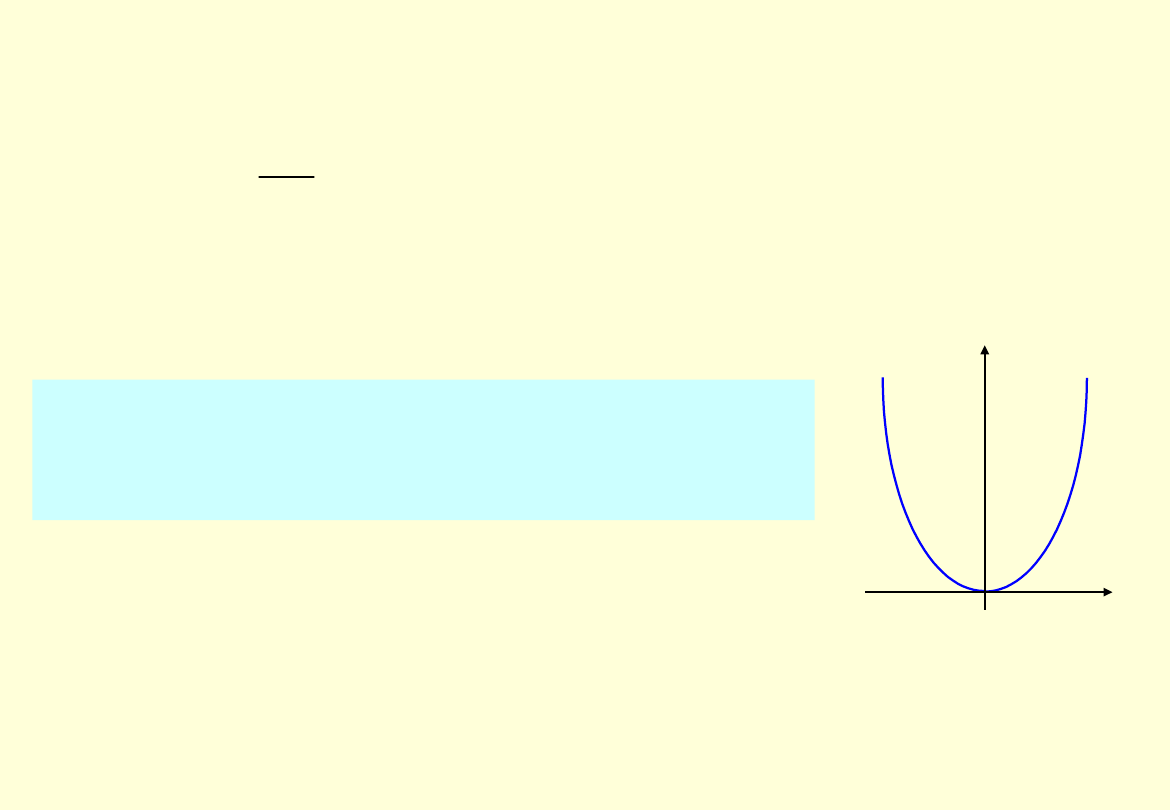
Oscylator

harmoniczny

W fizyce klasycznej oscylatorem harmonicznym nazywamy układ, spełniający
równanie:

)

α

t

Asin(ω

x(t)

x

ω

dt

x

d

0

2

2

2











gdzie x oznacza wielkość zmieniającą się cyklicznie i nazywaną „wychyleniem”,

ω

=2π/T jest stałą dodatnią – tzw. częstością drgań, zależną wyłącznie od

właściwości układu,

A

jest amplitudą, a

α

0

oznacza fazę początkową. Dwie

ostatnie wielkości zależą od sposobu pobudzenia układu do drgań.

Całkowita energia oscylatora jest sumą energii
kinetycznej i potencjalnej. Energia potencjalna
oscylatora jest proporcjonalna do kwadratu
wychylenia:

2

p

k

p

x

E

,

E

E

E







i może przyjmować, podobnie jak energia kinetyczna, dowolne wartości
nieujemne. Eneriga równa zero odpowiada stanowi równowagi.

x

E

p

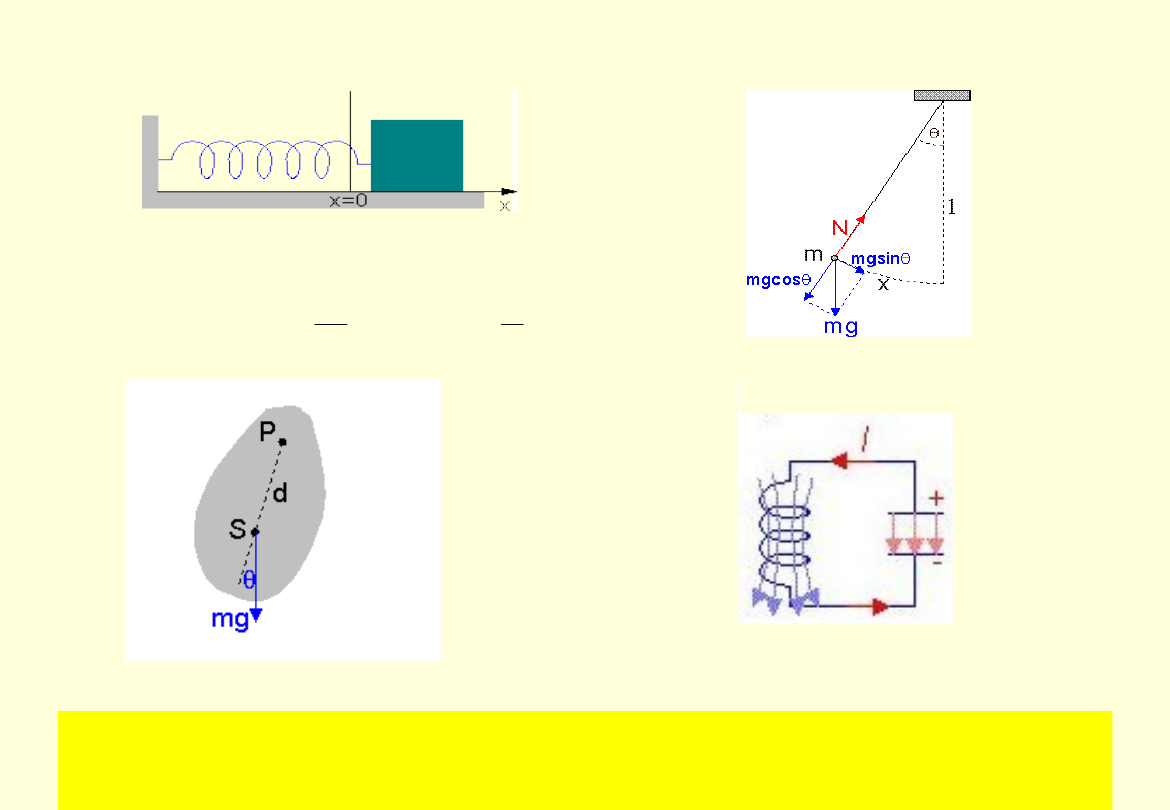
Oscylator -

przykłady

masa zamocowana na
sprężynie

wahadło matematyczne

wahadło fizyczne

układ elektryczny LC

2

p

2

x

kx

2

1

E

,

m

k

ω

kx,

F









Drgania zbliżone do harmonicznych wykonują atomy i cząsteczki w
ciele stałym. W ich opisie niezbędne jest uwzględnienie efektów
kwantowych.

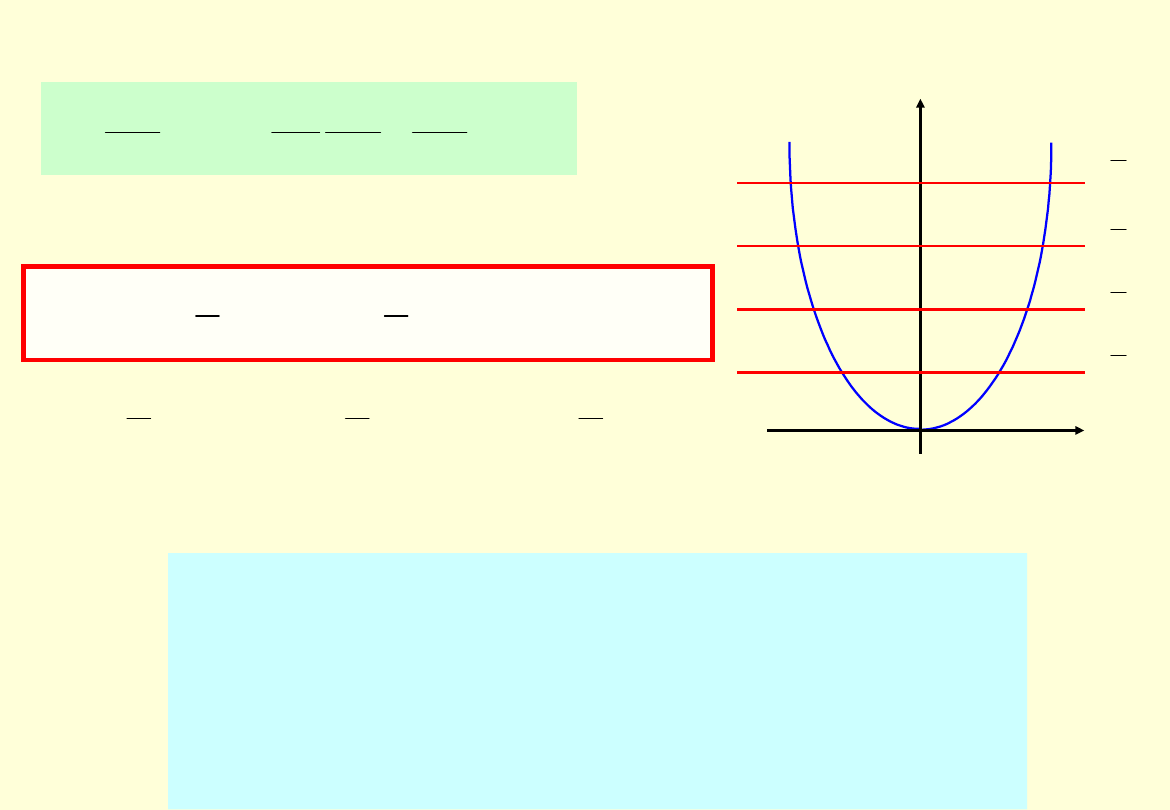
Kwantowy oscylator harmoniczny







E

2

kx

x

2m

2

kx

V

2

2

2

2

2

















ν

h

E

ν

h

2

5

E

ν,

h

2

3

E

ν,

h

2

1

E

0,1,2,3

n

ν,

)h

2

1

(n

ω

)

2

1

(n

E

2

1

0

n























x

E

ν

h

2

1

E

0



ν

h

2

5

E

0



ν

h

2

3

E

0



ν

h

2

7

E

0





Energia oscylatora jest skwantowana.



Poziomy energetyczne położone są w równych

odstępach.



Najniższa energia jest większa od zera (tzw.

drgania zerowe).



Stany energetyczne są niezdegenerowane.

Wynik
i:

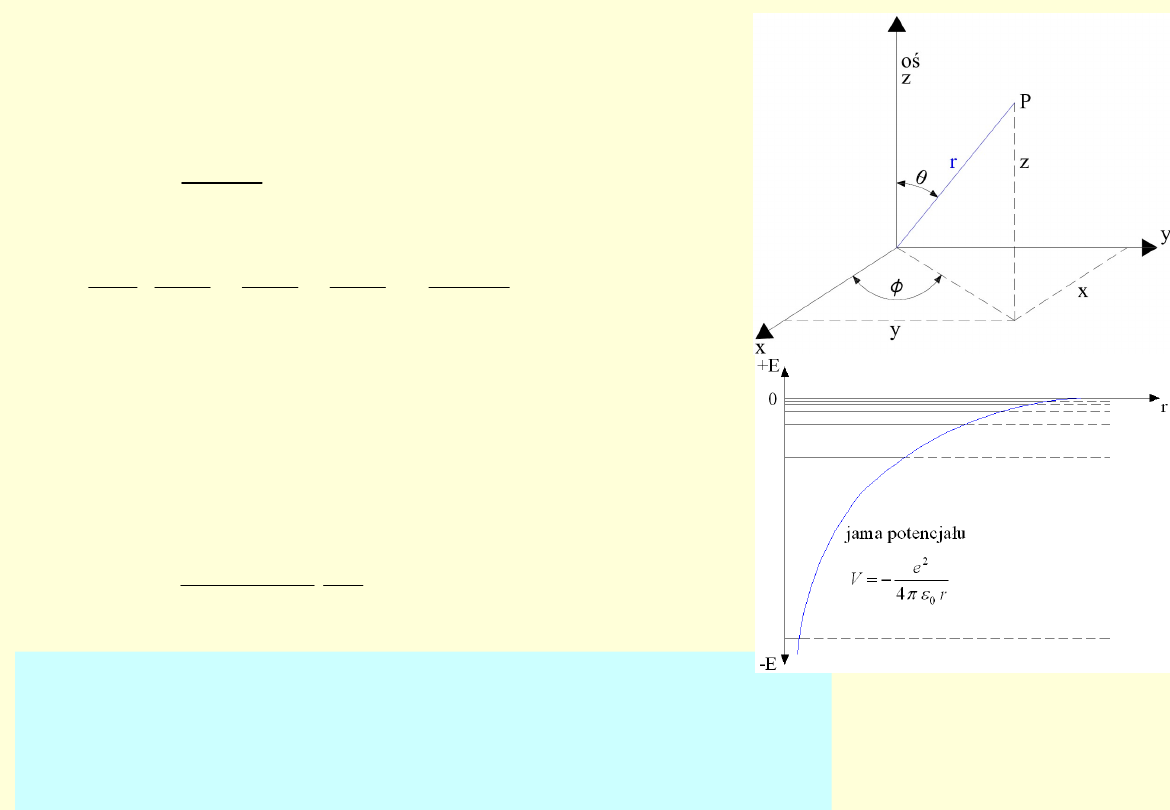
Atom wodoru











E

r

ε

4π

e

)

z

y

x

(

2m

r

ε

4π

e

V

0

2

2

2

2

2

2

2

2

0

2



























Równanie Schrödingera (trójwymiarowe)
dla atomu wodoru przyjmuje postać:

Rozwiązanie najłatwiej jest otrzymać
wykonując obliczenia we współrzędnych
sferycznych (r, θ, ):

Wynik
i:

4

,

3

,

2

,

1

,







n

2

2

0

2

4

n

n

1

ε

32π

me

E





Widmo energii jest skwantowane



Odstępy między poziomami są nierówne



Poziomy energetyczne sa wielokrotnie

zdegenerowane

Moment pędu elektronu w

atomie

Można pokazać, że funkcje falowe, odpowiadające poszczególnym poziomom
energetycznym, są jednocześnie funkcjami własnymi operatorów:



orbitalnego momentu pędu

L (liczba kwantowa l)



rzutu orbitalnego momentu pędu

L

z

na wybraną oś (liczba kwantowa m)



spinowego momentu pędu S



rzutu spinowego momentu pędu S

z

na wybraną oś (liczba kwantowa s)

Każdej energii E

n

odpowiada n funkcji falowych, różniących się liczbą

l - tzw orbitalną liczbą kwantową, kwantującą moment pędu:

1

n

,

0,1,2,

,

L









l

)

l(l 1



Każdej wartości

l

odpowiada 2

l

+1 funkcji różniących się tzw.

magnetyczną liczbą kwantową

m

taką, że:

l













,

3,

2,

1,

0,

m

,

m

L

z



Każdej wartości m odpowiadają 2 wartości tzw. spinowej liczby
kwantowej s, związanej z rzutem spinowego momentu pędu na oś z.

.

2

1

,

2

1

s

s,

S

,

S

z













2

3

W sumie mamy więc 2n

2

funkcji własnych odpowiadających energii E

n

.

Lˆ

z

Lˆ

Sˆ

z

Sˆ

Zakaz Pauliego

Cząstki elementarne mają własność zwaną

spinem

, zależnym od rodzaju

cząstek. Niektóre z nich mają spin wyrażający się poprzez liczbą całkowitą
(np. 1, 2, itp.) – nazywamy je

bozonami

(przykład: foton, fonon, atom helu).

Inne mają spin określany jako połówkowy (1/2, 3/2, itp.) – nazywamy je

fermionami

(przykład: elektron, proton, neutron, itp.).

Układ fizyczny może zawierać wiele jednakowych cząstek (np. w atomach jest
wiele elektronów). Wówczas funkcja falowa całego układu zależy od
współrzędnych (tzn. od współrzędnych przestrzennych i spinowych)
wszystkich tych cząstek.

Ponieważ cząstki na poziomie mikroskopowym są nierozróżnialne, więc proste
rozważania prowadzą do wniosku, że funkcja falowa układu fermionów musi
być antysymetryczna ze względu na przestawienie współrzędnych dwóch
cząstek, natomiast funkcja falowa układu bozonów – symetryczna.

Konsekwencją antysymetrii funkcji falowej jest

zakaz Pauliego

orzekający, że

w jednym stanie kwantowym może znaleźć się

co najwyżej jeden fermion

(inaczej:

nie może być w układzie

dwóch ani więcej fermionów o jednakowym zestawie liczb
kwantowych

).

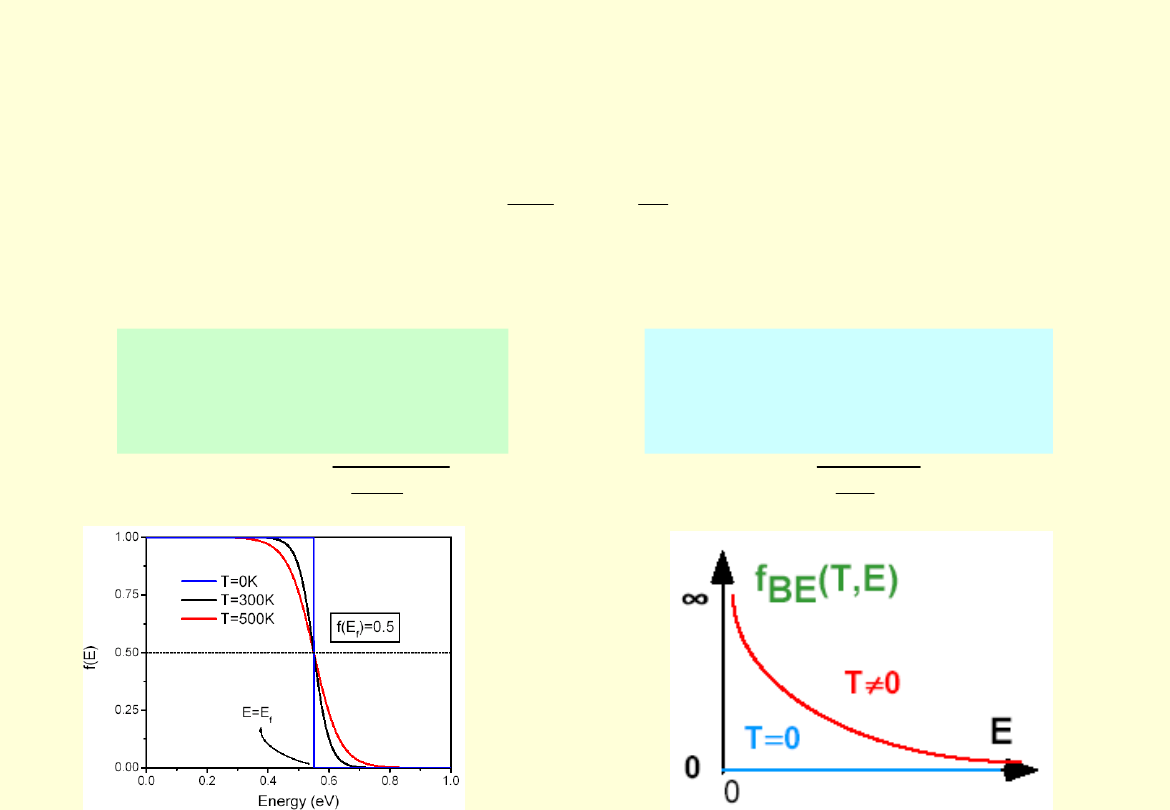
Statystyki kwantowe

W przypadku cząstek rozróżnialnych, takich jak ciała makroskopowe
opisywane przez fizykę klasyczną, liczba cząstek układu (N

i

), znajdujących się

w danym stanie energetycznym opisywana jest tzw. rozkładem kanonicznym,
z którego wynika, że:

kT

E

kT

μ

E

e

e

N











Dla cząstek nierozróżnialnych mamy:

Fermiony:

statystyka Fermiego-

Diraca

Bozony:

statystyka Bosego-

Einsteina

1

e

1

(E)

f

N

kT

E

E

FD

F









0

μ

,

1

e

1

(E)

f

N

kT

μ

E

BE











Zasada nieoznaczoności

Heisenberga

Zasada nieoznaczoności Heisenberga

dotyczy każdej pary wielkości

fizycznych A, B, których

operatory nie komutują ze sobą

(nie są

przemienne). Wielkości te nie mogą być jednocześnie znalezione idealnie
dokładnie, gdyż nieoznaczoność każdej z nich musi spełniać warunek:

/2

ΔB

ΔA







Takimi parami są
np.:

/2

Δx

Δp

x







/2

Δz

Δp

z







/2

Δt

ΔE







Przez nieoznaczoność rozumiemy średnie odchylenie od wartości średniej
wyników pomiaru.