MECHANIKA 2

 

 

Wykład Nr 10

MOMENT 

BEZWŁADNOŚCI

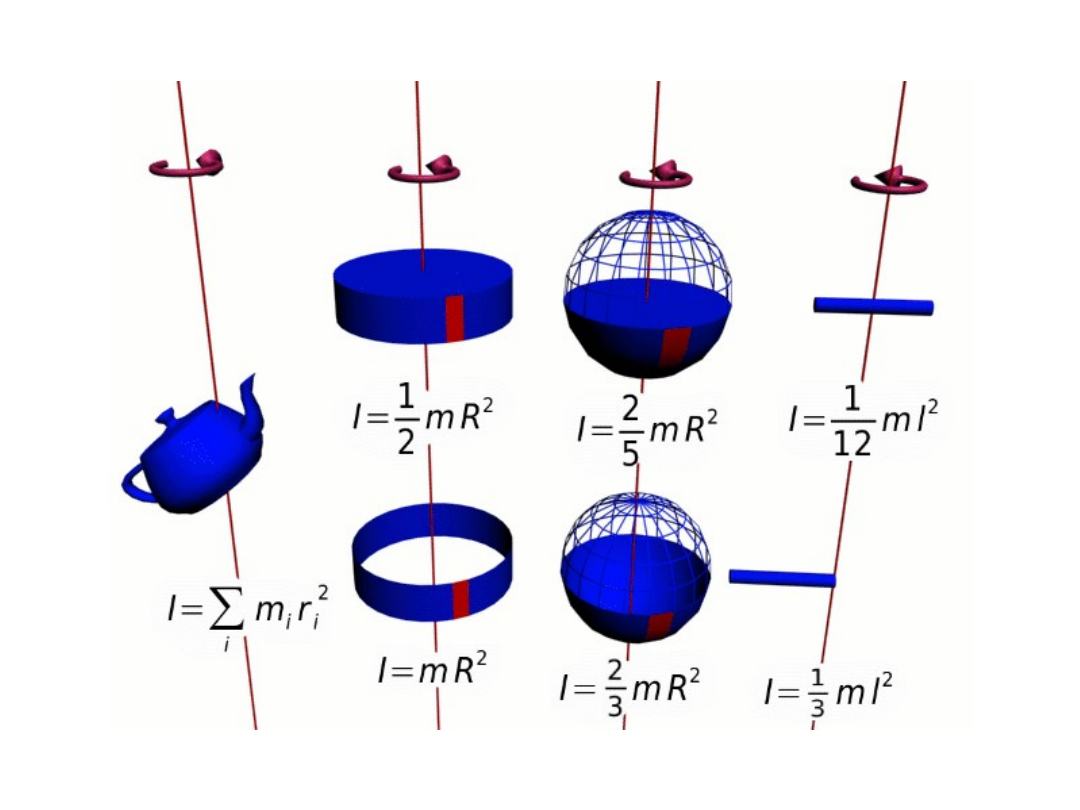
Definicja momentu bezwładności

Momentem 

bezwładności 

punktu 

materialnego  względem  płaszczyzny,  osi 
lub  bieguna  nazywamy  iloczyn  masy 
punktu  przez  kwadrat  odległości  tego 
punktu  od  danej  płaszczyzny,  osi  lub 
bieguna:

 

2

m

kg



I

Jednostką 
jest

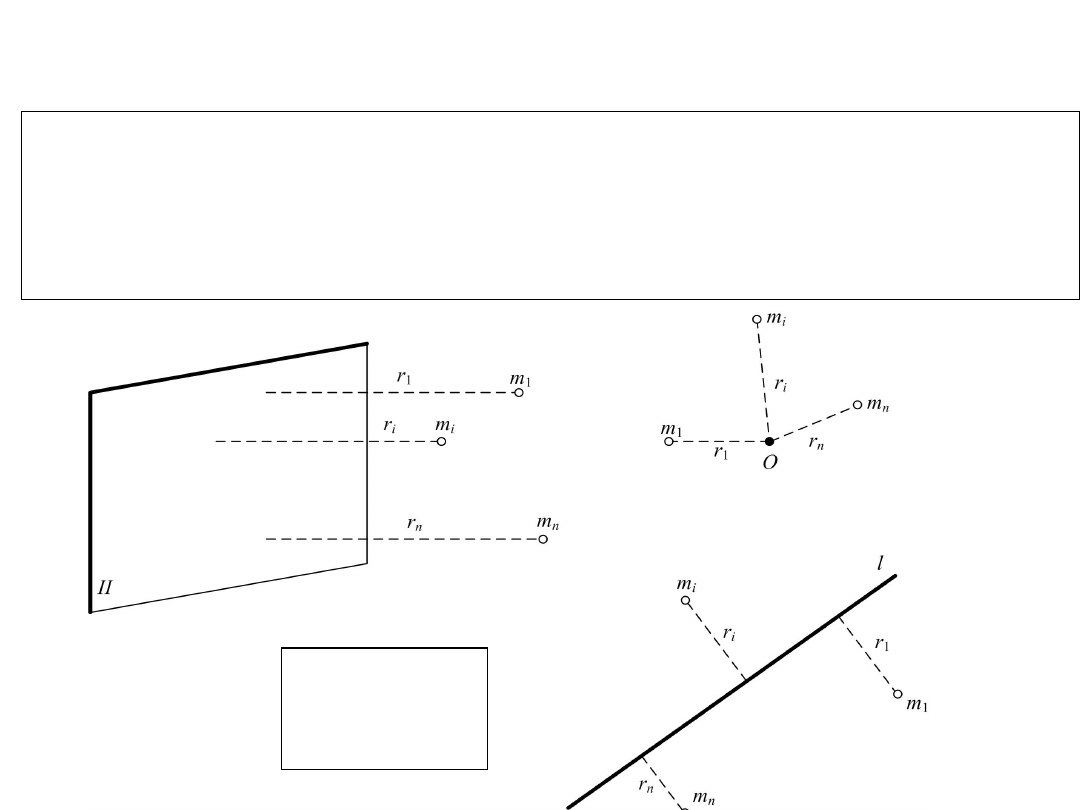
Momentem 

bezwładności 

układu 

punktów 

materialnych  względem  płaszczyzny,  osi  lub 
bieguna  nazywamy  sumę  momentów  bezwładności 
wszystkich  punktów  materialnych  względem  tej 
płaszczyzny, osi lub bieguna.

Moment bezwładności układu 

punktów

2

1

i

n

i

i

r

m

I







Moment bezwładności układu 

ciągłego

Momentem  bezwładności  układu 
ciągłego  (linii,  powierzchni  lub 
bryły 

materialnej) 

względem 

przyjętej  płaszczyzny,  osi  lub 
bieguna nazywamy całkę

rozciągniętą na całą masę 
układu. 

Promień bezwładności

Po 

przekształceniu 

wzoru

otrzymamy wzór na promień bezwładności

Masa zredukowana na 

odległość r

Masę  m

red

,  którą  należy  skupić  w 

odległości r od danej płaszczyzny, osi 
lub 

bieguna, 

aby 

jej 

moment 

bezwładności  był  równy  I,  nazywamy 
masą 

zredukowaną 

na 

daną 

odległość r. 

czyli 

Geometryczny moment 

bezwładności

 

Geometryczny 

moment 

bezwładności 

I 

(dla 

ciał 

jednorodnych) 

jest 

ilorazem 

masowego momentu bezwładności  
przez gęstość: 

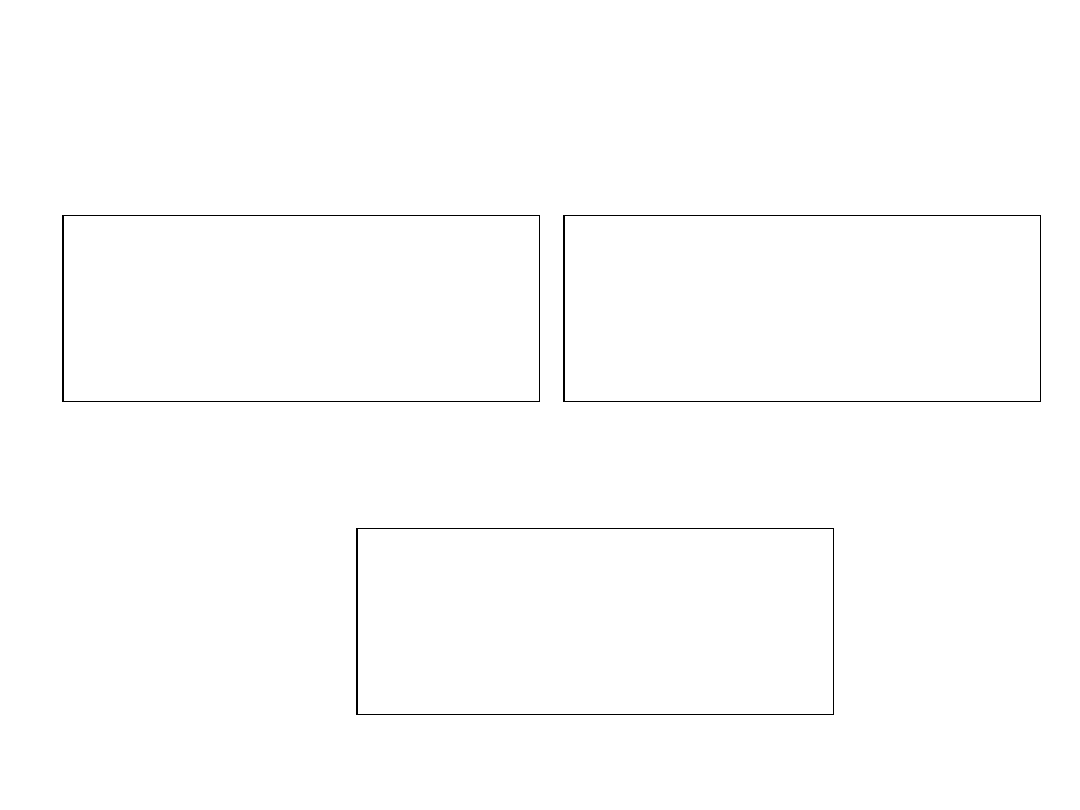
Moment bezwładności linii 

materialnej

Po podstawieniu do równania 

Otrzymamy  wzór  na  moment  bezwładności 
linii materialnej

Masy elementarnej w 
postaci:

Gdzie: 

l

 – jest gęstością liniową linii 

materialnej, kg/m

Geometryczny moment 

bezwładności linii materialnej

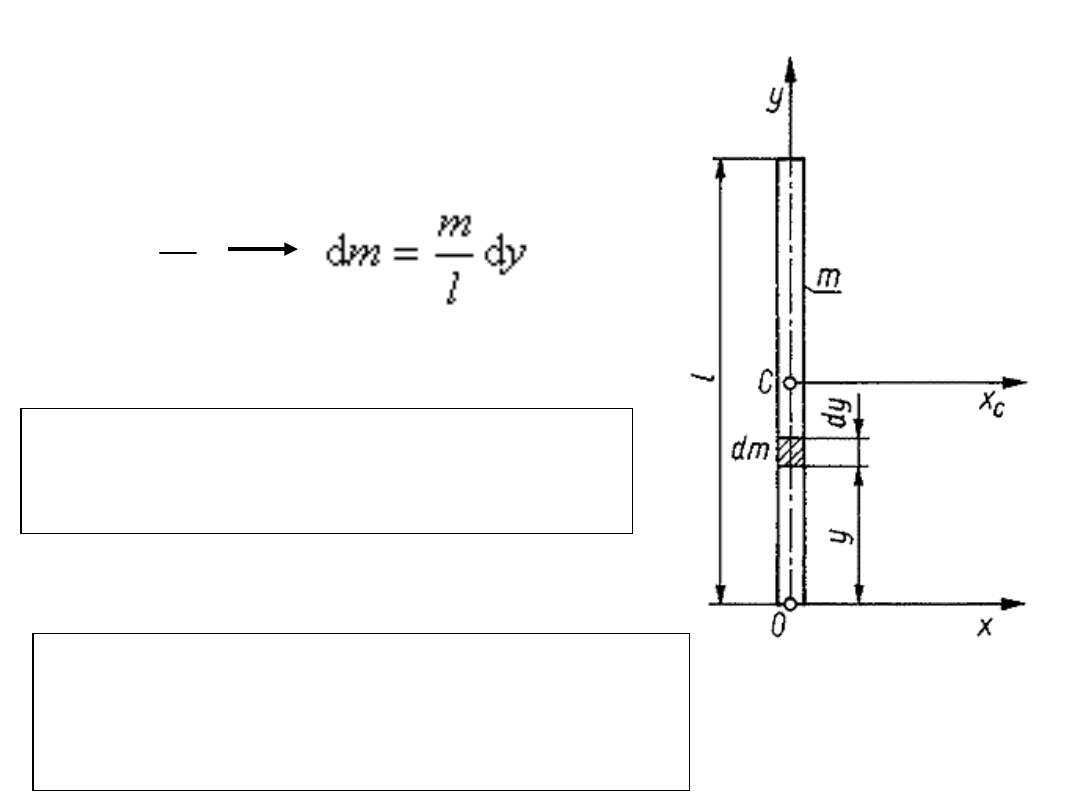
Przykład

Wyznacz moment bezwładności 
cienkiego jednorodnego pręta o masie 
m i długości l względem osi Ox i osi 
centralnej Cx

c

.

Pomijając wymiary poprzeczne pręta (z = 0) 
otrzymujemy

Moment bezwładności względem osi 
centralnej Cx

c

.

l

m

l





Moment powierzchni 

materialnej

Po podstawieniu do 
wzoru

Masy elementarnej w postaci:

Otrzymamy wzór na moment bezwładności powierzchni materialnej

Gdzie: 

s

 – jest gęstością powierzchni 

materialnej, kg/m

2

Geometryczny moment powierzchni materialnej

Jednostka J

S

 –  m

4

Moment bryły materialnej

Po podstawieniu do wzoru

Masy elementarnej w postaci:

Otrzymamy wzór na moment bezwładności bryły materialnej

Gdzie: 

s

 – jest gęstością bryły materialnej, kg/m

3

Moment bezwładności względem 

płaszczyzny

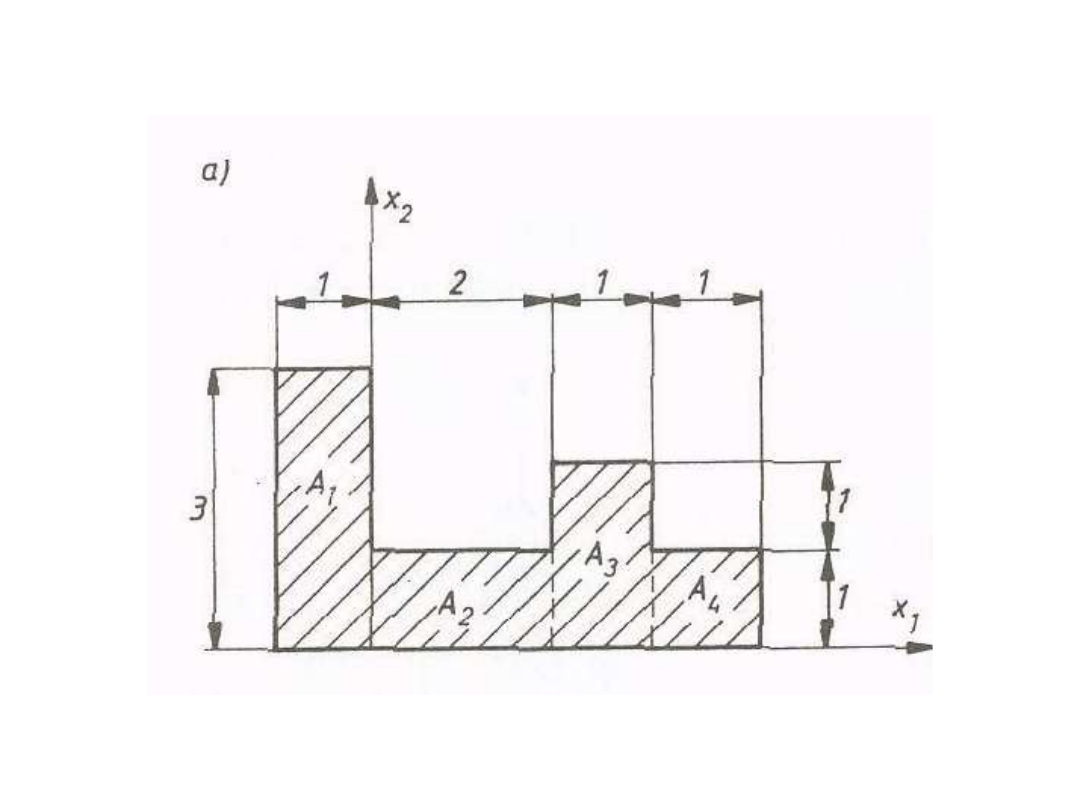
W układzie współrzędnych                 dany jest 
układ punktów materialnych o masach             
      . Współrzędne masy       oznaczymy             
. 
      Momenty bezwładności względem 
płaszczyzn układu współrzędnych określają 
wzory:    

z

y

x

,

,

n

m

m

m

,

,

,

2

1



i

m

i

i

i

z

y

x

,

,

Moment bezwładności względem osi

Moment bezwładności względem bieguna

Związki pomiędzy momentami

Suma 

momentów 

bezwładności 

względem 

dwóch 

płaszczyzn 

wzajemnie  prostopadłych 
jest  równa  momentowi 
bezwładności 

względem 

osi  pokrywającej  się  z 
krawędzią  przecięcia  się 
tych płaszczyzn.

Momenty 
bezwładności 
względem 
płaszczyzn  można 
wyrazić 

przez 

momenty osiowe:

Biegunowy moment bezwładności można wyrazić 
przez momenty osiowe 

Biegunowy  moment  bezwładności  jest  równy 
połowie  sumy  osiowych  momentów  bezwładności 
względem  trzech  prostopadłych  osi  przechodzących 
przez ten biegun.

Związki pomiędzy momentami

Biegunowy  moment  bezwładności  możemy  również  wyrazić 
przez momenty względem płaszczyzn

Moment  biegunowy  jest  sumą  momentów 
względem  trzech  prostopadłych  płaszczyzn 
przechodzących przez dany biegun.

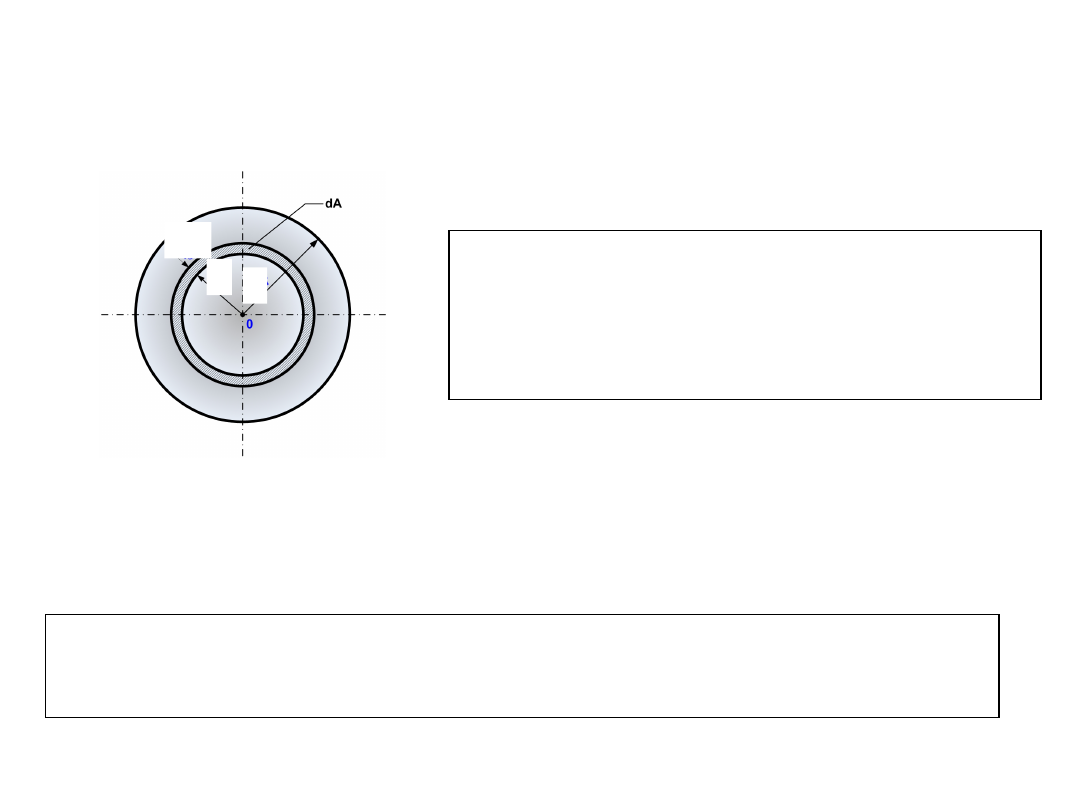
PRZYKŁAD 
1

Wyznaczyć biegunowy moment bezwładności przekroju 
kołowego.

r

dr

R

Elementarne  pole  dA  pierścienia  o  grubości  d



  jest 

równe 

Po  pominięciu  (d)

2

  -  wielkości  małej  wyższego 

rzędu 

Po podstawieniu otrzymamy: 

Aby  objąć  całkowaniem  cały  obszar  A,  zmienna  r 
powinna przybierać wartości od 0 do R:

Biegunowy  moment  bezwładności  przekroju  kołowego 
względem jego środka wynosi: 

 

 

lu
b

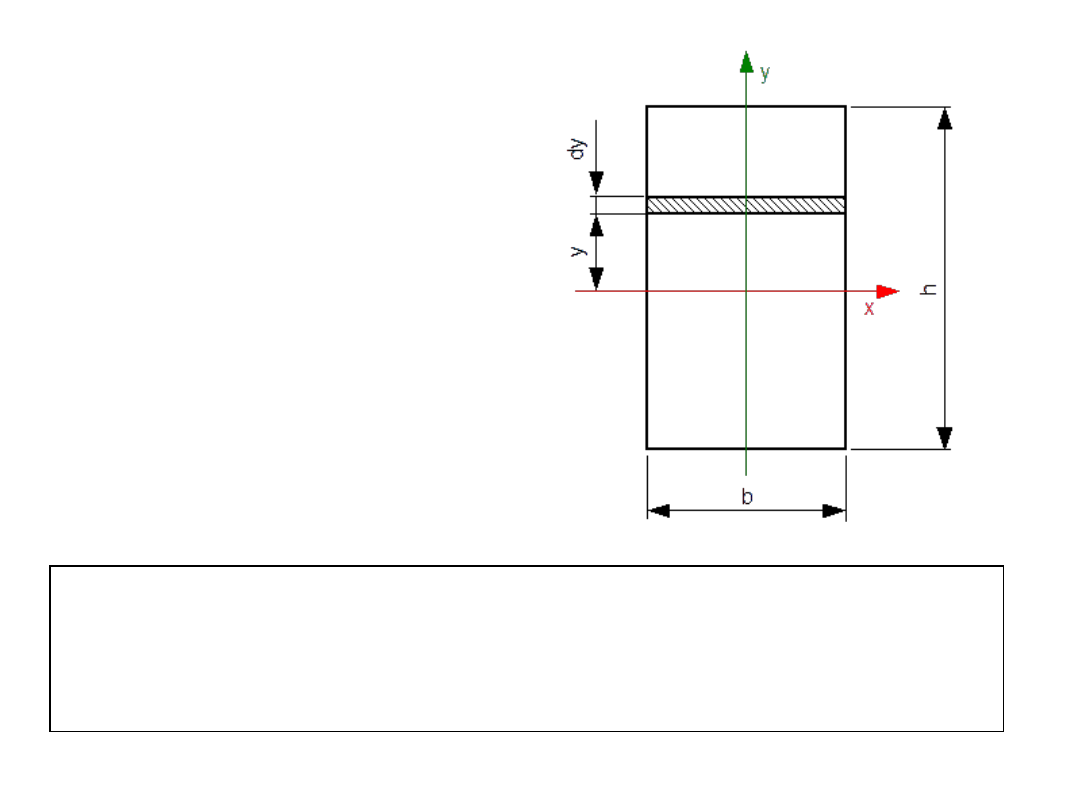
PRZYKŁAD 2

Obliczyć geometryczny 
moment bezwładności  
prostokąta o wym. b i h 
względem osi x.

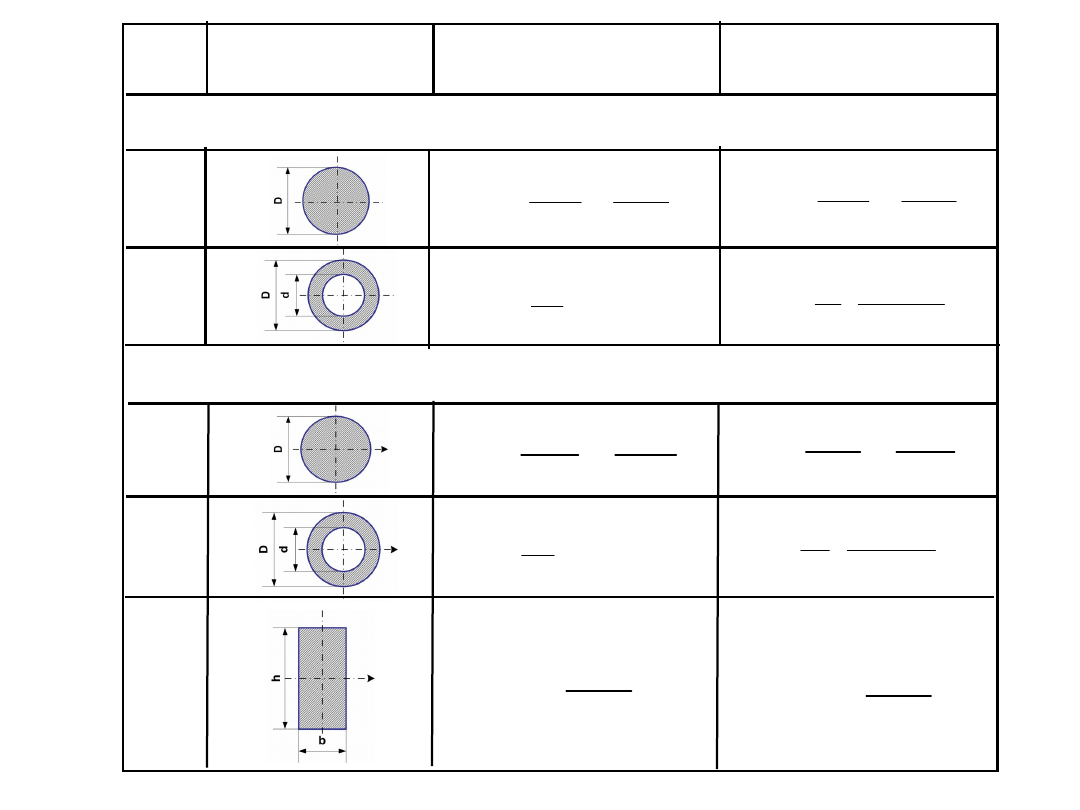
Lp.

 

Przekrój 

Moment 

bezwładności 

Wskaźnik 

wytrzymałości 

Względem środka (osiowy)

 

1.

2.

Względem osi zaznaczonej na rysunku 

3.

4.

5.

32

2

4

4

0

D

R

J













4

4

0

32

d

D

J







16

2

3

3

0

D

R

W

























D

d

D

W

4

4

0

16



64

4

4

4

D

R

J













4

4

64

d

D

J







12

3

bh

J 

6

2

bh

W 

















D

d

D

W

4

4

32



32

4

3

3

D

R

W









MOMENTY DEWIACJI

Momentem  dewiacji  punktu  materialnego 
względem płaszczyzn wzajemnie prostopadłych 
nazywamy 

iloczyn 

masy 

punktu 

przez 

odległości od danych płaszczyzn:

Momenty  zboczenia  mogą  być  dodatnie, 
ujemne i, w szczególności, równe zeru.

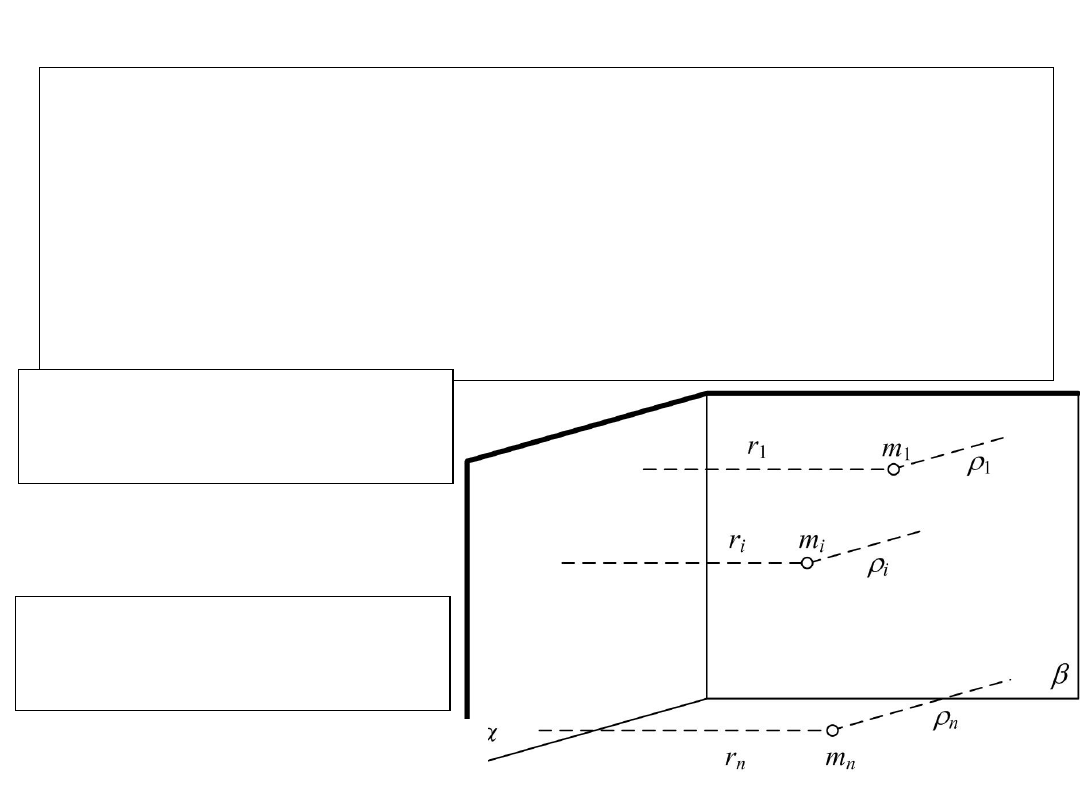
MOMENTY DEWIACJI

Momentem 

dewiacji 

układu 

punktów 

materialnych  względem  dwóch  wzajemnie 
prostopadłych  płaszczyzn  a  i  b  nazywamy 
sumę  momentów  dewiacji  poszczególnych 
punktów 

materialnych 

względem 

tych 

płaszczyzn.

Dla 

układu 

ciągłego

rozciągnięta, na całą masę.

MOMENTY DEWIACJI

W przestrzennym układzie współrzędnych układ 
punktów  materialnych  ma  trzy  momenty 
dewiacji:

W płaskim układzie współrzędnych układ 
materialny ma jeden moment dewiacji 

Geometryczny  moment  dewiacji  jest 
równy ilorazowi masowego momentu 
dewiacji przez gęstość  bryły.

GEOMETRYCZNY MOMENT DEWIACJI

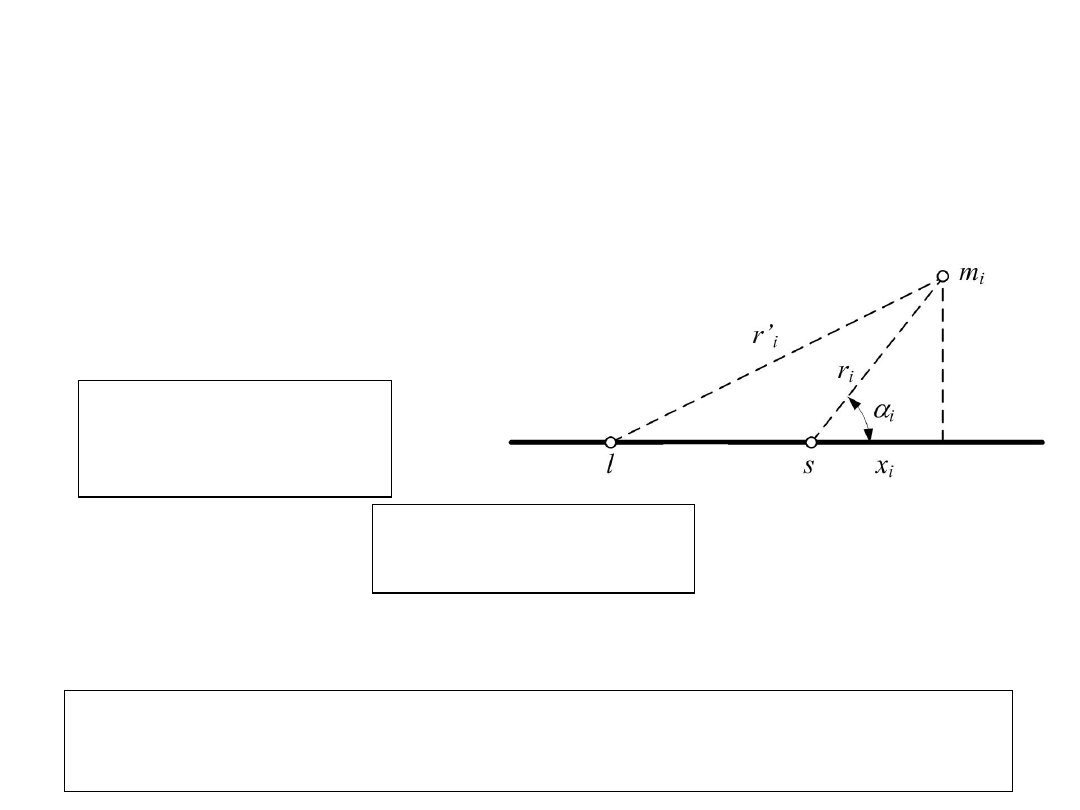
Transformacja równoległa momentów 

bezwładności

Weźmy 

pod 

uwagę 

układ 

punktów 

materialnych i dwie równoległe osie l, s.

Moment 
bezwładności 
względem osi l

a względem osi s

Pomiędzy odległościami       i         zachodzi zależność 

i

r

i

r

a

Po podstawieniu otrzymujemy

czyli

Założymy, że oś s przechodzi przez środek 
ciężkości układu materialnego, wtedy moment 
statyczny                ,  jest równy zero i wzór 
przybiera postać:     

0





i

i

x

m

Transformacja równoległa momentów 

bezwładności

Moment bezwładności względem dowolnej 
osi  jest  równy  momentowi  względem  osi 
równoległej  przechodzącej  przez  środek 
ciężkości  powiększonemu  o  iloczyn  masy 
całkowitej 

układu 

przez 

kwadrat 

odległości obu osi.

Iloczyn        jest zawsze dodatni, stąd wniosek, 
że  moment  bezwładności  względem  prostej 
przechodzącej  przez  środek  ciężkości  układu 
jest  najmniejszym  ze  wszystkich  momentów 
względem prostych do niej równoległych. 

2

ma

Transformacja równoległa momentów 

bezwładności

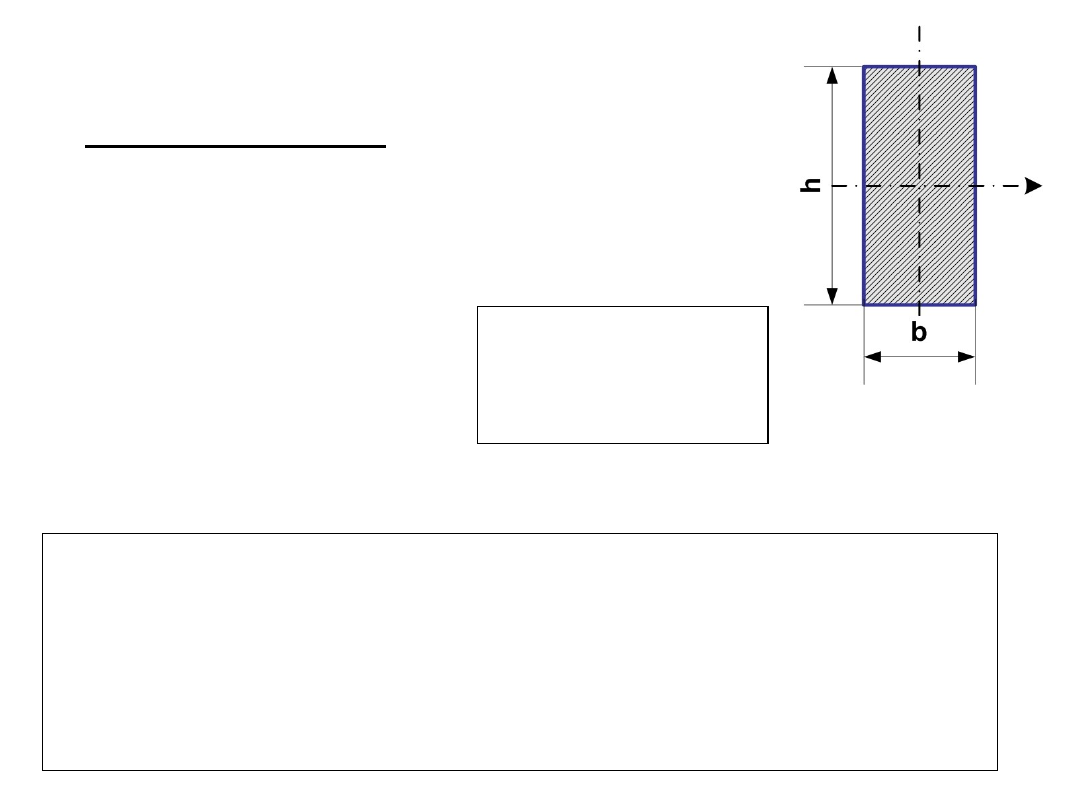
PRZYKŁAD

Geometryczny moment 
bezwładności prostokąta 
względem poziomej  osi x 
wynosi

Obliczyć moment bezwładności względem 
podstawy.

x

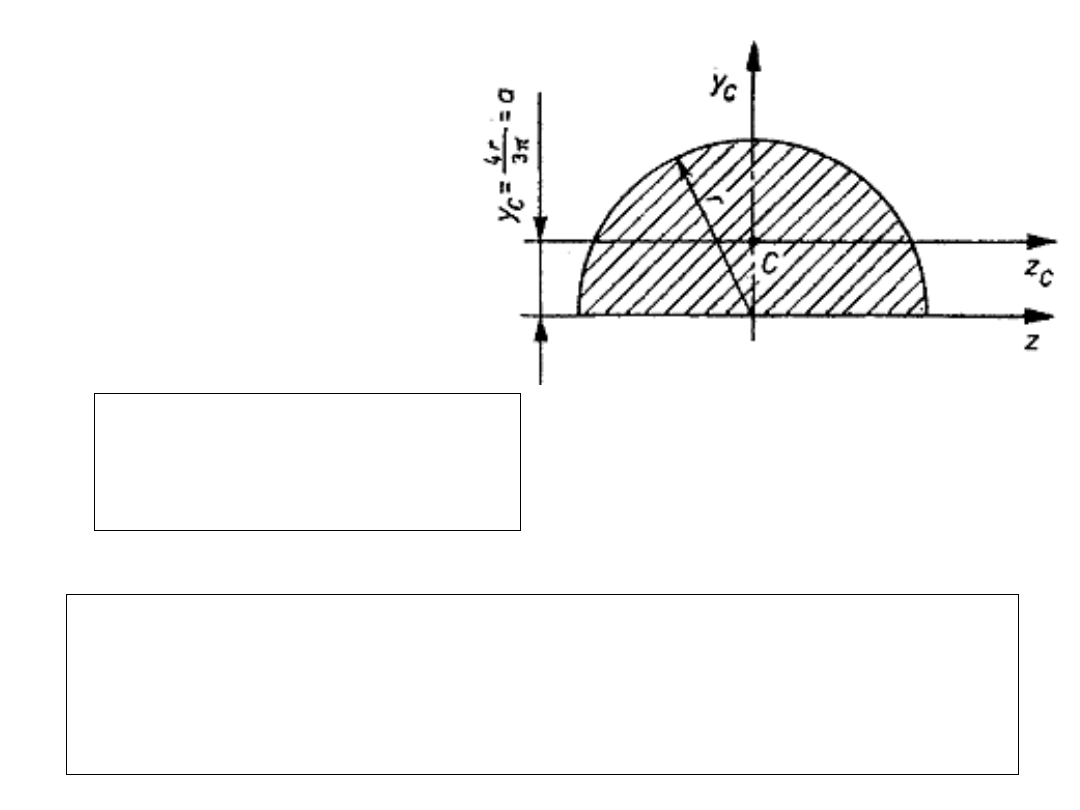
Przykład 1
Wyprowadź wzór na 
moment bezwładności 
półkola względem osi 
centralnej.

R o z w i ą z a n i e:
Moment bezwładności 
półkola względem osi z 
jest równy połowie 
momentu bezwładności 
całego koła

Stosując wzór Steinera, mamy

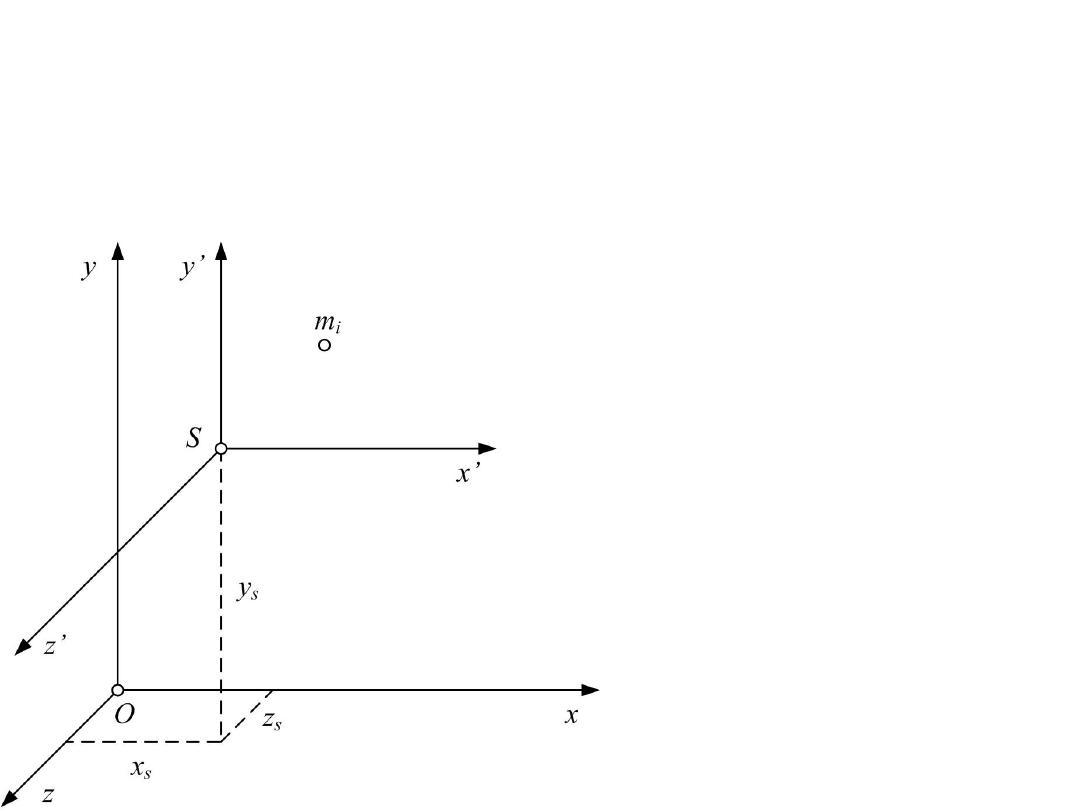
  Wyznaczymy  moment  dewiacji  względem  układu 
współrzędnych                               

z  początkiem 

umieszczony w środku ciężkości S.

z

y

x







,

,

Transformacja równoległa momentów 

dewiacji

Współrzędne dowolnej 
masy      w układzie          
    będą równe 

i

m

z

y

x ,

,

s

i

i

x

x

x







s

i

i

y

y

y







s

i

i

z

z

z







Moment dewiacji względem dwóch płaszczyzn (np. 
płaszczyzn       i       ) będzie równy 

zy

xz

Transformacja równoległa momentów 

dewiacji

Ale

Po zapisaniu analogicznych związków na       i       
otrzymamy:

yz

D

zx

D

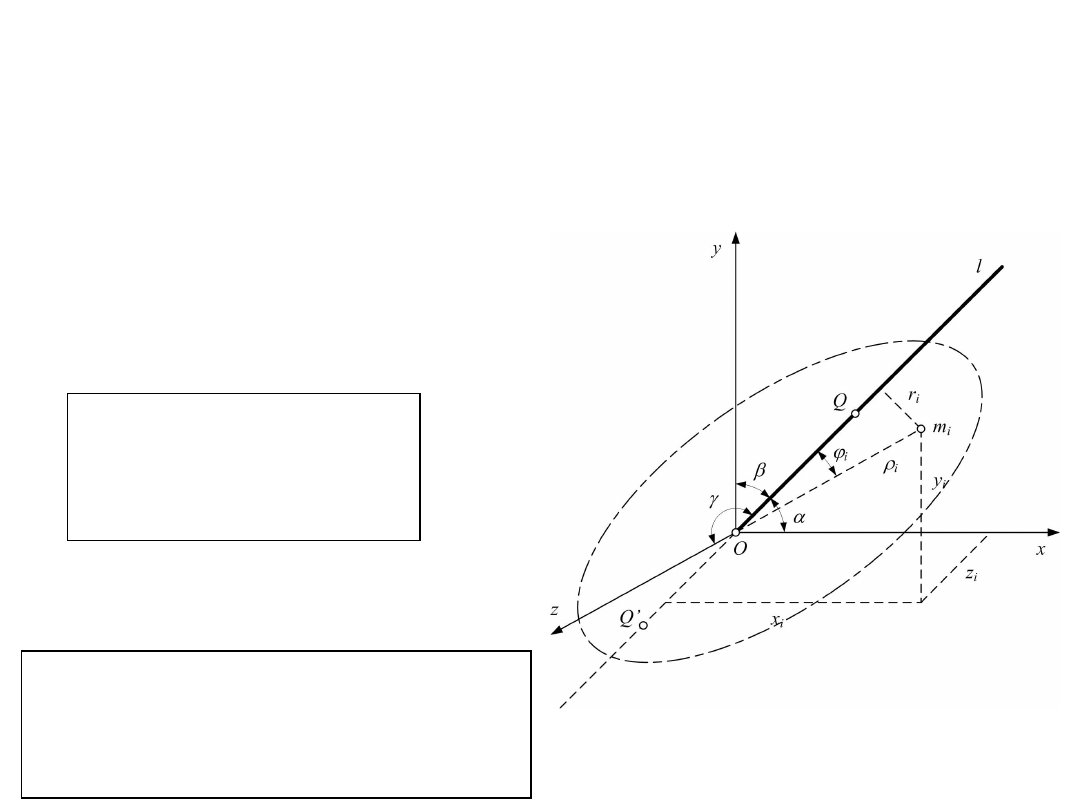
Transformacja obrotowa osiowych momentów 

bezwładności

Dane:                            oraz                        i              

n

m

m

m

,

,

,

2

1



z

y

x

I

I

I

,

,

xy

D

yz

D

zx

D

Należy 
wyznaczyć 
moment 
bezwładności 
względem osi l .

Odległość  r

i

  masy  m

i

  od 

osi  l    określona  jest 
równaniem



i

x

i

,y

i

,z

i

)

lub 

Rzut promienia       na oś l jest równy 

i



Uwzględniając, że

gdzie

Transformacja obrotowa osiowych momentów 

bezwładności

dochodzimy do równania

Grupując względem cosinusów otrzymamy

Po podstawieniu 

do

Transformacja obrotowa osiowych momentów 

bezwładności

Mnożymy  powyższe  równanie  przez  m

i

,  a 

otrzymane  iloczyny  sumujemy.  Uwzględniając, 
że

oraz

otrzymujemy ostatecznie

Transformacja obrotowa osiowych momentów 

bezwładności

  W  szczególności  dla  układu  płaskiego 
uwzględniając, że                      powyższe 
równanie przyjmuje postać: 













90

Transformacja obrotowa osiowych momentów 

bezwładności