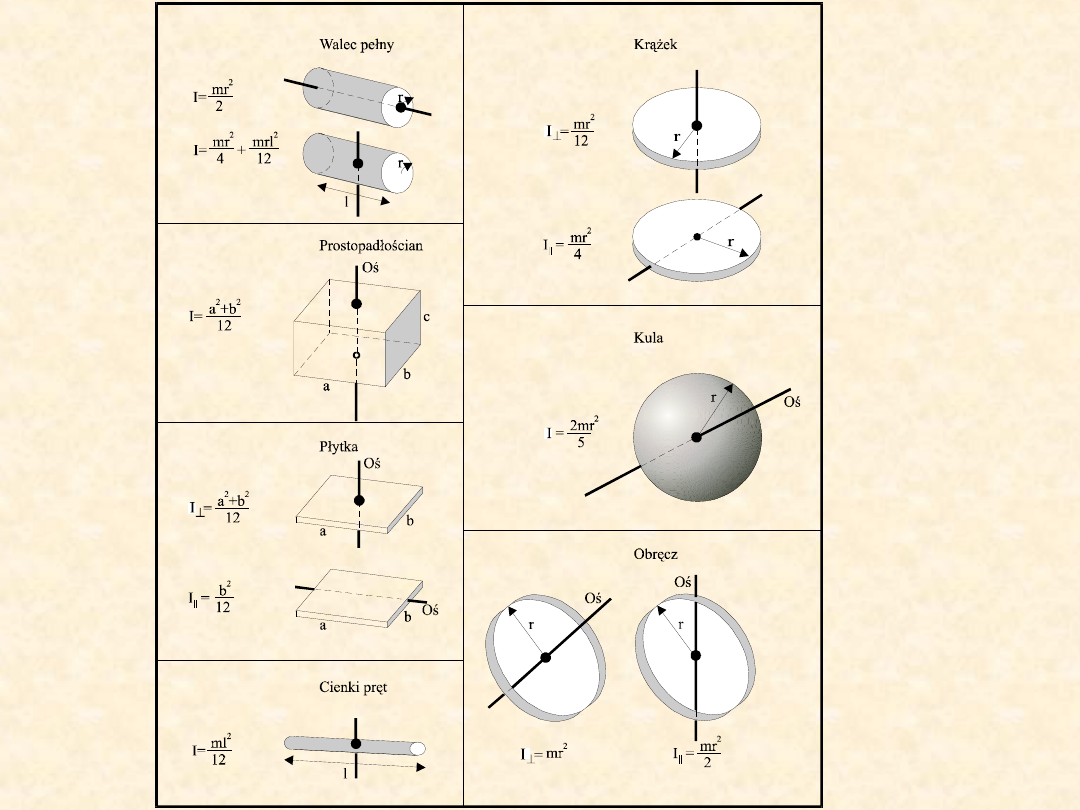
DYNAMIKA BRYŁY 

SZTYWNEJ

 

 

Dotychczas 

zajmowaliśmy 

się 

najprostszym 

przybliżeniem 

ciała, 

czyli 

modelem 

punktu 

materialnego

. Jednak w wielu przypadkach nie można 

pominąć  rozmiarów  ciała.  Dlatego  też  zajmiemy  się 
teraz  mechaniką  ciał  zajmujących  pewną  skończoną 
objętość w przestrzeni, czyli mechaniką 

brył

.

Jednak również w tym przypadku ograniczymy się do 
najprostszego 

modelu bryły sztywnej

.

 

 

Momenty masowe pierwszego 

stopnia

Momentem 

masowym 

pierwszego 

stopnia

 

(momentem 

statycznym) 

 

układu 

punktów 

materialnych  względem  dowolnego  punktu  O 
nazywamy  sumę  iloczynów  mas  punktów  i  ich 
wektorów wodzących

 







n

1

i

i

i

mr

S

W przypadku ciągłego układu punktów o stałej 
gęstości 











V

m

dV

dm

r

r

S

gdzie  dV = dxdydz jest elementem 
objętości ciała

 

 

 



















n

1

i

i

i

z

n

1

i

i

i

y

n

1

i

i

i

x

z

m

S

;

y

m

S

;

x

m

S

Suma  iloczynów  mas  punktów  i  ich  odległości  od 
danej  płaszczyzny  nazywana  jest 

momentem 

statycznym względem płaszczyzny

 



















n

1

i

i

i

xz

n

1

i

i

i

yz

n

1

i

i

i

xy

y

m

S

;

x

m

S

;

z

m

S

Z  porównania  otrzymujemy  równania  wiążące 
składowe  momentu  statycznego  względem  punktu  z 
odpowiednimi  momentami  statycznymi  względem 
płaszczyzn 

xy

z

xz

y

yz

x

S

S

;

S

S

;

S

S







 

 

Zawsze  można  znaleźć  taki  punkt  ciała  C  (czyli 

środek masy

 ciała), którego promień r

C

 pomnożony 

przez  masę  skupioną  w  tym  punkcie 

da wartość momentu statycznego 

S







n

1

i

i

m

m

C

n

1

i

i

i

m

m

r

r

S









Stąd można znaleźć położenie środka masy 

m

dm

m

m

m

m

m

C

n

1

i

i

n

1

i

i

i

C



















r

S

r

r

S

r

dla dyskretnego układu punktów              dla ciała 

ciągłego (bryły)

 

 

m

S

m

S

z

;

m

S

m

S

y

;

m

S

m

S

x

xy

z

C

xz

y

C

yz

x

C













Stąd wynikają dwa istotne wnioski:

1. Moment  statyczny  względem  płaszczyzny  (lub 

moment  statyczny  względem  punktu  będącego 
środkiem masy) przechodzącej przez środek masy 
jest równy zero.

2. Jeżeli  jednorodne  ciało  posiada  środek,  oś  lub 

płaszczyznę  symetrii,  to  środek  masy  będzie 
znajdował  się  na  tej  płaszczyźnie,  osi  lub  w  tym 
środku symetrii.

 

 

Momenty masowe drugiego 

stopnia

 

Momentem 

masowym 

stopnia 

drugiego

 

(

momentem  bezwładności

)  układu  punktów 

materialnych  lub  ciała  względem  płaszczyzny 
nazywamy  sumę  iloczynów  mas  punktów  i 
kwadratów ich odległości od płaszczyzny 



















n

1

i

2

i

i

yz

n

1

i

2

i

i

xz

n

1

i

2

i

i

xy

x

m

I

;

y

m

I

;

z

m

I

A dla układu ciągłego o stałej gęstości  

 

 































V

2

m

2

yz

V

2

m

2

xz

V

2

m

2

xy

dV

x

dm

x

I

dV

y

dm

y

I

dV

z

dm

z

I

Momentem  bezwładności  względem  osi

  układu 

punktów  materialnych  lub  ciała  nazywamy  sumę 
iloczynów mas i ich kwadratów odległości od osi.

dV

r

dm

r

I

r

m

I

V

2

m

2

n

1

i

2

i

i

















 

 

W układzie kartezjańskim Oxyz momenty bezwładności 
względem osi układu wyrazić można w następującej 
postaci

 





































n

1

i

2

i

2

i

i

z

n

1

i

2

i

2

i

i

y

n

1

i

2

i

2

i

i

x

y

x

m

I

;

z

x

m

I

;

z

y

m

I













dV

y

x

I

;

dV

z

x

I

;

dV

z

y

I

V

2

2

z

V

2

2

y

V

2

2

x

























yz

xz

z

yz

xy

y

xy

xz

x

I

I

I

;

I

I

I

;

I

I

I













Moment bezwładności względem osi równa się sumie 
momentów 

bezwładności 

względem 

płaszczyzn 

prostopadłych, których przecięciem jest ta oś 

 

 

Twierdzenie Steinera

 dla momentów bezwładności :

Momenty  bezwładności  względem  płaszczyzn  lub  osi 
nie  przechodzących  przez  środek  masy  ciała  można 
obliczyć jako

: 

1.     Dla 

momentów 

bezwładności 

względem 

płaszczyzn

2

aaC

aa

md

I

I





2. 

Dla momentów bezwładności 

względem osi

2

C

md

I

I





gdzie  indeks  C  oznacza  moment  bezwładności 
względem  płaszczyzny  lub  osi  równoległej  do 
rozpatrywanej 

i 

przechodzącej 

przez 

środek 

ciężkości,  d  jest  zaś  odległością  środka  ciężkości 
odpowiednio od płaszczyzny lub osi.

 

 

 

 

Definicja bryły sztywnej

Bryłą 

sztywną

 

nazywamy 

układ 

punktów 

materialnych 

o 

jednorodnej 

gęstości, 

których 

wzajemne  odległości  pozostają  stałe  w  trakcie  ruchu 
ciała.

Bryłą  sztywną  jest  takie  ciało,  w  którym  odległości 
między dowolnymi punktami są stałe i nie zmieniają 
się  pod  wpływem  sił  zewnętrznych  działających  na 
ciało. 

Bryła 

sztywna 

nie 

podlega 

zatem 

żadnym 

odkształceniom  pod  wpływem  działających  sił.  Wiele 
ciał  rzeczywistych  można  traktować  jako  bryły 
sztywne,  jeśli  działające  siły  są  dostatecznie  małe 
(zależy  to  od  właściwości  materiału,  z  którego 
wykonane jest ciało). 

 

 





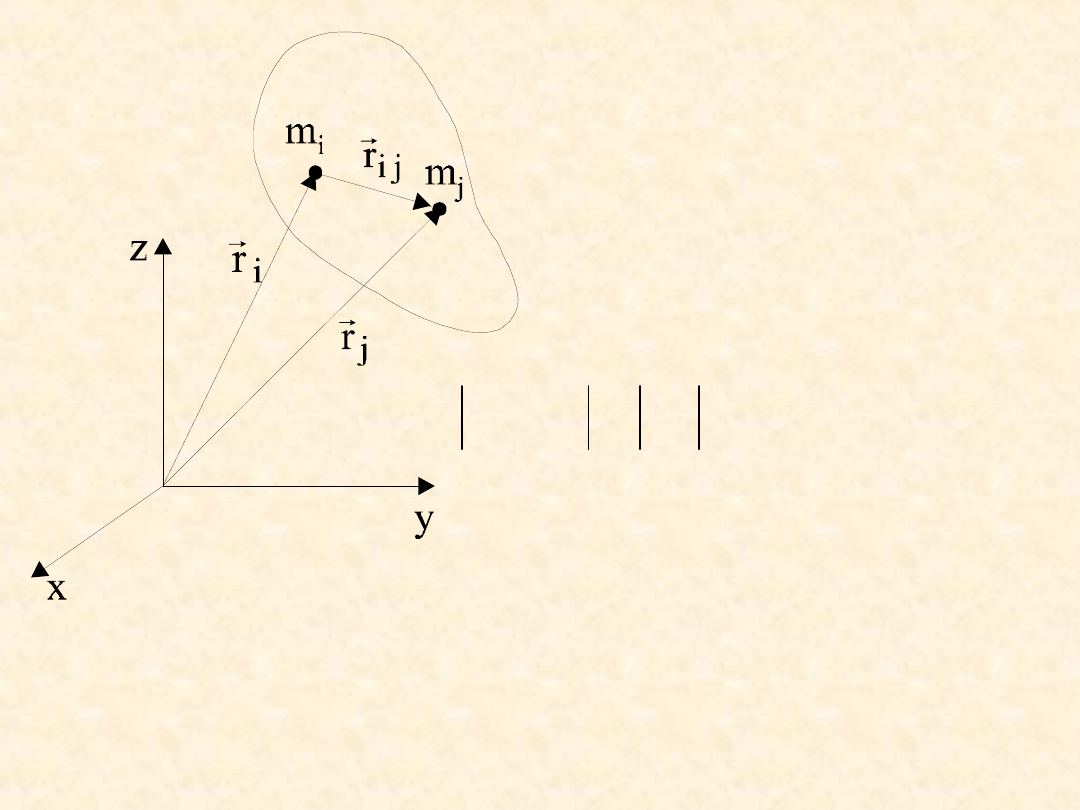
n

,...,

2

,

1

j

,

i

r

ij

ij

j

i









r

r

r

gdzie  r

i

  oraz  r

j

  są  wektorami  wodzącymi  i-tego  i  j-

tego  punktu  w  obranym  układzie  odniesienia, 
natomiast  r

ij

  jest  stałą  liczbą  wyrażającą  odległość 

między tymi punktami

. 

Warunek 

powyższy 

możemy 

zapisać 

następująco:

 

 

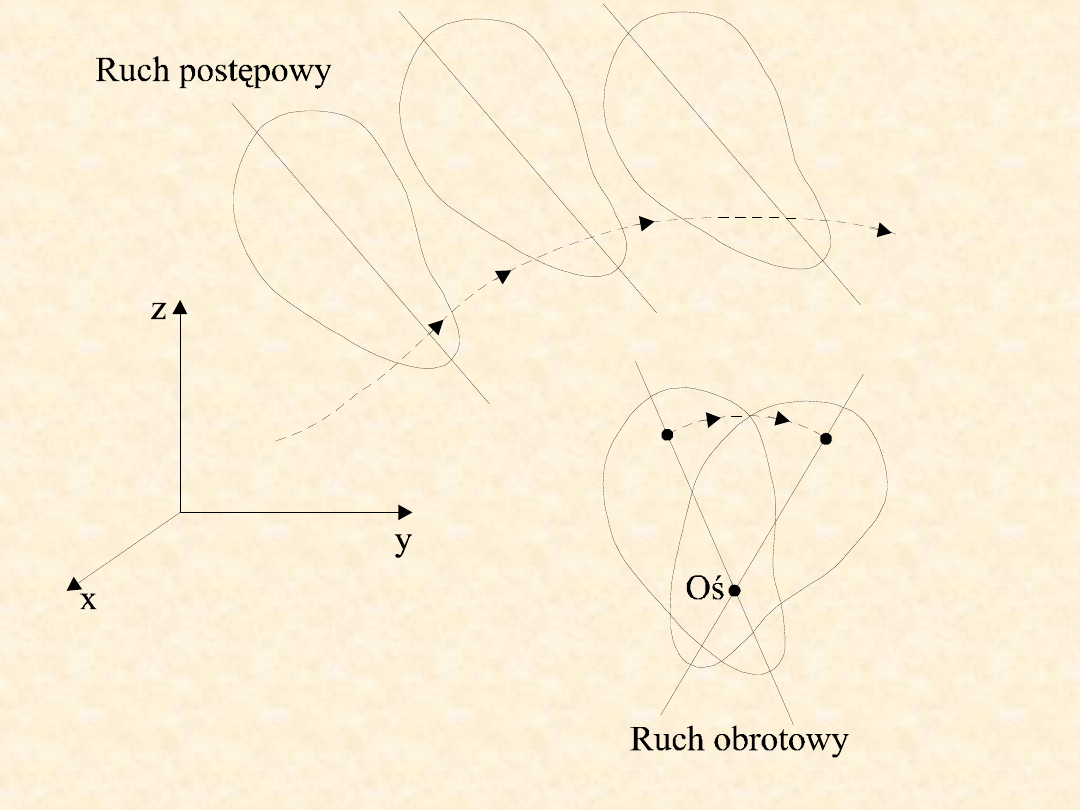
Rodzaje ruchów bryły sztywnej

Ruchem  postępowym  bryły  sztywnej

  nazywamy 

taki ruch, w którym dowolna prosta przeprowadzona 
przez  to  ciało  przesuwa  się  równolegle  do  samej 
siebie  (wektory  prędkości  wszystkich  punktów  ciała 
są w danej chwili jednakowe).

Bryła  sztywna  porusza  się  ruchem  obrotowym

, 

jeżeli  wszystkie  punkty  ciała  poruszają  się  po 
okręgach,  których  środki  leżą  na  jednej  prostej. 
Prostą  tę  nazywamy  chwilową  osią  obrotu.  Jeżeli 
położenie  osi  obrotu  nie  zmienia  się,  to  nosi  ona 
nazwę stałej osi obrotu.

 

 

 

 

Statyka układu sztywnego

Na każdy i-ty punkt bryły sztywnej może działać siła 
zewnętrzna  F

i

  oraz  siła  wewnętrzna  F

ij

  pochodząca 

od  innego  (j-tego)  punktu  bryły.  Wypadkowa  siła 
działająca  na  każdy  i-ty  punkt  bryły  jest  sumą  siły 
zewnętrznej 

(w 

ogólności 

wypadkowej 

sił 

działających  na  ciało)  oraz  sumy  sił  wewnętrznych 
pochodzących  od  wszystkich  pozostałych  punktów 
bryły  (punkt  nie  działa  sam  na  siebie,  czyli  F

ii

  =  0). 

Możemy więc zapisać dla i-tego punktu bryły:











1

n

1

j

ij

i

i

w

F

F

F

 

 

Takie  samo  wyrażenie  można  zapisać  dla  dowolnego 
innego  punktu  bryły.  Na  podstawie  trzeciej  zasady 
dynamiki siły wzajemnego oddziaływania punktów się 
równoważą:

ji

ij

F

F





Zatem  całkowita  siła  wypadkowa  działająca  na  całą 
bryłę :

















n

1

i

1

n

1

j

ij

n

1

i

i

w

F

F

F

ale  całkowita  suma  sił  wewnętrznych  się  zeruje, 
więc:







n

1

i

i

w

F

F

 

 

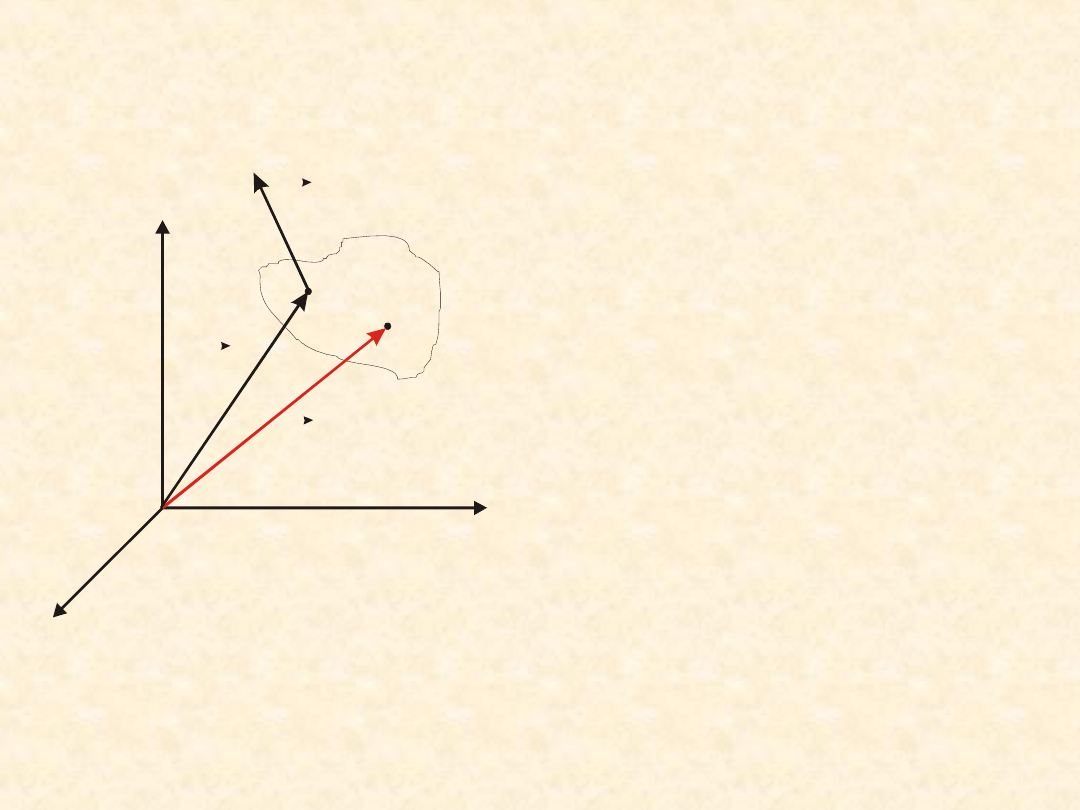
Siłą powodującą ruch ciała sztywnego może być tylko 
siła zewnętrzna.

 

C

x

y

z

r

C

F

i

r

i

i

Niech  na  i-ty  punkt 
bryły  sztywnej  działa 
siła 

F

i

. 

Układ 

współrzędnych 
kartezjańskich 

można 

przyjąć  tak,  aby  jego 
początek O był punktem 
obrotu  bryły.  Siła  F

i

 

działająca  na  i-ty  punkt 
wywołuje 

względem 

punktu O moment siły    
            równy: 

O

i

M

i

i

O

i

F

r

M





 

 

W  ogólnym  przypadku  na  bryłę  może  działać  więcej 
sił zewnętrznych. Wtedy należy rozważyć wypadkową 
siłę  zewnętrzną  oraz  wypadkowy  moment  względem 
punktu obrotu O: 













n

1

i

O
i

n

1

i

i

M

M

F

F

Równoważnymi  układami  sił

  nazywamy  takie 

układy  sił  zewnętrznych,  które  mają  równe 
wypadkowe  siły    i  momenty  sił  względem  punktu 
obrotu O .

Załóżmy,  że  istnieją  dwa  układy  sił  równoważne 
względem punktu O (początku układu współrzędnych 
z  poniższego  rysunku)  i  wprowadźmy  dodatkowo 
dowolny punkt P. Wtedy:

OP

r

r





i

P

i

 

 

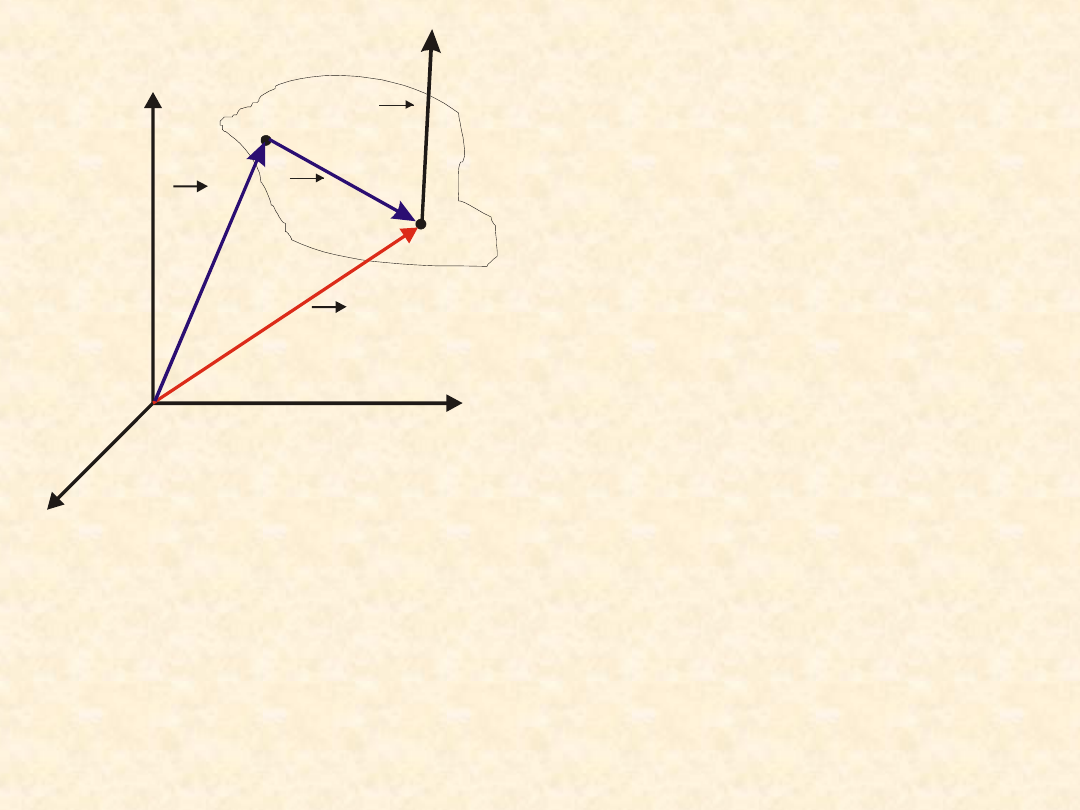
O

x

y

z

P

i

F

i

O P

r

i

r

i

P

Moment  sił  względem 
punktu  P  będzie  więc 
miał postać:

























































n

1

i

i

n

1

i

i

i

n

1

i

i

i

n

1

i

i

P

i

n

1

i

P

i

P

F

OP

F

r

F

OP

r

F

r

M

M

F

OP

M

M







O

P

 

 

Ponieważ  założyliśmy  występowanie  dwóch  układów 
równoważnych  względem  punktu  O  to,  z  równości  siły 
wypadkowej  i  momentu  względem  punktu  O  dla  tych 
dwóch  układów  wynika,  że  moment  siły  względem 
dowolnego  innego  punktu  dla  tych  dwóch  układów 
będzie  taki  sam.  Oznacza  to,  że 

układy  równoważne 

sił  są  układami  równoważnymi  dla  wszystkich 
punktów przestrzeni

.

 

Ponadto,  jeśli  wypadkowa  siła  zewnętrzna  F  =  0,  to 
momenty  sił  są  takie  same  względem  wszystkich 
punktów ponieważ:

 

O

p

M

M 

Wnioski:
  do  danego  układu  sił  można  dodawać  siły  o 

wypadkowej równej zero i zerowym momencie bez 
zmiany ruchu układu, 

 można  przesuwać  punkty  zaczepienia  sił  wzdłuż 

kierunku ich działania nie zmieniając ruchu ciała.

 

 

Parą  sił

  nazywamy  układ  dwóch  sił  równoległych, 

równych 

co 

do 

wartości 

lecz 

przeciwnie 

skierowanych  i  nie  leżących  na  jednej  prostej.  Z 
definicji  pary  sił  wynika,  że  F  =  0,  a  więc  moment 
pary sił jest jednakowy dla wszystkich punktów bryły. 
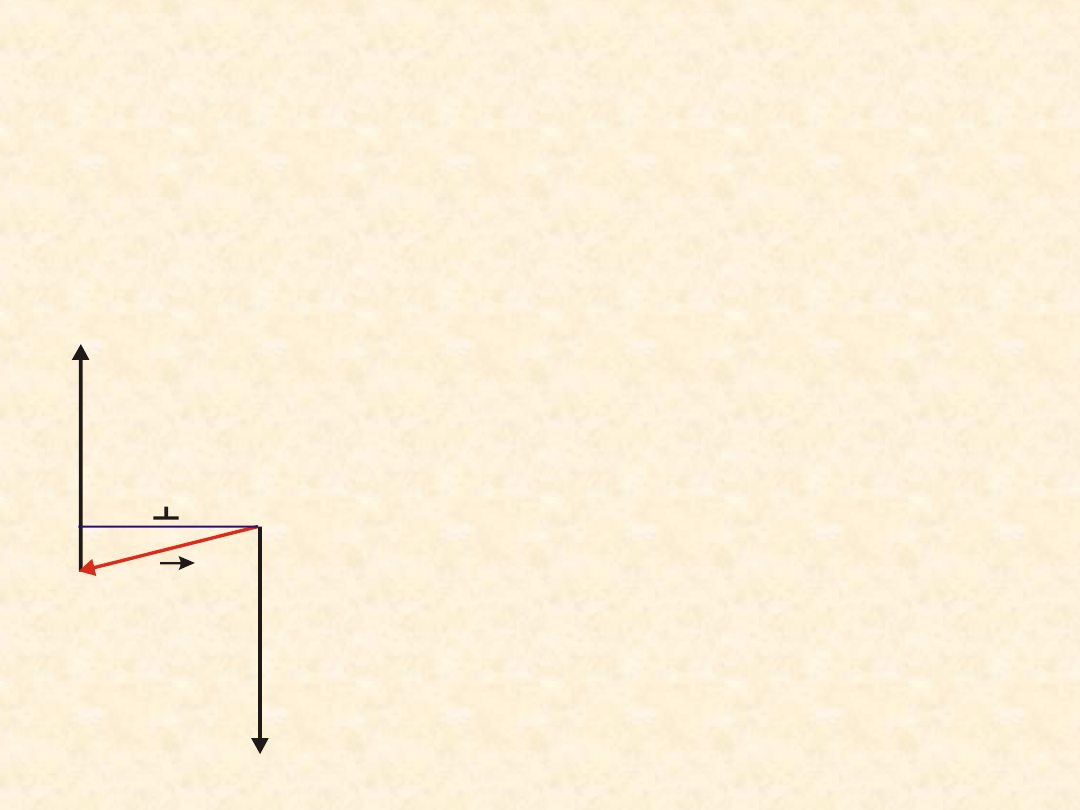
Obliczmy  moment  pary  sił  względem  punktu 
zaczepienia O jednej z sił tworzących parę.

F

- F

O

r

r

 

F

r

F

-

0

F

r

M













Wartość tego momentu pary 
wynosi: 

F

r

M





gdzie  r



  jest  rzutem  wektora  r  na 

kierunek  prostopadły  do  siły  F  i 
nazywa  się  ramieniem  działania 
pary sił. 

 

 

Moment  pary  sił  nie  zależy  zatem  od  jej  położenia 

(przesunięcia), jak również od obrotu w płaszczyźnie 
działania pary. Jeśli ponadto uwzględnimy, że para sił 
nie 

wprowadza 

siły 

wypadkowej, 

możemy 

sformułować 

twierdzenie o redukcji układu sił

:

Dowolny  układ  sił  działający  na  ciało  można 

sprowadzić  do  jednej  siły  równej  sumie  sil 
zewnętrznych działających na ciało i zaczepionej 
na linii działania tej sumy oraz jednej pary sił o 
momencie  równym  momentowi  całkowitemu  sił 
zewnętrznych  działających  na  ciało  względem 
punktu zaczepienia siły wypadkowej.

Z  przeprowadzonych  rozważań  wynika,  że  bryła 

sztywna  pozostanie  w  równowadze  tylko  wtedy,  gdy 
spełnione będą 

warunki równowagi bryły sztywnej

 

czyli równania:

0

i

0





M

F

 

 

Ruch bryły sztywnej

Równanie ruchu postępowego bryły sztywnej

Rozważmy  ruch  postępowy  bryły  sztywnej.  W  takim 
ruchu  prędkości  wszystkich  punktów  bryły,  a  zatem  i 
środka jej masy, są takie same, czyli dla każdego i oraz 
j:

j

i

v

v 

Oznaczając przez r

C

 promień wodzący środka masy, a 

przez v

C

 jego prędkość liniową dostajemy:

 

C

i

v

v 

 

 

Pamiętamy,  że  promień  środka  masy  jest  związany  z 
momentem statycznym bryły S:

m

m

m

n

1

i

i

i

C









r

S

r







n

1

i

C

i

C

m

m

r

r



Różniczkując to wyrażenie dwukrotnie po czasie 
otrzymamy: 

F

p

p

p

a

r



















dt

d

dt

d

dt

d

m

dt

d

m

n

1

i

i

n

1

i

i

C

2

C

2

Otrzymaliśmy  równanie  ruchu  postępowego  bryły 
sztywnej.  Wynika  z  niego,  że  wszystkie  punkty  bryły 
poruszają  się  tak,  jak  środek  jej  masy,  a  jego  ruch 
można  z  kolei  znaleźć  znając  wypadkową  siłę 
działającą na bryłę oraz masę bryły. 

 

 

Pęd w ruchu postępowym bryły sztywnej

Pęd bryły jest równy sumie pędów poszczególnych jej 
punktów, czyli:

C

C

n

1

i

i

C

n

1

i

C

i

n

1

i

i

i

n

1

i

i

m

m

m

m

p

v

v

v

v

p

p





























Pęd  bryły  sztywnej  w  ruchu  postępowym  jest 
więc  równy  pędowi  całkowitej  masy  bryły 
skupionej w jej środku masy.

 

 

Moment  pędu  w  ruchu  postępowym  bryły 
sztywnej

Moment pędu całej bryły jest sumą momentów pędów 
poszczególnych jej punktów, czyli:









C

n

1

i

i

i

n

1

i

C

i

i

n

1

i

i

i

i

n

1

i

i

m

m

m

v

r

v

r

v

r

L

L































Pierwszy czynnik iloczynu jest momentem statycznym 
pierwszego stopnia S, a zatem:

C

C

C

C

C

C

C

m

m

L

p

r

v

r

v

r

L















Moment  pędu  bryły  sztywnej  w  ruchu  postępowym 
jest  zatem  równy  momentowi  pędu  masy  punktu 
materialnego umieszczonego w środku masy tej bryły.

 

 

 

Dla 

dowolnego 

punktu, 

względem 

którego 

obliczamy  moment  pędu  w  środku  masy,  moment 
pędu  bryły  sztywnej  w  ruchu  postępowym 
względem  środka  masy  jest  równy  zeru.  Ponieważ 
druga  zasada  dynamiki  dla  momentu  pędu  ma 
postać  
to  prawdziwy  jest  następujący  warunek  ruchu 
postępowego bryły sztywnej: 

wypadkowy moment 

sił 

względem 

środka 

masy 

w 

ruchu 

postępowym bryły sztywnej jest równy zeru.

M

t

d

d



L

 

 

Energia  kinetyczna  w  ruchu  postępowym  bryły 
sztywnej

Energia  kinetyczna  bryły  sztywnej  jest  sumą  energii 
kinetycznych wszystkich punktów bryły:

2

mv

m

2

v

2

v

m

2

v

m

E

E

2
C

n

1

i

1

2

C

n

1

i

2

C

i

n

1

i

2

i

i

n

1

i

i

k

k



























Energia  kinetyczna  ruchu  postępowego  bryły 
sztywnej  jest  zatem  równa  energii  kinetycznej 
masy bryły skupionej w środku masy.

 

 

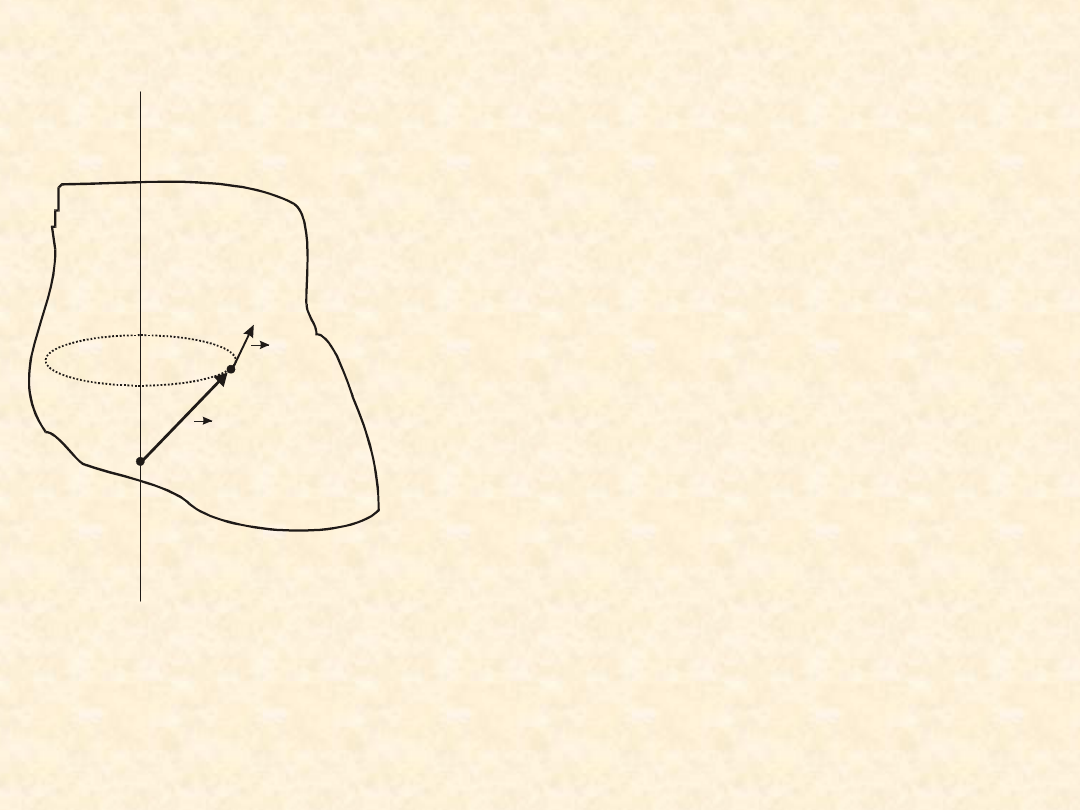
Równanie ruchu obrotowego bryły sztywnej

O

r

i

v

i

i

o ś   o b r o tu

Rozważmy 

ruch 

względem 

stałej 

osi 

przechodzącej 

przez 

środek 

układu 

inercjalnego  o  początku 
O. 

Prędkość 

liniowa 

punktu  i  wynosi  v

i

  oraz 

jest spełnione: 

i

i

i

r

ω

v





Ponieważ  prędkość  kątowa  jest  stała  dla  wszystkich 
punktów  bryły  (ruch  punktów  sztywno  związanych 
względem stałej osi) to:

i

i

r

ω

v





 

 

Pęd bryły sztywnej w ruchu obrotowym

Pęd  bryły  sztywnej  w  ruchu  obrotowym  jest 
(podobnie  jak  w  ruchu  postępowym)  równy  sumie 
pędów poszczególnych punktów bryły:









C

C

C

C

n

1

i

i

i

n

1

i

i

i

i

n

1

i

i

i

m

m

m

m

m

m

p

v

r

ω

r

ω

S

ω

r

ω

r

ω

v

p







































Stąd  wynika  wniosek,  że,  podobnie  jak  w  ruchu 
postępowym,  pęd  ruchu  obrotowego  bryły  sztywnej 
jest  równoważny  pędowi  masy  bryły  skupionej  w  jej 
środku  masy  C.  Jeżeli  oś  obrotu  przechodzi  przez 
środek  masy  bryły,  to  pęd  w  układzie  związanym  ze 
środkiem  masy  jest  równy  zero  ponieważ  moment 
statyczny  S  =  0.  Można  zatem  sformułować 
następujące  twierdzenie: 

Suma  pędów  wszystkich 

punktów  bryły  sztywnej  w  ruchu  obrotowym 
wokół osi przechodzącej przez środek masy bryły 
jest równa zeru.

 

 

Moment 

pędu 

bryły 

sztywnej 

w 

ruchu 

obrotowym

Moment  pędu  bryły  sztywnej  w  ruchu  obrotowym 
jest 

oczywiście 

sumą 

momentów 

pędu 

poszczególnych  punktów  bryły  względem  początku 
przyjętego układu współrzędnych:



































































n

1

i

i

i

i

i

n

1

i

i

1

i

i

n

1

i

i

i

i

n

1

i

i

i

n

1

i

i

m

m

m

r

ω

r

r

ω

r

v

r

p

r

L

L

















i

i

i

m

r

ω

r

L

Jest to ogólna postać momentu pędu względem punktu 
O dla ruchu obrotowego bryły sztywnej względem osi 
przechodzącej przez punkt O. 

 

 

Dla  każdego  punktu  materialnego,  a  więc  i  każdego 
punktu  bryły,  spełniona  jest  zależność  wynikająca  z 
drugiej zasady dynamiki:

M

L



t

d

d

i

i

t

d

d

M

L





ale  całkowity  moment  sił  względem  punktu  O 
działający  na  bryłę  jest  równy  sumie  momentów  sił 
względem  tego  punktu  działających  na  każdy  punkt 
bryły, czyli: 

t

d

d

dt

d

t

d

d

n

1

i

i

n

1

i

i

n

1

i

i

L

L

L

M

M





















Zatem dla dowolnego ruchu obrotowego druga zasada 
dynamiki przyjmuje następującą postać ogólną: 

t

d

dL

M 

 

 

Energia  kinetyczna  ruchu  obrotowego  bryły 
sztywnej

Energia  kinetyczna  ruchu  obrotowego  bryły  sztywnej 
jest 

oczywiście 

sumą 

energii 

kinetycznych 

poszczególnych punktów bryły: 









































n

1

i

i

i

i

n

1

i

2

i

i

i

n

1

i

2

i

i

n

1

i

i

k

k

2

m

2

m

2

v

m

E

E

r

ω

r

ω

r

ω

Wykorzystując tożsamość wektorową:









C

B

A

C

B

A











i

i

;

;

r

ω

C

r

B

ω

A









otrzymujemy  ogólny  wzór  na  energię  kinetyczną 
bryły sztywnej:





















2

2

m

2

m

2

2

m

E

n

1

i

i

n

1

i

i

i

i

n

1

i

i

i

i

n

1

i

i

i

i

k

ω

L

L

ω

v

r

ω

r

ω

r

ω

r

ω

r

ω





































 

 

Każdy  ruch  bryły  sztywnej  można  rozłożyć  na  ruch 
postępowy  i  obrotowy  względem  stałej  osi.  Należy 
wtedy  jednocześnie  wykorzystać  prawa  rządzące 
oboma rodzajami ruchów. 

Moment  bezwładności  bryły  sztywnej  wykonującej 
ruch  obrotowy  względem 

sztywnej  osi

  ma  moment 

pędu  względem  dowolnego  punktu  osi  obrotu  o 
niezerowych  składowych  w  kierunku  wszystkich  osi 
układu  współrzędnych.  Inaczej  mówiąc, 

kierunek 

wektora momentu pędu nie pokrywa się z kierunkiem 
wektora prędkości kątowej

. 

 

 

Szczególna postać II zasady 

dynamiki dla ruchu obrotowego 

względem osi symetrii

Druga zasada dynamiki w przypadku momentów 
sił ma postać 

M

L



t

d

d

Po  podstawieniu  momentu  pędu  dla  bryły  w  ruchu 
obrotowym względem sztywnej osi otrzymujemy:









M

k

j

i











z

yz

xz

I

I

I

dt

d

 

 

M

k

k

j

j

i

i































































t

d

d

t

d

d

I

t

d

d

dt

d

I

t

d

d

t

d

d

I

z

yz

xz

s

s

s

,

,

k

k

j

i

j

j

i

i

s

s





















cos

sin

sin

cos

Łatwo  zauważyć, 
że:

Na tej 
podstawie

 

0

t

d

d

t

d

d

t

d

d

sin

t

d

d

cos

t

d

d

dt

d

dt

d

cos

t

d

d

sin

t

d

d

s

s

s

s









































k

i

j

i

j

j

j

i

i

 

 

Wstawiając  te  wyrażenia  do  wzoru  na  pochodną 
momentu pędu bryły 

M

k

i

j

j

i























z

2

yz

yz

2

xz

xz

I

I

I

I

I



 



M

k

j

i























z

xz

2

yz

xz

yz

2

I

I

I

I

I

k

j

i

M

z

y

x

M

M

M







Powyższa równość będzie spełniona tylko 
wtedy, gdy: 





z

z

xz

yz

2

y

xz

yz

2

x

I

M

,

I

I

M

,

I

I

M























 

 

Zauważmy,  że  nawet  dla    =  0  (ruch  obrotowy 
jednostajny)  występują  niezerowe  momenty  sił 
względem  osi  Ox  i  Oy  wynikające  z  niezerowych 
momentów  dewiacji  ciała.  Jeżeli  oś  obrotu  jest 

swobodna

,  co  oznacza  możliwość  zmiany  jej 

kierunku,  to  momenty  sił  M

x

  i  M

y

  doprowadzą  do 

przyjęcia  takiego  ułożenia  osi,  w  którym  momenty 
dewiacyjne są równe zero. W takiej sytuacji moment 
pędu ma tylko składową zgodną z osią obrotu, a więc 
i  z  kierunkiem  prędkości  kątowej,  z  czego  wynika 
wniosek

W  trakcie  ruchu  obrotowego  bryły  sztywnej 
względem osi swobodnej kierunki momentu pędu 
bryły  i  prędkości  kątowej  są  zgodne.

  W  innym 

wypadku zasada ta nie jest spełniona.

Oś  swobodna  jest  osią  symetrii  ciała; 

osie  symetrii 

nazywamy  często  głównymi  osiami  bezwładności 
ciała.  Obrót  ciała  względem  jednej  z  głównej  osi 
bezwładności jest „trwały”

  

 

 

Dla  wszystkich  takich  ruchów  moment  pędu  bryły 
względem dowolnego punktu osi obrotu ma postać:

ω

L I



czyli 

druga 

zasada 

dynamiki 

dla 

ruchu 

obrotowego  bryły  sztywnej

  w  takich  szczególnych 

przypadkach przyjmuje postać: 

M

ε

M

ω





I

t

d

d

I

gdzie M jest składową momentu siły skierowaną 
zgodnie z osią obrotu bryły

 

 

 

Energia kinetyczna w takim ruchu wynosi: 

2

I

L

2

1

2

1

E

2

k











ω

L

a  pęd  jest  oczywiście  równy  pędowi  środka  masy 
bryły.  Jeżeli  oś  obrotu  przechodzi  przez  środek  masy 
(będzie osią symetrii), to: 

0



p