.

.

NIEKTÓRE ROZKŁADY

ZMIENNYCH LOSOWYCH

. NIEKTÓRE ROZKŁADY

ZMIENNEJ LOSOWEJ

SKOKOWEJ

.

.

Rozkład dwumianowy

(Bernoulliego)

R ozw ażm y w y nik badania jednej sztuki w y lo so w anej ze zbioru w y robó w , gdy jest

stosow ana klasy fi kacja alternaty w na na sztuki dobre i niedobre. F rakcję sztuk niedo bry ch w

zbiorze w y ro bów , nazy w ana w adliw ością tego zbio ru, oznacza się przez w . P raw do po do bieństw o

w y loso w ania sztuki niedobrej jest ró w ne w , a praw dopodo bieństw o w y lo so w ania sztuki do brej

jest ró w ne 1-w . J eżeli jest spełnio na podw ó jna nierów ność 0<w < 1 i sztukom niedobry m
przy porządko w ać w arto ść x

1

, a sztuko m dobry m w artość x

2

x

1

to w y nik badania w y lo sow anej

sztuki jest dw upunkto wą zm ienną losow ą X , przy jm ującą w arto ści x

1

i x

2

z

praw dopodo bieństw am i:

P X x

w

dla

w

P X x

w

(

)

(

)





 



 

1

2

0

1

1

W prakty ce przy jm uje się x

1

= 1 o raz x

2

= 0 i w ó w czas w y nik badania w y losow anej sztuki

jest zero- jedy nkową zm ienna loso w ą X o ro zkładzie określo ny m praw dopodo bieństw am i:

P X

w

dla

w

P X

w

(

)

(

)

 

 



 

1

0

1

0

1

W a r t oś ć o c z e k i w a n a i w a r i a n c j a z m i e n n e j l o s o w e j X o r o z kł a d z i e z e r o - j e d y n k o w y m

w y n o s zą o d p o w i e d n i o :

E X

w

V X

w

w

( )

( )

(

)





 

1

Z a kł a d a j ą c , ż e z p a r t i i w y r o b ó w o w a d l i w o ś c i w p o b r a n o p r ó b kę l o s o w ą p r o s t ą o l i c z n o ś c i

n s z t u k , w w y n i k u b a d ań p o s z c z e g ó l n y c h s z t u k u z y s k u j e s i ę w z a j e m n i e n i e z a l e ż n e z m i e n n e

l o s o w e X

1

, X

2

, . . . . , X

n

o j e d n a k o w y m r o z kł a d z i e z e r o - j e d y n k o w y m k aż d a . L i c z b a s z t u k

n i e d o b r y c h w p r ó b c e j e s t z m i e n ną l o s o w ą ( s t a t y s t y k ą ) Z o k r eś l o n ą w z o r e m :

Z

X

i

i

n







1

a c zę s t o ś ć z d a r z e n i a s z t u k a n i e d o b r a , c z y l i f r a k c j a s z t u k n i e d o b r y c h w p r ó b c e j e s t z m i e n ną

l o s o wą ( s t a t y s t y k ą ) H o k r eś l o n ą w z o r e m :

H

Z

n

n

X

i

i

n











1

1

p r z y c z y m X

i

j e s t w y n i k i e m b a d a n i a i - t e j s z t u k i w p r ó b c e ( 0 l u b 1 ) . S t a t y s t y k a Z m oż e

p r z y j m o w ać w a r t o ś c i z e z b i o r u l i c z b { 0 , 1 , 2 , . . . , n } n a t o m i a s t s t a t y s t y k a H = Z / n m oż e

p r z y j m o w ać w a r t o ś c i z e z b i o r u l i c z b { , , , . . . . . ,

, }

0

1 2

1

1

n n

n

n



p r z y c z y m p r a w d o p o d o b i eń s t w a

z d a r z eń Z = k o r a z H = k / n są j e d n a k o w e i o k r e ś l o n e w z o r e m :

P Z

k n w

P H

k

n

n w

n

k

w

w

d l a

w

o r a z k

n

k

n k

(

; ; )

(

; ; )

(

)

, , . . . . ,

( )











 









1

0

1

0 1

g d z i e

( ) (

)

!

! (

) !

n

k

n

n

k

n

k

n

k











j e s t l i c z bą r ó ż n y c h k o m b i n a c j i

k s z t u k n i e d o b r y c h w p r ó b c e o l i c z n oś c i n ( t a b l i c a 3 . 1 ) . R o z kł a d

p o w yż s z y n o s i n a z w ę r o z k ł a d u B e r n o u l i e g o l u b d w u m i a n o w e g o .

P ra w d o p o d o b ień s tw o , ż e w p ró b c e o lic z n o ś c i n bę d z ie c o n a j w y ż e j z s z tu k n ie d o b ry c h

lu b , ż e c z ę s to ś ć z d a rz e n ia s ztu k a n ie d o b r a bę d z ie c o n a j w y ż e j h = z /n je s t o k reś lo n e w z o re m :

P Z z n w

P H

z

n

n w

P Z

k n w

k

z

(

; ; )

(

; ; )

(

; ; )















0

D o o b lic z eń w y g o d n ie j e s t k o rz y s ta ć z e w z o ru re k u re n c y j n e g o :

P Z k

n w

n k

k

w

P Z

k n w

k

z

(

; ; )

(

)

(

) (

)

(

; ; )

 





  









1

1

1

0

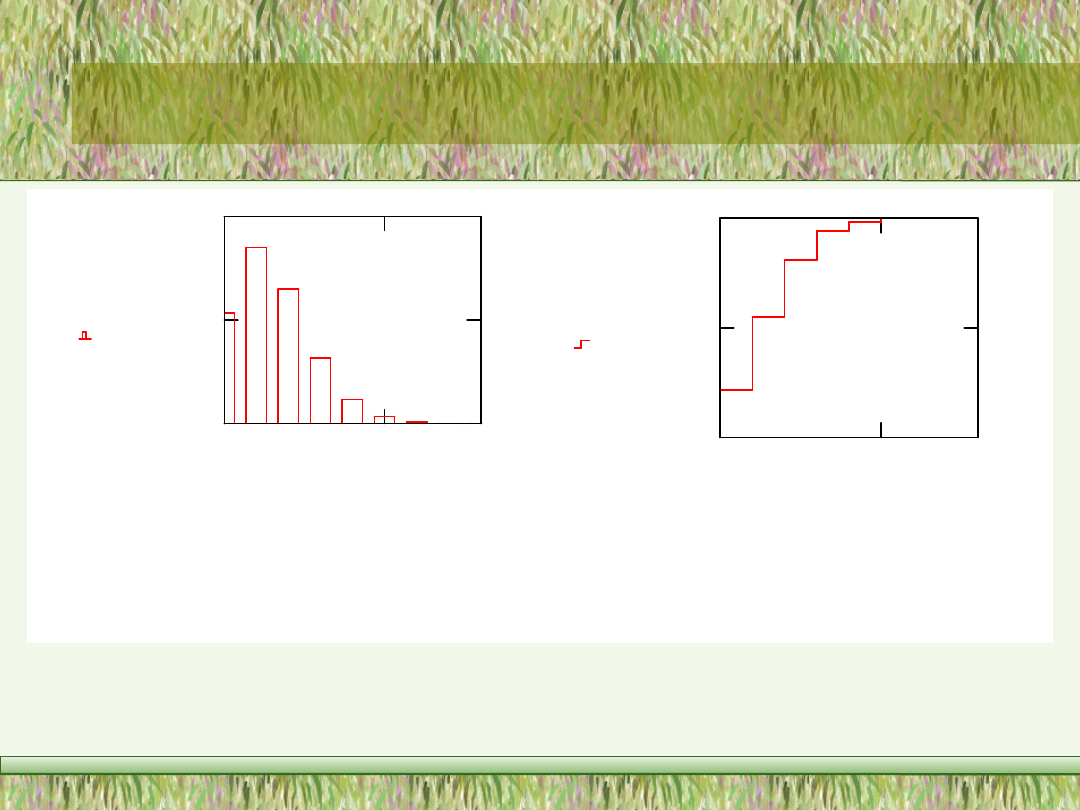
P rz y kła d ro z k ła d u P ( Z = k ) p o d a n o n a ry s . 4 .1 a ro z kła d u P ( Z



k ) n a ry s . 4 .2 .

0

5

0

0.2

0.4

dbinom

(

)

,

,

k np

k

0

5

0

0.5

1

pbin om

(

)

,

,

knp

k

Rys. 4.1. Przykład funkcji prawdopodobień-

stwa rozkładu dwumianowego: n = 30, w =

0.05

Rys. 4.2. Przykład prawdopodobieństwa
P(Zk) rozkładu dwumianowego: n = 30, w =

0.05

W a r toś c i o c z e k i w a n e i w a r i a n c j e s ta ty s ty k Z i H m a ją p o s ta ć :

E Z

n w

V Z

n w

w

E H

w

V H

w

w

n

( )

( )

(

)

( )

( )

(

)

 

   





 

1

1

a w s p ół c z y n n i k a s y m e tr i i ( s k o ś n o ś c i ) r o z k ł a d u d w u m i a n o w e g o m a w a r toś ć :

 





  

1 2

1

w

n w

w

(

)

S ta ty s ty k a H = Z / n bę d ą c a f r a k c j ą s z tu k n i e d o b r y c h w p r ó b c e l o s o w e j o l i c z n o ś c i n j e s t

s to c h a s ty c z n i e z b i eż n a d o w a d l i w o ś c i w r e p r e z e n to w a n e g o p r z e z tę p r ó b k ę z b i o r u w y r o b ó w .

O g ó l n i e u j m u j e to p r a w o w i e l k i c h l i c z b B e r n o u l l i e g o , k tó r e m ó w i , ż e c z ę s to ś ć z d a r z e n i a

l o s o w e g o w n j e d n a k o w y c h n i e z a l eż n y c h d o ś w i a d c z e n i a c h j e s t s to c h a s ty c z n i e z b i e ż n a d o

p r a w d o p o d o b i eń s tw a te g o z d a r z e n i a . F r a k c j a s z tu k n i e d o b r y c h w z b i o r z e , c z y l i w a d l i w o ś ć te g o

z b i o r u w , j e s t p r a w d o p o d o b i eń s tw e m z d a r z e n i a p o l e g a j ą c e g o n a w y l o s o w a n i u s z tu k i n i e d o b r e j , a

f r a k c j a s z tu k n i e d o b r y c h w p r ó b c e l o s o w e j p r o s te j o l i c z n oś c i n , c z y l i s ta ty s ty k a H = Z / n , j e s t

c zę s to ś c i ą te g o z d a r z e n i a w n n i e z a l eż n y c h j e d n a k o w y c h d o ś w i a d c z e n i a c h , p o l e g a j ą c y c h n a

b a d a n i u s z tu k w y l o s o w a n y c h z d a n e g o z b i o r u w y r o b ó w .

W s p ół c z y n n i k a s y m e tr i i  r o z kł a d u d w u m i a n o w e g o j e s t d o d a tn i p r z y w < 0 .5 i u j e m n y

p r z y w > 0 . 5 . P r z y w = 0 .5 w y n o s i  = 0 . M o d uł    j e s t f u n k c ją m a l e j ą c ą w a r to ś c i n i r o s ną c ą
w a r toś c i  0 .5 - w  . P r z y d o s ta te c z n i e d uż y m n m oż n a a p r o k s y m o w a ć r o z k ł a d d w u m i a n o w y

r o z kł a d e m n o r m a l n y m ( G a u s s a ) . J e s t to d o p u s z c z a l n e d l a ty m m n i e j s z e g o n i m m n i e j s z a j e s t
w a r toś ć  0 .5 - w  .

S u m a k n i e z a l eż n y c h s ta ty s ty k Z

1

, Z

2

, .. .. , Z

k

o r o z kł a d a c h d w u m i a n o w y c h z p a r a m e tr a m i

n

1

, n

2

, .. .. , n

k

i ty m s a m y m p a r a m e tr e m w m a r o z kł a d d w u m i a n o w y o p a r a m e tr a c h n = n

1

+ n

2

+

.. .. + n

k

o r a z w . M ó w i s ię , ż e r o z k ł a d d w u m i a n o w y j e s t a d d y ty w n y . Z a d d y ty w n oś c i r o z k ł a d u

d w u m i a n o w e g o k o r z y s ta s ię p r z y a n a l i z i e w y n i k ó w b a d a ń d w u l u b w i ę c e j n i e z a l e ż n y c h p r ó b e k

l o s o w y c h z te g o s a m e g o z b i o r u w y r o b ó w , r o z w aż a j ą c p r ó b k ę l o s o w ą ł ą c z n ą o l i c z n o ś c i r ó w n e j

s u m i e l i c z n oś c i p o s z c z e g ó l n y c h p r ó b e k i l i c z b i e s z tu k n i e d o b r y c h r ó w n e j s u m i e l i c z b s z tu k

n i e d o b r y c h w p o s z c z e g ó l n y c h p r ó b k a c h .

.

.

Rozkład Poissona

P r z y d uż e j w a r t o ś c i n i m ał e j w a d l i w o ś c i w , p r a k t y c z n i e p r z y n > 2 0 o r a z w < 0 . 2 r o z kł a d

d w u m i a n o w y m oż n a a p r o k s y m o w a ć r o z k ł a d e m P o i s s o n a o f u n k c j i p r a w d o p o d o b i eń s t w a :

P Z

k

k

e

d l a

o r a z k

g d z i e

n w

k

(

; )

!

, , , . . . .



























0

0 1 2

A p r o k s y m a c j a t a k a uł a t w i a o b l i c z e n i a , m o ż n a b o w i e m k o r z y s t a ć z ł a t w o d o s t ę p n y c h

t a b l i c r o z kł a d u P o i s s o n a ( t a b . 4 . 1 ) . K o r z y s t a ją c z t a b l i c w y z n a c z a s i ę p r a w d o p o d o b i e ń s t w o





P Z

k

P Z

k

P Z

k

(

; )

(

; )

;



















1

P r z y kł a d 4 . 1

Z d uż e j p a r t i i w y r o b ó w o w a d l i w o ś c i w = 5 % p o b r a n o p r ó b kę l o s o w ą o l i c z n o ś c i n = 4 0 s z t u k .

J a k i e j e s t p r a w d o p o d o b i eń s t w o , ż e w p r ó b c e t e j b ę d ą c o n a j w y ż e j 3 s z t u k i n i e d o b r e ? J a k i e j e s t

p r a w d o p o d o b i eń s t w o , ż e w p r ó b c e b ę d ą d o k ł a d n i e 3 s z t u k i n i e d o b r e ?

O d p o w i e dź n a p i e r w s z e p y t a n i e u z y s k u j e s i ę b e z p o ś r e d n i o z t a b l i c y 4 . 1

 = n w = 4 0 0 . 0 5 = 2

D l a  = 2 i k = 3 z t a b l i c y 4 . 1 o d c z y t u j e s ię :

P ( Z  3 ;  = 2 ) = 0 . 8 5 7

Prawdopodobieństwo, że w próbce będą co najwyżej 3 sztuki niedobre wynosi 0.857 (85.7%).

Odpowiedź na drugie pytanie uzyskamy jeśli od powyższego wyniku odejmiemy

prawdopodobieństwo tego, że w próbce będą co najwyżej 2 sztuki niedobre:

P(Z  2;  = 2) = 0.677

stąd

P(Z = 3;  = 2) = 0.857 - 0.677 = 0.18

Prawdopodobieństwo zdarzenia, że w próbce będą dokładnie 3 sztuki niedobre wynosi 0.18 (18

%).

Aproksymacja rozkładu dwumianowego nie jest jedynym zastosowaniem rozkładu

Poissona. Jeżeli przykładowo, czas pracy urządzenia wynosi t, a prawdopodobieństwo chwilowej,
samo usuwalnej niesprawności w jednostce czasu wynosi



to liczba niesprawności w przedziale

czasu (0, t



ma rozkład Poissona o parametrach



=



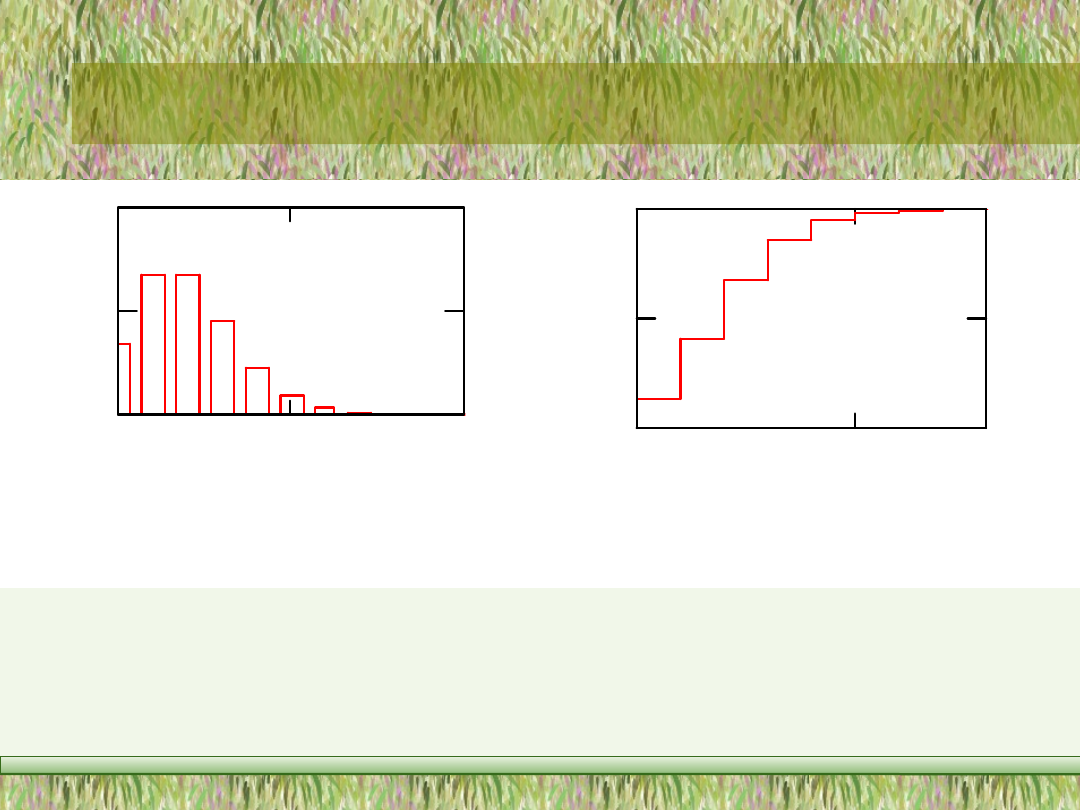
t. Przykład rozkładu Poissona podają

rysunki 4.3 i 4.4.

0

5

10

0

0.2

0.4

0

5

0

0.5

1

R

ys

. 4

.3

. F

u

n

k

c

ja

p

r

a

w

d

o

p

o

d

o

b

ień

s

tw

a

P

(Z

=

k

) ro

zkła

d

u

P

o

is

so

n

a

d

la



=

2

R

ys

. 4

.4

. D

ys

tr

yb

u

a

n

ta

ro

zkła

d

u

P

o

is

so

n

a

P

(Z



k

) d

la



=

2

P

o

d

s

ta

w

o

w

e

wła

ś

c

iw

o

ś

c

i r

o

z

k

ła

d

u

P

o

is

s

o

n

a

są

n

a

s

tę

p

u

ją

c

e

:



W

a

r

toś

ć

o

c

z

e

k

iw

a

n

a

i w

a

r

ia

n

c

ja

s

ą

s

o

b

ie

r

ó

w

n

e

i r

ó

w

n

e

p

a

r

a

m

e

tr

o

w

i



, c

z

y

li

E

(Z

) =

V

(Z

) =





W

s

p

ółc

z

y

n

n

ik

a

s

y

m

e

tr

ii





1



je

s

t z

a

w

s

z

e

d

o

d

a

tn

i i m

a

le

je

p

r

z

y

w

z

r

oś

c

ie

p

a

r

a

m

e

tr

u



,

dą

ż

ą

c

d

o

0

p

r

z

y



dą

ż

ą

c

y

m

d

o

n

ie

s

k

o

ń

c

z

o

n

o

ś

c

i.



P

r

z

y

d

o

s

ta

te

c

z

n

ie

d

uż

y

m

p

a

r

a

m

e

tr

z

e



r

o

z

kła

d

P

o

is

s

o

n

a

m

oż

n

a

a

p

r

o

k

s

y

m

o

w

a

ć

r

o

z

k

ła

d

e

m

n

o

r

m

a

ln

y

m

.



R

o

z

kła

d

P

o

is

s

o

n

a

je

s

t a

d

d

y

ty

w

n

y

, c

z

y

li ż

e

s

u

m

a

n

ie

z

a

le

ż

n

y

c

h

z

m

ie

n

n

y

c

h

lo

s

o

w

y

c

h

Z

1

, Z

2

, .... ,

Z

k

o

r

o

z

kła

d

a

c

h

P

o

is

s

o

n

a

z

p

a

r

a

m

e

tr

a

m

i



1

,



2

, .... ,



k

m

a

r

o

z

kła

d

P

o

is

s

o

n

a

o

p

a

r

a

m

e

tr

z

e



=



1

+



2

+

.... +



k

.

.

.

Rozkład geometryczny

W p r a k t y c e c zę s t o z a m i a s t b a d a ć p r ó b k ę l o s o w ą o u s t a l o n e j l i c z n o ś c i b a d a s i ę k o l e j n o

w y l o s o w a n e s z t u k i , aż t r a fi s i ę n a s z t u k ę n i e d o b r ą l u b n a o k r e ś l o n ą l i c z b ę s z t u k n i e d o b r y c h . J e s t

w ó w c z a s u s t a l o n a l i c z b a s z t u k n i e d o b r y c h w p r ó b c e k n a t o m i a s t l i c z n oś ć p r ó b k i j e s t z m i e n n ą

l o s o wą o z n a c z o n ą p r z e z N .

Z ał ó ż m y , ż e w a d l i w o ś ć b a d a n e j p a r t i i w y r o b ó w j e s t r ó w n a

w i b a d a n i a p r o w a d z i s ię d o

s t w i e r d z e n i a j e d n e j s z t u k i n i e d o b r e j , z a p e w n i a ją c j e d n a k o w e p r a w d o p o d o b i e ń s t w o w y l o s o w a n i a

d l a w s z y s t k i c h s z t u k w d a n e j p a r t i i w y r o b ó w . L i c z n oś ć p r ó b k i N j e s t w ó w c z a s z m i e n ną l o s o w ą

p r z y j m u ją c ą w a r t o ś c i n a t u r a l n e n = 1 , 2 , . . . . z p r a w d o p o d o b i eń s t w a m i :

....

,

2,

1

1

0

)

1(

)

;

(

1

















n

oraz

w

dla

w

w

w

n

N

P

n

g d yż p r a w d o p o d o b i e ń s t w o w y l o s o w a n i a s z t u k i n i e d o b r e j j e s t r ó w n e w a d l i w o ś c i p a r t i i w , a

p r a w d o p o d o b i eń s t w o w y l o s o w a n i a

n - 1 s z t u k d o b r y c h j e s t ( 1 - w )

n - 1

. R o z kł a d o k r e ś l o n y

p o w yż s z y m w z o r e m n a z y w a s i ę r o z k ł a d e m g e o m e t r y c z n y m o w a r t o ś c i o c z e k i w a n e j i w a r i a n c j i

z m i e n n e j l o s o w e j N o k r eś l o n y c h w z o r a m i :

E N

w

o r a z

V N

w

w

( )

( )







1

1

2

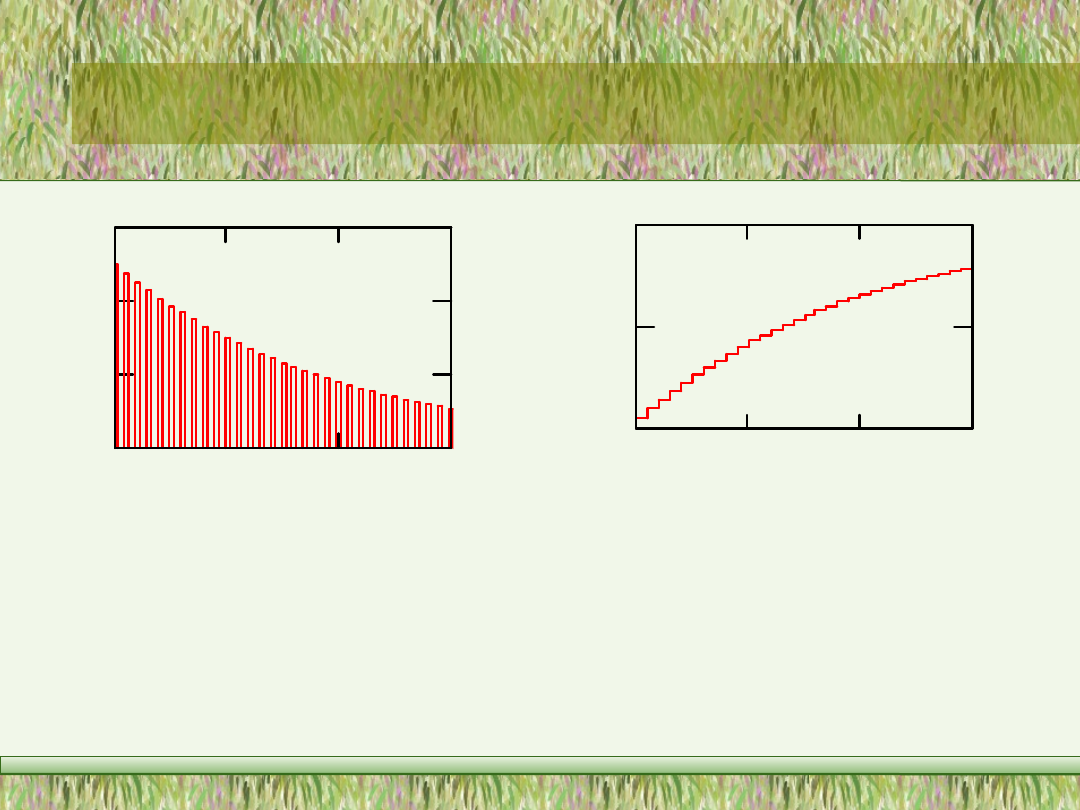
P r z y kł a d f u n k c j i p r a w d o p o d o b i e ń s t w a i d y s t r y b u a n t y p o k a z a n o o d p o w i e d n i o n a r y s . 4 . 5 i

4 . 6 .

0

10

20

30

0

0.02

0.04

0.06

0

10

20

30

0

0.5

1

R

ys. 4

.5

. F

u

n

k

cja

p

ra

w

d

o

p

o

d

o

b

ień

stw

a

ro

z-

kła

d

u

g

e

o

m

e

tryc

zn

e

g

o

d

la

w

=

0

.0

5

R

ys. 4

.6

D

ystryb

u

a

n

ta

ro

zkła

d

u

g

e

o

m

e

trycz-

n

e

g

o

d

la

w

=

0

.0

5

.

.

Rozkład Pascala

J eż e l i b a d a n i a p r o w a d z i s i ę d o s t w i e r d z e n i a k s z t u k n i e d o b r y c h to l i c z n oś ć p r ó b k i j e s t

z m i e n ną l o s o w ą N o r o z kł a d z i e P a s c a l a :

P N

n k w

n
k

w

w

p r z y

w

o r a z

n

k k

k

k

n k

(

; ; )

(

)

,

,

, . . . . .

(

)









 















1

1

1

0

1

1

2

g d z i e

(

)

n

k





1

1

j e s t l i c z bą k o m b i n a c j i k - 1 s z t u k n i e d o b r y c h wś r ó d n - 1 s z t u k z b a d a n y c h p r z e d

s tw i e r d z e n i e m k - te j s z tu k i n i e d o b r e j . W a r t oś ć o c z e k i w a n a i w a r i a n c j a z m i e n n e j l o s o w e j N o

r o z kł a d z i e P a s c a l a w y n o s z ą o d p o w i e d n i o :

E N

k

w

o r a z V N

k

w

w

( )

( )

(

)





 

1

2

R o z kł a d g e o m e tr y c z n y j e s t s z c z e g ó l n y m p r z y p a d k i e m r o z k ł a d u P a s c a l a p r z y k = 1 .

R o z kł a d P a s c a l a o p a r a m e tr a c h k i w j e s t s u mą k n i e z a l eż n y c h z m i e n n y c h l o s o w y c h o

j e d n a k o w y m r o z kł a d z i e g e o m e t r y c z n y m z p a r a m e t r e m w .

P r z y kł a d 4 . 2 .

Z e z b i o r u w y r o b ó w o b a r d z o d uż e j l i c z n o ś c i i w a d l i w o ś c i w = 1 0 % l o s o w a n o p o j e d n e j s z t u c e i

p o d d a w a n o b a d a n i o m . J a k i e j e s t p r a w d o p o d o b i eń s t w o , ż e d l a t r a fi e n i a n a s z t u k ę n i e d o b r ą

t r z e b a z b a d ać 5 s z t u k ? J a k i e j e s t p r a w d o p o d o b i e ń s t w o , ż e d l a t r a fi e n i a n a 2 s z t u k i n i e d o b r e

t r z e b a p r z e b a d ać 5 s z t u k ?

N a p i e r w s z e p y t a n i e o d p o w i e dź d a j e r o z k ł a d g e o m e t r y c z n y :

P ( X = 5 ; w = 0 . 1 ) = 0 . 1 ( 1 - 0 . 1 )

5 - 1

= 0 . 0 6 5 6

N a d r u g i e p y t a n i e o d p o w i e dź d a j e r o z k ł a d P a s c a l a :

P ( X = 5 ; k = 2 , w = 0 . 1 ) =

(

)

5

1

2

1





0 . 1

2

( 1 - 0 . 1 )

5 - 2

= 0 . 0 2 9 2

R o z kł a d P a s c a l a z m i e n n e j l o s o w e j N i r o z kł a d d w u m i a n o w y z m i e n n e j l o s o w e j Z są

z w ią z a n e z a l e ż n o ś c i ą :

P N

n k w

w P Z

k

n

w

(

; , )

(

;

, )













1

1

s ką d

P N

n k w

w P Z

k

n w

(

; , )

(

; , )













1

1

g d z i e N - 1 j e s t l i c z bą z b a d a n y c h s z t u k p o p r z e d z a j ą c y c h k - tą s z t u kę n i e d o b r ą .

Z e z w ią z k u m i ę d z y r o z k ł a d e m d w u m i a n o w y m , a r o z k ł a d e m P o i s s o n a w y n i k a

p r z y b l iż o n y z w i ą z e k m i ę d z y r o z k ł a d a m i P a s c a l a i P o i s s o n a :

P N

n k w

w P Z

k

n w

w

k

n

e

k

k

n w

(

; , )

(

;

)

(

) !



























 

1

1

1

1



sł u s z n y d l a w < 0 . 2 o r a z n > k . P r z y m ał y c h w a r t o ś c i a c h w r o z kł a d P a s c a l a m o ż n a

a p r o k s y m o w ać r o z k ł a d e m E r l a n g a , a r o z k ł a d g e o m e t r y c z n y r o z k ł a d e m w y k ł a d n i c z y m .