Rekurencje
Rekurencje
Króliki Fibonacciego
Fibonacci (Leonardo z Pizy; ur. około 1175 r. -
zm. 1250 r.) – włoski matematyk. Znany jako:
Leonardo Fibonacci, Filius Bonacci (syn
Bonacciego), Leonardo Pisano (z Pizy).
1202 rok – jak rozmnażają się króliki?
Króliki dorastają w ciągu jednego miesiąca.
Zawsze rodzi się jedna para królików (jeden
męski i jeden żeński królik).
Króliki nigdy nie umierają.
5. Rekurencje.
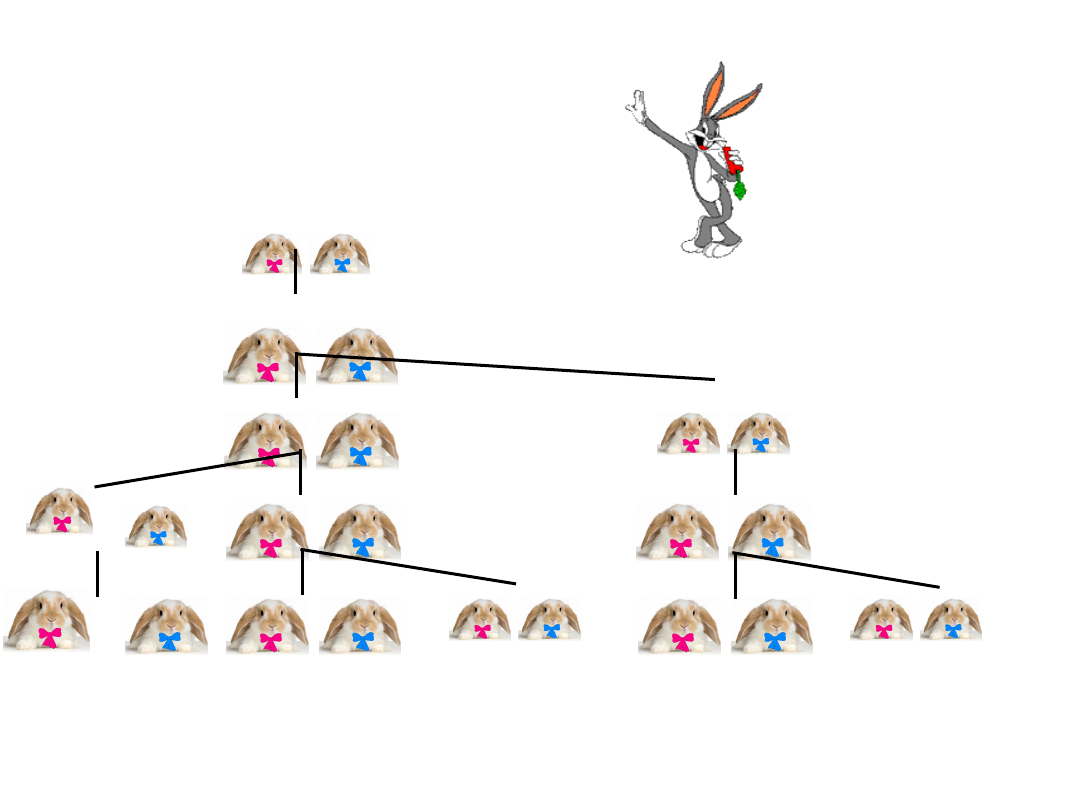
Króliki
Liczba par królików
1
1
2
3
5
Ciąg Fibonacciego
Liczba par królików na początku każdego
miesiąca wynosi:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…
Są to kolejne liczby ciągu Fibonacciego.
Dwie pierwsze liczby tego ciągu to 1.
Każda następna jest sumą dwóch
poprzednich.
Jeśli Fn oznacza n-tą liczbę Fibonacciego, to
F
n
=F
n -1
+F
n -2
;
F
0
=1, F
1
=1.
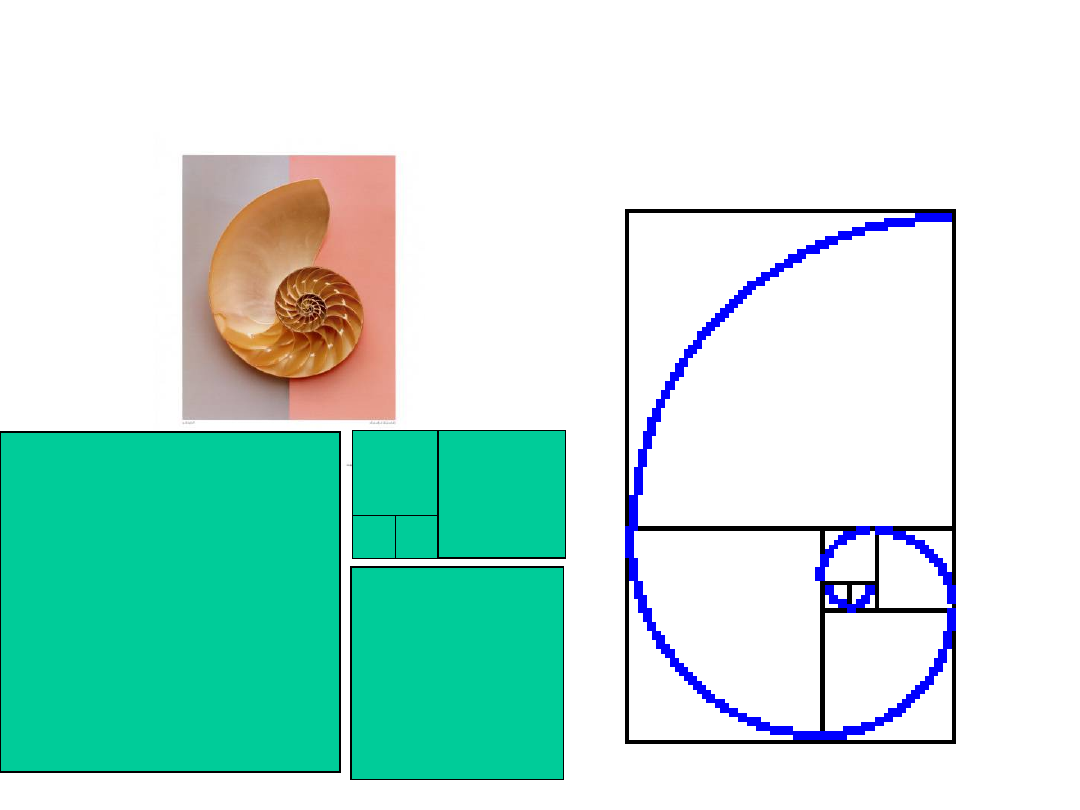
Kwadraty Fibonacciego i
muszle
1
2
3
5
8
1
Muszle - galeria
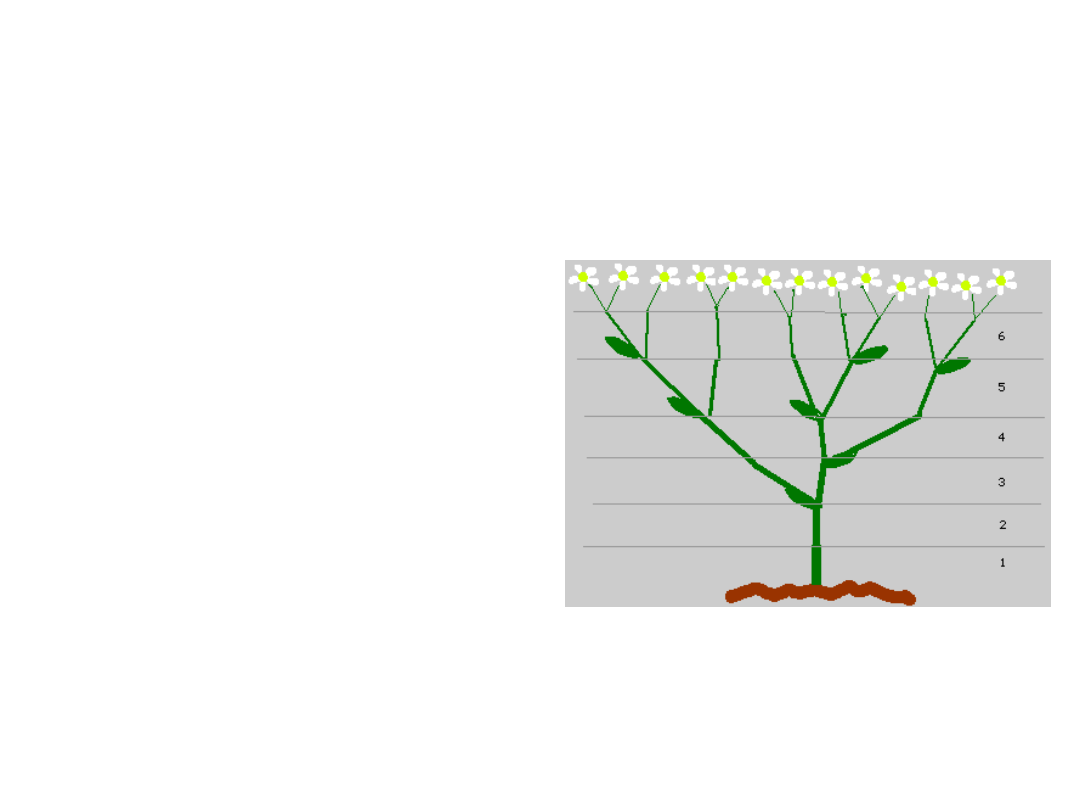
Liczby Fibonacciego a
wzrost roślin
Łodyga potrzebuje
dwóch miesięcy aby
wypuścić nową odnóżkę,
potem wypuszcza nowe
pędy co miesiąc.
Liczba łodyg w każdym
miesiącu stanowi kolejną
liczbę Fibonacciego.
Biolodzy potrafią
wskazać rośliny, które
tak się rozmnażają, np.
dąb lub krwawnik
kichawiec
(sneezwort).
1
1
2
3
5
8
Fibonacci a słoneczniki
Zliczając spirale prawo
i lewoskrętne
utworzone z ziaren
słonecznika
otrzymujemy dwie
sąsiednie liczby
Fibonacciego.
Fibonacci a szyszki
Zliczamy spirale prawo
i lewoskrętne
utworzone z łusek
szyszki od miejsca
przytwierdzenia do
gałązki.
Jeszcze więcej szyszek
5
8
Ananasy
Łuski ananasa są
sześciokątami,
dlatego możemy
wyróżnić trzy
rodzaje spiral.
13
8
5
Liczby Fibonacciego w
płatkach kwiatów
Kalia (white calla lily)– 1 płatek
Ostromlecz (euphorbia ) – 2 płatki
Trójlist (trillium) – 3 płatki
Liczby Fibonacciego w
płatkach kwiatów
Goździki – 5 płatków
Dzika róża – 5 płatków
Orlik (columbine) – 5 płatków
Liczby Fibonacciego w
płatkach kwiatów
Stokrotka – może
mieć 13, 21, 34, 55 lub 89
płatków
Krwiowiec (bloodroot) – 8 płatków
Stokrotka (shasta daisy) – 21 płatków
Nie zawsze Fibonacci…
Fuksja – 4 płatki
Krokus – 6 płatków
Narcyz – 6 płatków
Wieże Hanoi
Liniowa, jednorodna relacja rekurencji ze stałymi współczynnikami (*)
jest to relacja rekurencji postaci:
an=c1an-1+c2an-2+...
+ckan-k,
gdzie c1, c2, ... ,ck R i ck
0.
Liniowa oznacza, że każde ai jest w potędze co najwyżej pierwszej;
Jednorodna – że każdy człon po prawej stronie jest pomnożony przez
jakieś ai;
Relacja rekurencji
Wszystkie wpółczynniki ci są stałe (czyli niezależne od n);
Ponieważ ak zależy od k swoich poprzedników, więc rzędem relacji
jest k.
Aby rozwiązać relację rekurencji, będziemy potrzebowali k warunków
początkowych: a0 = c0, a1 = c1,..., ak = ck.
Przykłady.
1. sn = 2sn-1 – relacja (*) pierwszego rzędu
2. an = nan-1 jest liniowa i pierwszego rzędu. Ale współczynnik przy
an-1 nie jest stały;
3. bn = bn-1 + (n-1) jest relacją liniową pierwszego rzędu o stałych
współczynnikach. Ale ze względu na człon n-1 nie jest to relacja
jednorodna.
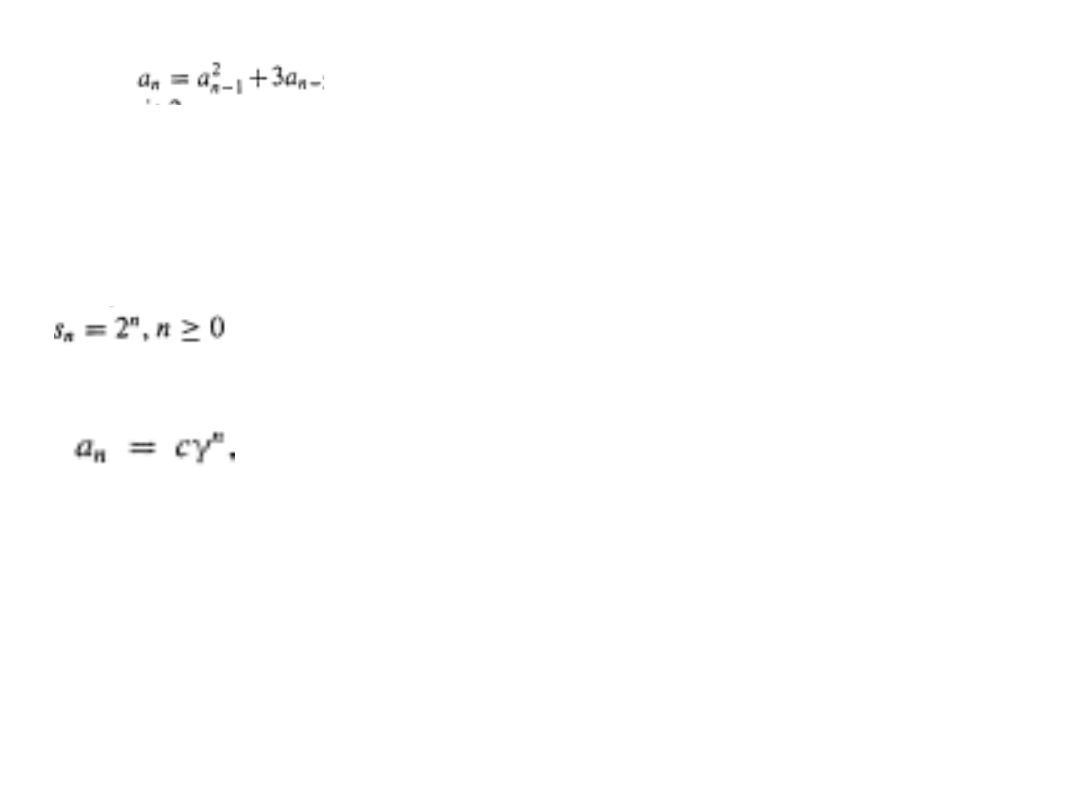
4.
jest jednorodna. Ale nie jest liniowa, bo an-1
występuje w drugiej potędze.
5. dn= 2dn-1+3 dn-6 jest relacją (*) rzędu 6.
Zauważmy, że rozwiązaniem równania sn = 2sn-1, gdzie s0 = 1 jest
Ogólniej, rozwiązaniem równania rekurencyjnego an =
an-1, gdzie a0 = c
jest
Rozważmy teraz równanie rekurencyjne typu (*) postaci:
an = a an-1 + b an-2,
gdzie a i b są niezerowymi stałymi.
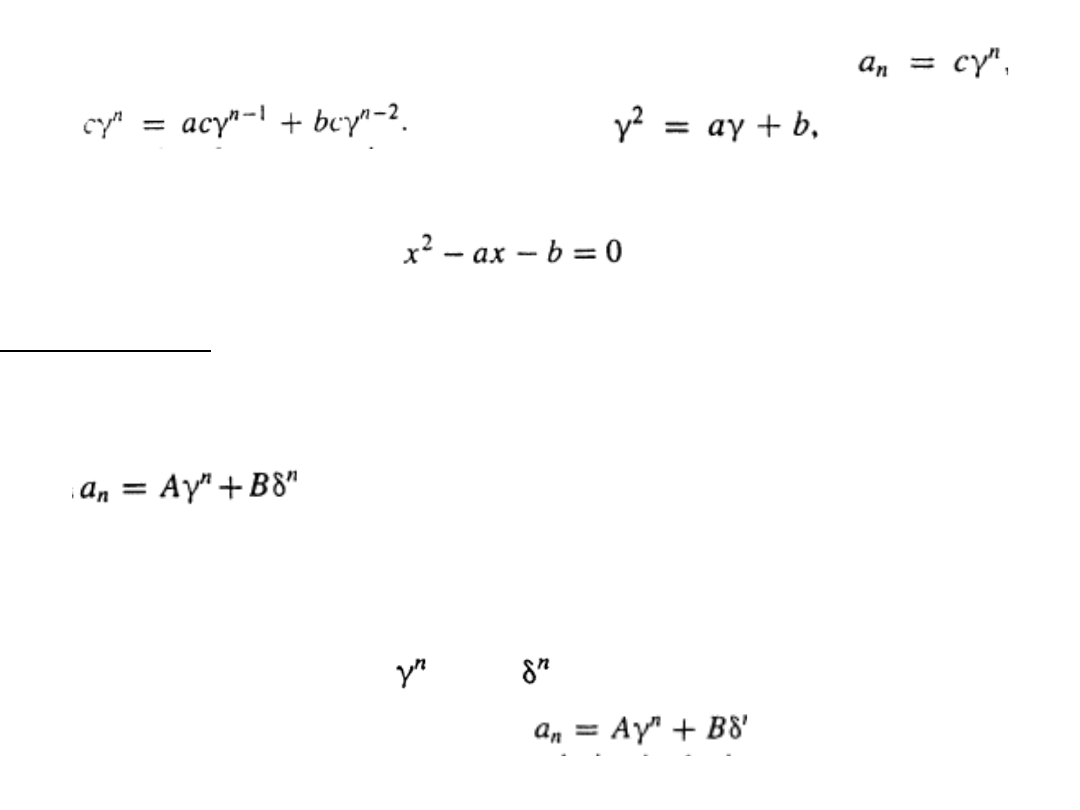
Jeśli to równanie posiada niezerowe rozwiązanie postaci
to
To daje
czyli
musi być rozwiązaniemrównania charakterystycznego:
Twierdzenie. Niech
i
będą różnymi rozwiązaniami równania
charakterystycznego, gdzie a, b
R i b
0. Wtedy każde rozwiązanie
Równania an = a an-1 + b an-2, gdzie a0 = c0 i a1 = c1 jest postaci
dla pewnych stałych A i B.
Zauważmy, że twierdzenie nie może być stosowane, jeśli
=
.
Można jednak je stosować, jeśli
i
są liczbami zespolonymi.
Rozwiązania
i
są to rozwiązania podstawowe.
Rozwiązanie relacji rekurencji
jest kombinacją liniową rozwiązań podstawowych.
Przykład. Rozwiązać relację a
n
= 5a
(n-1)-
6 a
(n-2),
gdzie a
0
= 4 i a
1
= 7.
Przykład. Rozwiązać relację rekurencji Fibonacciego
F
n
= F
(n-1)+
F
(n-2),
gdzie F
0
= 1 i F
1
= 1.
Zadanie
Zadanie
Zadanie
Funkcje tworzące.
Niech a1, a2,..., an,... będzie ciągiem liczb rzeczywistych.
Funkcją tworzącą dla ciągu (an) nazywamy funkcję postaci:
Funkcją tworzącą, którą będziemy najczęściej używać jest
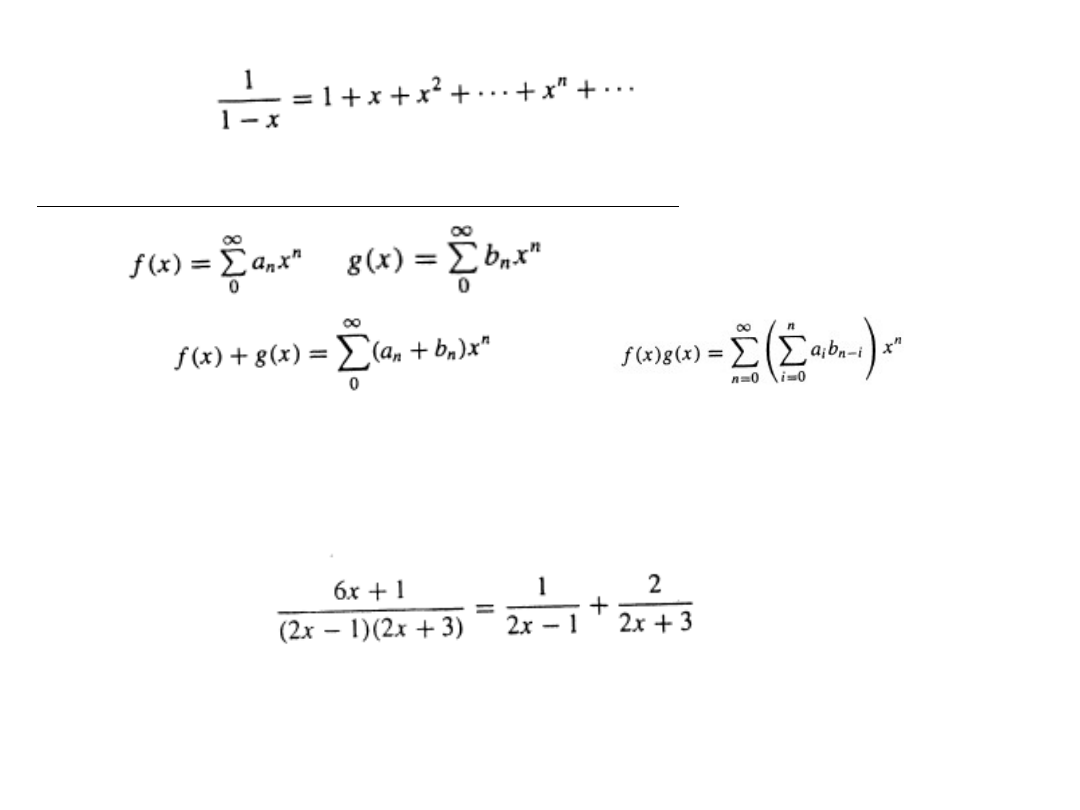
czyli
Dodawanie i mnożenie funkcji tworzących:
Niech
i
będą dwoma funkcjami tworzącymi.
Wtedy
oraz
Aby rozwiązać równanie rekurencyjne metodą funkcji tworzących,
potrzebny jest rozkład funkcji wymiernej na ułamki proste, np.
Przykład. Rozwiązać relację an= 5an-1-6 an-2, gdzie a0 = 4 i a1 = 7.
Przykład. Rozwiązać relację rekurencji Fibonacciego
Fn= Fn-1+Fn-2, gdzie F1 = 1 i F2 = 1.
