Modele i obliczenia

mechanizmów wciągarki

Dr inż. Piotr Kisiel

Zasada Hamiltona

Dla układu zachowawczego wymaga ona, aby

całka

miała wartość ekstremalną. Funkcja
podcałkowa L reprezentuje nadwyżkę energii

kinetycznej nad potencjalną tj.

L = Ak − Ap

gdzie:
L – funkcja Lagrange’a
Ak –energia kinetyczna
Ap - energia potencjalna

Równania ruchu dla układów zachowawczych
bez strat i wymuszeń zewnętrznych

Po obliczeniu wariacji całki względem kolejnych zmiennych
(współrzędnych

uogólnionych)

otrzymuje

się

równania

Lagrange’a drugiego rodzaju; dla układów zachowawczych, bez
strat i bez wymuszenia zewnętrznego:

dla j = 1,..., k
gdzie:

q j –współrzędne uogólnione
k – liczba stopni swobody

Równania ruchu dla układów nie zachowawczych
(rzeczywistych) ze stratami i wymuszeniami
zewnętrznymi

gdzie:

- funkcja strat
- funkcja wymuszenia

Stabilność oraz stany nieustalone

Stabilnością układu nazywamy jego skłonność powracania do
warunków równowagi statycznej, gdy został z nich wytrącony.
Zmiana wartości obciążenia lub siły elektromotorycznej silnika
powoduje zakłócenie równowagi ruchu napędu: zmianę
momentu dynamicznego oraz prędkości ruchu. Zakłócenia
równowagi ruchu napędu nazywamy stanem nieustalonym,
który trwa aż do osiągnięcia nowej stałej prędkości ruchu układu
napędowego.

Układ napędowy znajduje się w stanie równowagi gdy
Md = 0 tj. przy Ms (ω) = Mobc (ω). Stan równowagi dynamicznej
jest punktem pracy układu napędowego: jest to punkt przecięcia
się charakterystyki silnika z charakterystyką obciążenia.

Stabilność oraz stany nieustalone

Rys.1. Punkt pracy układu napędowego

M

M

obc

ω

p

ω

Punkt pracy

Charakterystyka

momentu silnika

M

s

Charakterystyka

momentu

obciążenia

Moment dynamiczny

Moment dynamiczny jest różnicą pomiędzy momentem silnika

(wymuszeniem zewnętrznym) a momentem oporu (obciążeniem).

Więzy sprężyste

Więzy sprężyste charakteryzuje współczynnik sztywności k
określany jako wartość siły potrzebnej dla jednostkowego
przesunięcia jednego końca więzów względem drugiego. Dla
przesunięcia prostoliniowego wartość tego współczynnika można
wyznaczyć wg wzoru :

gdzie:

F – siła rozciągająca więzy [N],
∆l – wydłużenie liniowe [m],
E – moduł sprężystości Younga [N / m2],
Q – przekrój poprzeczny [m2],
l – długość więzi [m].

Więzy sprężyste

Dla przesunięcia obrotowego współczynnik sztywności jest równy:

gdzie:

M – moment skręcający więzy [Nm],
∆α – skręcenie więzi [rad],
G – moduł sprężystości poprzecznej [N / m2],

d – średnica więzi [m].

Mechanizm podnoszenia
Model matematyczny (dwumasowy)

m

1

m

2

2

w

s

1

1

x

m



1

w

s

2

w

s

2

S

2

x

1

x

1

S

h

k

Równania ruchu
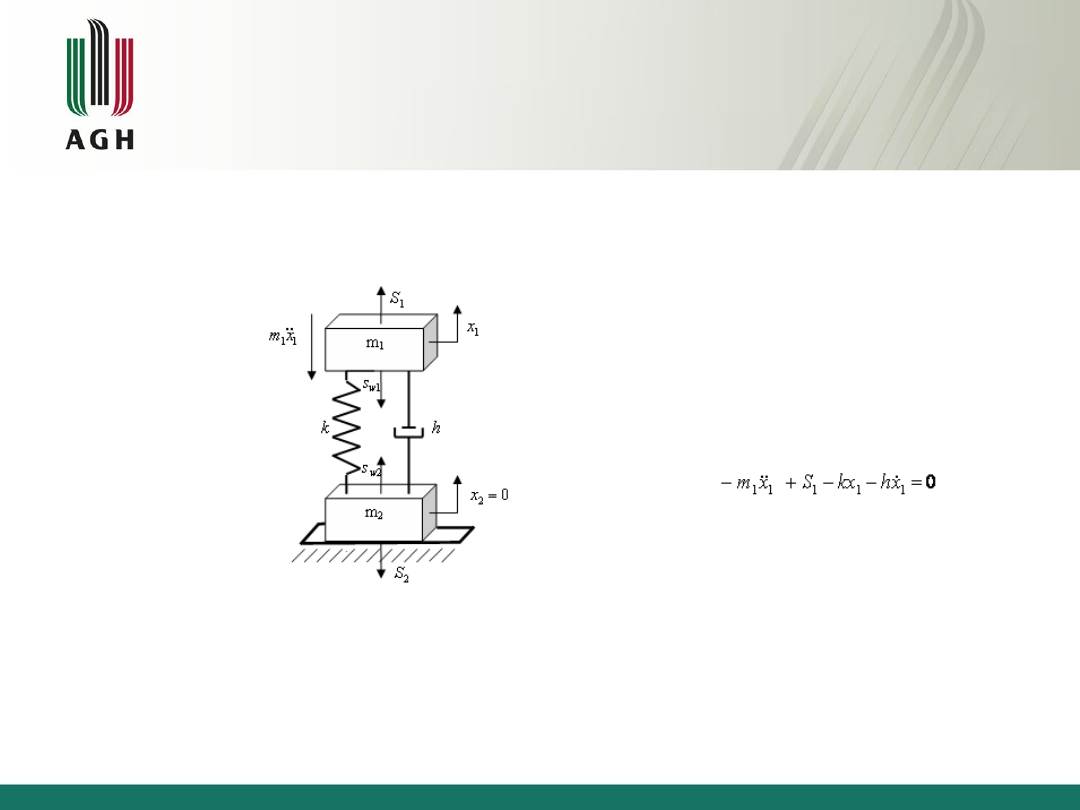
Rozruch – przypadek z napiętymi więzami

Równania ruchu przyjmują
postać:

Równania ruchu
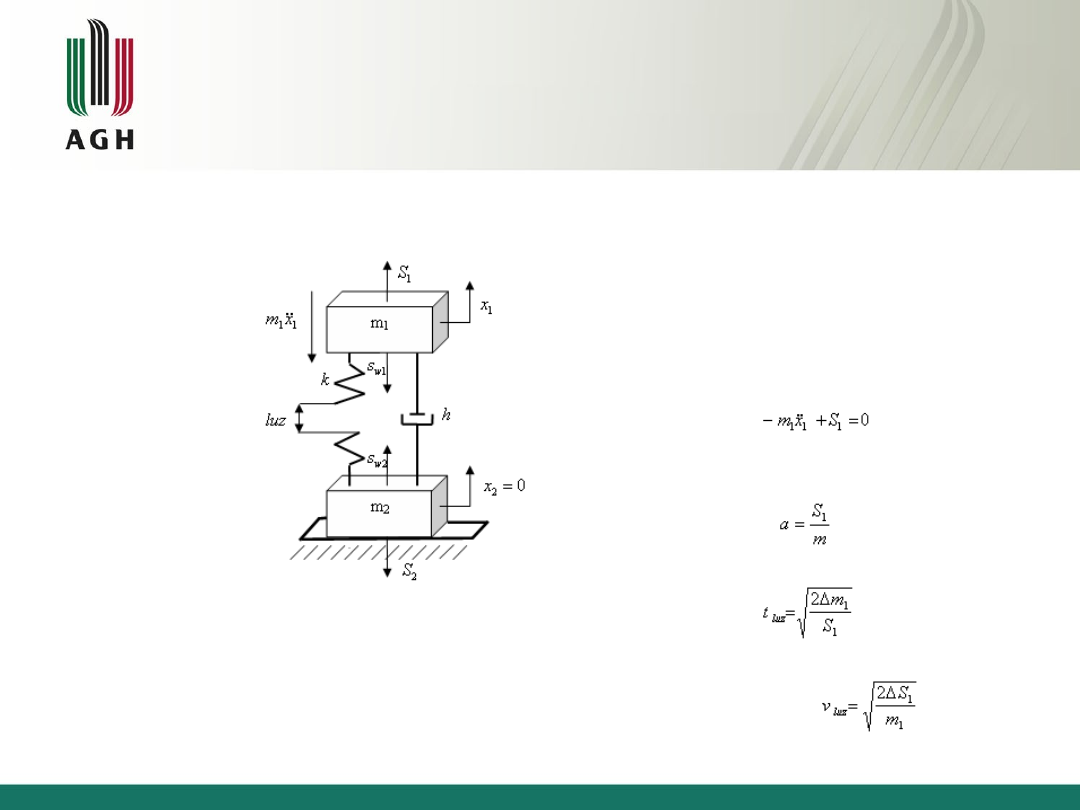
Rozruch – przypadek ze zluzowanymi więzami

Ładunek spoczywający na podłożu,

lina nie jest napięta. Ruch takiego

układu rozpoczyna się od fazy

napinania więzów, tj. początkowo

porusza się tylko masa m1, co

powoduje

stopniowe

rozciąganie

więzów. Faza ta trwa do chwili, w

której

siła

odkształcająca

więzy

osiągnie wartość równą sile S2 .

Układ ma tylko jeden stopień

swobody, a więc ruch układu opisuje

jedno równanie drugiego rzędu.

Równania ruchu
Rozruch – przypadek z nadmiernym luzem

Ładunek spoczywa na podłożu, lecz tym

razem liny są bardziej luźne. Ruch takiego

układu rozpoczyna się od fazy kasowania

luzu w więzach – porusza się tylko masa

m1 pociągając za sobą linę bez oporu, a

masa m2 spoczywa swobodnie na

podłożu.

W równaniu nie występują zewnętrzne ani

wewnętrzne siły oporu.

Ruch jest jednostajnie przyspieszony i trwa do

chwili wyczerpania luzu:

Czas kasowania luzów wyraża się wzorem:

Prędkość masy m1 w chwili skasowania luzu

jest równa:

Równania ruchu
Hamowanie przy opuszczaniu

Warunki początkowe określone są przez
prędkość ruchu przy opuszczaniu oraz
wydłużenie układu linowego pod wpływem
zawieszonego ciężaru:

Ruch opisują dwa równania różniczkowe:

Ruch tego układu składa się z dwóch faz:

− ruch obu mas – trwa do zatrzymania masy m1

siłą hamulca

− po zatrzymaniu masy m1 następuje faza,

w której masa m2 wykonuje swobodne

wahania pionowe opisane równaniem:

Równania ruchu
Hamowanie przy podnoszeniu

Równania ruchu w fazie pierwszej – ruch obu mas:

Faza ta trwa aż do chwili

w której nastąpi

zatrzymanie pierwszej masy m1,v=0. Druga
faza po zatrzymaniu masy m1 to ruch

wahadłowy drugiej masy m2

Obliczenie parametrów występujących
w równaniach ruchu

Tabela danych obliczeniowych mechanizmu podnoszenia

Obliczenie parametrów występujących
w równaniach ruchu

Obliczenie masy zredukowanej − m1

 obliczenie momentu zredukowanego Jzr1 dla masy m1

zatem:

2

1

1

4

b

zr

D

J

m





Obliczenie parametrów występujących
w równaniach ruchu

Obliczenie masy zredukowanej − m2

 obliczenie momentu zredukowane Jzr2 dla masy m2

gdzie

zatem

Obliczenie parametrów występujących
w równaniach ruchu

Obliczenie siły wymuszającej S1R dla rozruchu

 obliczenie M*silnika

zatem

Obliczenie parametrów występujących
w równaniach ruchu

Obliczenie siły wymuszającej SR2 dla rozruchu

Obliczenie siły wymuszającej S1H dla hamowania

Obliczenie siły wymuszającej S2H dla hamowania

Obliczenie parametrów występujących
w równaniach ruchu

Obliczenie współczynnika sprężystości liny

 k

Obliczenie współczynnika tłumienia

 h

Obliczenie parametrów występujących
w równaniach ruchu

Równania ruchu układu

- podczas rozruchu

- podczas hamowania

Tyle tej powtórki 

Zapraszam do udziału w laboratorium

z modelowania dynamiki wciągarki

przejezdnej !