T14. Dynamika układu punktów

materialnych. Dynamika bryły

sztywnej.



Pęd układu punktów materialnych.



Moment pędu układu punktów

materialnych.



Równania ruchu bryły sztywnej.



Momenty bezwładności bryły

sztywnej.



Przykład.

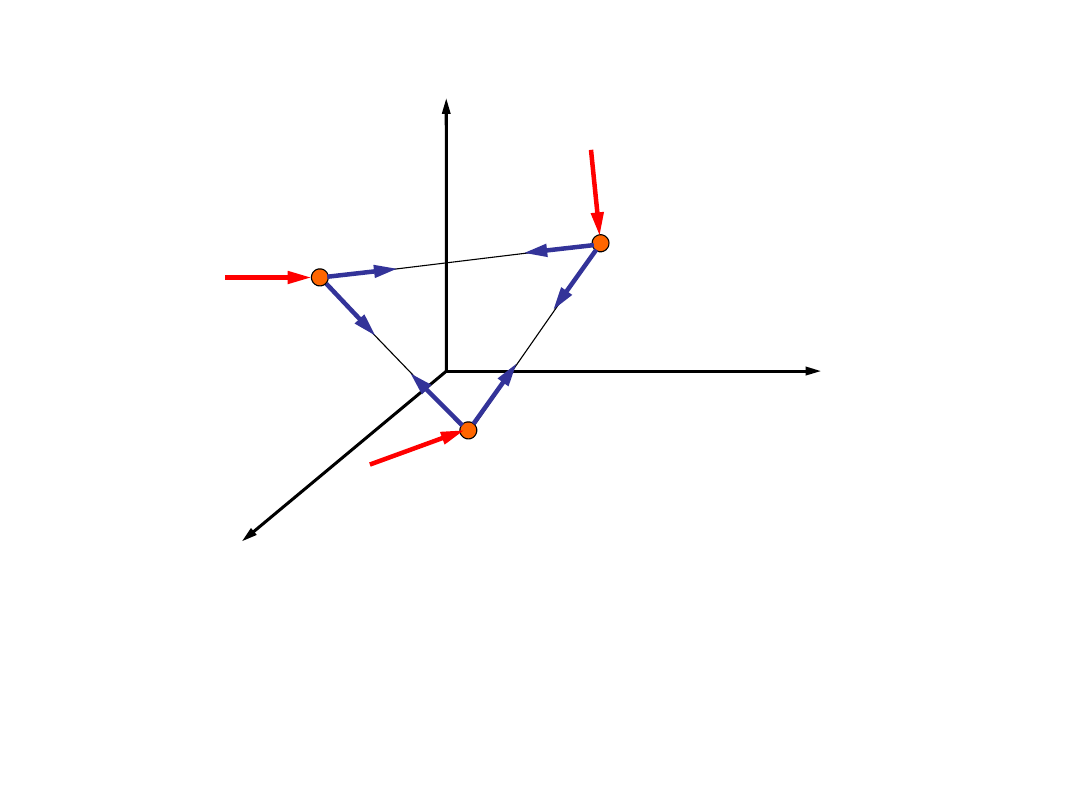
Pęd układu punktów
materialnych

0

x

y

z

- siły
wewnętrzne

- siły
zewnętrzne

Z III zasady dynamiki wynika,
że:

Ponieważ siły wewnętrzne
działają wzdłuż tych samych
prostych:

1

A

2

A

3

A

1,2

F

2,1

F

2,3

F

3,1

F

1,3

F

3,2

F

1

F

2

F

3

F

,

i j

F

i

F

,

,

i j

j i

F

F

=-

r

r

0

0

,

,

i j

j i

M

M

=-

r

r

Pęd układu punktów
materialnych

Wniosek:

Wypadkowa siła sił wewnętrznych układu
punktów materialnych równa jest zeru.

Wniosek:

Wypadkowy moment sił wewnętrznych układu
punktów materialnych równy jest zeru.

,

,

0

i j

j i

F

F

+

=

r

r

,

1

n

wi

i j

j

F

F

=

=

�

r

r

,

1

1

1

0

n

n

n

w

wi

i j

i

i

j

F

F

F

=

=

=

=

=

=

�

��

r

r

r

0

0

,

,

0

i j

j i

M

M

+

=

r

r

0

0 ,

1

n

wi

i j

j

M

M

=

=

�

r

r

0

0

0 ,

1

1

1

0

n

n

n

w

wi

i j

i

i

j

M

M

M

=

=

=

=

=

=

�

��

r

r

r

Pęd układu punktów
materialnych

Wniosek:

Szybkość zmian wypadkowego pędu układu
punktów materialnych równa jest wypadkowej
sił zewnętrznych.

i

wi

i

dP

F

F

dt

=

+

r

r

r

(

)

1

1

n

n

i

wi

i

i

i

dP

F

F

dt

=

=

=

+

�

�

r

r

r

1

1

1

n

n

n

i

wi

i

i

i

i

d

P

F

F

dt

=

=

=

=

+

� �

�

r

r

r

1

1

,

,

n

n

i

i

i

i

d

P F

P

P

F

F

dt

=

=

=

=

=

�

�

r

r

r

r

r

r

Pęd układu punktów
materialnych

Wniosek:

Szybkość zmian wypadkowego momentu pędu
układu punktów materialnych równa jest
wypadkowemu momentowi sił zewnętrznych.

0

0

0

i

wi

i

dK

M

M

dt

=

+

r

r

r

(

)

0

0

0

1

1

n

n

i

wi

i

i

i

dK

M

M

dt

=

=

=

+

�

�

r

r

r

0

0

0

1

1

1

n

n

n

i

wi

i

i

i

i

d

K

M

M

dt

=

=

=

=

+

�

�

�

r

r

r

0

0

0

0

0

0

1

1

,

,

n

n

i

i

i

i

d

K

M

K

K

M

M

dt

=

=

=

=

=

�

�

r

r

r

r

r

r

Pęd układu punktów
materialnych

Wniosek:

Pęd układu punktów materialnych możemy
wyrazić jako iloczyn sumy mas i prędkości
środka ciężkości.

- położenie środka masy układu punktów
materialnych

1

1

1

n

n

n

i

i

i i

i

i

i

i

dr

P

P

mu

m

dt

=

=

=

=

=

=

� �

�

r

r

r

r

1

n

i i

i

d

P

mr

dt

=

�

�

= �

�

�

�

�

r

r

1

1

,

n

n

i i

C

i

i

i

mr mr

m

m

=

=

=

=

�

�

r

r

(

)

C

C

C

dr

d

P

mr

m

mu

dt

dt

=

=

=

r

r

r

r

C

r

r

Pęd układu punktów
materialnych

Twierdzenie o ruchu środka masy:

Środek masy układu punktów materialnych
porusza się tak, jakby była w nim
skoncentrowana cała masa układu i działała na
niego wypadkowa siła.

C

du

d P

m

F

dt

dt

=

=

r

r

r

Pęd układu punktów
materialnych

Zasada zachowania pędu:

Jeżeli wypadkowa sił zewnętrznych jest równa
zeru, pęd układu punktów materialnych
pozostaje stały.

F - siła ciągu

0

0

d P

F

P const

dt

=

�

=

�

=

r

r

r

(

)

(

)

0

r

p

p

r

p

P

m m u

dm

d P

du

m m

u

dt

dt

dt

=

+

=

+

+

=

(

)

p

r

p

dm

du

m m

u

F

dt

dt

+

=-

=

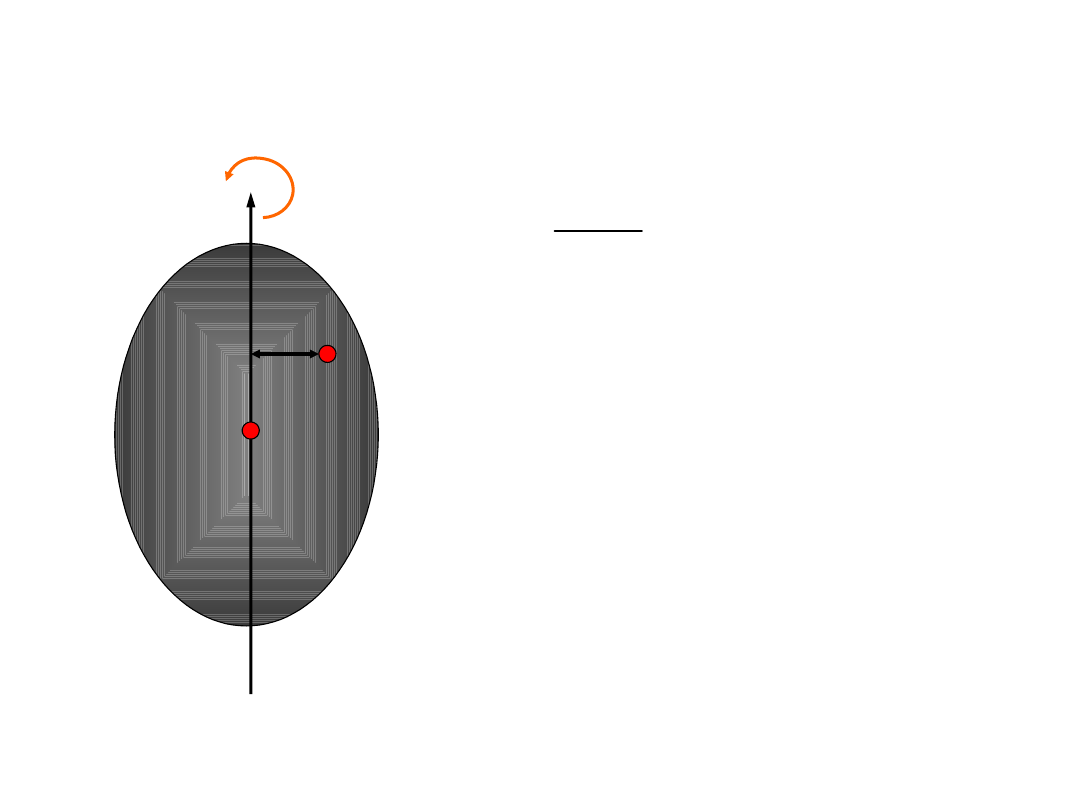
Równania ruchu bryły
sztywnej

Ruch obrotowy bryły sztywnej o jednym stopniu
swobody

C

z

I

z

–

moment bezwładności

bryły względem osi z

Cz

Cz

dK

M

dt

=

(

)

2

Czi

i i i

i

i

z

i

i i

z

K

muh m h

h mh

w

w

=

=

=

2

,

Czi

zi

z

zi

i i

K

I

I

mh

w

=

=

1

1

n

n

Cz

zi

z

z

zi

z z

i

i

K

I

I

I

w

w

w

=

=

=

=

=

�

�

i

h

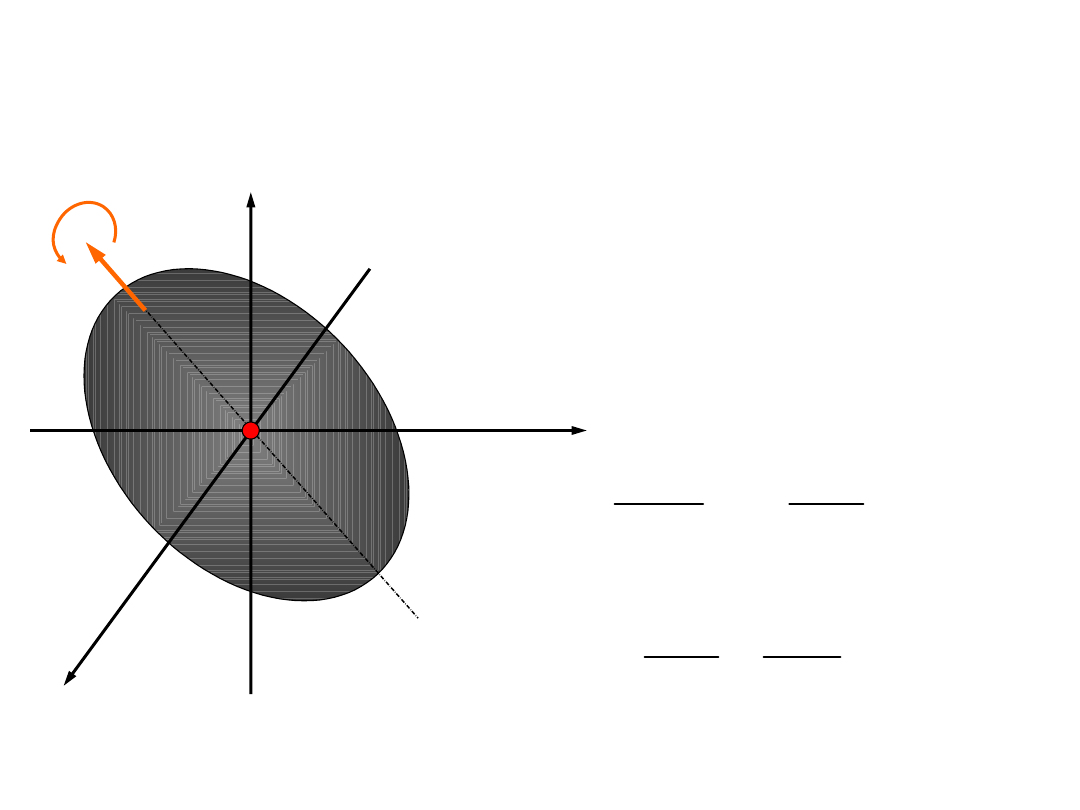
Równania ruchu bryły
sztywnej

Ruch obrotowy bryły sztywnej o trzech stopniach
swobody

C

z

y

x

Cx

x x

K

I

w

=

Cx

x

x

Cx

dK

d

I

M

dt

dt

w

=

=

Cy

y y

K

I

w

=

Cz

z z

K

I

w

=

x

Cx

x

x

d

M

dt

I

w

e

=

=

w

r

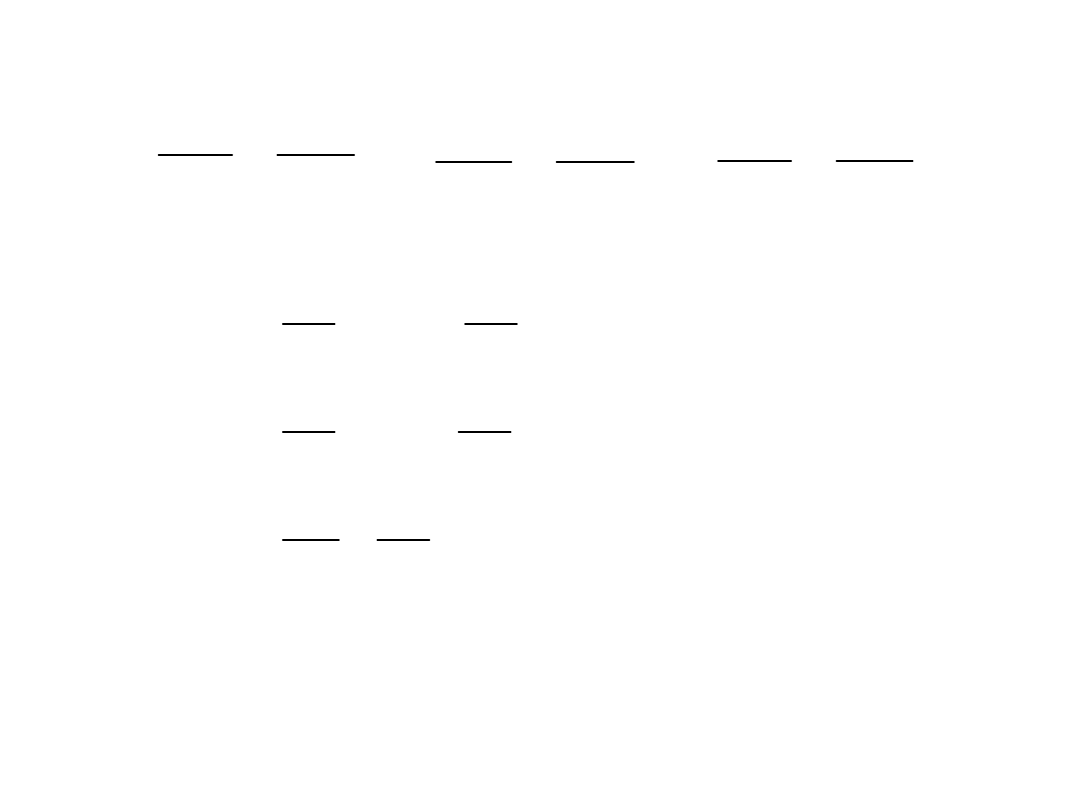
Równania ruchu bryły
sztywnej

x

Cx

x

d

M

dt

I

w

=

y

Cy

y

d

M

dt

I

w

=

Cz

z

z

M

d

dt

I

w

=

cos

sin sin

sin

sin cos

cos

x

y

z

d

d

dt

dt

d

d

dt

dt

d

d

dt

dt

J

j

y

J

y

w

J

j

y

J

y

w

y

j

J

w

+

=

-

=

+

=

0

0

0

0

0

0

(0)

,

(0)

,

(0)

(0)

,

(0)

,

(0)

x

x

y

y

z

z

w

w

w

w

w

w

y

y

J

J

j

j

=

=

=

=

=

=

Energia kinetyczna bryły
sztywnej

Energia kinetyczna w ruchu
obrotowym:

C

z

2

2 2

1

1

2

2

ki

i i

i

i

E

mu

m h

w

=

=

2 2

1

2

1

n

k

i

i

i

E

m h

w

=

=

�

i

h

2

2

2

1

1

2

2

1

n

k

i i

z

i

E

mh

I

w

w

=

=

=

�

Energia kinetyczna bryły
sztywnej

Energia kinetyczna w ruchu
postępowym:

Twierdzenie Koeniga:

Energia kinetyczna bryły sztywnej dla ruchu
dowolnego jest sumą energii kinetycznej ruchu
postępowego z prędkością równą prędkości
środka masy i energii kinetycznej w chwilowym
ruchu obrotowym ciała względem jego środka
masy

2

1

2

ki

i

E

mu

=

2

2

1

1

2

2

1

n

k

i

i

E

mu

mu

=

=

=

�

2

2

1

1

2

2

k

l

E

mu

I w

=

+

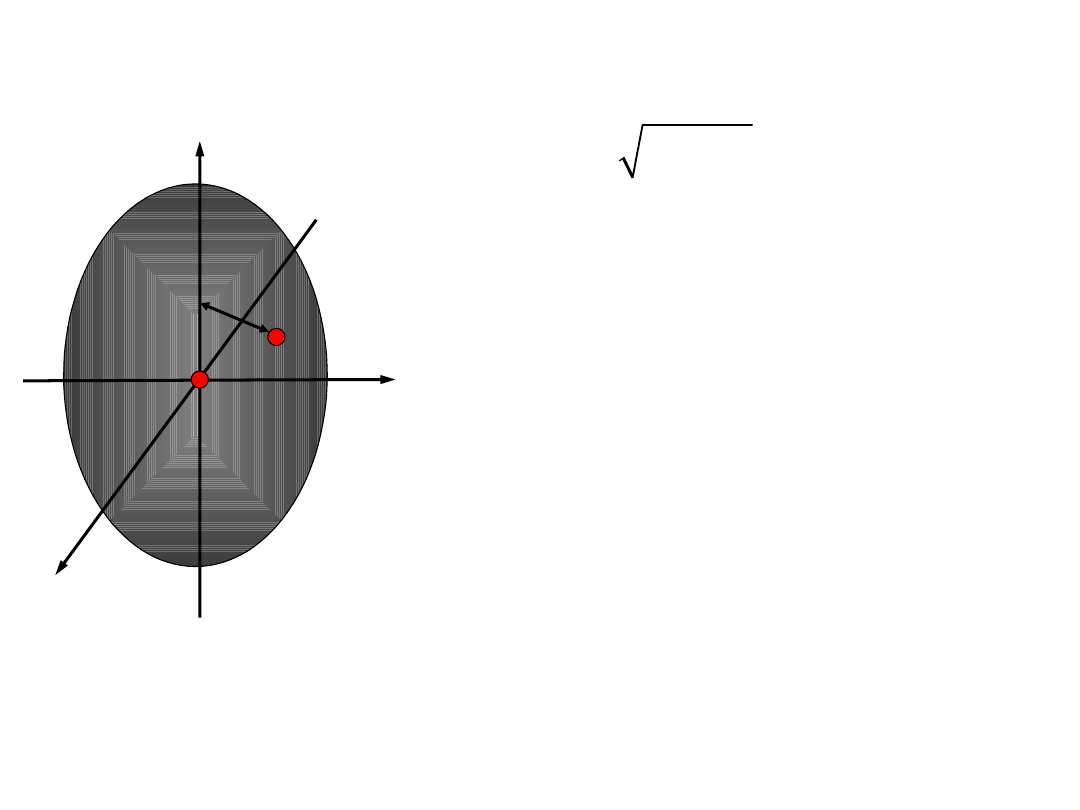
Momenty bezwładności
bryły

C

z

y

x

Podzielmy bryłę na jednakowe
elementy o objętości DV

i

h

2

2

2

(

)

zi

i i

i

i

I

mh

V x

y

r

=

= D

+

2

2

i

i

i

h

x

y

=

+

(

)

2

2

2

2

0

1

lim

(

)

n

z

i

i

V

i

V

I

V x

y

x

y dV

r

r

D �

=

=

D

+

=

+

�

�

(

)

(

)

2

2

2

2

,

x

y

V

V

I

y

z dV

I

x

z dV

r

r

=

+

=

+

�

�

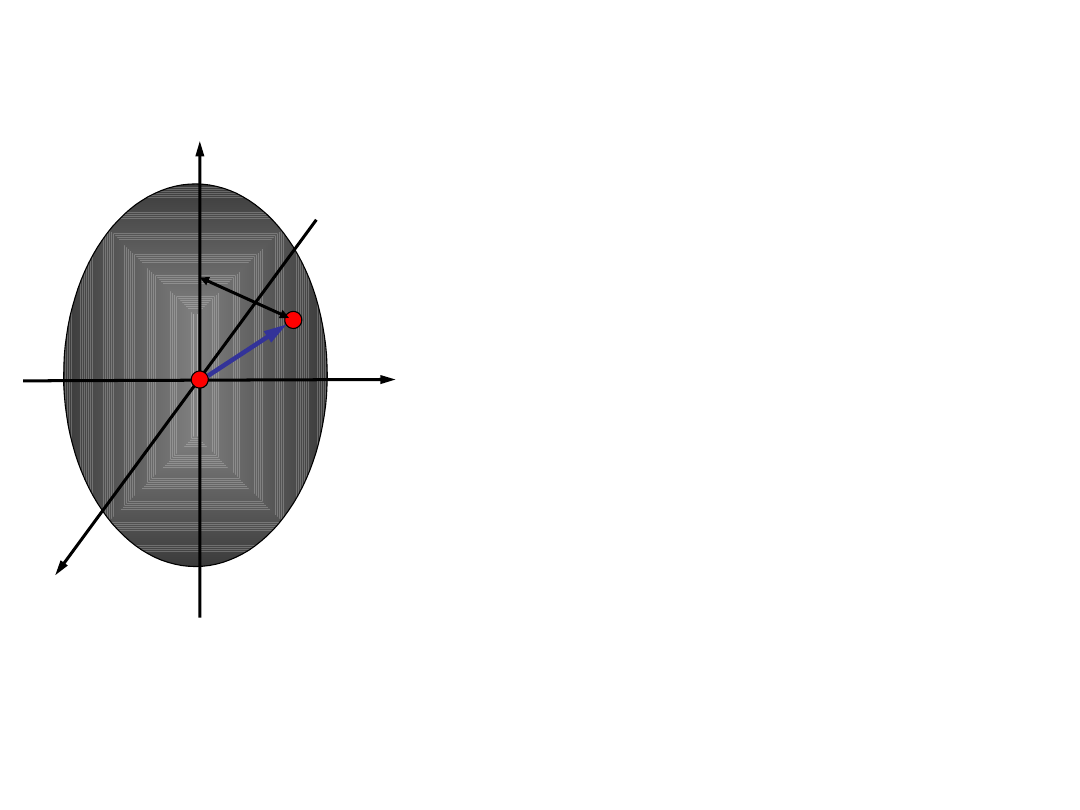
Momenty bezwładności
bryły

C

z

y

x

I

xz

–

moment bezwładności bryły

względem
płaszczyzny xz

moment bezwładności
bryły względem bieguna
C

i

h

(

)

2

x

y

z

xy

xz

yz

I

I

I

I

I

I

+ + =

+ +

2

2

x

xz

xy

V

V

I

y dV

z dV I

I

r

r

=

+

= +

�

�

i

r

r

(

)

2

2

2

2

x

y

z

V

I

I

I

x

y

z dV

+ + =

+ +

�

2

2

x

y

z

V

I

I

I

r dV

r

+ + =

�

2

C

V

I

r dV

r

=

�

Moment bezwładności bryły względem bieguna C
jest własnością bryły i nie zależy od orientacji osi
układu współrzędnych. Natomiast momenty
bezwładności względem osi zależą od tej
orientacji.
Można tak dobrać orientację osi, że momenty
bezwładności względem tych osi przybiorą
wartość ekstremalną. Takie osie nazywamy

głównymi osiami bezwładności

.

Momenty bezwładności
bryły

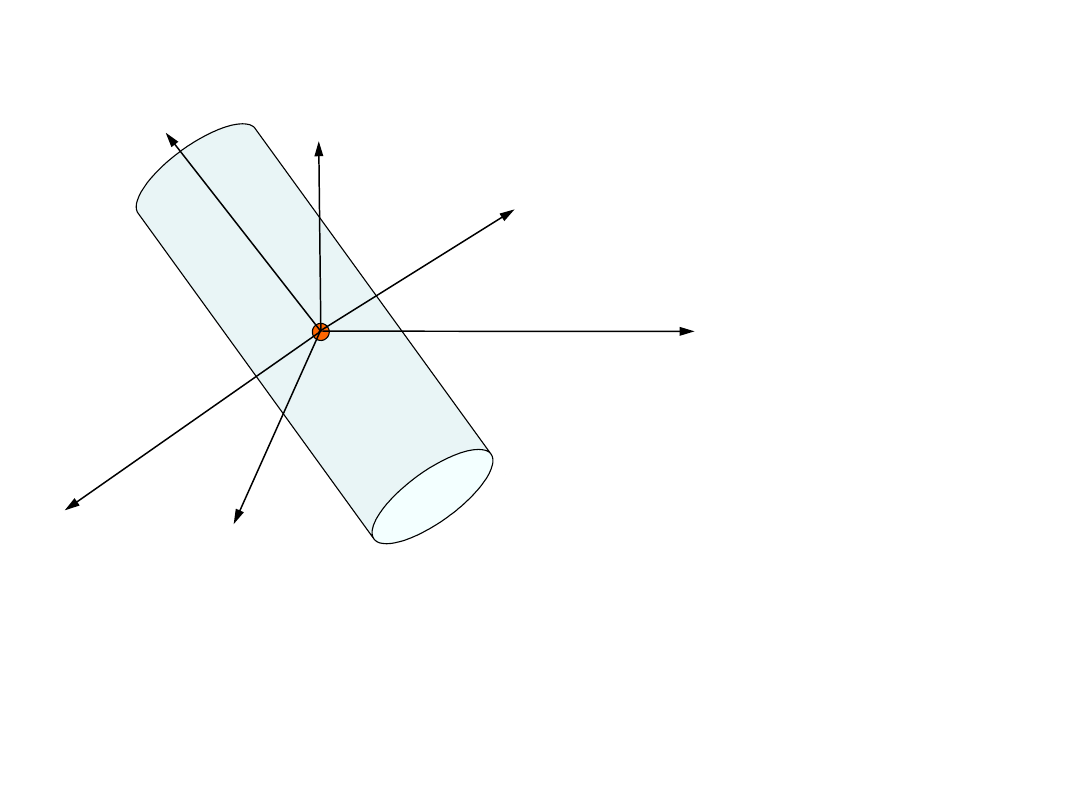
Momenty bezwładności
bryły

y

C

x

z

b

y

b

x

b

Momenty bezwładności względem głównych osi
bezwładności są właściwością bryły. Znając wartości
tych momentów i usytuowanie danej osi względem osi
głównych, możemy obliczyć wartość momentu
bezwładności względem tej osi.

min,

max

zb

xb

yb

I

I

I

=

=

=

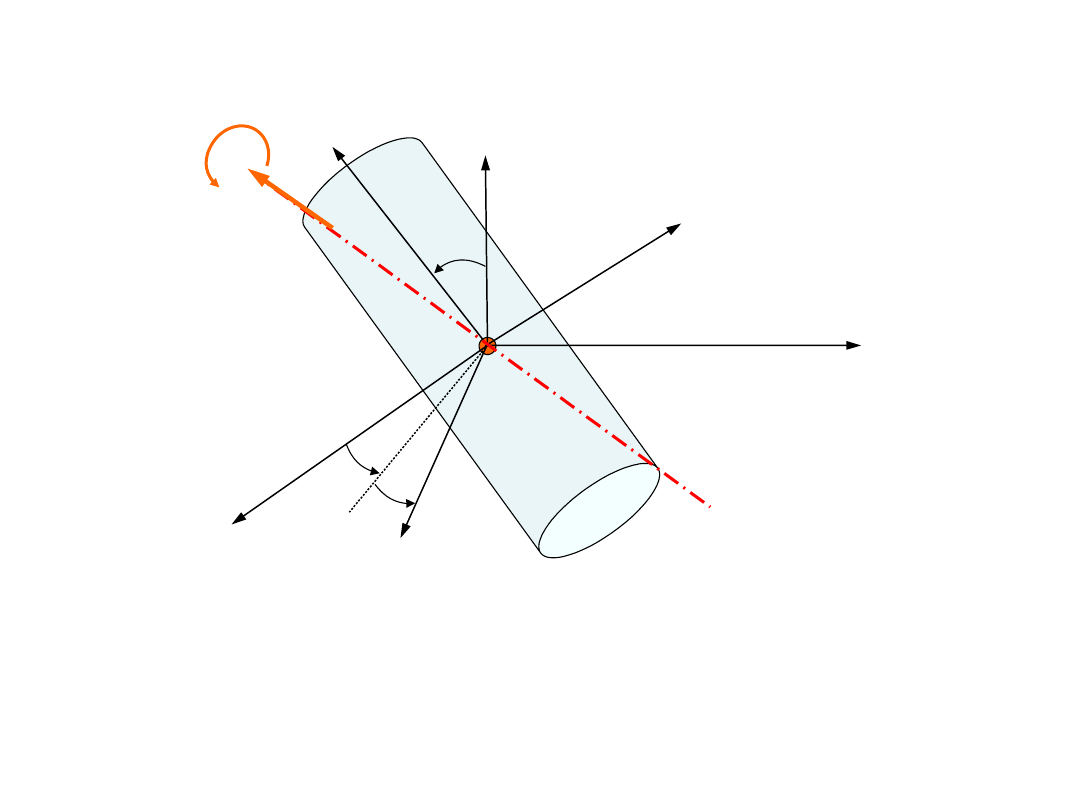
Momenty bezwładności
bryły

y

1

C

x

1

z

1

N

Przyjmujemy osie obracającego się układu
współrzędnych zgodne z głównymi osiami
bezwładności.

x

h

V

y

j

J

w

r

z

1

y

1

x

1

0

1

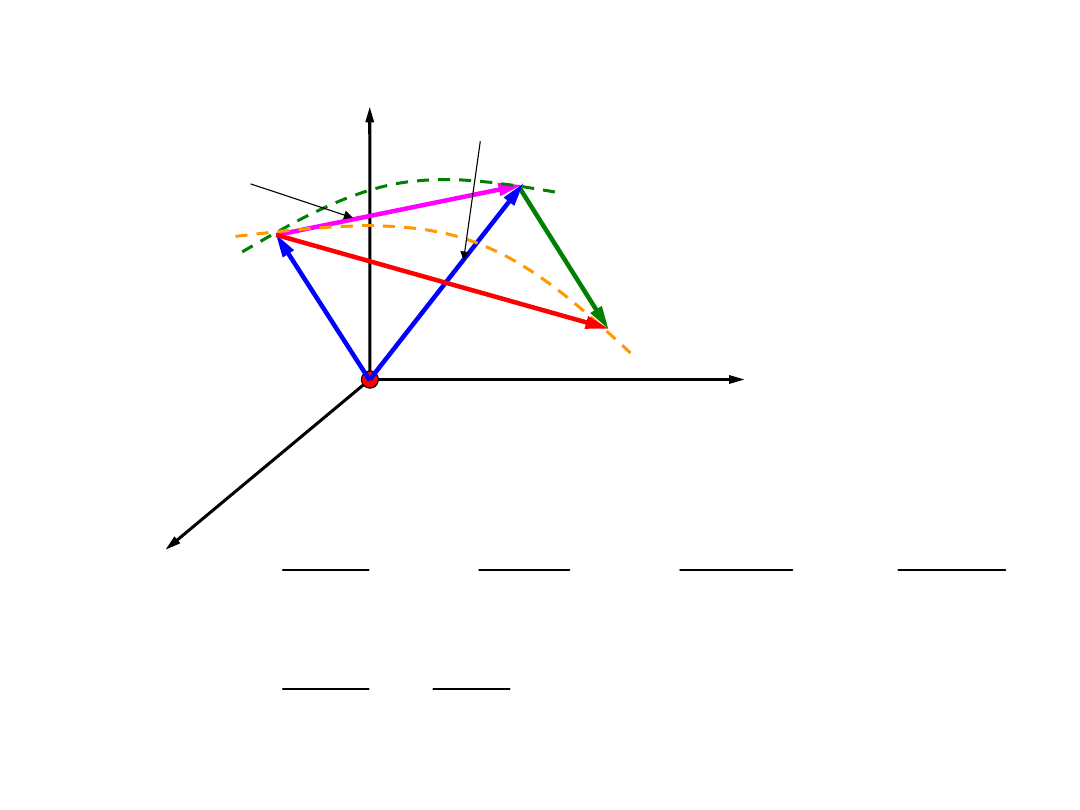
Równania ruchu bryły
sztywnej

1

( )

C

K t

r

1

(

)

C

K t

t

+D

r

1

( )

w C

K t

D

r

1

( )

C

K t

D

r

1

( )

r

C

K t

D

r

1

1

1

1

0

0

0

1

lim

lim

lim

C

C

w C

r

C

t

t

t

C

C

C

w

dK

K

K

K

dt

t

t

t

dK

dK

K

dt

dt

w

D �

D �

D �

D

D

D

=

=

+

D

D

D

�

�

=

+ �

�

�

�

�

r

r

r

r

r

r

r

Równania ruchu bryły
sztywnej

C

C

C

C

dK

K

K

M

dt

x

h

V

V

h

x

w

w

+

-

=

C

C

C

C

dK

K

K

M

dt

h

V

x

x

V

h

w

w

+

-

=

C

C

C

C

dK

K

K

M

dt

V

x

h

h

x

V

w

w

+

-

=

C

K

I

x

x x

w

=

C

K

I

h

h h

w

=

C

K

I

V

V V

w

=

Równania ruchu bryły
sztywnej

(

)

C

d

I

I

I

M

dt

x

x

h

V

V

h

x

w

w w

+

-

=

(

)

C

d

I

I

I

M

dt

h

h

V x

x

V

h

w

w w

+

-

=

(

)

C

d

I

I

I

M

dt

V

V

x h

h

x

V

w

w w

+

-

=

y

1

0

1

x

1

z

1

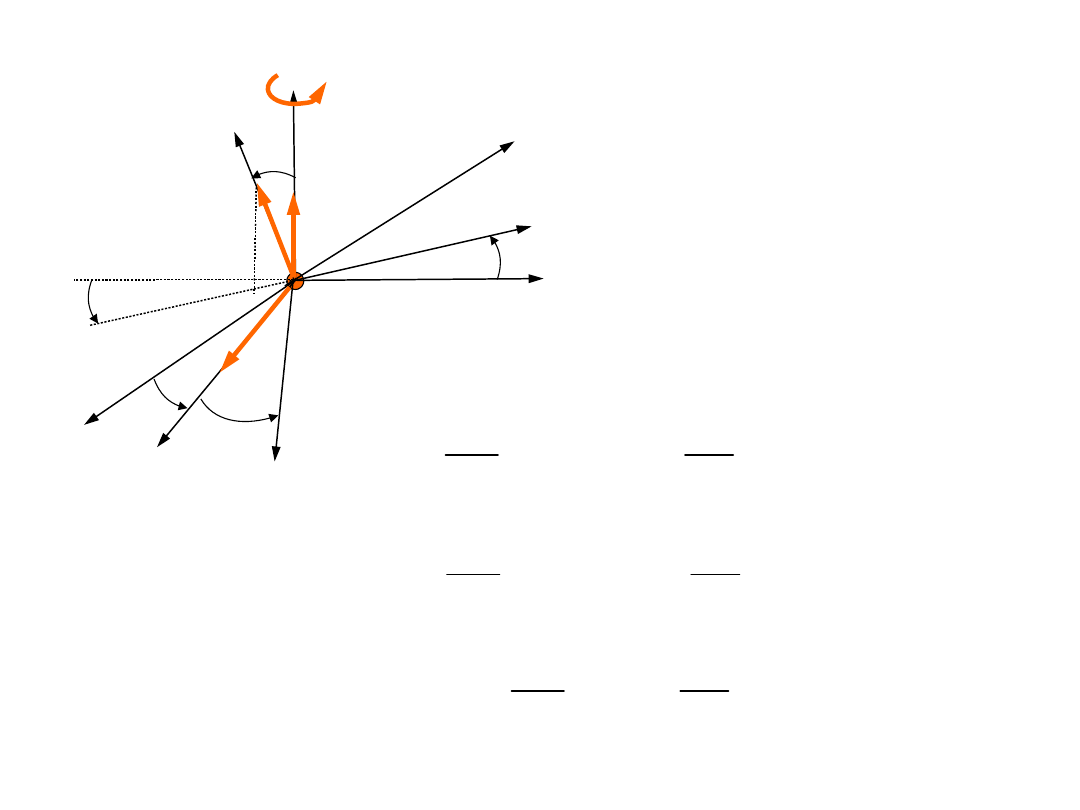
Równania ruchu bryły
sztywnej

y

x�

1

w

2

w

V

3

w

h�

y

3

1

cos

V

w w w

J

= +

sin cos

sin

d

d

dt

dt

h

y

J

J

j

j

w

-

=

J

y

1

2

sin sin

cos

x

w w

J

j

w

j

=

+

x

j

h

sin sin

cos

d

d

dt

dt

x

y

J

J

j

j

w

+

=

1

2

sin cos

sin

h

w w

J

j

w

j

=

-

cos

d

d

dt

dt

V

y

j

J

w

+

=

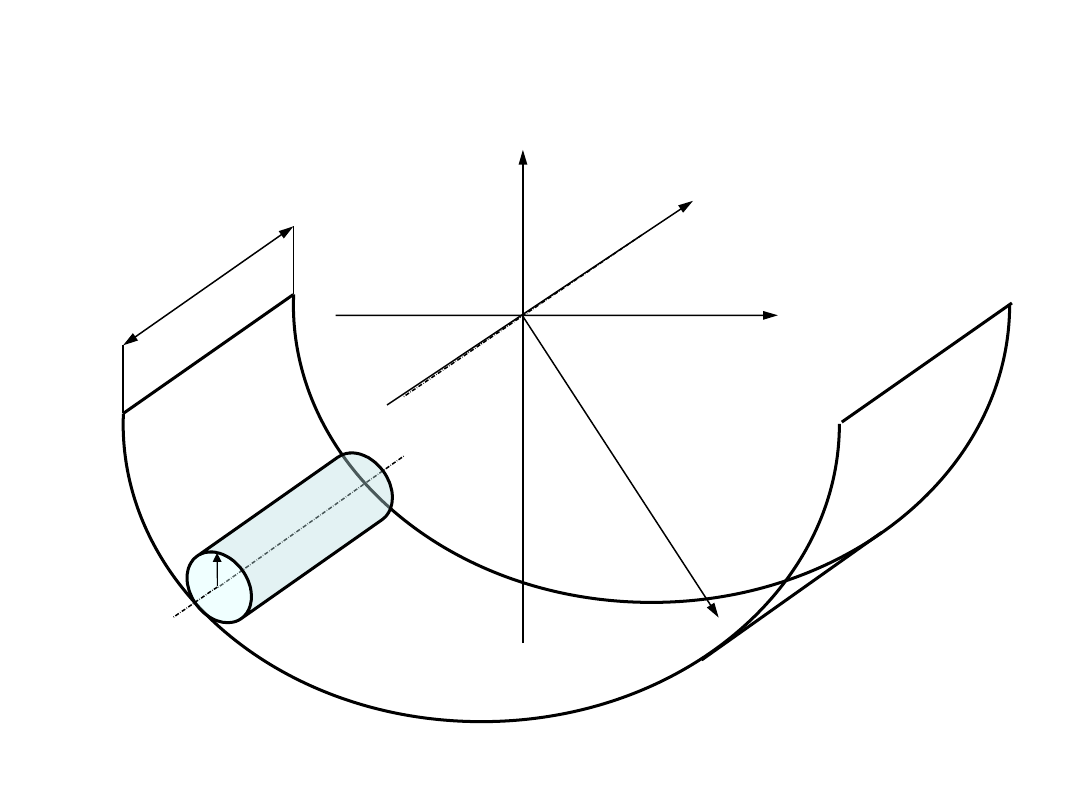
Równania ruchu bryły
sztywnej

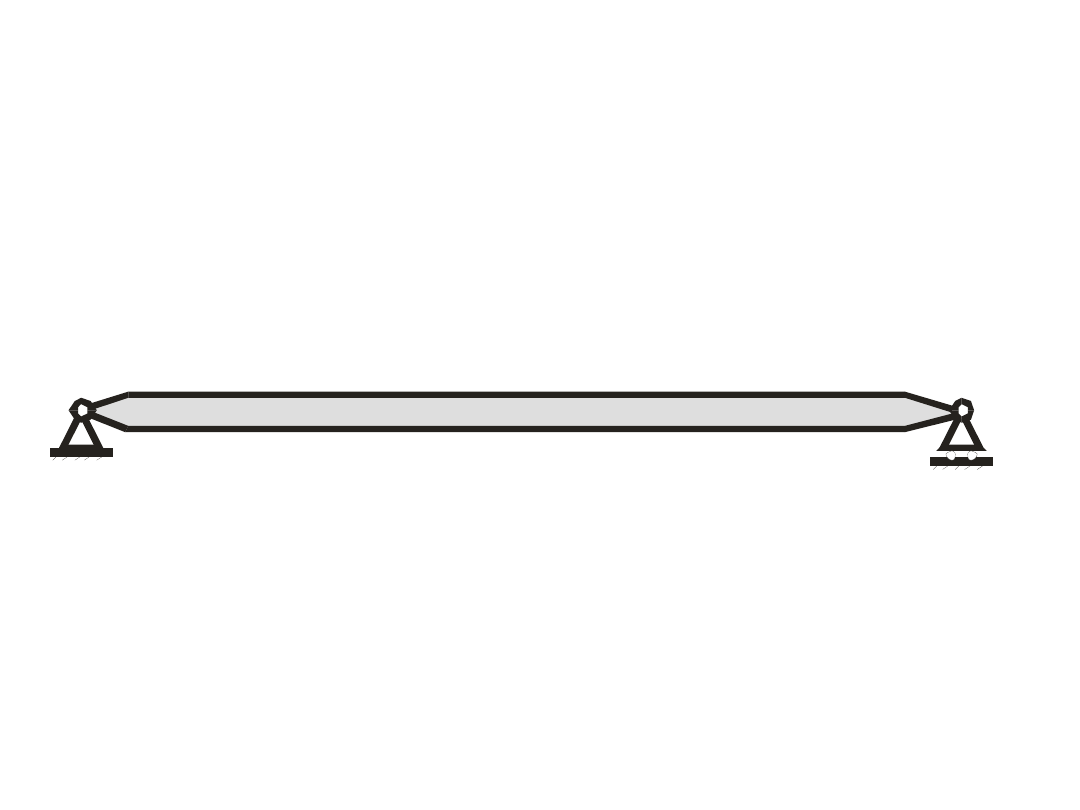
Przykład:

r

1

r

2

l

y

x

z

0

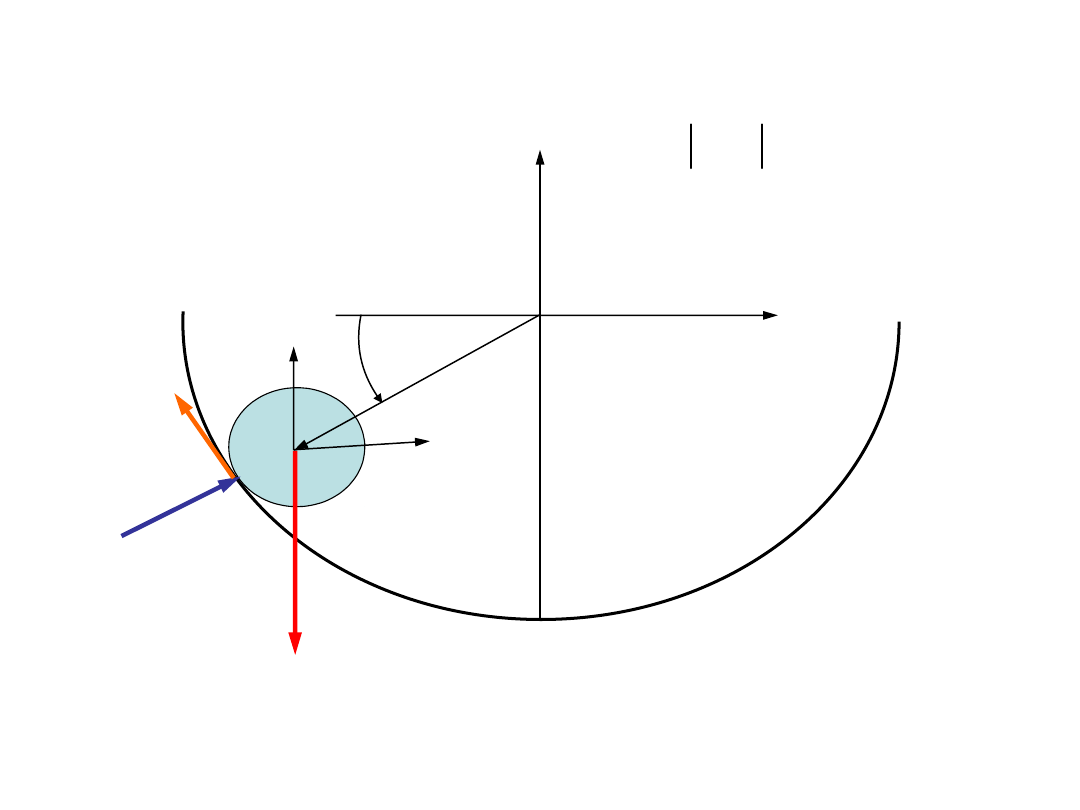
Równania ruchu bryły
sztywnej

Przykład:

y

x

0

x

1

y

1

G

R

T

C

0

( )

r t

r

0

1

2

( )

r t

r r

= -

r

( )

t

a

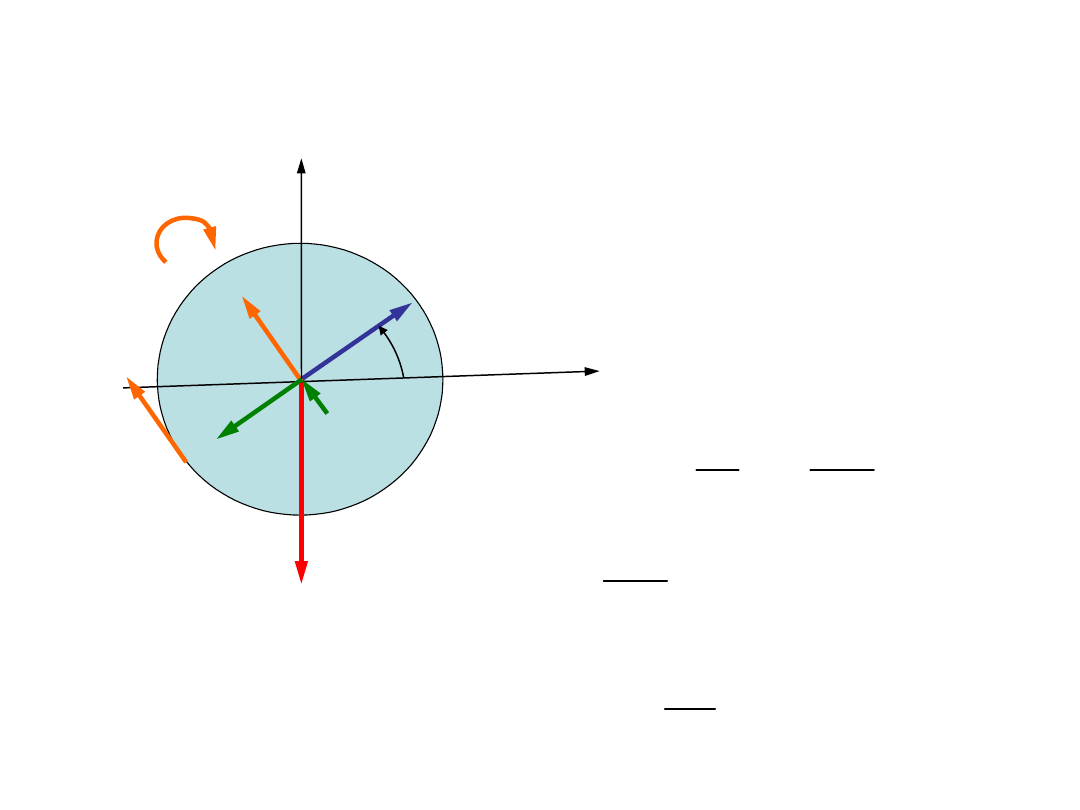
Równania ruchu bryły
sztywnej

x

1

y

1

G

R

T

M

T

=

-Tr

2

F

Bn

F

Bs

Opis ruchu
postępowego

T

sin ( ) 0

Bn

R F

G

t

a

-

-

=

( )

t

a

cos ( ) 0

Bs

T F

G

t

a

+

-

=

2

0

1

2

(

)

Bn

F

m

r r

w

=

-

0

1

2

(

)

Bs

d

du

F

m

m

r r

dt

dt

w

=

=

-

0

1

2

(

)

cos

d

m

r r

mg

T

dt

w

a

-

=

-

2

0

1

2

(

)

sin

R m

r r

mg

w

a

=

-

+

0

d

dt

a

w

=

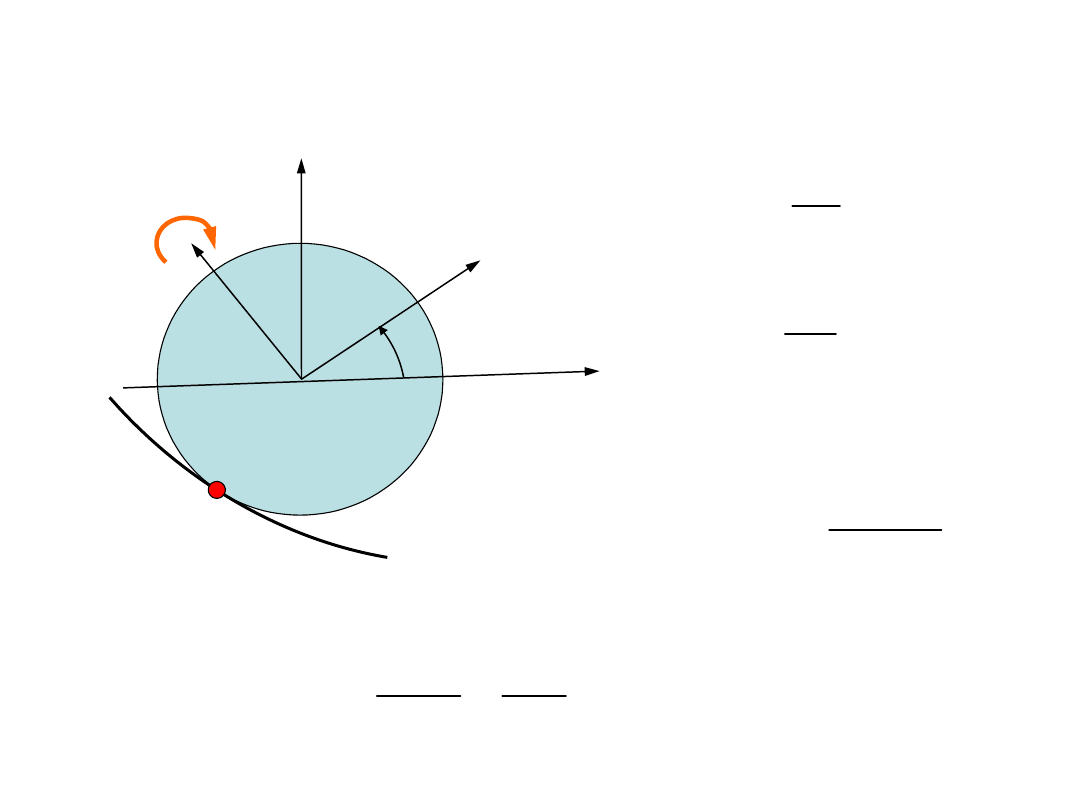
Równania ruchu bryły
sztywnej

x

1

y

1

M

T

=

-Tr

2

Opis ruchu obrotowego

A

Prędkość punktu A w układzie nieruchomym jest równa
zero.

( )

t

j

2

z

d

I

Tr

dt

w

=-

d

dt

j

w

=

x

h

(

)

2

0

1

2

0

r

r r

w

w

+

-

=

0

1

2

2

2

z

d

r r

I

Tr

r

dt

w

-

=

(

)

1

2

0

2

r r

r

w

w

-

=-

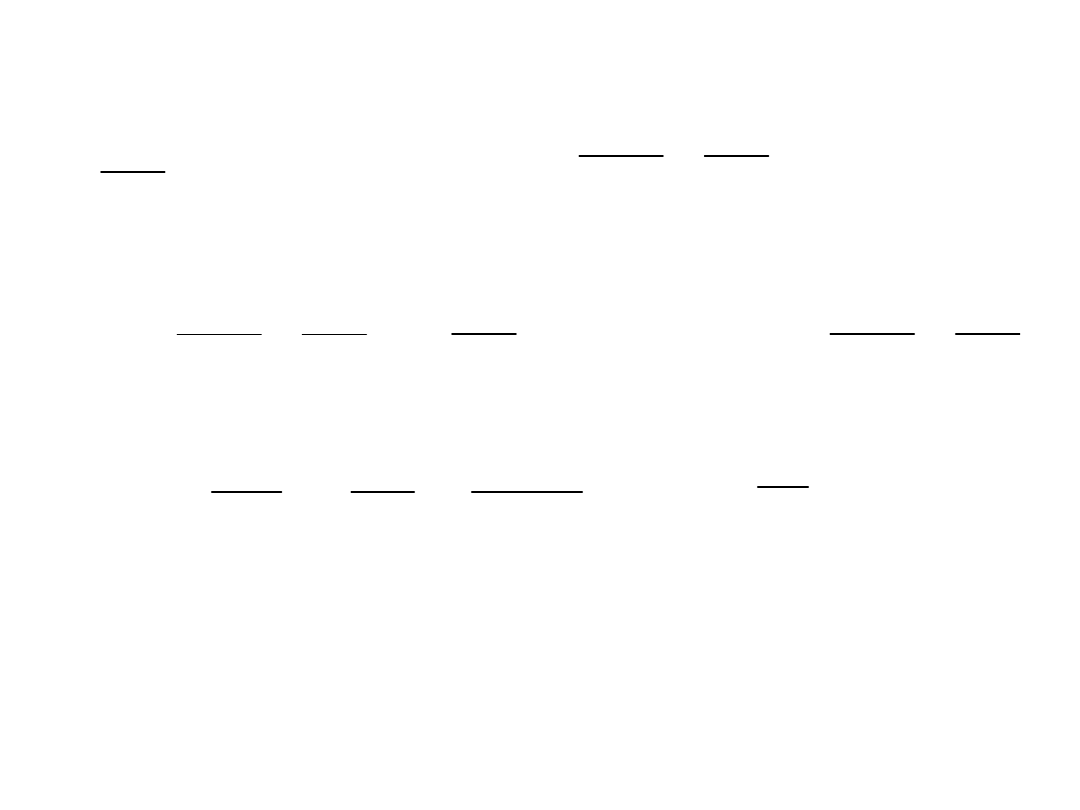
Równania ruchu bryły
sztywnej

0

1

2

(

)

cos

d

m

r r

mg

T

dt

w

a

-

=

-

0

1

2

2

2

z

d

r r

I

Tr

r

dt

w

-

=

0

1

2

2

2

z

d

r r

T

I

r

dt

w

-

=

0

0

1

2

1

2

2

2

(

)

cos

z

d

d

r r

m

r r

mg

I

dt

r

dt

w

w

a

-

-

=

-

0

2

2

1

2

cos

1

z

d

I

g

dt

mr

r r

w

a

�

�

+

=

�

�

-

�

�

0

d

dt

a

w

=

0

0

(0)

,

(0) 0

a

a

w

=

=

Równania ruchu bryły
sztywnej

2. Wyznaczamy prędkość kątową obrotu
walca:

3. Wyznaczamy kąt obrotu
walca:

1. Rozwiązując układ równań wyznaczamy funkcje:

1

0

2

( )

( )

r

t

t

r

w

w

=

0

( )

( )

t

t

d

j

w t t

=

�

0

( ), ( )

t

t

a

w

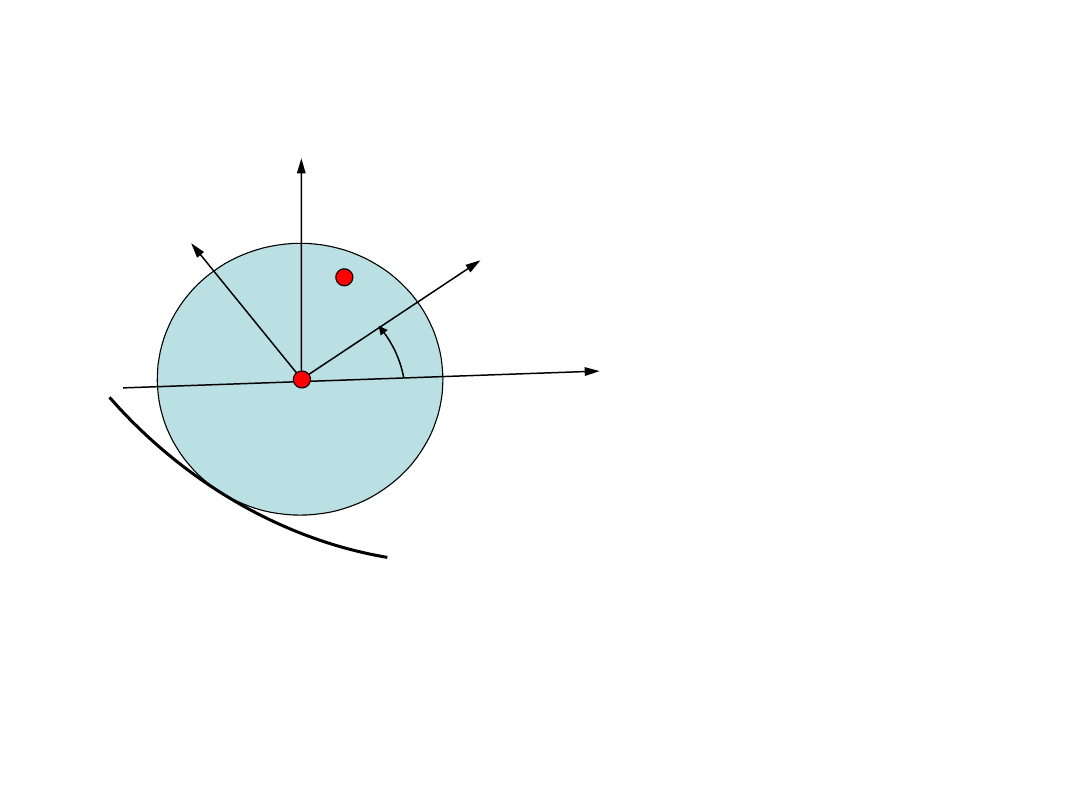
Równania ruchu bryły
sztywnej

x

1

y

1

A

C

( )

t

j

x

h

1

( )

( )

( )

( )

cos ( )

sin ( )

A

C

A

C

A

A

x t

x t

x t

x t

t

t

x

j

h

j

=

+

=

+

-

1

( )

( )

( )

( )

sin ( )

cos ( )

A

C

A

C

A

A

y t

y t

y t

x t

t

t

x

j

h

j

=

+

=

+

+

1

2

( ) (

)sin ( )

C

x t

r r

t

a

= -

1

2

( ) (

)cos ( )

C

y t

r r

t

a

= -

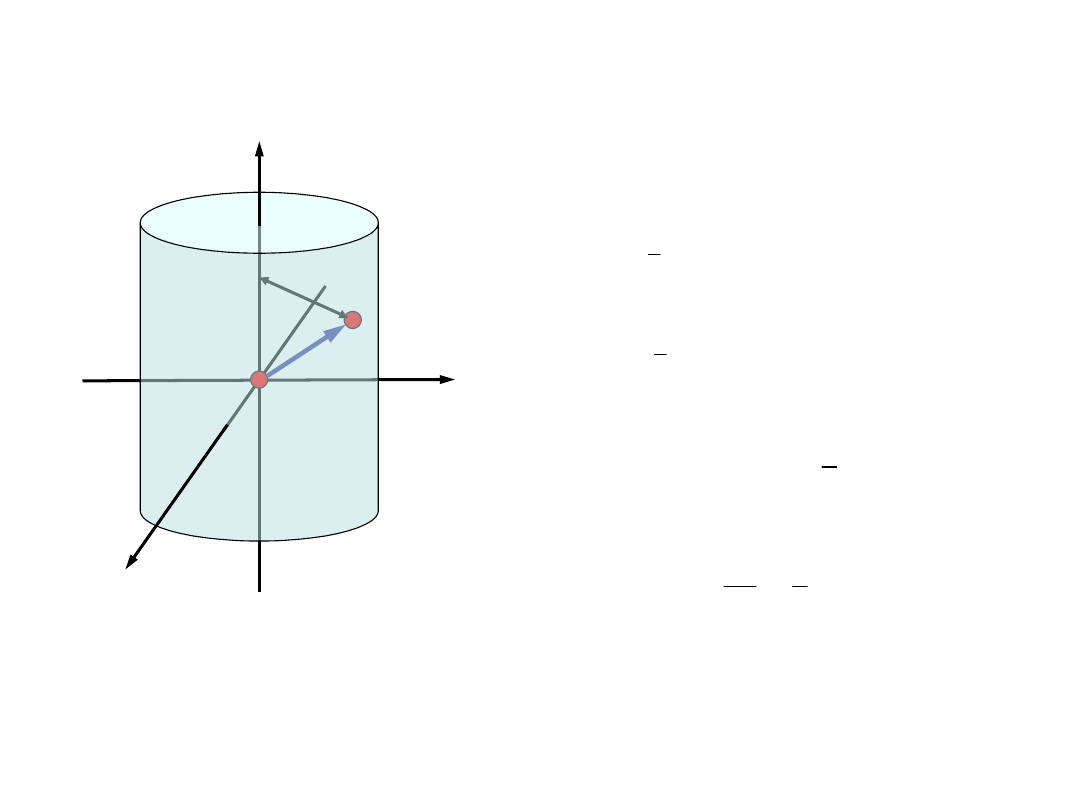
Równania ruchu bryły
sztywnej

C

z

y

x

i

h

i

r

r

(

)

2

2

z

V

I

x

y dV

r

=

+

�

2

2

2

2

0 0

2

l

r

z

l

I

h hd dhdz

p

r

j

-

=

���

2

3

4

1

2

2

0

2

r

z

I

l h dh

lr

pr

pr

=

=

�

2

2

m

lr

pr

=

2

1

2

2

z

I

r

m

=

Równania ruchu bryły
sztywnej

2

1

2

0

2

2

2

1

2

cos

1

r

d

g

dt

r

r r

w

a

�

�

+

=

�

�

-

�

�

(

)

0

1

2

1

2

cos

1

d

g

dt

r r

w

a

+ =

-

(

)

0

1

2

2 cos

3

d

g

dt

r r

w

a

=

-

0

d

dt

a

w

=

Dziękuję za uwagę