1
Wybrane rozkłady prawdopodobieństwa zmiennych
losowych
1.1
Podstawowe rozkłady typu dyskretnego
1. Zmienna losowa X ma rozkład jednopunktowy , skoncentrowany w punkcie x
0
jeśli przyjmuje z prawdopodobieństwem jeden wartość x
0
tj.
P (X = x
0
) = 1.
Podstawowe charakterystyki rozkładu:
EX = x
0
, V arX = 0.
Funkcja charakterystyczna:
ϕ
X
(t) = e
itx
0
.
2. Zmienna losowa X ma rozkład zerojedynkowy (rozkład Bernoulliego) z parame-
trem p, 0 < p < 1 (oznaczany B(1, p)) jeśli przyjmuje wartości ze zbioru {0, 1} z
prawdopodobieństwami:
P (X = 1) = p, P (X = 0) = 1 − p.
Podstawowe charakterystyki rozkładu:
EX = p, V arX = p(1 − p).
Funkcja charakterystyczna:
ϕ
X
(t) = 1 − p + pe
it
.
3. Zmienna losowa X ma rozkład jednostajny dyskretny jeżeli przyjmuje wartości
ze zbioru {x
1
, x
2
, ..., x
n
} z prawdopodobieństwami:
P (X = x
i
) =
1
n
, i = 1, 2, ..., n.
Podstawowe charakterystyki rozkładu:
EX =
1
n
n
X
i=1
x
i
, V arX =
1
n
n
X
i=1
(x
i
− EX)
2
.
Funkcja charakterystyczna:
ϕ
X
(t) =
1
n
n
X
i=1
e
itx
i
.
1
4. Zmienna losowa X ma rozkład dwumianowy z parametrami n, p, ( n ∈ N, 0 <
p < 1) (oznaczany B(n, p)), jeśli przyjmuje wartości ze zbioru {0, 1, 2, ..., n} z praw-
dopodobieństwami:
P (X = k) =
n
k
p
k
(1 − p)
k
, k = 0, 1, 2, ..., n, 0 < p < 1.
Podstawowe charakterystyki rozkładu:
EX = np, V arX = np(1 − p).
Funkcja charakterystyczna
ϕ
X
(t) = (1 − p + pe
it
)
n
.
Należy zauważyć, że jeżeli {X
1
, X
2
, ..., X
n
} jest ciągiem niezależnych zmiennych lo-
sowych o rozkładzie Bernoulliego z parametrem p B(1, p) to zmienna losowa
P
n
i=1
X
i
ma rozkład dwumianowy B(n, p).
5. Zmienna losowa X ma rozkład Poissona z parametrem λ, λ > 0 (oznaczany P(λ))
jeżeli przymuje ona wartości na zbiorze {0, 1, 2, ...} z prawdopodobieństwami
P (X = k) =
λ
k
k!
e
−λ
, k = 0, 1, 2, ...
Podstawowe charakterystyki rozkładu:
EX = λ, V arX = λ.
Funkcja charakterystyczna:
ϕ
X
(t) = e
λ(e
it
−1)
.
6. Zmienna losowa X ma rozkład geometryczny z parametrem p, 0 < p < 1
(oznaczany Ge(p)), jeżeli przyjmuje ona wartości ze zbioru {0, 1, 2, ...} z prawdopo-
dobieństwami:
P (X = k) = p(1 − p)
k
, k = 0, 1, 2, ...
Podstawowe charakterystyki rozkładu:
EX =
1 − p
p
, V arX =
p
(1 − p)
2
.
Funkcja charakterystyczna:
ϕ
X
(t) =
p
1 − (1 − p)e
it
.
2
7. Zmienna losowa X ma rozkład ujemny dwumianowy z parametrami n, p, (n ∈
N, 0 < p < 1) (oznaczany N B(n, p))jeżeli przyjmuje wartoście ze zbioru {0, 1, 2, ...}
z prawdopodobieństwami
P (X = k) =
k + n − 1
k
!
p
k
(1 − p)
n
, k = 0, 1, 2, ...
Podstawowe charakterystyki rozkładu:
EX =
np
1 − p
, V arX =
np
(1 − p)
2
.
Funkcja charakterystyczna:
ϕ
X
(t) =
1 − p
1 − pe
it
!
n
1.2
Podstawowe rozkłady typu ciągłego
1. Zmienna losowa X ma rozkład jednostajny (prostokątny)na odcinku (a, b)
(oznaczany U (a, b)), jeżeli jej gęstość f (x) wyraża się wzorem
f (x) =
1
b − a
1
(a,b)
(x).
Podstawowe charakterystyki rozkładu:
EX =
a + b
2
, V arX =
(b − a)
2
12
.
Funkcja charakterystyczna:
ϕ
X
(t) =
e
itb
− e
ita
(b − a)it
.
2. Zmienna losowa X ma rozkład normalny z parametrami µ, σ, (σ > 0, µ ∈ R)
(oznaczany N (µ, σ)), jeżeli jej gęstość f (x) jest określona wzorem
f (x) =
1
√
2πσ
exp
−
(x − µ)
2
2σ
2
!
x ∈ R).
Podstawowe charakterystyki rozkładu:
EX = µ, V arX = σ
2
.
Funkcja charakterystyczna
ϕ
X
(t) = e
itµ−
1
2
t
2
σ
2
.
Jeżeli zmienna losowa X ma rozkład normalny N (µ, σ) to zmienna losowa U =
X−µ
σ
ma rozkład N (0, 1), której dystrybuantę oznaczamy Φ(x). Ponadto mamy Φ(x) =
1 − Φ(−x).
3
3. Zmienna losowa X ma rozkład gamma z parametrami α, β, (α > 0, β > 0)
(oznaczany Γ(α, β)), jeżeli jej gęstość f (x) jest określona wzorem
f (x) =
1
β
α
Γ(α)
x
α−1
exp
−
x
β
!
1
(0,+∞)
(x),
gdzie funkcja gamma Γ(α) jest określona wzorem
Γ(α) =
Z
∞
0
x
α−1
e
−x
dx, α > 0, Γ(p + 1) = pΓ(p), Γ
1
2
=
√
π.
Podstawowe charakterystyki rozkładu:
EX = αβ, V arX = αβ
2
.
Funkcja charakterystyczna
ϕ
X
(t) =
1
(1 − itβ)
α
.
4. Zmienna losowa X ma rozkład wykładniczy z parametrem λ, (λ > 0) (oznaczany
Exp(λ)), jeżeli jej gęstość f (x) jest określona wzorem
f (x) =
1
λ
exp
−
x
λ
1
(0,+∞)
(x).
Podstawowe charakterystyki rozkładu:
EX = λ, V arX = λ
2
.
Funkcja charakterystyczna
ϕ
X
(t) =
1
1 − itλ
.
Warto zauważyć, że rozkład wykładniczy jest szczególnym przypadkiem rozkładu
gamma Γ(1, λ).
5. Zmienna losowa X ma rozkład χ
2
z parametrem n, n ∈ N) (oznaczany χ
2
(n)),
jeżeli jej gęstość f (x) określa wzór .
f (x) =
1
2
n/2
Γ(
n
2
x
n/2−1
exp
−
x
2
1
(0,+∞)
(x).
Podstawowe charakterystyki rozkładu:
EX = n, V arX = 2n.
Funkcja charakterystyczna
ϕ
X
(t) =
1
(1 − 2it)
n/2
.
4
Warto zauważyć, że rozkład χ
2
jest szczególnym przypadkiem rozkładu gamma
Γ(
n
2
, 2). Należy również zauważyć, że rozkład χ
2
jest dokładnym rozkładem staty-
styki
χ
2
=
n
X
i=1
U
2
i
=
n
X
i=1
X
i
− µ
σ
2
,
będącej funkcją próby prostej (X
1
, X
2
, ..., X
n
) pobranej z populacji o rozkładzie
N (µ, σ). Liczba stopni swobody jest parametrem rozkładu i ma wpływ na kształt
funkcji gęstości.
6. Zmienna losowa X ma rozkład beta z parametrami α, β, (α > 0, β > 0) (ozna-
czany B(α, β)), jeżeli jej gęstość f (x) wyraża się wzorem
f (x) =
1
B(α, β)
x
α−1
(1 − x)
β−1
1
(0,1)
(x),
gdzie funkcja beta B(α, β) określona jest wzorem
B(α, β) =
Z
1
0
x
α−1
(1 − x)
β−1
dx, α > 0, β > 0, B(α, β) =
Γ(α)Γ(β)
Γ(α + β)
.
Podstawowe charakterystyki rozkładu:
EX =
α
α + β
, V arX =
αβ
(α + β)
2
(α + β + 1)
.
7. Zmienna losowa X ma rozkład potęgowy z parametrami α, λ, (α > 0, λ > 0)
(oznaczany P o(α, λ)), jeżeli jej gęstość f (x) jest określona wzorem
f (x) =
αx
α−1
λ
α
1
(0,λ)
(x).
Podstawowe charakterystyki rozkładu:
EX =
αλ
α + 1
, V arX =
αλ
2
(α + 1)
2
(α + 2)
.
8. Zmienna losowa X ma rozkład Pareto z parametrami x
0
, α, ( x
0
> 0, α > 0),
(oznaczany P a(x
0
, α)), jeżeli jej gęstość f (x) jest posatci
f (x) =
α
x
0
x
0
x
α+1
1
(x
0
,∞)
(x).
Podstawowe charakterystyki rozkładu:
EX =
αx
0
α − 1
, V arX =
αx
2
0
(α − 1)
2
(α − 2)
.
5
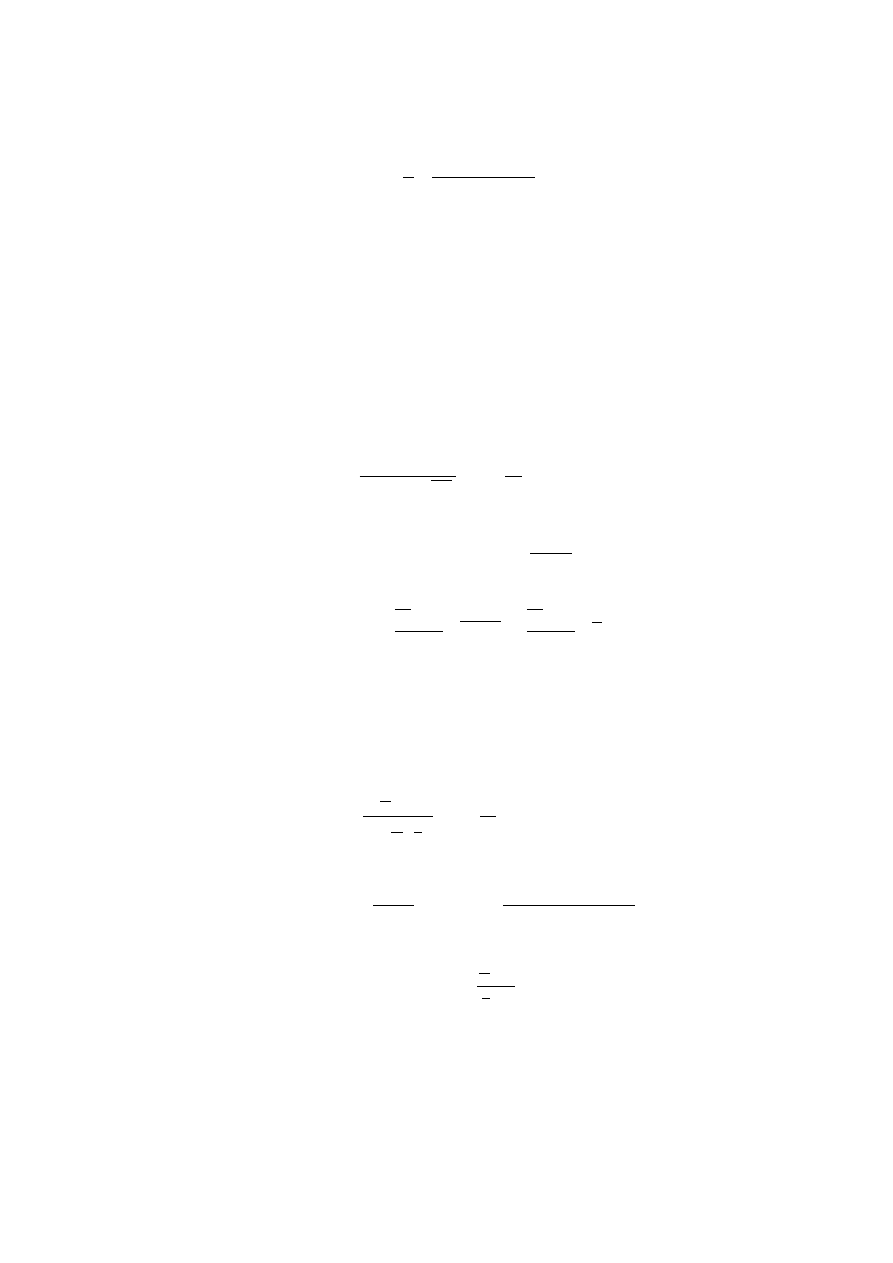
9. Zmienna losowa X ma rozkład Cauchy’ego z parametrami α, γ, (α ∈ R, λ > 0),
(oznaczany C(α, λ)), jeżeli jej gęstość f (x) jest wyrażona wzorem
f (x) =
1
π
λ
λ
2
+ (x − α)
2
!
, x ∈ R.
Podstawowe charakterystyki rozkładu:
EX − nieistnieje, V arX − nie istnieje.
Funkcja charakterystyczna:
ϕ
X
(t) = exp(iαt − λ|t|).
Standardowy rozkład Cauchy’ego jest postaci C(0, 1)
10. Zmienna losowa X ma rozkład t-Studenta z n stopniami swobody n ∈ N, (ozna-
czany t(n)), jeżeli jej gęstość f (x) jest określona wzorem
f (x) =
Γ((n + 1)/2)
Γ(n/2)
√
πn
1 +
x
2
n
!
−(n+1)/2
, x ∈ R.
Podstawowe charakterystyki rozkładu:
EX = 0, V arX =
n
n − 2
.
Należy zauważyć, że statystyka
T =
X − µ
S
√
n − 1 =
X − µ
b
S
√
n
będąca funkcją próby prostej (X
1
, X
2
, ..., X
n
) pobranej z populacji o rokładzie
N (µ, σ) ma rozkład t-Studneta o n − 1 stopniach swobody.
11. Zmienna losowa X ma rozkład F Snedecora z (m, n) stopniami swobody (m, n ∈
N), (oznaczany F (m, n)), jeżeli jej gęstość f (x) jest postaci
f (x) =
m
n
m/2
B
m
2
,
n
2
1 +
m
n
x
−(m+n)/2
1
(0,∞)
(x).
Podstawowe charakterystyki rozkładu:
EX =
n
n − 2
, V arX =
2n
2
(m + n − 2)
m(n − 2)
2
(n − 4)
.
Należy zauważyć, że statystyka określona wzorem
F =
1
m
χ
2
m
1
n
χ
2
n
,
gdzie zmienne χ
2
m
i χ
2
n
są niezależnymi zmiennymi losowymi takimi, że χ
2
m
ma
rozkład chi-kwadrat o m stopniach swobody, a χ
2
n
ma rozkład chi-kwadrat z n
stopniami swobody, ma rozkład F Snedecora o (m, n) stopniach swobody.
6