
Matematyka Dyskretna
Andrzej Szepietowski
25 marca 2004 roku


Rozdział 1
Teoria liczb
1.1
Dzielenie całkowitoliczbowe
Zacznijmy od przypomnienia szkolnego algorytmu dzielenia liczb naturalnych. Podziel-
my 174 przez 12.
1
4
1
7
4
:
1
2
1
2
5
4
4
8
6
W wyniku dzielenia otrzymali´smy iloraz 14 i reszt˛e 6 . Liczby te spełniaj ˛
a równanie
174 = 14
· 12 + 6
i reszta jest mniejsza od dzielnika. Podobnie mo˙zemy post ˛
api ´c dla dowolnych liczb natu-
ralnych a i b pod warunkiem, ˙ze b
6= 0.
Twierdzenie 1.1 Dla dowolnych liczb naturalnych a oraz b >
0 istnieje dokładnie jedna
para liczb naturalnych q i r spełniaj ˛
acych warunki:
• a = bq + r
• 0 ≤ r < b
q nazywa si˛e ilorazem całkowitoliczbowym a przez b, a r nazywa si˛e reszt ˛
a z dzielenia
Zauwa˙zmy, ˙ze iloraz q jest zaokr ˛
agleniem w dół normalnego ilorazu q
=
b
a
b
c. Iloraz
całkowitoliczbowy liczb a i b b˛edziemy oznacza´c przez
a
÷ b
lub
a
div b.
a reszt˛e przez
a
mod b.
3

4
Rozdział 1. Teoria liczb
Przykład 1.2
22
÷ 4 = 5 oraz 22 mod 4 = 2, poniewa˙z 22 = 5 · 4 + 2 oraz 0 ≤ 2 < 4.
Powy˙zsze definicje zakładały, ˙ze a i b s ˛
a naturalne. W przypadku, gdy a i b s ˛
a liczba-
mi całkowitymi, iloraz i ró˙znice mo˙zna róznie definiowa´c. Na przykład w j˛ezyku Pascal
iloraz dwóch liczb typu całkowitego oznacza si˛e przez
a div b
i jest to
b
a
b
c — zaokr ˛aglenie ilorazu
a
b
w dół, gdy
a
b
jest dodatnie i
d
a
b
e, — zaokr ˛aglenie
ilorazu
a
b
w gór˛e, gdy
a
b
jest ujemne. Reszta, któr ˛
a oznacza si˛e przez
a mod b,
jest okre´slona wzorem:
a mod b = a-(a div b)*b.
Mamy wi˛ec, na przykład:
22 div 4 = 5; (-22)div 4 = -5; 22 div(-4)= -5; (-22)div(-4)= 5;
22 mod 4 = 2; (-22)mod 4 = -2; 22 mod(-4)= 2; (-22)mod(-4)= -2.
1.2
Podzielno´s´c liczb
Mówimy, ˙ze liczba całkowita a
6= 0 dzieli liczb˛e całkowit ˛a b, je˙zeli istnieje liczba całko-
wita z, taka ˙ze:
b
= az.
B˛edziemy to oznacza´c przez a
|b. Zauwa˙zmy, ˙ze zachodzi wtedy:
b
mod a = 0.
Liczb˛e a nazywamy dzielnikiem liczby b.
Przykład 1.3
3
|6, 3| − 6 oraz 3|0.
Lemat 1.4 Je˙zeli a
|b oraz a|c , to a|(b + c) oraz a|(b − c)
Dowód. Je˙zeli a
|b i a|c, to istniej ˛a dwie liczby całkowite k i m, takie ˙ze:
b
= ak
oraz
c
= am.
Mamy wi˛ec:
b
+ c = ak + am = a(k + m)
oraz
b
− c = ak − am = a(k − m)
czyli a dzieli b
+ c oraz b
− c.
2

1.3. Relacja kongruencji
5
1.3
Relacja kongruencji
Niech m b˛edzie dowoln ˛
a liczb ˛
a naturaln ˛
a m
6= 0. Powiemy, ˙ze dwie liczby całkowite a i
b s ˛
a równowa˙zne (lub przystaj ˛
a) modulo m, je˙zeli
m
|(a − b).
B˛edziemy wtedy pisa´c:
a
= b (mod m).
Przykład 1.5
1 = 4 (mod 3),
3 = 0 (mod 3),
−1 = 2 (mod 3),
−1 = −7 (mod 3).
Je˙zeli a i b s ˛
a dodatnie, to a
= b (mod m) wtedy i tylko wtedy, gdy a i b maj ˛
a takie
same reszty z dzielenia przez m.
Lemat 1.6 Relacja przystawania modulo jest relacj ˛
a równowa˙zno´sci, czyli spełnia na-
st˛epuj ˛
ace trzy warunki:
• zwrotno´s´c, dla ka˙zdego a zachodzi
a
= a (mod m),
• symetri˛e, dla ka˙zdego a i b, je˙zeli
a
= b (mod m),
to
b
= a (mod m),
• przechodnio´s´c, dla ka˙zdego a, b i c,
je˙zeli
a
= b (mod m)
i
b
= c (mod m),
to
a
= c (mod m).
Dowód. Udowodnimy tylko przechodnio´s´c relacji. Je˙zeli m
|(a − b) oraz m|(b − c),
to m
|((a − b) + (b − c)), czyli m|(a − c).
2
Ponadto relacja modulo jest zgodna z dodawaniem, odejmowaniem i mno˙zeniem.
Twierdzenie 1.7 Je˙zeli
a
= b (mod m)
oraz
c
= d (mod m),
to:
a
+ c = b + d (mod m),
a
− c = b − d (mod m),
ac
= bd (mod m).
Dowód. Z zało˙zenia mamy:
m
|(a − b)
oraz
m
|(c − d),
z tego za´s łatwo wynika, ˙ze m dzieli:
(a + c)
− (b + d), (a − c) − (b − d) oraz ac − bd = a(c − d) + d(a − b),
czyli zachodzi teza twierdzenia.
2
Przykład 1.8 Twierdzenie 1.7 mo˙ze by´c u˙zyte do obliczania reszty z dzielenia Je˙zeli chce-
my policzy´c na przykład
1999 mod 3,

6
Rozdział 1. Teoria liczb
to pytamy, która z trzech liczb
{0, 1, 2} przystaje do 1999 modulo 3. Zróbmy najpierw
kilka prostych obserwacji. Po pierwsze:
10 = 1 (mod 3),
bo
3
|(10 − 1). Z twierdzenia 1.7 wynika, ˙ze ka˙zda pot˛ega liczby dziesi˛e´c przystaje do 1
modulo 3, czyli:
10
k
= 1 (mod 3)
dla ka˙zdego k. Mamy teraz:
1999 = 1000 + 9
· 100 + 9 · 10 + 9 = 1 + 9 + 9 + 9 = 1 (mod 3).
Podobnie, dla dowolnej liczby x, je˙zeli zapiszemy x w postaci dziesi˛etnej:
x
=
X
d
i
· 10
i
,
to
x
=
X
d
i
(mod 3),
czyli x ma takie same reszty modulo 3 co suma cyfr w zapisie dziesi˛etnym.
Przykład 1.9 Aby przekona´c si˛e, ˙ze
2002
· 1999 6= 4001999
wystarczy zauwa˙zy´c, ˙ze liczba
2002 jest parzysta, wi˛ec tak˙ze wynik mno˙zenia powinien
by˙z parzysty. Mówi ˛
ac inaczej
2002 = 0 (mod 2), wi˛ec na podstawie twierdzenia 1.7
mamy
2002
· 1999 = 0 (mod 2), a liczba 4001999 przystaje do jedynki modulo 2.
Podobnie mo˙zemy si˛e przekona´c, ˙ze
2002
· 1999 6= 4001996
wystarczy zauwa˙zy´c, ˙ze w iloczynie
2002
· 1999 ostatni ˛
a cyfr ˛
a powinno by´c 8 a nie 6.
Inaczej
2002 = 2 (mod 10) oraz 1999 = 9 (mod 10), wi˛ec na podstawie twierdze-
nia 1.7 mamy
2002
· 1999 = 8 (mod 10), a liczba 4001996 przystaje do 6 modulo
10.
1.4
Klasy abstrakcji
Dla relacji przystawania modulo m definiujemy klasy abstrakcji. Dla dowolnej liczby
całkowitej x, klas˛e abstrakcji elementu x definiujemy w nast˛epuj ˛
acy sposób:
[x] =
{y | y = x (mod m)}.
Innymi słowy, klasa abstrakcji liczby x to zbiór wszystkich liczb z ni ˛
a równowa˙znych.
Przykład 1.10 Dla m
= 3 mamy trzy klasy abstrakcji

1.5. Pier´scie´n Z
m
7
[0] =
{3k | k ∈ Z} = {. . . , −9, −6, −3, 0, 3, 6, 9, . . .}
[1] =
{3k + 1 | k ∈ Z} = {. . . , −8, −5, −2, 1, 4, 7, 10, . . .}
[2] =
{3k + 2 | k ∈ Z} = {. . . , −7, −4, −1, 2, 5, 8, 11, . . .}
Zauwa˙zmy, ˙ze klasy abstrakcji elementów równowa˙znych pokrywaj ˛
a si˛e.
Lemat 1.11 Je˙zeli
x
= y
(mod m),
to
[x] = [y].
Dowód. Je˙zeli z
∈ [x], to
z
= x
(mod m)
i z przechodnio´sci relacji mamy
z
= y
(mod m),
czyli z
∈ [y], a wi˛ec pokazali´smy, ˙ze:
[x]
⊂ [y].
Identycznie pokazujemy zawieranie odwrotne
[y]
⊂ [x].
2
Nast˛epna wa˙zna własno´s´c klas abstrakcji to ich rozł ˛
aczno´s´c.
Lemat 1.12 Je˙zeli
[x]
∩ [y] 6= ∅,
to
[x] = [y],
inaczej, dwie klasy abstrakcji
[x] i [y] albo s ˛
a identyczne, albo s ˛
a rozł ˛
aczne.
Dowód. Przypu´s´cmy, ˙ze klasy
[x] i [y] maj ˛
a wspólny element z. Wtedy:
z
= x (mod m)
oraz
z
= y
(mod m).
Z przechodnio´sci mamy wtedy
x
= y
(mod m),
a z lematu 1.11
[x] = [y].
2
1.5
Pier´scie ´n Z
m
Klasy abstrakcji relacji modulo m wygl ˛
adaj ˛
a nast˛epuj ˛
aco:
[0], [1], . . . , [m
− 1].
Dla dowolnego k z przedziału
0
≤ k ≤ m − 1, klasa [k] jest postaci:
[k] =
{jm + k | j ∈ Z}

8
Rozdział 1. Teoria liczb
(Z oznacza zbiór liczb całkowitych). Zbiór klas abstrakcji modulo m oznacza si˛e przez
Z
m
.
Poniewa˙z relacja modulo jest zgodna z działaniami dodawania i mno˙zenia, mo˙zemy
zdefiniowa´c dodawanie i mno˙zenie na klasach abstrakcji. Mówi ˛
ac w skrócie, aby wyko-
na´c działanie na dwóch klasach abstrakcji, wybieramy dowolnych przedstawicieli tych
klas i wykonujemy działania na tych przedstawicielach. Dokładniej, dodawanie klas abs-
trakcji definiujemy nast˛epuj ˛
aco:
[x] + [y] = [x + y].
Podobnie definiujemy odejmowanie i mno˙zenie:
[x]
− [y] = [x − y],
[x]
· [y] = [x · y].
Poni˙zszy lemat pokazuje, ˙ze działania te s ˛
a dobrze zdefiniowane; ˙ze wynik działania na
dwóch klasach nie zale˙zy od wyboru reprezentantów.
Lemat 1.13 Je˙zeli
[x] = [y]
oraz
[u] = [w],
to:
[x + u] = [y + w],
[xu] = [yw]
oraz
[x
− u] = [y − w].
Dowód. Z zało˙zenia mamy:
x
= y
(mod m)
oraz
u
= w
(mod m).
a z twierdzenia 1.7:
[x + u] = [y + w],
[x
− u] = [y − w] oraz [xu] = [yw].
2
Przykład 1.14 Niech m
= 3. Dla dowolnych dwóch liczb x
∈ [0] i y ∈ [1] ich suma
x
+ y nale˙zy do [0 + 1] = [1] a iloczyn do [0
· 1] = [0].
Lemat 1.15 Działania na klasach abstrakcji
[0], [1], . . . , [n
− 1]
spełniaj ˛
a nast˛epuj ˛
ace warunki:
• dodawanie oraz mno˙zenie s ˛
a przemienne i ł ˛
aczne,
• klasa [0] jest elementem neutralnym dodawania, to znaczy dla ka˙zdego a mamy
[a] + [0] = [a],
• dla ka˙zdej klasy [a] istnieje klasa do niej przeciwna [−a], taka ˙ze [a] + [−a] = [0],
• klasa [1] jest elementem neutralnym mno˙zenia, to znaczy dla dowolnego [x] mamy
[x]
· [1] = [x],
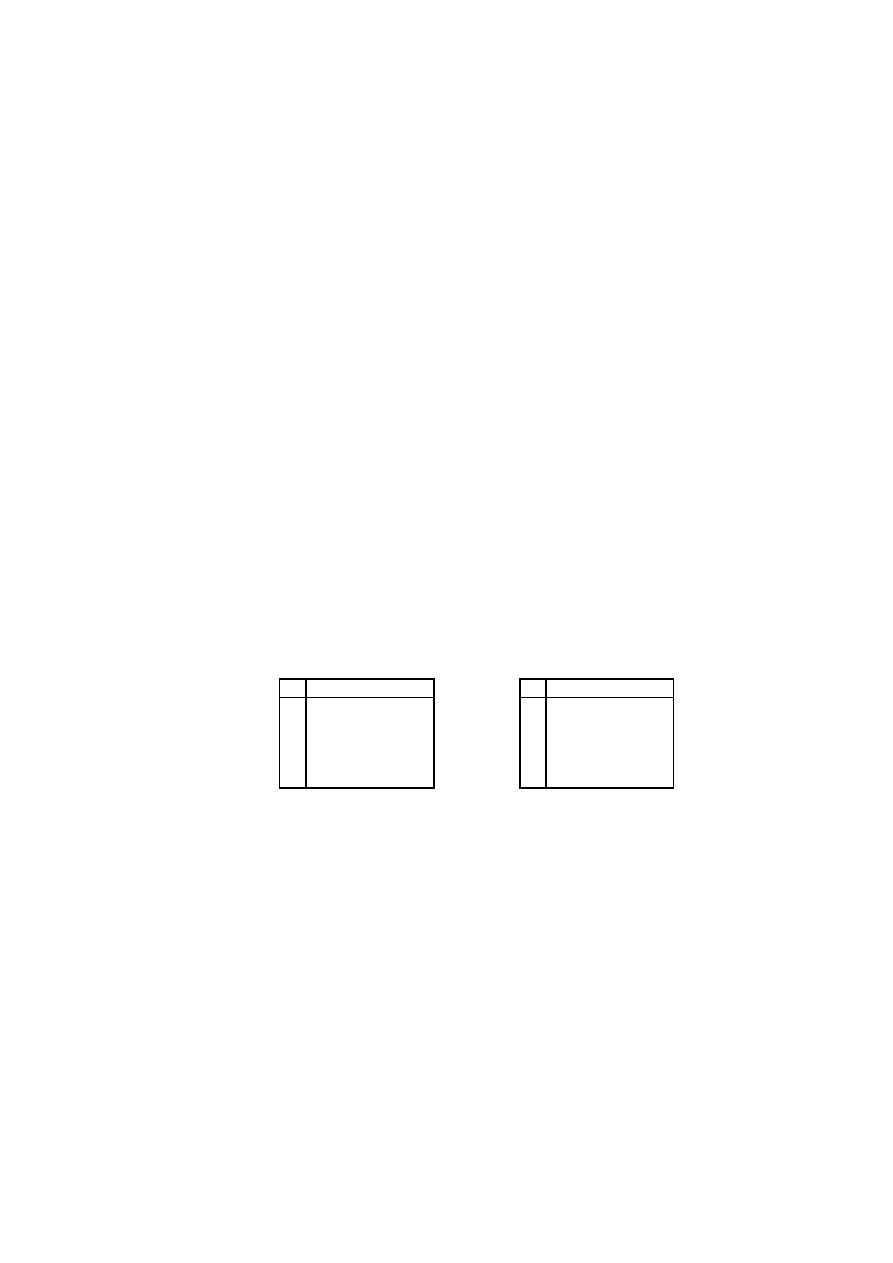
1.5. Pier´scie´n Z
m
9
• mno˙zenie jest rozdzielne wzgl˛edem dodawania, czyli dla ka˙zdych trzech klas [x],
[y], [z] mamy [x]([y] + [z]) = [x][y] + [x][z].
Zbiór z dwoma działaniami spełniaj ˛
acymi powy˙zsze warunki nazywa si˛e pier´scieniem
przemiennym z jedynk ˛
a.
Dowód: Udowodnimy tylko rozdzielno´s´c:
[x]([y] + [z]) = [x][y + z] = [x(y + z)] = [xy + xz] = [xy] + [xz] = [x][y] + [x][z].
Skorzystali´smy w tym dowodzie z rozdzielno´sci mno˙zenia wzgl˛edem dodawania dla liczb
całkowitych.
2
1.5.1
Pier´scie ´n Z
5
Rozwa˙zmy zbiór reszt modulo 5. Składa si˛e on z pi˛eciu klas:
[0], [1], [2], [3], [4],
dla prostoty b˛edziemy dalej opuszcza´c nawiasy. Mamy wi˛ec zbiór:
Z
5
=
{0, 1, 2, 3, 4}
z dodawaniem i mno˙zeniem okre´slonym nast˛epuj ˛
acymi tabelami:
+
0
1
2
3
4
0
0
1
2
3
4
1
1
2
3
4
0
2
2
3
4
0
1
3
3
4
0
1
2
4
4
0
1
2
3
·
0
1
2
3
4
0
0
0
0
0
0
1
0
1
2
3
4
2
0
2
4
1
3
3
0
3
1
4
2
4
0
4
3
2
1
Zauwa˙zmy, ˙ze ka˙zdy element oprócz zera ma w Z
5
element odwrotny wzgl˛edem mno˙ze-
nia, czyli dla ka˙zdego x
∈ Z
5
− {0} istnieje x
−1
, taki ˙ze xx
−1
= 1:
1
−1
= 1,
2
−1
= 3,
3
−1
= 2,
4
−1
= 4.
Dlatego Z
5
jest ciałem, czyli pier´scieniem przemiennym z jedynk ˛
a i z odwrotno´sci ˛
a
wzgl˛edem mno˙zenia.
1.5.2
Pier´scie ´n Z
4
Rozwa˙zmy teraz pier´scie´n reszt modulo 4:
Z
4
=
{0, 1, 2, 3},
gdzie dodawanie i mno˙zenie jest okre´slone nast˛epuj ˛
acymi tabelami:
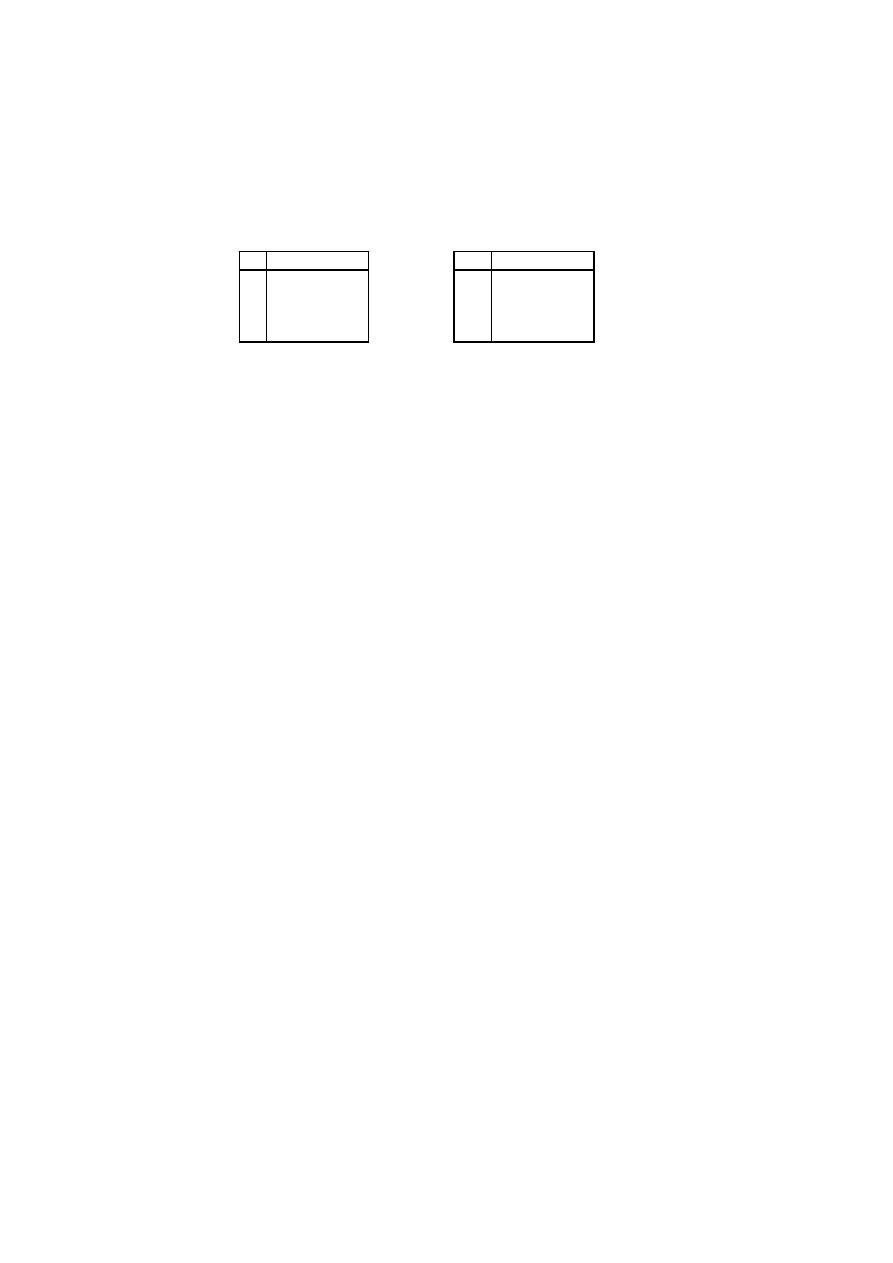
10
Rozdział 1. Teoria liczb
+
0
1
2
3
0
0
1
2
3
1
1
2
3
0
2
2
3
0
1
3
3
0
1
2
·
0
1
2
3
0
0
0
0
0
x 1
0
1
2
3
2
0
2
0
2
3
0
3
2
1
Z
4
nie jest ciałem, poniewa˙z nie ma w nim elementu odwrotnego do 2. Ponadto w Z
4
mamy:
2
· 2 = 0,
czyli zero mo˙zna przedstawi´c jako iloczyn dwóch liczb ró˙znych od zera.
Łatwo zauwa˙zy´c, ˙ze je˙zeli liczba m jest zło˙zona, m
= pq dla 1 < p, q < m, to w
pier´scieniu Z
m
mamy pq
= 0 i ani p, ani q nie maj ˛
a elementów odwrotnych. Przypu´s´cmy
bowiem, ˙ze istnieje p
−1
. Mamy wtedy:
0 = p
−1
0 = p
−1
(pq) = (p
−1
p
)q = 1q = q,
czyli q
= 0, sprzeczno´s´c. Tak wi˛ec Z
m
nie jest ciałem, je˙zeli m jest liczb ˛
a zło˙zon ˛
a.
W dalszej cz˛e´sci tego rozdziału zobaczymy, ˙ze je˙zeli m jest liczb ˛
a pierwsz ˛
a, to Z
m
jest
ciałem.
1.6
Najwi˛ekszy wspólny dzielnik
Dla dwóch liczb całkowitych a i b, ich najwi˛ekszy wspólny dzielnik to po prostu naj-
wi˛eksza liczba całkowita n, która dzieli a i b. Najwi˛ekszy wspólny dzielnik liczb a i b
b˛edziemy oznacza´c przez N W D
(a, b).
Przykład 1.16
N W D
(4, 6) = 2,
N W D
(4, 0) = 4,
N W D
(4,
−6) = 2.
1.7
Algorytm Euklidesa
Aby obliczy´c najwi˛ekszy wspólny dzielnik dwóch dodatnich liczb naturalnych a, b robi-
my co nast˛epuje
dopóki
a
· b 6= 0 wykonuj:
je˙zeli
a
≥ b, to
a
:= a mod b
w przeciwnym przypadku
b
:= b mod a;
NWD:=a+b
Powy˙zszy algorytm oblicza reszt˛e z dzielenia wi˛ekszej liczby przez mniejsz ˛
a tak długo,
a˙z otrzyma zero. Wtedy wynikiem działania algorytmu jest ta druga liczba (je˙zeli a
= 0,
to a
+ b = b, a je˙zeli b = 0, to a + b = a). W poni˙zszej tabeli pokazano kolejne kroki
działania algorytmu Euklidesa na parze liczb 36 i 15:
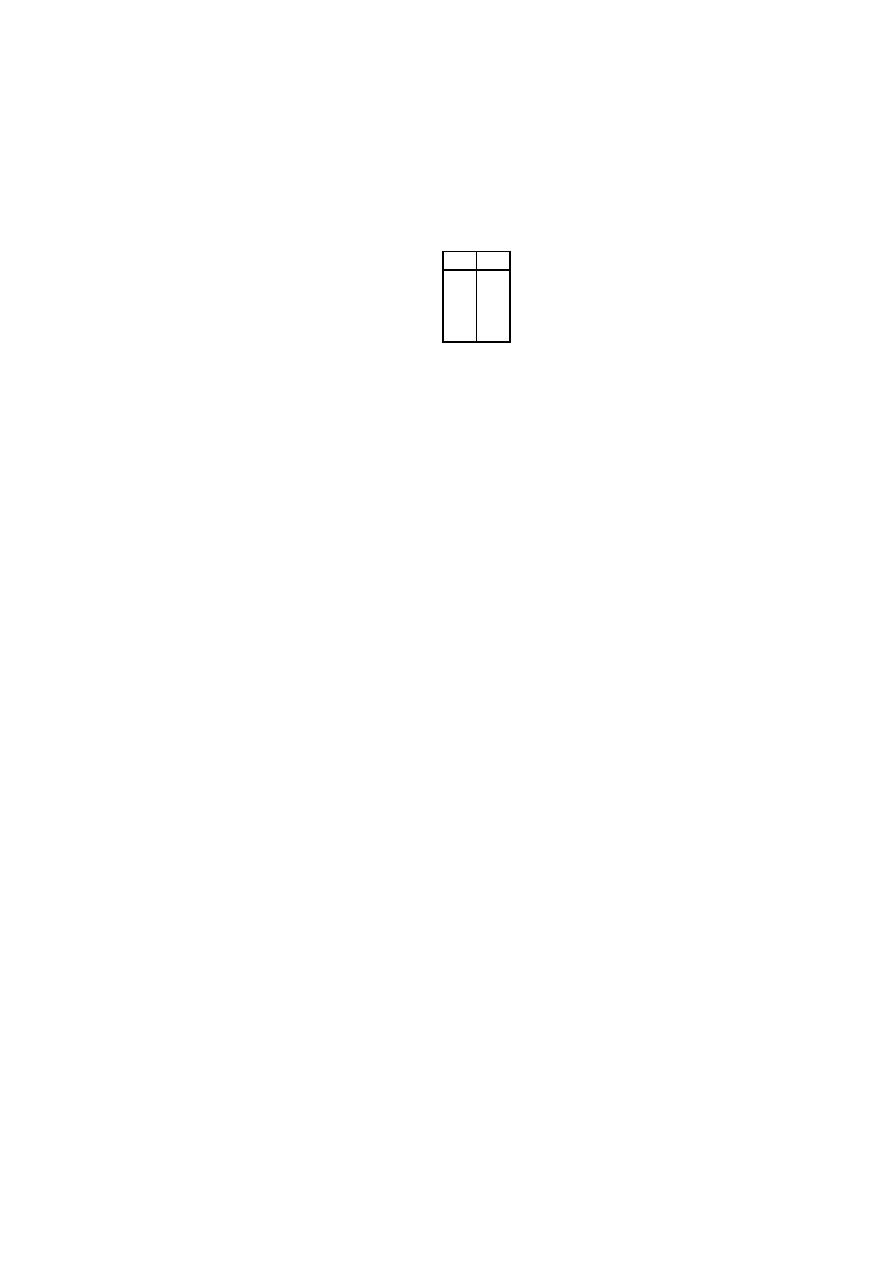
1.7. Algorytm Euklidesa
11
a
b
36
15
6
15
6
3
0
3
Tak wi˛ec 3 jest najwi˛ekszym wspólnym dzielnikiem liczb 15 i 36. Poprawno´s´c algorytmu
Euklidesa wynika z poni˙zszego lematu.
Lemat 1.17 Niech a i b b˛ed ˛
a dwoma liczbami naturalnymi i niech
0 < b
≤ a. Wtedy
para a, b ma taki sam zbiór wspólnych dzielników jak para a
mod b, b.
Dowód. Z definicji ilorazu i reszty mamy
a
= (a
÷ b) · b + a mod b.
Je˙zeli liczba r jest wspólnym dzielnikiem pary a, b, to r dzieli tak˙ze reszt˛e a
mod b, czyli
r jest wspólnym dzielnikiem pary
(a mod b), b. Na odwrót, je˙zeli liczba r jest wspólnym
dzielnikiem pary
(a mod b), b, to r dzieli tak˙ze a, czyli r jest wspólnym dzielnikiem pary
a, b.
2
Tak wi˛ec po ka˙zdej iteracji p˛etli
while
para a, b ma taki sam zbiór wspólnych dziel-
ników, a wi˛ec tak˙ze taki sam najwi˛ekszy wspólny dzielnik. Na ko ´ncu, gdy a
= 0 lub
b
= 0, N W D = a + b, czyli jest równy tej drugiej liczbie. Nale˙zy jeszcze pokaza´c, ˙ze
dla ka˙zdej pary dodatnich liczb naturalnych a i b algorytm zatrzyma si˛e. Ale to wynika z
faktu, ˙ze po ka˙zdej iteracji p˛etli dopóki liczba
max
{a, b}
jest coraz mniejsza, a poniewa˙z jest to zawsze liczba naturalna dodatnia, wi˛ec nie mo˙ze
zmniejsza´c si˛e w niesko ´nczono´s´c.
Twierdzenie 1.18 Niech a i b b˛ed ˛
a dwoma dodatnimi liczbami naturalnymi i niech d
=
N W D
(a, b). Wtedy istniej ˛
a liczby całkowite x i y, takie ˙ze:
xa
+ yb = d,
lub mówi ˛
ac inaczej, d jest kombinacj ˛
a całkowitoliczbow ˛
a liczb a i b.
Dowód. Niech a
0
i b
0
oznaczaj ˛
a pocz ˛
atkowe warto´sci zmiennych a i b, odpowiednio.
Poka˙zmy, ˙ze wszystkie warto´sci, jakie przyjmuj ˛
a zmienne a i b w trakcie wykonywania
algorytmu Euklidesa, s ˛
a całkowitoliczbowymi kombinacjami liczb a
0
i b
0
. Na pocz ˛
atku,
gdy a
= a
0
i b
= b
0
, mamy:
a
= 1a
0
+ 0b
0
,
b
= 0a
0
+ 1b
0
.
Załó˙zmy teraz, ˙ze po i-tej iteracji p˛etli a > b oraz ˙ze zachodzi:
a
= x
a
a
0
+ y
a
b
0
,
b
= x
b
a
0
+ y
b
b
0
.
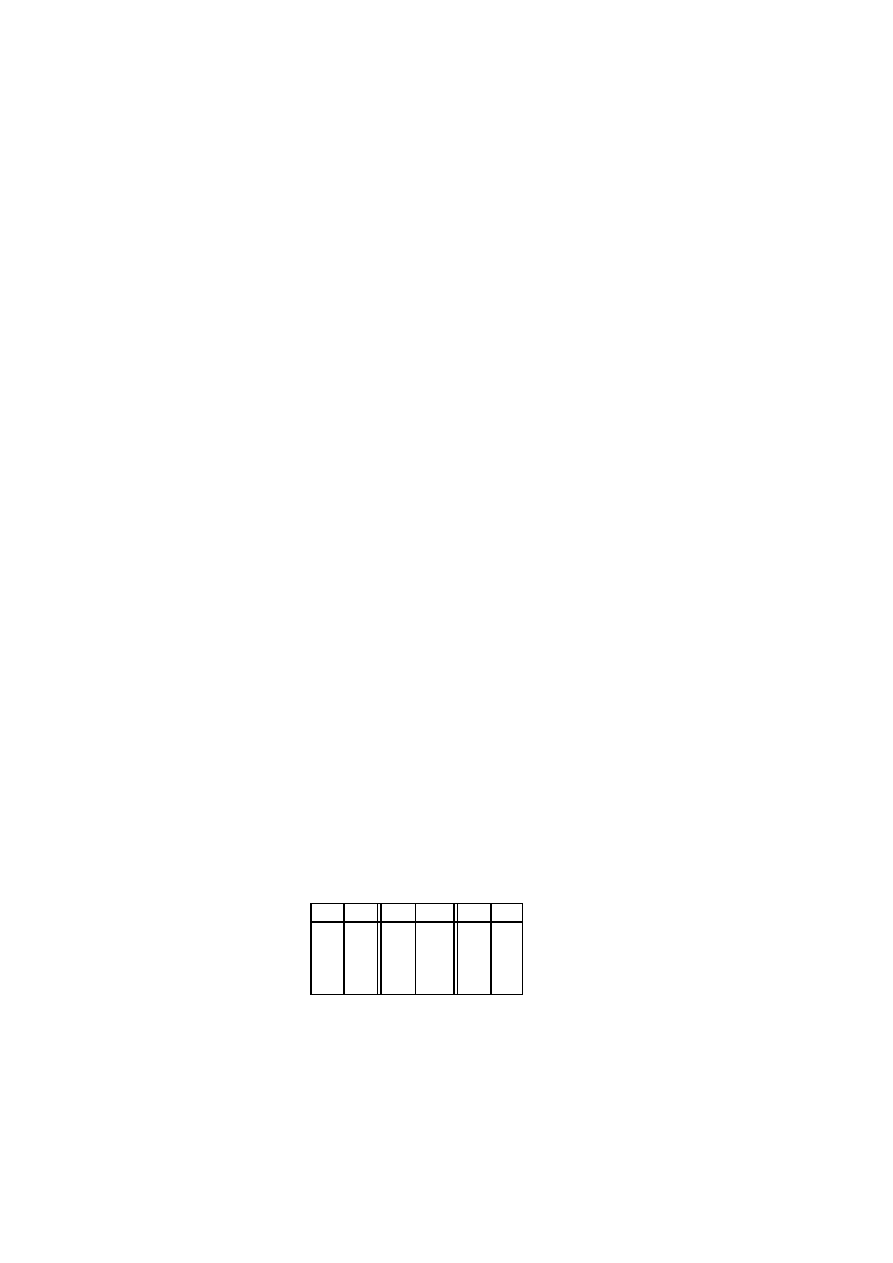
12
Rozdział 1. Teoria liczb
Wtedy w
(i + 1) iteracji a b˛edzie pomniejszone o b
· (a ÷ b) i b˛edziemy mieli:
a
= (x
a
− x
b
· (a ÷ b))a
0
+ (y
a
− y
b
· (a ÷ b))b
0
oraz
b
= x
b
a
0
+ y
b
b
0
.
Z tego wynika, ˙ze tak˙ze ostateczna warto´s´c d jest kombinacj ˛
a liczb a
0
i b
0
.
2
1.7.1
Rozszerzony algorytm Euklidesa
Algorytm Euklidesa mo˙zna tak zmodyfikowa´c, aby oprócz najwi˛ekszego wspólnego dziel-
nika N W D
(a, b), wyliczał tak˙ze liczby x i y, takie ˙ze:
xa
+ yb = N W D(a, b).
Oto ten algorytm
x
a
:= 1; y
a
:= 0;
x
b
:= 0; y
b
:= 1;
dopóki
a
· b 6= 0 wykonuj:
je˙zeli
a
≥ b, to
a
:= a mod b
x
a
:= x
a
− x
b
∗ (a ÷ b);
y
a
:= y
a
− y
b
∗ (a ÷ b)
w przeciwnym przypadku
b
:= b mod a;
x
b
:= x
b
− x
a
∗ (b ÷ a);
y
b
:= y
b
− y
a
∗ (b ÷ a)
N W D
:= a + b
je˙zeli
a >
0, to x := x
a
; y := y
a
;
je˙zeli
b >
0, to x := x
b
; y := y
b
;
W poni˙zszej tabeli pokazano kolejne kroki działania rozszerzonego algorytmu Eukli-
desa na parze liczb 36 i 15:
a
b
x
a
y
a
x
b
y
b
36
15
1
0
0
1
6
15
1
-2
0
1
6
3
1
-2
-2
5
0
3
5
-12
-2
5
Tak wi˛ec liczb˛e 3 mo˙zna przedstawi´c jako kombinacj˛e liczb 15 i 36 w nast˛epuj ˛
acy sposób:
3 = (
−2) · 36 + (5) · 15.

1.8. Liczby pierwsze i wzgl˛ednie pierwsze
13
Zauwa˙zmy, ˙ze je˙zeli jaka´s liczba r dzieli liczby a i b, to dzieli tak˙ze ka˙zd ˛
a ich kombinacj˛e
całkowit ˛
a
xa
+ yb,
a wi˛ec dzieli tak˙ze najwi˛ekszy wspólny dzielnik N W D
(a, b). Udowodnili´smy poni˙zszy
lemat.
Lemat 1.19 N W D
(a, b) jest podzielny przez ka˙zdy wspólny dzielnik liczb a i b.
Z lematu 1.19 wynika, ˙ze najwi˛ekszy wspólny dzielnik N W D
(a, b) mo˙ze by´c rów-
nowa˙znie zdefiniowany jako taki wspólny dzielnik liczb a i b, który jest podzielny przez
ka˙zdy wspólny dzielnik a i b.
Lemat 1.20 Liczba naturalna d jest najwi˛ekszym wspólnym dzielnikiem liczb a i b wtedy
i tylko wtedy gdy d jest wspólnym dzielnikiem a i b oraz istniej ˛
a liczby całkowite x i y,
takie ˙ze d
= xa + yb.
Dowód Je˙zeli N W D
(a, b) = d to d
|a, d|b oraz (z twierdzenia 1.18) istniej ˛a liczby całko-
wite x i y, takie ˙ze: d
= xa + yb.
Na odwrót, je˙zeli d dzieli a i b oraz xa
+ yb = d, to ka˙zdy wspólny dzielnik a i b
dzieli d, a wi˛ec d jest najwi˛ekszym wspólnym dzielnikiem a i b.
2
Wniosek 1.21 Je˙zeli istniej ˛
a liczby całkowite x i y, takie, ˙ze xa
+yb = 1, to N W D(a, b) =
1.
Przykład 1.22 Poniewa˙z:
2000
− 1998 = 2
oraz 2 jest wspólnym dzielnikiem 1998 i 2000, wi˛ec N W D
(1998, 2000) = 2.
2001
− 1999 = 2,
wi˛ec N W D
(1999, 2001) dzieli 2, a poniewa˙z 2 nie dzieli ani 1999, ani 2001, wi˛ec
N W D
(1999, 2001) = 1.
1.8
Liczby pierwsze i wzgl˛ednie pierwsze
Dwie liczby naturalne a i b s ˛
a wzgl˛ednie pierwsze, je˙zeli N W D
(a, b) = 1, a liczba
naturalna p jest pierwsza, je˙zeli p >
1 i jedynymi dzielnikami naturalnymi p s ˛
a jedynka i
samo p.
Oto wszystkie liczby pierwsze mniejsze od 50:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.
Liczba n >
1, która nie jest pierwsza jest zło˙zona. Istniej ˛
a wtedy dwie liczby k, m < n,
takie, ˙ze n
= k
· m.

14
Rozdział 1. Teoria liczb
1.9
Rozkład liczb na czynniki pierwsze
W tym rozdziale zobaczymy, ˙ze ka˙zd ˛
a liczb˛e naturaln ˛
a n >
1 mo˙zna rozło˙zy ´c na czynniki
pierwsze i ˙ze taki rozkład jest jednoznaczny z dokładno´sci ˛
a do kolejno´sci czynników. Na
przykład:
12 = 2
2
· 3
i
180 = 2
2
· 3
2
· 5.
Przyjmujemy przy tym, ˙ze je˙zeli liczba jest pierwsza, to jej rozład składa si˛e tylko z jednej
liczby.
Twierdzenie 1.23 Ka˙zd ˛
a liczb˛e naturaln ˛
a n >
1 mo˙zna przedstawi´c jako iloczyn liczb
pierwszych (niekoniecznie ró˙znych):
n
= q
1
q
2
· · · q
r
.
Dowód nie wprost. 2 jako liczba pierwsza ma trywialny rozkład składaj ˛
acy si˛e z jednej
liczby. Przypu´s´cmy, ˙ze istnieje liczba naturalna n, której nie mo˙zna przedstawi ´c jako
iloczynu liczb pierwszych i ˙ze n jest najmniejsz ˛
a tak ˛
a liczb ˛
a. n nie mo˙ze by ´c liczb ˛
a
pierwsz ˛
a (bo wtedy n
= q
1
), wi˛ec n jest liczb ˛
a zło˙zon ˛
a, czyli jest postaci:
n
= km
dla k, m < n. Ale poniewa˙z k i m s ˛
a mniejsze od n, wi˛ec mo˙zna je rozło˙zy ´c na czynniki
pierwsze
k
= p
1
p
2
· · · p
s
oraz
m
= r
1
r
2
· · · r
t
,
ale wtedy, wbrew zało˙zeniu, mamy rozkład liczby n na czynniki pierwsze:
n
= p
1
p
2
· · · p
s
r
1
r
2
· · · r
t
.
2
Aby pokaza´c, ˙ze rozkład jest jednoznaczny (z dokładno´sci ˛
a do kolejno´sci czynników),
musimy najpierw udowodni´c dwa lematy.
Lemat 1.24 Niech a i b b˛ed ˛
a dodatnimi wzgl˛ednie pierwszymi liczbami naturalnymi.
Wtedy dla dowolnej liczby c, je˙zeli a
|bc, to a|c.
Dowód. Z twierdzenia 1.18, istniej ˛
a dwie liczby całkowite x i y, takie ˙ze:
xa
+ yb = 1.
Pomnó˙zmy teraz obie strony tego równania przez c:
xac
+ ybc = c,
i zauwa˙zmy, ˙ze a dzieli oba składniki po lewej stronie równania, a wi˛ec dzieli praw ˛
a
stron˛e, czyli c.
2

1.10. Elementy odwracalne
15
Lemat 1.25 Je˙zeli liczba pierwsza p dzieli iloczyn liczb pierwszych
q
1
q
2
· · · q
r
(niekoniecznie ró˙znych), to wtedy p jest równe jednej z liczb q
i
.
Dowód przez indukcj˛e ze wzgl˛edu na r. Dla r
= 1 mamy p
|q
1
, a poniewa˙z q
1
jest
pierwsza i p >
1, wi˛ec p = q
1
.
Załó˙zmy teraz, ˙ze teza zachodzi dla r i przypu´s´cmy, ˙ze p dzieli
q
1
q
2
· · · q
r
q
r
+1
.
Mamy dwa przypadki: albo p dzieli q
r
+1
, albo nie. W pierwszym przypadku p
= q
r
+1
.
W drugim przypadku mamy N W D
(p, q
r
+1
) = 1, bo 1 i q
r
+1
to jedyne dzielniki liczby
q
r
+1
. Z lematu 1.24 wynika teraz, ˙ze p dzieli q
1
q
2
· · · q
r
, a z zało˙zenia indukcyjnego, ˙ze
p
= q
i
dla jakiego´s
1
≤ i ≤ r.
2.
Udowodnimy teraz, ˙ze rozkład liczby na czynniki pierwsze jest jednoznaczny, z dokład-
no´sci ˛
a do kolejno´sci czynników.
Twierdzenie 1.26 Ka˙zd ˛
a liczb˛e naturaln ˛
a n >
1 mo˙zna w dokładnie jeden sposób przed-
stawi´c w postaci iloczynu:
n
= p
α
1
1
p
α
2
2
. . . p
α
r
r
,
gdzie α
i
s ˛
a dodatnimi liczbami naturalnymi, p
i
s ˛
a liczbami pierwszymi oraz zachodzi
p
1
< p
2
< . . . < p
r
.
Dowód. Twierdzenie 1.23 orzeka, ˙ze liczba ma rozkład na czynniki pierwsze. Trzeba
pokaza´c, ˙ze jest to rozkład jednoznaczny. n
= 2 jako liczba pierwsza ma jednoznaczny
rozkład. Przypu´s´cmy, ˙ze n jest najmniejsz ˛
a liczb ˛
a z dwoma ró˙znymi rozkładami:
n
= p
α
1
1
p
α
2
2
. . . p
α
r
r
= q
β
1
1
q
β
2
2
. . . q
β
s
s
.
(1.1)
Wtedy z jednej strony p
1
nie mo˙ze wyst˛epowa´c po prawej stronie równania (1.1), bo
n
p
1
byłoby mniejsz ˛
a liczb ˛
a z niejednoznacznym rozkładem. Z drugiej strony p
1
dzieli praw ˛
a
stron˛e, a wi˛ec, z lematu 1.25 wyst˛epuje po prawej stronie. Mamy wi˛ec sprzeczno´s´c.
2
Lemat 1.27 Je˙zeli a i b s ˛
a wzgl˛ednie pierwsze, to ich rozkłady s ˛
a rozł ˛
aczne. To znaczy
maj ˛
a rozł ˛
aczny zbiór liczb pierwszych wyst˛epuj ˛
acych w ich rozkładach.
1.10
Elementy odwracalne
Definicja 1.28 Element a
∈ Z
m
jest odwracalny, je˙zeli istnieje b
∈ Z
m
, takie, ˙ze
a
· b = 1 (mod m).
b nazywamy elementem odwrotnym do a i oznaczamy przez a
−1
.

16
Rozdział 1. Teoria liczb
Przykład 1.29 Liczba
3 jest odwracalna w Z
8
bo
3
· 3 = 1 (mod 8). Oprócz 3 w Z
8
odwracalne s ˛
a tak˙ze
1, 5 i 7.
Lemat 1.30 Liczba a
∈ Z
m
jest odwracalna wtedy i tylko wtedy, gdy N W D
(a, m) = 1.
Dowód. Je˙zeli N W D
(a, m) = 1, to istniej ˛
a liczby całkowite x i y, takie ˙ze:
xa
+ ym = 1,
a wi˛ec m dzieli ax
− 1, czyli:
ax
= 1 (mod m).
Teraz wystarczy przyj ˛
a´c za a
−1
tak ˛
a liczb˛e z przedziału od 1 do m
− 1, która przystaje
do x modulo m.
Z drugiej strony je˙zeli istnieje element a
−1
odwrotny do a to
a
−1
a
= 1 (mod m)
czyli
a
−1
a
− 1 = k · m
dla jakiego´s k. Mamy wi˛ec
a
−1
a
+ (
−k)m = 1
czyli N W D
(a, m) = 1 (wniosek 1.21).
2
Z powy˙zszego dowodu wynika, ˙ze element odwrotny do a mo˙zna wyliczy ´c stosuj ˛
ac
algorytm Euklidesa. Na przykład, policzmy element odwrotny do 12 w pier´scieniu Z
17
.
Najpierw zastosujemy algorytm Euklidesa, aby obliczy´c x i y, takie ˙ze:
12x + 17y = 1.
Kolejne kroki algorytmu przedstawiono w tabeli:
a
b
x
a
y
a
x
b
y
b
17
12
1
0
0
1
5
12
1
-1
0
1
5
2
1
-1
-2
3
1
2
5
-7
-2
3
1
0
5
-7
-12
17
Mamy wi˛ec:
5
· 17 + (−7)12 = 1,
czyli:
(
−7)12 = 1 (mod 17),
ale:
−7 = 10 (mod 17),
czyli 10 jest elementem odwrotnym do 12 w pier´scieniu Z
17
.
1.11. Funkcja liniowa
17
Definicja 1.31 Zbiór elementów odwracalnych w Z
n
oznaczamy przez Z
∗
n
.
Przykład 1.32 Z
∗
8
=
{1, 3, 5, 7}.
Lemat 1.33 Je˙zeli liczba m jest pierwsza, to ka˙zdy element a
∈ Z
m
, a
6= 0, jest odwra-
calny, czyli pier´scie´n Z
m
jest ciałem.
Lemat 1.34 Je˙zeli a, b
∈ Z
∗
n
to ab
∈ Z
∗
n
oraz a
−1
∈ Z
∗
n
.
To oznacza, ˙ze Z
∗
n
z mno˙zeniem jest grup ˛
a.
Dowód: Elementem odwrotnym do iloczynu ab jest b
−1
a
−1
, a elementem odrotnym do
a
−1
jest a.
2
1.11
Funkcja liniowa
Zastanówmy si˛e jak w pier´scieniu Z
m
działa funkcja liniowa
f
(x) = a
· x (mod m).
Rozpatrzmy najpierw przypadek, gdy a i m s ˛
a wzgl˛ednie pierwsze, czyli gdy N W D
(a, m) =
1. Dla m = 8 i a = 3 warto´sci funkcji przedstawia tabela
x
0
1
2
3
4
5
6
7
3x
0
3
6
1
4
7
2
5
W takim przypadku istnieje a
−1
element odwrotny do a i funkcja g
(x) = a
−1
x, która
jest odwrotna do f . Rzeczywi´scie
f
(g(x)) = aa
−1
x
= x.
Z tego wynika, ˙ze f jest wzajemnie jednoznaczna i "na" oraz, ˙ze dla ka˙zdego b
∈ Z
m
równanie
ax
= b
ma dokładnie jedno rozwi ˛
azanie w pier´scieniu Z
m
, jest ono równe x
= a
−1
b.
Funkcja f jest permutacj ˛
a w Z
m
i wykorzystuje si˛e j ˛
a, gdy trzeba wymiesza´c (prze-
permutowa´c) elementy Z
m
. Zauwa˙zmy, ˙ze f jest tak˙ze permutacj ˛
a w Z
∗
m
. Rzeczywi´scie,
je˙zeli x
∈ Z
∗
m
, to na podstawie lematu 1.34 f
(x) = ax
∈ Z
∗
m
. Mamy wi˛ec
Lemat 1.35 Je˙zeli N W D
(a, m) = 1, to funkcja f (x) = ax jest funkcj ˛
a wzajemnie
jednoznaczn ˛
a w Z
m
i w Z
∗
m
.
Rozpatrzmy teraz przypadek, gdy a i m nie s ˛
a wzgl˛ednie pierwsze, czyli gdy N W D
(a, m) =
d >
1. Dla m = 8 i a = 6 warto´sci funkcji przedstawia tabela
x
0
1
2
3
4
5
6
7
6x
0
6
4
2
0
6
4
2
18
Rozdział 1. Teoria liczb
Zauwa˙zmy, ˙ze je˙zeli b jest warto´sci ˛
a funkcji f , czyli gdy
ax
= b (mod m)
to istnieje takie k, ˙ze
ax
− b = km,
a poniewa˙z d dzieli a i m, to d dzieli b, a wi˛ec warto´sciami funkcji f mog ˛
a by´c tylko
liczby podzielne przez d.
Lemat 1.36 Je˙zeli N W D
(a, m) = d oraz d
|b, to równania
ax
= b (mod m)
oraz
a
d
x
=
b
d
(mod
m
d
)
s ˛
a równowa˙zne, czyli maj ˛
a ten sam zbiór rozwi ˛
aza´n w zbiorze liczb całkowitych.
Dowód
ax
= b (mod m)
wtedy i tylko wtedy, gdy istnieje k takie ˙ze
ax
− b = km,
a to zachodzi wtedy i tylko wtedy, gdy istnieje k takie, ˙ze
a
d
x
−
b
d
= k
m
d
,
czyli wtedy i tylko wtedy, gdy
a
d
x
=
b
d
(mod
m
d
).
2
Przypu´s´cmy teraz, ˙ze d dzieli b i rozwi ˛
a˙zmy równanie
ax
= b
(1.2)
w pier´scieniu Z
m
, czyli szukamy takich x
∈ {0, . . . , m − 1}, ˙ze
ax
= b (mod m)
(1.3)
Z lematu 1.36, to równanie jest równowa˙zne równaniu
a
d
x
=
b
d
(mod
m
d
)
(1.4)

1.12. Szyfry liniowe
19
Ale teraz N W D
(
a
d
,
m
d
) = 1 i równanie (1.4) ma dokładnie jedno rozwi ˛
azanie x
0
∈
{0, . . . ,
m
d
− 1} takie ˙ze
a
d
x
0
=
b
d
(mod
m
d
).
Ale równania (1.4) i (1.3) s ˛
a spełnione tak˙ze przez liczby
x
0
, x
0
+
m
d
, x
0
+ 2
m
d
, . . . , x
0
+ (d
− 1)
m
d
.
S ˛
a to wszystkie liczby ze zbioru
{0, . . . , m − 1} spełniaj ˛ace równania (1.4) i (1.3), czyli
wszystkie rozwi ˛
azania równania (1.2) w pier´scieniu Z
m
.
Przykład 1.37 Rozwi ˛
a˙zmy równanie
6x = 9 (mod 15).
(1.5)
Poniewa˙z N W D
(6, 15) = 3, wi˛ec najpierw rozwi ˛
azujemy równanie
2x = 3 (mod 5)
W Z
5
mamy
2
−1
= 3 wi˛ec rozwi ˛
azaniem jest x
0
= 3
· 3 = 4. Tak wi˛ec rozwi ˛
azaniami
równaia (1.5) w Z
15
s ˛
a liczby
4, 9, 14.
1.12
Szyfry liniowe
Przypu´s´cmy, ˙ze mamy tekst zapisany za pomoc ˛
a 26 liter alfabetu łaci ´nskiego:
a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z,
i chcemy ten tekst zaszyfrowa´c. W tym celu uto˙zsamiamy zbiór liter z elementami pier-
´scienia Z
26
:
a
= 0,
b
= 1,
c
= 2, . . . , z = 25,
wybieramy dwie liczby a, b
∈ Z
26
, takie ˙ze N W D
(a, 26) = 1, i szyfrujemy litera po
literze według wzoru:
C
(x) = ax + b (mod 26).
Funkcja deszyfruj ˛
aca jest okre´slona wzorem:
D
(y) = a
−1
y
− a
−1
b
(mod 26).
Rzeczywi´scie:
D
(C(x)) = a
−1
(ax + b)
− a
−1
b
= a
−1
ax
+ a
−1
b
− a
−1
b
= x.
Z tego wynika, ˙ze funkcja szyfruj ˛
aca C
(x) jest wzajemnie jednoznaczna.
20
Rozdział 1. Teoria liczb
Przykład 1.38 Wybierzmy a
= 23 i b = 20 i zaszyfrujmy słowo
matematyka.
W tym celu musimy zaszyfrowa´c 6 liter: m, a, t, e, y oraz k. Obliczenia przedstawiono w
tabeli:
litera
x
C
(x)
szyfr
m
12
10
k
a
0
20
u
t
19
15
p
e
4
8
i
y
24
0
a
k
10
16
q
Słowo matematyka po zaszyfrowaniu wygl ˛
ada tak:
kupikupaqu.
Je˙zeli za´s zastosujemy ten sam szyfr do pocz ˛
atkowego zdania z wiersza Lokomotywa Ju-
liana Tuwima:
stoi na stacji lokomotywa,
to otrzymamy:
spewhuspuotwneqekepagu.
Szyfry liniowe s ˛
a bardzo starym wynalazkiem. W prostszej wersji z a
= 1 stosował je
ju˙z Juliusz Cezar. Ich wad ˛
a jest to, ˙ze bardzo łatwo daj ˛
a si˛e łama ´c. Czasami wystarcza od-
gadn ˛
a´c, jak zaszyfrowano dwie litery. Mo˙zna to zrobi´c analizuj ˛
ac cz˛esto´sci wyst˛epowania
liter w zaszyfrowanym tek´scie.
Przykład 1.39 (kontynuacja przykładu 1.38) W naszym drugim zaszyfrowanym tek´scie
litera e wyst˛epuje cztery razy, a litery p i u po trzy razy. Mo˙ze to nam pomóc w odgadni˛e-
ciu, ˙ze litera e koduje liter˛e o, a litera p koduje liter˛e t. Mamy wi˛ec dwa równania:
15 = 19a + b (mod 26),
4 = 14a + b (mod 26).
Po odj˛eciu tych równa´n stronami mamy:
11 = 5a (mod 26).
Korzystaj ˛
ac z algorytmu Euklidesa, mo˙zemy teraz wyliczy´c element odwrotny do 5 w pier-
´scieniu Z
26
. Jest to 21, poniewa˙z:
(
−5)5 + 26 = 1
oraz
− 5 = 21 (mod 26),
tak wi˛ec:
a
= 21
· 11 = 231 = 23 (mod 26).
Teraz z drugiego równania mo˙zemy wyliczy´c b:
b
= 15
− 19 · 23 = 20 (mod 26).

1.13. Chi ´nskie twierdzenie o resztach
21
1.13
Chi ´nskie twierdzenie o resztach
W staro˙zytnych Chinach generałowie u˙zywali pewnego ciekawego sposobu liczenia swo-
ich ˙zołnierzy. Dla kilku niewielkich liczb parami wzgl˛ednie pierwszych, na przykład dla:
m
1
= 3,
m
2
= 5,
m
3
= 7,
obliczano i zapami˛etywano reszty z dzielenia liczby ˙zołnierzy przez te liczby. W celu
obliczenia reszt kazano ˙zołnierzom ustawi´c si˛e trójkami, pi ˛
atkami i siódemkami. Je˙zeli
przy nast˛epnym apelu wszystkie trzy reszty były takie same, to znaczyło, ˙ze nie brakuje
˙zadnego ˙zołnierza.
Zobaczmy, jak ten sposób działa. We´zmy najpierw dwie liczby:
m
1
= 2
m
2
= 3.
W poni˙zszej tabeli mamy zestawione reszty modulo 2 i 3 liczb od 0 do 5:
a
a
(mod 2)
a
(mod 3)
0
0
0
1
1
1
2
0
2
3
1
0
4
0
1
5
1
2
Ka˙zda z liczb od 0 do
5 = 2
· 3 − 1 ma inny zestaw reszt oraz dla ka˙zdej pary reszt
(a
1
, a
2
), spełniaj ˛
acych warunek
0
≤ a
1
<
2, 0
≤ a
2
<
3, istnieje liczba a, taka ˙ze:
a
1
= a (mod 2),
a
2
= a (mod 3).
Oczywi´scie 6 ma takie same reszty jak 0:
0 = 6 (mod 2),
0 = 6 (mod 3),
i ogólnie, je˙zeli dwie liczby a i b
ró˙zni ˛
a si˛e o wielokrotno´s´c liczby
6 = 2
· 3, czyli:
a
= b + k
· 6
dla jakiego´s całkowitego k, to
a
(mod 2) = b (mod 2),
a
(mod 3) = b (mod 3).
Z tego wida´c, ˙ze sposób chi ´nskich generałów, z liczbami 2 i 3, liczy ˙zołnierzy z dokład-
no´sci ˛
a do pi˛eciu.

22
Rozdział 1. Teoria liczb
Sytuacja jest inna, je˙zeli m
1
i m
2
nie s ˛
a wzgl˛ednie pierwsze. Je˙zeli, na przykład,
m
1
= 4 i m
2
= 6, to w´sród liczb od 0 do 23 = 4
· 6 − 1 istniej ˛a takie, które maj ˛a takie
same reszty, na przykład 1 i 13:
1 (mod 4) = 13 (mod 4) = 1,
1 (mod 6) = 13 (mod 6) = 1.
Ponadto nie istnieje taka liczba a, dla której:
1 = a (mod 4),
0 = a (mod 6).
Rzeczywi´scie, z pierwszej równo´sci wynika, ˙ze a powinno by´c nieparzyste, a z drugiej,
˙ze parzyste.
Je˙zeli jednak m
1
i m
2
s ˛
a wzgl˛ednie pierwsze, to ka˙zda z liczb od 0 do m
1
· m
2
− 1 ma
inny zestaw reszt oraz dla ka˙zdej pary reszt
(a
1
, a
2
), spełniaj ˛
acych warunek
0
≤ a
1
<
m
1
,
0
≤ a
2
< m
2
, istnieje liczba a, taka ˙ze:
a
1
= a (mod m
1
),
a
2
= a (mod m
2
),
zachodzi bowiem poni˙zsze twierdzenie.
Twierdzenie 1.40 (chi ´nskie twierdzenie o resztach) Niech
m
1
, m
2
, . . . , m
r
b˛ed ˛
a dodatnimi liczbami wzgl˛ednie pierwszymi, to znaczy dla ka˙zdej pary
1
≤ i < j ≤ r
mamy N W D
(m
i
, m
j
) = 1, oraz niech
a
1
, a
2
, . . . , a
r
b˛ed ˛
a dowolnymi resztami. Wtedy istnieje liczba całkowita a, taka ˙ze:
a
1
= a (mod m
1
),
a
2
= a (mod m
2
),
(1.6)
. . .
a
r
= a (mod m
r
).
Ponadto je˙zeli liczby a i b s ˛
a rozwi ˛
azaniami układu kongruencji (??), to ich ró˙znica
a
− b dzieli si˛e przez iloczyn wszystkich liczb m
i
, czyli przez:
M
=
r
Y
i
=1
m
i
.

1.13. Chi ´nskie twierdzenie o resztach
23
Dowód. Najpierw udowodnimy drug ˛
a cz˛e´s´c twierdzenia. Dla ka˙zdego
1
≤ i ≤ r mamy:
a
i
= a (mod m
i
)
oraz
a
i
= b (mod m
i
).
Po odj˛eciu stronami tych dwóch równa ´n mamy:
0 = a
− b (mod m
i
),
czyli
m
i
|(a − b),
Druga cz˛e´s´c twierdzenia wynika z nast˛epuj ˛
acego lematu:
Lemat 1.41 Je˙zeli ka˙zda spo´sród liczb m
i
dzieli a
−b i liczby m
1
, . . . , m
r
s ˛
a wzgl˛ednie
pierwsze, to tak˙ze ich iloczyn M dzieli a
− b.
Dowód Lematu. Liczba m
1
dzieli a
− b, wi˛ec istnieje K
1
takie, ˙ze
a
− b = K
1
· m
1
.
Liczba m
2
te˙z dzieli a
− b, a poniewa˙z jest wzgl˛ednie pierwsza z m
1
, wi˛ec na podstawie
Lematu 1.24, m
2
dzieli K
1
i mamy
a
− b = K
2
· m
2
· m
1
,
dla jakiego´s K
2
. Podobnie, liczba m
3
jest wzgl˛ednie pierwsza z m
1
, wi˛ec dzieli iloczyn
K
2
· m
2
, ale jest tak˙ze wzgl˛ednie pierwsza z m
2
, wi˛ec dzieli K
2
i mamy
a
− b = K
3
· m
3
· m
2
· m
1
,
dla pewnego K
3
. Powtarzaj ˛
ac to rozumowanie
r
razy dochodzimy do wniosku, ˙ze
istnieje takie K
r
, ˙ze
a
− b = K
r
· m
r
· · · m
1
,
2
Dowód Lematu, ci ˛
ag dalszy. Zobaczymy teraz, ˙ze układ (1.6) ma rozwi ˛
azanie. Niech
M
i
=
M
m
i
, czyli:
M
i
= m
1
· · · m
i
−1
m
i
+1
. . . m
r
.
Poniewa˙z M
i
i m
i
maj ˛
a rozł ˛
aczne rozkłady, wi˛ec N W D
(m
i
, M
i
) = 1 oraz istnieje N
i
,
takie ˙ze:
M
i
N
i
= 1 (mod m
i
).
Zauwa˙zmy, ˙ze je˙zeli i
6= j, to m
i
|M
j
, oraz ˙ze ka˙zdy iloczyn m
i
M
i
ma nast˛epuj ˛
ac ˛
a
własno´s´c
m
i
M
i
= 1 (mod m
i
),
m
i
M
i
= 0 (mod m
j
)
dla
j
6= i,

24
Rozdział 1. Teoria liczb
We´zmy teraz:
a
=
r
X
i
=1
a
i
M
i
N
i
.
Z powy˙zszej własno´sci wynika, ˙ze
a
= a
i
(mod m
i
)
dla ka˙zdego i, a wi˛ec a jest rozwi ˛
azaniem układu równa ´n (1.6).
2
Przykład 1.42 W przypadku ukłau dwóch równa´n nasze rozumowanie mo˙zna troch˛e upro-
´sci´c. We´zmy, na przykład, układ
a
1
= a (mod 3),
(1.7)
a
2
= a (mod 5),
Poniewa˙z 3 i 5 s ˛
a wzgl˛ednie pierwsze, wi˛ec istniej ˛
a x i y takie, ˙ze
3x + 5y = 1
Za pomoc ˛
a rozszerzonego algorytmu mo˙zemy wyliczy´c x i y, mamy
3
· 2 + 5 · (−1) = 1
Teraz zauwa˙zmy, ˙ze iloczyny
3
· 2 oraz 5 · (−1) maj ˛
a nast˛epuj ˛
ace własno´sci
3
· 2 = 0 (mod 3),
3
· 2 = 1 (mod 5),
5
· (−1) = 1 (mod 3),
5
· (−1) = 0 (mod 5),
Dlatego liczba
a
2
· 3 · 2 + a
1
· 5 · (−1) = 1
jest rozwi ˛
azaniem układu 1.7
Przykład 1.43 Ka˙zda z liczb od 0 do
104 = 3
· 5 · 7 − 1 ma inny zestaw reszt wzgl˛edem
liczb 3, 5 i 7. Tak wi˛ec stosuj ˛
ac sposób chi´nskich generałów z liczbami 3, 5, 7 mo˙zemy
liczy´c ˙zołnierzy z dokładno´sci ˛
a do 104.
Ale sposób chi´nskich generałów pozwala tak˙ze stwierdzi´c, o ile zmieniła si˛e liczba
˙zołnierzy. Przypu´s´cmy bowiem, ˙ze na porannym apelu było x ˙zołnierzy i uzyskano reszty:
x
1
= x
(mod 3),
x
2
= x (mod 5),
x
3
= x
(mod 7),
a na apelu wieczornym było y ˙zołnierzy i otrzymano reszty:
y
1
= y
(mod 3),
y
2
= y
(mod 5),
y
3
= y
(mod 7),
wtedy ró˙znica x
− y spełnia nast˛epuj ˛acy układ kongruencji:
x
1
− y
1
= x
− y (mod 3),
x
2
− y
2
= x
− y (mod 5),
x
3
− y
3
= x
− y (mod 7).

1.14. Obliczenia na du˙zych liczbach
25
1.14
Obliczenia na du˙zych liczbach
Chi´nskie twierdzenie o resztach pozwala wnioskowa´c o du˙zych liczbach za pomoc ˛
a ope-
racji na małych liczbach. Zobaczmy teraz kilka przykładów.
Przykład 1.44 Rozwa˙zmy nast˛epuj ˛
ace równanie.
58 721 569
· 54 567 769 = 71 900 738 · 41 312 424 + 14 969 161 · 15 626 209.
Chi´nskie twierdzenie o resztach daje mo˙zliwo´s´c sprawdzenia tego równania operuj ˛
ac tyl-
ko na stosunkowo małych liczbach. Sprawdzamy to równanie licz ˛
ac modulo kilka niedu-
˙zych liczb wzgl˛ednie pierwszych, na przykład: m
1
= 999, m
2
= 1000, m
3
= 1001,
m
4
= 1003, m
5
= 1007, m
6
= 1009. Je˙zeli lewa strona równa si˛e prawej modulo
wszystkie te liczby, to równa si˛e tak˙ze w liczbach całkowitych, poniewa˙z iloczyn tych liczb
m
1
m
2
m
3
m
4
m
5
m
6
>
(10
3
)
6
= 10
18
jest wi˛ekszy od lewej i prawej strony.
Inny sposob, to sprawdzenie tej równo´sci modulo wszystkie liczby pierwsze mniejsze
od 50. Ich iloczyn jest wi˛ekszy od
10
17
.
Przykład 1.45 Zastanówmy si˛e teraz nad rozwi ˛
azaniem równania
x
· 56 606 581 = 71 900 738 · 41 312 424 + 14 969 161 · 15 626 209.
Je˙zeli spodziewamy si˛e, ˙ze rozwi ˛
azaniem jest liczba naturalna, to znowu mo˙zemy wy-
korzysta´c obliczenia modulo. Wybieramy du˙z ˛
a liczb˛e pierwsz ˛
a p, wi˛eksz ˛
a od ka˙zdej liczby
wyst˛epuj ˛
acej w tym równaniu, a nast˛epnie rozwi ˛
azujemy to równanie w ciele Z
p
x
= (56 606581)
−1
· (71 900 738 · 41 312 424 + 14 969 161 · 15 626 209).
Tak otrzymane rozwi ˛
azanie mo˙zemy zweryfikowa´c metod ˛
a z poprzedniego przykładu.
Stosuj ˛
ac t ˛
a metod˛e unikamy zaokr ˛
agle´n, które przy bardziej skomplikowanych rachun-
kach mog ˛
a si˛e kumulowa´c. Mo˙zna, na przykład, w ten sposób rozwi ˛
azywa´c du˙ze układy
równa´n liniowych, w których wszystkie współczynniki i rozwi ˛
azania s ˛
a liczbami całkowi-
tymi.
Przykład 1.46 Zastanówmy si˛e, ile wynosi reszta z dzielenia liczby
M
= 1 997 199 919
przez 15. Łatwo mo˙zna policzy´c, ˙ze: M
= 4 (mod 5) oraz M = 1 (mod 3), a wi˛ec:
M
= 4 (mod 15),
poniewa˙z 4 jest jedyn ˛
a liczb ˛
a z przedziału
0, 1, 2, . . . , 14, która posiada reszty 4 = 1
(mod 3) oraz 4 = 4 (mod 5).
26
Rozdział 1. Teoria liczb
1.15
Algorytm rosyjskich chłopów mno˙zenia liczb
W poprzednim podrozdziale obliczali´smy iloczyny typu
(x
· y) (mod m).
Je˙zeli wyra˙zenie to b˛edziemy oblicza´c najpierw mno˙z ˛
ac, a potem licz ˛
ac reszt˛e, to wynik
po´sredni x
· y mo˙ze by´c du˙zo wi˛ekszy ni˙z m. W tym podrozdziale poka˙zemy jak oblicza´c
takie wyra˙zenia bez du˙zych wyników po´srednich. W tym celu rozwa˙zmy nast˛epuj ˛
acy
algorytm mno˙zenia dwóch liczb. Algorytm ten był stosowany w Rosji.
Aby pomno˙zy´c dwie liczby a i b naturalne post˛epujemy w nast˛epuj ˛
acy sposób:
• Na pocz ˛atku dwóch kolumn wpisujemy a oraz b
• Powtarzamy nast˛epuj ˛acy ci ˛ag instrukcji dopóki na ko´ncu drugiej kolumny pojawi
si˛e 0.
Ostatni wyraz w pierwszej kolumnie mno˙zymy przez dwa,
Ostatni wyraz drugiej kolumny dzielimy przez 2 (bez reszty).
• Nast˛epnie dodajemy te wyrazy pierwszej kolumny, dla których w drugiej kolumnie
jest liczba nieparzysta.
Przykład 1.47 Poni˙zsza tabela ilustruje działanie algorytmu podczas obliczania
24
∗ 20.
Do kolumn z wart´sciami a i b dodali´smy na pocz ˛
atku kolumn˛e z numerem rz˛edu.
i
a
b
0
24
20
1
48
10
2
96
5
3
192
2
4
384
1
5
768
0
Teraz nale˙zy doda´c warto´sci z pierwszej kolumny, które znajduj ˛
a si˛e w drugim i czwartym
rz˛edzie, czyli
24
∗ 20 = 96 + 384 = 480.
Zauwa˙zmy, ˙ze rz˛edy s ˛
a numerowane od zera.
Poprawno´s´c algorytmu wynika z faktu, ˙ze b mo˙ze by´c przedstawione w postaci dwój-
kowej
b
=
j
X
i
=0
d
i
2
i
.
Poniewa˙z cyfry d
i
∈ {0, 1}, wi˛ec b jest sum ˛a pot˛eg dwójki. Na przykład
20 = 16 + 4 = 2
4
+ 2
2
.

1.16. Szybkie pot˛egowanie
27
Pot˛ega
2
i
wyst˛epuje w takiej sumie, je˙zeli w rozwini˛eciu dwójkowym b cyfra d
i
= 1.
Mno˙z ˛
ac
24 przez 20 mamy
24
· 20 = 24 · (2
4
+ 2
2
) = 24
· 2
4
+ 24
· 2
2
,
czyli iloczyn
24
· 20 jest sum ˛a wszystkich liczb postaci 24 · 2
i
, dla których d
i
= 1. Tak
wła´snie liczy algorytm rosyjskich chłopów. W i-tym rz˛edzie pierwszej kolumny mamy
warto´s´c a
∗ 2
i
. Je˙zeli wyraz w drugiej kolumnie jest nieparzysty to i-ty bit rozwini˛ecia b
jest równy d
i
= 1.
Zastosujmy teraz algorytm rosyjskich chłopów do obliczania iloczynu
a
·b (mod m).
Algorytm mno˙zenia
Dane wej´sciowe: czynniki mno˙zenia a oraz b.
Dane wyj´sciowe: Iloczyn a
· b mod m
iloczyn
:= 0
dopóki
b >
0 wykonuj
je˙zeli
b
mod 2 = 1 to
iloczyn
:= (iloczyn + a) mod m;
a
:= (2
∗ a) mod m;
b
:= b
÷ 2;
Zauwa˙zmy, ˙ze wyniki po´srednie, i ostateczny, nale˙z ˛
a do Z
m
i algorytm nie potrzebuje
zbyt du˙zej pami˛eci.
1.16
Szybkie pot˛egowanie
Teraz zastanowimy si˛e jak mo˙zna pot˛egowa´c, czyli jak obliczy´c a
k
mod n dla a
∈ Z
n
oraz k
∈ N. Pierwszy nasuwaj ˛acy si˛e algorytm pot˛egowania polega na k krotnym mno-
˙zeniu przez a:
y
:= 1;
dla
i
od
0
do
k
wykonuj
y
:= (y
∗ a) mod n
W kryptografii oblicza si˛e pot˛egi z wykładnikami posiadaj ˛
acymi po kilkaset bitów. Do
takich zastosowa ´n powy˙zszy algorytm jest nieprzydatny (wymaga on k mno˙ze ´n).
Poka˙zemy teraz jak mo˙zna pot˛egowa´c du˙zo szybciej. Zauwa˙zmy, ˙ze
a
· a = a
2
,
a
2
· a
2
= a
4
i ogólnie
a
2
i
· a
2
i
= a
2
i+1
.
Dlatego, aby obliczy´c pot˛eg˛e o wykładniku, który jest pot˛eg ˛
a dwójki k
= 2
j
nale˙zy
wykona´c

28
Rozdział 1. Teoria liczb
y
:= a;
dla
i
od
0
do
j
wykonuj
y
:= (y
∗ y) mod n
Przykład 1.48 Aby obliczy´c
2
16
w Z
21
obliczmy
2
2
= 2
· 2 = 4 (mod 21),
2
4
= 4
· 4 = 16 (mod 21),
2
8
= 16
· 16 = 4 (mod 21),
2
16
= 4
· 4 = 16 (mod 21).
Je˙zeli wykładnik jest sum ˛
a pot˛eg dwójki k
= 2
i
+ 2
j
, to
a
k
= a
2
i
· a
2
j
.
Przykład 1.49 Aby obliczy´c
2
20
mod 21 trzeba wymno˙zy´c
2
20
= 2
16
· 2
2
· 4 = 16 · 16 = 4 (mod 21).
Zauwa˙zmy, ˙ze ka˙zda liczba naturalna k jest sum ˛
a pot˛eg dwójki
k
=
j
X
i
=0
d
i
· 2
i
,
gdzie d
i
∈ {0, 1} to cyfry rozwini˛ecia dwójkowego k.
Powy˙zsze uwagi sugeruj ˛
a nast˛epuj ˛
acy algorytm obliczania pot˛egi
a
k
(mod m).
• Na pocz ˛atku dwóch kolumn wpisujemy a oraz k
• Powtarzamy nast˛epuj ˛acy ci ˛ag instrukcji dopóki na ko´ncu drugiej kolumny pojawi
si˛e 0.
Ostatni wyraz w pierwszej kolumnie podnosimy do kwadratu modulo m
Ostatni wyraz drugiej kolumny dzielimy przez 2.
• Nast˛epnie wymna˙zamy te wyrazy pierwszej kolumny, dla których w drugiej ko-
lumnie jest liczba nieparzysta.
Jak wida´c algorytm ten jest podobny do algorytmu mno˙zenia z poprzedniego rozdziału.
Przykład 1.50 Poni˙zsza tabela ilustruje działanie algorytmu podczas obliczania
8
5
(mod 21).
Do kolumn z wart´sciami a i k dodali´smy na pocz ˛
atku kolumn˛e z numerem rz˛edu.
i
a
k
0
8
5
1
1
2
2
1
1
3
1
0

1.17. Pierwiastki kwadratowe
29
Teraz nale˙zy wymno˙zy´c warto´sci z pierwszej kolumny, które znajduj ˛
a si˛e w zerowym, i
drugim rz˛edzie, czyli
8
5
= 8
· 1 = 8 (mod 5).
Zauwa˙zmy, ˙ze w i-tym wierszu pierwszej kolumny mamy pot˛eg˛e
2
2
i
. Je˙zeli wyraz w drugiej
kolumnie jest nieparzysty to i-ty bit rozwini˛ecia k jest równy d
i
= 1.
Poni˙zej mamy powy˙zszy algorytm w pseudo Pascalu.
Algorytm szybkiego pot˛egowania
Dane wej´sciowe: podstawa a oraz wykładnik k.
Dane wyj´sciowe: Pot˛ega a
k
mod n
potega
:= 1
dopóki
b >
0 wykonuj
je˙zeli
b
mod 2 = 1 to
iloczyn
:= (potega
· a) mod n;
a
:= (a
∗ a) mod n;
b
:= b
÷ 2;
Zauwa˙zmy, ˙ze wyniki po´srednie, i ostateczny, nale˙z ˛
a do Z
m
i algorytm nie potrzebuje
zbyt du˙zej pami˛eci. Algorytmu tego nie mo˙zna stosowa´c do obliczania a
k
w liczbach
całkowitych, je˙zeli k jest du˙ze. Wtedy wynik ostateczny oraz po´srednie b˛ed ˛
a zbyt du˙ze,
˙zeby mógł si˛e zmie´sci´c w pami˛eci komputera.
1.17
Pierwiastki kwadratowe
Definicja 1.51 Liczb˛e y nazywamy pierwiastkiem kwadratowym liczby x w pier´scieniu
Z
m
, je˙zeli
x
= y
2
(mod m).
Przykład 1.52 W Z
5
pierwiastkami 4 s ˛
a 2 i 3, poniewa˙z
2
2
= 3
2
= 4 (mod 5)
a
liczba 2 nie posiada pierwiastka.
Zauwa˙zmy, ˙ze je˙zeli y
2
= x
(mod m) to
(m
− y)
2
= m
2
− 2my + y
2
= y
2
= x (mod m),
czyli m
− y = −y (mod m), te˙z jest pierwiastkiem x.
Lemat 1.53 Je˙zeli m jest liczb ˛
a pierwsz ˛
a i x
= y
2
, to y i
−y s ˛
a jedynymi pierwiastkami
z x.
Dowód Je˙zeli z
2
= y
2
(mod m), to m dzieli z
2
− y
2
= (z
− y)(z + y), a poniewa˙z m
jest pierwsze to m dzieli z
− y lub z + y. W pierwszym przypadku z = y (mod m), w
drugim z
=
−y (mod m).
2

30
Rozdział 1. Teoria liczb
Przykład 1.54 Tak nie musi by´c, je˙zeli m nie jest liczb ˛
a pierwsz ˛
a. Na przykład w Z
15
mamy cztery pierwiastki z
1, s ˛
a to
1, 4, 11 i 14.
Ogólnie rozwa˙zmy liczb˛e m która jest iloczynem dwóch ró˙znych liczb pierwszych
p > q >
2. We´zmy teraz dowoln ˛
a liczb˛e y, dla której
y
mod p = 1 lub y mod p =
−1
oraz
y
mod q = 1 lub y mod q =
−1
Wtedy
y
2
mod p = 1 oraz y
2
mod q = 1
czyli z chi´nskiego twierdzenia o resztach wynika, ˙ze
y
2
= 1 (mod pq).
Poniewa˙z p > q >
2, to 1
6= −1 (mod p) oraz 1 6= −1 (mod q) i mamy wtedy
cztery ró˙zne pierwiastki z 1, y
1
, y
2
, y
3
, y
4
. S ˛
a to liczby dla których
y
1
mod p = 1,
y
1
mod q = 1,
y
2
mod p = 1,
y
2
mod q =
−1,
y
3
mod p =
−1,
y
3
mod q = 1,
y
4
mod p =
−1
y
4
mod q =
−1.
Zauwa˙zmy, ˙ze y
1
= 1 (mod n) oraz y
4
=
−1 (mod n).
1.18
Funkcja Eulera
Definicja 1.55 Funkcja Eulera, jest to funkcja, która liczbie m przypisuje φ
(m) liczb˛e
elementów odwracalnych w Z
m
. Z definicji przyjmujemy φ
(1) = 1.
Przykład 1.56 φ
(8) = 4, bo w Z
8
odwracalne s ˛
a
{1, 3, 5, 7}.
Podobnie φ
(2) = 1, φ(3) = 2, φ(4) = 2, φ(6) = 2, φ(9) = 6.
Lemat 1.57
a) Je˙zeli p jest liczb ˛
a pierwsz ˛
a, to dla dowolnego α
≥ 1, φ(p
α
) =
p
α
−1
(p
− 1). W szczególno´sci φ(p) = p − 1.
b) Je˙zeli m i n s ˛
a wzgl˛ednie pierwsze, to φ
(m
· n) = φ(m) · φ(n)
Dowód:
a)
Zauwa˙zmy ˙ze, w´sród liczb
0, . . . , p
α
wzgl˛ednie pierwsze z p
α
nie s ˛
a te, które s ˛
a po-
dzielne przez p, jest ich
p
α
p
= p
α
−1
, czyli
φ
(p
α
) = p
α
− p
α
−1
= p
α
−1
(p
− 1).

1.19. Małe twierdzenie Fermata
31
b)
Najpierw zauwa˙zmy, ze dla dowolnej liczby x,
0
≤ x < mn
N W D
(x, mn) = 1
wtedy i tylko wtedy gdy
N W D
(x, m) = 1 oraz N W D(x, n) = 1
a to zachodzi wtedy i tylko wtedy gdy reszty r
m
= x mod m oraz r
n
= x mod n speł-
niaj ˛
a warunki
N W D
(r
m
, m
) = 1 oraz N W D(r
n
, n
) = 1
(1.8)
Par reszt
(r
m
, r
n
) spełniaj ˛
acych warunek (1.8) jest φ
(m)
·φ(n), a z chi´nskiego twierdzenia
o resztach ka˙zdej liczbie x,
0
≤ x < mn odpowiada dokładnie jedna para reszt, i na
odwrót ka˙zdej parze reszt odpowiada jedna liczba. Tak wi˛ec liczb wzgl˛ednie pierwszych
z mn jest φ
(m)
· φ(n).
2
1.19
Małe twierdzenie Fermata
Twierdzenie 1.58 (Fermata) Niech a
∈ Z
∗
m
, wtedy
a
φ
(m)
= 1 (mod m).
Dowód Niech
a
1
, a
2
, . . . , a
φ
(m)
to b˛ed ˛
a wszystkie elementy Z
∗
m
. Je˙zeli pomno˙zymy je przez a
aa
1
, aa
2
, . . . , aa
φ
(m)
to zgodnie z lematem 1.35 otrzymamy te same elementy tylko w innej kolejno´sci.
Wymnó˙zmy teraz elemnty obu ci ˛
agów
φ
(m)
Y
i
=1
a
i
=
φ
(m)
Y
i
=1
aa
i
= a
φ
(m)
φ
(m)
Y
i
=1
a
i
(mod m).
Po pomno˙zeniu przez odwrotno´s´c
Q
φ
(m)
i
=1
a
i
otrzymamy tez˛e twierdzenia.
2
Wniosek 1.59 Je˙zeli p jest liczb ˛
a pierwsz ˛
a, to dla ka˙zdego a wzgl˛ednie pierwszego z p
mamy
a
p
−1
= 1 (mod p).

32
Rozdział 1. Teoria liczb
1.20
Szyfry RSA
W szyfrach one-pad opisanych w rozdziale o funkcjach boolowskich klucz do szyfrowa-
nia jest ten sam co klucz do deszfrowania. W szyfrach liniowych wprawdzie klucze do
szyfrowania i deszyfrowania s ˛
a ró˙zne, ale jaden łatwo mo˙zna wyliczy ´c z drugiego. Takie
szyfry nazywamy symetrycznymi.
Teraz zapoznamy si˛e ze sposobem szyfrowania, w których klucz do szyfrowania mo˙ze
by´c jawny, nawet ogłaszany publicznie, a klucz do deszyfrowania jest tajny i jest praktycz-
nie niemo˙zliwe wyliczenie klucza tajnego z klucza jawnego. Sposób ten zaproponowali
Rivest, Shamir i Adleman. Przypu´s´cmy, ˙ze Alicja chce utworzy´c swój klucz. Bierze w
tym celu dwie du˙ze liczby pierwsze p i q, ka˙zda mo˙ze zawiera ´c po kilkaset bitów. Tworzy
ich iloczyn n
= pq. Funkcja Eulera φ(n) = (p
− 1)(q − 1). Nast˛epnie Alicja losuje liczb˛e
e, która jest wzgl˛ednie pierwsza z φ
(n). Skoro N W D(e, φ(n)) = 1 to istnieje liczba
d, taka, ˙ze ed
= 1 (mod φ(n)). Teraz para (e, n) jest jawnym kluczem Alicji i mo˙ze
by´c publicznie ogłoszona. Para
(n, d) jest kluczem prywatnym Alicji, nie powinna go ona
nikomu zdradza´c. Alicja nie powinna te˙z zdradza´c rozkładu liczby n na czynniki. Je˙zeli
kto´s zna p i q, to mo˙ze wyliczy´c φ
(n) oraz d.
Przypu´s´cmy, ˙ze Bob chce przesła´c Alicji jak ˛
a´s zaszyfrowan ˛
a wiadomo´s´c x. Traktuje-
my t˛e wiadomo´s´c jako liczb˛e x < n. (Je˙zeli wiadomo´s´c jest ci ˛
agiem znaków, to kodujemy
ka˙zdy znak jako 8 bitów i cały ci ˛
ag mo˙ze by´c traktowany jako liczba w postaci dwójko-
wej.) Bob szyfruje wiadomo´s´c przy pomocy funkcji szyfruj ˛
acej
C
A
(x) = x
e
mod n
i przesyła j ˛
a Alicji. Alicja odszyfrowuje za pomoc ˛
a funkcji deszyfruj ˛
acej
D
A
(y) = y
d
mod n.
Poka˙zemy teraz, ˙ze je˙zeli N W D
(x, n) = 1, to
D
A
(C
A
(x)) = x.
Mamy
D
A
(C
A
(x)) = x
ed
mod n.
Ale
ed
= 1 (mod φ(n)), wi˛ec istnieje k takie, ˙ze ed = 1 + kφ(n), czyli
D
A
(C
A
(x)) = x
1+kφ(n)
= x
· x
kφ
(n)
(mod n)
ale poniewa˙z N W D
(x, n) = 1, wi˛ec mamy
x
kφ
(n)
= (x
φ
(n)
)
k
= 1 (mod n).
Tak wi˛ec D
A
(C
A
(x)) = x. W powy˙zszym rozumowaniu zakładali´smy, ˙ze N W D(x, n) =
1. Ale gdy kto´s trafi na wiadomo´s´c x, która nie jest wzgl˛ednie pierwsza z n, to Alicja ma
pecha, poniewa˙z wtedy mo˙zna dokona´c rozkładu liczby n i złama´c jej szyfr.
Łatwo te˙z mo˙zna pokaza´c, ˙ze C
A
(D
A
(x)) = x.

1.21. Testy pierwszo´sci
33
Niesymetryczne szyfry daj ˛
a nowe mo˙zliwo´sci. Mo˙zna ich na przykład u˙zywa´c do
podpisu. Aby podpisa´c jak ˛
a´s wiadomo´s´c m, Alicja szyfruje j ˛
a swoim szyfrem prywat-
nym D
A
(m) i jest to podpis wiadomo´sci m. Alicja wysyła Bobowi par˛e (m, D
A
(m)).
˙
Zeby sprawdzi´c, ˙ze wszystko si˛e zgadza Bob szyfruje podpis publicznym kluczem Alicji
i sprawdza czy
C
A
(D
A
(m)) = m.
1.21
Testy pierwszo´sci
W tym rozdziale zajmiemy si˛e zagadnieniem jak sprawdzi´c, czy liczba n jest pierwsza.
Mo˙zemy sobie wyobrazi´c, ˙ze n ma kilkaset bitów. Jak wida´c z poprzedniego rozdziału
du˙ze liczby pierwsze mog ˛
a by´c przydatne.
1.21.1
Test naiwny
Najprostszy sposób to, dzieli´c n przez kolejne liczby (pierwsze) a˙z do
√
n. Jednak ten
test jest zupełnie niepraktyczny, je˙zeli n ma kilkaset bitów.
1.21.2
Test Fermata
Drugi test jest algorytmem probabilistycznym i opiera si˛e na twierdzeniu Fermata 1.58.
Losujemy liczb˛e a < n i najpierw sprawdzamy, czy N W D
(a, n) = 1. Je˙zeli a i n
nie s ˛
a wzgl˛ednie pierwsze, i N W D
(a, n) = d > 1, to d jest dzielnikiem n i n nie jest
pierwsza.
Je˙zeli N W D
(a, n) = 1, to obliczamy a
n
−1
mod n. Je˙zeli a
n
−1
6= 1 (mod n), to
orzekamy, ˙ze n jest liczb ˛
a zło˙zon ˛
a. Je˙zeli a
n
−1
= 1 (mod n), to orzekamy, ˙ze liczba n
jest pierwsza.
Zauwa˙zmy, ˙ze je˙zeli wylosujemy liczb˛e a, dla której a
n
−1
6= 1 (mod n), to wte-
dy mamy pewno´s´c, ˙ze n nie jest liczb ˛
a pierwsz ˛
a. Wynika to bezpo´srednio z twierdze-
nia Fermata1.58. Je˙zeli jednak wylosujemy liczb˛e a wzgl˛ednie pierwsz ˛
a z n, dla której
a
n
−1
= 1 (mod n), to wtedy mo˙zemy popełni´c bł ˛
ad. Liczba n mo˙ze by´c zło˙zona, a
mimo to wylosujemy pechowo i a
n
−1
= 1 (mod n).
Przykład 1.60 W przykładzie 1.50 pokazano, ˙ze
8
5
= 8 (mod 21). Z tego wynika,
˙ze
8
10
= 8
2
= 1 (mod 21) oraz , ˙ze 8
20
= 1 (mod 21).
Definicja 1.61 Tak ˛
a liczb˛e a, dla której N W D
(a, n) = 1 oraz a
n
−1
6= 1 (mod n) b˛e-
dziemy nazywa´c ´swiadkiem zło˙zono´sci dla n, poniewa˙z za´swiadcza ona, ˙ze n jest zło˙zona.
Przykład 1.62 Jak pokazano wy˙zej
8 nie jest ´swiadkiem zło˙zono´sci dla 21. W przykła-
dzie 1.49 pokazali´smy, ˙ze
2
20
= 4 (mod 21), czyli 2 jest ´swiadkiem zło˙zono´sci
liczby
21.
Zachodzi nast˛epuj ˛
acy lemat.

34
Rozdział 1. Teoria liczb
Lemat 1.63 Je˙zeli istnieje takie a
∈ Z
∗
n
, ˙ze a
n
−1
6= 1 (mod n), to przynajmniej poło-
wa elementów Z
∗
n
jest ´swiadkiem Fermata dla n.
Dowód. Przypu´s´cmy, ˙ze
{b
1
, . . . , b
k
}
s ˛
a to wszystkie elementy Z
∗
n
, dla których b
n
−1
i
= 1 (mod n). Wtedy po pomno˙zeniu
przez a otrzymamy k elementów
{ab
1
, . . . , ab
k
}
ró˙znych mi˛edzy sob ˛
a (lemat 1.35), z których ka˙zdy jest ´swiadkiem Fermata. Rzeczywi-
´scie
(ab
i
)
n
−1
= a
n
−1
b
n
−1
i
= a
n
−1
6= 1 (mod n).
A wi˛ec ´swiadków zło˙zono´sci jest co najmniej połowa.
2
Je˙zeli n jest pierwsze, to z Twierdzenia Fermata, algorytm zawsze orzeknie dobrze.
Z lematu 1.63 wynika, ˙ze je˙zeli n jest zło˙zona i istnieje ´swiadek Fermata dla n, to takich
´swiadków jest co najmniej połowa, i nasz algorytm pomyli si˛e z prawdopodobie ´nstwem
1
2
. Prawdopodobie ´nsto, to mo˙zna zmniejszy´c poprzez powtórzenie algorytmu r razy, z
ró˙znymi wylosowanymi a.
Istniej ˛
a jednak liczby zło˙zone n, które nie maj ˛
a ´swiadków zło˙zono´sci. Na przykład
n
= 561. Kłopot bierze si˛e st ˛
ad, ˙ze
561 = 3
· 11 · 17, a 560 = 561 − 1 dzieli si˛e przez
2 = 3
− 1, 10 = 11 − 1 oraz przez 16 = 17 − 1. Dlatego dla dowolnego a, je˙zeli
N W D
(a, 561) = 1, to a jest wzgl˛ednie pierwsze z 3, 11 i 17 oraz mamy
a
560
= (a
2
)
280
= 1 (mod 3)
a
560
= (a
10
)
56
= 1 (mod 11)
a
560
= (a
16
)
35
= 1 (mod 17)
i z chi´nskiego twierdzenia o resztach wynika, ˙ze
a
560
= 1 (mod 561)
Takie liczby nazywaj ˛
a sie liczbami Carmichaela. Pierwsze trzy z nich to 561, 1105 i 1729.
Wyst˛epuj ˛
a one bardzo rzadko, jest ich tylko 255 w´sród liczb mniejszych od 100 000 000.
1.21.3
Test Millera-Rabina
Zakładamy, ˙ze n jest nieparzyste (2 jest jedyn ˛
a parzyst ˛
a liczb ˛
a pierwsz ˛
a). Najpierw spraw-
dzamy, czy n jest pot˛eg ˛
a jakiej´s liczby naturalnej. Dla α od 2 do
log
2
n sprawdzamy czy
n
= k
α
, dla jakiego´s k. W rozdziale o arytmetyce opisano jak za pomoc ˛
a binary search
stwierdzi´c, czy liczba jest pot˛eg ˛
a innej liczby. Je˙zeli n jest pot˛eg ˛
a, to jest zło˙zona.
Poniewa˙z n jest nieparzyste, to n
− 1 mo˙zemy przedstawi´c w postaci
n
− 1 = m · 2
k
.

1.21. Testy pierwszo´sci
35
dla jakiego´s m nieparzystego.
Losujemy a < n. Sprawdzamy, czy N W D
(a, n) = 1 (je˙zeli N W D(a, n) > 1, to n
jest zło˙zona).
Nast˛epnie obliczamy a
m
mod n. Je˙zeli a
m
mod n = 1, to koniec, stwierdzamy, ˙ze n
jest pierwsza. Je˙zeli a
m
mod n
6= 1, to obliczamy po kolei
a
m
2
mod n, a
m
2
2
mod n, . . . , a
m
2
k
mod n.
Zauwa˙zmy, ˙ze w tym ci ˛
agu ka˙zda liczba jest kwadratem poprzedniej. Je˙zeli w´sród tych
liczb nie ma jedynki, to z twierdzenia Fermata wynika, ˙ze n jest zło˙zona, bo wtedy
a
m
2
k
= a
n
−1
6= 1 (mod n).
Je˙zeli w tym ci ˛
agu jest jedynka, na przykład
a
m
2
i
= 1 (mod n)
to patrzymy na poprzedni element x
= a
m
2
i−1
. Je˙zeli x
6= −1, to orzekamy, ˙ze n jest
liczb ˛
a zło˙zon ˛
a. Znale˙zli´smy nietrywialny pierwiastek z 1, a z twierdzenia 1.53 wynika,
˙ze jest to mo˙zliwe tylko wtedy gdy n nie jest pierwsze. Je˙zeli x
=
−1, to orzekamy, ˙ze n
jest pierwsze.
Łatwo wi˛ec wida´c, ˙ze je˙zeli n jest pierwsze, to test zawsze odpowie prawidłowo,
niezale˙znie od losowania. Wiadomo te˙z, ˙ze je˙zeli n jest zło˙zona i nie jest pot˛eg ˛
a liczby
pierwszej, to z prawdopodobie ´nstwem wi˛ekszym ni˙z
1
2
wykryjemy to. Dowód tego faktu
wybiega poza zakres tej ksi ˛
a˙zki i pomijamy go.
Przykład 1.64 Prze´sled´zmy algorytm Millera-Rabina dla n
= 21 i a = 8.
n
− 1 = 20 = 5 · 2
2
.
W przykładzie 1.50 pokazali´smy, ˙ze
8
5
= 8 (mod 21).
Teraz podnosimy
8 do kwadratu i otrzymujemy
8
5·2
= 8
2
= 1 (mod 21).
W tym momencie algorytm znalazł nietrywialny pierwiastek 1 i orzeka, ˙ze
21 jest liczb ˛
a
zło˙zon ˛
a.
W praktyce stosujemy wszystkie trzy testy na raz. Maj ˛
ac nieparzyst ˛
a liczb˛e n, naj-
pierw sprawdzamy, czy dzieli si˛e ona przez kilka kolejnych liczb pierwszych
p
1
, p
2
, . . . , p
d
.
Dobór d zale˙zy od tego jak du˙ze liczby sprawdzamy. W ten sposób eliminujemy du˙z ˛
a
cz˛e´s´c liczb. Zauwa˙zmy, ˙ze obliczaj ˛
ac iloczyn tych liczb
x
=
d
Y
i
=1
p
i

36
Rozdział 1. Teoria liczb
i sprawdzaj ˛
ac, czy N W D
(x, n) = 1 mo˙zemy za jednym razem sprawdzi´c, czy n dzieli
si˛e przez któr ˛
a´s z tych liczb. Po przej´sciu pierwszego testu stosujemy test drugi, a gdy
liczba n go przejdzie stosujemy test trzeci. Poniewa˙z liczby Carmichaela s ˛
a do´s´c rzadkie,
wi˛ec drugi test wyeliminuje wi˛ekszo´s´c liczb zło˙zonych.
1.21.4
Losowanie liczb pierwszych
Je˙zeli chcemy wyklosowa´c liczb˛e pierwsz ˛
a to losujemy nieparzyst ˛
a liczb˛e, a mast˛epnie
sprawdzamy, czy jest ona pierwsza. Je˙zeli nie, to sprawdzamy nast˛epne liczby n
+ 2, n +
4, ....
1.22
Zadania
1. Podziel (oblicz ilorazy i reszty) liczb
175 oraz 1754 przez 11.
2. Dla ka˙zdej z liczb:x
= 8,
−8, 120 oraz −120 znajd´z liczb˛e y ∈ {0, 1, 2, 3, 4} tak ˛a,
˙ze x
= y
(mod 5).
3. Oblicz: a)
(50
· 51 + 15) mod 7, b) 15 · 36 mod 7; c) 15
3
· (37)
3
mod 7.
4. Oblicz: a)
26
4
∗ 18 + 2002) mod 5,
5. Oblicz: a)
10
39
mod 11, b) 2
39
mod 5 c) 7
40
mod 10.
6. Przedstaw klasy abstrakcji relacji kongruencji dla m
= 6.
7. Jak wygl ˛
adaj ˛
a działania dodawania i mno˙zenia w pier´scieniu Z
6
8. W pier´scieniu Z
8
wykonaj działania
7 + 6 oraz 7
· 6.
9. W pier´scieniu Z
8
rozwi ˛
a˙z równania: a)
1 + x = 0, b) 1 + x = 2, c) 5 + x = 0, d)
5 + x = 2.
10. Podaj tabliczk˛e dodawania i mno˙zenia w ciele Z
7
. Podaj elementy odwrotne do 5 i
6 w Z
7
.
11. Dla liczb a
= 600 i b = 1050 oblicz N W D(a, b) oraz liczby całkowite x i y
spełniaj ˛
ace równanie xa
+ yb = N W D(a, b).
12. Oblicz N W D
(667, 713).
13. Oblicz N W D
(199816, 199819).
14. W pier´scieniu Z
5
rozwi ˛
a˙z równania: a)
4
· x = 1, b) 4 · x = 2.
15. W pier´scieniu Z
8
rozwi ˛
a˙z równania: a)
3
· x = 1, b) 3 · x = 2.
16. W pier´scieniu Z
17
rozwi ˛
a˙z równania: a)
8x = 2,
b)
9x = 4.
17. W pier´scieniu Z
14
rozwi ˛
a˙z równania: a)
6x = 2, b) 6x = 9.

1.22. Zadania
37
18. Znajd´z liczby całkowite x i y spełniaj ˛
ace równanie:
17x + 40y = 1.
19. Podaj rozkład na czynniki pierwsze liczb
240 oraz 111.
20. Ile dzielników ma liczba
240?
21. Znajd´z elementy odwrotne do wszystkich elementów dwracalnych w Z
12
.
22. Udowodnij, ˙ze dla ka˙zdego a
∈ Z
m
istnieje co najwy˙zej jeden element odwrotny
a
−1
.
23. Przedstaw tabel˛e funkcji f
(x) = 4
· x + 5 w pier´scieniu Z
13
.
24. Przedstaw tabel˛e funkcji f
(x) = 4
· x + 5 w pier´scieniu Z
12
.
25. Rozwi ˛
a˙z układ kongruencji:
3 = a (mod 5),
5 = a (mod 6).
26. Sprawd´z, czy
100136 = 200146 (mod 30)
27. Dla jakich par reszt
(a
1
, a
2
) istniej ˛
a liczby a spełniaj ˛
ace układ kongruencji:
a
1
= a (mod 4),
a
2
= a (mod 6).
28. Które elementy Z
12
s ˛
a resztami kwadratowymi?
29. Które elementy Z
13
s ˛
a resztami kwadratowymi?
30. Ile jest pierwiastków z
1 w Z
30
?
31. Poka˙z, ˙ze w Z
105
jest osiem pierwiastków z
1.
32. Przy pomocy algorytmu szybkiego pot˛egowania oblicz: a)
4
14
mod 15; b)8
64
mod
65; c) 12
64
mod 65; d)14
64
mod 65; e) 10
32
mod 33.
33. Przeprowad´z test Fermata dla: a) n
= 15 oraz a = 4; b) n = 65 oraz a = 8; c)
n
= 65 oraz a = 12.
34. Przeprowad´z test Millera-Rabina dla: a) n
= 39 oraz a = 5; b) n = 65 oraz
a
= 8; a) n = 65 oraz a = 12.
35. Oblicz: a) φ
(24); b) φ(120).
36. Niech
Ω =
{0, 1, . . . , 59}, b˛edzie przestrzeni ˛a zdarze´n elementarnych z jednostaj-
nym rozkładem prawdopodobie ´nstwa. Okre´slmy na
Ω trzy zmienne losowe
X
4
(ω) = ω mod 4
X
5
(ω) = ω mod 5
X
6
(ω) = ω mod 6
Poka˙z, ˙ze zmienne X
5
i X
6
s ˛
a niezale˙zne, a zmienne X
4
i X
6
nie s ˛
a niezale˙zne.

38
Rozdział 1. Teoria liczb
37. Niech
Ω =
{0, 1, . . . , 104}, b˛edzie przestrzeni ˛a zdarze´n elementarnych z jedno-
stajnym rozkładem prawdopodobie ´nstwa. Okre´slmy na
Ω trzy zmienne losowe
X
3
(ω) = ω mod 3
X
5
(ω) = ω mod 5
X
7
(ω) = ω mod 7
Poka˙z, ˙ze zmienne X
5
, X
5
i X
7
s ˛
a niezale˙zne.
1.23
Problemy
1.23.1
Najwi˛ekszy wspólny dzielnik
1. Udowodnij, ˙ze ka˙zda liczba postaci xa
+ yb, dla x i y całkowitych, jest wielo-
krotno´sci ˛
a N W D
(a, b), i na odwrót, ka˙zda wielokrotno´s´c N W D(a, b) jest postaci
xa
+ yb, dla jaki´s x i y całkowitych.
2. Udowodnij, ˙ze N W D
(a, b) jest najmniejsz ˛
a dodatni ˛
a liczb ˛
a d, dla której istnieje x
i y całkowite, takie ˙ze xa
+ yb = d.
3. Zaprojektuj algorytm obliczania najwi˛ekszego wspólnego dzielnika trzech (lub k)
liczb.
4. Które z liczb całkowitych mo˙zna przedstawi´c w postaci x
· 10 + y · 21 (x i y ∈ Z)?
5. Które z liczb całkowitych mo˙zna przedstawi´c w postaci x
· 10 + y · 12 (x i y ∈ Z)?
6. Niech r
1
, ... , r
k
b˛edzie ci ˛
agiem kolejnych reszt uzyskiwanych w alorytmie Eukli-
desa. Poka˙z, ˙ze dla ka˙zdego i
≤ k − 2, mamy r
i
+2
<
r
i
2
.
1.23.2
Najmniejsza wspólna wielokrotno´s´c
Niech N W W
(a, b) oznacza najmniejsz ˛
a wspóln ˛
a wielokrotno´s´c liczb a i b.
1. Udowodnij, ˙ze N W W
(a, b) dzieli ka˙zd ˛
a inn ˛
a wspóln ˛
a wielokrotno´s´c liczb a i b.
2. Poka˙z, ˙ze N W W
(a, b)
· NW D(a, b) = a · b.
3. Jakie liczby całkowite dziel ˛
a si˛e jednocze´snie przez
24 i przez 54?
1.23.3
Liczby wzgl˛ednie pierwsze
Udowodnij, ˙ze je˙zeli m jest wzgl˛ednie pierwsze z a i b, to m jest wzgl˛ednie pierwsze z
iloczynem tych liczb ab.
Jako wniosek udowodnij, ˙ze je˙zeli m jest wzgl˛ednie pierwsze z ka˙zd ˛
a z liczb m
1
, ..., m
k
,
to m jest wzgl˛ednie pierwsze z iloczynem tych liczb
Q
k
i
=1
m
i
.

1.23. Problemy
39
1.23.4
Liczby pierwsze
1. Udowodnij, ˙ze dla ka˙zdego k istnieje ci ˛
ag k kolejnych liczb zło˙zonych.
2. Udowodnij, ˙ze liczb pierwszych jest niesko ´nczenie wiele.
3. Udowodnij, ˙ze je˙zeli dwie liczby x i y spełniaj ˛
a warunki: x
2
= y
2
(mod n) oraz
x
6= y (mod n) i x 6= −y (mod n), to NW D(x+y, n) = d jest nietrywialnym
dzielnikiem n.
1.23.5
Chi ´nskie twierdzenie o resztach
Z chi´nskiego twierdzenia o resztach wynika, ˙ze je˙zeli N W D
(m, n) = 1, to funkcja
f
(x) = (x mod m, x mod n)
stanowi wzajemnie jednoznaczne odwzorowanie pomi˛edzy Z
mn
a iloczynem kartezja ´n-
skim Z
m
× Z
n
.
Na iloczynie kartezja ´nskim Z
m
× Z
n
mo˙zemy okre´sli´c działania dodawania i mno˙ze-
nia w nast˛epuj ˛
acy sposób:
(a, b) + (c, d) = (a + b, c + d)
(a, b)
· (c, d) = (a · b, c · d).
Łatwo mo˙zna sprawdzi´c, ˙ze zbiór Z
m
× Z
n
z tak okre´slonymi działaniami, jest pier´scie-
niem. Ponadto funkcja f spełnia warunki f
(x+y) = f (x)+f (y) oraz f (x
·y) = f(x)·(y).
1.23.6
System one-pad
System „one-pad” (porównaj rozdział o funkcjach boolowskich) mo˙ze by ´c stosowany
do ci ˛
agów liter alfabetu łaci ´nskiego. Wtedy uto˙zsamiamy litery z liczbami od 0 do 25 i
zamiast operacji
⊕ stosujemy:
x
+ k
(mod 26),
czyli reszt˛e z dzielenia
(x + k) przez 26. Jak wygl ˛
ada wtedy operacja deszyfrowania?
Poka˙z, ˙ze system one-pad z literami jest równie bezpieczny jak system z dwoma cyframi
0 i 1.
1.23.7
Przestrze ´n liniowa
Zbiór B
=
{0, 1} z działaniami xor ⊕ oraz koniunkcji · jest ciałem Z
2
.
Udowodnij, ˙ze zbiór B
n
jest przestrzeni ˛
a liniow ˛
a nad ciałem
{0, 1}, z ⊕ jako doda-
waniem oraz mno˙zeniem przez skalar zdefiniowanym przez:
• 0 · x = 0 (tutaj zero po lewej stronie jest zerem z ciała, a zero po prawej stronie jest
wektorem zerowym),
• 1 · x = x.

40
Rozdział 1. Teoria liczb
1.23.8
Uogólnienie małego twierdzenia Fermata
Udowodnij
Twierdzenie 1.65 Niech G b˛edzie dowoln ˛
a grup ˛
a. Wtedy dla dowolnego a
∈ G
a
|G|
= 1
.
1.23.9
Algorytm Euklidesa dla wielomianów
Rozwa˙zmy zbiór wielomianów, którego współczynniki s ˛
a elementami jakiego´s ciała, na
przykład zbioru liczb rzeczywistych lub Z
2
. W pierwszym rozdziale pokazali´smy jak
mo˙zna dzieli´c wielomiany i dla dwóch wielomianów p i q wyliczy´c iloraz i reszt˛e z dzie-
lenia. Mówimy, ˙ze wielomian p dzieli wielomian q, je˙zeli istnieje wielomian r taki, ˙ze
p
· r = q. Mo˙zna te˙z dla wielomianów p i q zdefiniowa´c najwi˛ekszy wspólny dzielnik,
jako taki wielomian d, który dzieli p i q oraz jest podzielny przez ka˙zdy wspólny dzielnik
wielomianów p i q. Poka´z, ˙ze
1. Algorytm Euklidesa oblicza najwi˛ekszy wspólny dzielnik dla wielomianów.
2. Je˙zeli N W D
(p, q) = d, to istniej ˛
a wielomiany x i y, takie, ˙ze
p
· x + q · y = d.
3. Mo˙zna zdefiniowa´c w pier´scieniu wielomianów relacj˛e przystawania modulo wie-
lomian m, która ma podobne własno´sci do relacji kongruencji modulo w liczbach
całkowitych.
Wyszukiwarka
Podobne podstrony:
Matematyka dyskretna 2004 06 Teoria liczb
Matematyka dyskretna 2002 06 Teoria liczb
Matematyka dyskretna 2004 01 Podstawowe pojęcia, oznaczenia
Matematyka dyskretna 2004 04 Rachunek prawdopodobieństwa
Matematyka dyskretna 2004 04 Rachunek prawdopodobieństwa
Matematyka dyskretna 2004 01 Podstawowe pojęcia, oznaczenia
Matematyka dyskretna cz 1 Teoria liczb
PK-I-06, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka dyskretna i TPI, 04-10-2012
Egzamin 2004.06.07, rozwiazania zadań aktuarialnych matematyka finansowa
Z Ćwiczenia 06.04.2008, Zajęcia, II semestr 2008, Matematyka dyskretna i logika
Test-06, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka dyskretna i TPI, 04-10-2012
2004 06 21
matematyka dyskretna w 2 id 283 Nieznany
Denisjuk A Matematyka Dyskretna
Program nauczania Technik Informatyk 312[01] 2004 06 04
C2, Matematyka studia, Matematyka dyskretna
więcej podobnych podstron