
DEFINICJE GRANICY FUNKCJI
f : D → R, D ⊂ R
Def. Cauchy’ego:
lim
x→x
0
f (x) = g ⇔
∀ε > 0 ∃δ > 0 ∀x ∈ D
0 < |x − x
0
| < δ ⇒ |f (x) − g| < ε
Def. Heinego:
lim
x→x
0
f (x) = g ⇔
∀
(x
n
)
n∈N
x
n
6= x
0
lim
n→∞
x
n
= x
0
⇒ lim
n→∞
f (x
n
) = g
DEFINICJA CIA
¸ G LO´
SCI FUNKCJI
Funkcja f jest ci¸
ag la w punkcie x
0
, je´sli obie granice jednostronne istniej¸
a, s¸
a
sobie r´
owne
lim
x→x
+
0
f (x) = lim
x→x
−
0
f (x)
oraz s¸
a r´
owne warto´sci funkcji w punkcie
lim
x→x
0
f (x) = f (x
0
)
Funkcja f jest ci¸
ag la w zbiorze D, je´sli jest ci¸
ag la w ka˙zdym punkcie tego zbioru.
1

PUNKTY NIECIA
¸ G LO´
SCI FUNKCJI
Punkt nieci¸
ag lo´sci funkcji x
0
nazywamy punktem nieci¸
ag lo´
sci I-go rodzaju, je´sli
istniej¸
a sko´
nczone granice jednostronne funkcji w tym punkcie
lim
x→x
+
0
f (x) i
lim
x→x
−
0
f (x)
W przeciwnym przypadku, punkt nieci¸
ag lo´sci x
0
nazywamy punktem nieci¸
ag lo´
sci
II-go rodzaju.
NIEKT ´
ORE W LASNO´
SCI FUNKCJI CIA
¸ G LYCH
TWIERDZENIA m.in.:
-o ci¸
ag lo´sci funkcji z lo˙zonej,
-o ci¸
ag lo´sci funkcji odwrotnej,
-o lokalnym zachowaniu znaku,
-o wchodzeniu granicy do argumentu funkcji ci¸
ag lej,
-tw. Weierstrassa o osi¸
aganiu kres´
ow,
-tw. Darboux o przyjmowaniu warto´sci po´srednich.
TWIERDZENIE BOLZANO-CAUCHY (wniosek z tw. Darboux)
f : [a, b] → R - funkcja ci¸ag la, [a, b] ⊂ D.
Je´
sli f przyjmuje na ko´
ncach przedzia lu warto´
sci r´
o˙znych znak´
ow tzn.
f (a) · f (b) < 0 ⇒ ∃ c ∈ (a, b) f (c) = 0
DOW ´
OD TW:
LEMAT
Je´
sli funkcja f (x) jest ci¸
ag la w punkcie x = x
0
i warto´
s´
c f (x
0
) 6= 0, to dla
wszystkich argument´
ow x dostatecznie bliskich x
0
funkcja f (x) zachowuje taki sam
znak, jaki ma w punkcie x
0
.
2

Rozwa˙zmy teraz wszystkie punkty x = ¯
x przedzia lu [a, b], dla kt´
orych
f (¯
x) < 0. Do nich nale˙zy np. punkt a i (na podstawie lematu) najbli˙zsze mu
punkty. Zbi´
or {¯
x} jest ograniczony z g´
ory liczb¸
a b. Niech c = sup{¯
x}; twierdzimy,
˙ze f (c) = 0.
Za l´
o˙zmy, ˙ze jest przeciwnie. W´
owczas albo f (c) < 0 albo f (c) > 0. Gdyby by lo
f (c) < 0 (wtedy wiadomo, ˙ze c < b, bo f (b) > 0), to z Lematu, na prawo od c
znalaz lyby si¸e warto´sci ¯
x, dla kt´
orych f (¯
x) < 0, co by loby sprzeczne z definicj¸
a c
jako kresu g´
ornego dla {¯
x}.
Je´sliby za´s by lo f (c) > 0, to - znowu na podstawie Lematu - mieliby´smy f (x) > 0
tak˙ze i w s¸
asiedztwie lewostronnym, czyli w pewnym dostatecznie ma lym przedziale
(c − δ, c], a zatem w og´
ole nie by loby tam warto´sci ¯
x, co r´
ownie˙z jest niemo˙zliwe, bo
z definicji c jest kresem g´
ornym dla ¯
x.
Twierdzenie jest udowodnione.
DEFINICJA POCHODNEJ
f : D → R, D ⊂ R; x
0
∈ IntD
Pochodn¸
a funkcji f w punkcie x
0
nazywamy granic¸e (o ile istnieje) ilorazu r´
o˙znicowego
∆f
∆x
=
f (x
0
+ ∆x) − f (x
0
)
∆x
tej funkcji w punkcie x
0
, gdy przyrost ∆x d¸
a˙zy do 0 i oznaczamy f
0
(x
0
), czyli
f
0
(x
0
) = lim
∆x→0
f (x
0
+ ∆x) − f (x
0
)
∆x
= lim
x→x
0
f (x) − f (x
0
)
x − x
0
UWAGA:
Analogicznie definiuje si¸e pochodne jednostronne f
0
±
(x
0
), gdy istniej¸
a granice
jednostronne oraz pochodne wy˙zszych rz¸ed´
ow
f
00
= (f
0
)
0
, . . . , f
(n)
= (f
(n−1)
)
0
3
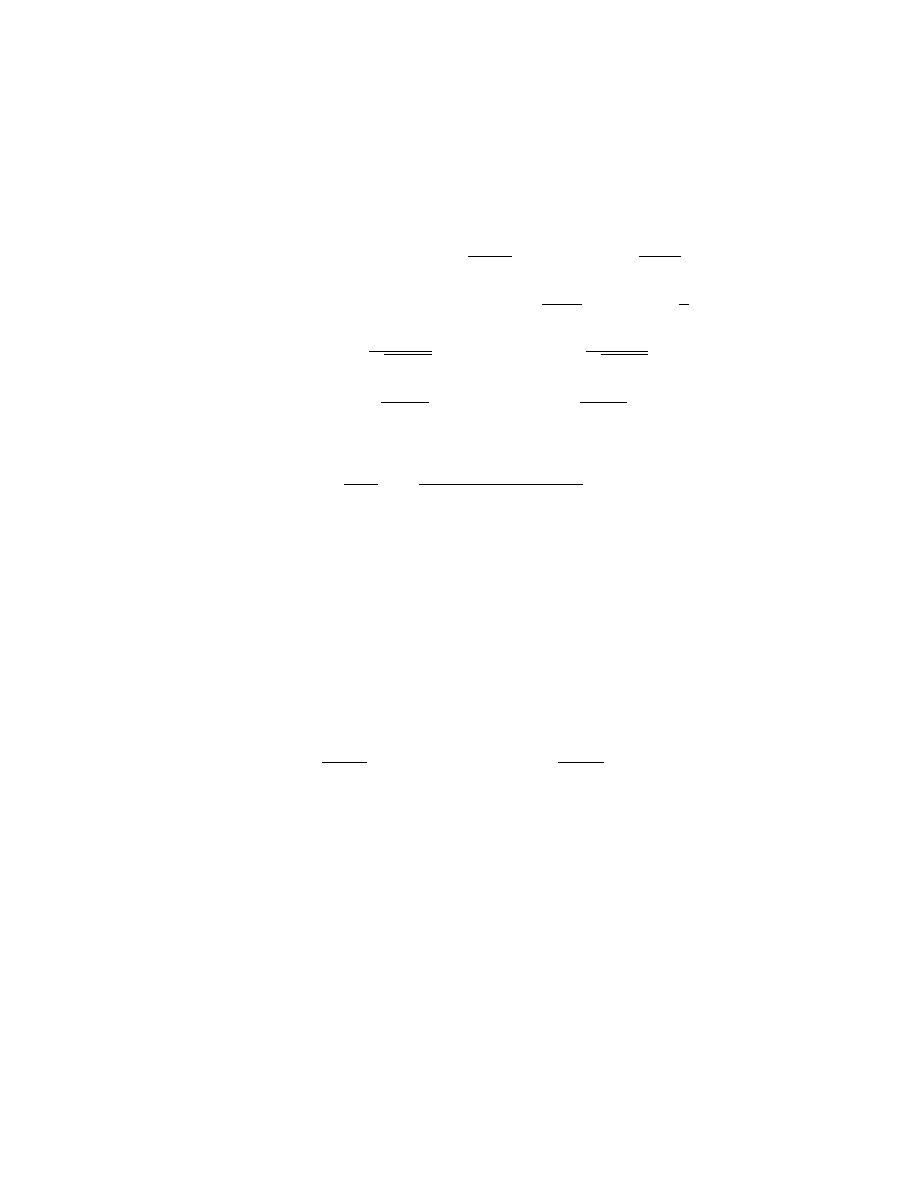
PODSTAWOWE WZORY
(c)
0
= 0
(x
α
)
0
= αx
α−1
, α 6= 0
(sin x)
0
= cos x
(cos x)
0
= − sin x
(tgx)
0
=
1
cos
2
x
(ctgx)
0
= −
1
sin
2
x
(a
x
)
0
= a
x
ln a
(e
x
)
0
= e
x
(log
a
x)
0
=
1
x ln a
(ln x)
0
=
1
x
(arcsin x)
0
=
1
√
1 − x
2
(arccos x)
0
= −
1
√
1 − x
2
(arctgx)
0
=
1
1 + x
2
(arcctgx)
0
= −
1
1 + x
2
[f (x) ± g(x)]
0
= f
0
(x) ± g
0
(x)
[f (x) · g(x)]
0
= f
0
(x)g(x) + f (x)g
0
(x)
f (x)
g(x)
0
=
f
0
(x)g(x) − f (x)g
0
(x)
g
2
(x)
NIEKT ´
ORE TWIERDZENIA RACHUNKU R ´
O ˙
ZNICZKOWEGO
TWIERDZENIE O POCHODNEJ FUNKCJI ODWROTNEJ
Niech f : D → W jest odwracalna i niech g : W → D b¸
edzie jej funkcj¸
a odwrotn¸
a
(g = f
−1
). Za l´
o˙zmy, ˙ze f ma pochodn¸
a sko´
nczon¸
a i r´
o˙zn¸
a od 0 w x
0
∈ D. Wtedy w
punkcie y
0
= f (x
0
) istnieje pochodna funkcji g oraz
g
0
(y
0
) =
1
f
0
(x
0
)
inaczej
[f
−1
(y
0
)]
0
=
1
f
0
(x
0
)
|
y
0
=f (x
0
)
TWIERDZENIE O POCHODNEJ FUNKCJI Z LO ˙ZONEJ
Za l´
o˙zmy, ˙ze funkcja u = ϕ(x) ma w punkie x
0
pochodn¸
a sko´
nczon¸
a ϕ
0
(x
0
) i ˙ze
funkcja y = f (u) ma w punkcie u
0
= ϕ(x
0
) pochodn¸
a sko´
nczon¸
a f
0
(u
0
). Wtedy
funkcja z lo˙zona y = f (ϕ(x)) ma w punkcie x
0
pochodn¸
a sko´
nczon¸
a r´
own¸
a iloczynowi
pochodnych funkcji f i ϕ w odpowiednich punktach
y
0
(x
0
) = [f (ϕ(x
0
))]
0
= [f ◦ ϕ]
0
(x
0
) = f
0
(ϕ(x
0
)) · ϕ
0
(x
0
) = f
0
(u
0
) · ϕ
0
(x
0
)
4

DOW ´
OD TW. O POCHODNEJ F-CJI ODWROTNEJ
Nadajmy warto´sci y = y
0
dowolny przyrost ∆y. Wtedy funkcja x = g(y) uzyska
odpowiedni przyrost ∆x. Zauwa˙zmy, ˙ze je´sli ∆y 6= 0, to wobec jednoznaczno´sci
funkcji y = f (x) tak˙ze i ∆x 6= 0. Otrzymujemy
∆x
∆y
=
1
∆x
∆y
Je´sli teraz ∆y → 0, to na mocy za lo˙zenia, ˙ze funkcja x = g(y) jest ci¸
ag la, r´
ownie˙z
∆x → 0. Ale wtedy mianownik po prawej stronie r´
owno´sci d¸
a˙zy do granicy f
0
(x
0
) 6=
0 i co za tym idzie, istnieje granica lewej strony r´
owna odwrotno´sci 1/f
0
(x
0
). Ta
granica jest w la´snie pochodn¸
a g
0
(y
0
).
DOW ´
OD TW. O POCHODNEJ F-CJI Z LO ˙ZONEJ
Tez¸e twierdzenia [f (ϕ(x))]
0
= f
0
u
(ϕ(x
0
))ϕ
0
(x
0
) mo˙zemy kr´
ocej zapisa´
c w postaci
y
0
x
= y
0
u
u
0
x
Nadajmy x dowolny przyrost ∆x, niech ∆u b¸edzie odpowiednim przyrostem
funkcji u = ϕ(x), a ∆y - przyrostem funkcji y = f (u) odpowiadaj¸
acym przyros-
towi ∆u. Zachodzi wz´
or
∆f (u
0
) = f
0
(u
0
)∆u + α∆u
gdzie α zale˙zy od ∆u i d¸
a˙zy do 0 wraz z ∆u. Dziel¸
ac obie strony tej r´
owno´sci przez
∆x otrzymamy
∆y
∆x
= y
0
u
∆u
∆x
+ α
∆u
∆x
Je´sli ∆x → 0 to i ∆u → 0, a wtedy r´
ownie˙z α → 0. Istnieje zatem granica
lim
∆→0
∆y
∆x
= y
0
u
lim
∆→0
∆u
∆x
= y
0
u
u
0
x
kt´
ora jest w la´snie szukan¸
a pochodn¸
a y
0
x
.
5

TWIERDZENIE ROLLE’A
Je´
sli funkcja f jest ci¸
ag la na przedziale [a, b] i r´
o˙zniczkowalna w ka˙zdym punkcie
przedzia lu (a, b) oraz f (a) = f (b), to istnieje taki punkt c ∈ (a, b), ˙ze f
0
(c) = 0.
DOW ´
OD
Opiera si¸e na nast¸epuj¸
acych twierdzeniach
TWIERDZENIE WEIERSTRASSA
Je´sli funkcja f : [a, b] → R jest ci¸ag la, to osi¸aga ona w tym przedziale sw´oj kres
g´
orny i dolny, tzn.
∃ c, d ∈ [a, b]
f (c) = sup{f (x) : x ∈ [a, b]}
f (d) = inf{f (x) : x ∈ [a, b]}
TWIERDZENIE FERMATA
Je´sli funkcja f okre´slona w przedziale I osi¸
aga warto´s´
c najwi¸eksz¸
a (najmniejsz¸
a)
w punkcie wewn¸etrznym x
0
tego przedzia lu i jest w tym punkcie r´
o˙zniczkowalna, to
f
0
(x
0
) = 0.
Z ci¸
ag lo´sci funkcji w przedziale domkni¸etym [a, b] wynika, zgodnie z tw. Weier-
strassa, ˙ze osi¸
aga ona w tym przedziale warto´s´
c najwi¸eksz¸
a i najmniejsz¸
a.
Oz-
naczmy je odpowiednio przez M i m. W´
owczas dla ka˙zdego x ∈ [a, b] prawdziwa
jest nier´
owno´s´
c m 6 f (x) 6 M .
Gdyby M = m, w´
owczas nier´
owno´s´
c ta oznacza laby, ˙ze funkcja jest sta la w [a, b].
W zwi¸
azku z tym w ka˙zdym punkcie c ∈ [a, b] pochodna f
0
(c) by laby r´
owna 0, co
ko´
nczy loby dow´
od.
Za l´
o˙zmy wi¸ec, ˙ze m < M . Zatem istniej¸
a dwa r´
o˙zne punkty α i β w przedziale
[a, b] takie, ˙ze f (α) = m i f (β) = M . Poniewa˙z f (a) = f (b), wi¸ec co najmniej jeden
z tych punkt´
ow musi le˙ze´
c mi¸edzy punktami a i b. Zgodnie z tw. Fermata pochodna
funkcji w tym punkcie jest r´
owna 0. To ko´
nczy dow´
od twierdzenia, bo jak wida´
c
szukanym punktem c mo˙ze by´
c jeden z punkt´
ow α lub β.
TWIERDZENIE LAGRANGE’A (o warto´sci ´sredniej)
Za l´
o˙zmy, ˙ze funkcja f : [a.b] → R jest ci¸ag la oraz posiada pochodn¸a w przedziale
(a, b). Wtedy
∃ c ∈ (a, b)
f (b) − f (a)
b − a
= f
0
(c)
6

WNIOSKI
1. Je´sli f
0
(x) = 0 dla ka˙zdego x ∈ (a, b), to f jest funkcj¸
a sta l¸
a w (a, b).
2. Je´sli f jest ´sci´sle rosn¸
aca (´sci´sle malej¸
aca) w (a, b), to f
0
(x) > 0 w (a, b)
(f
0
(x) 6 0 w (a, b)).
3. Je´sli f
0
(x) > 0 w (a, b) (f
0
(x) < 0 w (a, b)) z wyj¸
atkiem by´
c mo˙ze sko´
nczonej
liczby punkt´
ow, to f jest ´sci´sle rosn¸
aca w (a, b) (´sci´sle malej¸
aca w (a, b)).
DOW ´
OD TW. LAGRANGE’A
Rozpatrzmy funkcj¸e g : [a, b] → R okre´slon¸a wzorem
g(x) = f (x) − f (a) −
f (b) − f (a)
b − a
(x − a)
Zauwa˙zmy, ˙ze funkcja ta spe lnia wszystkie za lo˙zenia tw. Rolle’a. Jest ci¸
ag la w
[a, b] jako r´
o˙znica funkcji ci¸
ag lej i liniowej oraz jest r´
o˙zniczkowalna w ka˙zdym punkcie
x ∈ (a, b), poniewa˙z
g
0
(x) = f
0
(x) −
f (b) − f (a)
b − a
Ponadto g(a) = g(b). Zatem zgodnie z tym twierdzeniem, istnieje taki punkt c ∈
(a, b), ˙ze g
0
(c) = 0. Oznacza to, ˙ze
f
0
(c) =
f (b) − f (a)
b − a
co ko´
nczy dow´
od twierdzenia.
TWIERDZENIE DE L’HOSPITALA
Za l´
o˙zmy, ˙ze funkcje f i g s¸
a r´
o˙zniczkowalne w pewnym otoczeniu punktu x
0
, przy
czym g
0
(x) 6= 0 dla ka˙zdego x z tego otoczenia. Za l´
o˙zmy ponadto, ˙ze
lim
x→x
0
f (x) = lim
x→x
0
g(x) = 0
lub
lim
x→x
0
f (x) = lim
x→x
0
g(x) = ±∞
W´
owczas je´
sli istnieje granica (w la´
sciwa lub niew la´
sciwa) ilorazu pochodnych
lim
x→x
0
f
0
(x)
g
0
(x)
7

to istnieje r´
ownie˙z granica ilorazu tych funkcji lim
x→x
0
f (x)
g(x)
i s¸
a sobie r´
owne
lim
x→x
0
f (x)
g(x)
= lim
x→x
0
f
0
(x)
g
0
(x)
UWAGA
Twierdzenie pozostaje prawdziwe dla granic jednostronnych oraz granic w niesko´
nczono´sciach.
DOW ´
OD
twierdzenia przeprowadzimy w przypadku granic jednostronnych, tj. przy za lo˙zeniu,
˙ze
lim
x→x
+
0
f (x) = lim
x→x
+
0
g(x) = 0
Opiera si¸e on na nast¸epuj¸
acym uog´
olnieniu tw. Lagrange’a
TWIERDZENIE CAUCHY’EGO
Za l´
o˙zmy, ˙ze funkcje f, g : [a, b] → R s¸a ci¸ag le, r´o˙zniczkowalne w przedziale (a, b)
oraz g
0
(x) 6= 0 dla ka˙zdego x ∈ (a, b). Wtedy
∃ c ∈ (a, b)
f (b) − f (a)
g(b) − g(a)
=
f
0
(c)
g
0
(c)
Poka˙zemy prawdziwo´s´
c tw. de l’Hospitala w przypadku granic prawostronnych
d¸
a˙z¸
acych do 0.
Okre´slmy w tym celu funkcje f i g dodatkowo w punkcie x
0
przyjmuj¸
ac f (x
0
) =
g(x
0
) = 0. Tak rozszerzone funkcje f i g s¸
a ci¸
ag le w przedziale domkni¸etym [x
0
, x] ∀ x ∈
S, gdzie S jest s¸
asiedztwem punktu x
0
. S¸
a r´
ownie˙z r´
o˙zniczkowalne w przedziale ot-
wartym (x
0
, x).
Zauwa˙zmy, ˙ze g(x) 6= 0 dla x ∈ S. Gdyby bowiem w pewnym punkcie x ∈
S zachodzi la r´
owno´s´
c g(x) = 0, to funkcja g spe lnia laby za lo˙zenia tw. Rolle’a w
przedziale [x
0
, x] i st¸
ad wynika loby istnienie punktu c ∈ (x
0
, x), w kt´
orym g
0
(c) = 0,
co przeczy za lo˙zeniu, ˙ze g
0
(x) 6= 0 dla x ∈ S.
Tak wi¸ec g(x) 6= 0 dla x ∈ S.
8

Stosuj¸
ac do funkcji f i g w przedziale [x
0
, x] tw. Cauchy’ego, kt´
orego wszystkie
za lo˙zenia s¸
a spe lnione, mamy
∃ c ∈ (x
0
, x)
f (x) − f (x
0
)
g(x) − g(x
0
)
=
f
0
(c)
g
0
(c)
Poniewa˙z f (x
0
) = g(x
0
) = 0, wi¸ec ostatnia r´
owno´s´
c przyjmuje posta´
c
f (x)
g(x)
=
f
0
(c)
g
0
(c)
dla pewnego punktu c ∈ (x
0
, x).
Je´sli x → x
+
0
, to c → x
+
0
, poniewa˙z c ∈ (x
0
, x). W´
owczas zgodnie z za lo˙zeniem, ˙ze
istnieje granica ilorazu pochodnych, prawa strona ostatniej r´
owno´sci d¸
a˙zy do granicy
lim
x→x
+
0
f
0
(x)
g
0
(x)
Zatem lewa strona tzn. iloraz
f (x)
g(x)
d¸
a˙zy do tej samej granicy, co ko´
nczy dow´
od
twierdzenia w rozpatrywanym przypadku.
WZ ´
OR TAYLORA
Wz´
or Taylora jest uog´
olnieniem wzoru Lagrange’a z tw. o warto´sci ´sredniej
TWIERDZENIE
Je´
sli funkcja jest klasy C
n−1
w przedziale domkni¸
etym [a, b] i ma sko´
nczon¸
a n-
t¸
a pochodn¸
a wewn¸
atrz tego przedzia lu, to istnieje taki punkt c ∈ (a, b), ˙ze zachodzi
r´
owno´
s´
c
f (b) − f (a) = f
0
(a)(b − a) +
f
00
(a)
2!
(b − a)
2
+ . . . +
f
(n−1)
(a)
(n − 1)!
(b − a)
n−1
+
f
(n)
(c)
n!
(b − a)
n
Wz´
or Taylora cz¸esto zapisuje si¸e w nast¸epuj¸
acej postaci, gdy spe lnione s¸
a za lo˙zenia
twierdzenia w pewnym otoczeniu U punktu x
0
f (x) = f (x
0
) + f
0
(x
0
)(x − x
0
) +
f
00
(x
0
)
2!
(x − x
0
)
2
+ . . . +
f
(n−1)
(x
0
)
(n − 1)!
(x − x
0
)
n−1
+ R
n
(x)
9
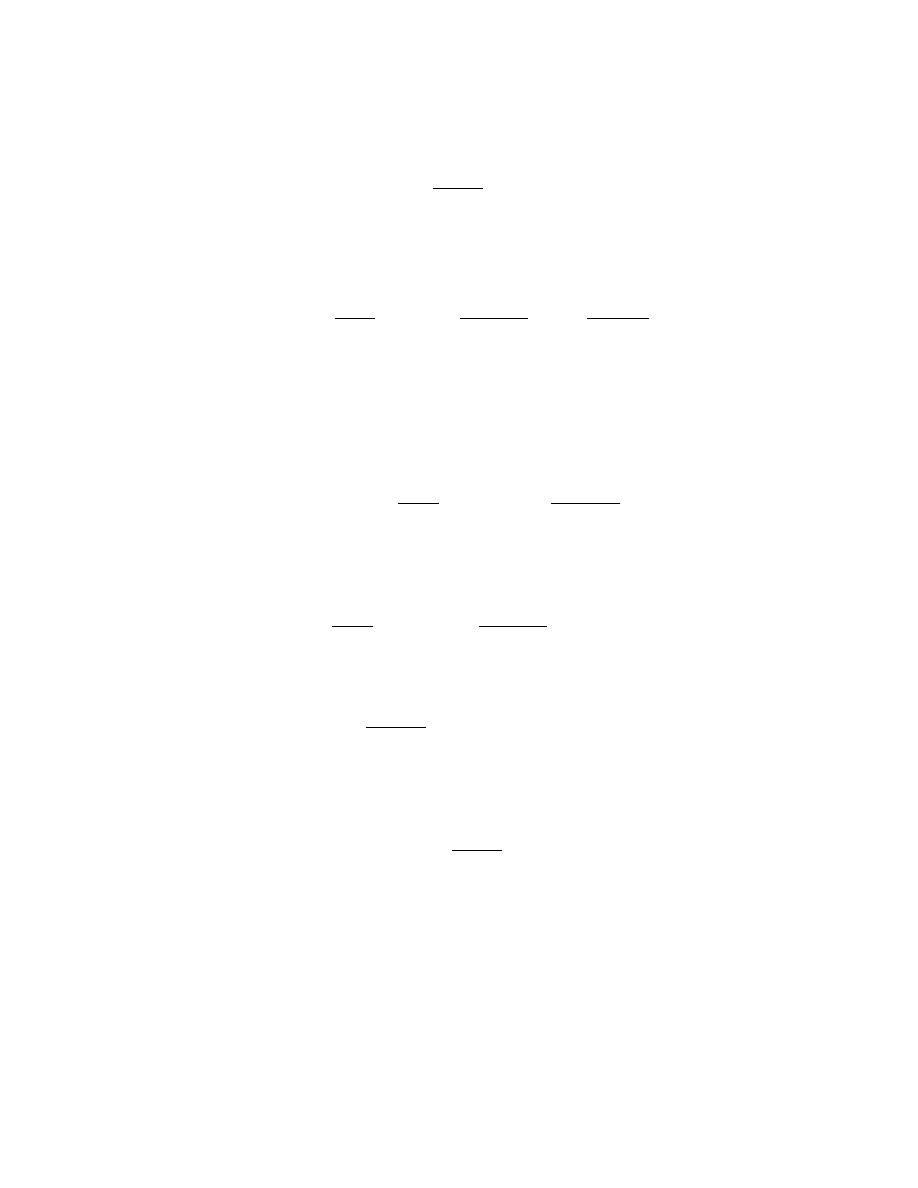
gdzie
R
n
(x) =
f
(n)
(c)
n!
(x − x
0
)
n
nazywamy reszt¸
a wzoru Taylora w postaci Lagrange’a.
Najprostsz¸
a posta´
c ma wz´
or Taylora, gdy x
0
= 0. Wtedy wz´
or przyjmuje posta´
c
f (x) = f (0) + f
0
(0)x +
f
00
(0)
2!
x
2
+ . . . +
f
(n−1)
(0)
(n − 1)!
x
n−1
+
f
(n)
(θx)
n!
x
n
,
θ ∈ (0, 1)
i jest nazywany wzorem Maclaurina
DOW ´
OD
Tworzymy funkcj¸e pomocnicz¸
a
g(x) = f (b)−f (x)−f
0
(x)(b−x)−
f
00
(x)
2
(b−x)
2
−. . .−
f
(n−1)
(x)
(n − 1)!
(b−x)
n−1
−A(b−x)
n
w kt´
orej A dobieramy tak, aby g(a) = 0, tzn. A mo˙zemy wyliczy´
c z r´
ownania
g(a) = 0
f (b)−f (a)−f
0
(a)(b−a)−
f
00
(a)
2
(b−a)
2
−. . .−
f
(n−1)
(a)
(n − 1)!
(b−a)
n−1
−A(b−a)
n
= 0
(?)
Zauwa˙zmy, ˙ze g(b) = 0. Funkcja g ma pochodn¸
a:
g
0
(x) = −
f
(n)
(x)
(n − 1)!
(b − x)
n−1
+ An(b − x)
n−1
kt´
ora istnieje ∀ x ∈ (a, b). Funkcja g spe lnia wi¸ec wszystkie za lo˙zenia tw. Rolle’a.
Zatem istnieje punkt c ∈ (a, b) taki, ˙ze g
0
(c) = 0. St¸
ad
A =
f
(n)
(c)
n!
i po podstawieniu do (?) otrzymujemy ˙z¸
adany wz´
or.
10
Wyszukiwarka
Podobne podstrony:
podstawy analizy matematycznej Nieznany
Podstawy analizy matematycznej, rachunek całkowy, szeregi, tom 2, Andrzej Kaczyński
pd podstawy całka nieoznaczona, Informatyka SGGW, Semestr 2, Analiza, Analiza matematyczna, analiza
Zadania domowe dotyczące metody podstawiania i całkowania przez części, 2 Semestr, Analiza matematyc
Analiza Matematyczna Podstawy
WYKLAD ANALIZA MATEMATYCZNA
Analiza matematyczna, lista analiza 2008 6 szeregi
Analiza Matematyczna 1 Gewert Skoczylas zadania
Analiza Matematyczna Twierdzenia
Analiza matematyczna 1
Praca domowa 2a Analiza Matematyczna
Zadania z Analizy Matematycznej, Matematyka
zestaw9, Matematyka stosowana, Analiza, Analiza matematyczna dla leniwych
Analiza matematycza opracowanie pytań
Kolos 3 Analiza matematyczna
analiza matematyczna 7
więcej podobnych podstron