WNIOSKOWANIE STATYSTYCZNE

WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH

ZADANIA PRZYKŁADOWE

1. Na losowo dobranej próbie 150 samochodów marki X zbadano zużycie benzyny po przejecha-

niu trasy 100 km. Średnie zużycie benzyny dla tej próby wyniosło 7,5 litra przy odchyleniu
standardowym 0,9 litra. Norma fabryczna wynosi 7,01 litra na 100 km. Czy rzeczywiste
zużycie benzyny różni się istotnie od normy fabrycznej na poziomie istotności 0,03 (zużycie
benzyny ma rozkład normalny)?

2. Wylosowano próbę składającą się z 12 pracowników pewnego zakładu i zbadano ich staż

pracy (w latach). Otrzymano następujące informacje:

3, 5, 5, 8, 8, 8, 9, 10, 10, 11, 12, 15.

Czy na podstawie tych obserwacji można twierdzić, że przeciętny staż pracy wszystkich
pracowników tego zakładu jest większy od 8 lat? Przyjmij poziom istotności 0,05. Jakie
dodatkowe założenie jest tutaj niezbędne?

3. Z populacji studentów zaocznych Uniwersytetu Szczecińskiego pobrano próbę losową 50

studentów i zapytano ich o średnią liczbę godzin, jakie spędzają na uczelni w ciągu jednego
dnia zjazdu. Otrzymano następujące wyniki: x = 8 godzin, S(x) = 1,5 godziny. Czy można
stwierdzić przy α = 0,01, że dla całej populacji studentów zaocznych liczba godzin, jaką
spędzają na uczelni w ciągu jednego dnia, jest mniejsza od 9? Zakładamy, że średnia liczba
godzin, spędzanych na uczelni przez studentów, ma rozkład normalny.

4. Automat ma produkować blaszki o nominalnej grubości 0,6 mm. Wylosowana próba 45

blaszek dała średnią 0,59 mm oraz wariancję równą 0, 05 mm

2

. Czy na podstawie tych danych

można stwierdzić, że automat działa prawidłowo? Przyjmujemy, że rozkład zmiennej jest
normalny, a współczynnik istotności wynosi 0,01.

5. W 1997 roku w Pomorskiej Akademii Medycznej prowadzono badania nad wpływem oty-

łości na reakcję pacjentów na pewne leki. W grupie kontrolnej miały znaleźć się osoby bez
niedowagi lub nadwagi. Wylosowano osiemnaście osób i po skontrolowaniu ich wagi otrzy-
mano średnią BMI 24,04 kg/m

2

oraz odchylenie standardowe 2,60 kg/m

2

. Przyjmuje się, że

osoba dorosła z prawidłową wagą powinna mieć BMI między 18 a 24,5 kg/m

2

. Na poziomie

istotności α = 0,05 zweryfikuj hipotezę, że wylosowane osoby pochodzą z populacji o wadze
zgodnej z normą.

6. W wylosowanych gminach wiejskich województwa szczecińskiego zbadano liczbę zlikwido-

wanych firm usługowych w II kwartale 1997 roku i otrzymano następujące informacje:

3, 5, 14, 1, 7, 2, 2, 3, 7, 4.

Na poziomie istotności 0,1 zweryfikuj hipotezę, że liczba zlikwidowanych firm w gminach
wiejskich różni się od średniej arytmetycznej o więcej niż 5 firm.

7. W 1996 roku badano zatrudnienie w budownictwie w gminach wiejskich województwa szcze-

cińskiego. Do badania wylosowano 12 gmin i otrzymano następujące informacje dotyczące
liczby osób pracujących w budownictwie w każdej z gmin:

14, 38, 23, 23, 16, 68, 22, 44, 25, 49, 17, 16.

1

Na poziomie istotności 0,05 zweryfikuj hipotezę, że odchylenie standardowe liczby pracują-
cych w budownictwie w gminach wiejskich badanego województwa nie przekracza 16 osób.

8. Na poziomie istotności 0,1 zweryfikuj hipotezę, że rozrzut wzrostu studentów jest mniejszy

niż 5 cm, jeżeli wybrano losowo 85 studentów i uzyskano odchylenie standardowe 6 cm.

9. Wysunięto hipotezę, że 40% studentów Uniwersytetu Szczecińskiego pali papierosy. Czy

jest to przypuszczenie słuszne, jeśli w wylosowanej próbie 250 studentów 120 osób paliło
papierosy (przyjmij α = 0,01)?

ROZWIĄZANIA I ODPOWIEDZI

1. Hipotezę roboczą stawiamy następująco: zużycie benzyny nie różni się istotnie od normy

podanej przez producenta. Będzie ona naszą testowaną hipotezą zerową.

Procedura testowania hipotezy zerowej (na zadanym poziomie istotności) polega na znalezie-
niu obszaru krytycznego (obszaru odrzucenia hipotezy zerowej) i sprawdzeniu, czy należy do
niego statystyka sprawdzająca. Wartość statystyki sprawdzającej obliczamy z odpowiednie-
go wzoru, podanego w tablicach; tablice kwantyli rozkładów służą natomiast do określenia
granic przedziału (przedziałów), stanowiącego obszar krytyczny. Jeśli statystyka sprawdza-
jąca należy do obszaru krytycznego, hipotezę zerową na danym poziomie istotności należy
odrzucić, jeśli nie należy – wówczas brak jest podstaw do odrzucenia hipotezy zerowej (uwaga
– nie oznacza to, że hipotezę należy przyjąć!).

Hipotezę zerową i hipotezę alternatywną w stosunku do niej sformułujemy następująco:

H

0

: µ = µ

0

H

1

: µ 6= µ

0

,

gdzie µ

0

jest wartością wzorcową.

W naszym przykładzie

H

0

: µ = 7,01

H

1

: µ 6= 7,01.

W zadaniu sprawdzamy wartość średnią, przy czym zastosujemy test dla dużej próby (n >
120), gdzie statystyka sprawdzająca jest dana wzorem (tablice, s.19)

u =

x − µ

0

S(x)

·

√

n,

Jej wartość wynosi 6,668.

Konstruujemy obszar krytyczny w oparciu o informację dotyczącą poziomu istotności. W
związku ze znakiem nierówności zawartej w hipotezie alternatywnej, mamy skonstruować
obszar dwustronny, dany jako

−∞; −u

1−

α

2

E

∪

D

u

1−

α

2

; +∞

. Skoro α = 0,03, to przy kon-

strukcji obszaru krytycznego szukamy w tablicy dystrybuanty rozkładu normalnego wartości
0,985 i odpowiadającego jej argumentu. Szukanym u

α

jest 2,17. Mamy zatem wyznaczony

obszar krytyczny, OK = (−∞; −2,17i ∪ h2,17; +∞) . Wartość statystyki sprawdzającej na-
leży do tego przedziału, u ∈ OK, dlatego też H

0

należy na zadanym poziomie istotności

2

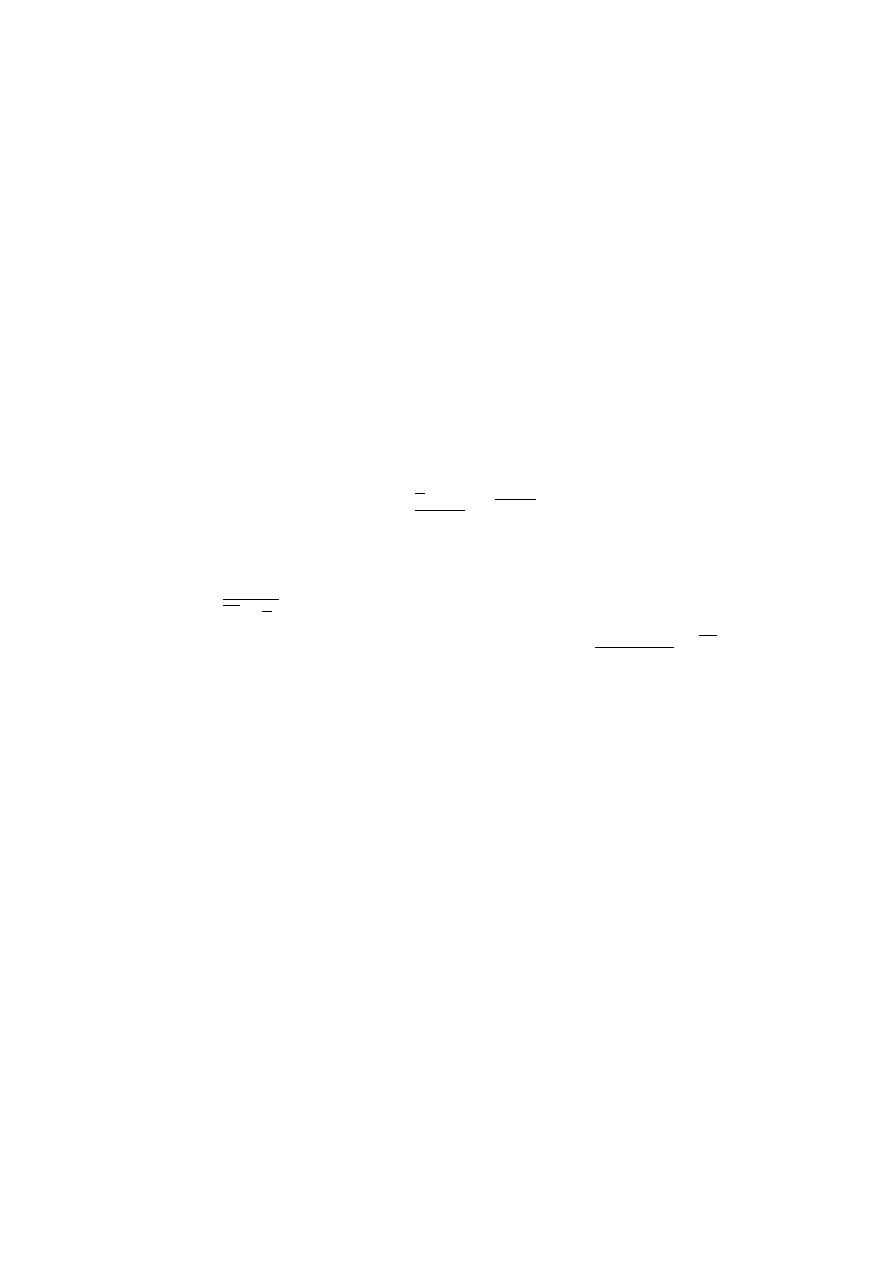
odrzucić na korzyść hipotezy alternatywnej, która stwierdza, że zużycie rzeczywiste benzyny
różni się istotnie od normy producenta.

2. Nie zawsze konstruujemy obszar krytyczny dwustronny, niekiedy – jak w tym zadaniu –

interesujące dla nas będzie sprawdzenie, czy badana statystyka jest większa (mniejsza) niż
pewna ustalona wartość.

Formułujemy hipotezę roboczą: przeciętny staż pracy pracowników badanego zakładu jest
większy od 8 lat. Będzie ona naszą hipotezą alternatywną (w hipotezie zerowej zawsze wystę-
puje równość, natomiast nierówności występować mogą jedynie w hipotezie alternatywnej).
Nasza hipoteza zerowa przyjmie postać

H

0

: µ = 8

natomiast hipoteza alternatywna (którą jesteśmy szczególnie zainteresowani, jest to bowiem
nasza hipoteza robocza) będzie sformułowana jako

H

1

: µ > 8.

Korzystając z odpowiedniego wzoru dla małej próby (tablice, s. 19) danego jako

t =

x − µ

0

S(x)

·

√

n − 1

obliczymy wartość statystyki testowej. W tym celu musimy obliczyć średnią z próby i od-
chylenie standardowe z próby. Średnia wynosi 8,6667. Odchylenie standardowe obliczymy
jako S(x) =

q

x

2

− x

2

. Średnia z kwadratów x jest równa 85,1667. Odchylenie standardowe

zatem wynosi 3,171. Obliczamy wartość statystyki testowej t =

8,6667 − 8

3,171

·

√

11 = 0,6973, a

następnie konstruujemy prawostronny obszar krytyczny OK = ht

2α

; +∞) (w przypadku hi-

potezy alternatywnej postaci H

1

: µ < µ

0

byłby to obszar lewostronny, OK = (−∞; −t

2α

i).

Szukamy w tablicy kwantyli rozkładu t-Studenta wartości odpowiadającej podwojonemu
poziomowi istotności 2 · α (α użylibyśmy, gdyby konstruowany był dwustronny obszar kry-
tyczny) i k = n − 1 = 11 stopniom swobody. Szukaną wartością jest t

2α

= 1,796. Oznacza

to, że obszarem krytycznym jest przedział OK = h1,796; +∞). Wartość statystyki spraw-
dzającej nie należy do tego przedziału, dlatego brak jest – na zadanym poziomie istotności
– podstaw do odrzucenia hipotezy zerowej mówiącej, że średni staż pracy pracowników
badanego zakładu wynosi 8 lat.

Wymagane jest założenie, że staż pracy pracowników tego przedsiębiorstwa ma rozkład
normalny.

3. OK = (−∞; −2,407i,

t ∈ OK,

H

0

należy odrzucić.

4. OK = (−∞; −2,692i ∪ h2,692; +∞),

t /

∈ OK, brak podstaw do odrzucenia H

0

, mówiącej

o tym, że średnia grubość blaszki wynosi 0,6 mm.

5. W tym zadaniu nie mamy dwustronnego obszaru krytycznego, ponieważ norma podana

jest jako przedział (18; 24,5). Aby sprawdzić, czy badane osoby mają przeciętną wagę zgod-
ną z normą musimy przeprowadzić dwa testy. Po pierwsze, zbadać, czy średnia waga nie
jest niższa niż dolny kraniec przedziału (tj. H

0

: µ = 18, H

1

: µ < 18), a następnie ana-

logicznie sprawdzić, czy średnia waga nie jest wyższa niż górny kraniec przedziału (tj.
H

0

: µ = 24,5, H

1

: µ > 24,5). W pierwszym przypadku t = 9,5783 > t

α

= −1,74, a więc

brak podstaw do odrzucenia H

0

mówiącej, że średnia waga jest równa 18. Podobnie jest

3

w drugim przypadku, t = −0,7295 < t

α

= 1,74 – tu również brak podstaw do odrzucenia

hipotezy zerowej mówiącej, że średnia waga jest równa 24,5.

6. x = 4,8, x

2

= 36,2, S

2

(x) = 13, 16.

χ

2

do testu dla wariancji liczymy według wzoru (tablice, s. 19)

χ

2

=

n · S

2

(x)

σ

2

0

,

gdzie σ

2

0

jest wzorcową wartością wariancji. Konstruujemy prawostronny obszar krytyczny

dla χ

2

α;n−1

(por. tablice, s. 21).

χ

2

= 5,264 /

∈ h14,684; +∞), brak podstaw do odrzucenia H

0

mówiącej o tym, że wariancja

jest równa 25 (odchylenie standardowe jest równe 5).

7. χ

2

= 11,98 /

∈ (0; 4,575i, brak podstaw do odrzucenia H

0

.

8. Tym razem próba jest duża, zatem szukamy statystyki u, danej wzorem

u =

q

2χ

2

−

√

2k − 1,

gdzie χ

2

obliczamy jak w zadaniach poprzednich, natomiast k = n − 1. Konstruujemy

lewostronny obszar krytyczny (−∞; u

1−α

i i sprawdzamy, czy u do niego należy.

u = 2,723 /

∈ (−∞; 1,29i, brak podstaw do odrzucenia H

0

mówiącej, że odchylenie standar-

dowe wzrostu studentów jest równe 5 cm.

9. Weryfikując hipotezę dotyczącą wskaźnika struktury korzystamy ze statystyki u danej wzo-

rem

u =

m

n

− p

0

r

p

0

· q

0

n

.

Konstruujemy dwustronny obszar krytyczny (nie badamy, czy odsetek jest mniejszy albo
większy niż wartość wzorcowa, a jedynie równość, zatem hipotezą alternatywną jest H

1

: p 6=

p

0

).

u = 2,582 ∈ (−∞; −2,58i ∪ h2,58; +∞) zatem H

0

należy odrzucić.

Pełne rozwiązania zadań od numeru 3 wzwyż oraz pozostałe testy (parametryczne i – jeśli
starczy nam czasu – nieparametryczne) pokażemy na zajęciach.

Paweł Baran

4