Ws zechnica Informa tyczna

Różnorodne algorytmy oblicze ń i ich komputerowe realizacje

prof. dr hab. Ma ciej M Sysło

prof. dr hab. Maciej M Sysło

Zes zyt dyda ktyczny opracowany w ramach proje ktu edukacyjnego

— pona dre giona lny program rozwijania kompete ncji

uczniów s zkół ponadgimna zjalnych w za kre sie te chnologii
informacyjno-komunika cyjnych (ICT).

Wars za ws ka Wyżs za Szkoła Informatyki

ul. Le wartows kie go 17, 00 -169 Wars zawa

Projekt graficzny: FRYCZ I WICHA

Wars za wa 2010
Copyright © Wa rs za wska Wyżs za Szkoła Informa tyki 2009
Publikacja nie jes t przezna czona do s prze da ży.

Uniwers ytet Wrocławski, UMK w Toruniu

s [e-mail], s [e-mail]

< 4 >

Informa tyka +

Kompute ry nie przes ta ły być ma s zynami mate ma tycznymi – jak kie dyś je na zywa no – i obe cnie służą równie ż
do wykonywa nia różnych oblicze ń. Kurs je s t poś wię cony m.in. a lgorytmom wyzna czania: dzies ię tnej i binar-
nej reprezenta cji liczb, oblicza nia wartoś ci wielomianu, najwię ks ze go ws pólnego dzielnika dwóch liczb (al-
gorytm Euklide s a) ora z wartoś ci potę gi. Motywa cją dla wprowa dze nia tych algorytmów jes t chę ć obja śnie -
nia metody s zyfrowania informacji z klucze m publicznym RSA, pows ze chnie s tos owa nej w kryptogra fii kom-
pute rowej.

Z pods ta w a lgorytmiki omawiane s ą m.in. specyfikacja problemu, s chematy blokowe a lgorytmów, pods tawo-
we s truktury danych (cią g i tablica) ora z pracochłonnoś ć algorytmów. Czę ś ć prakt yczna zaję ć je s t poś więco-
na wprowadzeniu pods ta wowych ins trukcji języka programowania (iteracyjnych i warunkowych ora z proce -
dury i funkcji nies ta ndardowej), wys ta rczających do zaprogramowa nia i uruchomienia komputerowych reali-
zacji omówionych a lgorytmów. Ję zyk programowania s łuży głównie do zapis ywania i tes towa nia rozwią zań
rozwa żanych proble mów, a nie jes t celem zaję ć s amym w s obie. Wykorzys tywane jes t równie ż oprogra mowa -
nie edukacyjne , uła twiające zrozumienie dzia łania a lgorytmów i umożliwiające wykonywa nie eks perymen-
tów z algorytma mi be z konie cznoś ci ich programowania. Przytoczono cie kawe przykłady za s tosowa ń oma -
wia nych zaga dnie ń.

W drugiej czę ści kurs u s ą przeds ta wiane wybra ne te chniki rozwią zywania problemów za pomocą kompute -
ra , m.in. podejś cie zachłanne (do wydawania re s zt y), prze s zukiwanie z na wrota mi (do us ta wia nia hetmanów
na s zachownicy) i rekure ncja w re alizacji wybranych algorytmów. Za ję cia prakt yczne s ą poś więcone kompu-
terowej realizacji wybranych te chnik algorytmicznych na odpowiednio dobranych przykłada ch problemów.

Rozwa żania s ą prowa dzone na ele mentarnym poziomie i do ich wys łucha nia ora z wzięcia udzia łu w wars zta -
tach wys tarczy znajomoś ć informa tyki wyniesiona z gimna zjum ora z mate ma tyki na poziomie s zkoły śre dniej.
Te za jęcia s ą adre s owane do ws zys tkich uczniów w s zkoła ch pona dgimna zjalnych, zgodnie bowiem z nową
pods tawą programową, ks ztałcenie m umiejętnoś ci algorytmiczne go rozwią zywania problemów mają być ob-
jęci ws zys cy uczniowie.

W tych ma teriałach dla s łucha czy, algorytmy s ą zapis ywane w ję zyku Pa s cal. Odpowiednie wersje w ję zyku
C++ bę dą prze ka za ne s łuchaczom na zajęciach.

> Różnorodne algorytmy obliczeń i ich komputerowe realiza cje

< 5 >

1. Wprowadze nie ............................................................................................................................................. 6

2. Warm-up – rozgrzewka ............................................................................................................................... 6

3. Oblicza nie wartoś ci wielomianu – s che mat Horne ra .................................................................................... 8

3.1. Wyprowa dze nie s chematu Horne ra ....................................................................................................... 9

3.2. Schema t blokowy s chematu Horne ra ...................................................................................................11

3.3. Komputerowa realizacja sche ma tu Hornera ......................................................................................... 13

4. Sys tem dzie siętny i s ys tem binarny ........................................................................................................... 15

4.1. Zamiany liczby bina rnej na liczbę dzies ię tną ...................................................................................... 16

4.2. Otrzymywanie binarne go rozwinię cia liczby dzies iętnej ...................................................................... 17

4.3. Długoś ć rozwinię cia binarnego liczby .................................................................................................. 18

5. Rekure ncja ............................................................................................................................................... 19

5.1. Wieże Hanoi......................................................................................................................................... 20

5.2. Króliki i chaotyczny profes or – liczby Fibonaccie go ............................................................................. 24

5.3. Inne s pojrzenie na sche ma t Hornera ................................................................................................... 28

5.4. Wyprowadzanie liczb od początku ...................................................................................................... 29

6. Szybkie oblicza nie wartoś ci potęgi ............................................................................................................ 32

7. Algorytm Euklide s a .................................................................................................................................... 34

8. Algorytmy za chłanne ................................................................................................................................. 37

8.1. Problem wyda wania re s zt y .................................................................................................................. 37

8.2. Zmartwienie kinoma na ........................................................................................................................ 40

8.3. Pakowanie najcenniejs zego plecaka ................................................................................................... 41

8.4. Na jdłużs za droga na piramidzie .......................................................................................................... 43

8.5. Inne przykłady użycia me tody zachła nnej ........................................................................................... 44

9. Prze s zukiwanie z nawrotami ...................................................................................................................... 45

9.1. Wyjś cie z la biryntu metodą zgłę biania ................................................................................................. 45

9.2. Rozmie s zcza nie he tma nów na s zachownicy ........................................................................................ 47

10. Dodatek. Algorytm, a lgorytmika i a lgorytmiczne rozwią zywanie problemów .......................................... 53

Lite ratura

............................................................................................................................................... 55

< 6 >

Informa tyka +

Kompute ry nadal – jak kie dyś – s łużą równie ż do wykonywania różnych obliczeń. Kurs je s t poś więcony m.in.
algorytmom: wyznaczania dzies ię tnej i binarnej repre zenta cji liczb, obliczania wartoś ci wielomianu, na jwięk-
s ze go wspólnego dzielnika dwóch liczb (algorytm Euklides a) ora z wartoś ci potę gi. Motywa cją dla wprowa -
dzenia tych a lgorytmów je s t chęć obja ś nienia me tody s zyfrowa nia informa cji z kluczem publicznym RSA, po-
ws ze chnie s tos owanej w kryptografii kompute rowej.

Częś ć prakt yczna zaję ć je s t poś wię cona wprowadzeniu pods tawowych ins trukcji ję zyka progra mowa nia (ite -
racyjnych i wa runkowych ora z proce dury i funkcji nies ta ndardowej), wys tarcza jących do za progra mowa nia
i uruchomienia komputerowych re aliza cji omówionych algorytmów. Ję zyk programowania służy głównie do
zapis ywania i tes towa nia rozwią zań rozwa żanych problemów, a nie je s t cele m zaję ć s a mym w s obie. Przyto-
czono cie kawe przykłady zas tos owań oma wia nych za gadnień.

W drugiej częś ci kursu s ą prze ds tawione wybrane techniki rozwią zywania proble mów za pomocą kompute -
ra , m.in. podejś cie zachłanne (do wydawania re s zt y), prze s zukiwanie z na wrota mi (do us ta wia nia hetmanów
na s zachownicy) i rekurencja w rea liza cji wybra nych algorytmów. Zaję cia prakt yczne bę dą poś wię cone kom-
puterowe j rea liza cji wybranych te chnik algorytmicznych na odpowiednio dobra nych przykładach proble mów.

Rozwa żania ogólne na tema t algorytmiki, a lgorytmiczne go myślenia i rozwią zywania problemów z pomocą
komputerów s ą zamies zczone w Doda tku (rozdz. 10). Ma teriał tam za wa rty może być dobrym pods umowa -
nie m zajęć.

Jako literaturę rozs zerzającą prowadzone tutaj rozwa ża nia polecamy podręczniki [2], a zwła s zcza

ksią żki [5] i [6].

W tym rozdziale , na s zym cele m jes t uruchomienie pierws zego programu. A za tem, Ci uczniowie, którzy ma ją
już pewne doś wia dczenie w programowaniu, mogą go pominą ć, zachę ca my ich jednak do s zybkie go zapo-
znania się z za wa rt ym tutaj ma teriałem.

Zacznijmy od bardzo pros tego proble mu. Ka żdy proble m, który bę dzie my rozwią zywa ć na t ych zaję -

ciach, bę dzie opis any s woją na zwą ora z wys zcze gólnieniem danych i wyników. Taki opis proble mu na zywa
się s pecyfika cją – patrz rozdz. 10. A wię c na s z problem ma pos tać:

Problem. Pole trójkąta
Dane :

a, b, c – trzy dodatnie liczby.

Wynik: S – pole trójką ta , które go boki ma ją długoś ci a , b i c.

Je śli ten problem ma rozwią zać za na s komputer, to mus imy go poinformować o danych, czyli o trze ch licz-
bach, ora z, co ma być wynikiem, czyli ja k pole trójką ta zależy od długoś ci je go boków – posłużymy się tutaj
wzore m Herona . Te czynnoś ci zapis zemy ja ko na s z pierws zy algorytm w pos ta ci lis ty kroków

1

, a powyżs zą

spe cyfika cję problemu przyjmiemy za s pecyfikację tego, co ma wykonać a lgorytm a później progra m.

Algorytm. Pole trójką ta
Dane :

a, b, c – trzy dodatnie liczby.

Wynik: S – pole trójką ta , które go boki ma ją długoś ci a , b i c.
Krok 1. Wprowa dź trzy liczby: a , b, c.
Krok 2. Oblicz połowę długoś ci obwodu trójkąta : p = (a + b + c)/ 2.
Krok 3. Oblicz pole trójką ta we dług wzoru:

1

Algorytmy, poza programami, mogą b yć przeds ta wione również w pos taci s che matów blokowych. Przykładowy s che ma t

blokowy je s t za mies zczony w p. 3.2.

> Różnorodne algorytmy obliczeń i ich komputerowe realiza cje

< 7 >

S=

√

p(p – a)(p – b)(p – c)

Progra m dla komputera w ję zyku Pa s cal, bę dący rea lizacją te go a lgorytmu, je s t prze ds tawiony w ta beli 1.

Ta bela 1.
Pie rws zy program

Wie rs ze programu

Obja ś nienia

Program Trojkat;

Program

i na zwa program, na końcu ś rednik

var a,b,c,p:real;

Dekla ra cja zmie nnych – real ozna cza , że wa rtoś ci t ych
zmiennych nie mus zą b yć ca łkowite

begin

Początek za s adniczej częś ci programu

read(a,b,c);

Czytanie wartoś ci zmiennych do programu

p:=(a+b+c)/2;

Oblicza nie pomocniczej wielkoś ci – połowy obwodu

write(sqrt(p*(p-a)*(p-b)*(p-c)))

Wypis ywanie wielkoś ci pola trójką ta o bokach a, b, c

end.

Koniec programu – na końcu kropka .

Przepis z progra m z tabeli 1 w edytorze języka Pa s cal i uruchom go dla różnych trójek da -

nych, np. 1, 1, 1; 2, 2, 2; 1, 2, 2; 1, 2, 4. Uruchom także dla danych: 1, 2, 3 ora z 1, 3, 1.

Ja kie wyniki dzia łania programu otrzymałe ś w os tatnich dwóch przypadkach da nych? Czy wies z, dlaczego?
Przypomnij wię c s obie , ja kie wa runki mus zą spe łniać trzy liczby, aby mogły być długoś ciami boków trójką -
ta? Jak więc wyglą da trójką t o bokach 1, 2, 3? A dlaczego nie otrzyma łe ś żadnego wyniku, tylko jakiś komu-
nikat, dla liczb 1, 3, 1?

Aby trzy liczby mogły być długoś cia mi boków trójką ta , mus zą s pe łniać warunek trójkąta , tzn. ka żda suma
dwóch długości boków musi być więks za od trzeciej liczby, czyli;

a + b > c, a + c > b, b + c > a .

Łatwo można sprawdzić, że te trzy nierównoś ci s ą równowa żne nierównoś ciom:

p – a > 0, p – b > 0, p – c > 0.

Uwzglę dnienie tych warunków w a lgorytmie przekła da s ię na modyfikację trze ciego kroku, który otrzymuje
pos ta ć:

Krok 3. Jeś li p*(p – a )*(p – b)*(p – c) < 0, to za kończ obliczenia z komunika tem, że podane trzy liczby nie s ą

długoś ciami boków w trójką cie. W prze ciwnym ra zie oblicz pole trójką ta we dług wzoru:

S=

√

p(p – a)(p – b)(p – c)

W tabeli 2 jes t zawarty program Trojkaty _ mod, w którym uwzglę dniono zmienioną pos tać kroku 3 – po-
jawia się ins trukcja warunkowa if … then … else.

< 8 >

Informa tyka +

Ta bela 2.
Zmodyfikowany progra m Trojkat _ mod

Wiers ze programu

Obja ś nienia

Program Trojkat _ mod;

Zmieniono na zwę.

var a,b,c,p,q:real;

Dodatkowa zmienna q.

begin

read(a,b,c);

p:=(a+b+c)/2;

q:=p*(p-a)*(p-b)*(p-c);

Wyra że nie pod pierwia s tkiem

if q <= 0 then writeln(’To nie sa boki trojkata

ʽ )

else write(’Pole trojkata =

ʽ ,sqrt(q))

Ins trukcja warunkowa :
if ... hen ...
else ...

end.

Uruchom program Trojkat _ mod z tabe li 2. Spra wdź jego dzia ła nie na trójkach liczb,

które spe łnia ją warunek trójką ta i na ta kich, które nie s pe łniają . W pierws zym przypa dku wybierz trój-
ki liczb, dla których zna s z pole trójkąta , np. 1, 1 i 1.4142.

Faktyczna moc komputerów objawia się dopiero przy wielokrotnym wykonywaniu tych s amych pleceń, być
może dla różnych danych. Pole cenie w algorytmie lub ins trukcja w ję zyku progra mowania , która umożliwia
powtarza nie pole ceń, na zywa s ię itera cją lub ins trukcja pę tli. W ta beli 3 przeds ta wia my jedną z ta kich in-
s trukcji – ins trukcję for – która w tym programie służy do powta rzenia obliczeń us ta loną liczbę ra zy n.

Ta bela 3.
Progra m Trojkaty – wielokrotne oblicza nie pola trójkąta dla różnych długoś ci boków

Wiers ze programu

Obja ś nie nia

Program Trojkaty;

var i,n: integer;

Zmienne użyte w ins trukcji for

a,b,c,p,q:real;

begin

read(n);

Wczytanie liczby p owtórzeń n

for i:=1 to n do begin

Ins trukcja ite ra cyjna for

write(

’

Boki trojkata:

ʽ

);

read(a,b,c);

p:=(a+b+c)/2;

q:=p*(p-a)*(p-b)*(p-c);

write(’Pola trojkata:

ʽ );

if q <= 0 then writeln(’To nie sa boki trojkata

ʽ )

else writeln(sqrt(q):3:3);

writeln;

end

Konie c ins trukcji for

end.

> Różnorodne algorytmy obliczeń i ich komputerowe realiza cje

< 9 >

Inne ins trukcje itera cyjne wprowadzimy
na da ls zych zaję ciach. Progra m w ta be -
li 3 s łuży do obliczania pola trójką ta dla
n trójek, bę dących długoś cia mi boków
trójką ta .

Uruchom program Trojkaty na t ych s amych danych, na których tes towałeś program

w ćwicz. 2. Porównaj wyniki.

Podsumowując rozgrze wkę z progra mowania , wykona liś my trzy progra my, o rozwijają cej się s trukturze:

■

pierws zy – za wiera , poza deklara cjami zmiennych, tylko lis tę poleceń;

■

w drugim – wykonywanie poleceń zale ży od spe łnienia warunku;

■

trze ci za ś wykonuje polecenia w pę tli.

Z ta kim, niewielkim a rs ena łem, możemy rozpoczą ć progra mować powa żniejs ze algorytmy.

Ja k wspomnieliś my już, je dnym z najwa żniejs zych kroków w algorytmach je s t powta rzanie tej s ame j czynno-
ś ci (operacji), czyli itera cja . W tym punkcie zilus trujemy itera cję na przykładzie s zybkie go spos obu oblicza -
nia wa rtoś ci wielomia nu.

Obliczanie wartoś ci wielomianu o za danych współczynnika ch je s t jedną z najczę ś ciej wykonywanych ope -
ra cji w komputerze. Wynika to z wa żne go faktu ma tematyczne go, zgodnie z którym ka żdą funkcję (np. funk-
cje trygonometryczne) można za s tą pić wielomia ne m, którego pos ta ć za le ży od funkcji i od te go, ja ką chcemy
uzyskać dokła dnoś ć obliczeń.

Na przykład, obliczanie wa rtoś ci funkcji cos x w przedzia le 0 ≤ x ≤ π/ 2 z błę dem nie więks zym niż

0.0009, można za s tąpić oblicza nie m wartoś ci nas tępującego wielomianu:

cos x = 1 – 0.49670x

2

+ 0.03705x

4

.

Za cznijmy od pros tych ćwicze ń. Jeś li dane s ą wartoś ci współczynników a, b i c wielomia nu s topnia 2:

w(x) = a x

2

+ bx + c,

to jego wartość można obliczyć wykonując zaznaczone mnożenia i dodawania: a∙x

•

x + b

•

x + c, czyli 3 mnożenia i dwa

dodawania. Można także nieco inaczej – wyłączmy x z dwóch pierwszych składników – wtedy otrzymamy:

w(x) = (a x + b)x + c

i dla tej pos ta ci oblicza nie wa rtoś ci tego wielomianu przyjmuje pos ta ć: (a

•

x + b)

•

x + c, czyli s ą wykonywane tyl-

ko 2 mnożenia i dwa doda wa nia .

W podobny spos ób można przeds ta wić wielomia n s topnia 3:

v(x) = a x

3

+ bx

2

+ cx + d

Ada Augus ta , córka Byrona , uznawana powszechnie
za pierws zą programis tkę komputerów, prze łomowe
znaczenie mas zyny analitycznej Ch. Babbage’a , pierwowzoru
późniejs zych komputerów, upatrywała właś nie „w możliwości
wielokrotnego wykonywania przez nią danego cią gu
ins trukcji, z liczbą powtórzeń z góry za daną lub zależną
od wyników obliczeń”.

< 10 >

Informa tyka +

najpierw wyłączam x z pierws zych trzech wyrazów, a następnie wyłączamy x z dwóch pierwszych wyrazów w nawiasie:

v(x) = a x

3

+ bx

2

+ cx + d = v(x) = v(x) = (a x

2

+ bx + c)x + d = ((a

•

x + b)

•

x + c)

•

x + d.

Widać z tego ostatniego wzoru, że wartość wielomiany stopnia 3 można obliczyć za pomocą 3 mnożeń i 3 dodawań.

Rozwa żmy tera z wielomian s topnia n:

w

n

(x) = a

0

x

n

+ a

1

x

n–1

+ ... + a

n–1

x + a

n

(1)

i za s tosujmy grupowa nie wyra zów podobnie, ja k w wielomianie s topnia 3 – na jpierw wyłą czamy x ze ws zys t-
kich wyra zów z wyjątkiem os ta tnie go, a na s tę pnie s tosujmy ten s a m krok wielokrotnie do wyra zów, które
bę dą pojawiały s ię w na jgłę bs zych nawia s a ch, a ż pozos tanie jednomian:

w

n

(x) = a

0

x

n

+ a

1

x

n –1

+ ... + a

n–1

x + a

n

= (a

0

x

n–1

+ a

1

x

n –2

+ ... + a

n –1

)x + a

n

= ((a

0

x

n–2

+ a

1

x

n–3

+ ... + a

n –2

)x+ a

n –1

)x + a

n

=

= (...((a

0

x + a

1

)x+ a

2

)x +... + a

n–2

)x+ a

n–1

)x + a

n

(2)

Przeds ta w w pos taci (2) na s tępujące wielomiany:

w(x) = 3x

4

– x

3

+ 5x

2

+ 7x – 2

w(x) = x

5

– x

3

+ 4 x

2

+ 3x – 1

w(x) = x

6

– x

3

+ x

Za pis zmy tera z s pecyfika cję , czyli dokładny opis rozwa ża ne go tutaj proble mu:

Proble m. Obliczanie wartoś ci wielomia nu
Dane:

n – nieujemna liczba ca łkowita – s topień wielomia nu;
a

0

, a

1

, ... a

n

– n+1 współczynników wielomianu;

z – wartoś ć a rgumentu.

Wynik: Wartoś ć wielomianu (2) s topnia n dla wartoś ci a rgumentu x = z.

Aby obliczyć ze wzoru (2) wartoś ć wielomianu dla wa rtoś ci argumentu z, należy pos tę powa ć na s tępująco
(y oznacza pomocniczą zmienną ):

y := a

0

y := yz + a

1

y := yz + a

2

...

y := yz + a

n–1

y := yz + a

n

Ws zys tkie wie rs ze , z wyjątkiem pierws zego można zapis ać w je dnolity spos ób – otrzymujemy wtedy:

y := a

0

(3)

y: = yz + a

i

dla i = 1, 2, ..., n.

Ten spos ób obliczania wartoś ci wielomianu na zywa się s chematem Horne ra .

Uwaga . W opisie algorytmu wys tę puje ins trukcja przypis ania

2

, wcze śniej już użyta , np. y := a

0

, w które j s ym-

bol := jes t złożony z dwóch znaków: dwukropka i równoś ci. Przypis a nie ozna cza na danie wielkoś ci (zmien-

2

Pole cenie przypis a nia je s t cza s em na zywane niep oprawnie pods ta wieniem.

Schemat Hornera zos tał podany przez jego autora w 1819 roku,
chocia ż znacznie wcześniej Is aac Newton s tosował podobną
metodę obliczania wartoś ci wielomianów w s woich rachunkach
fizycznych. W 1971 roku, A. Borodin udowodnił, że s chemat
Hornera jest optymalnym, pod względem liczby wykonywanych
działań, algorytmem obliczania wartości wielomianu.

> Różnorodne algorytmy obliczeń i ich komputerowe realiza cje

< 11 >

nej) s toją cej po le wej s trony te go s ymbolu wa rtoś ci równej wartoś ci wyra żenia (w s zczególnym przypadku to
wyra że nie może być zmienną ) zna jdują cego s ię po prawe j s tronie tego s ymbolu. Przypis anie jes t s tos owa ne
na przykład wte dy, gdy na leży zmienić wartoś ć zmiennej, np. i := i + 1 – w tym przypadku ta s ama zmienna wy-
s tępuje po le wej i po pra wej s tronie s ymbolu przypis ania . Polecenie przypis ania wys tę puje w więks zoś ci ję zy-
ków progra mowa nia , s tos owa ne s ą tylko różne s ymbole i ich upros zczenia dla je go ozna czenia .

Za s tos uj s che ma t Hornera do obliczenia wartoś ci wielomianów z ćwicz. 4 w punkcie z = 1.

Możemy więc tera z zapis a ć:
Algorytm: Schema t Hornera
Dane:

n – nieujemna liczba ca łkowita (s topie ń wielomianu);
a

0

, a

1

, ... , a

n

– n+1 współczynników wielomianu;

z – wartoś ć argumentu.

Wynik: y = w

n

(z) – wartoś ć wielomianu (1) s topnia n dla wartoś ci a rgumentu x = z.

Krok 1. y := a

0

– początkową wartoś cią jes t współczynnik przy najwyżs zej potędze .

Krok 2. Dla i = 1, 2, …, n oblicz wa rtoś ć dwumianu y := yz + a

i

Wynika s tą d, że aby obliczyć wartoś ć wielomia nu s topnia n wys ta rczy wykonać n mnożeń i n doda wań. Udo-
wodniono, że je s t to najs zybs zy s pos ób obliczania wartoś ci wielomianu.

Schema t blokowy algorytmu (zwany równie ż s iecią działań lub sie cią obliczeń) je s t graficznym opis em:
działa ń s kładających s ię na algorytm, ich wza jemnych powią zań i kolejnoś ci ich wykonywania . W informa -
tyce miejs ce s che ma tów blokowych je s t pomię dzy opis e m a lgorytmu w pos ta ci lis t y kroków, a programem,
na pis anym w wybra nym ję zyku progra mowania . Na le żą one do kanonu wie dzy informa tycznej, nie s ą jedna k
nie zbę dnym jej e le mente m, chocia ż mogą oka zać się ba rdzo przyda tne na począ tkowym e tapie proje kto-
wa nia algorytmów i progra mów komputerowych. Z drugiej s trony, w wielu publika cjach algorytmy s ą prze d-
s ta wiane w pos ta ci s chema tów blokowych, pożą da na je s t wię c umieję tnoś ć ich odczytywania i rozumienia .
Warto na dmienić, że te n s pos ób repre zentowa nia algorytmów poja wia się w zada niach ma turalnych z infor-
ma tyki.

Na rys. 1 je s t przeds ta wiony s chemat blokowy algorytmu Sche mat Hornera . Je s t on zbudowany z bloków, któ-
rych ks ztałty zale żą od rodza ju wykonywa nych w nich pole ce ń. I tak ma my:

■

blok począ tku i blok końca algorytmu;

■

blok wprowa dzania (wczytywa nia) danych i wyprowadza nia (drukowania) wyników – bloki te mają taki s am
ks zta łt;

■

blok ope racyjny, w którym s ą wykonywane operacje przypis ania;

■

blok wa runkowy, w którym je s t formułowa ny wa runek;

■

blok informa cyjny, który może służyć do komentowa nia fragmentów s chema tu lub łączenia ze s obą czę ś ci
wię ks zych s chematów blokowych.

Nie is tnieje pe łny układ za s ad popra wnego kons truowania s chematów blokowych. Można na tomia s t wymie -
nić doś ć naturalne za s ady, wynika jące z cha rakte ru bloków:

■

s che ma t za wiera dokła dnie jeden blok początkowy, ale może zwiera ć wiele bloków końcowych – począte k
algorytmu je s t je dnozna cznie okreś lony, a le algorytm może s ię kończyć na wiele różnych spos obów;

■

z bloków: początkowe go, wprowadzania danych, wyprowadzania wyników, operacyjne go wychodzi
dokładnie je dno połą czenie, może jednak wchodzić do nich wiele połączeń;

■

z bloku warunkowego wychodzą dwa połączenia , oznaczone wartoś ciami wa runku: Ta k lub Nie;

■

połączenia wychodzące mogą dochodzić do bloków lub do innych połącze ń.

< 12 >

Informa tyka +

START

Blok począ tku algorytmu

Blok wprowadzania

da nych

Blok wyprowa dze nia

wyniku

Wprowa dź liczbę n i n+1

da nych: a

0

, a

1

, a

2

, ..., a

n

ora z z

Blok operacyjny

i := 0

y := a

0

i := i + 1

y := yz + a

i

;

Wyprowa dź:

wynik y

STOP

Blok zakończe nia

a lgorytmu

Blok

warunkowy

Tak

Nie

i = n

Rysunek 1.
Realizacja s chematu Hornera w pos taci s chematu blokowe go

Za kreś l na sche macie blokowym na rys . 1 fra gmenty odpowiada jące pos zcze gólnym kro-

kom w opisie algorytmu Schema t Hornera . Zauwa ż, ten że s chema t blokowy zawiera równie ż fra gmen-
t y odpowiada jące wczytywa niu danym i wypis ywaniu wyników.

Blok wprowadza nia danych w schemacie na rys . 1 polega na wczytaniu liczby n a później

na wczyta niu n + 1 liczb a

i

. Narysuj s zcze gółowy s che ma t blokowy te go bloku.

Sche ma ty blokowe mają wady, trudne do wyeliminowania. Łat wo kons truuje s ię z ich pomocą algorytmy dla
obliczeń nie zawiera jących iteracji i warunków, którym w s che ma tach odpowia dają rozgałę zienia , nieco trud-
niej dla oblicze ń z rozga łę zienia mi, a trudniej dla oblicze ń iteracyjnych. Za pomocą s chema tów blokowych nie
można w naturalny s pos ób zapis a ć rekure ncji ora z obja śnić zna czenia wielu poję ć zwią zanych z algorytmiką,
takich np. ja k progra mowanie z użyciem procedur, czyli podprogramów z parame tra mi. .

W dals zej częś ci zajęć rzadko będzie my korzys ta ć ze sche ma tów blokowych, wys tarczy nam bowie m

umieję tnoś ć programowania .

> Różnorodne algorytmy obliczeń i ich komputerowe realiza cje

< 13 >

Sche ma t Hornera ma wiele za s tos owań. Może być wykorzys ta ny m.in. do:

■

oblicza nia wa rtoś ci dzies ię tnej liczb danych w innym s ys temie pozycyjnym (rozdz. 4);

■

s zybkiego oblicza nia wa rtoś ci potęgi (rozdz. 6).

Za nim podamy komputerową rea liza cję s chema tu Hornera , musimy us talić, w ja ki s pos ób będą repre ze nto-
wa ne w algorytmie dane i ja k będziemy je poda wa ć do algorytmu.

Da nymi dla sche ma tu Hornera s ą s topień wielomianu n, za pis ane w pos taci cią gu n + 1 liczb ws pół-

czynniki wielomianu a

0

, a

1

, a

2

, ..., a

n

ora z liczba z, dla której chcemy obliczyć wa rtoś ć wielomianu. Stopień wie -

lomianu jes t liczbą na turalną (czyli doda tnią liczbą całkowitą ), a pozos ta łe liczby mogą być całkowite lub rze -
czywis te , czyli np. dzie się tne (tj. z kropką ). Rodzaj da nych liczb na zywa s ię typem danych. Przyjmujemy, że
poza s topniem wielomia nu, pozos ta łe dane s ą rze czywis te , a wię c mogą zawierać kropkę.

Dla wygody będziemy zakładać, że wiemy, ile będzie danych i ta liczba da nych wys tępuje na począ tku

danych – je s t nią liczba n, s topień wielomianu.

Zbiór danych, który jes t prze twarzany za pomocą algorytmu, może być podawany (czytany) z kla wiatu-

ry, czyta ny z pliku lub może być zapis a ny w algorytmie w odpowiedniej s trukturze danych.

Za pis zemy tera z s chemat Hornera posługują c się pole ceniami ję zyka Pa s cal. Przyjmuje my na początku, że
dane s ą poda wane z klawiatury – na począ tku na le ży wpis ać liczbę ws zys tkich danych, a po niej kolejne e le -
menty da nych w podanej iloś ci. Po ka żdej dane j liczbie nacis kamy klawis z Ente r.

Program, który je s t za pis e m s che ma tu Hornera w ję zyku Pa s ca l, je s t umie s zczony w drugiej kolum-

nie w tab. 4. Ję zyk Pa s cal je s t zrozumia ły dla kompute rów, które s ą wypos a żone w s pe cjalne programy, tzw.
kompilatory, przekła da ją ce programy użytkowników na ję zyk we wnę trzny kompute rów. Progra m w ta b. 4
be z wię ks ze go trudu zrozumie ta kże człowiek dys ponują cy opis e m s che ma tu Horne ra w pos ta ci lis ty kro-
ków. Słucha cze tych za ję ć pozna li już e le ment y ję zyka Pa s ca l podcza s rozgrze wki (rozdz. 2), za tem tuta j
tylko kilka s łów kome ntarza . W wiers za ch nr 2 i 3 zna jdują się de klara cje zmie nnych – kompute r mus i wie -
dzie ć, ja kimi wie lkoś cia mi pos ługuje s ię a lgorytm i jakie to s ą liczby, czyli jakie go s ą one t ypu – inte-

ger

ozna cza liczby ca łkowite (np. s topie ń wie lomia nu jes t liczbą ca łkowitą ), real ozna cza liczby rze czy-

wis te , czyli np. liczby, które mogą za wiera ć kropkę dzie s ię tną . Pole ce nia w ję zykach progra mowa nia na zy-
wają s ię ins trukcjami. Jeś li chce my z kilku ins trukcji zrobić je dną , to t worzymy z nich blok, umie s zcza jąc
na je go począ tku s łowo begin, a na końcu – end. Poje dyncze ins trukcje kończymy ś re dnikie m. Na końcu
progra mu s ta wiamy kropkę . Pokrótce to ws zys tkie pods ta wowe za s a dy pis a nia progra mów w ję zyku Pa s -
ca l dla komputerów.

Je dna ins trukcja wyma ga wytłuma cze nie , chocia ż równie ż je s t doś ć oczywis ta i p oja wiła s ię

w rozdz. 2. W wie rs za ch 9 – 12 zna jdują s ię ins trukcje , które re a lizują Krok 2 a lgorytmu pole ga ją cy na wy-
kona niu je dne j ite ra cji s che ma tu Horne ra . Doda tkowo, wcze ś nie j je s t czyta ny kole jny ws półczynnik wie -
lomia nu. Ins trukcja , s łużą ca do wie lokrotne go wykona nia innych ins trukcji na zywa s ię ins trukcją ite ra -
cyjną lub ins trukcją pę tli. W progra mie w ta b. 4 ta ins trukcja za czyna s ię w wie rs zu nr 9 a kończy w wie r-
s zu nr 12:

for i:=1 to n do begin

...

end

Ta ins trukcja itera cyjna , jak na pis aliś my, s łuży do powtórzenia dwóch ins trukcji:

read(a);

y:=y*z+a

Inne rodzaje ins trukcji itera cyjnej bę dą wprowadzane s ukces ywnie.

Uwaga . Poniewa ż za łożyliśmy, że da ne s ą podawane z klawiatury, zmieniliś my ich kolejnoś ć w s tosunku
do s pecyfikacji – liczba z, dla której jes t oblicza na wartoś ć wielomianu, je s t podawana na początku, przed
współczynnikami wielomianu.

< 14 >

Informa tyka +

Ta bela 4.
Progra m w ję zyku Pa s cal (druga kolumna)

Lp.

Prog ram w ję zyku Pa s cal

Obja ś nienia

1.

Program Horner;

na zwa programu

2.

var i,n :integer;

deklaracja zmiennych i, n

3.

var a,y,z:real;

deklaracja zmiennych a , y, z

4 .

begin

p oczątek główne go bloku programu

5.

read(n);

czytaj(n)

6 .

read(z);

czytaj(z)

7.

read(a);

czytaj(a) – pierws zy współczynnik

8 .

y:=a;

począ tkowa wartoś ć wielomianu

9.

for i:=1 to n do begin

dla i:=1 do n wykona j

10.

read(a);

czytaj(a)

11.

y:=y*z+a

modyfikacja wartoś ci wielomianu

12.

end;

koniec iteracji

13.

write(y)

drukuj(y) – wartoś ć wie lomia nu

14.

end.

konie c. – na końcu s tawiamy kropkę

W wyniku wykonania tego programu, wypis ywa na jes t na ekra nie wartoś ć wielomianu y w punkcie z. Ta war-
toś ć je s t wypis ywana w pos taci normalne j, np. liczba 30 je s t wypis ywa na jako:

3.00000000000000E+001

czyli 3.00000000000000

•

10^ 1. Nie jes t to najwygodniejs za pos tać liczb, zwła s zcza liczb o niewielkich war-

toś cia ch. Aby wybra ć inny forma t wyprowa dzanych liczb, możemy napis a ć:

write(y:2:2)

co bę dzie ozna czać, że wartoś ć y zos ta nie wyś wie tlona (wydrukowa na , wyprowadzona) z dwoma cyframi
prze d kropką i z dwoma cyframi po kropce.

Uruchom program Horner i wykona j obliczenia dla wybranego wielomianu i kilku jego

a rgumentów.

Zmodyfikujemy te ra z na s z progra m tak, a by:

■

s topie ń i współczynniki wielomianu były czytane na począ tku i przechowywane w programie – do
prze chowa nia w programie ws półczynników użyjemy tablicy, która w języku programowa nia jes t
s ynonime m cią gu;

■

można było obliczyć wartoś ć wielomianu o wczyta nych ws półczynnikach dla wielu a rgumentów –
zakłada my w tym celu, że cią g argumentów je s t za kończony liczbą 0 (je s t to tak zwa ny wa rtownik cią gu,
gdyż je go rolą jes t pilnowanie końca ciągu.

Przy tych za łożeniach, program bę dący impleme ntacją

3

s chematu Horne ra , może mieć na s tępująca pos tać:

3

Terminem implementacja okreś la s ię w informat yce realiza cję algorytmu w pos taci programu komputerowe go.

Za głębiające
s ię bloki
ins trukcji

> Różnorodne algorytmy obliczeń i ich komputerowe realiza cje

< 15 >

Program Horner _ tablica;

var i,n:integer;

y,z:real;

a :array[0..100] of real;

{Przyjmujemy, ze wielomian ma stopien co najwyzej 100}

begin

read(n);

for i:=0 to n do read(a[i]);

writeln(’ z y‘);

read(z);

while z <> 0 do begin

y:=a[0];

for i:=1 to n do

y:=y*z+a[i];

write(’

ʽ ,y:2:5);

writeln;

read(z)

end

end.

Skomentowania wyma ga użyta ins trukcja warunkowa :

while z <> 0 do begin

y:=a[0];

for i:=1 to n do

y:=y*z+a[i];

write(’

ʽ ,y:2:5);

writeln;

read(z)

end

W bloku tej ins trukcji je s t wykonywany s chema t Horne ra dla kolejnych wa rtoś ci a rgumentu z tak długo, ja k
długo czytana liczba z je s t różna od 0 (z <> 0).

Doda tkowo, w programie wprowadziliśmy drukowa nie wyników w pos taci ta belki.

Uruchom program Horner _ tablica i wykonaj obliczenia dla wybrane go wielomia nu

i kilku wartoś ci je go a rgumentu. Popraw wygląd wyników.

Obecnie w pows zechnym użyciu je s t s ys te m dzie się tny, zwa ny te ż s ys temem dzies iątkowym. Komputery na -
tomia s t ws zys tkie opera cje wykonują w s ys te mie binarnym, zwa nym równie ż s ys te me m dwójkowym. Oba
s ys te my, to dwa przykła dy tzw. s ys temu pozycyjne go zapis ywania wa rtoś ci liczbowych. Powinny one być
Wam zna ne z lekcji ma temat yki. Przypomnijmy je dnak je den i drugi s ys tem.

Liczba zapis a na w s ys te mie dzie się tnym, np. 357, ozna cza wartoś ć, na którą skła da ją się trzy se tki,

pię ć dzies ią tek i s iede m je dnoś ci, a za tem wartoś ć tej liczby można zapis a ć ja ko 357 = 3

•

100 + 5

•

10 + 7

•

1,

a także ja ko 357 = 3

•

10

2

+ 5

•

10

1

+ 7

•

10

0

.

A zate m, dziesiętna liczba na tura lna złożona z n cyfr:

d

n–1

d

n –2

... d

1

d

0

< 16 >

Informa tyka +

oznacza wa rtoś ć:

d

n–1

10

n–1

+ d

n–2

10

n–2

+ ... + d

1

10

1

+ d

0

10

0

. (4)

Liczba 10 w tej reprezenta cji na zywa s ię pods ta wą s ys temu li-
cze nia. Do zapis ywania liczb w s ys temie dzies ię tnym s ą uży-
wa ne cyfry: 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9. Ten spos ób reprezento-
wa nia liczb na zywa się s ys te m pozycyjnym, gdyż w tym s ys te -
mie znaczenie cyfry zale ży od jej pozycji w cią gu cyfr, okreś la -
jącym liczbę. Na przykład, liczby 123 i 321 mają różną wartoś ć,
chocia ż s ą złożone z tych s amych cyfr, a liczba 111 jes t złożo-
na z trze ch je dynek, z których ka żda ma inne zna czenie dla wa r-
toś ci te j liczby.

Ws zys tkim s ą znane tzw. cyfry rzyms kie : I, V, X, L, C, D. M. Oznacza ją one odpowiednio

liczby: 1, 5, 10, 50, 100, 500, 1000. W tym s ys te mie , liczba III ma dzies ię tną wartoś ć 3, a za tem ka żda
z cyfr w tej liczbie ma takie s amo zna czenie, a wartoś ć je s t oblicza na prze z dodawanie wartoś ci cyfr. Za -
pis z w tym s ys temie liczby 2009 i 2012. Na liczbach rzymskich trudno wykonuje się pods ta wowe dzia -
łania: dodawanie, odejmowanie i mnoże nie. Liczby te były s tos owane prze z Rzymian głównie do zapi-
s ywania wartoś ci liczbowych, a nie do wykonywania na nich działań.

Za pods ta wę s ys temu liczenia można przyją ć dowolną liczbę na turalną p wię ks zą od 1, np. 2, 5, 8, 16 czy 60.
Jeś li p je s t pods tawą s ys temu liczenia , to liczby w tym s ys temie s ą zapis ywane za pomocą cyfr ze zbioru {0,
1, ..., p – 1}.

W rozwa żaniach, zwią za nych z kompute rami, poja wiają s ię liczby w s ys tema ch o pods ta wach 2, 8 i 16. Na s zą
uwa gę skupimy głównie na s ys temie o pods ta wie 2, a o innych s ys temach je s t mowa w ćwiczeniach.

Jeś li p = 2, to s ys te m na zywa się bina rnym lub dwójkowym – cy-
fry liczby, zapis anej w tym s ys te mie , mogą mieć wa rtoś ć 0 lub 1
i na zywają się bita mi. Liczba na turalna a dana w s ys temie dzie -
się tnym ma na s tępującą pos tać w s ys te mie binarnym dla pe w-
ne go n:

a = b

n–1

2

n–1

+ b

n–2

2

n–2

+ ... + b

1

2

1

+ b

0

2

0

,

(5)

gdzie ws półczynniki b

n–1

, b

n –2

, ..., b

1

, b

0

s ą liczbami 0 lub 1. W s krócie pis ze my zwykle a = (b

n –1

b

n–2

... b

1

b

0

)

2

i cią g bitów w na wia s ie na zywamy binarnym rozwinię ciem liczby a. Na przykła d ma my, 8 = (1000)

2

, 12 =

(1100)

2

, 7 = (111)

2

. Cyfra b

n–1

je s t na jbardzie j znaczą cą , a b

0

– na jmniej znaczą cą w rozwinię ciu liczby a .

Jeś li s ię dobrze przyjrzymy wzorom ozna czonym przez (4) i (5), to zauwa żymy, że przypominają one s pecja lne
wielomia ny – współczynnikami t ych wielomianów s ą cyfry rozwinię cia , a argumentem wielomia nu – jes t pod-
s tawa s ys temu liczenia . Aby wię c obliczyć wartoś ć dzie się tną liczby, da nej w innym s ys temie, możemy s ko-
rzys tać ze sche ma tu Hornera , ba rdzo efektywne go algorytmu oblicza nia wartości wielomia nu.

Binarne rozwinięcie dziesię tnej liczby na turalnej (prawa s trona we wzorze (5)) przypomina s woją postacią wie -
lomian (patrz wzór (1)), gdzie a je s t wartoś cią wielomia nu s topnia n – 1 o ws półczynnika ch b

n–1

, b

n–2

, ... b

1

, b

0

nale żących do zbioru {0, 1}, dla wartości argumentu x = 2. Z tej interpretacji rozwinię cia (5) wynika spos ób ob-
liczania dzie siętnej wartości liczby naturalnej a , gdy je s t dane jej bina rne rozwinięcie (b

n–1

b

n–2

... b

1

b

0

)

2

. Wys tar-

czy za s tos owa ć s chemat Hornera , który dla wielomia nu, dane go wzore m (5), przyjmuje na s tępującą pos tać:

Dwa tysiące la t prze d na s zą erą
Ba bilończycy s tos owali s ys te m
kopowy (tj. przy pods tawie 60)
– przypus zcza się , że s tą d wziął s ię
podzia ł kąta pe łnego na 360 s topni,
godziny – na 60 minut, a minuty
– na 60 se kund.

Za prekurs ora s ys temu binarnego
uwa ża się G.W. Leibniza, który w pracy
opublikowanej w 1703 roku zilus trowa ł
wykonywanie czterech podstawowych
dzia łań arytmetycznych na liczbach
binarnych.

> Różnorodne algorytmy obliczeń i ich komputerowe realiza cje

< 17 >

a = b

n–1

2

n–1

+ b

n–2

2

n–2

+ ... + b

1

2

1

+ b

0

2

0

= (...(b

n–1

2 + b

n–2

)2 + ... + b

1

)2 + b

0

(6)

Napis z program s łużący do obliczania dzie siętnej wa rtoś ci liczby a danej w pos ta ci bi-

narne go rozwinię cia (b

n–1

b

n –2

... b

1

b

0

)

2

.

Wska zówka . Zmodyfikuj odpowie dnio program Hornera _ Klawiatura. Zwróć uwagę, że kolejne cy-
fry rozwinię cia bina rne go liczby w pos ta ci (5) s ą ponume rowane odwrotnie niż ws półczynniki wielo-
mianu we wzorze (1) i zauwa ż przy tym, że indeks ws półczynnika odpowiada potędze liczby 2, prze d
którą s toi ten współczynnik. Nie powinno to je dna k utrudnić Ci wykonania te go ćwiczenia .

Postać rozwinięcia binarnego (6) sugeruje bardzo pros ty spos ób obliczania wartości liczby a za pomocą kalkulatora.

Oblicz za pomocą kalkulatora dzies ię tną wa rtoś ć liczby a , prze ds tawionej w pos taci roz-

winięcia binarnego. Wykorzys ta j algorytm wynikają cy z pos taci (6). Zauwa ż, że nie musis z korzys tać
z dodatkowej pamięci kalkula tora .
Wska zówka . Możes z s korzys ta ć z kalkula tora dos tę pne go wśród akce s oriów ś rodowis ka Windows .

Ws zys tkie fa kty poda ne powyżej przenos zą się na rozwinięcia liczby w s ys te mie przy dowolnej pods tawie p.

Zmodyfikuj program na pis any w ćwicz. 11 tak, a by mógł być s tos owa ny do oblicza nia

dziesiętnej wartoś ci liczby a danej w pos ta ci rozwinię cia przy pods tawie p.

Interes uje na s te ra z czynnoś ć odwrotna – otrzymanie bina rnego rozwinięcia dla danej d zie się tnej liczb y natu-
ra lnej a.

Zauwa żmy, że we wzorze (5), czyli w binarnym przeds ta wieniu liczby a , ws zys tkie s kładniki z wyjątkiem

os tatniego s ą podzielne prze z 2, a za tem ten os ta tni s kładnik, czyli b

0

je s t res ztą z dzielenia liczby a przez 2.

Bity b

1

, b

2

,..., to re s zty z dzielenia prze z 2 kolejno otrzymywanych ilora zów. Dzielenie kończymy, gdy ilora z

wynosi 0, gdyż wtedy kolejne res zty będą już ca ły cza s równe 0, a zera na początku rozwinięcia bina rnego nie
mają ża dne go znaczenia. Prześ ledź ten proces na przykładzie z rys . 2.

dziele nie

ilora z

res zta

749 | 2

374

1

374 | 2

187

0

187 | 2

93

1

93 | 2

46

1

46 | 2

23

0

23 | 2

11

1

11 | 2

5

1

5 | 2

2

1

2 | 2

1

0

1 | 2

0

1

Rysunek 2.
Przykład tworzenia binarnej reprezentacji liczby dzie się tnej 749. Otrzyma liśmy 749 = (1011101101)

2

Za uwa żmy, że w powyżs zym a lgorytmie bina rna re pre zentacja liczby je s t tworzona od końca , czyli od naj-
mniej znaczącego bitu. W punkcie 5.4 omawiamy generowa nie cyfr liczb od począ tku.

< 18 >

Informa tyka +

Wprowa dzimy tera z dwie operacje , wykonywane na liczbach całkowitych, których wyniki s ą równie ż liczba mi
ca łkowitymi, a które s ą przyda tne przy obliczaniu ilora zu i res zty z dzie lenia liczb ca łkowitych przez siebie.

Dla dwóch liczb całkowitych k i l definiujemy:
r = k mod l – r jes t res ztą z dzielenia k prze z l, czyli r spe łnia nie równoś ci 0 ≤ r < l, gdyż re s zta jes t nie -

ujemną liczbą mniejs zą od dzielnika;

q = k div l – q jes t ilora zem ca łkowitym z dzie lenia k przez l, czyli q je s t wynikiem dzielenia k prze z l z po-

minięciem częś ci ułamkowej.

Z definicji tych dwóch ope racji wynika na s tę pują ca równoś ć:

k = l

•

q + r = l

•

(k div l) + (k mod l)

(7)

Upe wnij s ię, że dobrze rozumie s z te dwie operacje , które czę s to wys tę pują w obliczenia ch kompute rowych
na liczbach całkowitych. .

Dla liczby naturalnej l = 6 i dla liczby na turalnej k, zmienia jącej s ię od 0 co 1 do 20 oblicz

wartoś ci k div l ora z k mod l i s pra wdź prawdziwoś ć równoś ci (7).

Przyjmij, że l = 2, a więc intere suje na s ilora z i re s zta z dzielenia liczby na turalnej k prze z

2. Poda j, w zależnoś ci od parzys toś ci liczby k, ile wynos i k mod 2 ora z k div 2.

Dotychcza s owa dyskus ja prowadzi na s do na s tę pują ce go a lgorytmu:

Algorytm: Za miana dzie siętne j liczby naturalnej na pos tać binarną
Dane:

Dzie się tna liczba naturalna a .

Wynik: Cią g bitów, t worzą cych binarne rozwinię cie liczby a, w kolejnoś ci od na jmniej znaczącego bitu.
Krok 1. Powta rzaj krok 2 dopóki a je s t liczbą więks zą od zera , w prze ciwnym ra zie zakończ a lgorytm.
Krok 2. Za kolejny bit (od końca) rozwinięcia przyjmij: a mod 2 i przypis z: a := a div 2.

Poniżej prze ds tawiamy imple mentację te go a lgorytmu w języku Pa s ca l.

Program Rozwiniecie _ binarne;

var a:integer;

begin

read(a);

while a <> 0 do begin

write(a mod 2,’ ‘);

a:=a div 2

end

end.

W powyżs zym progra mie , kolejne bity rozwinię cia bina rne go liczby a s ą wypis ywane

w kolejnoś ci od najmniej znaczą ce go, a wię c odwrotnie, niż to s ię przyjmuje. Zmodyfikuj ten program
ta k, a by bina rne rozwinię cie danej liczby było wyprowa dzane od najba rdziej znaczącego bitu.
Wska zówka . Pos łuż s ię tablicą , w której będą prze chowywane kolejno generowane bity.

Os oby, które nie zna ją logarytmu, mogą opuś cić ten podpunkt.

Liczby w komputerze s ą za pis ywa ne w pos ta ci bina rnej. Inte re sujące jes t wię c pytanie, ile miejs ca w kompu-
terze, czyli ile bitów, zajmuje liczba na tura lna a w pos taci binarnej. Odpowie dź na to pyta nie jes t bardzo wa ż-

> Różnorodne algorytmy obliczeń i ich komputerowe realiza cje

< 19 >

na w informatyce, nawe t dzisiaj, kiedy można korzys ta ć z niemal nie ograniczonej pamięci komputerów i nie
trzeba się obawiać, że jej za braknie.

Najpierw rozwa żymy odwrotne pytanie: Jaką najwięks zą liczbę na turalną można zapis a ć na n bitach?

Liczba taka ma ws zys tkie bity równe 1 w s woim rozwinięciu binarnym (11...11)

2

, a wię c jej wartoś ć, ja ko sumą

n począ tkowych wyra zów cią gu ge ome trycznego z ilora zem równym 2, wynos i:

2

n–1

+ 2

n–2

+ ... + 2

1

+ 2

0

= 2

0

+ 2

1

+ ... + 2

n–2

+ 2

n –2

= (1 – 2

n

)/ (1 – 2) = 2

n

– 1

Ta równoś ć ma cie kawą inte rpre tację. Wa rtoś ć sumy po le wej s tronie je s t liczbą o je den mniejs zą od liczby
(100...00)

2

, która w rozwinię ciu binarnym składa s ię z n+1 bitów i ma tylko jeden bit równy 1 – na jbardziej

znaczą cy. Tą liczbą je s t 2

n

. Na rys . 3 poka zano, ile bitów potrze ba do przeds ta wie nia w pos ta ci bina rnej liczb

z pos zczególnych przedzia łów. Z os tatniej równoś ci wynika , że liczba a może być za pis ana na n bita ch, je śli
spe łnia nierównoś ć:

2

n

– 1 ≥ a, czyli 2

n

≥ a + 1.

Dla danej liczby a wybie ramy na jmniejs ze n s pe łniają ce tę nierównoś ć, gdyż począ tkowe zera w rozwinię ciu
liczby nie mają znacze nia . Logarytmując obie s trony nie równoś ci można dokła dnie okreś lić wartoś ć n:

n =

log

2

(a + 1) .

Użyliśmy funkcji powała, której wartością jest najmniejsza liczba całkowita większa od liczby stojącej pod powałą, gdyż
liczba bitów w rozwinię ciu liczby a jest zawsze liczbą naturalną, a wartość logarytmu może nie być liczbą całkowitą ,

końce podzia łów

1

3

7

15

31

63

= 2

n

– 1

liczba bitów n

2

3

4

5

6

Rysunek 3.
Liczba bitów potrzebnych do zapamię tania liczb a z pos zczególnych przedzia łów

Z powyżs zych rozwa ża ń nale ży za pamię ta ć, że liczba bitów potrzebnych do zapamię tania w komputerze licz-
by na turalne j je s t w przybliżeniu równa logarytmowi przy pods ta wie 2 z wartoś ci tej liczby. na przykła d, licz-
ba 1000 jes t pamięta na na

log

2

(1000 + 1) = 10 bitach.

Przy tej oka zji porównaj s zybkoś ć wzra s tania funkcji liniowej i funkcji logarytmicznej.

Narysuj w jednym układzie współrzę dnych wykre s y dwóch funkcji, loga rytmicznej i linio-

we j. Utwórz ta kże tabelę wartoś ci obu funkcji dla liczb wybra nych z przedzia łu [1, 10

9

]. Zauwa ż, jak wol-

no roś nie funkcja logarytmiczna w porówna niu z funkcją liniową .

Funkcja logarytmiczna odgrywa bardzo wa żną rolę w informatyce.

W rozwią zywaniu problemów czę s to je s t s tos owana me toda , w której korzys ta my ze zna nych już rozwią zań
innych problemów. Dotyczy to nie t ylko proble mów tutaj rozpa trywa nych czy problemów ma tema tycznych,
ale tak pos tępujemy niemal w ka żdej dziedzinie.

Szcze gólnym przypadkie m metody, korzys tają cej z rozwią zań innych problemów, jes t me toda , w której

tymi „innymi problemami” jes t rozwią zywa ny wła ś nie problem, a le dla mnie js zych rozmiarów danych. W ta -

< 20 >

Informa tyka +

kiej s ytuacji je s t s tos owa ny algorytm rekurencyjny, czyli a lgorytm, który odwołuje się do s iebie. Rekurencję
można s tos ować nie tylko do przeds ta wiania rozwią zań problemów, ale także do opis u wykonywania pew-
nych czynnoś ci, które mają cha ra kter itera cyjny i powtarzana jes t ta s a ma czynnoś ć. Ogólnie , rekurencja to
spos ób myśle nia uła twia jący radzenie s obie z problema mi i ich rozwią zaniami. Ze względu na znaczenie te go
podejś cia do rozwią zywa nia problemów z użyciem komputerów, algorytmiczne ję zyki programowa nia , takie
jak Pa s cal i C++ umożliwia ją zapis ywa nie rozwią zań re kurencyjnych i ich wykonywanie. Rekurencyjne opis y
rozwią za ń komputerowych s ą na ogół bardzo zwarte – zobaczymy to na wielu pre zentowa nych tuta j przykła -
dach – jes t to jednak czę s to okupione efe kt ywnoś cią oblicze ń, znaczna częś ć organizacji obliczeń rekuren-
cyjnych je s t bowiem prze jmowa na przez komputer. Można wię c s pojrze ć na rekure ncję ja k na spos ób „prze -
rzuca nia roboty na kompute r” przy rozwią zywaniu problemów.

Przytoczymy tutaj dwa przykłady re kurencyjnych „proce dur” pos tępowania , które s ą da lekie od cha -

rakte ru na s zych rozwa żań – s formułowaliśmy je je dnak używa jąc ins trukcji ję zyka Pa s cal – a le ilus trują re ku-
re ncyjny spos ób myślenia . Pierws zy przykład pochodzi od zna ne go Radzieckiego informa tyka , Andrie ja Jer-
s zowa .

procedure Jedz kaszk

ę;

if talerz jest pusty then koniec jedzenia

else begin

we

ź ł yż kę kaszki;

Jedz kaszk

ę {wywoł anie rekurencyjne}

end

procedure Ta

ńcz;

if nie gra muzyka then koniec ta

ńczenia

else begin

zrób krok;

Ta

ńcz {wywoł anie rekurencyjne}

end

W obu przykłada ch, po if wys tę puje warune k, który gwa ra ntuje , że obie proce dury mogą kończyć działanie,
gdy tale rz będzie pus ty lub gdy przes tanie grać muzyka . Można sobie wyobra zić je dnak s ytuację , że muzyka
gra be z przerwy, wtedy druga proce dura opisuje nies kończony algorytm rekurencyjnego wykonywa nia kro-
ków tańca i dals ze go ta ńczenia . Stą d też wniose k dla opisów algorytmów komputerowych, o których na ogół
zakłada my, że kończą dzia ła nie – w opis ach rekurencyjnych powinien wys tą pić warune k zakończenia reku-
re ncji, nos i on na zwę warunku począ tkowe go.

Da lej w t ym rozdziale ilus truje my re kure ncyjny s pos ób rozwią zywa nia proble mów przykła da mi, o których
można powie dzie ć, że s ą wzię te z życia , ja k wie że Ha noi czy rozmna ża nie s ię królików. W rozwa żaniu t ych
proble mów można pos łużyć s ię s che ma ta mi gra ficznymi, co uła twia za obs erwowa nie odpowie dnich zale ż-
noś ci.

Ilus trujemy także , że poda ne wcze śniej rozwią zania niektórych proble mów można zapis a ć w pos taci

re kurencyjnej. Dotyczy to rozwią za ń za wie rających iterację . Z drugiej s trony, poka zuje my również, ze rozwią -
zania rekure ncyjne można za s tą pić rozwią za nia mi itera cyjnymi. Prowadzić to do konkluzji, że rekurencja je s t
fa ktycznie pewnym s pos obem za pisu powtarzających s ię czynnoś ci (np. obliczeń), czyli innym zapis em ite -
racji.

W da ls zych rozdzia łach wielokrotnie przeds ta wia my rozwią za nia rozwa ża nych proble mów równie ż

w pos taci rekurencyjnej, pa trz rozdz. 6, 7 i 9.

Tą na zwą opatruje się ła migłówkę logiczną , która jes t kla s ycznym przykłade m problemu algorytmiczne go
i służy w informa tyce ja ko ilus tracja wielu poję ć i me tod rozwią zywa nia problemów, w tym zwła s zcza reku-
re ncji. Zajrzyj na s tronę http:// wipos .p.lodz.pl/ zylla/ games/ hanoi3p.html, gdzie możes z zapoznać się z tą ła -
migłówką , pa trz rys .4.

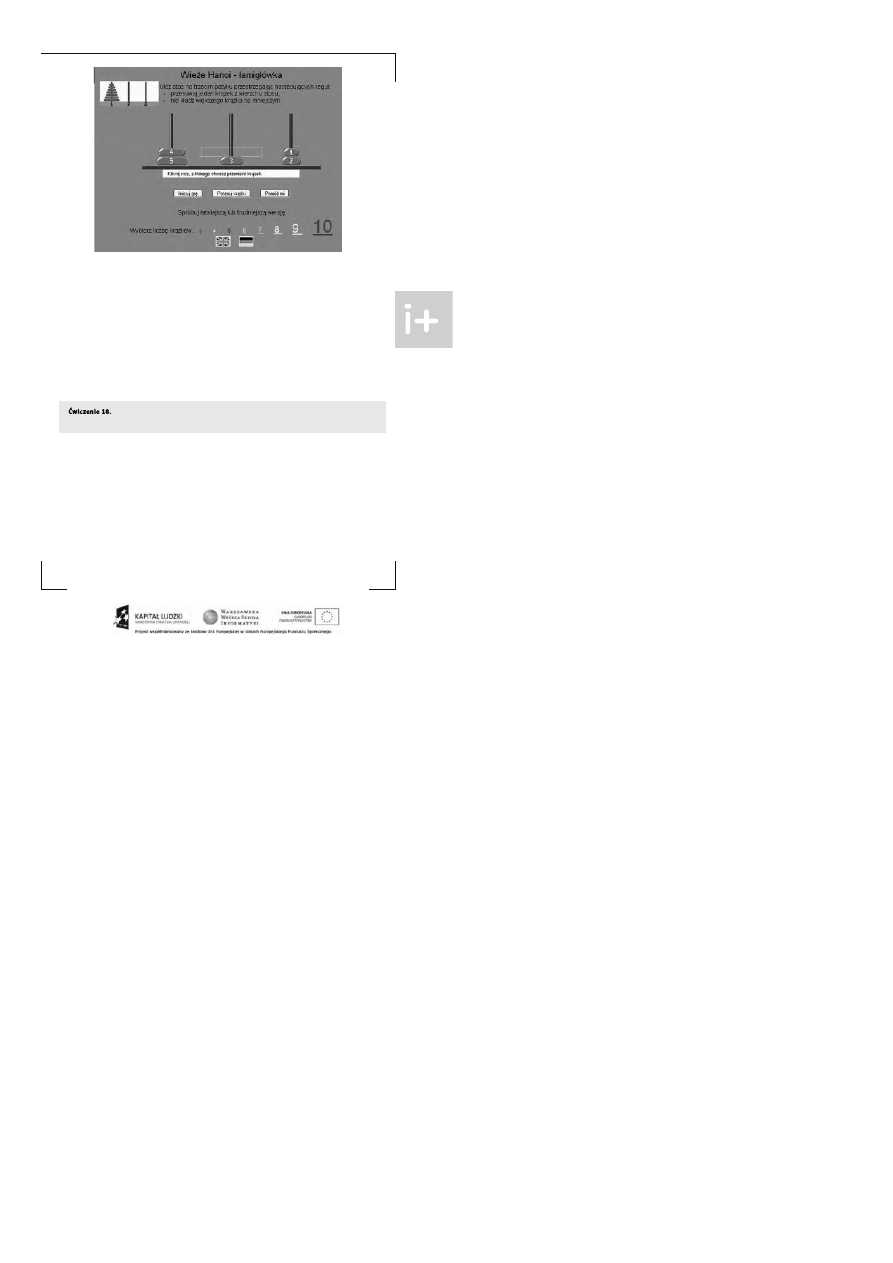
> Różnorodne algorytmy obliczeń i ich komputerowe realiza cje

< 21 >

Rysunek 4.
Rozwią zywanie łamigłówki Wież Hanoi w sie ci

W łamigłówce ma my trzy pa liki – oznaczmy je prze z A, B i C – ora z pe wną liczbę krą żków różnej wielkoś ci
z otworami, nanizanych na pa lik A w kolejnoś ci od najwięks zego do na jmniejs ze go, najwięks zy znajduje się
na dole. Łamigłówka polega na przenies ieniu ws zys tkich krą żków z palika A na palik B, z możliwoś cią pos łu-
żenia s ię przy t ym palikie m C, w taki s pos ób, że:

■

poje dynczy ruch polega na przenie sie niu jednego krą żka mię dzy dwoma palikami;

■

w żadnej chwili rozwią zywa nia ła migłówki, wię ks zy krą żek nie może le że ć na mniejs zym.

Jeś li na paliku A znajduje się jede n krą żek, to wys ta rczy prze nie ś ć go na pa lik B, a więc w t ym przypa dku wy-
s tarczy jeden ruch. Jeś li na A s ą dwa krą żki, to łamigłówka równie ż nie jes t trudna: górny przenos imy na palik
C, dolny na B i krą żek z C przenosimy na B. Zatem wykonuje my w tym przypadku 3 ruchy.

Na s tronie http:// wipos .p.lodz.pl/ zylla/ game s/ hanoi3p.html, najpie rw rozwią ż tę łami-

główkę dla 3 krą żków a później dla 4 i 5. W ilu ruchach ja rozwią za łe ś ?

Za pe wne podcza s tych prób poczyniłeś na s tę pujące spos trze żenia :

■

najmniejs zy krą żek zna jduje s ię za ws ze na górze któregoś z palików;

■

na górze dwóch pozos tałych palików, jeden z krą żków jes t mniejs zy od drugiego i tylko ten je den krą żek
można przenie ś ć — żaden inny ruch mię dzy tymi dwoma palikami nie jes t możliwy;

■

z poprze dnie go s pos trze żenia wynika , że najmniejs zy krą żek mus i być przenos zony co drugi ruch, a w co
drugim ruchu przenos zenie krą żka jes t jednoznacznie okre ślone – mus imy wię c jedynie okreś lić, na który
palik nale ży przenie ś ć na jmniejs zy krą że k – s zcze góły podajemy już w algorytmie.

Algorytm iteracyjny rozwią zania łamigłówki Wie ż Hanoi
Dane:

Trzy paliki A, B i C, ora z n krą żków o różnych ś re dnicach, na niza nych od najwię ks ze go do najmniej-
s ze go na pa lik A. Krą żki można prze nos ić między pa likami tylko poje dynczo i nigdy nie można poło-
żyć wię ks ze go na mniejs zym.

Wynik: Krą żki na niza ne na palik B lub C – do uzyskania tego wyniku można wykonywa ć je dynie dopus zczal-

ne przenos zenia .

< 22 >

Informa tyka +

Uwa ga: Paliki A, B i C traktuje my tak, jakby były us ta wione cyklicznie, zgodnie z ruche m wska zówek ze gara ,

zatem dla ka żde go palika je s t okreś lony nas tępny pa lik w tym porządku.

Krok 1. Przenieś na jmniejs zy krą żek z palika , na którym się zna jduje , na na s tępny pa lik. Jeśli ws zys tkie

krą żki s ą ułożone na jednym paliku, to za kończ algorytm.

Krok 2.

Wykonaj jedyne możliwe przeniesienie krążka, który nie jes t najmniejszym krążkiem i wróć do kroku 1.

Ponownie prze jdź na s tronę http:// wipos.p.lodz.pl/ zylla/ game s/ hanoi3p.html i rozwią ż

tę łamigłówkę dla 3, 4 i 5 krą żków pos ługując s ię powyżs zym algorytmem. Czy wykonałe ś tyle s amo
ruchów, co wykonując poprze dnie ćwiczenie?

Za cznijmy od pyta nia , które ma Ciebie naprowa dzić na rozwią zanie rekurencyjne: gdy wies z, jak rozwią za ć
ła migłówkę dla trze ch krą żków, czy potrafis z wykorzys tać to rozwią zanie , gdy ma s z o je den krą żek więcej?

Za s tanów się, ja ki powinien być układ krą żków, gdy wres zcie można najwięks zy z nich przenie ś ć z A na

B – pa mię taj przy tym, że te go najwięks ze go krą żka nie można położyć na żadnym innym, gdyż ws zys tkie po-
zos ta łe krą żki s ą od nie go mniejs ze. Za tem, gdy możemy przenieś ć najwięks zy krą żek, ws zys tkie pozos ta łe
krą żki mus zą być ułożone na paliku C zgodnie z ich wielkością. Stąd wynika , że możliwe je s t rozwią za nie , któ-
re składa się z trzech eta pów — za pis ze my je dla dowolnej liczby n krą żków na pa liku A:

1. Przenieś n – 1 górnych krą żków z pa lika A na palik C, używa jąc B.
2. Przenieś na jwięks zy krą żek z palika A na pa lik B.
3. Przenieś ws zys tkie krą żki z pa lika C na palik B, używając A.

Za tem, jeś li umiemy rozwią zać tę ła migłówkę z trze ma krą żkami, to powyżs zą me todą może my znale źć roz-
wią zanie dla czterech krą żków, na tej pods tawie – dla pię ciu krą żków itd. Może my skorzys tać z tej za s ady
równie ż w przypadku trzech krą żków, gdyż wiemy, jak przenos i się dwa krą żki. Pows ta je je dna k pyta nie , czy
opis ane wyżej kroki mogą być za ws ze wykonane? Krok 2 już obja śniliś my. Kroki 1 i 3 s ą podobne , a ich wy-
konalnoś ć wynika s tą d, że ma my do pe łnej dys pozycji trzy paliki, gdyż pa lik zawierający na jwięks zy krą żek
może być równie ż s wobodnie wykorzys ta ny prze z ws zys tkie pozos ta łe krą żki. Możemy więc być pe wni, że
kroki 1 i 3 mogą być również wykona ne. Powyżs zy opis posłuży nam tera z do zapis ania rekurencyjnego roz-
wią zania łamigłówki Wież Hanoi w pos ta ci algorytmu.

Algorytm rekure ncyjny rozwią zania ła migłówki Wie ż Hanoi
Dane: Trzy paliki A, B i C, ora z n krą żków o różnych śre dnicach, nanizanych od najwię ks zego do najmniejs ze -

go na palik A. Krą żki można przenos ić między palikami tylko poje dynczo i nigdy nie można położyć
wię ks ze go na mniejs zym.

Wynik: Krą żki naniza ne na pa lik B – do uzys kania tego wyniku można wykonywać jedynie dopus zcza lne prze -

nos zenia.

Krok 1. Je ś li n = 1, to przenieś krą że k z palika A na B i zakończ algorytm dla n = 1.
Krok 2. {W tym przypadku liczba krą żków na pa liku A je s t więks za od 1.}

2a . Stosując ten algorytm, przenieś n – 1 krą żków z A na C, używają c B.

2b. Przenieś pozos ta ły krą żek z A na B.

2c. Stosując ten algorytm, przenieś n – 1 krą żków z C na B, używając A.

Aby bardziej pre cyzyjnie opis a ć realizację powyżs ze go algorytmu, oznaczmy przez (X➝Y) przenie sienie krą ż-
ka z palika X na palik Y, a prze z (k,X,Y,Z) — prze nie sienie k krą żków z palika X na palik Y z wykorzys taniem pa -
lika Z, gdzie X, Y, Z oznacza ją różne paliki spośród A, B i C. Przy tych oznaczenia ch, powyżs zy algorytm moż-
na za pis ać na s tępująco:

Algorytm rekure ncyjny rozwią zania ła migłówki Wie ż Hanoi (n,A,B,C)
Krok 1. Jeś li n = 1, to (A➝B) i zakończ a lgorytm dla te go przypadku.
Krok 2. {W tym przypadku liczba krą żków na pa liku A jes t wię ks za od 1.}

2a . Za s tosuj ten algorytm dla (n – 1,A,C,B).

> Różnorodne algorytmy obliczeń i ich komputerowe realiza cje

< 23 >

2b. Prze nie ś pozos ta ły krą żek (A➝B).

2c. Za s tos uj ten algorytm dla (n – 1,C,B,A).

Można poczynić jes zcze da ls ze upros zczenia w tym algorytmie . Zauwa żmy, że w krokach 1 i 2b je s t wykony-
wa ne takie s amo przenie sienie krą żka , krok 1 je s t więc s zczególnym przypa dkiem kroku 2, w którym dla n =
1 przyjmujemy, że kroki 2a i 2c s ą pus te (czyli nic nie jes t wykonywane). Os ta tecznie otrzymuje my na s tępu-
jący algorytm rekure ncyjny:

Algorytm rekurencyjny rozwią zania ła migłówki Wie ż Hanoi (n,A,B,C)
Krok 1. Jeś li n = 0, to nic nie rób i zakończ a lgorytm dla te go przypadku.
Krok 2. {W tym przypadku liczba krą żków na paliku A jes t wię ks za od 0.}

2a . Za s tosuj ten a lgorytm dla (n – 1,A,C,B).

2b. Przenie ś pozos ta ły krą żek (A➝B).

2c. Za s tos uj ten algorytm dla (n – 1,C,B,A).

Opis y dwóch os ta tnich wers ji a lgorytmu rozwią zania łamigłówki Wie ż Hanoi s ą w pe łni rekurencyjne . Układ
parame trów w na zwie a lgorytmu umożliwia rekurencyjne wywoła nia wewną trz algorytmu.

Cieka we może być porównanie przebiegu obu wersji a lgorytmu ite racyjnego i rekurencyjnego.

Prze konaj s ię, że kolejnoś ć przemies zczania krą żków w rekure ncyjnym algorytmie roz-

wią za nia ła migłówki Wie ż Ha noi dla n = 3 je s t dokładnie taka s ama , jak w algorytmie ite racyjnym.

Imple mentacja rekurencyjne go rozwią zania łamigłówki Wież Ha noi ma bardzo pros tą pos tać w języku Pa scal:

procedure HanoiRek(n:integer; A,B,C:char);

{Rekurencyjne rozwiazanie zagadki Wiez Hanoi}

begin

if n>0 then begin

HanoiRek(n-1,A,C,B);

writeln(’Przenies ‘,n,’ z ‘,A,’ na ‘,B);

HanoiRek(n-1,C,B,A)

end

end; {HanoiRek}

Umie ś ć procedurę HanoiRek w programie i użyj s woje go programu do otrzyma nia roz-

wią za nia dla n = 3 i n = 4. Porównaj te rozwią za nia z otrzyma nymi wcześ niej.

Wcześ niej nie proponowaliśmy utworzenia implementacji a lgorytmu służące go do itera cyjnego rozwią zywa -
nia ła migłówki Wież Hanoi, gdyż je s t ona doś ć złożona . Je śli je dnak ma s z ochotę, to ut wórz ta ką .

His toria głosi, że łamigłówkę Wie ż Ha noi rozwią zują mnis i w jednym z kla s ztorów w Tybecie . Począ tkowo na
paliku A znajdowały się n = 64 krą żki i gdy ws zys tkie zos taną odpowiednio ułożone na paliku B, to na s tą pi ko-
nie c ś wiata . Dobrze jes t wię c wie dzie ć, ile zajmie im to cza su. Proponujemy na s tępujące ćwiczenie.

Przyjmij, że grupa mnichów w Tybe cie rozpoczę ła rozwią zywać ła migłówkę Wie ż Hanoi

z n = 64 krą żkami na początku na s zej ery i pracuje z prędkoś cią komputera średniej mocy przenos ząc
100 milionów pojedynczych krą żków na s e kundę ! Oblicz, kiedy na s tą pi konie c ś wiata .

< 24 >

Informa tyka +

Ozna czmy przez h

n

liczbę ruchów pojedynczymi krą żka mi, by rozwią zać ła migłówkę Wie ż Hanoi z n krą żka -

mi. Przypomnij s obie, ile wykona łe ś ruchów dla trzech i cztere ch krą żków – było to odpowiednio 7 i 15, a za -
tem h

3

= 7 i h

4

= 15. Co przypomina ją Ci te liczby? Na wet z nie wielkim obyciem w dzie dzinie algorytmów, moż-

na za uwa żyć, że te liczby s ą o je den mniejs ze od kolejnych potę g liczby 2, mamy więc h

1

= 1 = 2

1

– 1, h

2

= 3 =

2

2

– 1, h

3

= 7 = 2

3

– 1, i h

4

= 15 = 2

4

– 1 – potęga liczby 2 je s t równa indeks owi liczby h. Na tej pods ta wie mo-

że my przypus zczać, że h

n

= 2

n

– 1 dla dowolnej liczby krą żków n. Wyka że my, że tak je s t rze czywiś cie, ale s ą

to trochę trudniejs ze rozwa żania. Ilus truje my nimi również otrzymywanie za le żnoś ci re kurencyjnych na pod-
s tawie algorytm rekurencyjnego ora z pros ty s pos ób rozwią zywa nia takich zale żnoś ci.

Z rekurencyjne go algorytmu rozwią zywania ła migłówki Wież Hanoi wynika na s tę pują ca zale żnoś ć re -

kurencyjna między liczba mi h

n

– za uwa ż, że h

n

zależy od tej s amej wielkoś ci h

n–1

tylko z mniejs zym inde kse m:

1 n = 1

h

n

=

{

2h

n–1

+ 1 n ≥ 2

Jeś li bowiem n = 1, to wykonuje my je dno przenie sienie krą żka , a jeś li n > 1, to s tos uje my rekurencyjny krok
algorytmu, w którym dwa ra zy przenosimy t ym s amym algorytmem n – 1 krą żków (wykonują c przy tym h

n–1

przenies ień krą żków w obu przypadka ch) i ra z przenosimy na jwięks zy krą żek.

W ja ki spos ób na pods ta wie powyżs ze j za le żnoś ci rekurencyjnej można zna leźć wartoś ci liczb h

n

? W przypad-

ku tej zale żnoś ci jes t to doś ć pros te, gdyż możemy za s tos ować me todę ws ta wiania . Polega ona na tym, że
wielkoś ć s toją cą po prawej s tronie zale żnoś ci rekurencyjnej można równie ż wyra zić prze z tę s amą za leżnoś ć.
Za tem, dla n – 1 otrzymujemy z zale żnoś ci na s tę pują cą równoś ć h

n –1

= 2h

n–2

+ 1 i po ws ta wieniu do wzoru na

h

n

w zale żnoś ci powyżej otrzymuje my:

h

n

= 2h

n –1

+ 1 = 2(2h

n –2

+ 1) + 1 = 2

2

h

n –2

+ 2 + 1

Wykona jmy jes zcze jede n krok ws tawienia , by za uwa żyć pewną re gula rnoś ć. Z zale żnoś ć rekurencyjnej dla
n – 2 otrzymujemy h

n–2

= 2h

n–3

+ 1 i po ws ta wieniu do powyżs zego wzoru otrzymujemy:

h

n

= 2

2

h

n–2

+ 2 + 1 = 2

2

(2h

n–3

+ 1) + 2 + 1 = 2

3

h

n –3

+ 2

2

+ 2 + 1

Takie ws ta wianie kontynuujemy a ż do otrzyma nia h

1

po prawej s tronie zna ku równoś ci, wte dy bowiem może -

my prze rwa ć rekurencyjne za s tę powa nie we dług drugiej czę ś ci zależnoś ci rekurencyjnej i za s tą pić h

1

prze z

liczbę 1. Na s tępuje to po n – 1 ws ta wieniach. Wtedy wyra żenie na h

n

przyjmuje pos tać:

h

n

= 2

n–1

h

1

+ 2

n –2

+ 2

n–3

+ … + 2

2

+ 2 + 1 = 2

n–1

+ 2

n–2

+ 2

n–3

+ … + 2

2

+ 2 + 1

Wartoś ć sumy po pra wej s tronie os tatniej równoś ci jes t liczbą , która w rozwinię cie bina rnym ma n je dynek.
Na s tępna liczba , czyli wię ks za o 1, ma w rozwinięciu binarnym je dynkę na n + 1 pozycji, jes t więc równa 2

n

.

Stąd otrzymujemy os tatecznie:

h

n

= 2

n

– 1

tak, jak prze widywa liś my. Z pomocą tej równoś ci rozwią ż tera z ćwicz. 22.

Jedne z na jpopula rniejs zych liczb wys tępujących w informat yce s ą zwią zane z pytaniem, ja kie za warł Leonar-
do Fibonacci w s wojej ks ią żce Liber Abbaci opublikowanej w 1202 roku.

Pytanie Fibonacciego dotyczyło s zybkoś ci rozmna żania się królików. Na początku ma my parę nowona rodzo-
nych królików i o ka żdej parze królików za kła damy, że:

■

nowa para s taje s ię płodna po mies iącu życia;

> Różnorodne algorytmy obliczeń i ich komputerowe realiza cje

< 25 >

■

ka żda płodna pa ra rodzi je dną parę nowych królików w mies iącu;

■

króliki nigdy nie umierają .

Oryginalne pyta nie Fibonacciego brzmia ło: ile bę dzie par królików po roku cza su? Najczęś ciej pyta się , ile bę -
dzie par królików po upływie k mies ięcy – oznaczmy tę liczbę przez F

k

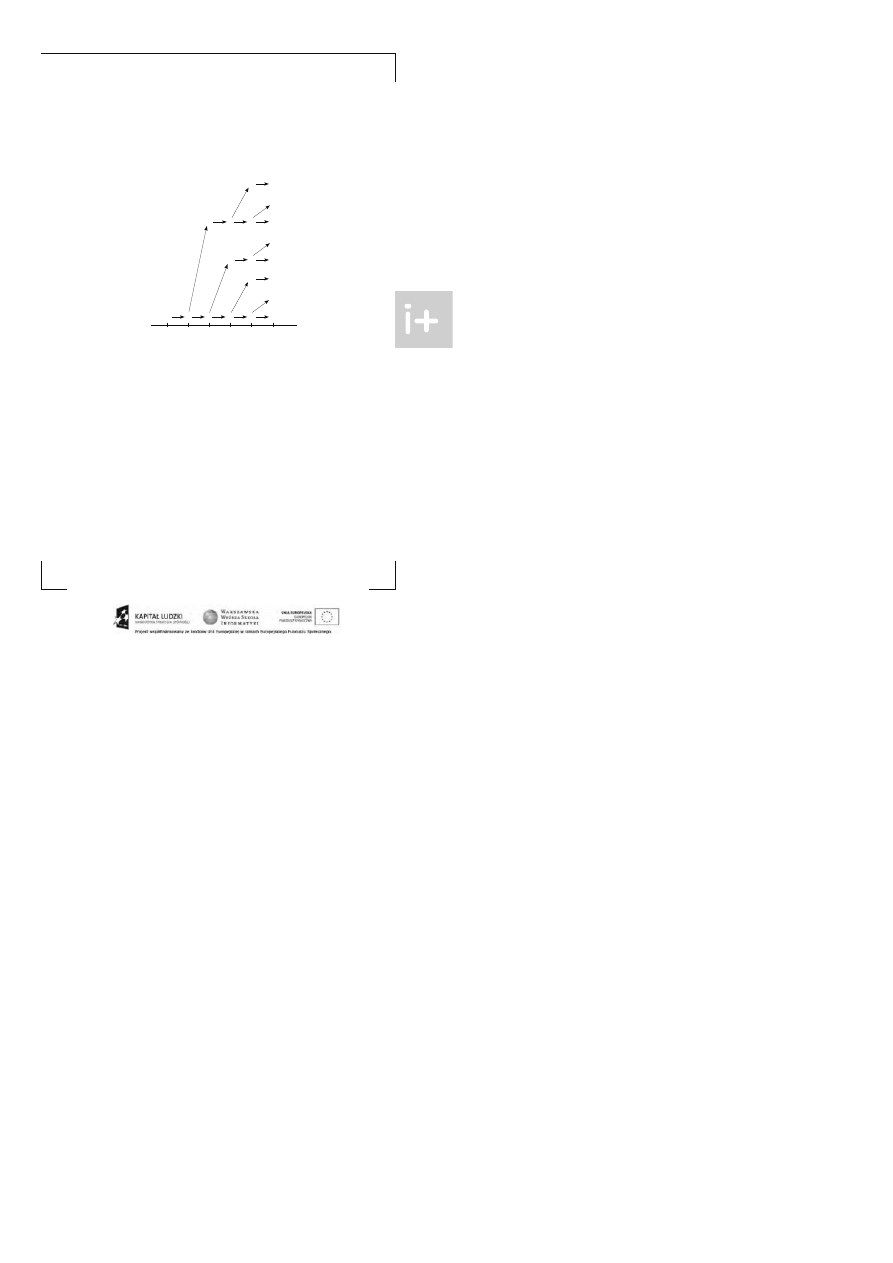
. Na rys . 5 przeds ta wiono rozra s ta nie

się s tada królików w cią gu kilku począ tkowych mie się cy (litera M oznacza pa rę młodych, a litera R – parę roz-
mna żających s ię już królików). W pierws zym i drugim mies iącu mamy tylko je dną parę , z tym że w drugim mie -
sią cu może ona dać już parę młodych. Za tem w trze cim mie siącu s ą już dwie pary, przy czym tylko ta s tars za
może da lej rodzić młode. Stąd, w czwa rtym miesiącu s ą już trzy pary, z których dwie , a więc tyle , ile było już
w poprze dnim mies iącu, mogą rodzić. Czyli w na s tępnym mie siącu mamy te trzy pary i dwie pary młodych, ra -
zem pię ć par. I tak da lej. Otrzymujemy więc ciąg liczb: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 itd.

M

R

M

M

R

R

R

M

M

R

R

M

R

M

M

R

R

R

R

R

miesiąc k

1

2

3

4

5

6

liczba par królików F

k

1

1

2

3

5

8

Rysunek 5.
Sche ma t rozra s tania się s ta da królików w orygina lnym pyta niu Fibonaccie go. M oznacza parę młodych, a R
oznacza parę dorosłych, czyli rozmna żają cych się królików

Z tego przykładu i z wa runków rozmna żania s ię królików wnioskujemy, że w kolejnym mies iącu liczba pa r kró-
lików będzie równa liczbie pa r z poprze dnie go mie sią ca , gdyż króliki nie wymiera ją , plus liczba par nowona ro-
dzonych królików, a tych jes t tyle, ile było par dwa mies iące wcze śniej. Za tem kolejna liczba Fibonacciego jes t
sumą dwóch poprzednich liczb Fibona cciego. Stos ują c oznaczenie na liczbę pa r królików w da nym mie sią cu,
ten wnios ek można zapis ać w na s tę pują cej pos taci F

k

= F

k–1

+ F

k–2

, gdzie k je s t równe przyna jmniej 3, a by moż-

na s ię było odwoływa ć do poprze dnich miesięcy. Mus imy za tem wartoś ci dwóch pierws zych liczb Fibona ccie -
go zde finiowa ć os obno i wpros t, nie odwołując się do ża dnych innych wartoś ci tego cią gu. Z tych rozwa żań
wynika wię c na s tę pująca pos ta ć liczb Fibona ccie go:

1 k = 1, 2

F

k

=

{

F

k–1

+ F

k–2

k ≥ 3

Ten wzór ma pos tać zale żnoś ci rekurencyjne j i można go za s tosować do oblicza nia wa rtoś ci dowolne j liczby
Fibonaccie go. Imple menta cja wzoru rekure ncyjne go w ję zyku Pa scal jes t niemal automa tyczna

function FibRek(k:integer):integer;

{Wartoscia funkcji jest k-ta liczba Fibonacciego, obliczona