
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
1
Olga Kopacz, Adam Łodygowski, Wojciech Pawłowski,
Michał Płotkowiak, Krzysztof Tymber
Konsultacje naukowe: prof. dr hab. J
ERZY
R
AKOWSKI
Poznań 2002/2003
MECHANIKA BUDOWLI 4
RÓWNANIE PRACY WIRTUALNEJ
Rozdział ten poświęcony jest wyprowadzeniu twierdzenia o pracy wirtualnej,
przygotowanej. W dalszej jego części omówimy praktyczne zastosowanie tego twier-
dzenia.
Słowa kluczowe: praca wirtualna, przemieszczenie wirtualne
1. TWIERDZENIE 1
1.1. Twierdzenie
Jeżeli na układ działa obciążenie rzeczywiste spełniające (warunki równo-
wagi), to obciążenie zewnętrzne wykonuje na przemieszczeniu wirtualnym pracę
równą pracy uogólnionych sił przekrojowych na wirtualnych odkształceniach
(na wirtualnych przemieszczeniach wewnętrznych).
1.2. Interpretacja
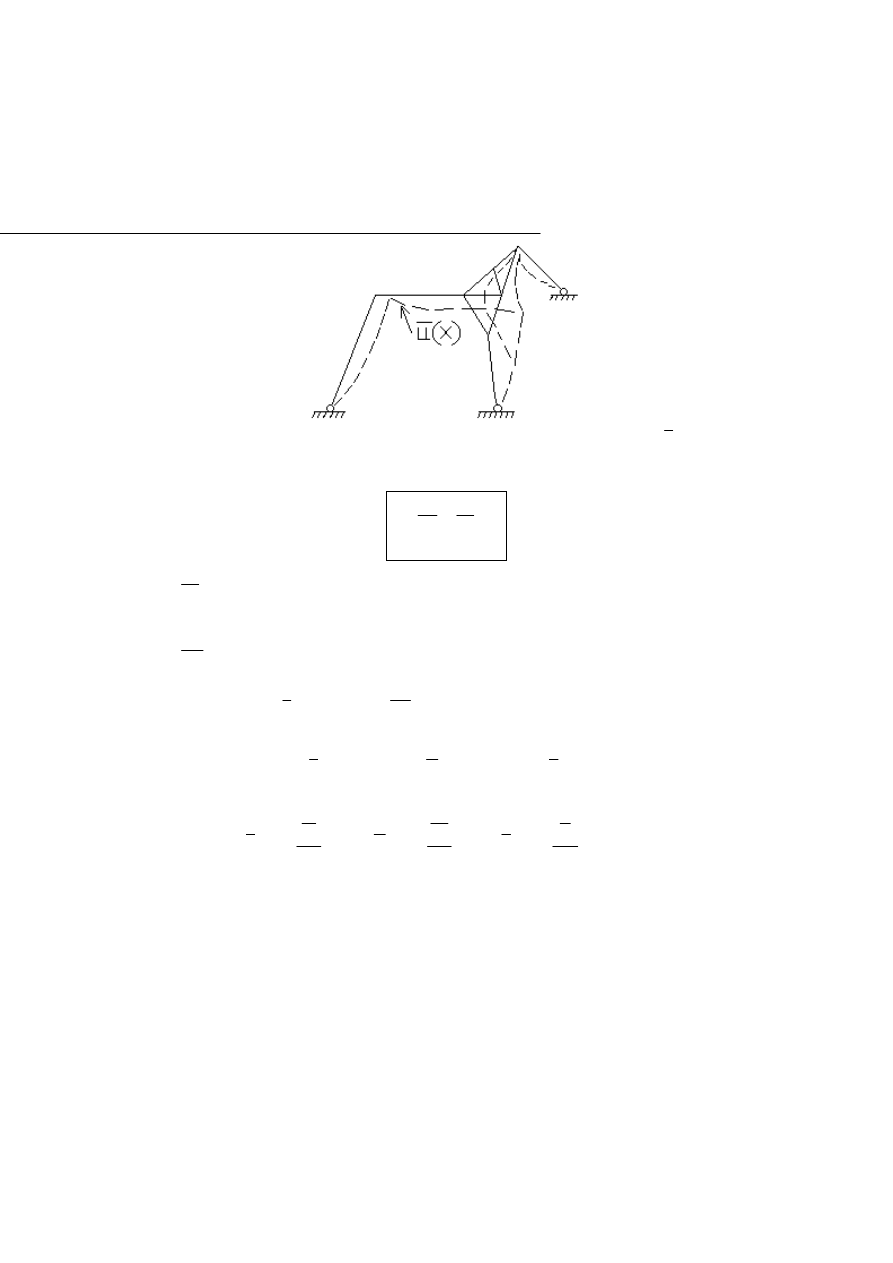
Przyjmujemy dowolny układ pozostający w równowadze
Rys.1.2.1. Rzeczywisty model układu prętowego, obciążony rzeczywistymi siłami
)
(x
p
pod wpływem, których doznaje przemieszczeń
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
2
Rys.1.2.2. Ten sam układ ale z wymuszonym przemieszczeniem wirtualnym
)
(x
u
(kinematycznie dopuszczalnym)
z
w
L
L
=
z
L
- praca wszystkich rzeczywistych sił czynnych obciążających układ oraz
biernych pracujących na przemieszczeniach wirtualnych (wymuszonych
kinematycznie)
W
L
- praca wszystkich sił wewnętrznych rzeczywistych na odkształceniach
wirtualnych (na wirtualnych przemieszczeniach wewnętrznych)
∑
∫
∫
∫
∑
∑∫
+
+
=
=
∆
+
n
s
s
s
k
k
k
n s
dx
x
x
T
dx
x
x
M
dx
x
x
N
R
dx
x
u
x
p
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
γ
κ
χ
ε
(1.2.1)
przy czym:
EA
N
x
=
)
(
ε
,
EJ
M
x
=
)
(
χ
,
GA
T
x
=
)
(
γ
(1.2.2)
1.3. Wyprowadzenie
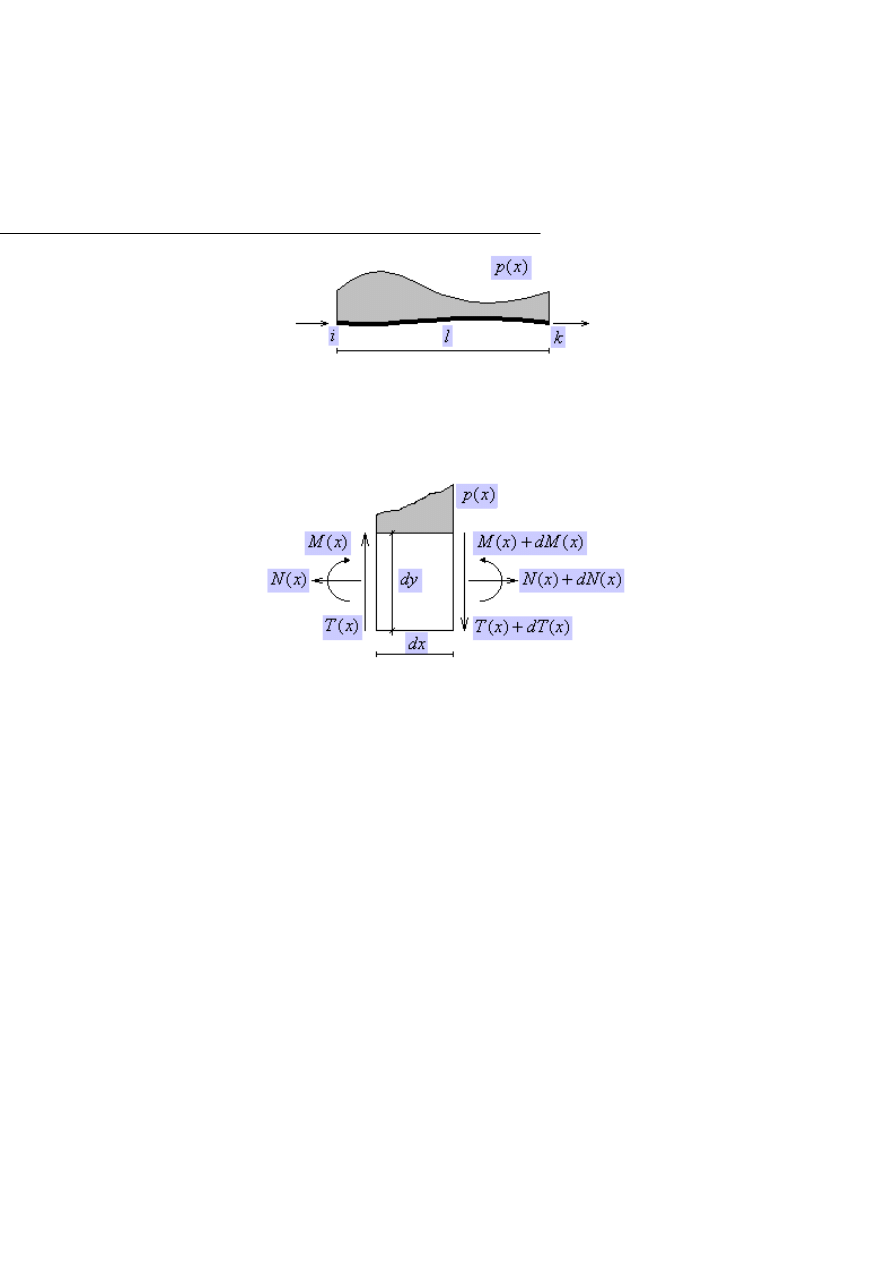
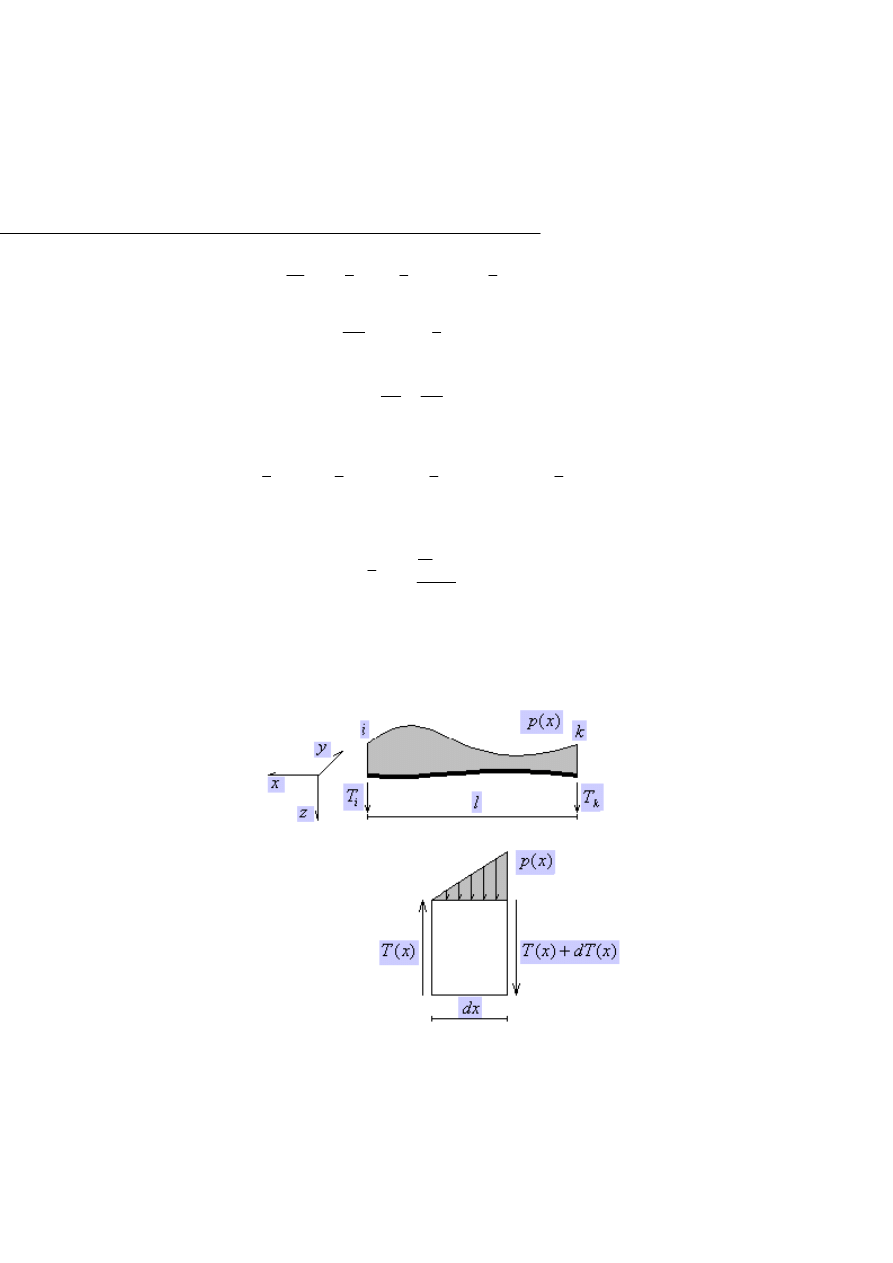
Przyjmujemy dowolny pręt (Rys.1.3.1.) o długości skończonej l i końcach
i,k oraz dowolnie obciążony siłami zewnętrznymi p(x):
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
3
Rys.1.3.1.
Wyobraźmy sobie następnie bardzo mały fragment tego pręta o długości dx
(Rys.1.3.2.). Działają na niego siły uogólnione wewnętrzne przyjmujące
dowolną kombinację normalnych, tnących i momentów.
Rys.1.3.2.
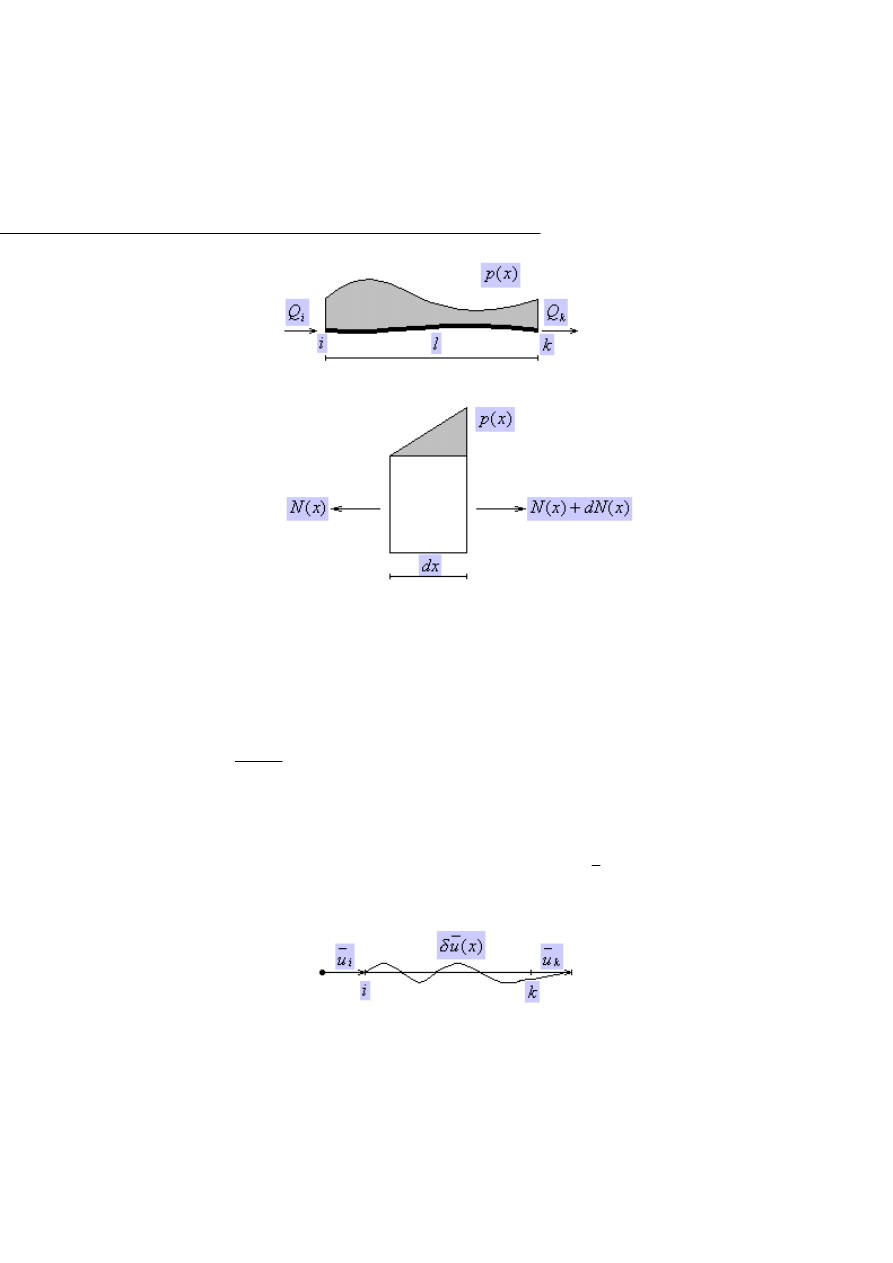
Upraszczając obliczenia sprowadzamy tę sytuację do następujących
przypadków:
1) Zakładamy, że dowolne obciążenie pręta siłą p(x) powoduje powstanie
tylko sił biernych poziomych Q
i
i Q
k
,
wobec czego na nasz element dx będzie
działała tylko uogólniona siła normalna (podłużna, osiowa) N(x) (Rys.1.3.3.):
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
4
Rys.1.3.3.
Zapisując równanie równowagi dla tego elementu (tzn. w każdym punkcie tego
pręta) otrzymujemy zapis:
0
)
(
)
(
:
/
0
)
(
)
(
0
)
(
)
(
)
(
)
(
0
=
+
=
+
=
+
−
+
⇒
=
∑
x
p
dx
x
dN
dx
dx
x
p
x
dN
dx
x
p
x
N
x
dN
x
N
X
(1.3.1)
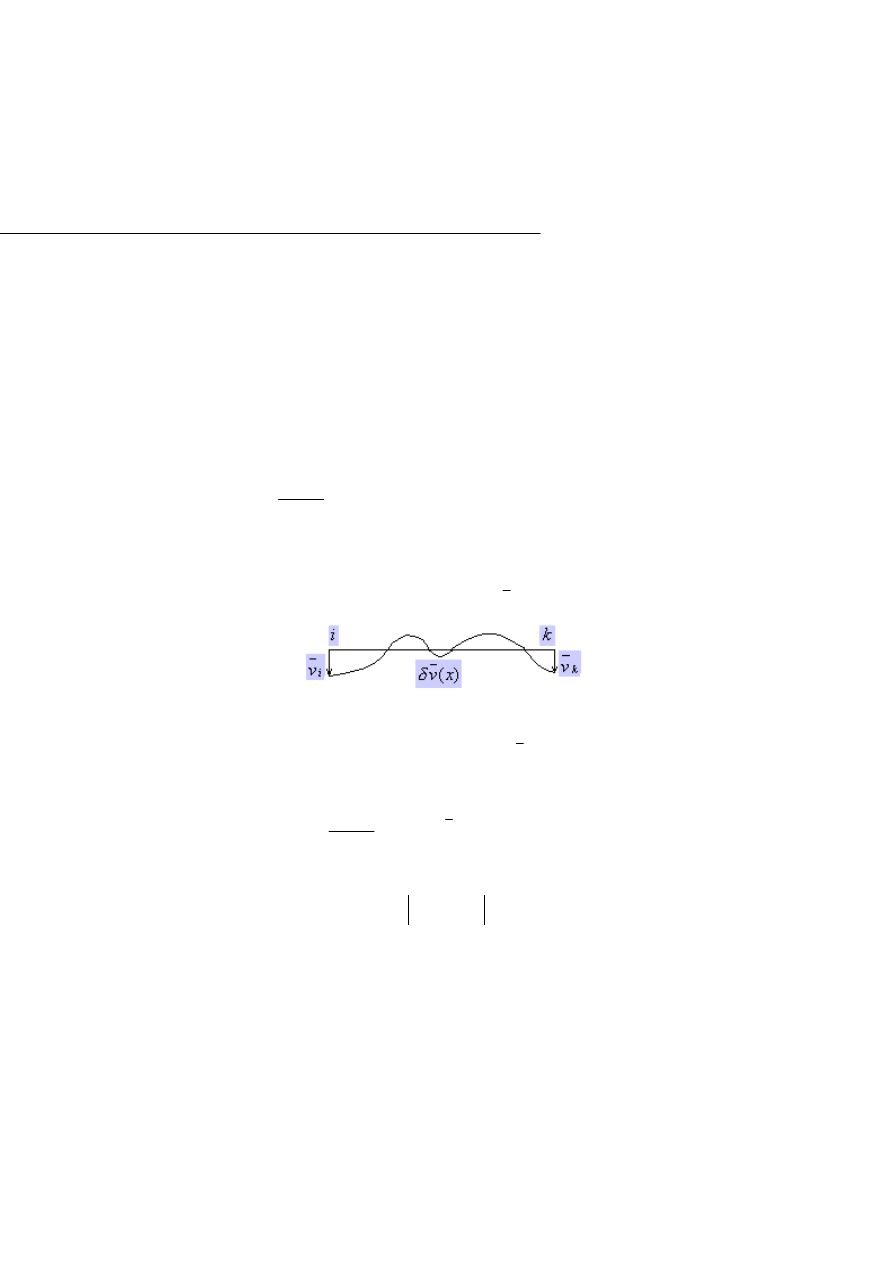
Następnie wprowadzamy do tego pręta pewne wirtualne przemieszczenie
(Rys.1.3.4.), zgodne z działaniem uogólnionych sił normalnych. Pamiętajmy, że
musi ono spełnić warunek kinematycznej dopuszczalności, musi być niezależne
od wszelkich obciążeń zewnętrznych oraz od czasu, małe w porównaniu z
wymiarami pręta i ciągłe. Przyjmiemy jego wartość równą:
)
(x
u
δ

W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
5
Rys.1.3.4.
Pomnóżmy równanie (1.3.1) obustronnie przez
)
(x
u
δ
i scałkujmy w granicach
od x = 0 do x =
L
0
)
(
)
(
)
(
)
(
0
)
(
)
(
)
(
0
)
(
)
(
)
(
0
0
0
=
+
=
+
=
+
∫
∫
∫
l
l
l
dx
x
p
x
u
dx
dx
x
dN
x
u
dx
x
p
dx
x
dN
x
u
x
u
x
p
dx
x
dN
δ
δ
δ
δ
(1.3.2)
aby obliczyć całkę:
∫
l
dx
dx
x
dN
x
u
0
)
(
)
(
δ
skorzystamy z całkowania przez części,
∫
∫
−
=
vdz
zv
zdv
)
(x
u
z
δ
=
dx
dx
x
dN
dv
)
(
=
dx
x
u
d
dz
))
(
(
δ
=
)
(
)
(
x
N
dx
dx
x
dN
v
=
=
∫
∫
∫
−
=
l
l
l
dx
dx
x
u
d
x
N
x
N
x
u
dx
x
dN
x
u
0
0
0
))
(
(
)
(
)
(
)
(
)
(
)
(
/
δ
δ
δ
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
6
Równanie (1.3.2) uzyska więc postać:
0
)
(
)
(
))
(
(
)
(
)
(
)
(
0
0
0
/
=
+
−
∫
∫
dx
x
u
x
p
dx
dx
x
u
d
x
N
x
N
x
u
l
l
l
δ
δ
δ
(
)
dx
dx
x
u
d
x
N
x
u
x
p
u
Q
u
Q
dx
x
u
x
p
dx
dx
x
u
d
x
N
u
N
u
N
l
l
i
i
k
k
l
l
L
L
∫
∫
∫
∫
=
+
−
−
=
+
−
−
0
0
0
0
0
0
))
(
(
)
(
)
(
)
(
0
)
(
)
(
))
(
(
)
(
δ
δ
δ
δ
δ
δ
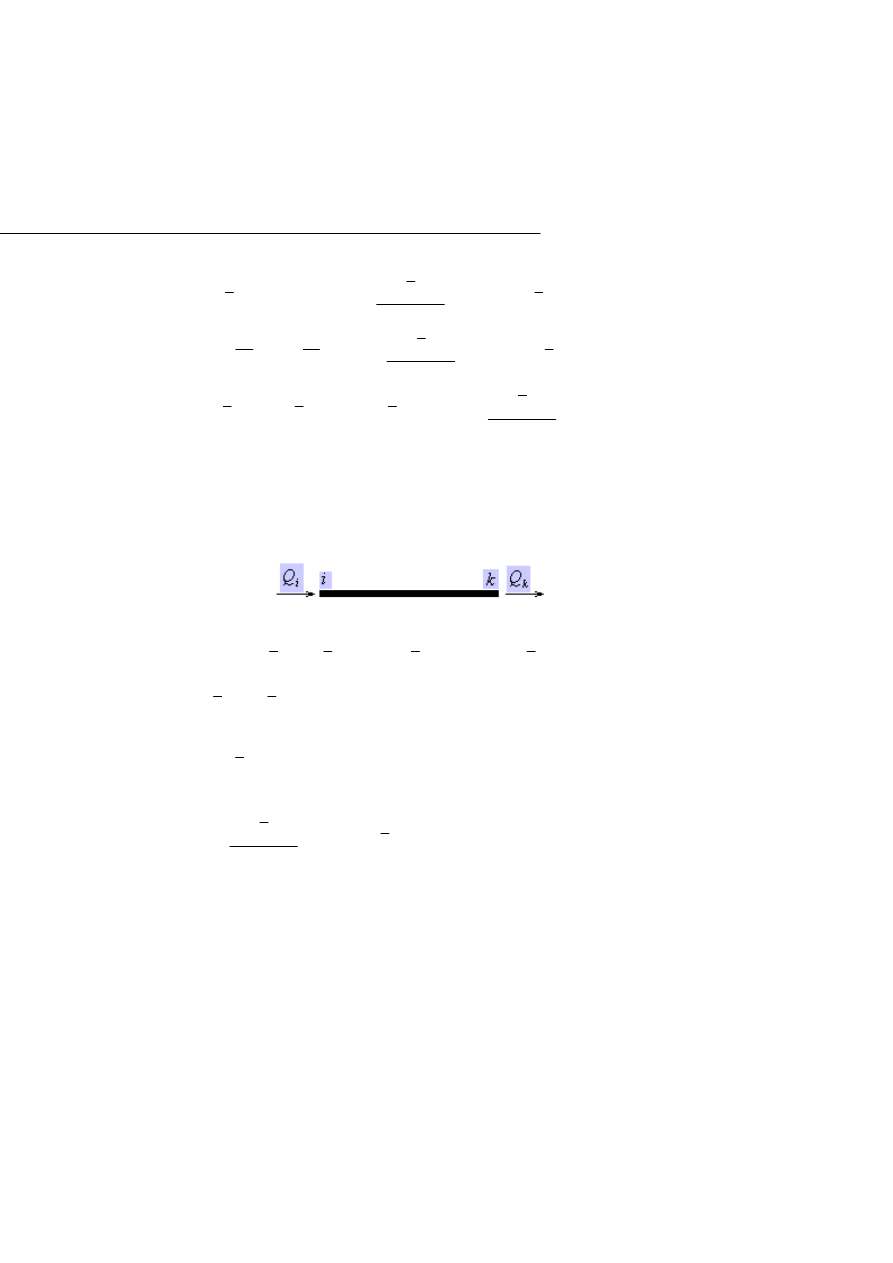
Znaki wynikają z tego, że znak dodatni siły N
0
jest przeciwny do
założonego dodatniego Q
i
a znak dodatni siły N
L
jest zgodny z
założonym dodatnim Q
k
(Na rys 1.3.5. przyjęto zasadę zgodności
dodatnich zwrotów sił Q
i
i Q
k
oraz przemieszczeń im odpowiada-
jących)
(1.3.3)
Rys.1.3.5. Znakowanie
∫
∫
=
+
+
l
l
i
i
k
k
dx
x
x
N
dx
x
u
x
p
u
Q
u
Q
0
0
)
(
)
(
)
(
)
(
ε
δ
i
i
k
k
u
Q
u
Q
+
- całkowita praca sił zewnętrznych (biernych) na
przemieszczeniach wirtualnych
dx
x
u
x
p
l
∫
0
)
(
)
(
δ
- całkowita praca sił zewnętrznych (czynnych) na
przemieszczeniach wirtualnych
∫
∫
=
l
l
dx
x
x
N
dx
dx
x
u
d
x
N
0
0
)
(
)
(
))
(
(
)
(
ε
δ
- całkowita praca sił we-
wnętrznych (normalnych) na odkształceniach wirtualnych (na wirtual-
nych przemieszczeniach wewnętrznych)
(1.3.4)
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
7
Wobec oznaczeń:
∫
+
+
=
l
i
i
k
k
z
dx
x
u
x
p
u
Q
u
Q
L
0
)
(
)
(
δ
∫
=
l
W
dx
x
x
N
L
0
)
(
)
(
ε
mamy:
W
Z
L
L
=
(1.3.5)
Wniosek:
∫
∑
∑
∑
=
+
+
l
n
n
n
i
i
i
j
j
j
dx
x
x
N
dx
x
u
x
q
u
P
u
Q
0
)
(
)
(
)
(
)
(
ε
Warto zaznaczyć, że we wzorze tym nadal obowiązują zależności
fizyczne odpowiadające stanowi wirtualnemu:
EA
x
N
x
)
(
)
(
=
ε
(1.3.6)
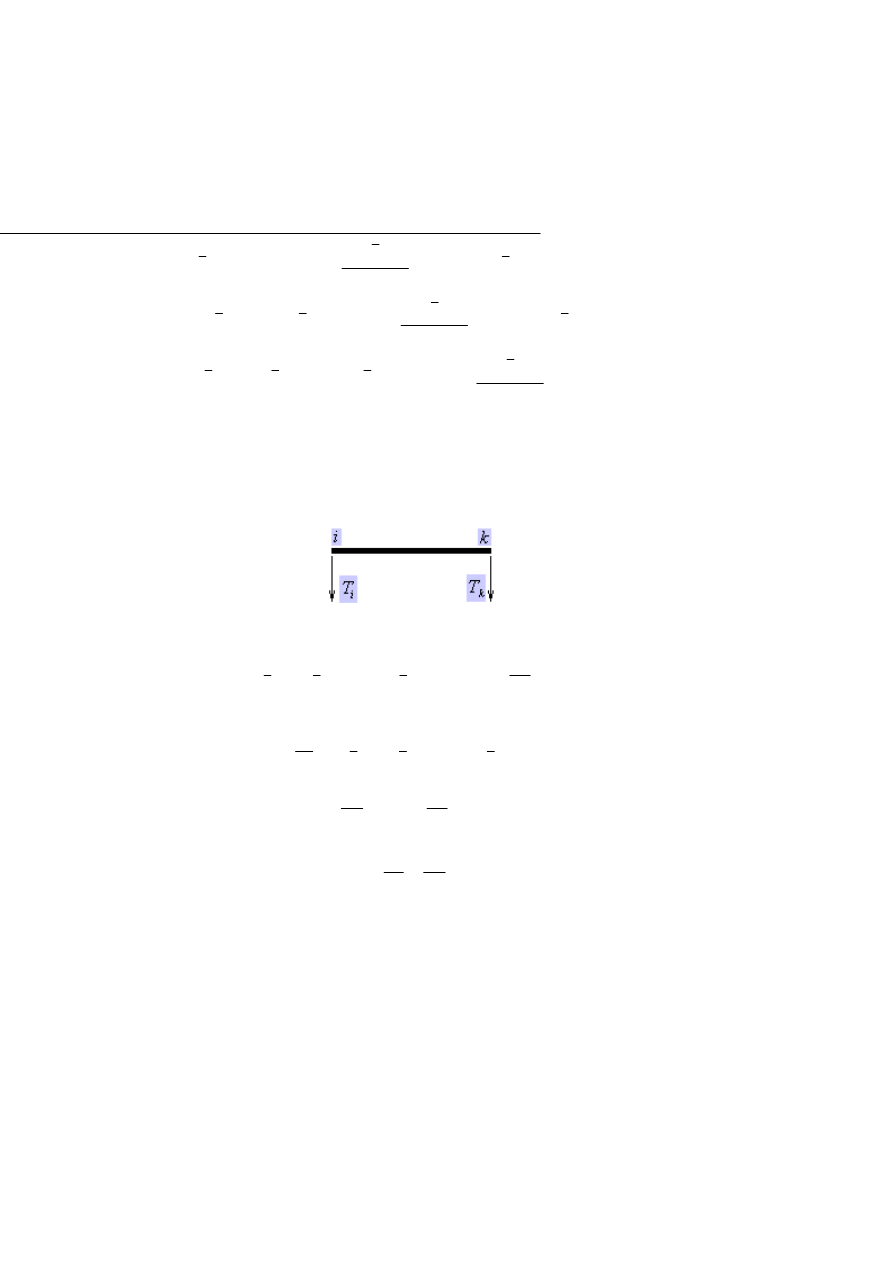
2) Zakładamy, że dowolne obciążenie pręta siłą p(x) powoduje powstanie
sił biernych pionowych T
i
i T
k
, wobec czego na nasz element dx będzie działała
uogólniona siła tnąca (poprzeczna) T(x) (Rys.1.3.6.):
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
8
Rys.1.3.6.
Zapisując równanie równowagi dla tego elementu (tzn. w każdym punkcie tego
pręta), otrzymujemy:
0
)
(
)
(
/
0
)
(
)
(
0
)
(
)
(
)
(
)
(
0
=
+
=
+
=
+
+
+
−
=
∑
x
p
dx
x
dT
dx
dx
x
p
x
dT
dx
x
p
x
dT
x
T
x
T
Z
(1.3.7)
Następnie wprowadzamy do tego pręta wirtualne przemieszczenie (spełniające te
same warunki, co wcześniej) zgodne z działaniem uogólnionych sił poprzecz-
nych (tnących), o niezerowej wartości równej:
)
(x
v
δ
Rys.1.3.7.
Pomnóżmy równanie (1.3.7) obustronnie przez
)
(x
v
δ
i scałkujmy w granicach
od x = 0 do x =
L
0
)
(
)
(
)
(
=
+
x
v
x
p
dx
x
dT
δ
(1.3.8)
Stosując przekształcenia jak wcześniej z tym, że w całkowaniu przez części bę-
dzie:
)
(x
T
v
=
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
9
(
)
∫
∫
∫
∫
∫
∫
=
+
−
−
=
+
−
−
=
+
−
l
l
i
i
k
k
l
l
L
L
l
l
l
dx
dx
x
v
d
x
T
dx
x
v
x
p
v
T
v
T
dx
x
v
x
p
dx
dx
x
v
d
x
T
x
v
T
x
v
T
dx
x
v
x
p
dx
dx
x
v
d
x
T
x
T
x
v
0
0
0
0
0
0
0
0
0
))
(
(
)
(
)
(
)
(
0
)
(
)
(
))
(
(
)
(
)
(
)
(
0
)
(
)
(
))
(
(
)
(
)
(
)
(
/
δ
δ
δ
δ
δ
δ
δ
δ
δ
Znaki wynikają z tego, że znak dodatni siły T
0
jest przeciwny do założo-
nego dodatniego T
i
a znak dodatni siły T
L
jest zgodny z założonym do-
datnim T
k
(Na rys 1.3.8. przyjęto zasadę zgodności dodatnich zwrotów
sił T
i
i T
k
oraz przemieszczeń im odpowiadających)
(1.3.9)
Rys.1.3.8. Znakowanie
∫
∫
=
+
+
l
sr
l
i
i
k
k
ds
x
x
T
ds
x
v
x
p
v
T
v
T
0
0
)
(
)
(
)
(
)
(
γ
δ
Wobec oznaczeń:
∫
+
+
=
l
i
i
k
k
z
dx
x
v
x
p
v
T
v
T
L
0
)
(
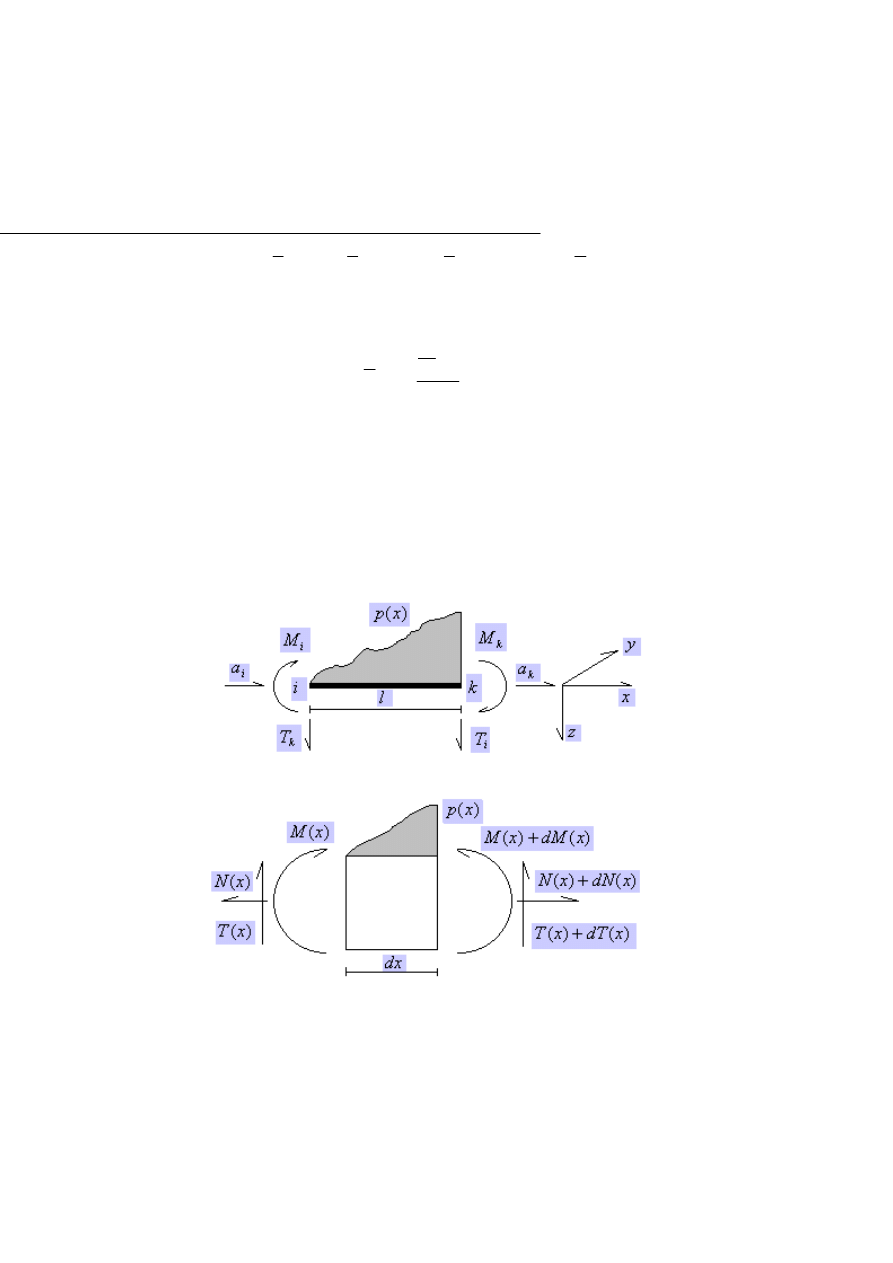
)
(
δ
∫
=
l
sr
W
dx
x
x
T
L
0
)
(
)
(
γ
mamy:
W
Z
L
L
=
(1.3.10)
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
10
Wniosek:
∫
∑
∑
∑
=
+
+
l
sr
n
n
n
i
i
i
j
j
j
dx
x
x
T
dx
x
v
x
q
v
P
v
T
0
)
(
)
(
)
(
)
(
γ
gdzie:
γ
κ
γ =
sr
Warto zaznaczyć, że we wzorze tym nadal obowiązują zależności fi-
zyczne odpowiadające stanowi wirtualnemu:
EA
x
T
x
)
(
)
(
=
γ
(1.3.11)
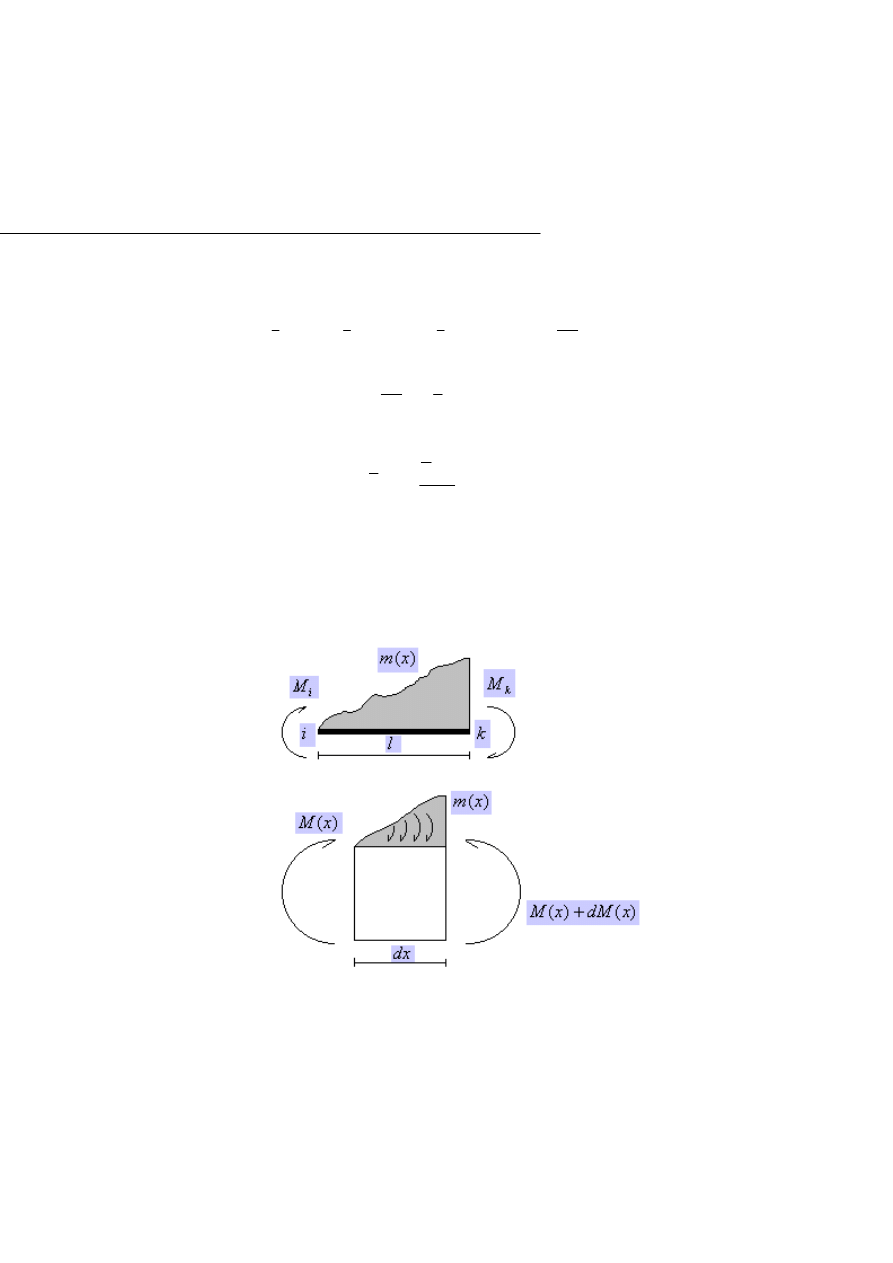
3) Zakładamy czyste zginanie tzn. dowolne obciążenie pręta m(x) powodu-
je powstanie tylko sił biernych w postaci momentów zginających M
i
i M
k
, stąd
na nasz myślowo wycięty element będzie działał tylko uogólniony moment
zginający M(x) (Rys.1.3.9.):
Rys.1.3.9.
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
11
Zapisując równanie równowagi otrzymujemy:
0
)
(
)
(
)
/(
0
)
(
)
(
0
)
(
)
(
)
(
)
(
0
=
−
−
=
+
−
=
+
−
−
=
∑
x
m
dx
x
dM
dx
dx
x
m
x
dM
dx
x
m
x
dM
x
M
x
M
M
(1.3.12)
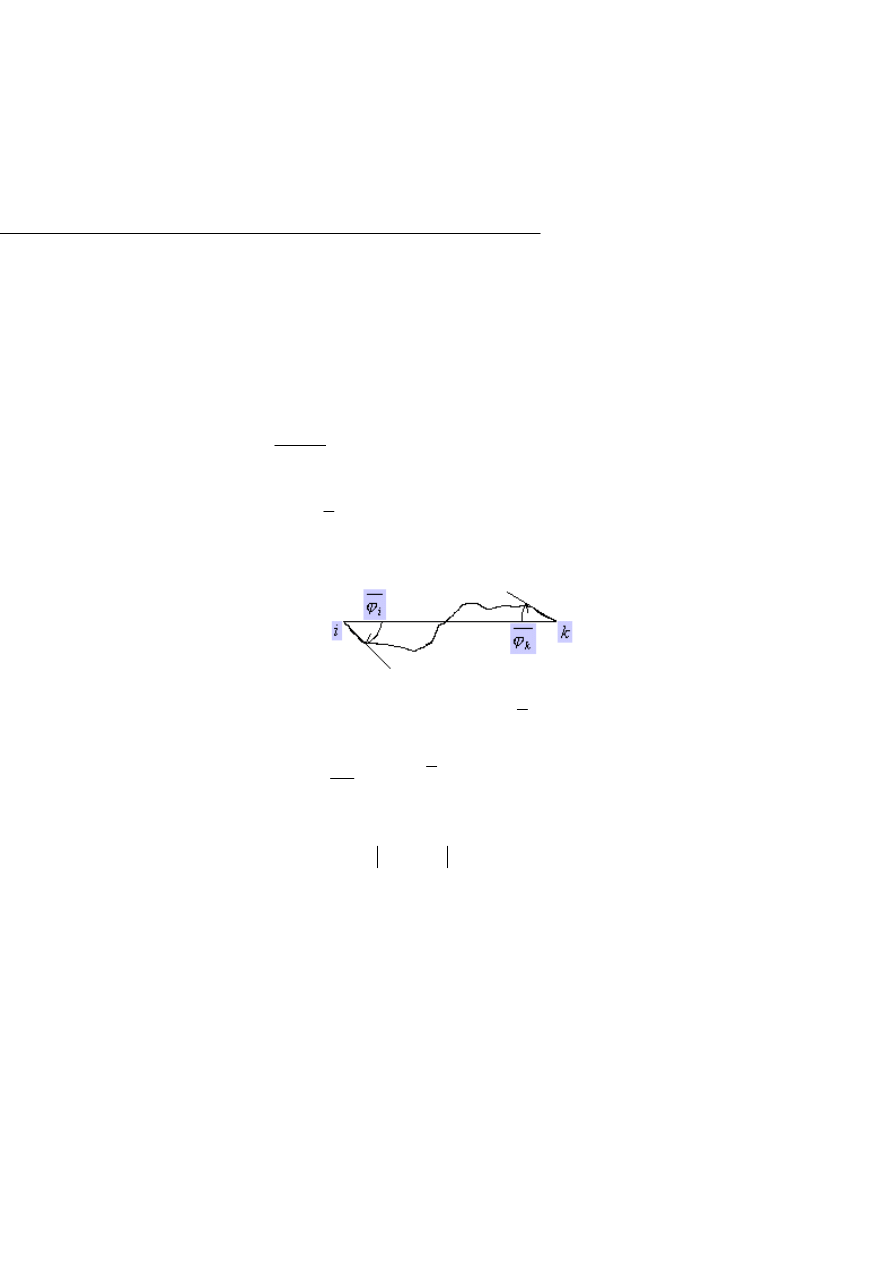
Postępując analogicznie jak w poprzednich przypadkach, wprowadzamy wirtual-
ne przemieszczenie zgodne z działaniem uogólnionych momentów zginających
o wartości równej:
)
(x
ϕ
δ
Rys.1.3.10.
Pomnóżmy równanie (1.3.12) obustronnie przez
)
(x
ϕ
δ
i scałkujmy w granicach
od x = 0 do x =
L
0
)
(
)
(
=
−
x
x
m
dx
d
ϕ
δ
ϕ
(1.3.13)
Stosując przekształcenia jak wcześniej z tym, że w całkowaniu przez części bę-
dzie:
)
(x
M
v
=
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
12
)
1
/(
))
(
(
)
(
)
(
)
(
0
)
(
)
(
))
(
(
)
(
)
(
)
(
0
)
(
)
(
))
(
(
)
(
)
(
)
(
0
0
0
0
0
0
0
0
0
/
−
−
=
−
−
−
=
−
+
−
=
−
+
∫
∫
∫
∫
∫
∫
l
l
i
i
k
k
l
l
L
L
l
l
l
dx
dx
x
d
x
M
dx
x
x
m
M
M
dx
x
x
m
dx
dx
x
d
x
M
x
M
x
M
dx
x
x
m
dx
dx
x
d
x
M
x
M
x
ϕ
δ
ϕ
δ
ϕ
ϕ
ϕ
δ
ϕ
δ
ϕ
δ
ϕ
δ
ϕ
δ
ϕ
δ
ϕ
δ
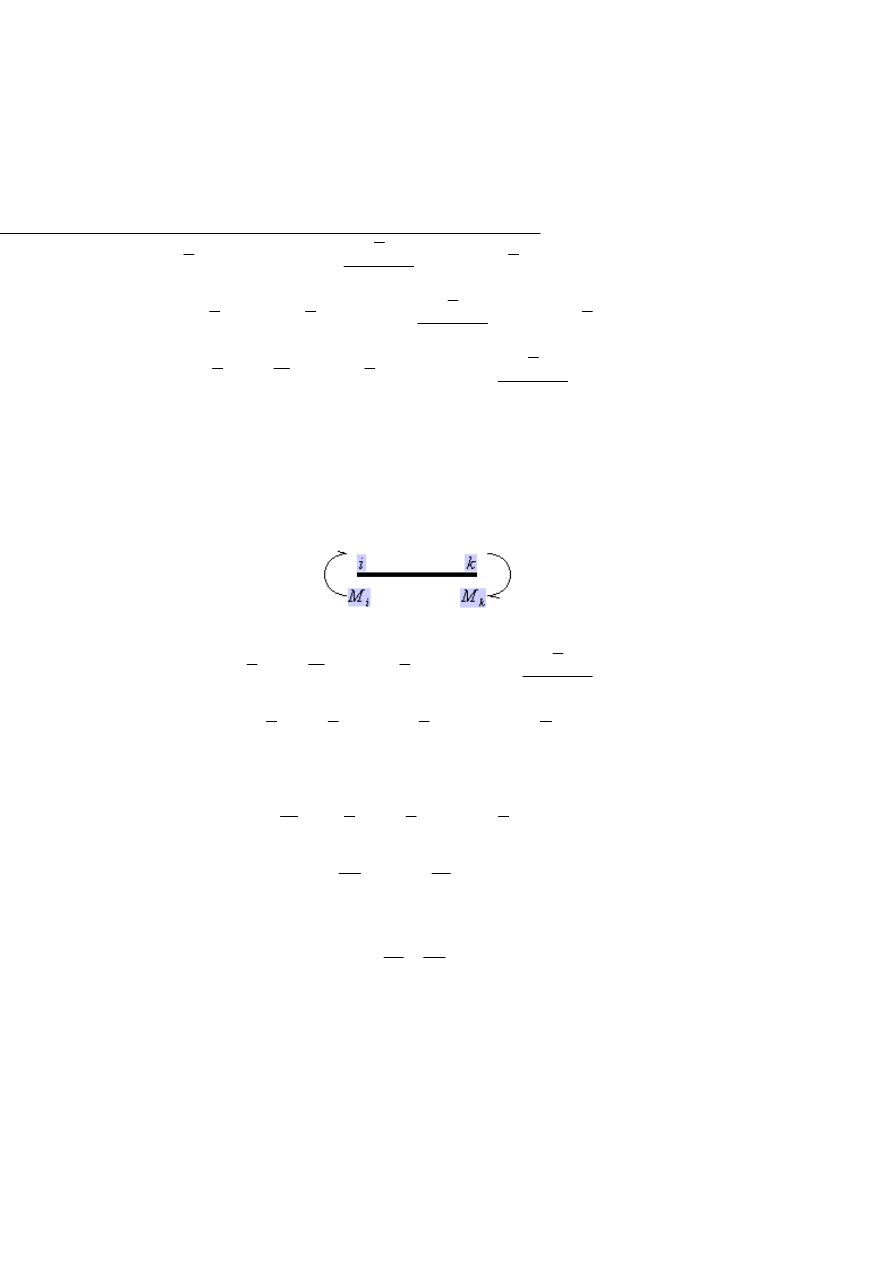
Znaki wynikają z tego, że dodatni moment M
0
jest zgodny z założonym
dodatnim momentem M
i
a dodatni moment M
L
jest przeciwny do założone-
go dodatniego M
k
(Na rys 1.3.11. przyjęto zasadę zgodności dodatnich
zwrotów M
i
i M
k
oraz przemieszczeń im odpowiadających)
Rys.1.3.11. Znakowanie
∫
∫
=
+
+
l
l
i
i
k
k
dx
dx
x
d
x
M
dx
x
x
m
M
M
0
0
))
(
(
)
(
)
(
)
(
ϕ
δ
ϕ
δ
ϕ
ϕ
∫
∫
=
+
+
l
l
i
i
k
k
dx
x
x
M
dx
x
x
m
M
M
0
0
)
(
)
(
)
(
)
(
χ
ϕ
δ
ϕ
ϕ
(1.3.14)
Wobec oznaczeń:
∫
+
+
=
l
i
i
k
k
z
dx
x
x
m
M
M
L
0
)
(
)
(
ϕ
δ
ϕ
ϕ
∫
=
l
W
dx
x
x
M
L
0
)
(
)
(
χ
mamy:
W
Z
L
L
=
(1.3.15)
Wniosek:
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
13
∫
∑
∑
∑
=
+
+
l
n
n
n
i
i
i
j
j
j
dx
x
x
M
dx
x
x
q
P
M
0
)
(
)
(
)
(
)
(
χ
ϕ
ϕ
ϕ
Warto zaznaczyć, że we wzorze tym nadal obowiązują zależności fi-
zyczne odpowiadające stanowi wirtualnemu:
EA
x
M
x
)
(
)
(
=
χ
(1.3.16)
4) Zakładamy, że dowolne obciążenie pręta p(x) powoduję powstanie do-
wolnych sił biernych w postaci uogólnionych sił poziomych, pionowych i
momentów zginających (Rys.1.2.9.):
Rys.1.3.12.

W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
14
Zapisując równania równowagi dla tego elementu (tzn. w każdym punkcie tego
pręta), otrzymujemy:
⇒
=
⇒
=
⇒
=
∑
∑
∑
0
0
0
M
Y
X
jak wcześniej z tym, że moment od sił tnących pomijamy, gdyż ramię
tych sił jest bliskie zeru.
(1.3.17)
Podsumowując: korzystając z zasady superpozycji dokonujemy sumowania po-
wyższych rozwiązań:
∑
∫
∫
∫
∑
∑
∑
+
+
=
=
+
+
∆
n
s
s
s
n
n
i
i
i
j
j
j
dx
x
M
dx
x
T
dx
x
N
dx
x
u
x
q
u
P
R
χ
γ
κ
ε
)
(
)
(
)
(
)
(
)
(
praca sił zewnętrznych = praca sił wewnętrznych na
na przemieszczeniach wirtualnych odkształceniach wirtualnych
gdzie:
∑
∆
j
j
j
R
- całkowita praca sił biernych (reakcji) na przemieszcze-
niach (osiadaniach) wirtualnych
∑
i
i
i
u
P
- całkowita praca sił skupionych na przemieszczeniach
wirtualnych
∑
n
n
dx
x
u
x
q
)
(
)
(
- całkowita praca obciążeń ciągłych na przemiesz-
czeniach wirtualnych
Warto zaznaczyć, że we wzorze tym nadal obowiązują zależności fi-
zyczne odpowiadające stanowi wirtualnemu:
EA
x
N
x
)
(
)
(
=
ε
,
EA
x
T
x
)
(
)
(
=
γ
,
EA
x
M
x
)
(
)
(
=
χ
(1.3.18)
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
15
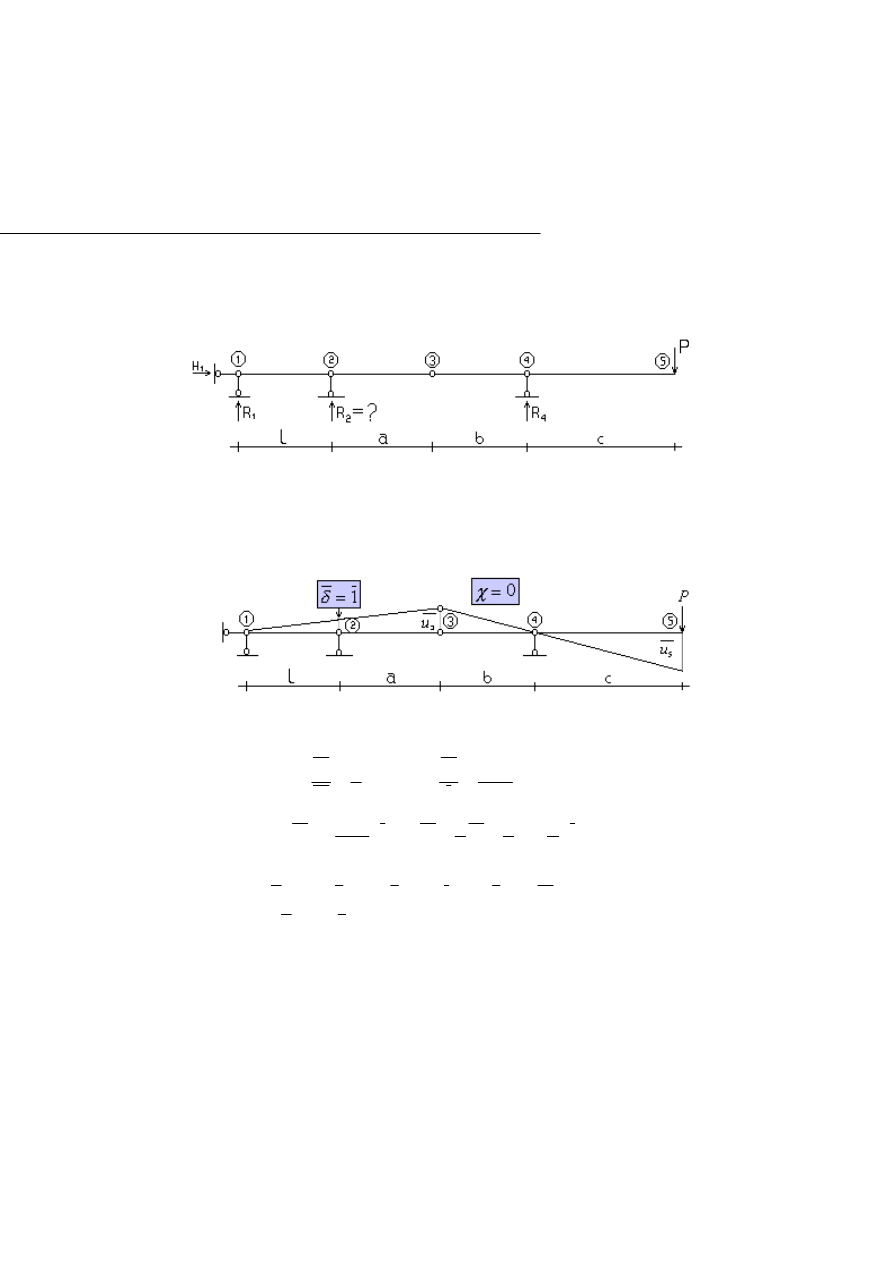
1.4. Przykład
Obliczyć pionową reakcję w punkcie R
2
belki przedstawionej na
Rys.1.4.1.
Rys.1.4.1.
Narzucamy możliwe przemieszczenie wirtualne, o jednostkowej wartości w punk-
cie R
2
(Rys. 1.4.2.).
Rys.1.4.2.
Z proporcji otrzymujemy:
b
c
u
u
=
3
5
v
l
a
l
u
+
=
1
3
1
3
+
=
l
a
l
u
1
1
3
5
+
=
=
l
a
b
c
u
b
c
u
(1.4.1)
Zapisujemy równania prac wirtualnych dla danej belki:
5
4
2
1
1
0
1
0
0
u
P
V
R
H
V
L
Z
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
0
0
1
=
⋅
=
W
L
(1.4.2)
Praca sił wewnętrznych jest równa zeru gdyż:
-
M = 0 – belka to bryła sztywna więc nie doznaje krzywizn (tzn. jej prze-
mieszczenia opisuje funkcja liniowa, której pochodna wynosi zero)

W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
16
-
T = 0 – jeżeli M = 0 to
0
=
=
dx
dM
T
-
N = 0 – nie uwzględniamy wpływu sił poziomych na przemieszczenia
pionowe
Po porównaniu prac otrzymujemy:
1
5
2
u
P
R
−
=
(1.4.3)
a po podstawieniu odpowiednich wartości otrzymujemy szukaną wielkość:
+
−
=
l
a
b
c
P
R
1
2
(1.4.4)
Wniosek:
Ten sam wynik otrzymalibyśmy korzystając z „klasycznych” równań rów-
nowagi.
2. TWIERDZENIE 2
2.1. Twierdzenie 2
Jeżeli na układ działa dowolne zewnętrzne obciążenie wirtualne,
spełniające warunki równowagi to wykonuje ono pracę na rzeczywistych
przemieszczeniach (wywołanych przez rzeczywiste obciążenie zewnętrzne)
równą pracy wirtualnych sił przekrojowych na rzeczywistych odkształceniach
(na rzeczywistych przemieszczeniach wewnętrznych).
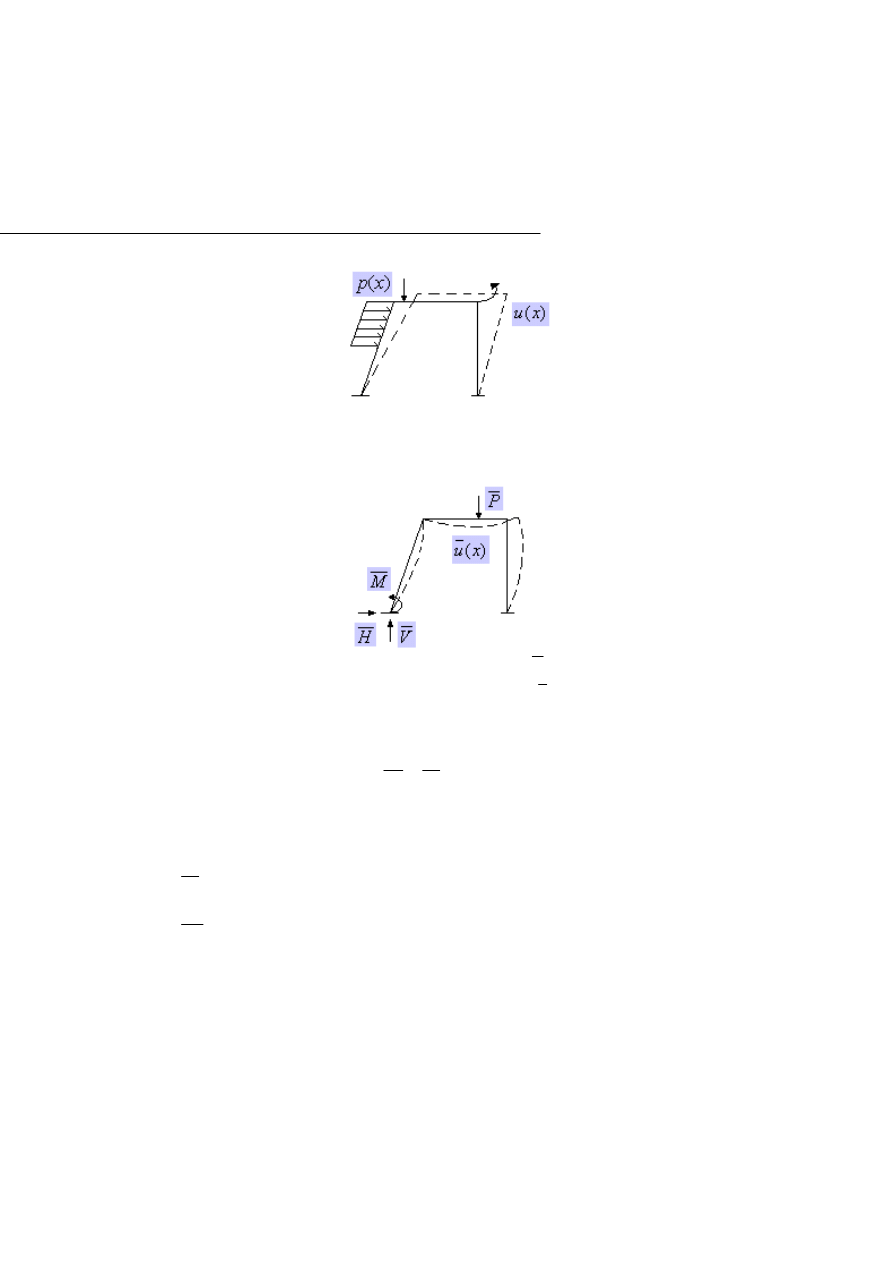
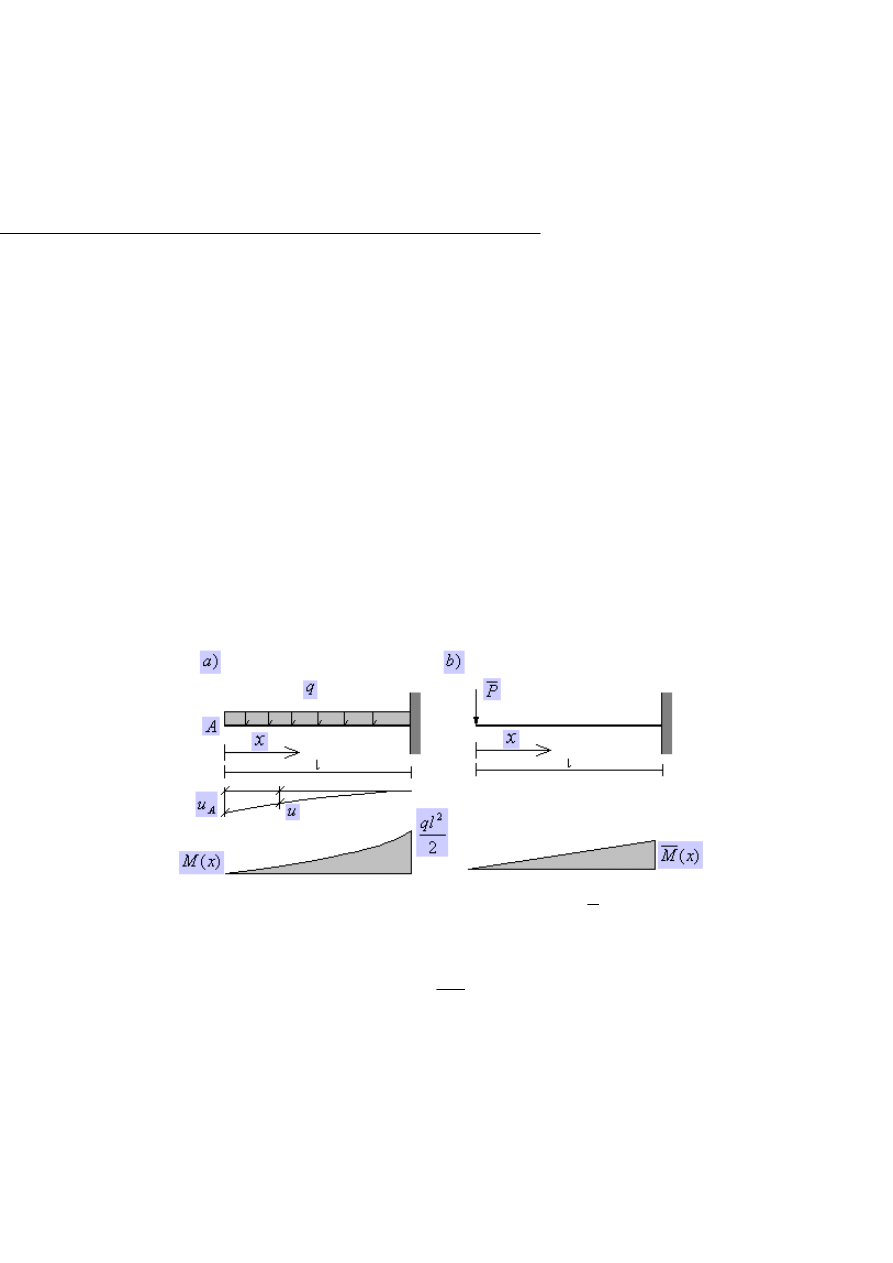
2.2. Interpretacja
Dotychczas korzystaliśmy z twierdzenia, że siły zewnętrzne wykonywały
pracę na wirtualnych przemieszczeniach. Teraz zróbmy odwrotnie tzn. stwórzmy
rzeczywisty model układu (Rys.2.2.1.), a następnie obciążmy go siłami wirtual-
nymi (pomyślanymi) (Rys.2.2.2.) i obliczmy rzeczywiste przemieszczenia nasze-
go układu prętowego. Musimy przy tym zaznaczyć, że wirtualne obciążenie speł-
nia warunki statycznej dopuszczalności, jest niezależne od obciążeń
zewnętrznych rzeczywistych i czasu, a zarazem jest obciążeniem stosunkowo
małym oraz ciągłym (przynajmniej raz różniczkowalnym).
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
17
Rys. 2.2.1. Rzeczywisty model układu prętowego, obciążony rzeczywistymi siłami
)
(x
p
pod wpływem, których doznaje przemieszczeń
Rys. 2.2.2. Ten sam układ, ale obciążony siłą wirtualną
)
(x
P
pod wpływem, której
doznaje przemieszczeń wirtualnym
)
(x
u
z
w
L
L
=
(2.2.1)
z
L
- praca sił wirtualnych pracujących na rzeczywistych przemieszczeniach
(tzn. wytworzonych przez rzeczywiste obciążenia zewnętrzne)
W
L
- praca wszystkich wirtualnych sił wewnętrznych pracujących na rzeczywi-
stych odkształceniach

W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
18
∑
∫
∫
∫
∑
∑∫
+
+
=
=
∆
+
n
s
s
s
k
k
k
n s
dx
x
x
T
dx
x
x
M
dx
x
x
N
R
dx
x
u
x
p
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
γ
κ
χ
ε
Przy czym:
EA
x
N
x
)
(
)
(
=
ε
,
EJ
x
M
x
)
(
)
(
=
χ
,
GA
x
T
x
)
(
)
(
=
γ
(2.2.2)
stąd:
∑
∫
∫
∫
∑
∑∫
+
+
=
=
∆
+
n
s
s
s
k
k
k
n s
dx
GA
x
T
x
T
dx
EJ
x
M
x
M
dx
EA
x
N
x
N
R
dx
x
u
x
p
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
κ
gdzie:
∑
∆
k
k
k
R
- całkowita praca wirtualnych sił biernych (reakcji) na
przemieszczeniach (osiadaniach) rzeczywistych
dx
x
u
x
p
n s
∑∫
)
(
)
(
- całkowita praca wirtualnych obciążeń na rze-
czywistych przemieszczeniach
)
(x
N
- funkcja sił normalnych wywołana od obciążenia ze-
wnętrznego (rzeczywistego)
)
(x
N
- funkcja sił normalnych wywołana od obciążenia wirtualnego
)
(x
T
- funkcja sił poprzecznych wywołana od obciążenia
zewnętrznego (rzeczywistego)
)
(x
T
- funkcja sił poprzecznych wywołana od obciążenia wirtualnego
)
(x
M
- funkcja momentów wywołana od obciążenia zewnętrznego
(rzeczywistego)
)
(x
M
- funkcja momentów wywołana od obciążenia wirtualnego
(2.2.3)
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
19
2.3. Wyprowadzenie
Dowód tego twierdzenia można pominąć, dokonując formalnej zmiany in-
terpretacji czynników iloczynów podcałkowych w równaniu I.
2.4. Przykład 1
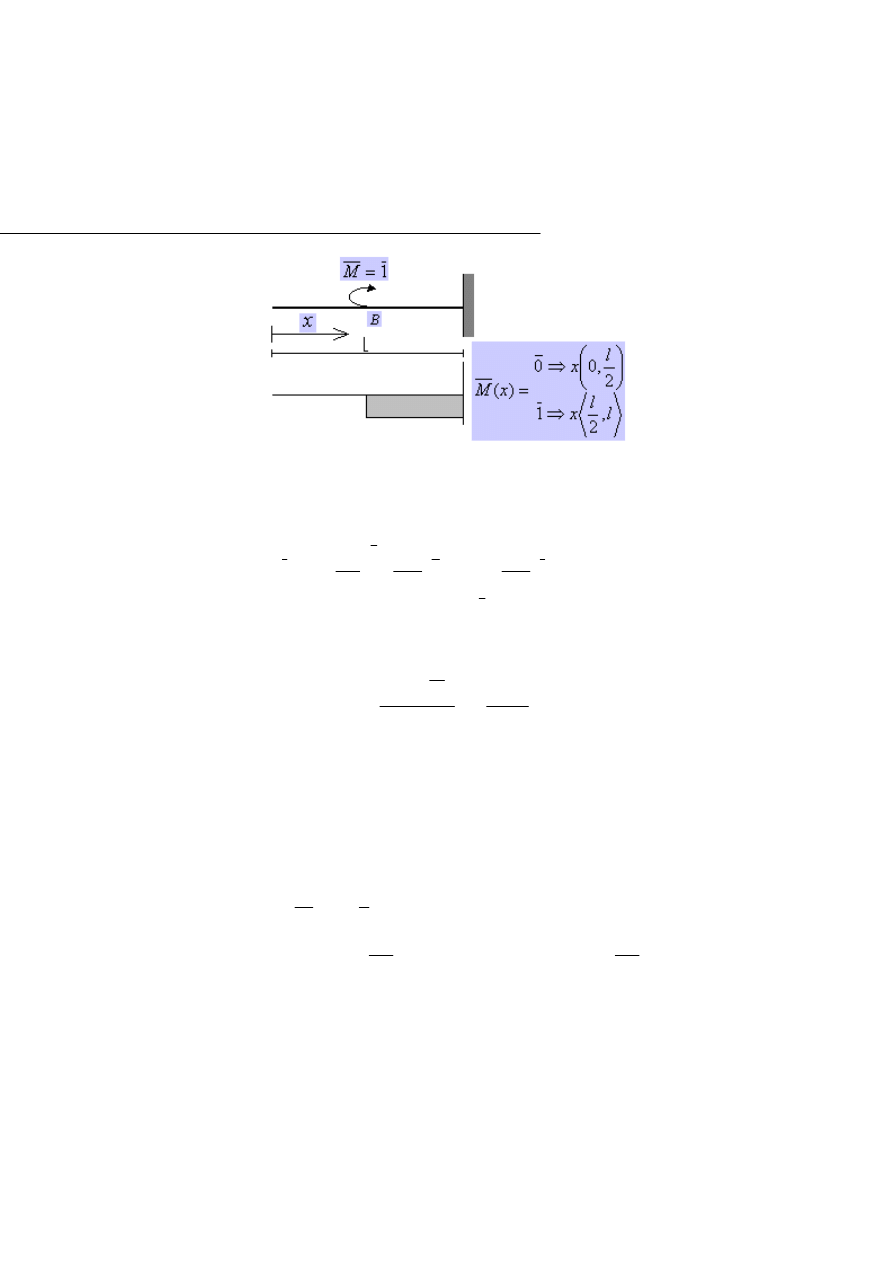
Obliczyć przemieszczenie pionowe punktu A belki wspornikowej przed-
stawionej na (Rys.2.4.1.a) oraz kąt obrotu w połowie rozpiętości tej belki:
Rys.2.4.1. a) belka wspornikowa obciążona siłą rzeczywistą q i z odkształceniami u
b) ta sama belka obciążona wirtualną siłą
P
Najpierw dokonujemy obliczeń sił wewnętrznych w układzie rzeczywistym
2
)
(
2
qx
x
M
−
=
(2.4.1)

W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
20
Następnie daną belkę obciążamy wirtualną siłą
P
=
1
[-] (Rys.2.4.1.b)
i ponownie obliczamy wartości sił wewnętrznych
1
)
(
⋅
−
=
x
x
M
(2.4.2)
Równania prac wirtualnych przyjmą więc postać:
0
1
⋅
+
⋅
=
R
u
L
A
Z
dx
EJ
qx
x
L
l
W
∫
⋅
=
2
1
2
(2.4.3)
Korzystając z twierdzenia drugiego, zapisujemy:
dx
EJ
qx
x
u
l
A
∫
=
2
1
1
2
(2.4.4)
Po scałkowaniu i przekształceniu otrzymujemy następujący wynik:
EJ
ql
l
EJ
q
u
A
8
4
2
4
4
=
⋅
=
(2.4.5)
W celu obliczenia kąta obrotu tej belki zamiast jedynkowej siły
P
= 1[-] przy-
kładamy jedynkowy moment
M
=
1
[-] w połowie jej długości (Rys 2.4.2.) i po-
nownie obliczamy wartości sił wewnętrznych:
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
21
Rys.2.4.2. Belka wspornikowa obciążona jedynkowym momentem wirtualnym
Postępując jak w przypadku pierwszym korzystamy z twierdzenia drugiego:
⋅
−
+
⋅
−
=
⋅
∫
∫
l
l
l
B
dx
qx
dx
qx
EJ
2
2
2
0
2
1
2
0
2
1
1
ϕ
(2.4.6)
Po scałkowaniu i przekształceniu otrzymujemy następujący wynik:
EJ
ql
EJ
l
l
q
B
48
7
6
8
3
3
3
−
=
−
−
=
ϕ
(2.4.7)
Minus w wyniku końcowym wskazuje nam na to, że belka ta obróci się w drugą
stronę niż założyliśmy.
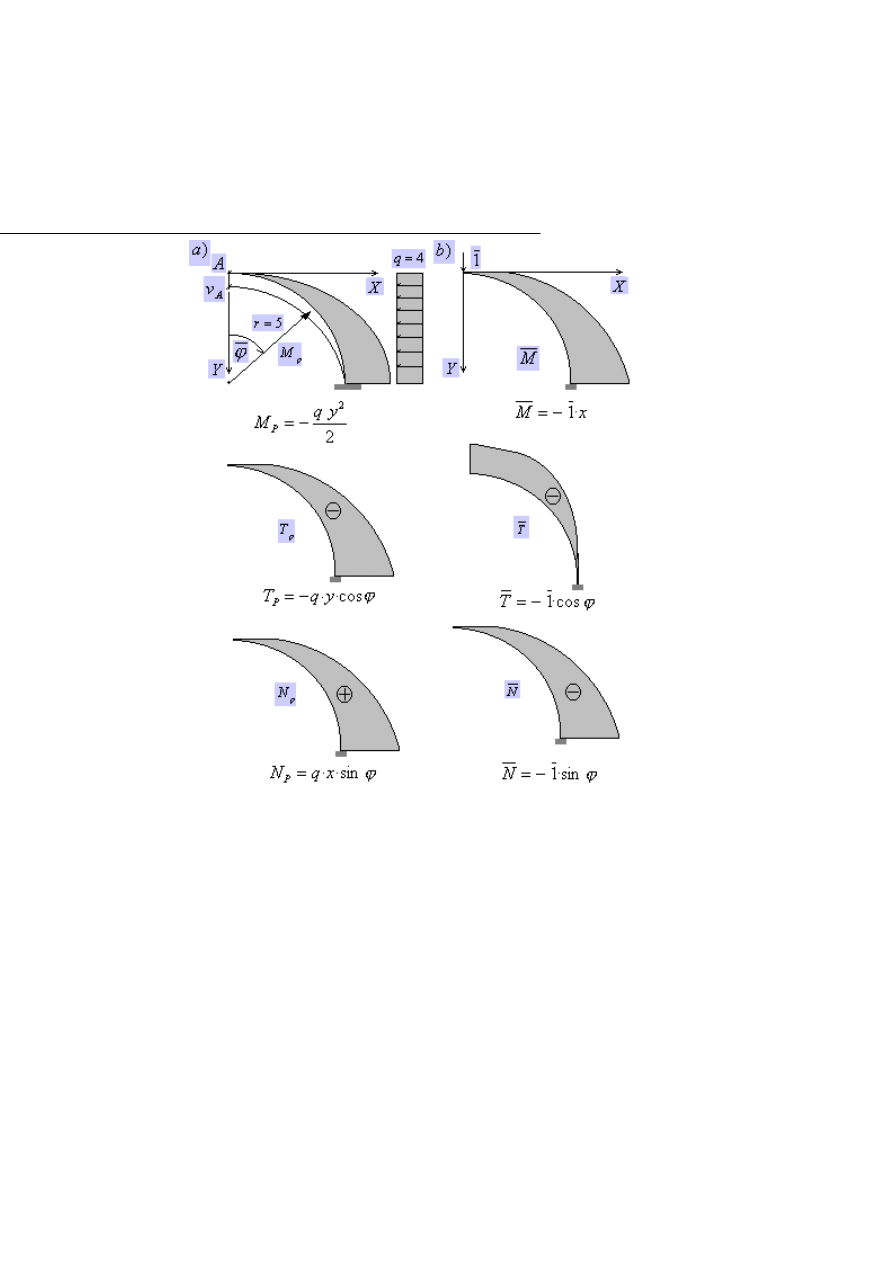
2.5. Przykład 2
Obliczyć przemieszczenie pionowe w punkcie A łuku o przekroju koło-
wym, przedstawionym na (Rys.2.5.1a).
Dane:
2
3
2
6
10
200
200
,
10
205
205
)
1
.
5
.
2
.
(
50
,
3
1
9
10
,
5
m
kN
MPa
m
kN
GPa
E
Rys
patrz
m
kN
M
m
r
dop
eks
⋅
=
=
⋅
=
=
⋅
=
=
=
=
σ
ν
κ
(2.5.1)

W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
22
2
3
10
76875
)
1
(
2
m
kN
E
G
⋅
=
+
=
ν
2
6
10
0
,
250
,
m
M
W
W
M
dop
eks
eks
dop
−
⋅
=
=
⇒
=
≥
σ
σ
σ
σ
m
W
R
R
R
W
2
3
3
3
10
83
,
6
7854
,
0
7854
,
0
4
−
⋅
=
=
⇒
=
= π
(2.5.2)
Przyjęliśmy: R = 0,069 m stąd:
4
8
4
4
2
4
2
10
1780
7854
,
0
4
,
10
150
m
R
R
I
m
R
A
−
−
⋅
=
≈
=
⋅
≈
=
π
π
(2.5.3)
Reasumując w zadaniu przyjęte zostały następujące wielkości:
2
3
2
6
4
8
2
4
10
76875
,
10
205
,
10
1780
,
10
150
m
kN
G
m
kN
E
m
I
m
A
⋅
=
⋅
=
⋅
=
⋅
=
−
−
(2.5.4)
Ponownie stosując tę samą metodę, przykładamy jedynkową siłę wirtualną w
punkcie A łuku (Rys.2.5.1b)
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
23
Rys.2.5.1.a) łuk obciążony siła rzeczywistą q z przemieszczeniem punktu A równym v
A
,
b) łuk obciążony jedynkową siłą wirtualną
W celu ułatwienia sobie obliczeń przyjmujemy biegunowy układ współrzędnych
(Rys.2.5.2.).
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
24
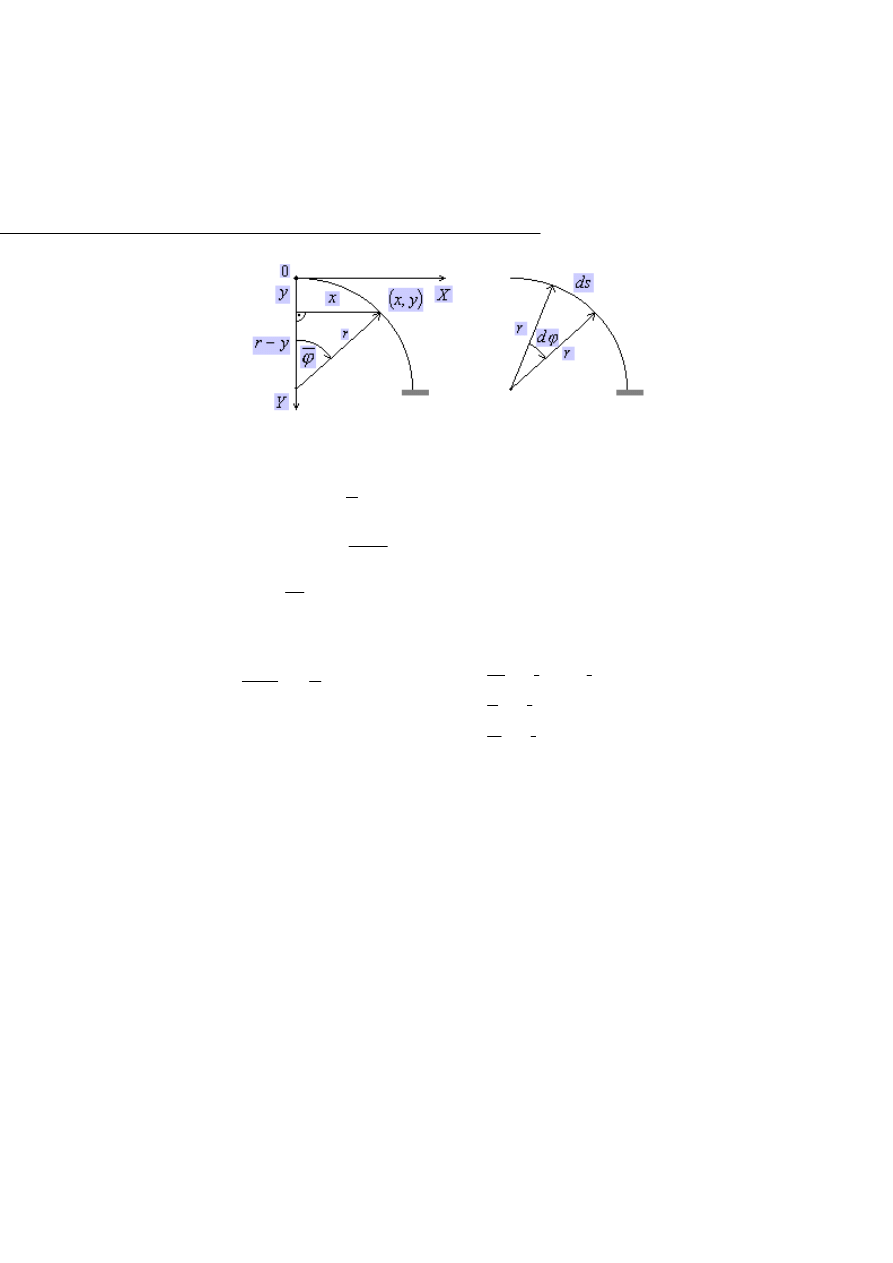
Rys.2.5.2. Przyjęcie układu biegunowego
r
y
r
r
x
−
=
=
ϕ
ϕ
cos
sin
)
cos
1
(
cos
sin
ϕ
ϕ
ϕ
−
=
−
=
=
r
r
r
y
r
x
ϕ
d
r
ds
=
r
d
ds
ϕ
=
(2.5.5)
Stąd:
(
)
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
2
2
2
2
sin
sin
)
cos
1
(
cos
cos
cos
1
2
2
r
q
x
q
N
r
q
y
q
T
r
q
y
q
M
P
P
P
=
=
−
−
=
−
=
−
−
=
−
=
ϕ
ϕ
ϕ
sin
1
cos
1
sin
1
1
⋅
−
=
⋅
−
=
⋅
−
=
⋅
−
=
N
T
r
x
M
(2.5.6)
Korzystając z drugiego twierdzenia o pracy wirtualnej uzyskamy:

W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
25
ϕ
ϕ
ϕ
ϕ
κ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
π
π
π
rd
r
q
GA
d
r
r
q
EA
d
r
r
q
r
EJ
v
A
)]
cos
1
(
cos
[
cos
1
sin
sin
1
1
)
cos
1
(
2
sin
1
1
1
2
0
2
0
2
2
0
2
2
−
−
⋅
−
+
+
⋅
−
+
+
−
−
⋅
−
=
∫
∫
∫
ϕ
ϕ
ϕ
κ
ϕ
ϕ
ϕ
ϕ
ϕ
π
π
π
d
GA
qr
d
EA
qr
d
EJ
qr
v
A
)
cos
1
(
cos
sin
)
cos
1
(
sin
2
2
0
2
2
2
0
3
2
2
0
2
4
−
+
+
−
−
=
∫
∫
∫
(2.5.7)
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
26
3
1
/
cos
3
1
cos
cos
/
3
2
2
)
2
1
(
)
1
(
sin
sin
cos
)
cos
1
(
sin
*
2
0
3
2
2
0
3
2
2
0
2
2
0
2
2
0
2
=
=
−
+
−
=
−
+
−
=
=
+
−
−
=
−
−
=
−
=
=
−
=
=
−
∫
∫
∫
Λ
π
π
π
π
π
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
t
t
t
dt
t
t
dt
t
dt
d
dt
d
t
d
(
)
( )
3
2
/
cos
3
1
cos
/
3
1
sin
sin
cos
cos
1
sin
sin
sin
sin
*
2
0
3
2
0
3
2
0
2
2
0
2
2
2
0
2
0
3
=
=
+
−
=
+
−
=
−
−
=
=
−
=
=
−
=
=
−
=
=
∫
∫
∫
∫
Κ
π
π
π
π
π
π
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
t
t
dt
t
dt
d
dt
d
t
d
d
d
(
)
( )
12
42
,
1
3
2
4
*
3
2
/
sin
3
1
sin
/
3
1
1
cos
sin
sin
1
cos
cos
*
*
4
/
2
sin
4
1
2
1
2
2
cos
1
cos
2
2
cos
1
cos
*
*
cos
cos
)
cos
1
(
cos
*
2
0
3
2
0
3
2
0
2
2
0
2
2
0
3
2
0
2
0
2
0
2
2
2
0
3
2
0
2
2
0
2
=
−
=
−
=
=
+
−
=
+
−
=
=
−
−
=
=
=
=
−
−
=
−
=
=
=
+
=
+
=
=
+
=
=
+
=
−
∫
∫
∫
∫
∫
∫
∫
∫
π
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
π
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
π
π
π
π
π
π
π
π
π
π
π
Κ
Κ
Κ
Κ
t
t
dt
t
dt
d
t
d
d
d
d
d
d
d
d
(2.5.8)
cm
m
GA
qr
EA
qr
EJ
qr
v
A
42
,
11
11418
,
0
00001
,
0
00002
,
0
11419
,
0
12
42
,
1
3
2
3
1
2
2
2
4
=
=
=
+
−
=
⋅
+
⋅
−
⋅
=
κ
(2.5.9)
Wniosek:
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
27
W zginanym łuku decydujący wpływ na przemieszczenia mają momenty zaś
wpływ pozostałych sił wewnętrznych możemy pominąć (łatwiej pręt zgiąć niż
na przykład ścisnąć czy rozciągnąć)
2.6. Przykład 3
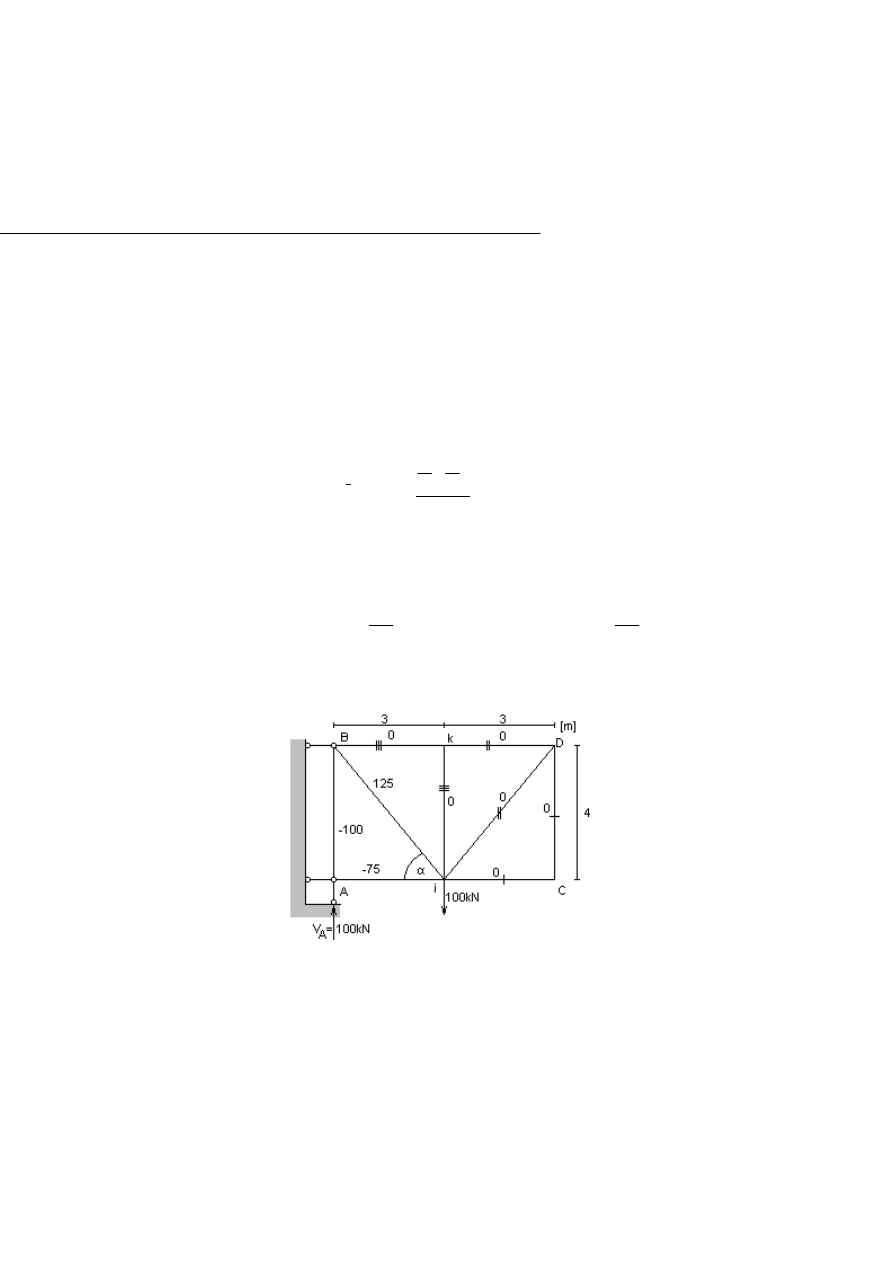
Dla układu kratowego przedstawionego na (Rys.2.6.1.) obliczyć:
a) pionowe przemieszczenie punktu i
b) kąt obrotu pręta S
ik
(obrót cięciwy ik)
c) wzajemny obrót prętów S
Bk
i S
kD
(wzajemny obrót cięciw)
d) skrócenie pręta S
ik
(zbliżenie punktów k, i)
Wzór:
j
j
j
j
j
i
l
A
E
N
N
∑
=
δ
1
(2.6.1)
Dane:
2
3
2
6
10
200
200
,
10
205
205
m
kN
MPa
m
kN
GPa
E
dop
⋅
=
=
⋅
=
=
σ
(2.6.2)
Rys.2.6.1 Kratownica z obciążeniem rzeczywistym

W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
28
dop
i
i
dop
N
A
A
N
σ
σ
σ
σ
=
⇒
=
≥
,
2
4
3
10
25
,
6
10
200
125
m
A
Bi
−
⋅
=
⋅
=
π
π
i
i
A
r
r
A
=
⇒
=
2
m
r
Bi
2
10
41
,
1
−
⋅
=
Przyjęliśmy:
m
r
Bi
2
10
50
,
1
−
⋅
=
stąd:
2
4
10
07
,
7
m
A
Bi
−
⋅
=
2
4
3
10
00
,
5
10
200
100
m
A
BA
−
⋅
=
⋅
=
m
r
Bi
2
10
26
,
1
−
⋅
=
Przyjęliśmy:
m
r
BA
2
10
30
,
1
−
⋅
=
stąd:
2
4
10
31
,
5
m
A
BA
−
⋅
=
2
4
3
10
75
,
3
10
200
75
m
A
Ai
−
⋅
=
⋅
=
m
r
Ai
2
10
09
,
1
−
⋅
=
Przyjęliśmy:
m
r
Ai
2
10
10
,
1
−
⋅
=
stąd:
2
4
10
80
,
3
m
A
Ai
−
⋅
=
(2.6.3)
Reasumując w zadaniu przyjęte zostały następujące wielkości:
2
4
2
4
2
4
2
3
2
6
10
80
,
3
,
10
31
,
5
,
10
07
,
7
10
200
200
,
10
205
205
m
A
m
A
m
A
m
kN
MPa
m
kN
GPa
E
Ai
BA
Bi
dop
−
−
−
⋅
=
⋅
=
⋅
=
⋅
=
=
⋅
=
=
σ
(2.6.4)
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
29
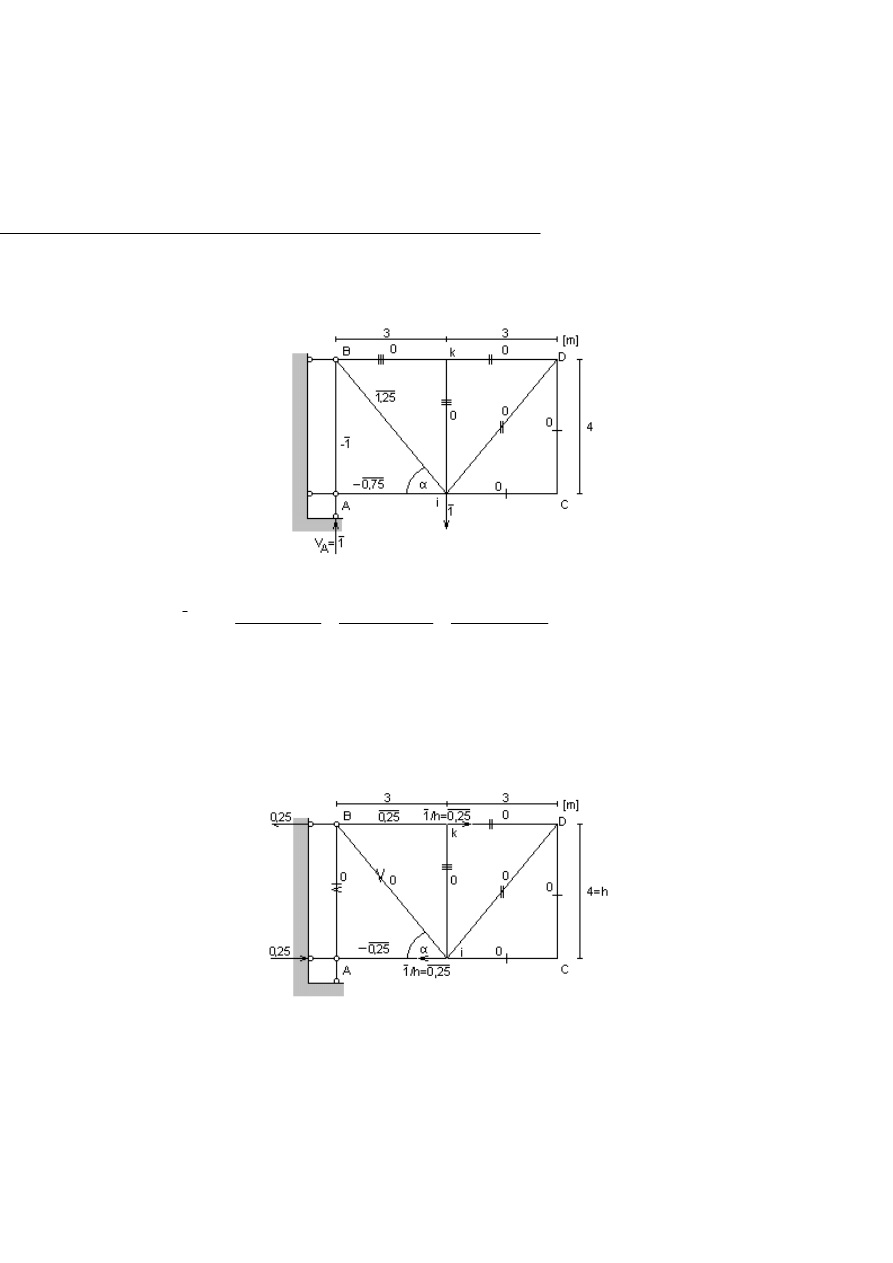
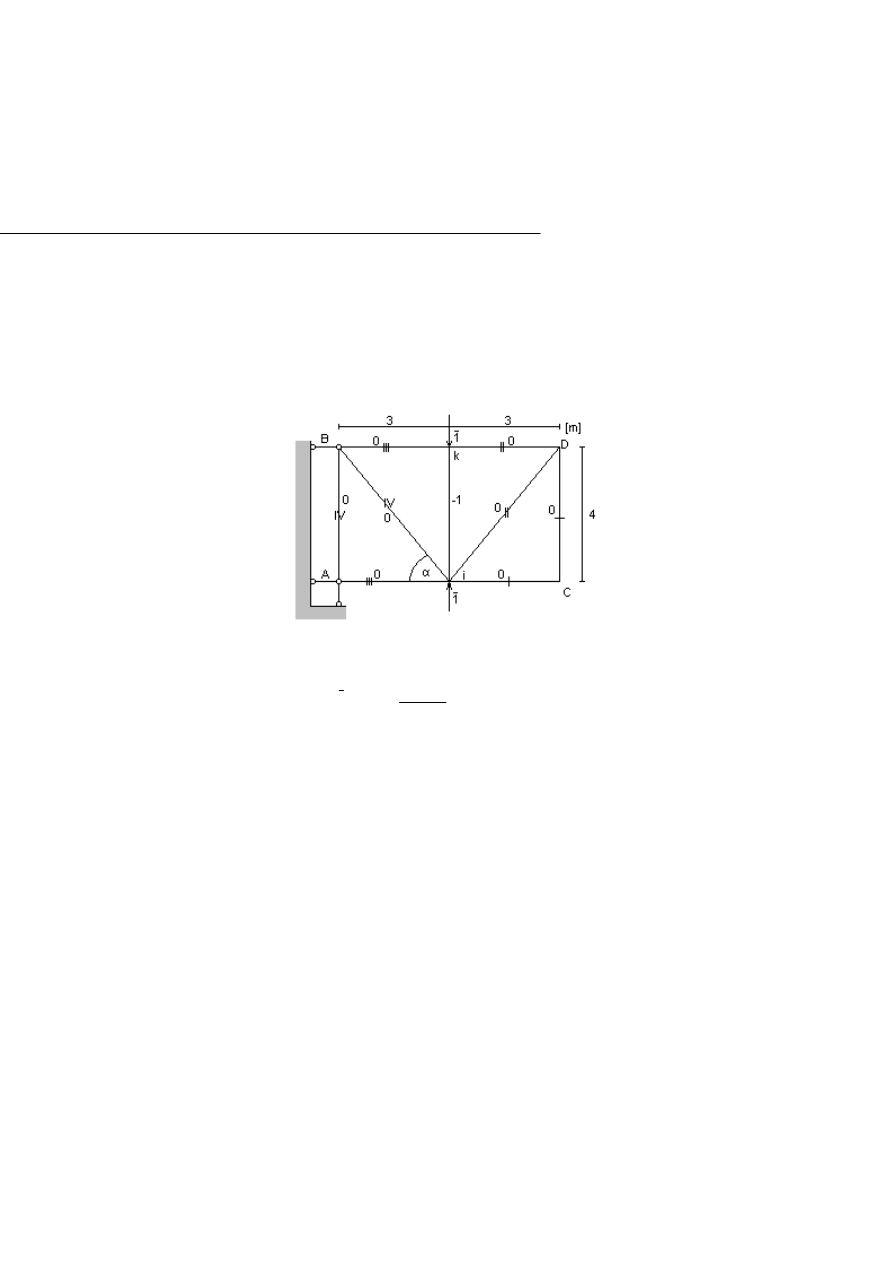
ad. a)
W celu obliczenia pionowego przemieszczenia punktu i, przykładamy w tym
punkcie jedynkową, pionową siłę wirtualną (Rys.2.6.2)
Rys.2.6.2 Kratownica z obciążeniem wirtualnym
m
E
E
E
v
A
2
4
4
4
10
12
,
1
10
07
,
7
5
125
25
,
1
10
31
,
5
4
100
1
10
8
,
3
3
75
75
,
0
1
−
−
−
−
⋅
=
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
=
⋅
(2.6.5)
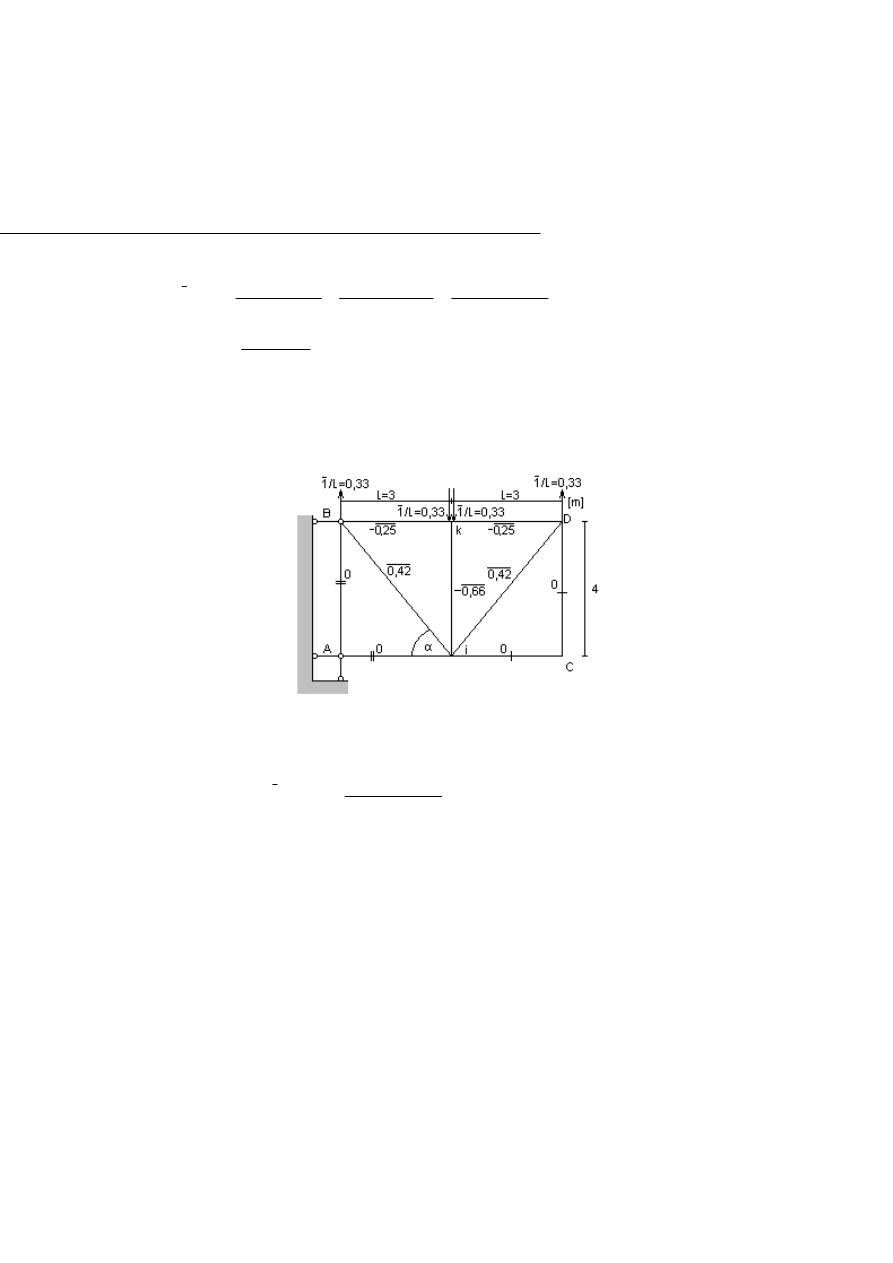
ad. b)
W celu obliczenia kąta obrotu pręta S
ik
(obrót cięciwy ik), przykładamy w koń-
cach tego pręta parę sił wirtualnych, które razem tworzą moment jedynkowy
(Rys.2.6.3)
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
30
Rys.2.6.3 Kratownica z obciążeniem wirtualnym
rad
A
E
E
E
E
v
Bk
ik
4
4
4
4
10
0
,
7
3
0
25
,
0
10
07
,
7
5
125
0
10
31
,
5
4
100
0
10
8
,
3
3
75
25
,
0
1
−
−
−
−
⋅
=
⋅
⋅
⋅
−
−
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
=
⋅
(2.6.6)
ad. c)
W celu obliczenia wzajemnego obrotu prętów S
Bk
i S
kD
(wzajemny obrót cięciw)
przykładamy w końcach każdego z tych prętów parę sił wirtualnych, które
razem tworzą moment jedynkowy (Rys.2.6.4)
Rys.2.6.4 Kratownica z obciążeniem wirtualnym
rad
E
D
k
B
4
4
10
0
,
18
10
07
,
7
5
125
42
,
0
1
−
−
⋅
=
⋅
⋅
⋅
⋅
=
⋅
ϕ
(2.6.7)
W
Y K Ł A D Y Z
M
E C H A N I K I
B
U D O W L I
R
ÓWNANIE PRACY WIRTUALNEJ
Politechnika Poznańska® Kopacz,
Łodygowski, Pawłowski, Płotkowiak, Tymber
31
ad. d)
W celu obliczenia skrócenia pręta S
ik
(zbliżenie punktów k, i) przykładamy w
końcach tego pręta, wzdłuż jego kierunku, parę sił wirtualnych, jedynkowy
(Rys.2.6.5)
Rys.2.6.5 Kratownica z obciążeniem wirtualnym
m
A
E
v
ki
ki
0
4
0
1
1
=
⋅
⋅
⋅
−
=
(2.6.8)
Wyszukiwarka
Podobne podstrony:
cwicz mechanika budowli przemieszczen metoda pracy wirtualnej
cwicz mechanika budowli przemieszczen metoda pracy wirtualnej
OBLICZANIE PRZEMIESZCZEŃ Z ZASTOSOWANIEM RÓWNANIA PRACY WIRTUALNEJ
wykl mechanika budowli 01 wstep przypomnienie praca na przemieszczeniach
wykl mechanika budowli 11 linie wplywu belki ciaglej
Obliczanie przemieszczeń układów statycznie wyznaczalnych z zastosowaniem równania pracy wirtualnej
Wykl Mechanika Budowli 15 Opis Ruchu Drgania Wlasne Tlumione
OBLICZANIE PRZEMIESZCZEŃ Z ZASTOSOWANIEM RÓWNANIA PRACY WIRTUALNEJ
wykl mechanika budowli 01 wstep przypomnienie praca na przemieszczeniach
Wykl Mechanika Budowli 13 Metoda Przemieszczen
wykl mechanika budowli 09 metoda sil cd
wykl mechanika budowli 07 twierdzenie o wzajemnosci
wykl mechanika budowli 02 praca sil wewnetrznych(1)
wykl mechanika budowli 12 luki statycznie niewyznaczalne
wykl mechanika budowli 06 metoda ciezarow sprezystych
wykl mechanika budowli 18 statecznosc ukladow pretowych
wykl mechanika budowli 15 opis ruchu drgania wlasne tlumione
więcej podobnych podstron