
Trzynaście Wykładów
z Matematyki Obliczeniowej
Leszek Plaskota
Instytut Matematyki Stosowanej i Mechaniki
Uniwersytet Warszawski

Spis treści
1 Specyfika obliczeń numerycznych
1
1.1 Zadania numeryczne, przykłady . . . . . . . . . . . . . .
1
1.2 Model obliczeniowy . . . . . . . . . . . . . . . . . . . . .
3
1.3 Arytmetyka fl
ν
. . . . . . . . . . . . . . . . . . . . . . .
5
2 Algorytmy i ich własności
11
2.1 Rozkład algorytmu względem informacji . . . . . . . . . 11
2.2 Problem wyboru algorytmu . . . . . . . . . . . . . . . . 12
2.3 Numeryczna poprawność algorytmu . . . . . . . . . . . . 13
2.4 Rola uwarunkowania zadania . . . . . . . . . . . . . . . . 15
2.5 Przykłady . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2.5.1 Iloczyn skalarny . . . . . . . . . . . . . . . . . . . 17
2.5.2 Całkowanie . . . . . . . . . . . . . . . . . . . . . 18
3 Układy równań liniowych
25
3.1 Układy z macierzą trójkątną . . . . . . . . . . . . . . . . 25
3.2 Eliminacja Gaussa . . . . . . . . . . . . . . . . . . . . . 26
3.3 Rozkład trójkątny macierzy . . . . . . . . . . . . . . . . 28
4 Analiza błędów w eliminacji Gaussa
39
4.1 Układy z macierzą trójkątną . . . . . . . . . . . . . . . . 39
4.2 Poprawność rozkładu trójkątnego . . . . . . . . . . . . . 40
4.3 Poprawność rozwiązywania układu . . . . . . . . . . . . 44
4.4 Uwarunkowanie macierzy, a błąd w fl
ν
. . . . . . . . . .
46
5 Zadanie wygładzania liniowego
51
5.1 Układ normalny . . . . . . . . . . . . . . . . . . . . . . . 51
i

ii
SPIS TREŚCI
5.2 Odbicia Hauseholdera . . . . . . . . . . . . . . . . . . . . 54
5.3 Algorytm dla zadania wygładzania . . . . . . . . . . . . 56
6 Interpolacja wielomianowa
65
6.1 Sformułowanie zadania interpolacji . . . . . . . . . . . . 65
6.2 Wybór bazy wielomianowej . . . . . . . . . . . . . . . . 67
6.3 Algorytm różnic dzielonych . . . . . . . . . . . . . . . . 69
6.4 Przypadek węzłów wielokrotnych . . . . . . . . . . . . . 71
7 Interpolacja a aproksymacja funkcji
77
7.1 Błąd interpolacji wielomianowej . . . . . . . . . . . . . . 77
7.2 Wielomiany Czebyszewa . . . . . . . . . . . . . . . . . . 80
7.3 Interpolacja kawałkami wielomianowa . . . . . . . . . . . 83
8 Interpolacja funkcjami sklejanymi
89
8.1 Co to są funkcje sklejane? . . . . . . . . . . . . . . . . . 89
8.2 Interpolacja i gładkość . . . . . . . . . . . . . . . . . . . 90
8.3 Kubiczne funkcje sklejane . . . . . . . . . . . . . . . . . 94
9 Całkowanie numeryczne
103
9.1 Co to są kwadratury? . . . . . . . . . . . . . . . . . . . . 103
9.2 Błąd kwadratur interpolacyjnych . . . . . . . . . . . . . 105
9.3 Kwadratury złożone . . . . . . . . . . . . . . . . . . . . 108
9.4 Przyspieszanie zbieżności kwadratur . . . . . . . . . . . . 110
10 Całkowanie a aproksymacja
117
10.1 Rząd kwadratury . . . . . . . . . . . . . . . . . . . . . . 117
10.2 Ciągi wielomianów ortogonalnych . . . . . . . . . . . . . 119
10.3 Kwadratury Gaussa . . . . . . . . . . . . . . . . . . . . . 123
11 Iteracje dla równań liniowych
131
11.1 Kiedy stosujemy iteracje? . . . . . . . . . . . . . . . . . 132
11.2 Metoda Czebyszewa . . . . . . . . . . . . . . . . . . . . . 134
11.3 Metoda najszybszego spadku . . . . . . . . . . . . . . . . 139
12 Iteracje dla równań nieliniowych
145
12.1 Bisekcja . . . . . . . . . . . . . . . . . . . . . . . . . . . 146
12.2 Iteracje proste . . . . . . . . . . . . . . . . . . . . . . . . 147

SPIS TREŚCI
iii
12.3 Metody interpolacyjne . . . . . . . . . . . . . . . . . . . 149
12.4 Obliczanie zer wielomianów . . . . . . . . . . . . . . . . 153

iv
SPIS TREŚCI

Rozdział 1
Specyfika obliczeń
numerycznych
Matematyka obliczeniowa jest dziedziną wiedzy zajmującą się proble-
mami obliczeniowymi i konstrukcją algorytmów rozwiązywania zadań
matematycznych.
Aby w ogóle mówić w problemie obliczeniowym, musimy najpierw
• określić dane początkowe i cel obliczeń, czyli dokładnie sformuło-
wać zadanie,
• określić środki obliczeniowe dzięki którym chcemy osiągnąć cel,
czyli zdefiniować model obliczeniowy.
1.1 Zadania numeryczne, przykłady
Sformułowanie zadania polega na sprecyzowaniu tego, co mamy i co
chcemy uzyskać. Formalnie polega to na zdefiniowaniu przestrzeni da-
nych F , przestrzeni wyników G i wskazaniu zależności f 7→ g, gdzie
f
∈ F i g ∈ G, między danymi a wynikami. Zależność tę repezentuje
operator rozwiązania
S
: F −→ G.
Będziemy zainteresowani przede wszystkim zadaniami numerycz-
nymi. Są to zadania, dla których wynikiem g jest zawsze skończony
1
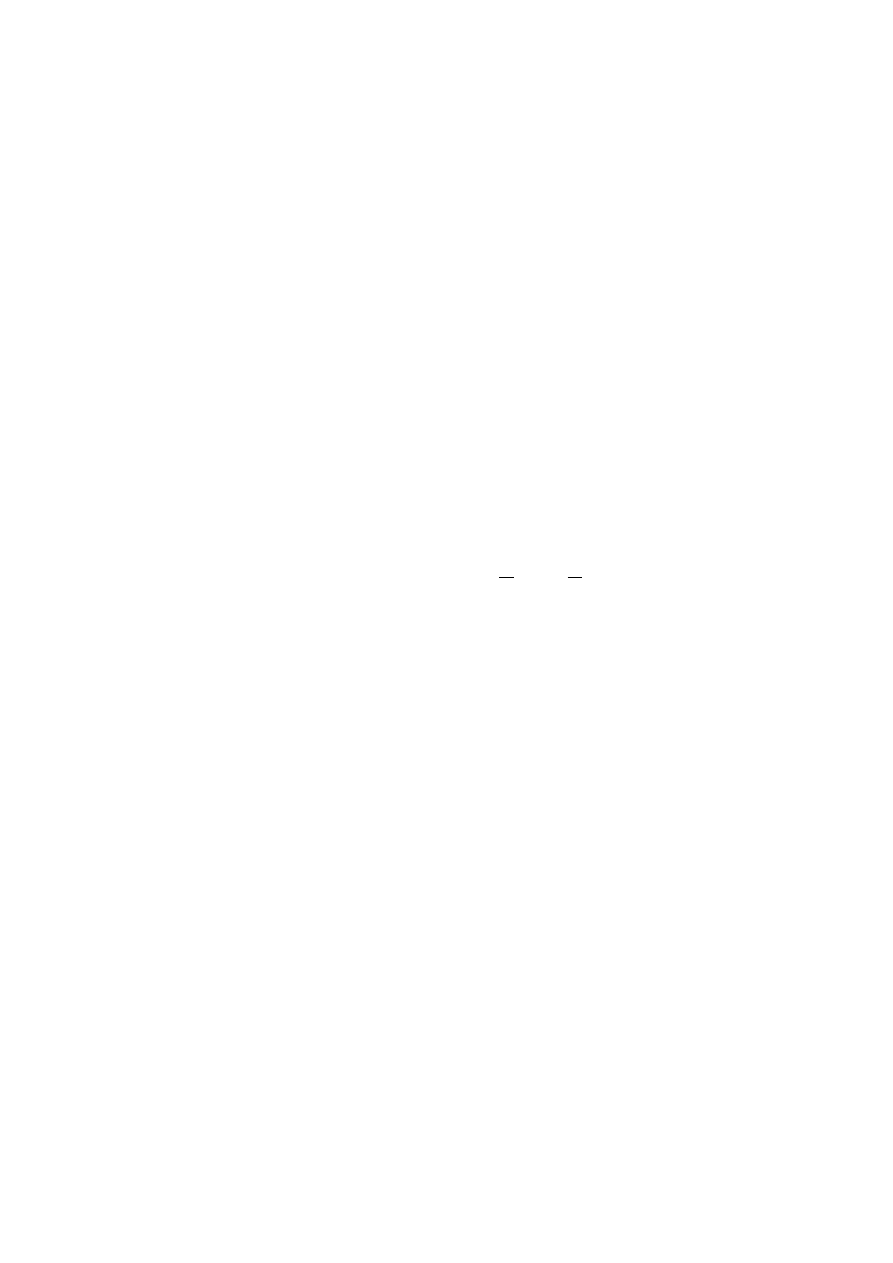
2
ROZDZIAŁ 1. SPECYFIKA OBLICZEŃ NUMERYCZNYCH
ciąg liczb rzeczywistych, czyli
G
⊂ ∪
∞
n=0
R
n
(przyjmujemy przy tym, że R
0
= pusty). Zbiór danych może być w
zasadzie dowolny, ale my będziemy dla uproszczenia rozpatrywać tylko
zadania dla których F ⊂ R
m
, albo ogólniej, dla których F jest pewną
klasą funkcji zdefiniowanych na ustalonym zbiorze D ⊂ R
d
.
Przykład 1.1 (Równanie kwadratowe.) Załóżmy, że chcemy obliczyć
wszystkie rzeczywiste pierwiastki równania
x
2
− 2p + q = 0,
dla danych liczb rzeczywistych p i q. Wtedy F = R
2
, G = R
0
∪R
1
∪R
2
,
oraz
S
(p, q) =
pusty
∆ < 0,
p
∆ = 0,
(p +
√
∆, p −
√
∆)
∆ > 0,
(1.1)
gdzie ∆ = p
2
− q.
Przykład 1.2 (Układ równań liniowych.) Rozpatrzmy zadanie roz-
wiązywania układu równań liniowych
A~x
= ~b,
dla nieosobliwej macierzy A = (a
i,j
)
n
i,j=1
i wektora ~b = (b
j
)
n
j=1
. Wtedy
F
= { (A,~b) ∈ R
n
2
+n
: det A 6= 0 },
G
= R
n
, oraz
S
(A,~b) = A
−1
~b.
Przykład 1.3 (Całkowanie.) Dla danej funkcji ciągłej f : [a, b]
→ R,
chcemy obliczyć całkę oznaczoną
I
(f) =
Z
b
a
f
(x) dx.
W tym przypadku G = R, ale dane stanowi pewna klasa funkcji cią-
głych określonych na odcinku [a, b], tzn. F ⊂ C([a, b]). Oczywiście S
jest operatorem całkowania, S = I.

1.2. MODEL OBLICZENIOWY
3
1.2 Model obliczeniowy
Aby zdefiniować nasz model obliczeniowy, posłużymy się pojęciem pro-
gramu. Zastosujemy przy tym notację podobną do tej z języka progra-
mowania Pascal.
Program składa się z deklaracji, czyli opisu obiektów, których bę-
dziemy używać, oraz z poleceń (instrukcji), czyli opisu akcji, które bę-
dziemy wykonywać.
Dostępnymi obiektami są stałe i zmienne typu całkowitego (inte-
ger), rzeczywistego (real), albo logicznego (Boolean). Zmienne mogą
być grupowane w wektory albo tablice.
Polecenia dzielimy na proste i złożone. Poleceniem prostym jest
•
Podstawienie
z
:= W;
gdzie z jest zmienną, a W jest wyrażeniem o wartościach tego samego
typu co z.
Wyrażeniem jest pojedyncza stała lub zmienna, albo złożenie skoń-
czonej liczby operacji elementarnych na wyrażeniach. Operacje elemen-
tarne to:
arytmetyczno–arytmetyczne: x
7→ −x, (x, y) 7→ x + y, (x, y) 7→
x
− y, (x, y) 7→ x ∗ y, (x, y) 7→ x/y, y 6= 0, gdzie x, y są stałymi
lub zmiennymi liczbowymi,
arytmetyczno–logiczne: (x, y)
7→ x < y, (x, y) 7→ x ≤ y, (x, y) 7→
x
= y, (x, y) 7→ x 6= y, gdzie x, y są stałymi lub zmiennymi
liczbowymi,
logiczno–logiczne: p
7→ not p, (p, q) 7→ p and q, (p, q) 7→ p or q, gdzie
p, q
są stałymi lub zmiennymi logicznymi.
Dla niektórych zadań wygodnie jest (a czasem koniecznie) uzu-
pełnić ten zbiór o dodatkowe operacje, takie jak obliczanie wartości
niektórych funkcji standardowych (√ , cos(), sin(), exp(), log(), itp.),

4
ROZDZIAŁ 1. SPECYFIKA OBLICZEŃ NUMERYCZNYCH
czy nawet funkcji bardziej skomplikowanych. Na przykład, zastosowa-
nie “szkolnych” wzorów na obliczanie pierwiatków równania kwadrato-
wego z Przykładu 1.1 byłoby niemożliwe, gdyby pierwiastkowanie było
niemożliwe. Należy jednak przy tym pamiętać, że w praktyce funk-
cje standardowe (o ile są dopuszczalne) są obliczane używając czterech
podstawowych operacji arytmetycznych.
Mamy trzy podstawowe polecenia złożone.
•
Warunkowe
if
W then A
1
else
A
2
;
gdzie W jest wyrażeniem o wartościach logicznych, a A
1
i A
2
są pole-
ceniami, przy czym dopuszczamy polecenia puste.
•
Powtarzane
while
W do A;
gdzie W jest wyrażeniem o wartościach logicznych, a A jest poleceniem.
•
Kombinowane
begin
A
1
; A
2
; . . . ; A
n
end;
gdzie A
j
są poleceniami.
Na podstawie tych trzech poleceń można tworzyć inne, takie jak
pętle for i repeat, czy case, itd.
Mamy też dwa szczególne polecenia, które odpowiadają za ”wejście”
i ”wyjście”.
•
Wprowadzanie danych
IN (x, t);
gdzie x jest zmienną rzeczywistą, a t “adresem” pewnego funkcjonału
L
: F → R należącym to pewnego zbioru T . W wyniku wykonania tego
polecenia w zmiennej x zostaje umieszczona wartość L
t
(f).
Polecenie to pozwala zdobyć informację o danej f. Jeśli F = R
n
to
zwykle mamy T = {1, 2, . . . , n} i L
i
(f) = f
i
, co w praktyce odpowiada

1.3. ARYTMETYKA FL
ν
5
wczytaniu i-tej współrzędnej wektora danych. W szczególności, ciąg po-
leceń IN (x[i], i), i = 1, 2, . . . , n, pozwala uzyskać pełną informację o
f
. Jeśli zaś F jest pewną klasą funkcji f : [a, b] → R, to możemy mieć
np. T = [a, b] i L
t
(f) = f(t). W tym przypadku, wykonanie polecenia
IN (x, t) odpowiada w praktyce skorzystaniu ze specjalnej procedury
(albo urządzenia zewnętrznego) obliczającej (mierzącego) wartość funk-
cji f w punkcie t.
•
Wyprowadzanie wyników
OUT (W);
gdzie W jest wyrażeniem o wartościach rzeczywistych. Polecenie to po-
zwala “wskazać” kolejną współrzędną wyniku.
Zakładamy, że na początku procesu obliczeniowego wartości wszyst-
kich zmiennych są nieokreślone, oraz że dla dowolnych danych wykona-
nie programu wymaga wykonania skończonej liczby operacji elementar-
nych. Wynikiem obliczeń jest skońćzony ciąg liczb rzeczywistych (albo
puste
), którego kolejne współrzędne pokazywane są poleceniem OUT .
1.3 Arytmetyka
fl ν
Przedstawiony model obliczeniowy jest modelem idealistycznym, tzn.
zakłada on, że wszystkie operacje są wykonywane bezbłędnie. Dlatego
w tym przypadku będziemy mówić o arytmetyce idealnej. W praktyce
jednak, np. wykonując obliczenia na maszynie cyfrowej, operacje aryt-
metyczne na liczbach rzeczywistych wykonywane są z pewnym błędem.
Matematycznym modelem arytmetyki maszyny cyfrowej jest arytme-
tyka fl
ν
(albo arytmetyka zmiennoprzecinkowa), którą teraz przedsta-
wimy.
Dowolną liczbę rzeczywistą x 6= 0 można przedstawić w postaci
x
= s · 10
c
· m,
gdzie s ∈ {−1, 1} jest znakiem, c ∈ Z cechą, a m ∈ [0.1, 1.0) mantysą
liczby x. Zauważmy, że taki rozkład jest jednoznaczny i odpowiada prze-
suwaniu przecinka w rozwinięciu dziesiętnym liczby do pierwszej cyfry

6
ROZDZIAŁ 1. SPECYFIKA OBLICZEŃ NUMERYCZNYCH
znaczącej, tj. różnej od zera. Mantysa ma w ogólności nieskończenie
wiele cyfr c
j
w swoim rozwinięciu dziesiętnym,
m
=
∞
X
j=1
c
j
10
−j
,
gdzie c
j
∈ {0, 1, 2, . . . , 9} i c
1
6= 0. Jako taka nie może więc być zapa-
miętana dokładnie w pamięci maszyny cyfrowej. Zakładając, że pamię-
tamy tylko t cyfr znaczących i ostatnią cyfrę zaokrąglamy, zamiast m
pamiętamy
m
t
=
t
X
j=1
c
j
10
−j
+ d
t
10
−j
,
gdzie
d
t
=
(
0
gdy 0 ≤ c
t+1
≤ 4},
1
gdy 5 ≤ c
t+1
≤ 9}.
Stąd x będzie reprezentowana przez liczbę
rd (x) = s
· 10
c
· m
t
.
Między liczbą x (x 6= 0) a jej reprezentacją rd(x) zachodzi więc
nierówność
|x − rd(x)|
|x|
= |
m
− m
t
|
|m|
≤
5 · 10
−(t+1)
10
−1
= 5 · 10
−t
,
charakteryzująca dokładność arytmetyki. Liczby rzeczywiste są więc w
arytmetyce fl
ν
reprezentowane z dokładnością względną ν = 5·10
−t
. (We
współczesnych maszynach cyfrowych w pojedynczej precyzji mamy co
najmniej t = 8.) Zauważmy, że t jest największą spośród liczb natural-
nych j spełniających bierówność rd(1 + 10
−j
) > 1.
Ostatnią nierówność wygodnie jest zapisać w równoważny sposób
jako
rd (x) = x(1 + ε),
gdzie |ε| ≤ ν.
W arytmetyce fl
ν
zakładamy ponadto, że działania arytmetyczne na
liczbach rzeczywistych (a raczej na ich reprezentacjach) są wykonywane
dokładnie i tylko wynik jest zaokrąglany. Mamy więc
fl
ν
(x 2 y) = rd ( rd(x) 2 rd(y) ) ,

1.3. ARYTMETYKA FL
ν
7
gdzie 2 ∈ {+, −, ∗, /}, Ogólniej, jeśli W
1
i W
2
są wyrażeniami o war-
tościach rzeczywistych, to dla dowolnych wartości zmiennych
fl
ν
(W
1
2
W
2
) = rd ( fl
ν
(W
1
) 2 fl
ν
(W
2
)) .
Zwykle dla prostoty będziemy również zakładać podobną zależność dla
niektórych funkcji standardowych, o ile należą one do zbioru operacji
elementarnych (chociaż w rzeczywistości są one obliczane przez pro-
cedury używające czterech podstawowych operacji arytmetycznych). I
tak będziemy mieć np.
fl
ν
√
W
=
q
fl
ν
(W)
(1 + β
1
),
fl
ν
(W) = (cos(fl
ν
(W))) (1 + β
2
),
gdzie |ε
j
| ≤ ν, oraz β
j
≤ K
j
ν
i K
j
są “niewielkimi” stąłymi.
Podobnie, jeśli △ jest operatorem porównania, △ ∈ {<, ≤, =, 6=},
to wartością wyrażenia logicznego W
1
△W
2
w fl
ν
jest dokładna wartość
wyrażenia fl
ν
(W
1
)△fl
ν
(W
2
).
Uwagi i uzupełnienia
U. 1.1 W maszynie cyfrowej cecha c liczby rzeczywistej nie może oczywi-
ście mieć dowolnie dużej wartości bezwzględnej, |c| ≤ c
max
. Powoduje to
powstanie zjawiska nadmiaru gdy c > c
max
, oraz zjawiska niedomiaru gdy
c <
−c
max
. W pierwszym przypadku liczba jest tak duża (co do modułu),
że nie zawiera się w przedziale liczb reprezentowalnych, a w drugim jest tak
mała, że musi być reprentowana przez zero, przy czym błąd względny repre-
zentacji wynosi wtedy 1 a nie ν. W dalszych rozważaniach zjawiska nadmiaru
i niedomiaru będziemy dla uproszczenia zaniedbywać.
U. 1.2 W następnych rozdziałach często będziemy się posługiwać normami
wektorów ~x = (x
j
)
n
j=1
∈ R
n
i macierzy A = (a
i,j
)
n
i,j=1
∈ R
n×n
, a w szcze-
gólności błędami reprezentacji wektorów i macierzy w normie. Najczęściej
używanymi normami wektorowymi będą normy p-te,
k~xk = k~xk
p
=
n
X
j=1
|x
j
|
p
1/p
,
1 ≤ p < +∞,

8
ROZDZIAŁ 1. SPECYFIKA OBLICZEŃ NUMERYCZNYCH
oraz
k~xk
∞
= lim
p→+∞
k~xk
p
= max
1≤j≤n
|x
j
|.
Normą macierzową jest norma euklidesowa (albo Frobeniusa)
kAk
E
=
v
u
u
t
n
X
i,j=1
|a
i,j
|
2
,
a także normy indukowane przez normy wektorowe (np. przez normy p-te)
kAk = sup
x6=0
kA~xk
k~xk
= sup
kxk=1
kA~xk.
Jeśli norma macierzowa jest indukowana przez normę wektorową, to dla
dowolnego wektora mamy
kA~xk ≤ kAkk~xk.
U. 1.3 Przypomnijmy, że w przestrzeniach liniowych skończenie wymiaro-
wych (a więc także w R
n
i w przestrzeni macierzy wymiaru n × n) każde
dwie normy są równoważne. To znaczy, że jeśli mamy dwie normy k · k i k · k
′
w przestrzeni skończenie wymiarowej X, to istnieją stałe 0 < K
1
≤ K
2
<
∞
takie, że
K
1
kxk ≤ kxk
′
≤ K
2
kxk,
∀x ∈ X.
W szczególności dla ~x ∈ R
n
mamy
k~xk
∞
≤ k~xk
1
≤ n k~xk
∞
,
(1.2)
k~xk
∞
≤ k~xk
2
≤
√
n
k~xk
∞
,
(1.3)
1
√
n
k~xk
1
≤ k~xk
2
≤ k~xk
1
,
(1.4)
a dla A = (a
i,j
)
n
i,j=1
mamy
kAk
2
≤ k |A| k
2
≤ kAk
E
≤
√
n
kAk
2
,
(1.5)
gdzie |A| = (|a
i,j
|)
n
i,j=1
.

1.3. ARYTMETYKA FL
ν
9
Ćwiczenia
Ćw. 1.1 Podać przykłady liczb x i y, które są dokładnie reprezentowane w
fl
ν
, ale fl
ν
(x2y) 6= x2y, gdzie 2 ∈ {+, −, ∗, /}.
Ćw. 1.2 Uzasadnić, że jeśli x ≤ y to rd(x) ≤ rd(y) oraz fl
ν
(x/y) ≤ 1.
Podać przykład wyrażenia W takiego, że dla pewnych wartości zmiennych
W < 0, ale fl
ν
(W) > 0.
Ćw. 1.3 Jak zabezpieczyć się przed powstaniem nadmiaru albo niedomiaru
przy obliczaniu wyrażenia
p
x
2
+ y
2
, gdy x i y leżą w przedziale liczb repre-
zentowalnych w fl
ν
, ale x
2
lub y
2
nie?
Ćw. 1.4 Uzasadnić nierówności (1.2)–(1.5).
Ćw. 1.5 Pokazać, że dla macierzy A = (a
i,j
)
n
i.j=1
∈ R
n×n
mamy
kAk
∞
= max
1≤i≤n
n
X
j=1
|a
i,j
|
oraz
kAk
1
= kA
T
k
∞
= max
1≤j≤n
n
X
i=1
|a
i,j
|.
Ćw. 1.6 Dla wektora ~x = (x
j
)
n
j=1
∈ R
n
, niech rd(~x) = (rd(x
j
))
n
j=1
. Poka-
zać, że
k~x − rd(~x)k
p
≤ ν k~xk
p
dla 1 ≤ p ≤ ∞.
Ćw. 1.7 Dla macierzy A = (a
i,j
)
n
i,j=1
, niech rd(A) = (rd(a
i,j
))
n
i,j=1
. Poka-
zać, że
kA − rd(A)k
p
≤ ν kAk
p
,
dla p = 1, ∞, oraz
kA − rd(A)k
2
≤ kA − rd(A)k
E
≤ ν kAk
E
≤
√
n ν
kAk
2
.
æ

10
ROZDZIAŁ 1. SPECYFIKA OBLICZEŃ NUMERYCZNYCH

Rozdział 2
Algorytmy i ich własności
Algorytm to dokładnie określona i dozwolona w danym modelu oblicze-
niowym sekwencja akcji, pozwalająca na rozwiązanie danego zadania
(w sposób dokładny lub przybliżony).
2.1 Rozkład algorytmu względem infor-
macji
Z każdym algorytmem związany jest operator
Φ : F −→ G,
taki że Φ(f) jest wynikiem działania algorytmu w arytmetyce idealnej
dla danej f.
Zauważmy, że wynik Φ(f) działania algorytmu nie zależy bezpo-
średnio od f, ale raczej od informacji o f (uzyskanej dzięki poleceniu
IN ). Informacja ta może być pełna albo tylko częściowa. Informacja
jest pełna gdy, np. f = (f
1
, . . . , f
n
) ∈ R
n
i wczytamy wszystkie współ-
rzędne f
i
. Informacja może być częściowa, gdy f jest funkcją. Wtedy
wiele danych może posiadać tę samą informację, co łatwo zaobserwować
na przykładzie zadania całkowania.
Niech N : F → ∪
∞
n=0
R
n
będzie operatorem informacji, tzn.
N
(f) = (y
1
, y
2
, . . . , y
n
)
11

12
ROZDZIAŁ 2. ALGORYTMY I ICH WŁASNOŚCI
jest informacją o f zebraną przy idealnej realizacji algorytmu. Za-
uważmy, że nformacja jest pełna gdy N jest przekształceniem różnowar-
tościowym, tzn. jeśli f
1
6= f
2
implikuje N(f
1
) 6= N(f
2
). W przeciwnym
przypadku mamy do czynienia z informacją częściową.
Każdy algorytm Φ może być przedstawiony jako złożenie operatora
informacji i pewnego operatora ϕ : N(F ) → G zdefiniowanego równo-
ścią
ϕ
(N(f)) = Φ(f).
Zauważmy, że w przypadku informacji częściowej zwykle nie istnieje
algorytm dający dokładne rozwiązanie zadania dla każdej danej f ∈ F ,
ponieważ dla danych o tej samej informacji mogą istnieć różne rozwią-
zania.
2.2 Problem wyboru algorytmu
Wybór algorytmu jest najistotniejszą częścią całego procesu numerycz-
nego rozwiązywania zadania. Kierujemy się przy tym przede wszystkim
następującymi kryteriami:
• dokładnością algorytmu,
• złożonością algorytmu,
• własnościami numerycznymi algorytmu.
Przez dokładność algorytmu rozumiemy różnicę między rozwiąza-
niem dokładnym S(f), a rozwiązaniem Φ(f) dawanym przez algorytm
w arytmetyce idealnej. Jeśli Φ(f) = S(f), ∀f ∈ F , to algorytm nazy-
wamy dokładnym.
Mówiąc o złożoności, mamy na myśli złożoność pamięciową (zwy-
kle jest to liczba stałych i zmiennych używanych przez algorytm), jak
również złożoność obliczeniową. Na złożoność obliczeniową algorytmu
dla danej f składa się koszt uzyskania infomacji y = N(f) (zwykle jest
on proporcjonalny do liczby wywołań polecenia IN ), oraz koszt kombi-
natoryczny przetworzenia tej informacji, aż do uzyskania wyniku ϕ(y).
Koszt kombinatoryczny zwykle mierzymy liczbą operacji arytmetycz-
nych wykonywanych przez algorytm.

2.3. NUMERYCZNA POPRAWNOŚĆ ALGORYTMU
13
Przez własności numeryczne algorytmu rozumiemy jego własności
przy realizacji w arytmetyce fl
ν
. Temu ważnemu tematowi poświęcimy
teraz osobny paragraf.
2.3 Numeryczna poprawność algorytmu
Pożądane jest, aby algorytm dawał “dobry” wynik zarówno w arytme-
tyce idealnej, jak i w arytmetyce fl
ν
. Niestety, jak zobaczymy, nie zawsze
jest to możliwe. Nawet jeśli algorytm jest dokładny to w wyniku jego
realizacji w fl
ν
możemy otrzymać wynik fl
ν
(Φ(f)) daleko odbiegający
od S(f). W szczególności, prawie zawsze mamy
S
(f) 6= fl
ν
(Φ(f)) .
Zauważmy również, że o ile z reguły znamy dokładne zachowanie się al-
gorytmu w arytmetyce idealnej dla danej informacji, to nie można tego
samego powiedzieć o jego zachowaniu się w arytmetyce fl
ν
. W związku
z tym powstaje pytanie, jak kontrolować błąd algorytmów wynikający z
błędów zaokrągleń i jakie algorytmy uznamy za te o najwyższej jakości
numerycznej.
Istnienie błędów reprezentacji liczb rzeczywistych powoduje, że in-
formacja y = N(f) o danej f nie jest w ogólności reprezentowana do-
kładnie. Znaczy to, że zamiast na informacji dokładnej, dowolny al-
gorytm będzie operować na informacji nieco zaburzonej y
ν
, tzn. zabu-
rzonej na poziomie błędu reprezentacji. Tak samo wynik dawany przez
algorytm będzie w ogólności zaburzony na poziomie błędu reprezenta-
cji. W najlepszym więc wypadku wynikiem działania algorytmu w fl
ν
będzie (ϕ(y
ν
))
ν
zamiast ϕ(y). Algorytmy dające tego rodzaju wyniki
uznamy za posiadające najlepsze własności numeryczne w arytmetyce
fl
ν
i nazwiemy numerycznie poprawnymi.
Dokładniej, powiemy, że ciąg rzeczywisty a
ν
= (a
ν,1
, . . . , a
ν,n
) (a
właściwie rodzina ciągów {a
ν
}
ν
) jest nieco zaburzonym ciągiem a =
(a
1
, . . . , a
n
), jeśli istnieje stała K taka, że dla wszystkich dostatecznie
małych ν zachodzi
|a
ν,j
− a
j
| ≤ K ν |a
j
|,
1 ≤ j ≤ n,
(2.1)

14
ROZDZIAŁ 2. ALGORYTMY I ICH WŁASNOŚCI
albo ogólniej
ka
ν
− ak ≤ K ν kak,
(2.2)
gdzie k · k jest pewną normą w R
n
. W pierwszym przypadku mówimy
o zaburzeniu “po współrzędnych”, a w drugim o zaburzeniu w normie
k · k.
Zauważmy, że niewielkie zaburzenia po współrzędnych pociągają za
sobą niewielkie zaburzenia w normie. Rzeczywiście, jeśli (2.1) to również
ka
ν
− ak
∞
= max
1≤j≤n
|a
ν,j
− a
j
| ≤ K ν max
1≤j≤n
|a
j
| = K ν kak
∞
,
i korzystając z faktu, że w przestrzeni skończenie wymiarowej wszystkie
normy są równoważne otrzymujemy dla pewnych stałych K
1
i K
2
ka
ν
− ak ≤ K
1
ka
ν
− ak
∞
≤ K
1
K ν
kak
∞
≤ K
2
K
1
K ν
kak,
czyli nierówność (2.2) ze stałą K
2
K
1
K
zamiast K.
Definicja 2.1 Algorytm Φ rozwiązywania zadania nazywamy nume-
rycznie poprawnym w zbiorze danych F
0
⊂ F , jeśli dla każdej danej
f
∈ F
0
wynik fl
ν
(Φ(f)) działania algorytmu w arytmetyce fl
ν
można
zinterpretować jako nieco zaburzony wynik algorytmu w arytmetyce
idealnej dla nieco zaburzonej informacji y
ν
= (N(f))
ν
∈ N(F ) o f,
przy czym poziom zaburzeń nie zależy od f.
Formalnie znaczy to, że istnieją stałe K
1
, K
2
, oraz ν
0
>
0 takie, że
spełniony jest następujący warunek. Dla dowolnej ν ≤ ν
0
oraz informa-
cji y ∈ N(F
0
) można dobrać y
ν
∈ N(F ) oraz (ϕ(y
ν
))
ν
takie, że
ky
ν
− yk ≤ K
1
ν
kyk,
k (ϕ(y
ν
))
ν
− ϕ(y
ν
)k ≤ K
2
ν
kϕ(y
ν
)k,
oraz
fl
ν
(Φ(f)) = fl
ν
(ϕ(N(f))) = (ϕ(y
ν
))
ν
.
2
Zauważmy,że jeśli f ∈ R
n
, N(f) = (f
1
, . . . , f
n
), oraz algorytm jest
dokładny, Φ ≡ ϕ ≡ S, to numeryczną poprawność algorytmu można
równoważnie zapisać jako
fl
ν
(Φ(f)) = (S(f
ν
))
ν
.

2.4. ROLA UWARUNKOWANIA ZADANIA
15
2.4 Rola uwarunkowania zadania
Niech Φ(·) = ϕ(N(·)) będzie algorytmem numerycznie poprawnym dla
danych F
0
⊂ F . Wtedy jego błąd w fl
ν
można oszacować następująco:
kS(f) − fl
ν
(Φ(f))k = kS(f) − (ϕ(y
ν
))
ν
k
≤ kS(f) − ϕ(y)k + kϕ(y) − ϕ(y
ν
)k + kϕ(y
ν
) − (ϕ(y
ν
))
ν
k
≤ kS(f) − Φ(f)k + kϕ(y) − ϕ(y
ν
)k + K
2
ν
kϕ(y
ν
)k
≤ kS(f) − Φ(f)k + (1 + K
2
ν
)kϕ(y) − ϕ(y
ν
)k + K
2
ν
kϕ(y)k,
przy czym ky
ν
− yk ≤ K
1
ν
kyk. Stąd w szczególności wynika, że jeśli
algorytm jest numerycznie poprawny i ciągły ze względu na informację
y
, to
lim
ν→0
kS(f) − fl
ν
(Φ(f))k = kS(f) − Φ(f)k.
To znaczy, że dla dostatecznie silnej arytmetyki algorytm będzie się
zachowywał w fl
ν
prawie tak jak w arytmetyce idealnej.
Z powyższych wzorów wynika, że błąd w fl
ν
algorytmu numerycznie
poprawnego zależy w dużym stopniu od:
• dokładności algorytmu w arytmetyce idealnej,
• dokładności ν arytmetyki fl
ν
,
• wrażliwości algorytmu na małe względne zaburzenia informacji y.
Ponieważ dwa pierwsze punkty są raczej oczywiste, poświęcimy tro-
chę więcej uwagi jedynie trzeciemu.
Jeśli ϕ spełnia warunek Lipschitza ze stałą L, a dokładniej
kϕ(y
ν
) − ϕ(y)k ≤ L ky
ν
− yk,
to
kS(f) − fl
ν
(Φ(f))k
≤ kS(f) − Φ(f)k + (1 + K
2
ν
)Lky
ν
− yk + K
2
ν
kϕ(y)k
≤ kS(f) − Φ(f)k + (1 + K
2
ν
)LK
1
ν
kyk + K
2
ν
kϕ(y)k.
W tym przypadku błędy zaokrągleń zwiększają błąd bezwzględny al-
gorytmu proporcjonalnie do ν.

16
ROZDZIAŁ 2. ALGORYTMY I ICH WŁASNOŚCI
Bardziej jednak interesuje nas błąd względny. Wybierzmy “małe”
η
≥ 0 i przypuśćmy, że
kϕ(y
ν
) − ϕ(y)k ≤ M K
1
ν
max(η, kϕ(y)k),
dla pewnej M niezależnej od y, tzn. błąd względny informscji, ky
ν
−
y
k ≤ K
1
ν
kyk, przenosi się na błąd względny wyniku (w arytmetyce
idealnej) ze “współczynnikiem wzmocnienia” M, albo na błąd bez-
względny ze współczynnikiem Mη. (Zauważmy, że gdybyśmy wzięli
η
= 0 to dla y takiej, że ϕ(y) = 0 musiałoby być ϕ(y
ν
) = 0, co zwykle,
choć nie zawsze, nie jest prawdą.) Wtedy
kS(f) − fl
ν
(Φ(f))k
≤ kS(f) − Φ(f)k + (1 + K
2
ν
)MK
1
ν
max(η, kϕ(y)k) + K
2
ν
kϕ(y)k
= kS(f) − Φ(f)k + ν
M K
1
(1 + K
2
ν
) + K
2
max(η, kϕ(y)k).
W szczególności, gdy algorytm jest dokładny i korzysta z pełnej infor-
macji o f, tzn. S ≡ Φ ≡ ϕ, to błąd
kS(f) − fl
ν
(Φ(f))k
max(η, kS(f)k)
≤
M K
1
(1 + K
2
ν
) + K
2
ν
≈ (M K
1
+ K
2
) ν.
Stąd wynika, że jeśli (MK
1
+ K
2
)ν ≪ 1 to błąd względny algorytmu w
fl
ν
jest mały, o ile kS(f)k ≥ η. Błąd względny jest proporcjonalny do
dokładności ν, arytmetyki fl
ν
, współczynników proporcjonalności K
i
algorytmu numerycznie poprawnego, oraz do wrażliwości M zadania S
na małe względne zaburzenia danych.
Zwróćmy uwagę na istotny fakt, że interesują nas właściwie tylko
te zaburzenia danych (informacji), które powstają przy analizie algo-
rytmu numerycznie poprawnego. I tak, jeśli algorytm jest numerycznie
poprawny z pozornymi zaburzeniami danych w normie, to trzeba zba-
dać wrażliwość zadania ze względu na zaburzenia danych w normie.
Jeśli zaś mamy pozorne zaburzenia “po współrzędnych” (co oczywiście
implikuje pozorne zaburzenia w normie) to wystarczy zbadać uwarun-
kowanie zadania ze względu na zaburzenia “po współrzędnych”, itd.
Zadania, które nie są zbyt wrażliwe na “małe” względne zaburze-
nia danych, tzn. dla których M jest “niewielkie”, nazywamy ogólnie
zadaniami dobrze uwarunkowanymi.

2.5. PRZYKŁADY
17
2.5 Przykłady
Podamy teraz proste przykłady zadań, które mogą być rozwiązane al-
gorytmami mumerycznie poprawnymi. Oszacujemy też błędy tych al-
gorytmów.
2.5.1 Iloczyn skalarny
Załóżmy. że dla danych ciągów rzeczywistych o ustalonej długości n,
a
j
, b
j
, 1 ≤ j ≤ n, chcemy obliczyć
S
(a, b) =
n
X
j=1
a
j
b
j
.
Rozpatrzymy algorytm dokładny zdefiniowany powyższym wzorem i
korzystający z pełnej informacji o kolejnych współrzednych.
Oznaczmy przez ˜a
j
i ˜b
j
reprezentacje liczb a
j
i b
j
w fl
ν
, ˜a
j
= a
j
(1 +
α
j
), ˜b
j
= b
j
(1 + β
j
), oraz przez γ
j
i δ
j
błędy względne powstałe przy
kolejnych mnożeniach i dodawaniach. Oczywiście |α
j
|, |β
j
|, |γ
j
|, |δ
j
| ≤ ν.
Otrzymujemy
fl
ν
n
X
j=1
a
j
b
j
=
(fl
ν
(
n−1
X
j=1
a
j
b
j
) + ˜a
n
˜b
n
(1 + γ
n
)
(1 + δ
n
) = . . .
=
· · ·
˜a
1
˜b
1
(1 + γ
1
) + ˜a
2
˜b
2
(1 + γ
2
)
(1 + δ
2
)
+ · · · + ˜a
n
˜b
n
(1 + γ
n
)
(1 + δ
n
)
= ˜a
1
˜b
1
(1 + γ
1
)(1 + δ
2
) · · · (1 + δ
n
)
+ · · · + ˜a
j
˜b
j
(1 + γ
j
)(1 + δ
j
) · · · (1 + δ
n
)
=
n
X
j=1
a
j
b
j
(1 + e
j
),
gdzie w przybliżeniu (tzn. gdy ν → 0) mamy |e
1
| ˜
≤ (n+2)ν i |e
j
| ˜
≤ (n−
j
+4)ν, 2 ≤ j ≤ n. Algorytm naturalny jest więc numerycznie poprawny
w całym zbiorze danych, gdyż wynik otrzymany w fl
ν
można zinterpre-
tować jako dokładny wynik dla danych a
ν,j
= a
j
i b
ν,j
= b
j
(1 + e
j
), przy
czym kb
ν
− bk
p
˜
≤ (n + 2)νkbk
p
.
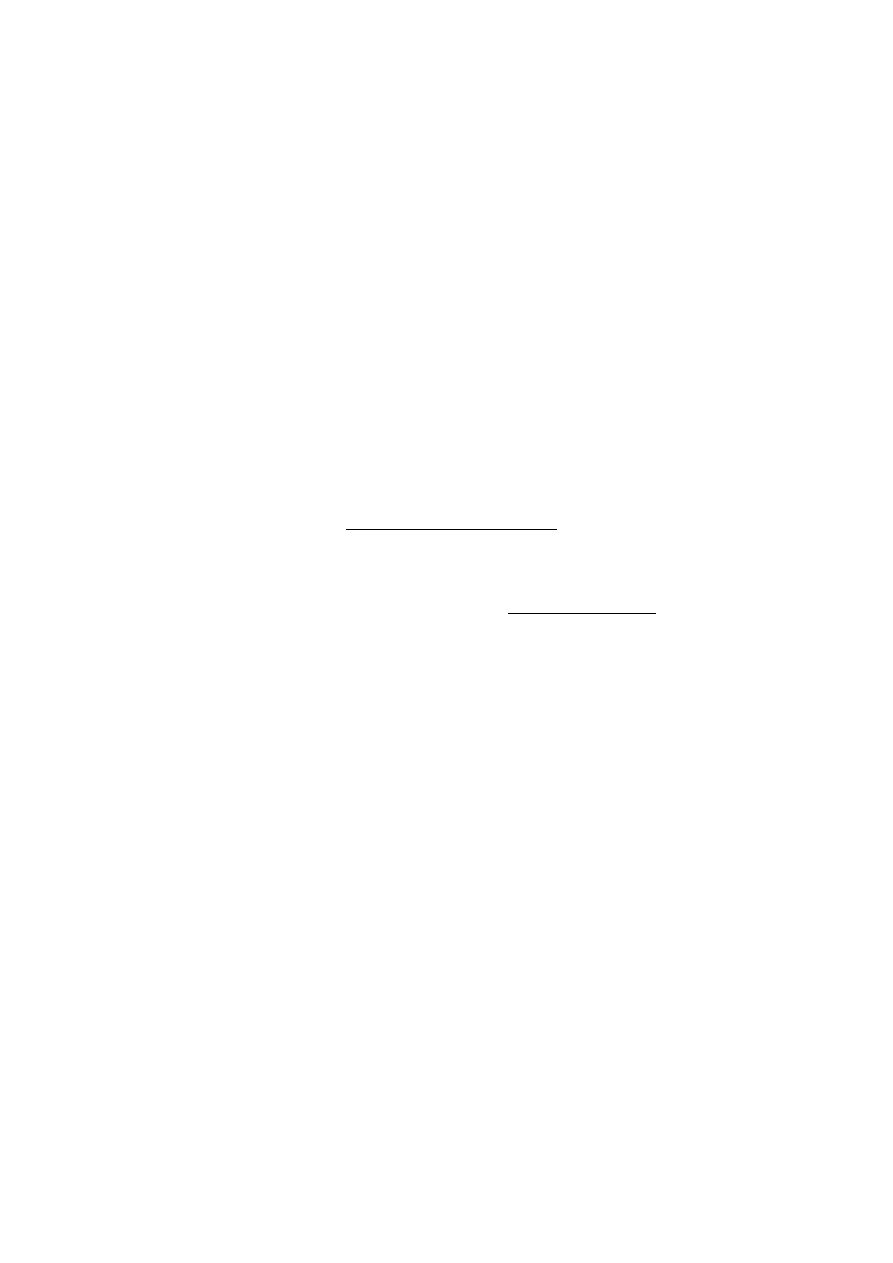
18
ROZDZIAŁ 2. ALGORYTMY I ICH WŁASNOŚCI
Zobaczmy teraz, jak błąd we współrzędnych b
j
wpływa na błąd
wyniku. Mamy
n
X
j=1
a
j
b
j
− fl
ν
n
X
j=1
a
j
b
j
=
n
X
j=1
a
j
b
j
−
n
X
j=1
a
j
b
j
(1 + e
j
)
=
n
X
j=1
e
j
a
j
b
j
≤
n
X
j=1
|e
j
||a
j
b
j
|
˜
≤ (n + 2)ν
n
X
j=1
|a
j
b
j
|.
Stąd dla η ≥ 0
|
P
n
j=1
a
j
b
j
− fl
ν
(
P
n
j=1
a
j
b
j
)|
max(η, |
P
n
j=1
a
j
b
j
|)
˜
≤ K
η
(n + 2) ν,
gdzie
K
η
= K
η
(a, b) =
P
n
j=1
|a
j
b
j
|
max(η, |
P
n
j=1
a
j
b
j
|)
.
Zauważmy, że jeśli iloczyny a
j
b
j
są wszystkie dodatnie albo wszyst-
kie ujemne, to K
η
= 1, tzn. zadanie jest dobrze uwarunkowane, a błąd
względny jest zawsze na poziomie co najwyżej nν. W tym przypadku
algorytm zachowuje się bardzo dobrze, o ile liczba n składników nie
jest horendalnie duża. W ogólności jednak K
η
może być liczbą dowol-
nie dużą i wtedy nie możemy być pewni uzyskania dobrego wyniku w
fl
ν
.
2.5.2 Całkowanie
Zadanie całkowania z Przykładu 1.3 często rozwiązuje się (a raczej przy-
bliża) stosując formułę
Φ(f) = ϕ(y) =
n
X
j=1
c
j
y
j
,
gdzie informacja y
j
= f(t
j
). t
j
są tu ustalonymi punktami z [a, b], a c
j
ustalonymi współczynnikami rzeczywistymi, niezależnymi od f. Algo-

2.5. PRZYKŁADY
19
rytmy korzystające z takich formuł nazywamy kwadraturami, a przy-
kładem jest zwykła suma Riemanna,
Φ
R
(f) =
1
n
n
X
j=1
f
(t
∗
j
),
gdzie t
∗
j
należy do przedziału [a + (j − 1)(b − a)/n, a + j(b − a)/n],
1 ≤ j ≤ n.
Z analizy algorytmu obliczającego iloczyn skalarny wynika, że kwa-
dratura jest algorytmem numerycznie poprawnym. Mamy bowiem
fl
ν
n
X
j=1
c
j
f
(t
j
)
=
n
X
j=1
c
j
y
j
(1 + e
j
),
gdzie |e
j
| ˜
≤ (n + 1)ν. (W porównaniu z iloczynem skalarnym mamy tu
n
+ 1 zamiast n + 2, bo c
j
nie jest daną i nie podlega zaburzeniu.) Stąd
błąd bezwzględny kwadratury w fl
ν
można oszacować następująco:
Z
b
a
f
(x) dx − fl
ν
n
X
j=1
c
j
f
(t
j
)
≤
Z
b
a
f
(x) dx −
n
X
j=1
c
j
f
(t
j
)
+ (n + 1) ν
n
X
j=1
|c
j
f
(t
j
)|.
Uwagi i uzupełnienia
U. 2.1 Wprowadzimy teraz formalną definicję zastosowanej już wcześniej
przybliżonej nierówności ˜
≤ . Dla dwóch funkcji piszemy
|h
1
(ν)| ˜≤ |h
2
(ν)|
gdy
lim sup
ν→0
|h
1
(ν)|/|h
2
(ν)| ≤ 1.
Na przykład, jeśli |h(ν)| ≤
P
n
j=1
K
j
ν
j
(K
1
> 0), to
|h(ν)| ˜
≤ K
1
ν, co już
zauważyliśmy w przykładzie z iloczynem skalarnym. Zapis ten wyraża prosty
fakt, że dla praktycznych wartości ν (ν ≤ 10
−8
) wyrazy typu ν
2
, ν
3
, itd. są
tak małe w porównaniu z ν, że można je zaniedbać.

20
ROZDZIAŁ 2. ALGORYTMY I ICH WŁASNOŚCI
Łatwo sprawdzić, że przy notacji ˜
≤ zachodzą następujące fakty. Jeśli
|ε| ˜
≤ Kν, |ε
1
| ˜
≤ K
1
ν i
|ε
2
| ˜
≤ K
2
ν (gdzie ε, ε
1
, ε
2
są funkcjami ν), to
(1 + ε
1
)(1 + ε
2
) = (1 + δ),
gdzie
|δ| ˜
≤ (K
1
+ K
2
)ν, (2.3)
(1 + ε)
−1
= (1 + δ),
gdzie
|δ| ˜
≤ Kν,
(2.4)
(1 + ε)
1/2
= (1 + δ),
gdzie
|δ| ˜
≤
1
2
Kν,
(2.5)
i ogólnie
(1 + ε)
p
= (1 + δ),
gdzie
|δ| ˜
≤ |p|ν.
(2.6)
U. 2.2 Rozpatrzymy teraz zadanie obliczenia wszystkich pierwiastków rze-
czywistych równania kwadratowego z Przykładu 1.1. Będziemy zakładać, że
model obliczeniowy dopuszcza obliczanie pierwiastków kwadratowych z liczb
nieujemnych oraz fl
ν
(√x) = rd(
p
rd (x)).
Okazuje się, że nie umiemy pokazać numerycznej poprawności “szkol-
nego” algorytmu obliczającego pierwiastki równania bezpośrednio ze wzorów
(1.1). Można jednak pokazać numeryczną poprawność drobnej jego modyfi-
kacji wykorzystującej wzory Viete’a.
∆ := p ∗ p − q;
if (∆ = 0) then OUT (p) else
if (∆ > 0) then
begin
∆1 := sqrt(d);
if (p ≥ 0) then
begin
x1 := p + ∆1;
x2 := q/x1;
end else
begin
x2 := p
− ∆1;
x1 := q/x2;
end;
OUT (x1); OUT (x2)
end.
Mamy bowiem
fl
ν
(∆(p, q)) =
p
2
(1 + α)
2
(1 + ε
1
) − q(1 + β)
(1 + ε
2
)
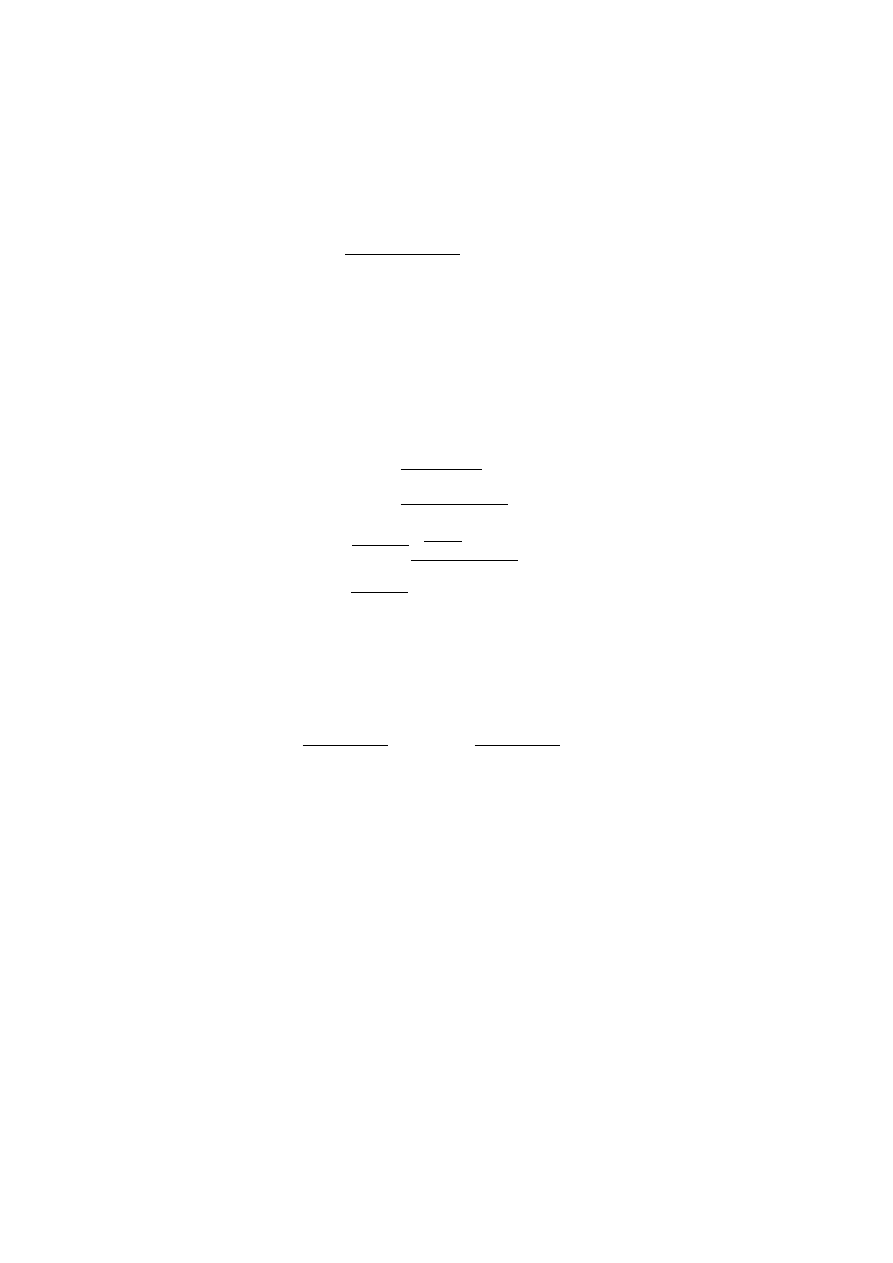
2.5. PRZYKŁADY
21
=
p
2
− q
(1 + β)
(1 + α)
2
(1 + ε
1
)
(1 + ε
2
)(1 + α)
2
(1 + ε
1
)
=
p
2
− q(1 + δ)
(1 + γ) = ∆(p, q(1 + δ))(1 + γ),
gdzie |δ|, |γ| ˜≤ 4ν. Wyróżnik obliczony w fl
ν
jest więc nieco zaburzonym wy-
różnikiem dokładnym dla danych p i q
ν
= q(1 + δ). W szczególności
sgn(fl
ν
(∆(p, q))) = sgn(∆(p, q
ν
)).
Jeśli p ≥ 0 to
fl
ν
(x1(p, q)) =
p(1 + α) +
q
fl
ν
(∆(p, q))(1 + ε
3
)
(1 + ε
4
)
=
p(1 + α) +
q
∆(p, q
ν
)(1 + γ)(1 + ε
3
)
(1 + ε
4
)
=
p +
q
∆(p, q
ν
)
√
1 + γ(1 + ε
3
)
1 + α
!
(1 + ε
4
)(1 + α)
=
p +
q
∆(p, q
ν
)
(1 + e
1
),
gdzie |e
1
| ˜
≤ 6ν. Zauważmy, że ostatnia równość zachodzi dlatego, że doda-
jemy liczby tego samego znaku. (Inaczej |e
1
| mogłaby być dowolnie duża i
tak byłoby w algorytmie szkolnym.) Dla drugiego pierwiastka mamy
fl
ν
(x2(p, q)) =
q(1 + β)
fl
ν
(x1(p, q))
(1 + ε
5
) =
q
ν
fl
ν
(x1(p, q))
(1 + e
2
),
gdzie |e
2
| ≤ 8ν.
Podobny wynik otrzymalibyśmy dla p < 0. Algorytm zmodyfikowany
jest więc numerycznie poprawny, gdyż otrzymane w fl
ν
pierwiastki są nieco
zaburzonymi dokładnymi pierwiatkami dla danych p
ν
= p i q
ν
= q(1 + δ).
Aby oszacować błąd algorytmu, wystarczy zbadać uwarunkowanie zada-
nia ze względu na zaburzenie danej q, ponieważ pokazaliśmy, że zaburzenia
p można przenieść na zaburzenia q i wyniku. Niestety, choć algorytm jest nu-
merycznie poprawny, zaburzenia q mogą sprawić, że nawet znak wyróżnika
∆ może być obliczony nieprawidłowo. Na przykład dla p = 1 i q = 1 ± 10
t+1
mamy ∆(p, q) = ∓10
t+1
, ale ∆(rd(p), rd(q)) = ∆(1, 1) = 0. Ogólnie
|fl
ν
(∆(p, q)) − ∆(p, q)| ˜≤ 4ν(p
2
+ 2|q|),

22
ROZDZIAŁ 2. ALGORYTMY I ICH WŁASNOŚCI
a więc tylko dla |∆(p, q)| = |p
2
− q| > 4ν(p
2
+ 2|q|) możemy być pewni
obliczenia właściwego znaku ∆. Przy tym warunku oraz ∆ > 0 błąd danych
przenosi się w normie euklidesowej na błąd wyniku następująco:
(x1(p, q) − x1(p, q
ν
))
2
+ (x2(p, q) − x2(p, q
ν
))
2
1/2
=
√
2|δq|
p
p
2
− q +
p
p
2
− q
ν
˜
≤ 2
√
2ν
|q|
p
p
2
− q
= 2
√
2ν
|q|/p
2
p
1 − q/p
2
max(η/|p|,
p
2(1 + (1 − q/p
2
)))
· max(η, (x1(p, q)
2
+ x2(p, q)
2
)
1/2
).
Stąd widać, że zadanie jest dobrze uwarunkowane dla q/p
2
≪ 1 i może być
źle uwarunkowane dla q/p
2
≈ 1. W ostatnim przypadku nie możemy być
pewni otrzymania dobrego wyniku w fl
ν
.
Ćwiczenia
Ćw. 2.1 Pokazać równości (2.3)–(2.6).
Ćw. 2.2 Niech 0 < a
1
< a
2
<
· · · a
n
. Czy z punktu widzenia błędów w fl
ν
lepiej jest policzyć sumę tych liczb w kolejności od najmniejszej do najwięk-
szej czy odwrotnie?
Ćw. 2.3 Aby obliczyć S(a, b) = a
2
− b
2
można zastosować dwa algorytmy:
Φ
1
(a, b) = a ∗ a − b ∗ b oraz Φ
2
(a, b) = (a + b) ∗ (a − b). Pokazać, że oba
algorytmy są numerycznie poprawne, ale drugi z nich wywołuje mniejszy
błąd względny wyniku w przypadku, gdy rd(a) = a i rd(b) = b.
Ćw. 2.4 Pokazać, że naturalny algorytm obliczania cosinusa kąta między
dwoma wektorami ~a,~b ∈ R
n
,
cos(a, b) =
P
n
j=1
a
j
b
j
r
P
n
j=1
a
2
j
P
n
j=1
b
2
j
,
jest numerycznie poprawny. Oszacować błąd względny wyniku w fl
ν
.

2.5. PRZYKŁADY
23
Ćw. 2.5 Pokazać, że naturalny algorytm obliczania kA~xk
2
dla danej ma-
cierzy A ∈ R
n×n
i wektora ~x ∈ R
n
jest numerycznie poprawny. Dokładniej,
fl
ν
(kA~xk
2
) = (A + E)~x,
gdzie kEk
2
˜
≤ 2(n + 2)
√
nν
kAk
2
. Ponadto, jeśli A jest nieosobliwa to
|fl
ν
(kA~xk
2
) − kA~xk
2
| ˜
≤ 2(n + 2)
√
n ν
kAk
2
kA
−1
k
2
kA~xk
2
.
Ćw. 2.6 Niech Φ będzie algorytmem numerycznie poprawnym w zbiorze
danych f ∈ F
0
, przy czym dla małych ν, fl
ν
(Φ(f)) = ϕ(y
ν
), gdzie ky
ν
−yk ≤
Kν
kyk i K nie zależy od ν i f (y = N(f)). Pokazać, że w ogólności Φ nie
musi być “numerycznie poprawny po współrzędnych”, tzn. w ogólności nie
istnieje bezwzględna stała K
1
taka, że dla małych ν i dla dowolnej f ∈ F
0
|y
ν,j
− y
j
| ≤ K
1
ν
|y
j
|,
1 ≤ j ≤ n,
gdzie y = (y
1
, . . . , y
n
).
æ ææ

24
ROZDZIAŁ 2. ALGORYTMY I ICH WŁASNOŚCI

Rozdział 3
Układy równań liniowych
Rozpoczynamy analizę metod dokładnych rozwiązywania układów rów-
nań liniowych postaci
A ~x
= ~b,
(3.1)
gdzie A = (a
i,j
)
n
i,j=1
jest macierzą nieosobliwą (det A 6= 0) wymiaru
n
× n, a ~b = (b
i
)
n
i=1
jest wektorem z R
n
. Zakładamy, że informacja
o zadaniu dana jest przez współczynniki a
i,j
macierzy i współrzędne
b
i
wektora. W wyniku powinniśmy uzyskać współrzędne x
∗
j
wektora
rozwiązania ~x
∗
= (x
∗
j
)
n
j=1
,
~x
∗
= A
−1
~b.
Przypomnijmy, że nieosobliwość macierzy A zapewnia, że rozwiązanie
~x
∗
istnieje i jest wyznaczone jednoznacznie.
3.1 Układy z macierzą trójkątną
Szczególnym przypadkiem (3.1) jest układ z macierzą trójkątną A.
Będą nas szczególnie interesować macierze trójkątne górne, dla których
a
i,j
= 0 gdy i > j, oraz macierze trójkątne dolne z jedynkami na prze-
kątnej, tzn. a
i,j
= 0, i < j, oraz a
i,i
= 1. Macierze pierwszego rodzaju
będziemy oznaczać przez R, a drugiego rodzaju przez L.
Układ z macierzą trójkątną górną
R ~x
= ~c,
(3.2)
25

26
ROZDZIAŁ 3. UKŁADY RÓWNAŃ LINIOWYCH
R
= (r
i,j
), ~c = (c
j
), można rozwiązać stosując algorytm:
x
∗
n
:= c
n
/r
n,n
;
for i := n
− 1 downto 1 do
x
∗
i
:=
c
i
−
P
n
j=i+1
r
i,j
x
∗
j
/r
i,i
.
(Algorytm ten jest wykonalny, ponieważ nieosobliwość macierzy impli-
kuje, że r
i,i
6= 0, ∀i.) Podobnie, układ L~x = ~c rozwiązujemy algoryt-
mem:
x
∗
1
:= c
1
;
for i := 2 to n do
x
∗
i
:= c
i
−
P
i−1
j=1
l
i,j
x
∗
j
.
Oba algorytmy wymagają rzędu n
2
/
2 mnożeń lub dzieleń i n
2
/
2 doda-
wań lub odejmowań, a więc rzędu n
2
wszystkich działań arytmetycz-
nych.
3.2 Eliminacja Gaussa
Eliminacja Gaussa jest algorytmem dokładnym rozwiązywania ukła-
dów równań z macierzą pełną A, polegającym na sprowadzeniu układu
wyjściowego (3.1) do układu trójkątnego (3.2).
W postaci rozwiniętej układ (3.1) ma postać
a
1,1
x
1
+ a
1,2
x
2
+ · · · + a
1,n
x
n
= b
1
a
2,1
x
1
+ a
2,2
x
2
+ · · · + a
2,n
x
n
= b
2
. . .
a
n,1
x
1
+ a
n,2
x
2
+ · · · + a
n,n
x
n
= b
n
.
Zauważmy, że jeśli od i-tego wiersza tego układu odejmiemy wiersz
pierwszy pomnożony przez l
i,1
= a
i,1
/a
1,1
, dla i = 2, 3, . . . , n (zakła-
damy, że a
1,1
6= 0) to otrzymamy układ równoważny A
(1)
~x
= ~b
(1)
,
a
1,1
x
1
+ a
1,2
x
2
+ · · · + a
1,n
x
n
= b
1
a
(1)
2,2
x
2
+ · · · + a
(1)
2,n
x
n
= b
(1)
2
. . .
a
(1)
n,2
x
2
+ · · · + a
(1)
n,n
x
n
= b
(1)
n
,

3.2. ELIMINACJA GAUSSA
27
z wyrugowaną zmienną x
1
z równań od drugiego do n-tego. Teraz z
kolei możemy od i-tego wiersza odjąć wiersz drugi pomnożony przez
l
i,2
= a
(1)
i,2
/a
(1)
2,2
, dla i = 3, 4, . . . , n (o ile a
(1)
2,2
6= 0), aby otrzymać układ
A
(2)
~x
= ~b
(2)
z wyrugowanymi zmiennymi x
1
i x
2
z równań od trzeciego
do n-tego. Postępując tak dalej otrzymujemy po n − 1 krokach układ
A
(n−1)
~x
= ~b
(n−1)
postaci
a
(0)
1,1
x
1
+ a
(0)
1,2
x
2
+ · · · + a
(0)
1,n
x
n
= b
1
a
(1)
2,2
x
2
+ · · · + a
(1)
2,n
x
n
= b
(1)
2
...
a
(n−1)
n,n
x
n
= b
(n−1)
n
.
Układ ten jest trójkątny górny, R~x = ~c, z macierzą R = A
(n−1)
i
wektorem ~c = ~b
(n−1)
, można go więc rozwiązać znaną już metodą.
Kolejne operacje w eliminacji Gaussa można zapisać następująco:
for k := 1 to n
− 1 do
for i := k + 1 to n do
begin
l
i,k
:= a
(k−1)
i,k
/a
(k−1)
k,k
;
b
(k)
i
:= b
(k−1)
i
− l
i,k
∗ b
(k−1)
k
;
for j := k + 1 to n do
a
(k)
i,j
:= a
(k−1)
i,j
− l
i,k
∗ a
(k−1)
k,j
end.
Zauważmy, że k-ty krok wymaga rzędu (n − k)
2
dodawań lub odejmo-
wań i tyle samo mnożeń lub dzieleń. Koszt całej eliminacji wynosi więc
2
P
n−1
k=1
(n − k)
2
≈ (2/3)n
3
operacji arytmetycznych. Ponieważ układ
trójkątny potrafimy rozwiązać kosztem n
2
, całkowity koszt rozwiązania
układu A~x = ~b jest również rzędu (2/3)n
3
.
Opisany powyżej proces eliminacyjny załamie się gdy dla pewnego
k
element a
(k−1)
k,k
będzie zerem. W takim przypadku prosta modyfikacja
polegająca na przestawieniu wiersza k-tego układu z wierszem s
k
-tym
(k + 1 ≤ s
k
≤ n) dla którego a
(k−1)
s
k
,k
6= 0, pozwala kontynuować elimi-
nację. Taki niezerowy element oczywiście istnieje, bo inaczej macierz
A
(k−1)
, a tym samym i macierz A, byłaby osobliwa.

28
ROZDZIAŁ 3. UKŁADY RÓWNAŃ LINIOWYCH
Najczęściej wybieramy s
k
tak, aby
|a
(k−1)
s
k
,k
| = max
k+1≤i≤n
|a
(k−1)
i,k
|,
co wymaga dodatkowo rzędu n
2
/
2 porównań liczb rzeczywistych i żad-
nych operacji arytmetycznych. Taki wybór elementu niezerowego pro-
wadzi do eliminacji Gaussa z wyborem elementu głównego w kolumnie.
Wtedy współczynniki l
i,k
= a
(k−1)
i,k
/a
(k−1)
k,k
są wszystkie co do modułu
nie większe od jedności co, jak się przekonamy później, ma niebaga-
telne znaczenie dla własności numerycznych całego algorytmu.
3.3 Rozkład trójkątny macierzy
Podamy teraz ważne twierdzenia wiążące eliminację Gaussa z rozkła-
dem trójkątno-trójkątnym macierzy A.
Twierdzenie 3.1 Eliminacja Gaussa bez przestawień wierszy (o ile
jest wykonalna) jest równoważna rozkładowi macierzy A na iloczyn ma-
cierzy trójkątnej dolnej L = (l
i,j
) (z jedynkami na przekątnej) i trójkąt-
nej górnej R = (r
i,j
). Dokładniej,
A
= L · R,
gdzie
l
i,j
=
a
(i−1)
i,j
/a
(i−1)
i,i
i > j,
1
i
= j,
0
i < j,
oraz
r
i,j
=
(
a
(i−1)
i,j
i < j,
0
i
≥ j.
Dowód Zauważmy, że rugowanie elementów pod główną przekątną
w k-tej kolumnie (k = 1, 2, . . . , n − 1) odpowiada mnożeniu układu

3.3. ROZKŁAD TRÓJKĄTNY MACIERZY
29
A
(k−1)
~x
= ~b
(k−1)
z lewej strony przez macierz
L
k
=
1
1
...
1
−l
k+1,k
1
...
...
−l
n,k
1
.
Stąd
L
n−1
L
n−2
· · · L
2
L
1
A
= R
i
A
= (L
−1
1
L
−1
2
· · · L
−1
n−2
L
−1
n−1
) R.
Łatwo sprawdzić, że macierz L
−1
k
różni się od L
k
tylko tym, że ele-
menty −l
i,k
dla k + 1 ≤ i ≤ n zmieniają się na l
i,k
. Ponadto, mnożenie
macierzy L
−1
k
przez siebie w podanej kolejności odpowiada ”przepisy-
waniu” elementów l
i,k
do macierzy wynikowej tak, że ostatecznie mamy
L
−1
1
· · · L
−1
n−1
= L i A = LR.
2
Zobaczmy teraz jak wybór elementu głównego w kolumnie i prze-
stawianie odpowiednich wierszy macierzy układu wpływa na rozkład
macierzy A z Twierdzenia 3.1.
Przestawienie wiersza k-tego z s-tym w danej macierzy jest formal-
nie równoważne pomnożeniu tej macierzy z lewej strony przez macierz
permutacji elementarnej P
k,s
. Jest to macierz, która powstaje z macie-
rzy jednostkowej przez przestawienie jej k-tego wiersza z s-tym (albo
k
-tej kolumny z s-tą). Eliminacja Gaussa z wyborem elementu głów-
nego w kolumnie odpowiada więc mnożeniu macierzy A z lewej strony
kolejno przez macierze permutacji elementarnej P
k,s
k
i macierze “elimi-
nacji” L
k
tak, że
L
n−1
P
n−1,s
n−1
L
n−2
P
n−2,s
n−2
· · · L
2
P
2,s
2
L
1
P
1,s
1
A
= R.
Ponieważ P
2
k,l
= I (identyczność), mamy
P
2,s
2
L
1
P
1,s
1
A
= (P
2,s
2
L
1
P
2,s
2
)(P
2,s
2
P
1,s
1
A
) = L
(1)
1
(P
2,s
2
P
1,s
1
A
),

30
ROZDZIAŁ 3. UKŁADY RÓWNAŃ LINIOWYCH
gdzie L
(1)
1
różni się od L
1
tym, że zostały przestawione elementy (2, 1)
i (s
2
,
1). Następnie,
P
3,s
3
L
2
L
(1)
1
(P
2,s
2
P
1,s
1
A
)
= (P
3,s
3
L
2
P
3,s
3
)(P
3,s
3
L
(1)
1
P
3,s
3
)(P
3,s
3
P
2,s
2
P
1,s
1
A
)
= L
(2)
2
L
(2)
1
(P
3,s
3
P
2,s
2
P
1,s
1
A
),
gdzie L
(2)
1
różni się od L
(1)
1
tym, że zostały przestawione elementy (3, 1)
i (s
3
,
1), a L
(2)
2
różni się od L
2
przestawieniem elementów (3, 2) i (s
3
,
2).
Postępując tak dalej otrzymujemy
L
n−1
P
n−1,s
n−1
· · · L
2
P
2,s
2
L
1
P
1,s
1
A
= L
(n−1)
n−1
L
(n−1)
n−1
· · · L
(n−1)
2
L
(n−1)
1
(P
n−1,s
n−1
· · · P
2,s
2
P
1,s
1
)A = R,
gdzie L
(n−1)
k
różni się od L
k
jedynie pewną permutacją elementów w
k
-tej kolumnie pod główną przekątną,
L
(n−1)
k
= P
n−1,s
n−1
· · · P
k+1,s
k+1
L
k
P
k+1,s
k+1
· · · P
n−1,s
n−1
.
Postępując dalej tak, jak w przypadku eliminacji bez przestawień wier-
szy, otrzymujemy następujący wniosek.
Wniosek 3.1 Eliminacja Gaussa z wyborem elementu głównego w ko-
lumnie jest wykonalna i jest równoważna rozkładowi
P
· A = L · R,
gdzie P = P
n−1,s
n−1
· · · P
2,s
2
P
1,s
1
jest macierzą permutacji, a L i R są
macierzami konstruowanymi tak jak w Twierdzeniu 3.1, ale dla macie-
rzy P A zamiast A. Ponadto wszystkie elementy macierzy L są co do
modułu nie większe od jedności.
2
Dodajmy, że znalezienie czynników rozkładu P A = LR dla danej
macierzy A kosztuje tyle samo co eliminacja Gaussa z wyborem ele-
mentu głównego, czyli (2/3)n
3
operacji arytmetycznych i n
2
/
2 porów-
nań.
W praktycznej realizacji rozkładu P A = LR oczywiście nie musimy
przy przestawieniu wierszy dokonywać fizycznie przepisań elementów

3.3. ROZKŁAD TRÓJKĄTNY MACIERZY
31
danego wiersza do innego. Wystarczy mieć dodatkowy n-wymiarowy
wektor permutacji p[] interpretowany w ten sposób, że p[i] jest wskaź-
nikiem do i-tego wiersza macierzy A. Przestawienie wierszy możemy
wtedy realizować po prostu przez zamianę wskaźników, czyli elemen-
tów wektora p. (Zob. U. 3.5.)
Twierdzenie 3.1 i Wniosek 3.1 mają nie tylko teoretyczne znaczenie.
Rozkładu macierzy na czynniki trójkątne (co w praktyce sprowadza się
do pamiętania kolejnych permutacji i mnożników l
i,j
) opłaca się doko-
nywać w przypadku, gdy zadanie polega na rozwiązaniu nie jednego,
ale wielu układów równań z tą samą macierzą A i ze zmieniającym się
wektorem prawej strony,
A ~x
= ~b
s
,
dla 1 ≤ s ≤ k.
Jeśli każdy z tych układów rozwiązujemy “od początku” to musimy
wykonać (2/3)n
3
k
operacji arytmetycznych. Koszt ten możemy znacz-
nie zredukować, jeśli dokonamy wstępnego rozkładu P A = LR. Wtedy
układ A~x = ~b
s
jest równoważny układowi LR~x = P~b
s
, a więc jego
rozwiązanie sprowadza się do rozwiązania dwóch znanych już układów
trójkątnych:
L ~y
= P ~b
s
i
R ~x
= ~y.
Taki sposób postępowania wymaga tylko (2/3)n
3
+2n
2
k
= 2n
2
(n/3+k)
operacji arytmetycznych, co np. przy k = n powoduje obniżenie rzędu
kosztu z n
4
do n
3
.
Uwagi i uzupełnienia
U. 3.1 Zaproponowany algorytm dla układów R~x = ~c z macierzą trójkątną
R ma prawie optymalną złożoność kombinatoryczną (n
2
) wśród algorytmów
dokładnych. Zauważmy bowiem, że jeśli algorytm jest dokładny to wykorzy-
stuje wszystkie dane r
i,j
i c
j
, 1 ≤ i, j ≤ n (zob. Ćw.3.1). Ponieważ każda
kolejna operacja arytmetyczna (+, −, ∗, /) może wykorzystywać co najwyżej
dwie nowe dane, a wszystkich danych jest n(n + 1)/2 + n ≈ n
2
/2, algorytm
dokładny musi wykonywać co najmniej n
2
/4 działań.

32
ROZDZIAŁ 3. UKŁADY RÓWNAŃ LINIOWYCH
U. 3.2 Znane są algorytmy dokładne, które rozwiązują układ równań z ma-
cierzą pełną kosztem proporcjonalnym do n
p
, gdzie p < 3, a więc mniejszym
niż w eliminacji Gaussa. Algorytmy te są jednak nieużyteczne ze względu na
skomplikowaną konstrukcję, zwykle dużą stłą przy n
p
, a także ze względu na
złe własności numeryczne. Oczywiście, ograniczeniem dolnym na wykładnik
p w koszcie rozwiązania układu z macierzą pełną jest 2 (bo mamy rzędu n
2
danych), ale nie wiadomo, czy może on być osiągnięty przez jakiś algorytm.
U. 3.3 Układy równań z tą samą macierzą, ale ze zmieniającą się prawą
stroną równania powstają często przy rozwiązywaniu, np. równań różniczko-
wych cząstkowych, gdzie prawa strona układu odpowiada zmieniającym się
warunkom brzegowym. Z wieloma układami tego typu mamy również do czy-
nienia gdy chcemy znaleźć macierz odwrotną do danej macierzy A ∈ R
n×n
.
Rzeczywiście, kolejne kolumny macierzy A
−1
są rozwiązaniami układów
A ~x = ~e
j
,
1 ≤ j ≤ n,
gdzie ~e
j
oznacza j-ty wersor.
U. 3.4 Obok wyboru elementu głównego w kolumnie dokonuje się również
wyboru elementu gównego w całej macierzy. To znaczy, w k-tym kroku eli-
minacyjnym wybiera się element a
(k−1)
s
k
,t
k
, k ≤ s
k
, t
k
≤ n, taki, że
|a
(k−1)
s
k
,t
k
| = max
k≤i,j≤n
|a
(k−1)
i,j
|,
a następnie przestawia się wiersze k-ty z s
k
-tym i kolumny k-tą z t
k
-tą w
macierzy A
(k−1)
. Zauważmy, że przestawienie kolumn macierzy odpowiada
mnożeniu jej z prawej strony przez macierz permutacji P
k,t
k
. Przyjmując
P = P
1,t
1
P
2,t
2
· · · P
n−1,t
n−1
i korzystając z Twierdzenia 3.1 i Wniosku 3.1
mamy, że eliminacja Gaussa z wyborem elementu głównego w całej macierzy
jest równoważna rozkładowi
P A P = L R.
U. 3.5 Podamy teraz jedną z możliwych implementacji algorytmu rozkładu
macierzy na iloczyn macierzy trójkątnych, P A = LR. W poniższym pro-
gramie współczynniki macierzy wyjściowej są pamiętane w tablicy a[, ]. Po
wykonaniu programu, informacja o permutacji wierszy zapamiętana będzie
w wektorze p[]. W a[p[i], j] będą elementy (i, j) macierzy L dla i > j, oraz
macierzy R dla i ≤ j.

3.3. ROZKŁAD TRÓJKĄTNY MACIERZY
33
{ inicjacja wskaźników }
for i := 1 to n do p[i] := i;
for j := 1 to n − 1 do
begin
{ wybór elementu głównego }
im := j;
val := abs(a[p[j], j]);
for i := j + 1 to n do
begin
v := abs(a[p[i], j]);
if v > val then
begin
im := i;
val := i
end;
{ zamiana wskaźników }
s := p[im];
p[im] := p[j];
p[j] := s;
{ eliminacja }
v := a[s, j];
for i := j + 1 to n do
begin
im := p[i];
l := a[im, j]/v;
a[im, j] := l;
for k := j + 1 to n do
a[im, k] := a[im, k]
− l ∗ a[s, k]
end;
end;
end.
U. 3.6 Przedstawiony algorytm eliminacji Gaussa rozwiązuje układy z ma-
cierzami dowolnej postaci. Jeśli macierz A jest szczególnej postaci to czasem
proste jego modyfikacje pozwalają znacznie zmniejszyć koszt uzyskania roz-
wiązania. Na przykład, niech A będzie macierzą trójdiagonalną postaci
A =
a
1
c
1
b
2
a
2
c
2
b
3
a
3
c
3
... ... ...
b
n
a
n
.
Wtedy układ A~x = ~e można rozwiązać stosując tzw. algorytm “przegania-
nia”:

34
ROZDZIAŁ 3. UKŁADY RÓWNAŃ LINIOWYCH
d
1
:= a
1
;
f
1
:= e
1
;
for i := 2 to n do
begin
l := b
i
/a
i−1
;
d
i
:= a
i
− l ∗ c
i−1
;
f
i
:= e
i
− l ∗ f
i−1
end;
x
∗
1
:= f
n
;
for i := n − 1 downto 1 do
x
∗
i
:= f
i
− c
i
∗ x
∗
i+1
.
Okazuje się, że jeśli macierz A ma dominującą przekątną, tzn.
|a
i
| ≥ |b
i
| + |c
i
|,
1 ≤ i ≤ n,
(3.3)
(b
1
= 0 = c
n
) i przynajmniej dla jednego i mamy powyżej nierówność <,
to algorytm przeganiania jest wykonalny bez przestawień wierszy. Ponadto
wymaga on 7n operacji arytmetycznych, a więc jest prawie optymalny.
U. 3.7 Innym ważnym przykładem macierzy szczególnej postaci są macierze
symetryczne i dodatnio określone. Są to macierze spełniające A = A
T
oraz
~x
T
A~x > 0,
∀~x 6= 0.
Dla takich macierzy można nieco zmniejszyć koszt kombinatoryczny i zużycie
pamięci przeprowadzając eliminację tak, aby otrzymać rozkład
A = L
· D · L
T
zamiast P A = LR, przy czym L jest tu jak zwykle macierzą trójkątną
dolną z jedynkami na przekątnej, a D jest macierzą diagonalną z dodatnimi
elementami na diagonali.
Rozkład taki przeprowadzamy mnożąc macierz A przez znane już ma-
cierze eliminacji nie tylko z lewej, ale też i z prawej strony, bez przestawień
wierszy. Bez zmniejszenia ogólności rozpatrzymy tylko pierwszy krok. W
tym celu, zauważmy najpierw, że a
1,1
= ~e
T
1
A~e
1
> 0 (gdzie ~e
1
jest pierw-
szym wersorem), a więc nie musimy przestawiać wierszy, bo element na
diagonali jest niezerowy. W pierwszym kroku mnożymy macierz A z lewej
strony przez odpowiednią macierz L
1
, a potem z prawej przez L
T
1
. Kluczem
do zrozumienia algorytmu jest uwaga, że efektem mnożenia macierzy L
1
A

3.3. ROZKŁAD TRÓJKĄTNY MACIERZY
35
z prawej strony przez L
T
1
jest wyzerowanie elementów pierwszego wiersza
poza a
1,1
i pozostawienie niezmienionych pozostałych elementów. Ponadto
macierz A
(1)
= L
1
AL
T
1
jest symetryczna i dodatnio określona. Rzeczywiście,
A
(1)
T
= (L
1
AL
T
1
)
T
= (L
T
1
)
T
A
T
L
T
1
= L
1
AL
T
1
,
oraz dla ~x 6= 0
~x
T
A
(1)
~x = ~x
T
L
1
AL
T
1
~x = (L
T
1
~x)
T
A(L
T
1
~x) > 0,
bo ~x 6= 0 implikuje L
T
1
~x
6= 0. Stąd a
(1)
2,2
= ~e
T
2
A
(1)
~e
2
> 0. Postępując tak dalej
otrzymujemy
L
n−1
L
n−2
· · · L
2
L
1
AL
T
1
L
T
2
· · · L
T
n−2
L
T
n−1
= D,
przy czym macierz D jest diagonalna i dodatnio określona, a więc wyrazy
na diagonali są dodatnie. Oznaczając
L = L
−1
1
L
−1
2
· · · L
−1
n−1
dostajemy żądany rozkład.
Zauważmy, że przy praktycznej realizacji rozkładu A = LDL
T
wystarczy
modyfikować jedynie wyrazy pod i na głównej przekątnej macierzy wyjścio-
wej, ponieważ, jak zauważyliśmy, wszystkie kolejne macierze A
(k)
są syme-
tryczne. Pozwala to zmniejszyć koszt kombinatoryczny o połowę do n
3
/3
operacji arytmetycznych. Opisany sposób rozkładu macierzy A = A
T
> 0
nosi nazwę metody Banachiewicza-Choleskiego. (Zob. Ćw. 3.9.)
U. 3.8 Rozkład trójkątno-trójkątny macierzy może być zastosowany rów-
nież do policzenia wyznacznika macierzy A. Jeśli bowiem P A = LR to
detA = (−1)
s
r
1,1
r
2,2
· · · r
n,n
,
gdzie s jest liczbą przestawień wierszy w eliminacji.
Ćwiczenia
Ćw. 3.1 Pokazać, że jeśli algorytm rozwiązywania układu równań z ma-
cierzą pełną (lub trójkątną) nie wykorzystuje wszystkich współczynników
macierzy i wektora, to istnieją macierz A i wektor ~b takie, że algorytm dla
tych danych nie daje dokładnego rozwiązania w arytmetyce idealnej.

36
ROZDZIAŁ 3. UKŁADY RÓWNAŃ LINIOWYCH
Ćw. 3.2 Znaleźć macierz odwrotną do macierzy trójkątnej.
Ćw. 3.3 Pokazać, że iloczyn elementarnych macierzy permutacji jest ma-
cierzą, która w każdym wierszu i w każdej kolumnie ma dokładnie jedną
jedynkę. I odwrotnie, jeśli pewna macierz ma w każdym wierszu i kolumnie
dokładnie jedną jedynkę to jest ona iloczynem pewnej liczby elementarnych
macierzy permutacji.
Ćw. 3.4 Pokazać, że jeśli dla danej macierzy A i permutacji P istnieje co
najwyżej jeden rozkład P A = LR na macierz trójkątną dolną L z jedynkami
na przekątnej i na macierz trójkątną górną R.
Ćw. 3.5 Pokazać, że w algorytmie eliminacji Gaussa (bez przestawień) ele-
menty l
i,j
i r
i,j
obliczane są według wzorów
l
i,j
= (a
i,j
−
j−1
X
k=1
l
i,k
r
k,j
)/r
j,j
,
j = 1, 2 . . . , i
− 1,
r
i,j
= a
i,j
−
i−1
X
k=1
l
i,k
r
k,j
,
j = i, i + 1, . . . , n,
dla i = 1, 2, . . . , n. Wywnioskować stąd rozkład A = LR z Twierdzenia 3.1.
Ćw. 3.6 Pokazać, że przy spełnieniu warunku (3.3) algorytm “przegania-
nia” z U. 3.6 jest wykonalny bez przestawień wierszy. Opracować algorytm
rozwiązywania układu z macierzą trójdiagonalną nie spełniającą warunku
(3.3).
Ćw. 3.7 Pokazać, że jeśli macierz pełna A ma dominującą przekątną, tzn.
2|a
i,i
| >
n
X
j=1
|a
i,j
|,
1 ≤ i ≤ n,
to jest to macierz dodatnio określona, ~x
T
A~x > 0 dla ~x
6= 0. Ponadto, elimi-
nacja Gaussa jest dla takich macierzy wykonalna bez przestawień wierszy.
Ćw. 3.8 Opracować algorytm eliminacyjny dla rozwiązywania układów li-
niowych z macierzą Hessembega, czyli macierzą dla której a
i,j
= 0, o ile
i
≥ j + 2.

3.3. ROZKŁAD TRÓJKĄTNY MACIERZY
37
Ćw. 3.9 Opracować program rozkładający macierz symetryczną i dodatnio
określoną A na iloczyn A = LDL
T
według metody Banachiewicza-Choleskie-
go z U. 3.7. Obliczenia przeprowadzać w tej samej macierzy A pozostawiając
elementy na i nad diagonalą nie zmienione i otrzymując w wyniku macierz
L pod główną diagonalą macierzy A, a macierz D jako dodatkowy wektor.
æ

38
ROZDZIAŁ 3. UKŁADY RÓWNAŃ LINIOWYCH

Rozdział 4
Analiza błędów w eliminacji
Gaussa
Zastanowimy się teraz, jak przebiega w arytmetyce fl
ν
realizacja algo-
rytmu eliminacji Gaussa z wyborem elementu głównego w kolumnie.
4.1 Układy z macierzą trójkątną
Najpierw pokażemy, że algorytmy rozwiązywania układów trójkątnych
zaprezentowane w Rozdziale 3.1 są numerycznie poprawne. Rozpatrzmy
najpierw układ trójkątny górny, R~x = ~c. Wykorzystując fakt, że licze-
nie iloczynu skalarnego jest numerycznie poprawne, mamy
fl
ν
(x
∗
n
) =
c
n
(1 + β
n
)
r
n,n
(1 + α
n,n
)
(1 + δ
n
) =
c
ν
n
r
ν
n,n
i dla i = n − 1, n − 2, . . . , 1,
fl
ν
(x
∗
i
)
=
c
i
(1 + β
i
) −
P
n
j=i+1
r
i.j
(1 + α
i,j
)fl
ν
(x
∗
j
)(1 + γ
i,j
)
(1 + ω
i
)
r
i,i
(1 + α
i,i
)(1 + δ
i
)
−1
=
c
ν
i
−
P
n
j=i+1
r
ν
i,j
fl
ν
(x
∗
j
)
r
ν
i,i
,
gdzie c
ν
i
= c
i
(1 + β
i
), r
ν
i,i
= r
i,i
(1 + α
i,i
)(1 + δ
i
)
−1
, r
ν
i,j
= r
i,j
(1 + α
i,j
)(1 +
γ
i,i
), czyli |c
ν
i
− c
i
| ≤ ν|c
i
| i |r
ν
i,j
− r
i,j
| ˜
≤ (n + 1)ν|r
i,j
|. Stąd otrzymane w
39

40 ROZDZIAŁ 4. ANALIZA BŁĘDÓW W ELIMINACJI GAUSSA
fl
ν
rozwiązanie jest dokładnym rozwiązaniem dla danych R
ν
= (r
ν
i,j
)
i,j
i ~c
ν
= (c
ν
j
)
j
, przy czym
kR
ν
− Rk
∞
˜
≤ (n + 1) ν kRk
∞
i
k~c
ν
− ~ck
∞
˜
≤ ν k~ck
∞
.
Zauważmy, że macierz zaburzona R
ν
jest nieosobliwa. Powyższy algo-
rytm jest więc numerycznie poprawny w klasie nieosobliwych macierzy
trójkątnych górnych.
Zauważmy również, że jeśli wektor prawej strony ~c jest reprezento-
wany dokładnie (β
i
= 0), to błąd pochodzący z odejmowania można
przenieść na zaburzenia r
i,i
tak, że ~c
ν
= ~c. Fakt ten wykorzystamy
później.
Przeprowadzając podobną analizę dla układu L~x = ~c z macierzą
trójkątną dolną z jedynkami na przekątnej dostajemy, że otrzymane w
fl
ν
rozwiązanie jest dokładnym rozwiązaniem układu L
ν
~x
= ~c
ν
, gdzie
kL
ν
− Lk
∞
˜
≤ (n + 1) ν kLk
∞
i
k~c
ν
− ~ck
∞
˜
≤ ν k~ck
∞
.
4.2 Poprawność rozkładu trójkątnego
Zajmiemy się teraz jakością numeryczną rozkładu macierzy na iloczyn
trójkątno-trójkątny. W poniższym twierdzeniu norma macierzy jest do-
wolna, ale ustalona.
Twierdzenie 4.1 Niech A
∈ R
n×n
będzie macierzą nieosobliwą. Dla
dostatecznie silnej arytmetyki (tzn. dla dostatecznie małego ν) rozkład
trójkątno-trójkątny macierzy za pomocą eliminacji Gaussa z wyborem
elementu głównego w kolumnie jest wykonalny w arytmetyce fl
ν
. Otrzy-
mane w wyniku macierze permutacji P
ν
, trójkątna górna R
ν
i trójkątna
dolna L
ν
(z jedynkami na przekątnej i elementami co do modułu nie
większymi od jedności) spełniają równość
P
ν
· (A + E) = L
ν
· R
ν
,
gdzie
kEk ≤ K(n) ν kAk,
a K(n) jest pewną stałą niezależną od ν i A.

4.2. POPRAWNOŚĆ ROZKŁADU TRÓJKĄTNEGO
41
Dowód Załóżmy najpierw dla uproszczenia, że eliminacja jest w fl
ν
wykonalna i że nie musimy dokonywać przestawień wierszy, tzn. w
k
-tym kroku elementem głównym jest obliczona wartość a
(k−1)
k,k
.
Zobaczmy jak zmieniają się elementy a
(k)
i,j
przy realizacji algorytmu
Gaussa w arytmetyce fl
ν
. Dla uniknięcia nadmiaru indeksów, będziemy
oznaczać przez ˜
w
wartość w obliczoną w fl
ν
. Rozpatrzymy dwa przy-
padki, i ≤ j i i > j.
Niech najpierw i ≤ j. Niech ε
(s)
i,j
będzie błędem bezwzględnym wy-
tworzonym przy obliczaniu wartości a
(s)
i,j
mając obliczone a
(s−1)
i,j
, l
i,s
i
a
(s−1)
s,j
. (Błąd ten oszacujemy później). Ponieważ a
(k)
i,j
= a
(k−1)
i,j
−l
i,k
a
(k−1)
k,j
,
otrzymujemy
˜a
(k)
i,j
= ˜a
(k−1)
i,j
− ˜l
i,k
˜a
(k−1)
k,j
+ ε
(k)
i,j
(4.1)
= ˜a
(k−2)
i,j
− ˜l
i,k−1
˜a
(k−2)
k−1,j
+ ε
(k−1)
i,j
− ˜l
i,k
˜a
(k−1)
k,j
+ ε
(k)
i,j
= . . .
= ˜a
(0)
i,j
+
k−1
X
s=1
−˜l
i,s
˜a
(s−1)
s,j
+ ε
(s)
i,j
.
Wobec tego, że a
(0)
i,j
= a
i,j
, mamy ˜a
(0)
i,j
= a
i,j
+ ε
(0)
i,j
z |ε
(0)
i,j
| ≤ ν|a
i,j
|.
Ponadto ˜a
(i−1)
i,j
= ˜r
i,j
, bo i-ty wiersz jest modyfikowany tylko w krokach
od 1-go do (i − 1)-szego. Stąd, podstawiając k = i − 1, otrzymujemy
˜r
i,j
= ˜a
(i−1)
i,j
= a
i,j
+
i−1
X
s=0
ε
(s)
i,j
−
i−1
X
s=1
˜l
i,s
˜r
s,j
,
albo
a
i,j
+ e
i,j
= ˜r
i,j
+
i−1
X
s=1
˜l
i,s
˜r
s,j
,
(4.2)
gdzie e
i,j
=
P
i−1
s=0
ε
(s)
i,j
.
Dla i > j mamy podobnie
˜a
(j−1)
i,j
= a
i,j
+ ε
(0)
i,j
+
j−1
X
s=1
−˜l
i,s
˜a
(s−1)
s,j
+ ε
(s)
i,j
.
(4.3)
Wobec tego, że
˜l
i,j
=
˜a
(j−1)
i,j
˜a
(j−1)
j,j
(1 + δ
i,j
),

42 ROZDZIAŁ 4. ANALIZA BŁĘDÓW W ELIMINACJI GAUSSA
otrzymujemy
˜a
(j−1)
i,j
= ˜l
i,j
˜a
j−1
j,j
+ ε
(j)
i,j
,
|ε
(j)
i,j
| ≤ ν|˜a
(j−1)
i,j
|,
a stąd, (4.3) i z faktu, że ˜a
(s−1)
s,j
= ˜r
i,j
,
a
i,j
+ e
i,j
=
j
X
s=1
˜l
i,s
˜r
s,j
,
(4.4)
gdzie e
i,j
=
P
j
s=0
ε
(s)
i,j
.
Z (4.2) i (4.4) wynika równość
(A + E) = ˜
L
· ˜
R
(4.5)
z macierzą E = (e
i,j
). Ponadto elementy ˜l
i,j
są co do modułu nie większe
od jedności, ponieważ |˜a
(j−1)
i,j
| ≤ |˜a
(j−1)
j,j
| (zob. Ćw. 1.2).
Aby zakończyć dowód, trzeba jeszcze oszacować błąd |e
i,j
|. W tym
celu zauważmy, że dla k ≥ 1
˜a
(k)
i,j
=
˜a
(k−1)
i,j
− ˜l
i,k
˜a
(k−1)
k,j
(1 + ω
1
)
(1 + ω
2
),
ω
1
, ω
2
≤ ν. Stąd i z (4.1) otrzymujemy
ε
(k)
i,j
= ˜a
(k)
i,j
− ˜a
(k−1)
i,j
+ ˜l
i,k
˜a
(k−1)
k,j
= ˜a
(k)
i,j
−
˜a
(k)
i,j
1 + ω
2
+ ω
1
˜l
i,k
˜a
(k−1)
k,j
=
ω
2
1 + ω
2
˜a
(k)
i,j
+ ω
1
˜l
i,k
˜a
(k−1)
k,j
oraz
|ε
(k)
i,j
| ≤
ν
1 − ν
(|˜a
(k)
i,j
| + |˜a
(k−1)
k,j
|).
Niech teraz G
0
= max
i,j
|a
i,j
|,
G
k
= max
i,j
|˜a
(k)
i,j
|,
oraz G = max
0≤k≤n−1
G
k
. Dla i ≤ j mamy
|e
i,j
| ≤
i−1
X
s=0
|ε
(s)
i,j
| ≤
ν
1 − ν
G
0
+
i−1
X
s=1
(G
s−1
+ G
s
)
=
ν
1 − ν
G
i−1
+ 2
i−2
X
s=0
G
s
≤
ν
1 − ν
(2i − 1)G,

4.2. POPRAWNOŚĆ ROZKŁADU TRÓJKĄTNEGO
43
a dla i > j
|e
i,j
| ≤
j
X
s=0
|ε
(s)
i,j
| ≤
ν
1 − ν
G
0
+
j
X
s=1
(G
s−1
+ G
s
)
=
ν
1 − ν
G
j
+ 2
j−1
X
s=0
G
s
≤
ν
1 − ν
(2j + 1)G.
W obu przypadkach
|e
i,j
| ≤
2ν
1 − ν
nG.
(4.6)
Łatwo zauważyć, że ˜a
(1)
i,j
˜
≤ (|a
i,j
| + |a
k,j
|)(1 + 2ν) oraz
|˜a
(k)
i,j
| ≤ (|˜a
(k−1)
i,j
| + |˜a
(k−1)
k,j
|)(1 + ν),
co implikuje G
k
˜
≤ 2G
k−1
, a w konsekwencji
G ˜
≤ 2
n−1
max
i,j
|a
i,j
|.
Ostatnia nierówność oraz (4.6) dają
|e
i,j
| ˜
≤ n2
n
ν
max
i,j
|a
i,j
|,
a ponieważ dla dowolnej macierzy B ∈ R
n×n
mamy
1
n
kBk
∞
≤ max
i,j
|a
i,j
| ≤ kBk
∞
,
to
kEk
∞
≤ K(n) ν kAk
∞
,
gdzie K(n) jest na poziomie n
2
2
n
. Z równoważności norm w R
n×n
wy-
nika, że podobna nierówność zachodzi dla dowolnej, innej niż k · k
∞
normy, ale być może z inną stałą K(n).
Oczywiście, ewentualne permutacje wierszy nie zmieniają tych osza-
cowań, a powodują jedynie przemnożenie lewej strony równości (4.5)
przez pewną macierz permutacji.

44 ROZDZIAŁ 4. ANALIZA BŁĘDÓW W ELIMINACJI GAUSSA
Aby zakończyć dowód, trzeba jeszcze pokazać, że dla dostatecznie
małych ν rozkład jest wykonalny, co jest równoważne temu, że macierz
(A + E) jest nieosobliwa. Rzeczywiście, weźmy ν > 0 spełniające
ν K
(n) kAk
∞
kA
−1
k
∞
<
1.
(4.7)
Jeśliby macierz (A + E) była osobliwa to dla pewnego niezerowego
wektora ~x mielibyśmy (A+E)~x = A(I +A
−1
E
)~x = 0, a w konsekwencji
kA
−1
E~x
k
∞
= k~xk
∞
i
1 ≤ kA
−1
E
k
∞
≤ kA
−1
k
∞
kEk
∞
≤ K(n)νkAk
∞
kA
−1
k
∞
,
co przeczy (4.7).
2
Zauważmy, że warunek (4.7) na wykonalność rozkładu w fl
ν
zależy
od macierzy A poprzez wielkość
cond(A) = kAk kA
−1
k.
Wielkość tą nazywa się uwarunkowaniem macierzy. Z Twierdzenia 4.1
oraz warunku (4.7) wynika ważny wniosek o numerycznej poprawności
rozkładu w klasie macierzy o uwarunkowaniu wspólnie ograniczonym
przez pewną stałą.
Wniosek 4.1 Niech M > 0. W klasie macierzy nieosobliwych A ta-
kich, że
cond(A) =
kAk kA
−1
k ≤ M
rozkład P A = LR jest numerycznie poprawny. Dokładniej, dla ν <
1/(MK(n)) rozkład w fl
ν
jest wykonalny, a otrzymane macierze P
ν
,
L
ν
i R
ν
pochodzą z dokładnego rozkładu macierzy (A+E), gdzie
kEk ≤
K
(n)νkAk.
2
4.3 Poprawność rozwiązywania układu
Przypomnijmy, że algorytm eliminacji Gaussa rozwiązywania układów
równań A~x = ~b polega na rozkładzie macierzy na iloczyn P A = LR, a
następnie na rozwiązaniu dwóch układów trójkątnych (albo, równoważ-
nie, na sprowadzeniu układu do postaci trójkątnej i rozwiązaniu go).
Numeryczna poprawność każdego z tych etapów algorytmu daje nam
również numeryczną poprawność całego algorytmu.

4.3. POPRAWNOŚĆ ROZWIĄZYWANIA UKŁADU
45
Twierdzenie 4.2 Niech M > 0. Algorytm eliminacji Gaussa z wybo-
rem elementu głównego w kolumnie zastosowany do rozwiązania układu
równań
A~x
= ~b
jest numerycznie poprawny w klasie danych wektorów ~b
∈ R
n
oraz ma-
cierzy nieosobliwych A
∈ R
n×n
spełniających
cond(A)
≤ M.
Dowód Dla dostatecznie silnej arytmetyki, rozkład macierzy A daje
w fl
ν
P
1
(A + E
1
) = L
1
R
1
, gdzie kE
1
k ≤ K
1
ν
kAk. W drugim kroku,
otrzymane w fl
ν
rozwiązanie ~y
1
układu L
1
~y
= P
1
~b jest dokładnym roz-
wiązaniem układu (L
1
+ E
2
)~y = P
1
(~b + ~e), gdzie kE
2
k ≤ K
2
ν
kL
1
k
oraz k~ek ≤ K
3
ν
k~bk. Z kolei w ostatnim kroku algorytmu, rozwiązując
układ R
1
~x
= ~y
1
dostajemy w fl
ν
rozwiązanie ~x
ν
, które jest dokład-
nym rozwiązaniem układu (R
1
+ E
3
)~x = ~y
1
, gdzie kE
3
k ≤ K
3
ν
kR
1
k.
(Zauważmy, że wektor ~y
1
nie jest zaburzony, bo jest on reprezentowany
dokładnie, zob. Rozdział 4.1). Stąd otrzymane w fl
ν
rozwiązanie ~x
ν
jest
dokładnym rozwiązaniem układu
A
ν
~x
= ~b
ν
,
gdzie ~b
ν
= ~b + ~e, a A
ν
= A + E spełnia równanie
P
1
(A + E) = (L
1
+ E
2
) (R
1
+ E
3
).
Aby zakończyć dowód, należy teraz oszacować kEk. Ponieważ P
1
(A +
E
1
) = L
1
R
1
, mamy
P
1
E
= P
1
E
1
+ L
1
E
3
+ E
2
R
2
+ E
2
E
3
.
Stąd
kEk
∞
≤ kE
1
k
∞
+ kL
1
k
∞
kE
3
k
∞
+ kE
2
k
∞
kR
2
k
∞
+ kE
2
k
∞
kE
3
k
∞
˜
≤ νK
1
kAk
∞
+ kL
1
k
∞
νK
3
kR
1
k
∞
+ kR
1
k
∞
νK
2
kL
1
k
∞
= ν
K
1
kAk
∞
+ (K
2
+ K
3
)kL
1
k
∞
kR
1
k
∞
.
Ponieważ elementy macierzy L
1
są co do modułu nie większe od jedno-
ści, mamy kL
1
k
∞
≤ n. Jak zauważyliśmy wcześniej, mamy też kR
1
k
∞
≤

46 ROZDZIAŁ 4. ANALIZA BŁĘDÓW W ELIMINACJI GAUSSA
n
2
n−1
kAk
∞
. Przyjmując K = K
1
+ (K
2
+ K
3
)n
2
2
n−1
ostatecznie otrzy-
mujemy
kEk
∞
≤ K ν kAk
∞
,
czyli numeryczną poprawność, ponieważ stała K nie zależy od ν i A.
2
4.4 Uwarunkowanie macierzy, a błąd w
fl
ν
Pokazaliśmy, że eliminacja Gaussa jest numerycznie poprawna w klasie
macierzy A ∈ R
n×n
takich, że
cond(A) ≤ M,
gdzie M < ∞ jest jakąkolwiek stałą niezależną od A. Okazuje się, że
wielkość uwarunkowania macierzy, cond(A), ma też zasadniczy wpływ
na błąd zadania rozwiązywania układu równań. Rzeczywiście, mamy
bowiem następujące twierdzenie. (Poniżej norma wektorowa jest do-
wolna, ale ustalona, a norma macierzowa jest przez nią indukowana,
zob. U. 1.2.)
Twierdzenie 4.3 Niech E i ~e będą zaburzeniami odpowiednio macie-
rzy A i wektora ~b takimi, że
kEk ≤ K
1
ν
kAk
i
k~ek ≤ K
2
ν
k~bk,
Jeśli
K
1
νcond(A) < 1
to układ zaburzony (A + E)~x = (~b + ~e) ma jednoznaczne rozwiązanie ~z
∗
spełniające
k~z
∗
− ~x
∗
k ≤ (K
1
+ K
2
) ν
cond(A)
1 − K
1
νcond(A)
k~x
∗
k.

4.4. UWARUNKOWANIE MACIERZY, A BŁĄD W FL
ν
47
Dowód Zauważmy najpierw, że jeśli F jest macierzą taką, że
kF k < 1
to macierz (I − F ) (gdzie I jest macierzą identycznościową) jest nie-
osobliwa oraz
k(I − F )
−1
k ≤
1
1 − kF k
.
(4.8)
Rzeczywiście, gdyby (I−F ) była osobliwa to istniałby niezerowy wektor
~x
taki, że (I − F )~x = 0, co implikuje kF~xk/k~xk = 1 i w konsekwencji
kF k ≥ 1. Aby pokazać (4.8) zauważmy, że
1 = kIk = k(I − F )(I − F )
−1
k
≥ k(I − F )
−1
k − kF k k(I − F )
−1
k
= (1 − kF k) k(I − F )
−1
k,
skąd bezpośrednio wynika (4.8).
Po podstawieniu F = −A
−1
E
mamy teraz
kF k ≤ kA
−1
k kEk ≤ K
1
ν
kAk kA
−1
k < 1,
co wobec równości A + E = A(I + A
−1
E
) daje, że macierz (A + E)
jest nieosobliwa i układ zaburzony ma jednoznaczne rozwiązanie ~z
∗
.
Przedstawmy to rozwiązanie w postaci ~z
∗
= ~x
∗
+ (~z
∗
− ~x
∗
). Rozpisując
układ zaburzony i wykorzystując równość A~x
∗
= ~b otrzymujemy, że
(A + E)(~z
∗
− ~x
∗
) = ~e − E~x
∗
, czyli
~z
∗
− ~x
∗
= (I + A
−1
E
)
−1
A
−1
(~e − E~x
∗
),
a stąd
k~z
∗
− ~x
∗
k ≤ k(I + A
−1
E
)
−1
k kA
−1
k (k~ek + kEk k~x
∗
k
≤
kA
−1
k
1 − K
1
ν
kAk kA
−1
k
K
2
ν
k~bk + K
1
ν
kAk k~x
∗
k
≤
kAk kA
−1
k
1 − K
1
ν
kAk kA
−1
k
(K
1
+ K
2
) ν k~x
∗
k,
co kończy dowód.
2
Podsumowując Twierdzenia 4.2 i 4.3 otrzymujemy wniosek, który
jest końcowym wynikiem tego rozdziału.

48 ROZDZIAŁ 4. ANALIZA BŁĘDÓW W ELIMINACJI GAUSSA
Wniosek 4.2 Niech A będzie macierzą nieosobliwą. Dla dostatecznie
silnej arytmetyki,
ν K
(n) cond(A) ≪ 1
(gdzie K(n) jest pewną stłą niezależną od A i ν), eliminacja Gaussa z
wyborem elementu głównego w kolumnie, zastosowana do rozwiązania
układu A~x = ~b, jest w fl
ν
wykonalna i daje wynik fl
ν
(~x
∗
) spełniający
nierówność
kfl
ν
(~x
∗
) − ~x
∗
k ˜
≤ K(n) ν cond(A) k~x
∗
k.
2
Uwagi i uzupełnienia
U. 4.1 Jak zauważyliśmy w dowodzie Twierdzenia 4.1 stała kumulacji K(n)
zależy zasadniczo od wzrostu maksymalnego elementu G
k
w macierzach A
(k)
powstających w kolejnych krokach eliminacji. Okazuje się, że uzyskane, pe-
symistyczne oszacowanie G = max
k
G
k
≤ 2
n−1
G
0
jest praktycznie nie spo-
tykane, choć teoretycznie może być osiągnięte. Przykładem jest macierz
1
0
0 · · ·
0 1
−1
1
0
... 1
−1 −1
1
... 1
...
0
...
1 1
−1 −1 −1 · · · −1 1
,
dla której G
k
= 2
k
G
0
, 0 ≤ k ≤ n − 1, oraz G = 2
n−1
G
0
.
U. 4.2 Eliminacja Gaussa bez przestawień wierszy jest numerycznie po-
prawna, gdy element maksymalny w kolejnych macierzach A
(k)
wzrasta w
sposób niezależny od A. Na przykład, gdy G
k
≤ mG
k−1
to G ≤ m
k−1
G
0
i w
Twierdzeniu 4.1 mamy K(n) = 2n
2
m
k−1
. Ma to miejsce wtedy gdy A jest
symetryczna i dodatnio określona, albo ma dominującą główną przekątną,
zob. U. 4.3 oraz Ćw. 4.5 i 4.6.
U. 4.3 Dla macierzy symetrycznych i dodatnio określonych, A = A
T
> 0,
eliminacja Gaussa jest wykonalna bez przestawień wierszy, zob. U. 3.7. W
klasie tych macierzy eliminacja bez przestawień wierszy jest też numerycz-
nie poprawna, a więc w szczególności algorytm Banachiewicza-Choleskiego
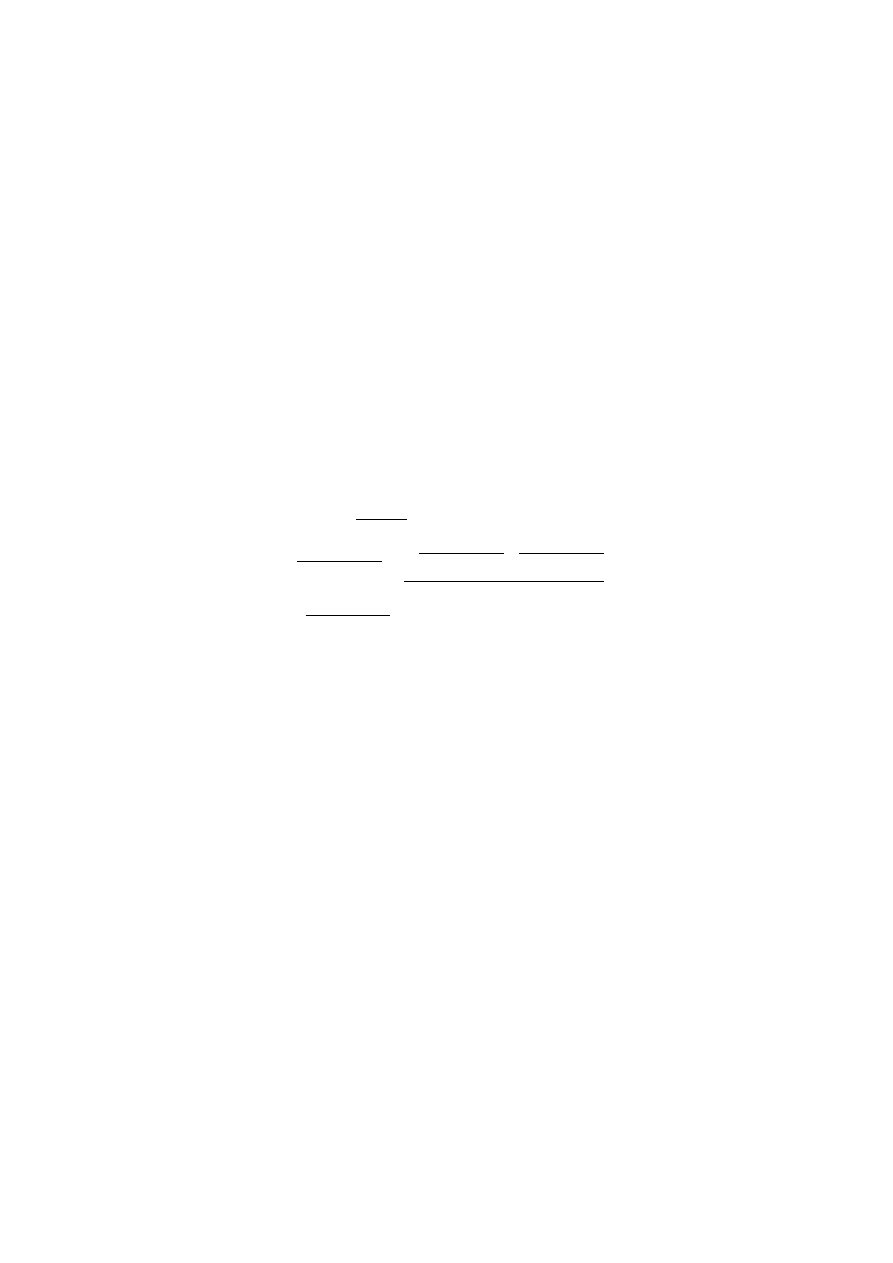
4.4. UWARUNKOWANIE MACIERZY, A BŁĄD W FL
ν
49
jest numerycznie popeawny. Wykażemy to pokazując, że maksymalny ele-
ment w kolejnych macierzach A
(k)
wzrasta co najwyżej dwukrotnie, tzn.
G
k
≤ 2G
k−1
, 1 ≤ k ≤ n. W tym celu wykorzystamy fakt, że dla dowolnej
symetrycznej i dodatnio określonwj macierzy B = (b
i,j
) mamy b
i,i
> 0, oraz
spełniona jest nierówność
b
2
i,j
< b
i,i
b
j,j
,
∀i, j
(4.9)
(zob. Ćw. 4.1). Jak wykazaliśmy w U. 3.7, każda z macierzy A
(k)
jest syme-
tryczna i dodatnio określona, Stąd
|a
(k)
i,j
| = |a
(k−1)
i,j
− l
i,k
a
(k−1)
k,j
|
≤ |a
(k−1)
i,j
| +
|a
(k−1)
i,k
|
|a
(k−1)
k,k
|
|a
(k−1)
k,j
|
≤
r
a
(k−1)
i,i
a
(k−1)
j,j
+
q
a
(k−1)
i,i
a
(k−1)
k,k
q
a
(k−1)
k,k
a
(k−1)
j,j
a
(k−1)
k,k
= 2
r
a
(k−1)
i,i
a
(k−1)
j,j
≤ 2 max(a
(k−1)
i,i
, a
(k−1)
j,j
),
a w konsekwencji G
k
≤ 2G
k−1
.
Ćwiczenia
Ćw. 4.1 Wykazać, że macierz symetryczna 2 × 2
a c
c b
!
jest dodatnio określona wtedy i tylko wtedy, gdy a > 0 i ab > c
2
. Wywnio-
skować stąd nierównosc (4.9) dla macierzy symetrycznych i dodatnio określo-
nych dowolnego wymiaru. Ponadto, największy co do modułu element takiej
macierzy leży na głównej diagonali.
Ćw. 4.2 Wykazać, że macierz A jest dodatnio określona wtedy i tylko wtedy
gdy dla każdego ~x ∈ R
n
wektory A~x i ~x tworzą w R
n
kąt ostry.

50 ROZDZIAŁ 4. ANALIZA BŁĘDÓW W ELIMINACJI GAUSSA
Ćw. 4.3 Pokazać, że jeśli eliminację Gaussa z wyborem elementu głównego
w kolumnie zastosujemy do macierzy trójdiagonalnej, to wzrost elementu
maksymalnego macierzy nie będzie zależał od n. Dokładniej,
max
i,j,k
|a
(k)
i,j
| ≤ 2 max
i,j
|a
i,j
|.
Ćw. 4.4 Pokazać, że dla macierzy Hessenberga (a
i,j
= 0 dla i ≥ j + 2)
eliminacja Gaussa z wyborem elementu głównego w kolumnie daje
max
i,j,k
|a
(k)
i,j
| ≤ (k + 1) max
i,j
|a
i,j
|.
Ćw. 4.5 Pokazać numeryczną poprawność algorytmu przeganiania z U. 3.6.
Ćw. 4.6 Wykazać numeryczną poprawność eliminacji Gaussa bez przesta-
wień wierszy dla macierzy z dominującą przekątną, tzn. gdy
2|a
i,i
| >
n
X
j=1
|a
i,j
|,
1 ≤ i ≤ n.
Wskazówka. Zauważyć, że max
i,j
|a
(k)
i,j
| ≤ 2 max
i,j
|a
(k−1)
i,j
|.
Ćw. 4.7 Jeśli
(A + E)~z = ~b,
(4.10)
gdzie kEk
p
≤ KνkAk
p
, to oczywiście dla residuum ~r = ~b − A~z mamy
k~rk
p
≤ KνkAk
p
k~zk
p
.
(4.11)
Pokazać, że dla p = 1, 2, ∞ zachodzi też twierdzenie odwrotne, tzn. jeśli
spełniony jest warunek (4.11) to istnieje macierz pozornych zaburzeń E taka,
że kEk
p
≤ KνkAk
p
oraz spełniona jest równość (4.10).
Wskazówka. Rozpatrzyć E = ~r(sgn z
i
)
T
1≤i≤n
/
k~zk
1
dla p = 1, E = ~r~z
T
/
k~zk
2
2
dla p = 2, oraz E = ~r(sgn z
k
)~e
T
k
/
k~zk
∞
dla p = ∞, gdzie k jest indeksem dla
którego |z
k
| = k~zk
∞
.

Rozdział 5
Zadanie wygładzania
liniowego
W tym rozdziale zajmiemy się zadaniem wygładzania liniowego, na-
zywanym też liniowym zadaniem najmniejszych kwadratów. Jest ono
uogólnieniem zadania rozwiązywania kwadratowych układów równań
liniowych do przypadku, gdy układ jest nadokreślony.
5.1 Układ normalny
Niech A będzie daną macierzą o m wierszach i n kolumnach, A ∈ R
m×n
,
taką, że
m
≥ n = rank(A),
albo równoważnie, taką że jej wektory kolumny są liniowo niezależne.
Niech także dany będzie wektor ~b ∈ R
m
. Jasne jest, że wtedy układ
równań A~x = ~b nie zawsze ma rozwiązanie - mówimy, że układ jest
nadokreślony.
Zadanie wygładzania liniowego polega na znalezieniu wektora ~x
∗
∈
R
n
, który minimalizuje wektor residualny ~r = ~b −A~x w normie drugiej,
tzn.
k~b − A~x
∗
k
2
= min
~
x∈
R
n
k~b − A~xk
2
.
Przykład 5.1 Przypuśćmy, że dla pewnej funkcji f : [a, b]
→ R ob-
serwujemy jej wartości f
i
(dokładne lub zaburzone) w punktach t
i
,
51

52
ROZDZIAŁ 5. ZADANIE WYGŁADZANIA LINIOWEGO
1 ≤ i ≤ m. Funkcję tą chcielibyśmy przybliżyć inną funkcją w nale-
żącą do pewnej n wymiarowej przestrzeni liniowej W , np. przestrzeni
wielomianów stopnia mniejszego niż n. Jakość przybliżenia mierzymy
wielkością
m
X
i=1
(f
i
− w(t
i
))
2
.
(5.1)
Wybierając pewną bazę (w
j
)
n
j=1
w W i rozwijając w w tej bazie, w(t) =
P
n
j=1
c
j
w
j
(t), sprowadzamy problem do minimalizacji
m
X
i=1
f
i
−
n
X
j=1
c
j
w
j
(t
i
)
2
względem c
j
, a więc do zadania wygładzania liniowego. Rzeczywiście,
kładąc A = (a
i,j
) ∈ R
m×n
z a
i,j
= w
j
(t
i
), ~b = (f
i
)
m
i=1
i ~x = (c
j
)
n
j=1
,
wielkość (5.1) jest równa k~b − A~xk
2
2
.
Lemat 5.1 Zadanie wygładzania liniowego ma jednoznaczne rozwiąza-
nie ~x
∗
, które spełnia układ równań
A
T
A~x
= A
T
~b.
(5.2)
Dowód Niech P
⊂ R
m
będzie obrazem A jako odwzorowania liniowego
z R
n
w R
m
,
P
= { A~x : ~x ∈ R
n
}.
Ponieważ kolumny macierzy A są liniowo niezależne, tworzą one bazę
w P . Stąd dim(P ) = n i odwzorowanie A : R
n
→ P jest różnowar-
tościowe. Ponadto przestrzeń R
m
z normą drugą jest przestrzenią uni-
tarną. Residuum jest więc minimalizowane dla wektora ~x
∗
∈ R
n
ta-
kiego, że A~x
∗
jest rzutem prostopadłym wektora ~b na podprzestrzeń P .
(Przypomnijmy, że skończony wymiar P zapewnia, że taki rzut istnieje
i jest wyznaczony jednoznacznie.) Równoważnie można powiedzieć, że
residuum ~b − A~x
∗
jest prostopadłe do P ,
(A~x)
T
(~b − A~x
∗
) = 0,
∀~x ∈ R
n
,
albo
x
T
( ~
A
T
~b − A
T
A~x
∗
) = 0.
∀~x ∈ R
n
.

5.1. UKŁAD NORMALNY
53
Otrzymaliśmy więc, że wektor A
T
~b − A
T
A~x
∗
jest prostopadły w R
n
do
każdego innego wektora. Ponieważ jedynym wektorem o tej własności
jest wektor zerowy, to A
T
A~x
∗
= A
T
~b.
2
Zauważmy, że jeśli macierz A jest kwadratowa, m = n, to rozwią-
zaniem jest ~x
∗
= A
−1
~b i residuum jest zerem. Zadanie wygładzania li-
niowego jest więc uogólnieniem rozwiązywania kwadratowych układów
równań liniowych.
Równanie (5.2) nazywa się układem normalnym. Może ono nam
sugerować sposób rozwiązania zadania wygładzania liniowego. Wystar-
czy bowiem pomnożyć macierz A
T
przez A i rozwiązać układ normalny.
Zauważmy ponadto, że macierz A
T
A
jest symetryczna i dodatnio okre-
ślona, bo (A
T
A
)
T
= A
T
A
i dla ~x 6= 0 mamy ~x
T
(A
T
A
)~x = (A~x)
T
(A~x) =
kA~xk
2
>
0, przy czym ostatnia nierówność wynika z faktu, że kolumny
macierzy A są liniowo niezależne i dlatego A~x 6= ~0. Przy mnożeniu A
T
przez A wystarczy więc obliczyć tylko elementy na głównej przekątnej
i pod nią, a do rozwiązania równania z macierzą A
T
A
można zastoso-
wać algorytm Banachiewicza-Choleskiego opisany w U. 3.7. Jak łatwo
się przekonać, koszt takiego algorytmu wynosi n
2
(k + n/3), przy czym
dominuje koszt mnożenia obliczenia macierzy A
T
A
.
Ma on jednak pewne wady. Mnożenie macierzy powoduje w fl
ν
po-
wstanie “po drodze” dodatkowych błędów, które mogą nawet zmienić
rząd macierzy. Na przykład, dla macierzy
A
=
1 1 1 1
ε
ε
ε
ε
mamy
A
T
A
=
1 + ε
2
1
1
1
1
1 + ε
2
1
1
1
1
1 + ε
2
1
1
1
1
1 + ε
2
.
Jeśli ε
2
< ν
to fl
ν
(1+ε
2
) = 1, co implikuje rank(fl
ν
(A
T
A
)) = 1, podczs
gdy rank(fl
ν
(A)) = 4.

54
ROZDZIAŁ 5. ZADANIE WYGŁADZANIA LINIOWEGO
Poniżej przedstawimy inną metodę rozwiązywania zadania wygła-
dzania liniowego, która oparta jest na specjalnych przekształceniach
zwanych odbiciami Hauseholdera.
5.2 Odbicia Hauseholdera
Dla danego wektora ~
w
∈ R
m
o normie k~wk
2
=
√
~
w
T
~
w
= 1, odbicie
(macierz) Hauseholdera zdefiniowane jest jako
H
= I − 2~w ~w
T
.
Zauważmy, że
H~x
= ~x − 2(~w
T
~x
) ~
w,
a ponieważ ( ~
w
T
~x
) ~
w
= h~x, ~wi
2
~
w
jest rzutem prostopadłym ~x na kieru-
nek wektora ~
w
(h·, ·i
2
oznacza iloczyn skalarny), to H~x jest odbiciem
lustrzanym wektora ~x względem hiperpłaszczyzny (wymiaru m − 1)
prostopadłej do ~
w
.
Odbicia Hauseholdera są przekształceniami nieosobliwymi spełnia-
jącymi
H
−1
= H = H
T
.
Rzeczywiście, ponieważ ~
w
ma normę jednostkową, mamy
H
2
= (I − 2~w ~w
T
)
2
= I − 4~w ~w
T
+ 4 ~
w
( ~
w
T
~
w
) ~
w
T
= I,
oraz
H
T
= (I − 2~w ~w
T
)
T
= I − 2(~w
T
)
T
~
w
T
= I.
W szczególności H jest więc przekształceniem ortogonalnym, H
−1
=
H
T
, czyli nie zmienia długości wektora,
kH~xk
2
=
q
(H~x)
T
(H~x) =
q
~x
T
(H
T
H
)~x =
√
~x
T
~x
= k~xk
2
.
Odbicia Hauseholdera zastosujemy do przeprowadzenia danego wek-
tora ~a 6= ~0 na kierunek innego niezerowego wektora, powiedzmy ~e, tzn.
H~a
= (I − 2~w ~w
T
)~a = α ~e.

5.2. ODBICIA HAUSEHOLDERA
55
Załóżmy dla uproszczenia, że k~ek
2
= 1. Aby wyznaczyć H zauważmy,
że
~
w
=
~a
− α~e
2( ~
w
T
~a
)
,
a ponieważ α = ±k~ak
2
i k~wk
2
= 1 to
~
w
=
~a
∓ k~ak
2
~e
k~a ∓ k~ak
2
~e
k
2
.
W szczególności, jeśli ~e = ~e
1
jest pierwszym wersorem to powyższe
wzory dają
H
= I −
~u~u
T
γ
,
gdzie
u
i
=
(
a
1
∓ k~ak
2
i
= 1,
a
i
2 ≤ i ≤ m,
oraz
γ
=
1
2k
~u
k
2
2
=
1
2
(a
1
∓ k~ak
2
)
2
+
m
X
i=2
a
2
i
=
1
2
m
X
i=1
a
2
i
+ k~ak
2
2
∓ 2a
1
kak
2
= kak
2
2
∓ a
1
kak
2
.
Otrzymaliśmy dwa odbicia Hauseholdera przekształcające dany wektor
~a
na kierunek pierwszego wersora, w zależności od wybranego znaku
przy k~ak
2
. Ustalimy ten znak na plus gdy a
1
≥ 0, oraz na minus gdy
a
1
<
0, co pozwoli na obliczenie u
1
i γ z małym błędem względem w
fl
ν
. Wtedy bowiem mamy
u
1
=
(
a
1
+ kak
2
a
1
≥ 0,
a
1
− kak
2
a
1
<
0,
oraz γ = k~ak
2
2
+ |a
1
| k~ak
2
, czyli zawsze dodajemy liczby tych samych
znaków. Ponadto pierwsza współrzędna wektora H~a jest równa −k~ak
2
dla a
1
≥ 0, oraz +k~ak
2
dla a
1
<
0.

56
ROZDZIAŁ 5. ZADANIE WYGŁADZANIA LINIOWEGO
5.3 Algorytm dla zadania wygładzania
Odbić Hauseholdera można użyć do rozkładu macierzy A ∈ R
m×n
na
iloczyn ortogonalno-trójkątny.
Niech A = (~a
1
, ~a
2
, . . . , ~a
n
), gdzie ~a
j
są wektorami-kolumnami macie-
rzy A. Wybierzmy pierwsze odbicie Hauseholdera H
1
= I
m
− ~u
1
~u
T
1
/γ
1
tak, aby przekształcało pierwszy wektor-kolumnę macierzy A na kieru-
nek ~e
1
. Efektem pomnożenia macierzy A z lewej strony przez H
1
będzie
wtedy macierz
A
(1)
= (~a
(1)
1
, . . . , ~a
(1)
n
) = (H
1
~a
1
, . . . , H
1
~a
n
),
w której pierwsza kolumna ~a
(1)
1
ma niezerową tylko pierwszą współ-
rzędną. W następnym kroku wybieramy drugie przekształcenie Hause-
holdera ¯
H
2
= I
m−1
− ~v
2
~v
T
2
/γ
2
wymiaru m − 1 tak, aby przeprowadzało
wektor (a
(1)
i,2
)
m
i=2
na kierunek pierwszego wersora w R
m−1
. Rozszerzając
~v
2
∈ R
m−1
do wektora ~u
2
∈ R
m
przez dodanie zera jako pierwszej
współrzędnej, ~u
2
= (0, ~v
2
)
T
, otrzymujemy przekształcenie (macierz)
Hauseholdera H
2
= I
m
− ~u
2
~u
T
2
/γ
2
w R
m
postaci
H
2
=
1 ~0
T
~0 ¯
H
2
!
.
Pomnożenie macierzy A
(1)
z lewej strony przez H
2
spowoduje teraz
wyzerowanie drugiej kolumny macierzy pod elementem a
(1)
2,2
, przy czym
pierwszy wiersz i pierwsza kolumna pozostaną niezmienione. Postępując
tak dalej n razy (albo n − 1 razy gdy m = n) otrzymujemy
H
n
H
n−1
· · · H
2
H
1
A
= R,
gdzie R ∈ R
m×n
jest uogólnioną macierzą trójkątną górną, tzn. r
i,j
= 0
dla i > j. Stąd, podstawiając Q = H
1
H
2
· · · H
n
, dostajemy rozkład
macierzy na iloczyn ortogonalno-trójkątny
A
= Q · R.
(5.3)
Rzeczywiście, macierz Q ∈ R
m×m
jest ortogonalna, bo
Q
−1
= (H
1
H
2
· · · H
n
)
−1
= H
−1
n
· · · H
−1
2
H
−1
1
= H
T
n
· · · H
T
2
H
T
1
= (H
1
H
2
· · · H
n
)
T
= Q
T
.

5.3. ALGORYTM DLA ZADANIA WYGŁADZANIA
57
Dyspunując rozkładem (5.3) zadanie wygładzania liniowego można
rozwiązać następująco. Ponieważ mnożenie przez macierz ortogonalną
nie zmienia normy drugiej wektora, mamy
k~rk
2
= k~b − A~xk
2
= k~b − QR~xk
2
= kQ(Q
T
~b − R~x)k
2
= k~c − R~xk
2
,
gdzie ~c = Q
T
~b = H
n
· · · H
2
H
1
~b. Rozbijając wektor ~c na ~c = (~c
I
, ~c
II
)
T
,
gdzie ~c
I
∈ R
n
i ~c
II
∈ R
m−n
, oraz macierz R na
R
=
R
I
0
!
,
gdzie R
I
∈ R
n×n
jest macierzą trójkątną górną, a 0 jest macierzą zerową
wymiaru (m − n) × n, otrzymujemy
k~rk
2
2
= k~c
I
− R
I
~x
k
2
2
+ k~c
II
k
2
2
.
Rozwiązanie ~x
∗
zadania wygładzania jest więc rozwiązaniem układu
liniowego trójkątnego,
~x
∗
= R
−1
I
~c
I
,
oraz k~r
∗
k
2
= k~b − A~x
∗
k
2
= k~c
II
k
2
.
Zastanówmy się nad praktyczną realizacją tego algorytmu. Każde z
kolejnych przekształceń Hauseholdera H
k
wyznaczamy przez obliczenie
γ
k
oraz współrzędnych wektora ~u
k
. Wektor ten ma tylko m − k + 1
współrzędnych niezerowych, a ponadto u
k,i
= a
(k−1)
i,k
dla k + 1 ≤ i ≤ m.
Dzięki takiej reprezentacji H
k
, mnożenia H
k
~x
możemy dla dowolnego
~x
realizować według wzoru
(H
k
~x
)
i
= x
i
− s u
k,i
,
gdzie s = ~u
T
k
~x/γ
k
.
Uwzględnizjąc obecność zerowych elementów w ~u
k
, przejście od ma-
cierzy A
(k−1)
do A
(k)
kosztuje rzędu 4(m−k+1)(n−k) operacji arytme-
tycznych i obliczenie jednego pierwiastka kwadratowego. Cały rozkład
A
= QR kosztuje więc rzędu (dla dużych m i n)
n
X
k=1
4(m − k + 1)(n − k) ≈
4
3
n
3
+ 2n
2
(m − n) = 2n
2
(m − n/3)

58
ROZDZIAŁ 5. ZADANIE WYGŁADZANIA LINIOWEGO
operacji arytmetycznych i n pierwiastków kwadratowych. Zauważmy,
że w przypadku m = n, a więc dla kwadratowego układu równań, koszt
ten wynosi (4/3)n
3
i jest dwa razy większy od kosztu eliminacji Gaussa.
Uwagi i uzupełnienia
U. 5.1 Pokazaliśmy, że rozwiązaniem zadania wygładzania liniowego jest
wektor ~x
∗
= A
+
~b, gdzie
A
+
= (A
T
A)
−1
A
T
.
Macierz A
+
∈ R
n×m
nazywa się macierzą pseudoodwrotną do A ∈ R
m×n
,
rank(A) = n. Dla nieosobliwych macierzy kwadratowych mamy oczywiście
A
+
= A
−1
, ponieważ wtedy ~x
∗
= A
−1
.
U. 5.2 Pokażemy, że każdą macierz A
m×n
, rank(A) = n, można rozłożyć
na iloczyn
A = U Σ V
T
,
(5.4)
gdzie U ∈ R
m×m
i V ∈ R
n×n
są macierzami ortogonalnymi, a Σ ∈ R
m×n
jest macierzą diagonalną (tzn. σ
i,j
= 0 dla i 6= j) o dodatnich wyrazach σ
i,i
.
Ponieważ macierz A
T
A jest symetryczna i dodatnio określona, znane
twierdzenie z algebry liniowej mówi, że istnieje w R
n
baza ortonormalna
(~ξ
j
)
n
j=1
wektorów własnych tej macierzy, a odpowiadające im wartości własne
są rzeczywiste i dodatnie, tzn.
h~ξ
i
, ~
ξ
j
i
2
=
(
0
i
6= j,
1
i = j,
oraz (A
T
A)~
ξ
j
= λ
j
~
ξ
j
, gdzie
λ
1
≥ λ
2
≥ · · · ≥ λ
n
> 0.
Zauważmy, że wektory ~η
i
= λ
−1/2
i
(A~ξ
i
) są ortonormalne w R
m
, bowiem
h~η
i
, ~η
j
i
2
= (λ
i
λ
j
)
−1/2
hA~ξ
i
, A~
ξ
j
i
2
= (λ
i
λ
j
)
−1/2
h(A
T
A)~
ξ
i
, ~
ξ
j
i
2
= (λ
i
λ
j
)
−1/2
λ
i
h~ξ
i
, ~
ξ
j
i
2
=
(
0
i
6= j,
1
i = j.

5.3. ALGORYTM DLA ZADANIA WYGŁADZANIA
59
Wektory ~η
i
, 1 ≤ i ≤ n, można uzupełnić m − n dodatkowymi wektorami
tak, aby cały układ (~η
i
)
m
i=1
był bazą ortonormalną w R
m
. Zdefiniujmy teraz
macierze ortogonalne U o kolumnach ~η
i
, 1 ≤ i ≤ m, oraz V o kolumnach
~
ξ
j
, 1 ≤ j ≤ n. Bezpośredni rachunek pokazuje, że macierz U
T
AV jest dia-
gonalna z wyrazami na przekątnej
p
λ
j
. Stąd A = UΣV
T
z σ
j,j
=
p
λ
j
,
1 ≤ j ≤ n.
Liczby
p
λ
j
nazywa się wartościami szczególnymi macierzy A, a rozkład
(5.4) rozkładem macierzy według wartości szczególnych.
Zauważmy jeszcze, że jeśli A = UΣV
T
to A
+
= V Σ
+
U
T
oraz Σ
+
∈
R
n×m
jest macierzą diagonalną z wyrazami na diagonali równymi 1/
p
λ
j
.
Rozwiązanie zadania wygładzania liniowego można więc zapisać jako
~x
∗
= V Σ
+
U
T
~b.
U. 5.3 Przedstawimy teraz jedną z możliwych implementacji algorytmu
Hauseholdera rozkładu macierzy na iloczyn A = QR. Po wykonaniu poniż-
szego programu wyrazy r
i,j
macierzy R dla 1 ≤ i ≤ j zostaną zapamiętane
na miejscach a[i, j], współrzędne u
j,i
wektora ~u
j
dla j + 1 ≤ i ≤ m na miej-
scach a[i, k], a współrzędna u
j,j
i liczba γ
j
odpowiednio na u[j] i gam[j],
1 ≤ j ≤ n.
for k := 1 to n do
begin
{ obliczanie kolejnego odbicia Hauseholdera }
norm2 := 0.0;
for l := k to m do
begin
aa := a[l, k];
norm2 := norm2 + aa
∗ aa
end;
norm := sqrt(norm2);
aa := a[k, k];
if (aa ≥ 0.0) then
begin
uu := aa + norm;
akk :=
−norm
end
else
begin
uu := aa
− norm;
akk := norm

60
ROZDZIAŁ 5. ZADANIE WYGŁADZANIA LINIOWEGO
end;
gamma := norm2 + abs(aa)
∗ norm;
u[k] := uu;
gam[k] := gamma;
{ modyfikacja kolumn macierzy }
a[k, k] := akk;
for j := k + 1 to n do
begin
s := uu
∗ a[k, j];
for l := k + 1 to m do
s := s + a[l.k]
∗ a[l, j];
s := s/gamma;
a[k, j] := a[k, j]
− s ∗ uu;
for l := k + 1 to m do
a[l, j] := a[l, j]
− s ∗ a[l, k]
end;
end.
U. 5.4 Można pokazać, że przedstawiony algorytm Hauseholdera rozkładu
macierzy na iloczyn ortogonalno-trójkątny jest numerycznie poprawny. To
znaczy, otrzymane w fl
ν
macierz trójkątna górna R
ν
i ortogonalna Q
ν
(re-
prezentowana przez n wektorów ~u
k
i liczb γ
k
) spełniają (A + E) = Q
ν
R
ν
,
gdzie kEk ≤ K(m, n)νkAk.
U. 5.5 Zadanie wygładzania liniowego można również rozwiązać stosując
innego rodzaju rozkład ortogonalno-trójkątny macierzy A ∈ R
m×n
; miano-
wicie przez zastosowanie ortogonalizacji Grama-Schmidta do wektorów ko-
lumn ~a
j
macierzy A. W wyniku otrzymujemy ciąg wektorów ~q
j
, 1 ≤ j ≤ n,
tworzący układ ortonormalny w R
m
, oraz spełniający
span{~q
1
, ~q
2
, . . . , ~q
j
} = span{~a
1
, ~a
2
, . . . , ~a
j
},
1 ≤ j ≤ n.
(5.5)
Zauważmy, że jeśli z wektorów ~q
j
stworzymy macierz Q = (~q
1
, ~q
2
, . . . , ~q
n
) ∈
R
m×n
, to (5.5) implikują istnienie kwadratowej macierzy trójkątnej górnej
R
∈ R
n×n
takiej, że
A = Q
· R.
(W odróżnieniu od efektu działania algorytmu Hauseholdera, macierz Q nie
jest tu kwadratowa, ale za to kwadratowa jest macierz R.)

5.3. ALGORYTM DLA ZADANIA WYGŁADZANIA
61
Wektory ortonormalne ~q
j
oraz współczynniki r
i,j
macierzy R można wy-
znaczyć z układu równań
~a
j
=
j
X
s=1
r
s,j
~q
s
,
1 ≤ j ≤ n.
Mnożąc j-te równanie skalarnie przez ~q
i
, 1 ≤ i ≤ j, otrzymujemy r
i,j
=
h~a
j
, ~q
i
i
2
= ~q
T
i
~a
j
, a stąd wzory rekurencyjne
for j := 1 to n do
begin
for i := 1 to j − 1 do r
i,j
:= h~q
i
, ~a
j
i
2
;
~
p
j
:= ~a
j
−
P
j−1
s=1
r
s,j
~q
s
;
r
j,j
:= k~p
j
k
2
;
~q
j
:= ~p
j
/r
j,j
end.
Dysponując rozkładem A = QR, rozwiązanie ~x
∗
zadania wygładzania
wyznaczamy z równania R~x = Q
T
~b. Rzeczywiście, układ (~q
j
)
n
j=1
można for-
malnie uzupełnić do układu ortonormalnego w R
m
dodając do niego pewne
wektory ~q
j
dla n+1 ≤ j ≤ m. Tworząc macierz ortogonalną Q = (~q
1
, . . . , ~q
m
)
i rozszerzając macierz R ∈ R
n×n
do macierzy R ∈ R
m×n
przez dodanie do
niej (m−n) zerowych wierszy, otrzymujemy A = Q R, a więc rozkład taki jak
w algorytmie Hauseholdera. Postępując dalej tak, jak w analizie algorytmu
Hauseholdera, otrzymujemy żądany wynik.
U. 5.6 Okazuje się, że algorytm ortogonalizacyjny Grama-Schmidta z U.
5.5 ma niedobre własności numeryczne, gdy wektory-kolumny macierzy wyj-
ściowej A są “słabo liniowo niezależne”; tzn. otrzymane w fl
ν
wektory ~q
(1)
j
mogą być wtedy “słabo” ortogonalne. W takim wypadku należy stosować
podwójną ortogonalizację, najpierw do wektorów ~a
j
, a potem do ~q
(1)
j
, 1 ≤
j
≤ n. (Zob. Ćw. 5.7.)
Ćwiczenia
Ćw. 5.1 Pokazać, że dla macierzy pseudoodwrotnej A
+
do danej macierzy
A
∈ R
m×n
, rank(A) = n, macierz A
+
A = I
n
jest identycznością w R
n×n
,
natomiast
AA
+
=
I
n
0
0
0
!
∈ R
m×m
,

62
ROZDZIAŁ 5. ZADANIE WYGŁADZANIA LINIOWEGO
czyli AA
+
jest rzutem prostopadłym na podprzestrzeń rozpiętą na pierw-
szych n wersorach w R
m
.
Ćw. 5.2 Niech A ∈ R
m×n
. Uzasadnić, że jądro macierzy A
T
,
ker(A
T
) = { ~y ∈ R
m
: A
T
~y = ~0
},
jest podprzestrzenią prostopadłą do obrazu A,
im(A) = { A~x ∈ R
m
: ~x ∈ R
n
}.
Ćw. 5.3 Pokazać, że macierze A
T
A i AA
T
mają takie same niezerowe war-
tości własne, a podprzestrzenie własne im odpowiadające mają ten sam wy-
miar.
Ćw. 5.4 Uzasadnić, że dana macierz kwadratowa Q ∈ R
m×m
jest ortogo-
nalna wtedy i tylko wtedy gdy jej kolumny (wiersze) tworzą bazę ortonor-
malną w R
m
.
Ćw. 5.5 Niech ~u będzie niezerowym wektorem w R
m
oraz γ = k~uk
2
2
/2.
Uzasadnić, że algorytm obliczania
H~x = ~x
− s~u,
s = (~u
T
~x)/γ,
według powyższego wzoru, jest numerycznie poprawny ze względu na dany
wektor ~x ∈ R
m
.
Ćw. 5.6 Policzyć złożoność algorytmu ortogonalizacyjnego opisanego w U.
5.5 rozwiązania zadania wygładzania liniowego.
Ćw. 5.7 Zastosujmy ortogonalizację Grama-Schmidta do dwóch wektorów
liniowo niezależnych ~a i ~b o normach k~ak
2
= 1 = k~bk
2
. Załóżmy dla uprosz-
czenia, że w obliczeniach jedynie iloczyn skalarny tych wektorów s = h~a,~bi
2
liczy się z błędem, fl
ν
(s) = s(1 + ε), gdzie |ε| jest dodatnie i na poziomie
ν. Pokazać, że wtedy dla otrzymanej w wyniku ortogonalizacji unormowanej
pary wektorów ~a i ~c mamy
h~a,~ci
2
=
−εs
p
1 − s
2
(1 − ε
2
)
.
Wywnioskować stąd, że gdy ~a i ~b są “prawie liniowo zależne”, to ~a i ~c są
dalekie od ortogonalnych.

5.3. ALGORYTM DLA ZADANIA WYGŁADZANIA
63
Ćw. 5.8 Zaprogramować algorytm Grama-Schmidta z U. 5.5 (z podwójną
ortogonalizacją) rozwiązujący zadanie wygładzania.
Ćw. 5.9 Zaprogramować algorytm obliczający macierz odwrotną do danej
nieosobliwej macierzy A ∈ R
n×n
wykorzystujący rozkład Hauseholdera A =
QR.
æ

64
ROZDZIAŁ 5. ZADANIE WYGŁADZANIA LINIOWEGO

Rozdział 6
Interpolacja wielomianowa
Dotychczas rozpatrywaliśmy zadania, w których danymi są ciągi liczb
rzeczywistych. Teraz zajmiemy się zadaniami, w których danymi są
funkcje o wartościach rzeczywistych. Pierwszym z nich jest zadanie in-
terpolacji wielomianowej.
6.1 Sformułowanie zadania interpolacji
Niech D ⊂ R i niech F będzie pewnym zbiorem funkcji f : D → R.
Niech x
0
, x
1
, . . . , x
n
będzie ustalonym zbiorem parami różnych punktów
z D, zwanych później węzłami.
Powiemy, że wielomian w interpoluje funkcję f ∈ F w węzłach x
j
,
gdy
w
(x
j
) = f(x
j
),
0 ≤ j ≤ n.
Oznaczmy przez Π
n
przestrzeń liniową wielomianów stopnia co naj-
wyżej n o współczynnikach rzeczywistych,
Π
n
= { w(x) = a
n
x
n
+ a
n−1
x
n−1
+ · · · + a
1
x
+ a
0
: a
j
∈ R, 0 ≤ j ≤ n }.
Lemat 6.1 Dla dowolnej funkcji f : D
→ R istnieje dokładnie jeden
wielomian w
f
∈ Π
n
interpolujący f w węzłach x
j
, 0
≤ j ≤ n.
Dowód Wybierzmy w Π
n
dowolną bazę wielomianów ϕ
j
, 0 ≤ j ≤ n,
Π
n
= span{ ϕ
0
, ϕ
1
, . . . , ϕ
n
}.
65

66
ROZDZIAŁ 6. INTERPOLACJA WIELOMIANOWA
Wtedy każdy wielomian z Π
n
można jednoznacznie przedstawić w po-
staci rozwinięcia względem wybranej bazy. Warunkiem koniecznym i
dostatecznym na to, aby wielomian w
f
(·) =
P
n
j=0
c
j
ϕ
j
(·) interpolował
f
jest spełnienie układu n + 1 równań liniowych
n
X
j=0
c
j
ϕ
j
(x
i
) = f(x
i
),
0 ≤ i ≤ n,
z n + 1 niewiadomymi c
j
, który w postaci macierzowej wygląda nastę-
pująco:
ϕ
0
(x
0
) ϕ
1
(x
0
) · · · ϕ
n
(x
0
)
ϕ
0
(x
1
) ϕ
1
(x
1
) · · · ϕ
n
(x
1
)
...
ϕ
0
(x
n
) ϕ
1
(x
n
) · · · ϕ
n
(x
n
)
c
0
c
1
...
c
n
=
f
(x
0
)
f
(x
1
)
...
f
(x
n
)
.
(6.1)
Aby wykazać, że układ ten ma jednoznaczne rozwiązanie wystarczy, aby
wektor zerowy był jedynym rozwiązaniem układu jednorodnego. Rze-
czywiście, układ jednorodny odpowiada interpolacji danych zerowych,
f
(x
i
) = 0, ∀i. Istnienie niezerowego rozwiązania byłoby więc równo-
ważne istnieniu niezerowego wielomianu stopnia nie większego od n,
który miałby n + 1 różnych zer x
i
, co jest niemożliwe.
2
Zadanie znalezienia dla danej funkcji f jej wielomianu interpolacyj-
nego stopnia co najwyżej n jest więc dobrze zdefiniowane, tzn. rozwią-
zanie istnieje i jest wyznaczone jednoznacznie. Zauważmy, że wielomian
interpolacyjny w
f
jako taki nie może być wynikiem obliczeń w naszym
modelu obliczeniowym, możemy natomiast wyznaczyć jego współczyn-
niki c
j
w wybranej bazie.
Definicja 6.1 Niech (ϕ
j
)
n
j=0
będzie bazą w przestrzeni Π
n
wielomianów
stopnia co najwyżej n. Zadanie (obliczeniowe) interpolacji wielomino-
wej polega na obliczeniu dla danej funkcji f współczynników c
j
takich,
że wielomian
w
f
(·) =
n
X
j=0
c
j
ϕ
j
(·)
(6.2)
interpoluje f w punktach x
j
, 0
≤ j ≤ n.

6.2. WYBÓR BAZY WIELOMIANOWEJ
67
6.2 Wybór bazy wielomianowej
Można powiedzieć, że trudność zadania interpolacji jest zdetermino-
wana przez trudność rozwiązania układu (6.1), ta zaś zależy w istotny
sposób od wybranej bazy (ϕ
j
)
n
j=0
. W naturalny sposób powstaje więc
problem wyboru “wygodnej” bazy w Π
n
. Rozpatrzymy trzy bazy: La-
grange’a, potęgową i Newtona.
Baza Lagrange’a (kanoniczna)
Zdefiniujmy dla 0 ≤ j ≤ n wielomiany
l
j
(x) =
(x − x
0
)(x − x
1
) · · · (x − x
j−1
)(x − x
j+1
) · · · (x − x
n
)
(x
j
− x
0
)(x
j
− x
1
) · · · (x
j
− x
j−1
)(x
j
− x
j+1
) · · · (x
j
− x
n
)
.
(6.3)
Zauważmy, że każdy z l
j
jest stopnia dokładnie n oraz
l
j
(x
i
) =
(
0
i
6= j,
1
i
= j.
Stąd łatwo widać, że wielomiany te stanowią bazę w Π
n
, którą nazy-
wamy bazą Lagrange’a. Macierz układu (6.1) jest identycznością i w
konsekwencji c
j
= f(x
j
), ∀j. Wielomian interpolacyjny dla funkcji f
można więc w tym przypadku zapisać jako
w
f
(·) =
n
X
j=0
f
(x
j
)l
j
(·).
Koszt kombinatoryczny rozwiązania zadania interpolacji jest przy tym
zerowy.
Przypuśćmy, że chcielibyśmy obliczyć wartość wielomianu interpo-
lacyjnego w
f
w punkcie x różnym od x
j
, 0 ≤ j ≤ n. Podstawiając
a
j
=
1
(x
j
− x
0
)(x
j
− x
1
) · · · (x
j
− x
j−1
)(x
j
− x
j+1
) · · · (x
j
− x
n
)
oraz a(x) = (x − x
0
) · · · (x − x
n
) mamy
w
f
(x) = a(x)
n
X
j=0
a
j
f
(x
j
)
x
− x
j
,
(6.4)

68
ROZDZIAŁ 6. INTERPOLACJA WIELOMIANOWA
albo
w
f
(x) =
P
n
j=0
q
j
(x)f(x
j
)
P
n
j=0
q
j
(x)
,
gdzie q
j
(x) = a
j
/
(x − x
j
). W ostatniej równości wykorzystaliśmy fakt,
że a(x) ≡ (
P
n
j=0
q
j
(x))
−1
, co wynika z (6.4) po podstawieniu f ≡ 1.
Baza potęgowa (naturalna)
Znacznie prościej można obliczyć wartość wielomianu interpolacyj-
nego, (a także jego pochodnych), gdy jest on dany w najczęściej uży-
wanej bazie potęgowej, ϕ
j
(x) = x
j
, ∀j. Jeśli bowiem
w
f
(x) = a
0
+ a
1
x
+ · · · + a
n
x
n
,
to również
w
f
(x) = (· · · (a
n
x
+ a
n−1
)x + a
n−2
)x + · · · + a
1
)x + a
0
,
co sugeruje zastosowanie następującego schematu Hornera do obliczenia
w
f
(x):
v
n
:= a
n
;
for j := n
− 1 downto 0 do
v
j
:= v
j+1
∗ x + a
j
,
Po wykonaniu tego algorytmu w
f
(x) = v
0
. Schemat Hornera wymaga
wykonania tylko n mnożeń i n dodawań. Ma on również głębszy sens,
zob. Ćw. 6.2.
Zauważmy jednak, że w przypadku bazy potęgowej macierz (x
j
i
)
n
i,j=0
układu (6.1) jest pełna. Jest to tzw. macierz Vandermonde’a. Obli-
czenie współczynników wielomianu interpolacyjnego w bazie potęgowej
bezpośrednio z tego układu, stosując jedną ze znanych nam już metod,
kosztowałoby rzędu n
3
operacji arytmetycznych.
Baza Newtona
Rozwiązaniem pośrednim, które łączy prostotę obliczenia współ-
czynników z prostotą obliczenia wartości w
f
(x) jest wybór bazy New-
tona,
p
0
(x) = 1,
p
j
(x) = (x − x
0
)(x − x
1
) · · · (x − x
j−1
),
1 ≤ j ≤ n.

6.3. ALGORYTM RÓŻNIC DZIELONYCH
69
W tym przypadku współczynniki rozwinięcia wielomianu interpolacyj-
nego będziemy oznaczać przez b
j
,
w
f
=
n
X
j=0
b
j
p
j
.
Zwróćmy od razu uwagę na ważną własność bazy Newtona. Jeśli w
f,j
∈
Π
j
jest wielomianem interpolacyjnym dla funkcji f opartym na węzłach
x
0
, x
1
, . . . , x
j
, 0 ≤ j ≤ n, to w
f,0
= b
0
oraz
w
f,j
= w
f,j−1
+ b
j
p
j
,
1 ≤ j ≤ n.
(6.5)
Wartość w
f
(x) można obliczyć stosując prostą modyfikację algo-
rytmu Hornera:
v
n
:= b
n
;
for j := n
− 1 downto 0 do
v
j
:= v
j+1
∗ (x − x
j
) + b
j
.
Ponadto układ równań (6.1) jest trójkątny dolny (tzn. p
j
(x
i
) = 0 dla
i < j
), co pozwala na obliczenie b
j
algorytmem z Rozdziału 3.1 o koszcie
n
2
,
b
0
:= f(x
0
);
for j := 1 to n do
b
j
:=
f
(x
j
) −
P
j−1
s=0
b
s
p
s
(x
j
)
/p
j
(x
j
).
Zwykle jednak do obliczania współczynników b
j
stosuje się nieco
inny algorytm, który teraz predstawimy.
6.3 Algorytm różnic dzielonych
Różnicę dzieloną funkcji f opartą na różnych węzłach t
0
, t
1
, . . . , t
s
, gdzie
s
≥ 1, definiuje się indukcyjnie jako
f
(t
0
, t
1
, . . . , t
s
) =
f
(t
1
, t
2
, . . . , t
s
) − f(t
0
, t
1
, . . . , t
s−1
)
t
s
− t
0
.
(6.6)
Zachodzi następujące ważne twierdzenie.

70
ROZDZIAŁ 6. INTERPOLACJA WIELOMIANOWA
Twierdzenie 6.1 Współczynniki b
j
wielomianu interpolacyjnego New-
tona dla danej funkcji f dane są przez różnice dzielone f w węzłach
x
0
, x
1
, . . . , x
j
, tzn.
b
j
= f(x
0
, x
1
, . . . , x
j
),
0 ≤ j ≤ n.
Dowód Dla 0
≤ i ≤ j ≤ n, oznaczmy przez w
i,j
wielomian z Π
j−i
in-
terpolujący f w węzłach x
i
, x
i+1
, . . . , x
j
. Wtedy ma miejsce następująca
równość (i < j):
w
i,j
(x) =
(x − x
i
)w
i+1,j
(x) − (x − x
j
)w
i,j−1
(x)
x
j
− x
i
,
∀x.
(6.7)
Aby ją pokazać wystarczy, że prawa strona tej równości, którą ozna-
czymy przez v(x), przyjmuje wartości f(x
s
) dla x = x
s
, i ≤ s ≤ j.
Rzeczywiście, jeśli i + 1 ≤ s ≤ j − 1 to
v
(x
s
) =
(x
s
− x
i
)f(x
s
) − (x
s
− x
j
)f(x
s
)
x
j
− x
i
= f(x
s
).
Ponadto
v
(x
i
) = −
(x
i
− x
j
)
x
j
− x
i
f
(x
i
) = f(x
i
),
oraz podobnie v(x
j
) = f(x
j
). Stąd v jest wielominem z Π
j−i
interpolu-
jącym f w węzłach x
s
, i ≤ s ≤ j, czyli w
i,j
= v.
Dalej postępujemy indukcyjnie ze względu na stopień n wielomianu
interpolacyjnego. Dla n = 0 mamy oczywiście b
0
= f(x
0
). Niech n ≥ 1.
Ponieważ, jak łatwo zauważyć,
w
0,n
(x) = w
0,n−1
(x) + b
n
p
n
(x),
z założenia indukcyjnego mamy b
j
= f(x
0
, . . . , x
j
) dla 0 ≤ j ≤ n − 1.
Aby pokazać podobną równość dla b
n
, wykorzystamy równość (6.7) z
i
= 0 i j = n, która ma wtedy postać
w
0,n
(x) =
(x − x
0
)w
1,n
(x) − (x − x
n
)w
0,n−1
(x)
x
n
− x
0
.
Zauważmy teraz, że b
n
jest współczynnikiem przy x
n
w wielomianie
w
0,n
. Z założenia indukcyjnego wynika, że współczynniki przy x
n−1
w

6.4. PRZYPADEK WĘZŁÓW WIELOKROTNYCH
71
wielomianach w
1,n
i w
0,n−1
są ilorazami różnicowymi opartymi odpo-
wiednio na węzłach x
1
, . . . , x
n
i x
0
, . . . , x
n−1
. Stąd
b
n
=
f
(x
1
, . . . , x
n
) − f(x
0
, . . . , x
n−1
)
x
n
− x
0
= f(x
0
, x
1
, . . . , x
n
),
co kończy dowód.
2
Różnicę dzieloną f(x
0
, x
1
, . . . , x
n
) można łatwo obliczyć na podsta-
wie wartości f(x
j
), 0 ≤ j ≤ n, budując następującą tabelkę:
x
0
f
(x
0
)
x
1
f
(x
1
) f(x
0
, x
1
)
x
2
f
(x
2
) f(x
1
, x
2
)
f
(x
0
, x
1
, x
2
)
... ...
...
...
...
x
n
f
(x
n
) f(x
n−1
, x
n
) f(x
n−2
, x
n−1
, x
n
) · · · f(x
0
, x
1
, . . . , x
n
).
Zauważmy przy tym, że “po drodze” obliczamy f(x
i
, x
i+1
, . . . , x
j
) dla
wszystkich 0 ≤ i < j ≤ n, a więc w szczególności również interesu-
jące nas różnice dzielone f(x
0
, x
1
, . . . , x
j
). Stąd i z Twierdzenia 6.1 na-
tychmiast wynika algorytm obliczania współczynników b
j
wielomianu
interpolacyjnego Newtona. Po wykonaniu następującego programu,
for j := 0 to n do b[j] := f (x[j]);
for j := 1 to n do
for k := n downto j
do
b
[k] := (b[k] − b[k − 1])/(x[k] − x[k − j]),
współczynniki b
j
zostaną umieszczone w tablicy b[j].
6.4 Przypadek węzłów wielokrotnych
Uogólnieniem rozpatrzonego zadania interpolacji jest zadanie interpo-
lacji Hermite’a. Zakładamy, że oprócz (różnych) węzłów x
j
dane są
również ich krotności n
j
, 0 ≤ j ≤ k, przy czym
P
k
j=0
n
j
= n + 1. Należy
skonstruować wielomian w
f
∈ Π
n
taki, że
w
(i)
f
(x
j
) = f
(i)
(x
j
)
dla
0 ≤ i ≤ n
j
− 1, 0 ≤ j ≤ k.
Oczywiście zakładamy przy tym, że odpowiednie pochodne funkcji f
istnieją.

72
ROZDZIAŁ 6. INTERPOLACJA WIELOMIANOWA
Lemat 6.2 Zadanie interpolacji Hermite’a ma jednoznaczne rozwiąza-
nie.
Dowód Istnienie i jednoznaczność rozwiązania można uzasadnić tak
samo jak w przypadku węzłów jednokrotnych. Przedstawiając wielo-
mian w dowolnej bazie otrzymujemy układ n + 1 równań z n + 1 nie-
wiadomymi, który dla zerowej prawej strony ma jedynie rozwiązanie
zerowe. Inaczej bowiem istniałby wielomian niezerowy stopnia nie więk-
szego niż n, który miałby zera o łącznej krotności większej niż n.
2
Nas oczywiście interesuje konstrukcja wielomianu w
f
. W tym celu
ustawimy węzły x
j
w ciąg
(¯x
0
,
¯x
1
, . . . ,
¯x
n
) = (x
0
, . . . , x
0
|
{z
}
n
0
, x
1
, . . . , x
1
|
{z
}
n
1
, . . . , x
k
, . . . , x
k
|
{z
}
n
k
)
i zdefiniujemy uogólnioną bazę Newtona w Π
n
jako
p
0
(x) = 1,
p
j
(x) = (x − ¯x
0
)(x − ¯x
1
) · · · (x − ¯x
j−1
),
1 ≤ j ≤ n.
Uogólnimy również pojęcie różnicy dzielonej na węzły powtarzające
się kładąc
f
(¯x
i
,
¯x
i+1
, . . . ,
¯x
j
) =
f
(j−i)
(¯x
i
)
(j − i)!
dla ¯x
i
= ¯x
i+1
= · · · = ¯x
j
, oraz
f
(¯x
i
,
¯x
i+1
, . . . ,
¯x
j
) =
f
(¯x
i+1
, . . . ,
¯x
j
) − f(¯x
i
, . . . , x
j−1
)
¯x
j
− ¯x
i
dla ¯x
i
6= ¯x
j
. Zauważmy, że przy tej definicji różnice f(¯x
i
, . . . ,
¯x
j
) mo-
żemy łatwo obliczyć stosując schemat podobny do tego z przypadku
węzłów jednokrotnych.
Twierdzenie 6.2 Współczynniki b
j
wielomianu interpolacyjnego Her-
mite’a w bazie Newtona,
w
f
(·) =
n
X
j=0
b
j
p
j
(·),
dane są przez odpowiednie różnice dzielone, tzn.
b
j
= f(¯x
0
,
¯x
1
, . . . ,
¯x
j
),
0 ≤ j ≤ n.

6.4. PRZYPADEK WĘZŁÓW WIELOKROTNYCH
73
Dowód Dowód przeprowadzimy podobnie jak dla węzłów jednokrot-
nych. Niech w
i,j
∈ Π
j−i
oznacza wielomian interpolacyjny Hermite’a
oparty na (być może powtarzających się) węzłach ¯x
i
,
¯x
i+1
, . . . ,
¯x
j
. To
znaczy, w
i,j
interpoluje f w węzłach x
s
takich, że x
s
występuje w ciągu
¯x
i
, . . .
¯x
j
, a jego krotność jest liczbą powtórzeń x
s
w tym ciągu.
Zauważmy najpierw, że dla ¯x
i
6= ¯x
j
zachodzi znany nam już wzór
(6.7),
w
i,j
(x) =
(x − ¯x
i
)w
i+1,j
(x) − (x − ¯x
j
)w
i,j−1
(x)
¯x
j
− ¯x
i
.
(6.8)
Rzeczywiście, oznaczmy przez v(x) prawą stronę powyższej równości.
Dla k mniejszego od krotności danego węzła x
s
w ciągu ¯x
i
, . . .
¯x
j
, mamy
w
(k−1)
i+1,j
(x
s
) = w
(k−1)
i,j−1
(x
s
), a ponieważ
v
(k)
(x) =
k
(w
(k−1)
i+1,j
(x) − w
(k−1)
i,j−1
(x))
¯x
j
− ¯x
i
+
(x − ¯x
i
)w
(k)
i+1,j
(x) − (x − ¯x
j
)w
(k)
i,j−1
(x)
¯x
j
− ¯x
i
,
to
v
(k)
(x
s
) =
(x
s
− ¯x
i
)w
(k)
i+1,j
(x
s
) − (x
s
− ¯x
j
)w
(k)
i,j−1
(x
s
)
¯x
j
− ¯x
i
.
Korzystając z tego wzoru sprawdzamy, że v spełnia odpowiednie wa-
runki interpolacyjne, a stąd w
i,j
= v.
Dalej postępujemy indukcyjnie ze względu na n. Dla n = 0 mamy
b
0
= f(x
0
). Dla n ≥ 1 wystarczy pokazać, że b
n
= f(¯x
0
,
¯x
1
, . . . ,
¯x
n
). W
tym celu rozpatrzymy dwa przypadki.
Jeśli ¯x
0
= ¯x
n
to mamy jeden węzeł x
0
o krotności n + 1. Wielomian
interpolacyjny jest wtedy postaci
w
f
(x) =
n
X
j=0
f
(j)
(x
0
)
j
!
(x − x
0
)
j
,
a stąd b
n
= f
(n)
(x
0
)/(n!) = f(x
0
, . . . , x
0
|
{z
}
n+1
). Jeśli zaś ¯x
0
6= ¯x
j
to równość
b
n
= f(¯x
0
,
¯x
1
, . . . ,
¯x
n
) wynika z (6.8) po podstawieniu i = 0 i j = n,
oraz z założenia indukcyjnego.
2

74
ROZDZIAŁ 6. INTERPOLACJA WIELOMIANOWA
Uwagi i uzupełnienia
U. 6.1 Algorytm Hornera okazuje się optymalny. Każdy inny algorytm ob-
liczający dokładną wartość wielomianu znając jego współczynniki wymaga
wykonania co najmniej n mnożeń i n dodawań. Algorytm Hornera jest też
numerycznie poprawny, zob. Ćw. 6.1.
U. 6.2 Mając obliczone współczynniki b
j
wielomianu interpolacyjnego w
postaci Newtona, można łatwo przejść do jego współczynników a
j
w bazie
potęgowej. Algorytm wynika bowiem z następującego wzoru rekurencyjnego.
Dla i = n, n − 1, . . . , 0, niech a
(i)
j
, i ≤ j ≤ n, będą odpowiednimi współ-
czynnikami w rozwinięciu
b
i
+b
i+1
(x−x
i
)+· · ·+b
n
(x−x
i
) · · · (x−x
n−1
) = a
(i)
i
+a
(i)
i+1
x+
· · ·+a
(i)
n
x
n−i
.
Wtedy a
(i)
n
= b
n
oraz
a
(i)
j
= a
(i+1)
j
− x
i
∗ a
(i+1)
j+1
,
i
≤ j ≤ n − 1.
Uwzględniając fakt, że poszukiwanymi współczynnikami są a
j
= a
(0)
j
, 0 ≤
j
≤ n, algorytm może być zrealizowany następująco:
for j := 0 to n do a[j] := b[j];
for i := n − 1 downto 0 do
for j := i to n − 1 do
a[j] := a[j]
− x[i] ∗ a[j + 1].
U. 6.3 Okazuje się, że przy realizacji w fl
ν
algorytmu różnic dzielonych
istotną rolę odgrywa porządek węzłów. Można pokazać, że algorytm liczenia
f (t
0
, . . . , t
n
) jest numerycznie poprawny ze względu na dane interpolacyjne
f
(i)
(t
j
), o ile węzły są uporządkowane nierosnąco lub niemalejąco, zob. Ćw.
6.5.
U. 6.4 Zauważmy, ze pojęcie różnicy dzielonej formalnie zdefiniowaliśmy je-
dynie dla ciągu węzłów postaci x
0
, . . . , x
0
, x
1
, . . . , x
1
, . . . , x
k
, . . . , x
k
, gdzie x
j
są parami różne. Tą definicję można rozszerzyć do dowolnego ciągu węzłów.
Można bowiem powiedzieć, że f(t
0
, t
1
, . . . , t
n
) jest współczynnikiem przy x
n
wielomianu w
t
0
,...,t
n
∈ Π
n
interpolującego f w węzłach t
j
(uwzględniając
krotności). Równoważnie,
f (t
0
, t
1
, . . . , t
n
) =
w
(n)
t
0
,...,t
n
n!
.

6.4. PRZYPADEK WĘZŁÓW WIELOKROTNYCH
75
Ćwiczenia
Ćw. 6.1 Pokazać numeryczną poprawność algorytmu Hornera obliczania
wartości wielomianu ze względu na dane współczynniki a
j
tego wielomianu.
Ćw. 6.2 Pokazać, że algorytm Hornera obliczania wartości w(ξ) wielomianu
danego w postaci potęgowej jest jednocześnie algorytmem dzielenia tego wie-
lomianu przez jednomian (x − ξ). Dokładniej, jeśli w(x) =
P
n
j=0
a
j
x
j
to
w(x) =
n
X
j=1
v
j
x
j−1
∗ (x − ξ) + v
0
,
gdzie v
j
są zdefiniowane tak jak w algorytmie Hornera.
Ćw. 6.3 Zaproponować możliwie tani algorytm obliczający współczynniki
wielomianu w bazie Newtona, dysponując współczynnikami tego wielomianu
w bazie potęgowej.
Ćw. 6.4 Pokazać, że dla różnych węzłów t
0
, . . . , t
n
mamy
f (t
0
, t
1
, . . . , t
n
) =
n
X
j=0
f (t
j
)
(t
j
− t
0
) · · · (t
j
− t
j−1
)(t
j
− t
j+1
) · · · (t
j
− t
n
)
.
Ćw. 6.5 Niech t
0
< t
1
< . . . < t
n
. Pokazać, że realizując w fl
ν
algo-
rytm różnic dzielonych, zamiast dokładnej wartości f(t
0
, t
1
, . . . , t
n
) otrzymu-
jemy fl
ν
f (t
0
, t
1
, . . . , t
n
)
, która jest dokładną różnicą dzieloną dla danych
f (t
j
)(1 + ε
j
), gdzie |ε
j
| ≤ Kν, 0 ≤ j ≤ n.
Wskazówka Rozpatrzyć najpierw proste przypadki n = 1, 2. Dla dowolnego
n skorzystać z Ćw. 6.4.
Ćw. 6.6 Uzasadnić, że iloraz różnicowy jest funkcją symetryczną, tzn. dla
dowolnej permutacji t
i
0
, . . . , t
i
s
węzłów t
0
, . . . , t
s
mamy
f (t
i
0
, . . . , t
i
s
) = f(t
0
, . . . , t
s
).
Ćw. 6.7 Niech w będzie wielomianem stopnia dokładnie n. Pokazać, że dla
ustalonych t
1
, t
2
, . . . , t
s
funkcja
w
t
1
,...,t
s
(t) = w(t, t
1
, t
2
, . . . , t
s
),
t
∈ R,
jest wielomianem stopnia dokładnie n − s dla s ≤ n, oraz jest zerem dla
s
≥ n + 1.

76
ROZDZIAŁ 6. INTERPOLACJA WIELOMIANOWA
Ćw. 6.8 Pokazać, że jeśli funkcja f : D → R jest n-krotnie różniczkowalna
na D w sposób ciągły, f ∈ C
(n)
(D), to
f (t
0
, t
1
, . . . , t
n−1
, t
0
) = lim
t
n
→t
0
f (t
0
, t
1
, . . . , t
n−1
, t
n
).
Ćw. 6.9 Stosując algorytm różnic dzielonym znależć wielomian w postaci
Hermite’a interpolujący funkcję f(x) = x
4
w trzech dwukrotnych węzłach
równych 0, 1 i 2.
æ

Rozdział 7
Interpolacja a aproksymacja
funkcji
Gdy mamy do czynienia z funkcją, która jest “skomplikowana” to często
dobrze jest zastąpić ją funkcją “prostszą”. Mówimy wtedy o aproksyma-
cji (przybliżaniu) funkcji. Funkcję musimy również aproksymać wtedy,
gdy nie jesteśmy w stanie uzyskać pełnej o niej informacji. Na przykład,
gdy funkcja reprezentuje pewien proces fizyczny to często zdarza się,
że dysponujemy jedynie ciągiem próbek, czyli wartościami tej funkcji
w pewnych punktach. Jasne jest, że chcielibyśmy przy tym, aby błąd
aproksymacji był możliwie mały.
Z tego punktu widzenia, intepolacja wielomianowa może być trak-
towana jako jeden ze sposobów aproksymacji funkcji, opartym na prób-
kowaniu. Naturalnym staje się więc pytanie o błąd takiej aproksymacji.
7.1 Błąd interpolacji wielomianowej
Niech x
0
, x
1
, . . . , x
n
będą (niekoniecznie różnymi) węzłami należącymi
do pewnego (być może nieskończonego) przedziału D ⊂ R. Dla da-
nej funkcji f : D → R, przez w
f
oznaczymy, tak jak w poprzednim
rozdziale, wielomian interpolacyjny stopnia co najwyżej n interpolu-
jący f w zadanych węzłach. W przypadku węzłów wielokrotnych jest
to oczywiście wielomian interpolacyjny Hermite’a.
77

78ROZDZIAŁ 7. INTERPOLACJA A APROKSYMACJA FUNKCJI
Lemat 7.1 Dla dowolnego punktu ¯
x
∈ D błąd interpolacji w ¯x wyraża
się wzorem
f
(¯x) − w
f
(¯x) = (¯x − x
0
)(¯x − x
1
) · · · (¯x − x
n
)f(x
0
, x
1
, . . . , x
n
,
¯x). (7.1)
Jeśli ponadto f
∈ C
(n+1)
(D), czyli pochodna f
(n+1)
w D istnieje i jest
ciągła, to
f
(¯x) − w
f
(¯x) = (¯x − x
0
)(¯x − x
1
) · · · (¯x − x
n
)
f
(n+1)
(ξ)
(n + 1)!
,
gdzie ξ = ξ(¯
x
) jest pewnym punktem należącym do najmniejszego prze-
działu zawierającego punkty x
0
, x
1
, . . . , x
n
,
¯x.
Dowód Możemy założyć, że ¯
x
nie jest żadnym z węzłów x
j
, 0 ≤ j ≤
n
. Niech ¯
w
f
∈ Π
n+1
będzie wielomianem interpolacyjnym funkcji f
opartym na węzłach x
0
, . . . , x
n
i dodatkowo na węźle ¯x. Mamy wtedy
¯
w
f
(x) = w
f
(x) + (x − x
0
)(x − x
1
) · · · (x − x
n
)f(x
0
, x
1
, . . . , x
n
,
¯x),
a ponieważ z warunku interpolacyjnego f(¯x) = ¯
w
f
(¯x), to mamy też
(7.1).
Aby pokazać drugą część lematu, rozpatrzmy funkcję ψ : D → R,
ψ
(x) = f(x) − ¯
w
f
(x)
= f(x) − w
f
(x) − (x − x
0
)(x − x
1
) · · · (x − x
n
)f(x
0
, . . . , x
n
,
¯x).
Z warunków interpolacyjnych na ¯
w
f
∈ Π
n+1
wynika, że funkcja ψ ma
punkty zerowe o łącznej krotności co najmniej n + 2. Wykorzystując
twierdzenie Rolle’a wnioskujemy stąd, że ψ
′
ma zera o łącznej krotności
co najmniej n + 1, ψ
′′
ma zera o łącznej krotności co najmniej n, itd. W
końcu funkcja ψ
(n+1)
zeruje się w co najmniej jednym punkcie ξ = ξ(¯x)
należącym do najmniejszego przedziału zawierającego x
0
, x
1
, . . . , x
n
,
¯x.
Wobec tego, że w
(n+1)
f
≡ 0, a (n + 1)-sza pochodna wielomianu (x −
x
0
) · · · (x − x
n
) wynosi (n + 1)!, mamy
0 = ψ
(n+1)
(ξ) = f
(n+1)
(ξ) − (n + 1)!f(x
0
, . . . , x
n
,
¯x).
Stąd
f
(x
0
, x
1
, . . . , x
n
,
¯x) =
f
(n+1)
(ξ)
(n + 1)!
,

7.1. BŁĄD INTERPOLACJI WIELOMIANOWEJ
79
co kończy dowód.
2
Zwykle interesuje nas nie tyle błąd w ustalonym punkcie ¯x ∈ D, ale
na całym przedziale D. Zakładając teraz, że przedział D jest domknięty,
czyli
D
= [a, b]
dla pewnych −∞ < a < b < +∞, błąd ten będziemy mierzyć w normie
jednostajnej (Czebyszewa). Dla funkcji ciągłej g : [a, b]
→ R, norma ta
jest zdefiniowana jako
kgk
C
([a,b])
= max
x∈D
|g(x)|.
Niech F
r
M
([a, b]), gdzie r ≥ 0, będzie klasą funkcji
F
r
M
([a, b]) = { f ∈ C
(r+1)
([a, b]) : kf
(r+1)
k
C
([a,b])
≤ M },
gdzie 0 < M < ∞. Mamy następujące twiedzenie.
Twierdzenie 7.1 Załóżmy, że każdą funkcję f
∈ F
r
M
([a, b]) aproksy-
mujemy jej wielomianem interpolacyjnym w
f
∈ Π
r
opartym na r + 1
węzłach x
0
, . . . , x
r
∈ [a, b]. Wtedy maksymalny błąd takiej aproksymacji
wynosi
e
(F
r
M
([a, b]); x
0
, x
1
, . . . , x
r
) =
max
f ∈F
r
M
([a,b])
kf − w
f
k
C
([a,b])
=
M
(r + 1)! ·
max
a≤x≤b
|(x − x
0
) · · · (x − x
r
)|.
Dowód Oszacowanie górne wynika bezpośrednio z Lematu 7.1, bo-
wiem dla f ∈ F
r
M
([a, b]) mamy
kf − w
f
k
C
([a,b])
= max
a≤x≤b
|f(x) − w
f
(x)|
= max
a≤x≤b
|(x − x
0
) · · · (x − x
r
)|
|f
(r+1)
(ξ(x))|
(r + 1)!
≤
M
(r + 1)!
max
x∈D
|(x − x
0
) · · · (x − x
r
)|.
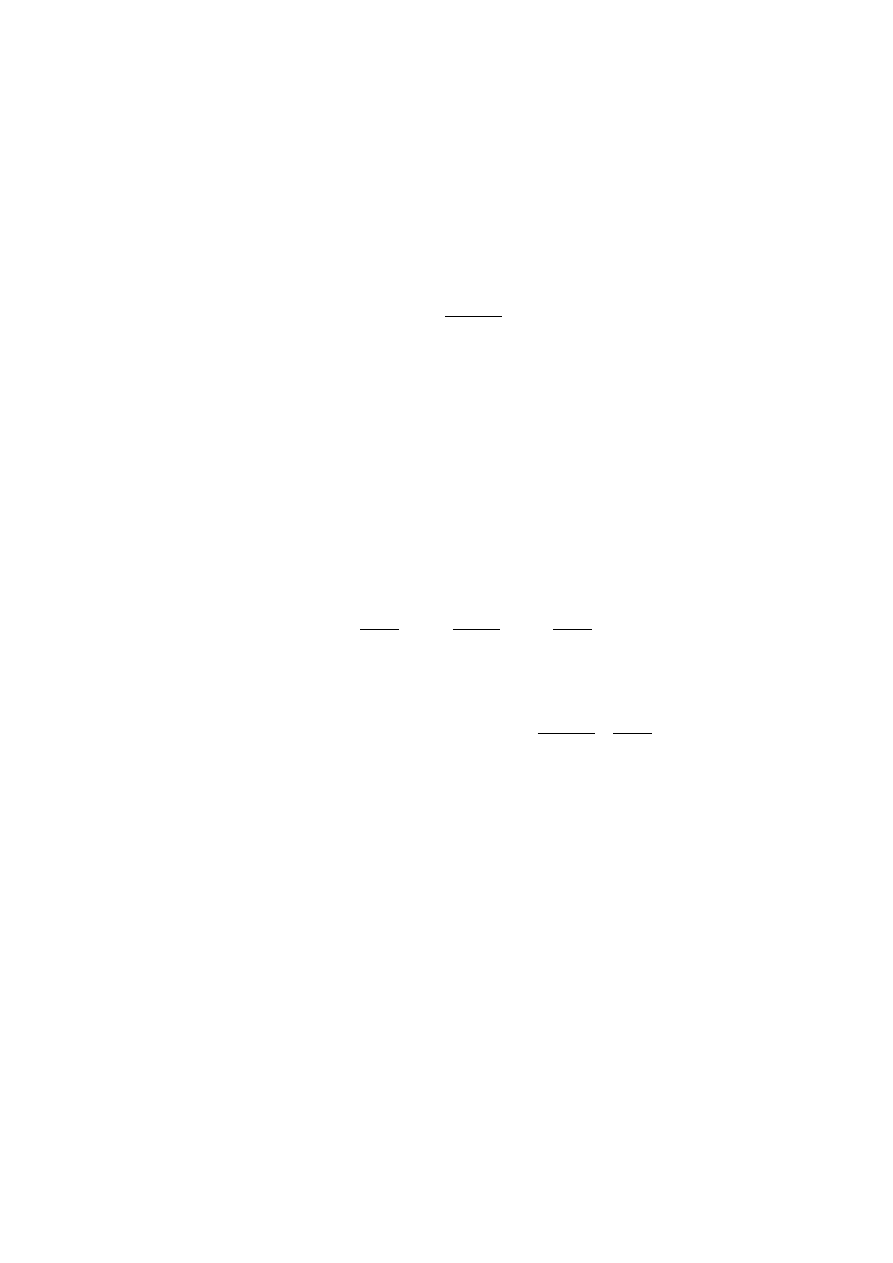
80ROZDZIAŁ 7. INTERPOLACJA A APROKSYMACJA FUNKCJI
Z drugiej strony zauważmy, że dla wielomianu v(x) = Mx
r+1
/
(r+1)!
mamy v ∈ F
r
M
([a, b]) oraz
kv − w
v
k
C
([a,b])
=
M
(r + 1)! ·
max
a≤x≤b
|(x − x
0
) · · · (x − x
r
)|,
co kończy dowód.
2
Zauważmy, że błąd aproksymacji e(F
r
M
([a, b]); x
0
, . . . , x
r
) w istotny
sposób zależy od wyboru węzłów x
j
. Naturalne jest więc teraz następu-
jące pytanie. W których punktach x
j
przedziału [a, b] należy obliczać
wartości funkcji, aby błąd był minimalny? Problem ten sprowadza się
oczywiście do minimalizacji wielkości max
a≤x≤b
|(x − x
0
) · · · (x − x
r
)|
względem węzłów x
j
.
Twierdzenie 7.2 Błąd aproksymacji F
r
M
([a, b])(x
0
,
· · · , x
r
) jest mini-
malny gdy węzły
x
∗
j
=
b
− a
2 ·
cos
2j + 1
2r + 2
π
+
a
+ b
2
,
0 ≤ j ≤ r.
Ponadto, dla węzłów optymalnych x
∗
j
mamy
e
(F
r
M
([a, b]); x
∗
0
, . . . , x
∗
r
) =
2M
(r + 1)!
b
− a
4
!
r+1
.
Dowód tego twierdzenia opiera się na własnościach pewnego waż-
nego ciągu wielomianów, który teraz przedstawimy.
7.2 Wielomiany Czebyszewa
Ciąg {T
k
}
k≥0
wielomianów Czebyszewa (pierwszego rodzaju) zdefinio-
wany jest indukcyjnie jako
T
0
(x) = 1,
T
1
(x) = x,
T
k+1
(x) = 2xT
k
(x) − T
k−1
(x),
dla
k
≥ 1.
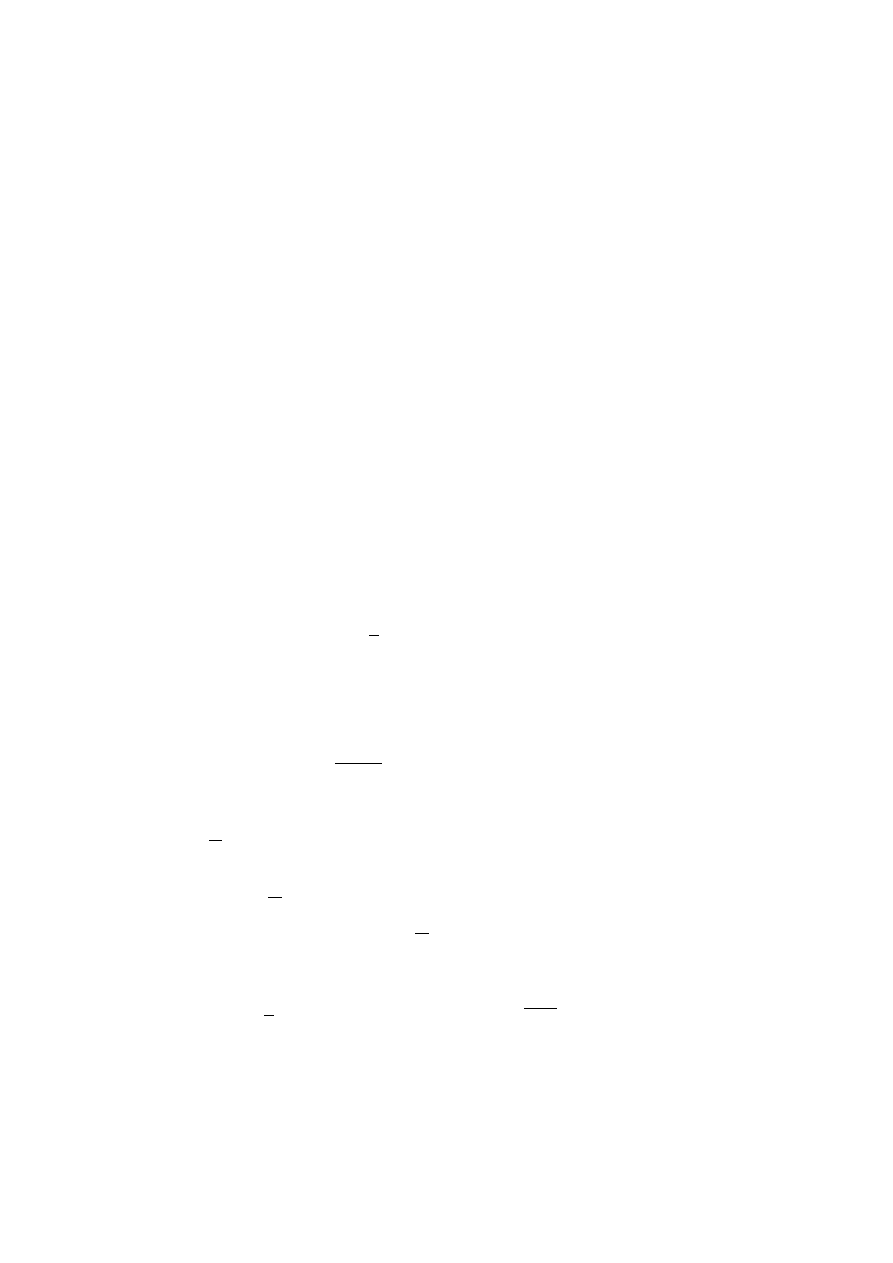
7.2. WIELOMIANY CZEBYSZEWA
81
Zauważmy, że T
k
jest wielomianem stopnia dokładnie k o współ-
czynniku przy x
k
równym 2
k−1
(k ≥ 1). Ponadto wielomian T
k
można
dla |x| ≤ 1 przedstawić w postaci
T
k
(x) = cos(k arccos x).
(7.2)
Rzeczywiście, łatwo sprawdzić, że jest to prawdą dla k = 0, 1. Stosując
podstawienie cos t = x, 0 ≤ t ≤ π, oraz wzór na sumę cosinusów
otrzymujemy dla k ≥ 1
cos((k + 1)t) = 2 · cos t cos(kt) − cos((k − 1)t),
co jest równoważne formule rekurencyjnej dla T
k+1
.
Ze wzoru (7.2) wynikają również inne ważne własności wielomianów
Czebyszewa. Norma wielomianu Czebyszewa na [−1, 1] wynosi
kT
k
k
C
([−1,1])
= max
−1≤x≤1
|T
k
(x)| = 1
i jest osiągana w k + 1 punktach tego przedziału równych
y
j
= cos
j
k
π
,
0 ≤ j ≤ k,
(7.3)
przy czym T
k
(y
j
) = (−1)
j
.
W końcu, k-ty wielomian Czebyszewa T
k
ma dokładnie k pojedyn-
czych zer w [−1, 1] równych
z
j
= cos
2j + 1
2r
π
,
0 ≤ j ≤ k − 1.
Konsekwencją wymienionych własności jest następujący lemat, któ-
ry jest kluczem do dowodu Twierdzenia 7.2.
Przez Π
k
oznaczymy klasę wielomianów stopnia k o współczynniku
wiodącym równym 1, tzn.
Π
k
= { w ∈ Π
k
: w(x) = x
k
+ · · · }.
Lemat 7.2 Niech k
≥ 1. W klasie Π
k
minimalną normę jednostajną
na przedziale [
−1, 1] ma wielomian w
∗
= 2
1−k
T
k
, tzn.
min
w∈Π
k
kwk
C
([−1,1])
= kw
∗
k
C
([−1,1])
=
1
2
k−1
.

82ROZDZIAŁ 7. INTERPOLACJA A APROKSYMACJA FUNKCJI
Dowód Zauważmy najpierw, że w
∗
∈ Π
k
oraz kw
∗
k
C
([−1,1])
= 2
1−k
.
Wystarczy więc pokazać, że norma każdego wielomianu z Π
k
jest nie
mniejsza niż 2
1−k
.
Załóżmy, że jest przeciwnie, tzn. istnieje wielomian w ∈ Π
k
taki, że
kwk
C
([−1,1])
<
1
2
k−1
= kw
∗
k
C
([−1,1])
.
Rozpatrzmy funkcję ψ = w
∗
− w. Ponieważ dla punktów “maksy-
malnych” zdefiniowanych w (7.3) mamy w
∗
(y
k−j
) = (−1)
j
2
1−k
oraz
|w(y
k−j
)| < 2
1−k
, to
ψ
(y
k−j
)
(
>
0
j
-parzyste,
<
0
j
-nieparzyste.
0 ≤ j ≤ k. Stąd ψ ma co najmniej jedno zero w każdym z przedziałów
(y
i
, y
i+1
) dla 0 ≤ i ≤ k − 1, czyli w sumie k zer. Z drugiej strony, ψ jest
wielomianem stopnia co najwyżej k − 1 (bo współczynniki przy x
k
w
wielomianach w
∗
i w redukują się), a więc ψ = 0 i w
∗
= w.
2
Dowód Twierdzenia 7.2 wynika teraz bezpośrednio z Lematu 7.2. Za-
uważmy bowiem, że wielomian (x − x
0
)(x − x
1
) · · · (x − x
r
) jest w klasie
Π
r+1
. Stąd dla [a, b] = [−1, 1] optymalnymi węzłami są zera z
j
wielo-
mianu Czebyszewa, przy których
(x − z
0
)(x − z
1
) · · · (x − z
r
) =
T
r+1
(x)
2
r
.
Jeśli przedział [a, b] jest inny niż [−1, 1], należy dokonać liniowej za-
miany zmiennych tak, aby przeszedł on na [−1, 1]. Bezpośrednie spraw-
dzenie pokazuje, że w klasie Π
r+1
minimalną normę Czebyszewa na
przedziale [a, b] ma wielomian
w
∗
a,b
(x) =
b
− a
2
r+1
w
∗
2x − (a + b)
b
− a
!
.
Stąd
kw
∗
a,b
k
C
([a,b])
=
b
− a
2
r+1
1
2
r
= 2
b
− a
4
r+1
i węzły x
∗
j
są optymalne.
2

7.3. INTERPOLACJA KAWAŁKAMI WIELOMIANOWA
83
7.3 Interpolacja kawałkami wielomiano-
wa
W praktyce interesuje nas konstrukcja nie jednej, a raczej ciągu aprok-
symacji, które przybliżałyby daną funkcję f z coraz większą dokładno-
ścią. Cel ten można spróbować osiągnąc przez wzięcie jako n-tej aprok-
symacji wielomianu interpolacyjnego w
f,n
∈ Π
n
opartego na pewnych
węzłach x
j
, 0 ≤ j ≤ n. Rzeczywiście, jeśli f jest na [a, b] nieskończenie
wiele razy różniczkowalna to n-ty błąd dla dowolnego układu węzłów
jest ograniczony przez
kf − w
f,n
k
C
([a,b])
≤
kf
(n+1)
k
C
([a,b])
(n + 1)!
(b − a)
n+1
,
(7.4)
a więc szybko dąży zera wraz z n → ∞, gdy np. wszystkie pochodne
funkcji f są wspólnie ograniczone przez pewną stałą. Tak jest np. dla
f
(x) = e
x
. Jeszcze lepsze oszacowanie dostaniemy, gdy wybierzemy
węzły Czebyszewa.
Podejście to ma jednak pewne wady. Zwiększając stopień wielo-
mianu interpolacyjnego sprawiamy, że aproksymacja, a także obliczenie
współczynników wielomianu interpolacyjnego, stają się coraz bardziej
skomplikowane, a tego chcielibyśmy uniknąć. Poza tym, założenie o
istnieniu i wspólnej ograniczoności wszystkich pochodnych funkcji nie
zawsze jest spełnione (np. w rozpatrywanej już klasie F
r
M
([a, b])), co po-
woduje, że oszacowanie (7.4) nie zawsze jest prawdziwe, a nawet błąd
kf − w
f,n
k
C
([a,b])
może nie maleć do zera, zob. U. 7.1.
Podamy teraz inny sposób konstrukcji ciągu aproksymacji, który
zapewnia zbieżność w klasie F
r
M
([a, b]), ale nie wymaga nadmiernego
zwiększania stopnia wielomianu interpolacyjnego.
Postąpimy zgodnie ze znaną zasadą “dziel i rządź”. Podzielimy
przedział [a, b] na k równych podprzedziałów [t
i−1
, t
i
], 1 ≤ i ≤ k, i
zastosujemy na każdym z nich interpolację wielomianową stopnia r.
Dokładniej, dla każdego i wybieramy (być może wielokrotne) węzły
x
i,j
∈ [t
i−1
.t
i
], 0 ≤ j ≤ r, po czym aproksymujemy f na [t
i−1
, t
i
] jej
wielomianem interpolacyjnym opartym na tych węzłach. Tak skonstru-
owaną kawałkami wielomianową aproksymację funkcji f : [a, b] → R

84ROZDZIAŁ 7. INTERPOLACJA A APROKSYMACJA FUNKCJI
oznaczymy przez ¯
w
f
. Zauważmy, że ¯
w
f
wykorzystuje na całym [a, b]
węzły o łącznej krotności n spełniającej nierówność
n
≤ k(r + 1).
(7.5)
Twierdzenie 7.3 Błąd aproksymacji kawałkami wielomianowej w kla-
sie funkcji F
r
M
([a, b]) jest ograniczony przez
max
f ∈F
r
M
([a,b])
kf − ¯
w
f
k
C
([a,b])
≤
M
(r + 1)!
b
− a
k
r+1
≤ C ·
1
n
r+1
,
gdzie
C
=
M
(b − a)
r+1
(r + 1)
r+1
(r + 1)!
.
Jeśli ponadto węzły x
i,j
, 0
≤ j ≤ r, są na każdym przedziale [t
i−1
, t
i
]
węzłami Czebyszewa, to dla odpowiedniej aproksymacji ¯
w
∗
f
mamy
max
f ∈F
r
M
([a,b])
kf − ¯
w
∗
f
k
C
([a,b])
=
2M
(r + 1)!
b
− a
4k
r+1
= C
∗
·
1
n
r+1
,
gdzie
C
∗
=
1
2
2r+1
C
=
2M(b − a)
r+1
(r + 1)
r+1
4
r+1
(r + 1)!
.
Dowód Niech f
∈ F
r
M
([a, b]) i x ∈ [t
i−1
, t
i
]. Z Lematu 7.1 wynika, że
|f(x) − ¯
w
f
(x)| =
|f
(r+1)
(ξ(x))|
(r + 1)!
|(x − x
i,0
)(x − x
i,1
) · · · (x − x
i,r
)|,
a ponieważ |x − x
i,j
| ≤ t
i
− t
i−1
= (b − a)/k, to
|f(x) − ¯
w
f
(x)| ≤
M
(r + 1)!
b
− a
k
r+1
.
Ta nierówność wraz z (7.5) dowodzi pierwszą część twierdzenia.
Dla dowodu drugiej części wystarczy wykorzystać Twierdzenie 7.2,
aby zauważyć, że
kf − ¯
w
∗
f
k
C
([a,b])
= max
a≤x≤b
|f(x) − ¯
w
∗
f
(x)| ≤
2M
(r + 1)!
b
− a
4k
r+1

7.3. INTERPOLACJA KAWAŁKAMI WIELOMIANOWA
85
oraz, że dla f(x) = Mx
r+1
/
(r + 1)! mamy powyżej równość.
2
Otrzymaliśmy, że interplacja kawałkami wielomianami stopnia r ko-
rzystająca z n wartości funkcji daje w klasie funkcji F
r
M
([a, b]) błąd
rzędu n
−(r+1)
. Błąd ten zbiega więc do zera, gdy liczba n wartości funk-
cji rośnie do nieskończoności, przy czym charakter zbieżności (tzn. przy
zaniedbaniu stałej przy n
−(r+1)
) nie zależy ani od długości przedziału
[a, b], ani od doboru “wewnętrznyh” węzłów x
i,j
, 0 ≤ j ≤ r.
Można pokazać, że powyższa aproksymacja jest w klasie F
r
M
([a, b])
optymalna, tzn. błąd dowolnej innej metody aproksymacji korzystającej
z wartości funkcji w n punktach dąży do zera nie szybciej niż n
−(r+1)
;
zob. U.7.2.
Uwagi i uzupełnienia
U. 7.1 Niech f(x) = (1 + x
2
)
−1
. Okazuje się, że jeśli w
f,n
jest wielomia-
nem interpolacyjnym dla f opartym na węzłach równoodległych przedziału
[−5, 5], tzn. x
j
= −5 + 10j/n, 0 ≤ j ≤ n, to ciąg w
f,n
(x) jest zbieżny do
f (x) dla
|x| < 3.63... i rozbieżny dla |x| > 3.63.... To znaczy, błąd interpo-
lacji funkcji f na całym przedziale [−5, 5] nie maleje do zera, gdy stopień
wielomianu interpolacyjnego rośnie do ∞.
U. 7.2 Pokażemy teraz, że aproksymacja funkcjami kawałkami wielomia-
nowymi jest optymalna w F
r
M
([a, b]) ze względu na rząd zbieżności błędu.
Dokładniej pokażemy, że dla dowolnej aproksymacji A(f) funkcji f wykorzy-
stującej wartości f lub jej pochodnych w co najwyżej n różnych punktach,
tzn. dla A postaci
A(f ) = φ(f (x
1
), . . . , f
(r+1)
(x
1
), . . . , f(x
n
), . . . , f
(r+1)
(x
n
))
mamy
sup
f ∈F
r
M
([a,b])
kf − A(f)k
C
([a,b])
≥ C
1
M n
−(r+1)
,
(7.6)
gdzie C
1
> 0 jest pewną stałą niezależną od A, M i n.
W tym celu wybierzmy dowolną niezerową funkcję ψ : R → R spełnia-
jącą warunki:
1. ψ ∈ F
r
1
(R),

86ROZDZIAŁ 7. INTERPOLACJA A APROKSYMACJA FUNKCJI
2. ψ(x) = 0 dla x 6∈ [0, 1].
Niech s będzie takim indeksem, że h
s
= x
s+1
− x
s
≥ (b − a)/(n + 1). Wtedy
dla funkcji ψ
i
, i = 1, 2, zdefiniowanych jako
ψ
1
(x) = −ψ
2
(x) = Mh
r+1
s
ψ
x
− x
s
h
s
mamy ψ
i
∈ F
r
M
([a, b]) oraz informacja o ψ
i
jest zerowa, ψ
(p)
i
(x
j
) = 0 dla
0 ≤ p ≤ r + 1, 1 ≤ j ≤ n. Stąd φ
0
= φ(0, . . . , 0
|
{z
}
n(r+2)
) jest aproksymacją dla obu
funkcji ψ
i
i z nierówności trójkąta dla norm dostajemy
max{kψ
1
− φ
0
k
C
([a,b])
,
kψ
2
− φ
0
k
C
([a,b])
}
≥ kψ
1
− ψ
2
k
C
([a,b])
/2 =
kψ
1
k
C
([a,b])
= Mh
r+1
s
kψk
C
([0,1])
≥ M
b
− a
n + 1
r+1
kψk
C
([0.1])
.
Nierówność (7.6) zachodzi więc z C
1
= (2(b − a))
r+1
kψk
C
([0.1])
. (Zob. też
Ćw. 8.3.)
U. 7.3 Załóżmy, że funkcje z klasy F
r
M
([a, b]) chcemy aproksymować z do-
kładnością ε > 0 w normie Czebyszewa używając możliwie mało obliczeń
wartości funkcji. Z Twierdzenia 7.3 i U. 7.2 wynika, że musimy wtedy obli-
czać co najmniej rzędu (1/ε)
r+1
wartości funkcji. Co więcej, aproksymacja
kawałkami wielomianowa daje błąd ε obliczając właśnie tyle wartości funkcji.
Mówimy, że złożoność informacyjna zadania jest rzędu (1/ε)
r+1
.
Ćwiczenia
Ćw. 7.1 Niech dane będą ε > 0 i funkcja f : [a, b] → R, która jest nieskoń-
czenie wiele razy różniczkowalna i wszystkie jej pochodne są na [a, b] ograni-
czone przez M. Napisać program znajdujący stopień n oraz współczynniki
w bazie Newtona wielomianu w
f,n
∈ Π
n
interpolacyjnego f z błędem
kf − w
f,n
k
C
([a,b])
≤ ε.
Rozpatrzyć dwa przypadki: gdy węzły interpolacji są równoodległe, oraz gdy
węzły są czebyszewowskie.

7.3. INTERPOLACJA KAWAŁKAMI WIELOMIANOWA
87
Ćw. 7.2 Pokazać, że dla k ≥ 1 mamy
T
k
(x) =
(x +
√
x
2
− 1)
k
+ (x −
√
x
2
− 1)
k
2
,
gdzie T
k
jest k-tym wielomianem Czebyszewa.
Ćw. 7.3 Pokazać, że wielomiany Czebyszewa tworzą układ ortogonalny w
przestrzeni L
2
ρ
(−1, 1), gdzie waga ρ(x) = (1 − x
2
)
−1/2
, tzn. iloczyn skalarny
hT
i
, T
j
i =
Z
1
−1
T
i
(x)T
j
(x)
√
1 − x
2
dx =
π
i = j = 0,
π/2
i = j
6= 0,
0
i
6= j.
Ćw. 7.4 Wielomiany Czebyszewa T
k
, 0 ≤ k ≤ n, tworzą bazę w przestrzeni
Π
n
. Podać algorytm obliczający współczynniki danego wielomianu w bazie
Czebyszewa na podstawie jesgo współczynników w bazie potęgowej, albo w
bazie Newtona.
Ćw. 7.5 Podać algorytm typu algorytmu Hornera oblicząjący wartość wie-
lomianu w(x) danego przez jego współczynniki w bazie Czebyszewa {T
k
}
k≥0
.
Ćw. 7.6 Niech w będzie wielomianem, którego rozwinięciem w bazie Cze-
byszewa jest w(x) =
P
n
k=0
a
k
T
k
(x). Pokazać, że wielomian
w
1
(x) =
n−1
X
k=0
a
k
T
k
(x)
najlepiej przybliża w w normie Czebyszewa na przedziale [−1, 1] spośród
wszystkich wielomianów stopnia co najwyżej n − 1, oraz
kw − w
1
k
C
([−1,1])
= |a
n
|.
Czy w
2
(x) =
P
n−2
k=0
a
k
T
k
(x) najlepiej przybliża w w tej samej normie w
klasie Π
n−2
?
Ćw. 7.7 Załóżmy, że wielomian w(x) =
P
n
k=0
a
k
T
k
(x) aproksymujemy wie-
lomianem w
i
(x) =
P
n−i
k=0
a
k
T
k
(x). Uzasadnić, że
kw − w
i
k
C
([−1,1])
≤
n
X
k=n−i+1
|a
k
|.
Kiedy w tej nierówności mamy równość?

88ROZDZIAŁ 7. INTERPOLACJA A APROKSYMACJA FUNKCJI
Ćw. 7.8 Niech dany będzie przedział skończony [a, b] nie zawierający zera,
oraz liczba c. Niech
˜
Π
k
= { w ∈ Π
k
: w(0) = c }.
Pokazać, że w klasie ˜
Π
k
najmniejszą normę Czebyszewa na [a, b] ma wielo-
mian
w(x) = c
·
T
k
2x−(a+b)
b−a
T
k
a+b
a−b
i wynosi ona
kwk
C
([a,b])
=
c
T
k
a+b
a−b
.
Jakie jest rozwiązanie, gdy 0 ∈ [a, b]?

Rozdział 8
Interpolacja funkcjami
sklejanymi
Interpolacja kawałkami wielomianami interpolacyjnymi daje mały błąd
aproksymacji, ma jednak również pewne wady. Zauważmy, że w punk-
tach t
j
podziału przedziału [a, b] na podprzedziały funkcja aproksymu-
jąca ¯
w
f
nie jest w ogólności ciągła. W najlepszym wypadku, nawet gdy
węzły x
i,j
na przedziale [t
i−1
, t
i
] wybierzemy tak, że x
i,0
= t
i−1
i x
i,r
= t
i
,
∀i, to ¯
w
f
(x) co prawda będzie ciągła, ale nie będzie różniczkowalna w
x
i
. Ta własność jest niepożądana w przypadku gdy wiemy, że funk-
cja którą aproksymujemy jest “gładka”. Wtedy lepiej jest zastosować
innego rodzaju interpolację, np. posługując się funkcjami sklejanymi.
8.1 Co to są funkcje sklejane?
W ogólności przez funkcję sklejaną rozumie się każdą funkcję przedzia-
łami wielomianową. Nas będą jednak interesować szczególne funkcje
tego typu i dlatego termin funkcje sklejane zarezerwujemy dla funk-
cji przedziałami wielomianowych i posiadających dodatkowe własności,
które teraz określimy.
Niech dany będzie przedział skończony [a, b] i węzły
a
= x
0
< x
1
<
· · · < x
n
= b,
przy czym n ≥ 1.
89

90
ROZDZIAŁ 8. INTERPOLACJA FUNKCJAMI SKLEJANYMI
Definicja 8.1 Funkcję s : R
→ R nazywamy funkcją sklejaną rzędu
r (r
≥ 1) odpowiadającą węzłom x
j
, 0
≤ j ≤ n, jeśli spełnione są
następujące dwa warunki:
(i) s jest wielomianem stopnia co najwyżej 2r
− 1 na każdym z prze-
działów [x
j−1
, x
j
], tzn. s
|[x
j−1
,x
j
]
∈ Π
2r−1
, 1
≤ j ≤ n,
(ii) s jest (2r
− 2)-krotnie różniczkowalna w sposób ciągły na całej
prostej, tzn. s
∈ C
(2r−2)
(R).
Jeśli ponadto
(iii) s jest wielomianem stopnia co najwyżej r
− 1 poza (a, b), tzn.
s
|(−∞,a]
, s
|[b,+∞)
∈ Π
r−1
,
to s jest naturalną funkcją sklejaną.
Klasę naturalnych funkcji sklejanych rzędu r opartych na węzłach x
j
będziemy oznaczać przez S
r
(x
0
, . . . , x
n
), albo po prostu S
r
, jeśli węzły
są ustalone.
Na przykład, funkcją sklejaną rzędu pierwszego (r = 1) jest funkcja
ciągła i liniowa na poszczególnych przedziałach [x
j−1
, x
j
]. Jest ona na-
turalna, gdy poza (a, b) jest funkcją stała. Tego typu funkcje nazywamy
liniowymi funkcjami sklejanymi.
Najważniejszymi a praktycznego punktu widzenia są jednak funkcje
sklejane rzędu drugiego odpowiadające r = 2. Są to funkcje, które są
na R dwa razy różniczkowalne w sposób ciągły, a na każdym z pod-
przedziałów są wielomianami stopnia co najwyżej trzeciego. W tym
przypadku mówimy o kubicznych funkcjach sklejanych. Funkcja skle-
jana kubiczna jest naturalna, gdy poza (a, b) jest wielomianem linio-
wym.
8.2 Interpolacja i gładkość
Pokażemy najpierw ważny lemat, który okaże się kluczem do dowodu
dalszych twierdzeń.

8.2. INTERPOLACJA I GŁADKOŚĆ
91
Niech W
r
(a, b) będzie klasą funkcji f : [a, b] → R takich, że f jest
(r−1) razy różniczkowalna na [a, b] w sposób ciągły oraz f
(r)
(x) istnieje
prawie wszędzie na [a, b] i jest całkowalna z kwadratem, tzn.
W
r
(a, b) = { f ∈ C
(r−1)
([a, b]) : f
(r)
(x) istnieje p.w. na [a, b]
oraz f
(r)
∈ L
2
(a, b) }.
Oczywiście każda funkcja sklejana rzędu r (niekoniecznie naturalna)
należy do W
r
(a, b).
Lemat 8.1 Niech f
∈ W
r
(a, b) będzie funkcją zerującą się w węzłach,
tzn.
f
(x
j
) = 0,
0 ≤ j ≤ n.
Wtedy dla dowolnej naturalnej funkcji sklejanej s
∈ S
r
mamy
Z
b
a
f
(r)
(x)s
(r)
(x) dx = 0.
Dowód Dla r = 1 funkcja s
′
jest przedziałami stała. Oznaczając przez
a
j
jej wartość na [x
j−1
, x
j
] dostajemy
Z
b
a
f
′
(x)s
′
(x) dx =
n
X
j=1
Z
t
j
t
j−1
f
′
(x)a
j
dx
=
n
X
j=1
a
j
(f(x
j
) − f(x
j−1
)) = 0,
ponieważ f zeruje się w t
j
.
Rozpatrzmy teraz przypadek r ≥ 2. Ponieważ
(f
(r−1)
s
(r)
)
′
= f
(r)
s
(r)
+ f
(r−1)
s
(r+1)
,
to
Z
b
a
f
(r)
(x)s
(r)
(x) dx = f
(r−1)
(x)s
(r)
(x)
b
a
−
Z
b
a
f
(r−1)
(x)s
(r+1)
(x) dx.
Wobec tego, że s jest poza przedziałem (a, b) wielomianem stopnia co
najwyżej r − 1 oraz s
(r)
jest ciągła na R, mamy s
(r)
(a) = 0 = s
(r)
(b), a
stąd
f
(r−1)
(x)s
(r)
(x)
b
a
= 0.

92
ROZDZIAŁ 8. INTERPOLACJA FUNKCJAMI SKLEJANYMI
Postępując podobnie, tzn. całkując przez części r −1 razy otrzymujemy
w końcu
Z
b
a
f
(r)
(x)s
(r)
(x) dx = (−1)
r−1
Z
b
a
f
′
(x)s
(2r−1)
(x) dx.
Funkcja s
(2r−1)
jest przedziałami stała, a więc możemy teraz zastosować
ten sam argument jak dla r = 1, aby pokazać, że ostatnia całka jest
równa zeru.
2
Funkcje sklejane chcielibyśmy zastosować do interpolacji funkcji.
Ważne jest więc, aby odpowiednie zadanie interpolacyjne miało jed-
noznaczne rozwiązanie.
Twierdzenie 8.1 Jeśli n+1
≥ r, to dla dowolnej funkcji f : [a, b] → R
istnieje dokładnie jedna naturalna funkcja sklejana s
f
∈ S
r
interpolu-
jąca f w węzłach x
j
, tzn. taka, że
s
f
(x
j
) = f(x
j
),
0 ≤ j ≤ n.
Dowód Pokażemy najpierw, że jedyną naturalną funkcją sklejaną in-
terpolującą dane zerowe jest funkcja zerowa. Rzeczywiście, jeśli s(x
j
) =
0 dla 0 ≤ j ≤ n, to podstawiając w Lemacie 8.1 f = s otrzymujemy
Z
b
a
s
(r)
(x)
2
dx
= 0.
Stąd s
(r)
jest funkcją zerową, a więc s jest wielomianem stopnia co
najwyżej r − 1 zerującym się w co najmniej n + 1 punktach x
j
. Wobec
tego, że n + 1 > r − 1, otrzymujemy s ≡ 0.
Zauważmy teraz, że problem znalezienia naturalnej funkcji skleja-
nej s interpolującej f można sprowadzić do rozwiązania kwadratowego
układu równań liniowych. Na każdym przedziale [x
i−1
, x
i
], 1 ≤ i ≤ n,
jest ona postaci
s
(x) = w
i
(x) =
2r−1
X
j=0
a
i,j
x
j
,
dla pewnych współczynników a
i,j
∈ R, a na (−∞, a] i [b, ∞) mamy
odpowiednio
s
(x) = w
0
(x) =
r−1
X
j=0
a
0,j
x
j

8.2. INTERPOLACJA I GŁADKOŚĆ
93
i
s
(x) = w
n+1
(x) =
r−1
X
j=0
a
n+1,j
x
j
.
Aby wyznaczyć s, musimy więc znaleźć ogółem 2r(n + 1) współczynni-
ków a
i,j
, przy czym są one związane (2r − 1)(n + 1) warunkami jedno-
rodnymi wynikającymi z gładkości,
w
(k)
i
(x
i
) = w
(k)
i+1
(x
i
)
dla 0 ≤ i ≤ n i 0 ≤ k ≤ 2r − 2, oraz n + 1 niejednorodnymi warunkami
interpolacyjnymi,
w
i
(x
i
) = f(x
i
)
dla 0 ≤ i ≤ n. Otrzymujemy więc układ 2r(n + 1) równań liniowych ze
względu na 2r(n + 1) niewiadomych a
i,j
.
Naturalna funkcja sklejana interpolująca f jest wyznaczona jedno-
znacznie wtedy i tylko wtedy, gdy układ ten ma jednoznaczne roz-
wiązanie. To zaś zachodzi, gdy zero jest jedynym rozwiązaniem układu
jednorodnego. Rzeczywiście, układ jednorodny odpowiada zerowym wa-
runkom interpolacyjnym, przy których, jak pokazaliśmy wcześniej, ze-
rowa funkcja sklejana (której odpowiada a
i,j
= 0, ∀i, j) jest jedynym
rozwiązaniem zadania interpolacyjnego.
2
Naturalne funkcje sklejane możemy więc używać do interpolacji
funkcji. Pokażemy teraz inną ich własność, która jest powodem dużego
praktycznego zainteresowania funkcjami sklejanymi.
Twierdzenie 8.2 Niech f
∈ W
r
(a, b) i niech s
f
∈ S
r
będzie naturalną
funkcją sklejaną rzędu r interpolującą f w węzłach x
j
, 0
≤ j ≤ n.
Wtedy
Z
b
a
f
(r)
(x)
2
dx
≥
Z
b
a
s
(r)
f
(x)
2
dx.
(8.1)
Dowód Jeśli przedstawimy f w postaci f = s
f
+ (f − s
f
), to
Z
b
a
f
(r)
(x)
2
dx
=
Z
b
a
s
(r)
f
(x)
2
dx
+
Z
b
a
(f − s
f
)
(r)
(x)
2
dx
2
Z
b
a
s
(r)
f
(x)(f − s
f
)
(r)
(x) dx.

94
ROZDZIAŁ 8. INTERPOLACJA FUNKCJAMI SKLEJANYMI
Funkcja f −s
f
jest w klasie W
r
(a, b) i zeruje się w węzłach x
j
, 0 ≤ j ≤ n.
Z Lematu 8.1 wynika więc, że
R
b
a
s
(r)
f
(x)(f −s
f
)
(r)
(x)dx = 0, a stąd (8.1).
2
Wartość całki
R
b
a
(f
(r)
(x))
2
dx
może być w ogólności uważana za miarę
gładkości funkcji. Nierówność (8.1) możemy więc zinterpretować w na-
stępujący sposób. Naturalna funkcja sklejana jest w klasie W
r
(a, b) naj-
gładszą funkcją spełniającą dane warunki interpolacyjne w wybranych
węzłach x
j
.
Konsekwencją Lematu 8.1 są również inne aproksymacyjne własno-
ści naturalnych funkcji sklejanych, zob. U. 8.2.
Jak już wspomnieliśmy, najczęściej używanymi są kubiczne funkcje
sklejane. Dlatego rozpatrzymy je oddzielnie.
8.3 Kubiczne funkcje sklejane
Jeśli zdecydowaliśmy się na użycie kubicznych funkcji sklejanych to
powstaje problem wyznaczenia s
f
∈ S
2
interpolującej daną funkcję f,
tzn. takiej, że s
f
(x
i
) = f(x
i
) dla 0 ≤ i ≤ n. W tym celu, na każdym
przedziale [x
i
, x
i+1
] przedstawimy s
f
w postaci jej rozwinięcia w szereg
Taylora w punkcie x
i
,
s
f
(x) = w
i
(x) = a
i
+ b
i
(x − x
i
) + c
i
(x − x
i
)
2
2
+ d
i
(x − x
i
)
3
6
,
i podamy algorytm obliczania a
i
, b
i
, c
i
, d
i
dla 0 ≤ i ≤ n − 1.
Warunki brzegowe i warunki ciągłości dla s
′′
f
dają nam w
′′
0
(x
0
) =
0 = w
′′
n−1
(x
n
) oraz w
′′
i
(x
i+1
) = w
′′
i+1
(x
i+1
), czyli
c
0
= 0,
c
i
+ d
i
h
i
= c
i+1
,
0 ≤ i ≤ n − 2,
c
n−1
+ d
n−1
h
n−1
= 0,
gdzie h
i
= x
i+1
− x
i
. Stąd, przyjmując dodatkowo c
n
= 0, otrzymujemy
d
i
=
c
i+1
− c
i
h
i
,
1 ≤ i ≤ n − 1.
(8.2)

8.3. KUBICZNE FUNKCJE SKLEJANE
95
Z warunków ciągłości dla s
′
f
dostajemy z kolei
b
i
+ c
i
h
i
+ d
i
h
2
i
/
2 = b
i+1
,
0 ≤ i ≤ n − 2,
i uwzględniając (8.2)
b
i+1
= b
i
+ h
i
(c
i+1
+ c
i
)/2,
0 ≤ i ≤ n − 2.
(8.3)
Warunki ciągłości s
f
dają w końcu
a
i
+ b
i
h
i
+ c
i
h
2
i
/
2 + d
i
h
3
i
/
6 = a
i+1
,
0 ≤ i ≤ n − 2.
(8.4)
Równania (8.2),(8.3) i (8.4) definiują nam na odcinku [a, b] naturalną
kubiczną funkcję sklejaną. Ponieważ poszukiwana funkcja sklejana s
f
ma interpolować f, mamy dotatkowych n + 1 warunków interpolacyj-
nych w
i
(x
i
) = f(x
i
), 0 ≤ i ≤ n − 1, oraz w
n−1
(x
n
) = f(x
n
), z których
a
i
= f(x
i
),
0 ≤ i ≤ n − 1.
(8.5)
Teraz możemy (8.4) przepisać jako
f
(x
i+1
) = f(x
i
) + b
i
h
i
+ c
i
h
2
i
+ d
i
h
3
i
/
6,
przy czym wzór ten zachodzi również dla i = n − 1. Po wyrugowaniu
b
i
i podstawieniu d
i
z (8.2), mamy
b
i
= f(x
i
, x
i+1
) + h
i
(c
i+1
+ 2c
i
)/6,
0 ≤ i ≤ n − 1,
(8.6)
gdzie f(x
i
, x
i+1
) jest odpowiednią różnicą dzieloną. Możemy teraz po-
wyższe wyrażenie na b
i
podstawić w równaniach (8.3), aby otrzymać
c
i
h
i
/
6 + c
i+1
(h
i
+ h
i+1
)/3 + c
i+1
h
i+1
/
6 = f(x
i+1
, x
i+2
) − f(x
i
, x
i+1
).
Wprowadzając oznaczenie
c
∗
i
= c
i
/
6,
(8.7)
możemy to równanie przepisać jako
h
i
h
i
+ h
i+1
c
∗
i
+ 2 c
∗
i+1
+
h
i+1
h
i
+ h
i+1
c
∗
i+2
= f(x
i
, x
i+1
, x
i+2
),

96
ROZDZIAŁ 8. INTERPOLACJA FUNKCJAMI SKLEJANYMI
0 ≤ i ≤ n − 2, albo w postaci macierzowej
2 w
1
u
2
2
w
2
u
3
2
w
3
... ...
...
u
n−2
2
w
n−2
u
n−1
2
c
∗
1
c
∗
2
c
∗
3
...
c
∗
n−2
c
∗
n−1
=
v
1
v
2
v
3
...
v
n−2
v
n−1
,
(8.8)
gdzie
u
i
=
h
i−1
h
i−1
+ h
i
,
w
i
=
h
i
h
i−1
+ h
i
,
v
i
= f(x
i−1
, x
i
, x
i+1
).
Ostatecznie, aby znaleźć współczynniki a
i
, b
i
, c
i
, d
i
należy najpierw roz-
wiązać układ równań (8.8), a potem zastosować wzory (8.7), (8.2), (8.6)
i (8.5).
Zauważmy, że macierz układu (8.8) jest trójdiagonalna i ma domi-
nującą przekątną. Układ można więc rozwiązać kosztem proporcjonal-
nym do wymiaru n używając algorytmu przeganiania z U. 3.6. Koszt
znalezienia wszystkich współczynników kubicznej funkcji sklejanej in-
terpolującej f jest więc też proporcjonalny do n.
Na końcu oszacujemy jeszcze błąd interpolacji naturalnymi kubicz-
nymi funkcjami sklejanymi na przedziale [a, b]. Będziemy zakładać, że
f
jest dwa razy różniczkowalna w sposób ciągły.
Twierdzenie 8.3 Jeśli f
∈ F
1
M
([a, b]) to
kf − s
f
k
C
([a,b])
≤ 5 M max
1≤i≤n
(x
i
− x
i−1
)
2
.
W szczególności, dla podziału równomiernego x
i
= a + (b − a)i/n, 0 ≤
i
≤ n, mamy
kf − s
f
k
C
([a,b])
≤ 5 M
b
− a
n
2
.

8.3. KUBICZNE FUNKCJE SKLEJANE
97
Dowód Wykorzystamy obliczoną wcześniej postać interpolującej funk-
cji sklejanej s
f
. Dla x ∈ [x
i
, x
i+1
] mamy
w
i
(x) = f(x
i
) +
f
(x
i+1
) − f(x
i
)
h
i
− h
i
(c
∗
i+1
+ 2c
∗
i
)
!
(x − x
i
)
+ 3c
∗
i
(x − x
i
)
2
+
c
∗
i+1
− c
∗
i
h
i
(x − x
i
)
3
.
Z rozwinięcia f w szereg Taylora w punkcie x
i
dostajemy f(x) = f(x
i
)+
f
′
(x
i
)(x − x
i
) + f
′′
(ξ
1
)(x − x
i
)
2
/
2 oraz (f(x
i+1
) − f(x
i
))/h
i
= f
′
(x
i
) +
h
i
f
′′
(ξ
2
)/2. Stąd
f
(x) − s
f
(x) = f(x) − w
i
(x)
=
f
′′
(ξ
1
)
2
(x − x
i
)
2
−
f
′′
(ξ
2
)
2
− (c
∗
i+1
+ 2c
∗
i
)
!
h
i
(x − x
i
)
−3c
∗
i
(x − x
i
)
2
−
c
∗
i+1
− c
∗
i
h
i
(x − x
i
)
3
,
oraz
|f(x) − s
f
(x)| ≤ (M + 2|c
∗
i+1
| + 6|c
∗
i
|)h
2
i
= (M + 8 max
1≤i≤n−1
|c
∗
i
|)h
2
i
.
Niech teraz max
1≤i≤n−1
|c
∗
i
| = |c
∗
s
|. Z postaci układu (8.8) otrzymujemy
|c
∗
s
| = 2|c
∗
s
| − |c
∗
s
|(u
s
+ w
s
) ≤ |u
s
c
∗
s−1
+ 2c
∗
s
+ w
s
c
s+1
|
= |f(x
s−1
, x
s
, x
s+1
)| ≤
f
′′
(ξ
3
)
2
≤
1
2
M,
a stąd i z (8.9)
|f(x) − s
f
(x)| ≤ 5Mh
2
i
,
co kończy dowód.
2
Uwagi i uzupełnienia
U. 8.1 Zamiast terminu funkcje sklejane używa się też często terminów
splajny (ang. spline-sklejać), albo funkcje gięte.

98
ROZDZIAŁ 8. INTERPOLACJA FUNKCJAMI SKLEJANYMI
U. 8.2 W Rozdziale 7 pokazaliśmy, że aproksymacja kawałkami wielomia-
nowa stopnia r jest optymalna (co do rzędu zbieżności) w klasie F
r
M
([a, b]),
wśród wszystkich aproksymacji korzystających jedynie z informacji o warto-
ściach funkcji w danej liczbie n punktów. Okazuje się, że podobne optymalne
własności wykazują funkcje sklejane, ale w innych klasach funkcji.
Niech
W
r
M
(a, b) =
n
f
∈ W
r
(a, b) :
Z
b
a
f
(r)
(x)
2
dx
≤ M
o
.
Ustalmy węzły a = x
0
<
· · · < x
n
= b. Dla f ∈ W
r
M
(a, b), niech s
f
będzie
naturalną funkcją sklejaną interpolującą f w x
j
, 0 ≤ j ≤ n, a a
f
dowolną
inną aproksymacją korzystającą jedynie z informacji o wartościach f w tych
węzłach , tzn.
a
f
= φ(f(x
0
), . . . , f(x
n
)).
Załóżmy, że błąd aproksymacji mierzymy nie w normie Czebyszewa, ale w
normie średniokwadratowej, zdefiniowanej jako
kgk
L
2
(a,b)
=
s
Z
b
a
(g(x))
2
dx.
Wtedy
sup
f ∈W
r
M
(a,b)
kf − s
f
k
L
2
(a,b)
≤
sup
f ∈W
r
M
(a,b)
kf − a
f
k
L
2
(a,b)
.
Aproksymacja naturalnymi funkcjami sklejanymi jest więc optymalna w kla-
sie W
r
M
(a, b).
Można również pokazać, że interpolacja s
∗
f
naturalnymi funkcjami skle-
janymi na węzłach równoodległych x
j
= a + (b − a)j/n, 0 ≤ j ≤ n, jest
optymalna co do rzędu w klasie W
r
M
(a, b), wśród wszystkich aproksymacji
korzystających jedynie z informacji o wartościach funkcji w n + 1 dowolnych
punktach, oraz
max
f ∈W
r
M
(a,b)
kf − s
∗
f
k
L
2
(a,b)
≍ n
−r
.
U. 8.3 Tak jak wielomiany, naturalne funkcje sklejane interpolujące dane
funkcje można reprezentować przez ich współczynniki w różnych bazach.
Do tego celu można na przykład użyć bazy kanonicznej K
j
, 0 ≤ j ≤ n,
zdefiniowanej równościami
K
j
(x
i
) =
(
0
i
6= j,
1
i = j,

8.3. KUBICZNE FUNKCJE SKLEJANE
99
przy której s
f
(x) =
P
n
j=0
f (x
j
)K
j
(x). Baza kanoniczna jest jednak niewy-
godna w użyciu, bo funkcje K
j
w ogólności nie zerują się na żadnym pod-
przedziale, a tym samym manipulowanie nimi jest utrudnione.
Częściej używa się bazy B-sklejanej B
j
, 0 ≤ j ≤ n. W przypadku funkcji
kubicznych, r = 2, jest ona zdefiniowana przez następujące warunki:
B
j
(x
j
) = 1,
dla 0 ≤ j ≤ n,
B
j
(x) = 0,
dla x ≤ x
j−2
, j
≥ 2, oraz dla x ≥ x
j+2
, j
≤ n − 2.
Dla B
0
i B
1
dodatkowo żądamy, aby
B
′′
0
(x
0
) = 0 = B
′′
1
(x
0
),
B
1
(x
0
) = 0,
a dla B
n−1
i B
n
podobnie
B
′′
n−1
(x
n
) = 0 = B
′′
n
(x
n
),
B
n−1
(x
n−1
) = 0.
Wtedy B
j
nie zeruje się tylko na przedziale (x
j−2
, x
j+2
), Wyznaczenie współ-
czynników rozwinięcia w bazie {B
i
}
n
i=0
funkcji sklejanej interpolującej f wy-
maga rozwiązania układu liniowego z macierzą trójdiagonalną {B
j
(x
i
)}
n
i,j=0
,
a więc koszt obliczenia tych współczynników jest proporcjonalny do n.
U. 8.4 Oprócz naturalnych funkcji sklejanych często rozpatruje się też okre-
sowe funkcje sklejane. Są to funkcje ˜
s : R
→ R spełniające warunki (i), (ii)
z Rozdziału 8.1, oraz warunek:
(iii)’ ˜s
(i)
jest dla 0 ≤ i ≤ r − 1 funkcją okresową o okresie (b − a), tzn.
˜s
(i)
(x) = ˜s
(i)
(x + (b − a)), ∀x.
Klasę okresowych funkcji sklejanych rzędu r oznaczymy przez ˜
S
r
. Funkcje
te mają podobne własności jak naturalne funkcje sklejane. Dokładniej, niech
˜
W
r
(a, b) = { f ∈ W
r
(a, b) : f
(i)
(a) = f
(i)
(b), 0 ≤ i ≤ r − 1 },
(8.9)
tzn. ˜
W
r
(a, b) jest klasą funkcji z W
r
(a, b), które można przedłużyć do funkcji,
krórych wszystkie pochodne do rzędu r − 1 włącznie są (b − a)-okresowe na
R. Wtedy dla dowolnej funkcji f ∈ ˜
W
r
(a, b) zerującej się w węzłach x
j
, oraz
dla dowolnej ˜s ∈ ˜
S
r
mamy
Z
b
a
f
(r)
(x)˜s
(r)
(x) dx = 0.
(8.10)

100 ROZDZIAŁ 8. INTERPOLACJA FUNKCJAMI SKLEJANYMI
Jest to odpowiednik Lematu 8.1 w przypadku okresowym. W szczególno-
ści wynika z niego jednoznaczność rozwiązania zadania interpolacyjnego dla
okresowych funkcji f (tzn. takich, że f(a) = f(b)), jak również odpowiednia
własność minimalizacyjna okresowych funkcji sklejanych. Dokładniej, jeśli
f
∈ ˜
W
r
(a, b) oraz ˜s
f
∈ ˜
S
r
interpoluje f w węzłach x
j
, 0 ≤ j ≤ n, to
Z
b
a
f
(r)
(x)
2
dx
≥
Z
b
a
˜s
(r)
f
(x)
2
dx.
U. 8.5 Klasyczne zadanie aproksymacyjne w przestrzeniach funkcji defi-
niuje się w następujący sposób.
Niech F będzie pewną przestrzenią liniową funkcji f : [a, b] → R, w
której określona została norma k · k. Niech V
n
⊂ F będzie podprzestrzenią
w F wymiaru n. Dla danej f ∈ F , należy znaleźć funkcję v
f
∈ F taką, że
kf − v
f
k = min
v∈V
n
kf − vk.
Okazuje się, że tak postawione zadanie ma rozwiązanie v
f
, choć nie zawsze
jest ono wyznaczone jednoznacznie, zob. Ćw. 8.6.
Jako przykład, rozpatrzmy F = W
r
(a, b). Utożsamiając funkcje f
1
, f
2
∈
W
r
(a, b) takie, że f
1
(x) − f
2
(x) ∈ Π
r−1
, zdefiniujemy w W
r
(a, b) normę
kfk =
s
Z
b
a
f
(r)
(x)
2
dx.
Dla ustalonych węzłów a = x
0
<
· · · < x
n
= b, niech
V
n+1
= S
r
będzie podprzestrzenią w W
r
(a, b) naturalnych funkcji sklejanych rzędu r
opartych węzłach x
j
, 0 ≤ j ≤ n. Oczywiście dimS
r
= n + 1, co wynika z
jednoznaczności rozwiązania w S
r
zadania interpolacji. Okazuje się, że wtedy
optymalną dla f ∈ W
r
(a, b) jest naturalna funkcja sklejana s
f
interpolująca
f w węzłach x
j
, tzn.
kf − s
f
k = min
s∈S
r
kf − sk.
Rzeczywiście, ponieważ norma w przestrzeni W
r
(a, b) generowana jest
przez iloczyn skalarny
hf
1
, f
2
i =
Z
b
a
f
(r)
1
(x)f
(r)
2
(x) dx,

8.3. KUBICZNE FUNKCJE SKLEJANE
101
jest to przestrzeń unitarna. Znane twierdzenie mówi, że w przestrzeni uni-
tarnej najbliższą danej f funkcją w dowolnej domkniętej podprzestrzeni V
jest rzut prostopadły f na V , albo równoważnie, taka funkcja v
f
∈ V
n+1
, że
iloczyn skalarny
hf − v
f
, v
i = 0,
∀v ∈ V.
W naszym przypadku, ostatnia równość jest równoważna
Z
b
a
(f − v
f
)
(r)
(x)s
(r)
(x) dx = 0,
∀s ∈ S
r
.
To zaś jest na mocy Lematu 8.1 prawdą gdy v
f
interpoluje f w punktach
x
j
, czyli v
f
= s
f
.
Dodajmy jeszcze, że nie zawsze interpolacja daje najlepszą aproksymację
w sensie klasycznym, zob. Ćw. 8.7.
Ćwiczenia
Ćw. 8.1 Dla z ∈ R, niech
z
+
= max(0, z) =
(
z
z
≥ 0,
0
z < 0.
Pokazać, że każdą funkcję sklejaną s rzędu r można przedstawić w postaci
s(x) = w(x) +
n
X
j=0
a
j
(x − x
j
)
+
2r−1
,
gdzie a
j
są pewnymi współczynnikami rzeczywistymi, a w ∈ Π
2r−1
. Ponadto,
jeśli s jest naturalna, to w ∈ Π
r−1
, a współczynniki a
j
spełniają równania
n
X
j=0
a
j
x
i
j
= 0,
0 ≤ i ≤ r − 1.
Ćw. 8.2 Niech h > 0 i c ∈ R. Wyznaczyć współczynniki kubicznej funkcji
sklejanej s opartej na pięciu węzłach −2h, −h, 0, h, 2h i spełniającej dodat-
kowo następujące warunki interpolacyjne:
s(0) = c,
s
(k)
(±2h) = 0,
k = 0, 1, 2,

102 ROZDZIAŁ 8. INTERPOLACJA FUNKCJAMI SKLEJANYMI
Ćw. 8.3 Wykorzystując Ćw. 8.2 wykazać, że dla dowolnego układu węzłów
a
≤ x
1
<
· · · x
n
≤ b mamy
max{ kf
′′
k
C
([a,b])
: f ∈ F
1
M
([a, b]), f(x
i
) = 0, 1 ≤ i ≤ n } ≥
M
24
b
− a
n + 1
2
.
Stąd i z U. 7.6 wywnioskować, że dla każdej aproksymacji a
f
korzystającej
jedynie z wartości f w n punktach,
max
f ∈F
1
M
([a,b])
kf − a
f
k
C
([a,b])
≥
M
24
b
− a
n + 1
2
.
Ćw. 8.4 Pokazać, że funkcje B
j
, 0 ≤ j ≤ n, zdefiniowane w U. 8.3 istnieją
i tworzą bazę w przestrzeni S
r
.
Ćw. 8.5 Pokazać jednoznaczność rozwiązania zadania interpolacyjnego w
przypadku okresowych funkcji sklejanych (zob. U. 8.4), oraz własność mini-
malizacyjną (8.9).
Wskazówka. Zastosować technikę dowodową podobną do tej z przypadku
naturalnych funkcji sklejanych.
Ćw. 8.6 Pokazać, że ogólnie postawione zadanie aproksymacyjne z U. 8.5
ma rozwiązanie.
Wskazówka. Zauważyć, że jeśli v
f
istnieje to kv
f
k ≤ 2kfk, oraz wykorzystać
ciągłość odwzorowania v 7→ kf − vk, v ∈ V , oraz fakt, że dimV < ∞.
Ćw. 8.7 Niech F = C([a, b]) z normą Czebyszewa, albo F = L
2
(a, b) z
normą średniokwadratową. Niech V
n+1
= Π
n
. Uzasadnić na przykładach, że
w ogólności nie istnieją węzły x
j
, 0 ≤ j ≤ n, o następującej własności: dla
każdej funkcji f ∈ F , wielomian w
f
∈ Π
n
interpolujący f w węzłach x
j
jest
elementem optymalnym w sensie aproksymacji klasycznej, zdefiniowanej w
U. 8.5.
æ

Rozdział 9
Całkowanie numeryczne
Zajmiemy się teraz zadaniem całkowania numerycznego. Polega ono na
obliczeniu (a raczej przybliżeniu) całki oznaczonej
S
(f) =
Z
b
a
f
(x) dx,
gdzie −∞ < a < b < +∞, a f należy do pewnej klasy F funkcji
rzeczywistych określonych i całkowalnych w sensie Riemanna na całym
przedziale [a, b].
Będziemy zakładać, że mamy możliwość obliczania wartości funkcji
f
, a w niektórych przypadkach również jej pochodnych, o ile istnieją.
Dokładna całka S(f) będzie więc w ogólności przybliżana wartością
A
(f), która zależy tylko od wartości f i ew. jej pochodnych w skończo-
nej liczbie punktów.
9.1 Co to są kwadratury?
Kwadraturami nazywamy funkcjonały liniowe Q : F
→ R postaci
Q
(f) =
n
X
i=0
a
i
f
(x
i
),
albo ogólniej
Q
(f) =
k
X
i=0
n
i
−1
X
j=0
a
i,j
f
(j)
(x
i
),
(9.1)
103

104
ROZDZIAŁ 9. CAŁKOWANIE NUMERYCZNE
gdzie x
i
są punktami z [a, b], a a
i
(albo a
i,j
) są pewnymi współczyn-
nikami rzeczywistymi. Zauważmy, że obliczenia kwadratur są dopusz-
czalne w naszym modelu obliczeniowym, mogą więc służyć jako sposób
przybliżania całki.
Jeden z możliwych sposobów konstrukcji kwadratur jest następu-
jący. Najpierw wybieramy węzły x
j
(pojedyncze lub wielokrotne), bu-
dujemy wielomian interpolacyjny odpowiadający tym węzłom, a na-
stępnie całkujemy go. Ponieważ postać wielomianu interpolacyjnego
zależy tylko od danej informacji o f, otrzymana w ten sposób wartość
też będzie zależeć tylko od tej informacji, a w konsekwencji funkcjonał
wynikowy będzie postaci (9.1). Są to tzw. kwadratury interpolacyjne.
Definicja 9.1 Kwadraturę Q
I
opartą na węzłach o łącznej krotności
n
+ 1 nazywamy interpolacyjną, jeśli
Q
I
(f) =
Z
b
a
w
f
(x) dx,
gdzie w
f
jest wielomianem interpolacyjnym funkcji f stopnia co najwy-
żej n, opartym na tych węzłach.
Współczynniki kwadratur interpolacyjnych można łatwo wyliczyć.
Rozpatrzmy dla uproszczenia przypadek, gdy węzły są jednokrotne.
Zapisując wielomian interpolacyjny w postaci jego rozwinięcia w bazie
kanonicznej Lagrange’a l
i
(zob. (6.3)), otrzymujemy
Q
I
(f) =
Z
b
a
n
X
i=0
f
(x
i
)l
i
(x) dx =
n
X
i=0
f
(x
i
)
Z
b
a
l
i
(x) dx,
a stąd i z postaci l
i
,
a
i
=
Z
b
a
(x − x
0
) · · · (x − x
i−1
)(x − x
i+1
) · · · (x − x
n
)
(x
i
− x
0
) · · · (x
i
− x
i−1
)(x
i
− x
i+1
) · · · (x
i
− x
n
)
dx,
0 ≤ i ≤ n.
Podamy teraz kilka przykładów.
Kwadratura prostokątów jest oparta na jednym węźle x
0
= (a + b)/2,
Q
I
0
(f) = (b − a)f
a
+ b
2
.

9.2. BŁĄD KWADRATUR INTERPOLACYJNYCH
105
Kwadratura trapezów jest oparta na jednokrotnych węzłach x
0
= a,
x
1
= b i jest równa polu odpowiedniego trapezu,
Q
I
1
(f) = T (f) =
b
− a
2
f
(a) + f(b)
.
Kwadratura parabol (Simpsona) jest oparta na jednokrotnych węzłach
x
0
= a, x
1
= b, x
2
= (a + b)/2, i jest równa polu pod parabolą interpo-
lującą f w tych węzłach,
Q
I
2
(f) = P (f) =
b
− a
6
f
(a) + 4f
a
+ b
2
+ f(b)
.
Zauważmy, że kwadratury trapezów i parabol są oparte na węzłach
jednokrotnych i równoodległych, przy czym x
0
= a i x
n
= b. Ogólnie,
kwadratury interpolacyjne oparte na węzłach równoodległych x
i
= a +
(b − a)i/n, 0 ≤ i ≤ n, nazywamy kwadraturami Newtona–Cotesa.
9.2 Błąd kwadratur interpolacyjnych
Zajmiemy się teraz błędem kwadratur interpolacyjnych. Przypomnijmy,
że F
n
M
([a, b]) oznacza klasę funkcji (n + 1) razy różniczkowalnych w
sposób ciągły i takich, że |f
(n+1)
(x)| ≤ M, ∀x.
Twierdzenie 9.1 Niech Q
I
będzie kwadraturą interpolacyjną opartą
na (jednokrotnych lub wielokrotnych) węzłach x
i
, 0
≤ i ≤ n. Jeśli f ∈
F
n
M
([a, b]) to
|S(f) − Q
I
(f)| ≤
M
(n + 1)!
(b − a)
n+2
.
(9.2)
W klasie F
n
M
([a, b]), maksymalny błąd kwadratury Q
I
wynosi
sup
f ∈F
n
M
([a,b])
|S(f)−Q
I
(f)| =
M
(n + 1)!
Z
b
a
|(x−x
0
)(x−x
1
) · · · (x−x
n
)| dx.
Dowód Korzystając ze znanego nam już wzoru na błąd interpolacji
wielomianowej z Lematu 7.1, mamy
S
(f) − Q
I
(f) =
Z
b
a
(x − x
0
)(x − x
1
) · · · (x − x
n
)f(x
0
, x
1
, . . . , x
n
, x
) dx.
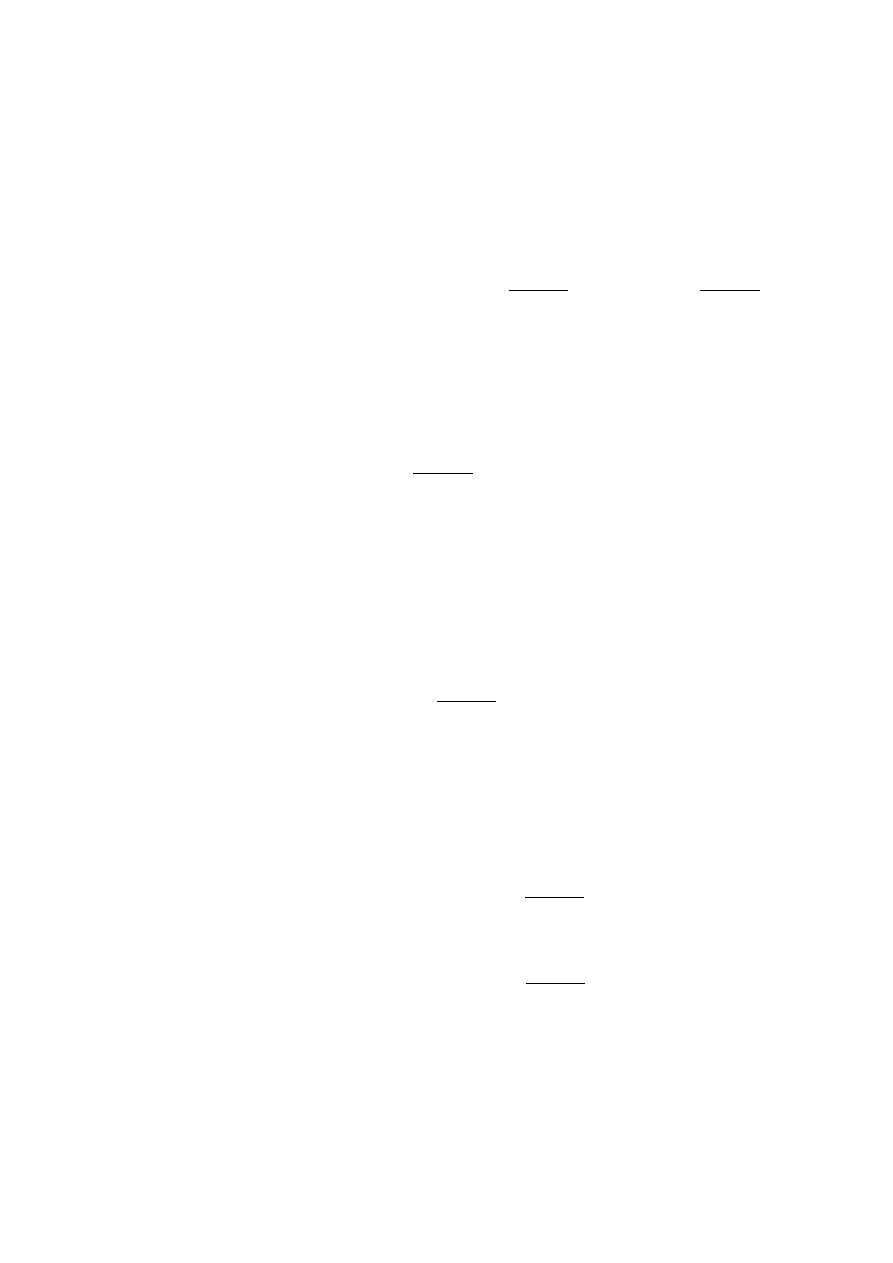
106
ROZDZIAŁ 9. CAŁKOWANIE NUMERYCZNE
Stąd, jeśli f ∈ F
n
M
([a, b]) to
|S(f) − Q
I
(f)| ≤
Z
b
a
(b − a)
n+1
M
(n + 1)!
dx
= (b − a)
n+2
M
(n + 1)!
.
Ograniczenie górne w dokładnej formule na błąd w klasie F
n
M
([a, b])
wynika bezpośrednio z oszacowania (9.2). Aby pokazać ograniczenie
dolne zauważmy, że dla funkcji g takiej, że g
(n+1)
przyjmuje na prze-
działach (a, x
0
), (x
0
, x
1
), . . ., (x
n
, b
) naprzemiennie wartości M i −M
mamy
|S(g) − Q
I
(g)| =
M
(n + 1)!
Z
b
a
|(x − x
0
)(x − x
1
) · · · (x − x
n
)| dx.
Co prawda, g nie jest w F
n
M
[a, b], ale może być dla dowolnego ε > 0
przybliżana funkcjami f
ε
∈ F
n
M
([a, b]) w ten sposób, że całka
Z
b
a
|(x − x
0
) · · · (x − x
n
)(f − g)
(n+1)
(x)| dx ≤ ε (n + 1)!.
Zapisując f
ε
= g + (f
ε
− g) mamy
|S(f
ε
) − Q
I
(f
ε
)| ≤ |S(g) − Q
I
(g)| + |S(f
ε
− g) − Q
I
(f
ε
− g)|
≤
M
(n + 1)!
Z
b
a
|(x − x
0
) · · · (x − x
n
)| dx + ε,
co wobec dowolności ε daje dowód twierdzenia.
2
W szczególnych przypadkach kwadratur trapezów T i parabol P
możemy otrzymać innego rodzaju formuły na błąd.
Twierdzenie 9.2 (i) Jeśli f
∈ C
(2)
([a, b]) to dla kwadratury trapezów
mamy
S
(f) − T (f) = −
(b − a)
3
12
f
(2)
(ξ
1
).
(ii) Jeśli f
∈ C
(4)
([a, b]) to dla kwadratury parabol mamy
S
(f) − P (f) = −
(b − a)
5
2280
f
(4)
(ξ
2
).
(ξ
1
, ξ
2
∈ [a, b]).
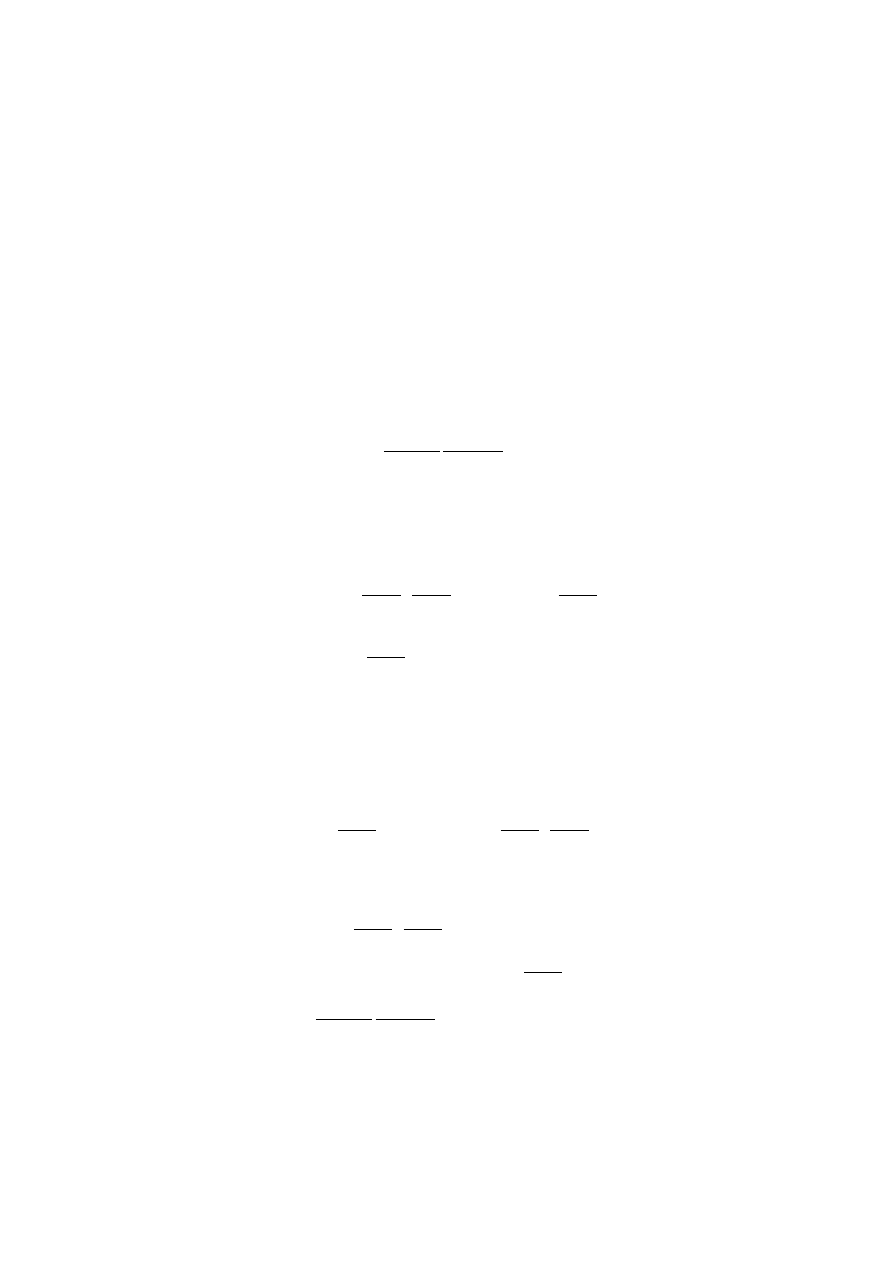
9.2. BŁĄD KWADRATUR INTERPOLACYJNYCH
107
Dowód (i) Ze wzoru (9.2)
S
(f) − T (f) =
Z
b
a
(x − a)(x − b)f(a, b, x) dx.
Ponieważ funkcja x 7→ f(a, b, x) jest ciągła, a wielomian (x − a)(x − b)
przyjmuje jedynie wartości nieujemne, można zastosować twierdzenie o
wartości średniej dla całki, aby otrzymać
S
(f) − T (f) = f(a, b, c)
Z
b
a
(x − a)(x − b) dx
= −
f
(2)
(ξ
1
)
2!
(b − a)
3
6
,
dla pewnych c, ξ
1
∈ [a, b].
(ii) Niech w
f,2
∈ Π
2
i w
f,3
∈ Π
3
będą wielomianami interpolacyjnymi
funkcji f odpowiednio dla węzłów a, b, (a + b)/2 oraz a, b, (a + b)/2, (a +
b
)/2. Wtedy
w
f,3
(x) = w
f,2
(x) + f
a, b,
a
+ b
2
,
a
+ b
2
(x − a)
x
−
a
+ b
2
(x − b).
Wobec
Z
b
a
(x − a)
a
+ b
2
(x − b) dx = 0
mamy
P
(f) =
Z
b
a
w
f,2
(x) dx =
Z
b
a
w
f,3
(x) dx.
Stąd i ze wzoru na błąd interpolacji Hermite’a otrzymujemy
S
(f) − P (f) =
Z
b
a
(f − w
f,3
)(x) dx
=
Z
b
a
(x − a)
x
−
a
+ b
2
2
(x − b)f
a, b,
a
+ b
2
,
a
+ b
2
, x
dx.
Ponieważ wielomian (x − a)(x − (a + b)/2)
2
(x − b) jest niedodatni na
[a, b], możemy znów zastosować twierdzenie o wartości średniej. Mamy
S
(f) − P (f) = f
a, b,
a
+ b
2
,
a
+ b
2
, c
Z
b
a
(x − a)
x
−
a
+ b
2
2
(x − b) dx
= −
f
(4)
(ξ
2
)
4!
(b − a)
5
120
,

108
ROZDZIAŁ 9. CAŁKOWANIE NUMERYCZNE
co kończy dowód.
2
9.3 Kwadratury złożone
Podobnie jak w przypadku zadania interpolacji chcielibyśmy, aby błąd
kwadratur malał do zera, gdy liczba węzłów rośnie do nieskończoności.
Można to osiągnąć stosując np. kwadratury złożone. Są to kwadratury,
które powstają przez scałkowanie funkcji kawałkami wielomianowej in-
terpolującej f.
Prostym przykładem kwadratury złożonej jest suma Riemanna,
¯
Q
(f) =
n
X
i=0
(t
i+1
− t
i
)f(x
i
),
gdzie a = t
0
< t
1
<
· · · < t
n+1
= b oraz x
i
∈ [t
i
, t
i+1
]. Jeśli średnica
podziału, max
0≤i≤n
(t
i
− t
i−1
), maleje do zera to lim
n→∞
¯
Q
(f) = S(f).
Będziemy rozpatrywać kwadratury złożone postaci
¯
Q
(f) =
Z
b
a
¯
w
f
(x) dx,
gdzie ¯
w
f
jest kawałkami wielomianem z Rozdziału 7.3. To znaczy, dla
danego n kładziemy t
i
= a + (b − a)i/k, 0 ≤ i ≤ k, a następnie dla
każdego i wybieramy dowolne węzły x
i,j
∈ [t
i−1
, t
i
], 0 ≤ j ≤ r. Wtedy
¯
w
f
jest na każdym przedziale wielomianem interpolacyjnym funkcji f
stopnia co najwyżej r opartym na węzłach x
i,j
. Kwadratura ¯
Q
korzysta
z węzłów o łącznej krotności n ≤ k(r + 1).
Twierdzenie 9.3 Błąd kwadratury złożonej ¯
Q
(f) w klasie F
r
M
([a, b])
jest ograniczony przez
sup
f ∈F
r
M
([a,b])
|S(f) − ¯
Q
(f)| ≤
(b − a)
r+2
k
r+1
M
(r + 1)! ≤
C
1
n
r+1
,
gdzie
C
=
M
(r + 1)
r+1
(b − a)
r+2
(r + 1)!
.

9.3. KWADRATURY ZŁOŻONE
109
Dowód Twierdzenie to jest bezpośrednim wnioskiem z Twierdzenia
9.1. Mamy bowiem
|S(f) − ¯
Q
(f)| ≤
k
X
i=1
Z
t
i
t
i−1
|f(x) − ¯
w
f
(x)| dx
≤
k
X
i=1
b
− a
k
r+2
M
(r + 1)!
=
(b − a)
r+2
k
r+1
M
(r + 1)!
,
co kończy dowód.
2
W klasie F
r
M
([a, b]), błąd kwadratur złożonych jest rzędu n
−(r+1)
,
czyli jest taki sam jak błąd interpolacji kawałkami wielomianowej. I
tak jak przy interpolacji można pokazać, że błąd każdej innej metody
całkowania korzystającej jedynie z wartości funkcji w n punktach nie
może w klasie F
r
M
([a, b]) maleć szybciej niż n
−(r+1)
, zob. U. 9.1. Podane
kwadratury złożone mają więc optymalny rząd zbieżności.
Zajmiemy się teraz błędem szczególnych kwadratur złożonych, mia-
nowicie złożonych kwadratur trapezów ¯
T
k
i parabol ¯
P
k
. Powstają one
przez zastosowanie na każdym przedziale [t
i−1
, t
i
] odpowiednio kwadra-
tur trapezów T i parabol P . Jak łatwo się przekonać,
¯
T
k
(f) =
b
− a
k
f
(a) + f(b)
2
+
k−1
X
j=1
f
j
k
,
oraz
¯
P
k
(f) =
b
− a
3k
f
(a) + f(b)
2
+
k−1
X
j=1
f
j
k
+ 2
k
X
j=1
f
2j − 1
2k
.
Twierdzenie 9.4 (i) Jeśli f
∈ C
(2)
([a, b]) to
S
(f) − ¯
T
k
(f) = −
(b − a)
2
12 k
2
f
(2)
(ξ
1
).
(ii) Jeśli f
∈ C
(4)
([a, b]) to
S
(f) − ¯
P
k
(f) = −
(b − a)
4
2280 k
4
f
(4)
(ξ
2
).

110
ROZDZIAŁ 9. CAŁKOWANIE NUMERYCZNE
Dowód Dla kwadratury trapezów mamy
S
(f) − ¯
T
k
(f) = −
k
X
i=1
(b − a)
3
12k
3
f
(2)
(α
i
)
= −
(b − a)
2
12k
2
k
X
i=1
b
− a
k
f
(2)
(α
i
) = −
(b − a)
2
12k
2
f
(2)
(ξ
1
),
a dla kwadratury parabol podobnie
S
(f) − ¯
P
k
(f) = −
k
X
i=1
(b − a)
5
2280k
5
f
(4)
(β
i
)
= −
(b − a)
4
2280k
4
k
X
i=1
b
− a
k
f
(4)
(β
i
) = −
(b − a)
4
2280k
4
f
(4)
(ξ
2
). 2
Kwadratura parabol ma więc optymalny rząd zbieżności nie tylko
w klasie F
2
M
([a, b]), ale też w F
3
M
([a, b]).
9.4 Przyspieszanie zbieżności kwadratur
W praktyce często stosuje się obliczanie kwadratur poprzez zagęszcza-
nie podziału przedziału [a, b]. Na przykład, dla złożonej kwadratury
trapezów zachodzi następujący wygodny wzór rekurencyjny:
¯
T
2k
=
1
2
¯
T
k
(f) +
b
− a
k
k
X
i=1
f
2i − 1
2k
!
.
(9.3)
Pozwala on obliczyć ¯
T
2k
(f) na podstawie ¯
T
k
(f) poprzez “doliczenie”
wartości funkcji w punktach “gęstszej” siatki. W ten sposób możemy
obserwować zachowanie się kolejnych przybliżeń ¯
T
2
s
(f) (s ≥ 0) całki
S
(f). Jest to szczególnie istotne wtedy, gdy nie mamy żadnej informa-
cji a priori o kf
′′
k
C
([a,b])
, a przez to nie potrafimy oszacować liczby n
węzłów, dla której osiągniemy pożądaną dokładność, zob. U. 9.2.
Jeśli funkcja jest więcej niż dwa razy różniczkowalna to użycie złożo-
nych kwadratur trapezów zdaje się tracić sens. Wtedy istnieją przecież
kwadratury, których błąd maleje do zera szybciej niż n
−2
. Okazuje się

9.4. PRZYSPIESZANIE ZBIEŻNOŚCI KWADRATUR
111
jednak, że kwadratury ¯
T
k
mogą być podstawą dla prostej rekurencyjnej
konstrukcji innych kwadratur posiadających już optymalną zbieżność.
Konstrukcja ta bazuje na następującym ważnym lemacie.
Lemat 9.1 (Formuła Eulera-Maclaurina)
Dla funkcji f
∈ C
(2m+2)
([a, b]), błąd złożonej kwadratury trapezów ¯
T
k
wyraża się wzorem
S
(f) − ¯
T
k
(f) =
m
X
i=1
c
i
h
2i
f
(2i−1)
(b) − f
(2i−1)
(a)
+ c
m+1
h
2m+2
(b − a)f
(2m+2)
(ξ
m,k
),
gdzie h = (b
− a)/k, ξ
m,k
∈ [a, b], a c
i
są pewnymi stałymi liczbowymi.
Mamy c
1
= −1/12, c
2
= −1/720 i, ogólnie, c
i
= B
i
/
(2i)!, gdzie B
i
są
tzw. liczbami Bernoulliego.
2
Dowód tego lematu pominiemy.
Formułę Eulera-Maclaurina można przepisać w postaci
S
(f) − ¯
T
k
(f) =
m
X
i=1
c
(0)
i
(f) k
−2i
+ c
(0)
m+1,k
(f) k
−(2m+2)
,
gdzie c
(0)
i
(f) = c
i
(b − a)
2i
(f
(2i−1)
(b) − f
(2i−1)
(a)), 1 ≤ i ≤ m, oraz
c
(0)
m+1,k
(f) = c
m+1
(b − a)
2m+2
f
(2m+2)
(ξ
m+1,k
). Zauważmy przy tym, że
jeśli f ∈ F
2m+1
M
([a, b]) to współczynniki c
(0)
m+1,k
(f) są wspólnie ograni-
czone przez c
m+1
(b − a)
2m+2
M
.
Definiując teraz kwadraturę
¯
T
1
k
(f) =
4 ¯
T
2k
(f) − ¯
T
k
(f)
3
,
dla f ∈ C
(4)
([a, b]) mamy
S
(f) − ¯
T
1
k
(f) =
4 (S(f) − ¯
T
2k
(f) − (S(f) − ¯
T
k
(f))
3
=
4
3
c
(0)
1
(f)
4k
2
+
c
(0)
2,2k
(f)
4
2
k
4
−
1
3
c
(0)
1
(f)
k
2
+
c
(0)
2,k
(f)
k
4
=
c
(1)
2,k
(f)
k
4
,

112
ROZDZIAŁ 9. CAŁKOWANIE NUMERYCZNE
gdzie c
(1)
2,k
(f) = (1/12)c
(0)
2,2k
(f) − (1/3)c
(0)
2,k
(f) i jest wspólnie ograniczone
dla f ∈ F
3
M
([a, b]). Kwadratura T
1
k
ma więc optymalny w F
3
M
([a, b]) rząd
zbieżności k
−4
. Proces ten można kontynuować dalej tworząc kolejne
kwadratury o coraz to wyższym rzędzie zbieżności. Dokładniej, połóżmy
¯
T
0
k
(f) = ¯
T
k
(f) oraz, dla s ≥ 1,
¯
T
s
k
(f) =
4
s
¯
T
s−1
2k
(f) − ¯
T
s−1
k
(f)
4
s
− 1
.
(9.4)
Wtedy, dla f ∈ F
2m+1
M
([a, b]), rząd zbieżności kwadratury ¯
T
m
k
wynosi
k
−(2m+2)
. Rzeczywiście, sprawdziliśmy, że jest to prawdą dla m = 0, 1.
Niech m ≥ 2. Postępując indukcyjnie ze względu na s = 1, 2, . . . , m
mamy
S
(f) − ¯
T
s
k
(f) =
4
s
(S(f) − ¯
T
s−1
2k
(f)) − (S(f) − ¯
T
s−1
k
(f))
4
s
− 1
=
4
s
m
X
i=s
c
(s−1)
i
(f)(2k)
−2i
+ c
(s−1)
m+1,2k
(f)(2k)
−(2m+2)
!
−
m
X
i=s
c
(s−1)
i
(f)k
−2i
+ c
(s−1)
m+1,k
(f)k
−(2m+2)
!!
1
4
s
− 1
=
m
X
i=s+1
c
(s)
i
(f)k
−2i
+ c
(s)
m+1,k
(f)k
−(2m+2)
,
ponieważ współczynniki przy k
−2s
redukują się. c
(s)
i
(f) są tutaj pew-
nymi nowymi stałymi, a c
(s)
m+1,k
(f) może być w klasie F
2m+1
M
([a, b]) ogra-
niczona przez stałą niezależną od f. Ostatecznie, dla s = m mamy więc
S
(f) − ¯
T
m
k
(f) = c
(m)
m+1,k
(f)k
−(2m+2)
i w klasie F
2m+1
M
([a, b])
|S(f) − ¯
T
m
k
(f)| ≤ c
m
k
−(2m+2)
dla pewnej stałej c
m
niezależnej od f.
Zauważmy jeszcze, że ¯
T
m
k
wykorzystuje n = k2
m
+ 1 wartości f
w punktach równoodległych na [a, b] co oznacza, że w terminach n
rząd zbieżności wynosi też n
−(2m+2)
, a więc jest optymalny w klasie
F
2m+1
M
([a, b]).

9.4. PRZYSPIESZANIE ZBIEŻNOŚCI KWADRATUR
113
Kwadratury ¯
T
s
k
nazywane są kwadraturami Romberga. Dla danej
funkcji f, można je łatwo konstruować budując następującą tablicę trój-
kątną:
¯
T
0
1
(f)
¯
T
0
2
(f)
¯
T
1
1
(f)
¯
T
0
4
(f)
¯
T
1
2
(f)
¯
T
2
1
(f)
¯
T
0
8
(f)
¯
T
1
4
(f)
¯
T
2
2
(f)
¯
T
3
1
(f)
...
...
...
...
...
¯
T
0
2
s
(f) ¯
T
1
2
s−1
(f) ¯
T
2
2
s−2
(f) ¯
T
3
2
s−3
(f) · · · ¯
T
s
1
(f),
(9.5)
w której pierwsza kolumna jest tworzona indukcyjnie zgodnie ze wzorem
(9.3), a kolejne zgodnie z (9.4).
Uwagi i uzupełnienia
U. 9.1 Pokażemy, że jeśli dowolny algorytm A daje przybliżoną wartość
całki S(f) =
R
b
a
f (x)dx na podstawie jedynie wartości lub pochodnych funk-
cji f w n różnych punktach, tzn.
A(f ) = φ(f (x
1
), . . . , f
(r+1)
(x
1
), . . . , f(x
n
), . . . , f
(r+1)
(x
n
))
dla pewnych x
i
∈ [a, b], to błąd takiego przybliżenia w klasie F
r
M
([a, b]),
sup
f ∈F
r
M
([a,b])
|S(f) − A(f)| ≥ C
1
M n
−(r+1)
,
(9.6)
gdzie C
1
jest pewną stałą dodatnią niezależną od A i n.
W tym celu, podobnie jak w U. 7.2, wybierzmy dowolną nieujemną funk-
cję ψ : R → R spełniającą warunki:
1. ψ ∈ F
r
1
(R),
2. ψ(x) = 0 dla x 6∈ [0, 1].
Oznaczmy x
0
= a, x
n+1
= b, h
i
= x
i+1
− x
i
, 0 ≤ i ≤ n, oraz zdefiniujmy
funkcje
ψ
i
(x) = Mh
r+1
i
ψ
x
− x
i
h
i
.

114
ROZDZIAŁ 9. CAŁKOWANIE NUMERYCZNE
Wtedy dla g
1
(x) = −g
2
(x) =
P
n
i=0
ψ
i
(x) mamy g
l
∈ F
r
M
([a, b]) oraz infor-
macja o g
l
jest zerowa, g
(p)
l
(x
j
) = 0 dla 0 ≤ p ≤ r + 1, 1 ≤ j ≤ n. Stąd
φ
0
= φ(0, . . . , 0
|
{z
}
n(r+2)
) jest aproksymacją dla całek obu funkcji ψ
l
i
max{|S(g
1
) − φ
0
|, |S(g
2
) − φ
0
|} ≥ |S(g
1
) − S(g
2
)|/2 = S(g
1
)
=
n
X
i=0
Z
x
i
x
i−1
ψ
i
(x) dx = M
n
X
i=0
h
r+1
i
Z
x
i
x
i−1
ψ
x
− x
i
h
i
dx
= M
Z
1
0
ψ(x) dx +
n
X
i=0
h
r+2
i
.
Zauważmy jeszcze, że suma
P
n
i=0
h
r+2
i
jest minimalna dla h
i
= (b−a)/(n+1),
∀i, a stąd
S(g
1
) ≥ M
(b − a)
r+2
(n + 1)
r+1
Z
1
0
ψ(x) dx.
Nierówność (9.6) zachodzi więc z C
1
= (2(b − a))
r+1
R
1
0
ψ(x)dx.
U. 9.2 Jeśli f ∈ C
(2)
([a, b]) i f
′
(a) 6= f
′
(b) to dla dużych k mamy
S(f )
− ¯
T
k
(f) ≈ c(f)k
−2
,
gdzie c(f) = −(b − a)
2
(f
′
(b) − f
′
(a))/12. Stąd
¯
T
k
(f) − ¯
T
k/2
(f) = (S(f) − ¯
T
k/2
(f)) − (S(f) − ¯
T
k
(f))
≈
c(f )
k
2
−
c(f )
(k/2)
2
= −
3c(f)
k
2
≈ −3 (S(f) − ¯
T
k
(f)),
a więc
S(f )
− ¯
T
k
(f) ≈
1
3
( ¯
T
k/2
(f) − ¯
T
k
(f)),
gdy k → ∞. Ostatnia przybliżona równość może sugerować kryterium koń-
czenia obliczeń, gdy chcemy otrzymać przybliżenie całki S(f) z zadaną do-
kładnością ε > 0. Mianowicie, obliczając kolejne kwadratury ¯
T
2
s
(f) dla
s = 0, 1, . . ., sprawdzamy jednocześnie, czy
| ¯
T
2
s−1
(f) − ¯
T
2
s
(f)| ≤ 3 ε.
Jeśli ten warunek jest spełniony dla kilku kolejnych s to z dużym prawdo-
podobieństwem możemy stwierdzić, że |S(f) − ¯
T
2
s
(f)| ≤ ε.
Oczywiście, podobne kryteria kończenia obliczeń mogą być konstruowane
dla innych ciągów kwadratur, jeśli tylko znamy teoretyczne zachowanie się
błędu.

9.4. PRZYSPIESZANIE ZBIEŻNOŚCI KWADRATUR
115
Ćwiczenia
Ćw. 9.1 Pokazać, że w kwadraturze Newtona-Cotesa opartej na n + 1 rów-
noodległych węzłach x
i
= a + (b − a)i/n, współczynniki a
i
dane są wzorami
a
i
=
(−1)
n−i
(b − a)
n i!(n
− i)!
Z
n
0
x(x
− 1) · · · (x − (i − 1))(x − (i + 1)) · · · (x − n) dx.
Ćw. 9.2 Pokazać, że jeśli f ∈ C
(2)
([a, b]) to dla kwadratury prostokątów
Q
0
(f) = f((a + b)/2)(b − a)/2 mamy
S(f )
− Q
0
(f) =
(b − a)
3
24
f
(2)
(ξ
0
),
(ξ
0
∈ [a, b]), a w konsekwencji
max
f ∈F
1
M
([a,b])
|S(f) − Q
0
(f)| =
M (b
− a)
3
24
.
Błąd w klasie F
1
M
([a, b]) jest więc dla kwadratury prostokątów dwa razy
mniejszy niż dla kwadratury trapezów. Wywnioskować stąd, że złożona kwa-
dratura prostokątów,
¯
Q
0
(f) =
b
− a
k
k
X
i=1
f
2i − 1
2k
,
ma optymalny rząd zbieżności nie tylko w klasie F
0
M
([a, b]), ale też w klasie
F
1
M
([a, b]).
Ćw. 9.3 Rozpatrzmy kwadratury interpolacyjne oparte na dwóch węzłach
x
0
, x
1
∈ [a, b]. Pokazać, że wśród tych kwadratur najmniejszy błąd w klasie
F
1
M
([a, b]) jest osiągany przez kwadraturę
Q
I
(f) =
b
− a
2
f
3a + b
4
+ f
a + 3b
4
,
a jej błąd
sup
f ∈F
1
M
([a,b])
|S(f) − Q
I
(f)| =
M (b
− a)
3
32
.

116
ROZDZIAŁ 9. CAŁKOWANIE NUMERYCZNE
Ćw. 9.4 Uzasadnić, że jeśli kwadratura interpolacyjna Q
I
oparta jest na
węzłach Czebyszewa
x
i
=
a + b
2
+
b
− a
2
cos
2i + 1
2r + 2
π
,
0 ≤ i ≤ r,
to dla f ∈ F
r
M
([a, b]) błąd
|S(f) − Q
I
(f)| ≤
M (b
− a)
r+2
2
2r+1
(r + 1)!
,
a dla odpowiadającej węzłom Czebyszewa kwadratury złożonej
|S(f) − ¯
Q
I
(f)| ≤
M (b
− a)
r+2
2
2r+1
(r + 1)!
1
k
r+1
.
Ćw. 9.5 Rozpatrzmy kwadraturę
¯
Q
k
(f) = ¯
T
k
(f) −
(b − a)
2
12k
2
(f
′
(b) − f
′
(a)).
Pokazać, nie korzytając z formuły Eulera-Maclaurina, że jeśli f ∈ F
2
M
([a, b])
to błąd |S(f) − ¯
Q
k
(f)| zbiega do zera co najmniej tak szybko jak k
−4
, gdy
k
→ ∞. W szczególności, dla funkcji spełniających f
′
(a) = f
′
(b) rząd zbież-
ności złożonej kwadratury trapezów wynosi k
−4
.
Ćw. 9.6 Opracować ekonomiczny algorytm obliczania ciągu kolejnych zło-
żonych kwadratur parabol ¯
P
2
s
(f) dla s = 0, 1, 2, . . ..
Ćw. 9.7 Opracować kryterium kończenia obliczeń analogiczne do tego z U.
9.2, dla ciągu złożonych kwadratur parabol ¯
P
2
s
(f), s = 0, 1, . . ..
Ćw. 9.8 Pokazać, że drugą kolumnę tabeli (9.5) kwadratur Romberga two-
rzą złożone kwadratury parabol, tzn.
¯
P
k
(f) =
4 ¯
T
2k
(f) − ¯
T
k
(f)
3
.
Ćw. 9.9 Opracować program obliczający wartość ¯
T
s
1
(f) kwadratury Rom-
berga, korzystając ze wzorów (9.3) i budując tabelę (9.4).
æ

Rozdział 10
Całkowanie a aproksymacja
W poprzednim rozdziale badaliśmy kwadratury ze względu na kryte-
rium błędu w pewnych klasach funkcji. W tym rozdziale zajmiemy się
badaniem kwadratur ze względu na inne, bardziej klasyczne kryterium,
którym jest rząd kwadratury. Będziemy przy tym rozpatrywać nieco
ogólniejsze zadanie całkowania, tzw. całkowanie z wagą,
S
(f) = S
ρ
(f) =
Z
b
a
f
(x)ρ(x) dx,
gdzie waga ρ jest prawie wszędzie dodatnia i jest całkowalna,
Z
b
a
|ρ(x)| dx < +∞.
Dopuścimy również możliwość nieskończonych przedziałów całkowania,
a więc −∞ ≤ a < b ≤ +∞.
10.1 Rząd kwadratury
Zaczniemy od definicji.
Definicja 10.1 Rzędem kwadratury Q nazywamy taką liczbę r, że
(i) kwadratura Q daje dokładną wartość całki dla wszystkich wielomia-
nów stopnia mniejszego niż r,
Q
(w) = S
ρ
(w),
∀w ∈ Π
r−1
,
117

118
ROZDZIAŁ 10. CAŁKOWANIE A APROKSYMACJA
(i) istnieje wielomian stopnia r dla którego kwadratura nie jest równa
całce,
∃w
∗
∈ Π
r
,
Q
(w
∗
) 6= S
ρ
(w
∗
).
Rząd kwadratury Q oznaczymy przez rz(Q). Dla przykładu, za-
łóżmy, że ρ ≡ 1 i przedział [a, b] jest skończony. Wtedy rząd kwa-
dratury prostokątów wynosi 2, tak jak rząd kwadratury trapezów T ,
natomiast rząd kwadratury parabol P wynosi 4. Rzeczywiście, to wy-
nika bezpośrednio ze wzorów na błędy tych kwadratur danych w Ćw.
9.2 i Twierdzeniu 9.2. Ogólniej, mamy następujące twierdzenie, które
przytaczamy bez dowodu.
Twierdzenie 10.1 Niech waga ρ
≡ 1 i niech przedział [a, b] będzie
skończony. Rząd kwadratury Newtona-Cotesa Q
N C
n
, tzn. opartej na jed-
nokrotnych węzłach równoodległych x
i
= a + (b − a)i/n, 0 ≤ i ≤ n,
wynosi
rz(Q
N C
) =
(
n
+ 1
dla n nieparzystych,
n
+ 2
dla n parzystych.
2
Jasne jest, że interesują nas kwadratury o jak najwyższym rzędzie.
Chcielibyśmy wiedzieć, jaki jest maksymalny rząd kwadratury korzy-
stającej z ustalonej liczby węzłów i jak konstruować kwadratury o mak-
symalnym rzędzie. Jak przekonamy się później, nie jest to tylko aka-
demickie pytanie, bowiem kwadratury o maksymalnym rzędzie mają
również dobre własności ze względu na błąd.
Częściową odpowiedź na pytanie o maksymalny rząd kwadratur
daje następujący lemat.
Lemat 10.1 Niech Q będzie kwadraturą opartą na węzłach o łącznej
krotności n + 1.
(i) Jeśli rz(Q)
≥ n + 1 to Q jest kwadraturą interpolacyjną.
(ii) Jeśli Q jest kwadraturą interpolacyjną to
n
+ 1 ≤ rz(Q) ≤ 2(n + 1).

10.2. CIĄGI WIELOMIANÓW ORTOGONALNYCH
119
Dowód (i) Dla dowolnej funkcji f , niech w
f
będzie wielomianem inter-
polacyjnym dla f stopnia co najwyżej n, opartym na tej samej informa-
cji o f, z jakiej korzysta kwadratura Q. Wtedy mamy Q(f) = Q(w
f
),
a ponieważ rz(Q) ≥ n + 1 to również Q(w
f
) = S
ρ
(w
f
). Stąd
Q
(f) = S
ρ
(w
f
),
a to oznacza, że Q jest interpolacyjna.
(ii) Jeśli Q jest interpolacyjna to dla każdego w ∈ Π
n
mamy Q(w) =
S
ρ
(w), bo w jest dla siebie wielomianem interpolacyjnym. Stąd rz(Q) ≥
n
+ 1.
Dla dowodu drugiej nierówności załóżmy, że Q korzysta z węzłów
x
0
, x
1
, . . . , x
n
(być może powtarzających się). Wtedy dla wielomianu
w
1
(x) = (x − x
0
)
2
(x − x
1
)
2
· · · (x − x
n
)
2
mamy w
1
∈ Π
2(n+1)
oraz S
ρ
(w
1
) > 0, bo w
1
jest prawie wszędzie do-
datni. Z drugiej strony, Q(w
1
) = 0, bo informacja o w
1
jest zerowa.
Stąd
Q
(w
1
) 6= S
ρ
(w
1
)
i w konsekwencji rz(Q) ≤ 2(n + 1). 2
Lemat 10.1 mówi nam, że w poszukiwaniu kwadratur o najwyż-
szym rzędzie możemy ograniczyć się do kwadratur interpolacyjnych.
Ponadto, maksymalny rząd jest na pewno nie mniejszy niż n + 1 i na
pewno nie większy niż 2(n + 1). Aby jednak odpowiedzieć na pytanie
jaki jest rzeczywisty maksymalny rząd, musimy odwołać się do pewnych
faktów z teorii aproksymacji w przestrzeniach unitarnych, a ściślej, do
własności ciągów wielomianów ortogonalnych.
10.2 Ciągi wielomianów ortogonalnych
Waga ρ definiuje nam przestrzeń L
2,ρ
(a, b) funkcji ciaągłych o warto-
ściach rzeczywistych, określonych na przedziale (a, b) i takich, że całka
R
b
a
f
2
(x)ρ(x) dx istnieje i jest skończona. W L
2,ρ
(a, b) wprowadzimy ilo-
czyn skalarny
hf, gi =
Z
b
a
f
(x)g(x)ρ(x) dx

120
ROZDZIAŁ 10. CAŁKOWANIE A APROKSYMACJA
i generowaną przez ten iloczyn normę
kfk =
q
hf, fi =
s
Z
b
a
f
2
(x)ρ(x) dx.
W ten sposób, L
2,ρ
(a, b) jest przestrzenią unitarną i można mówić o
ortogonalności (prostopadłości) elementów w tej przestrzeni.
Definicja 10.2 Ciąg wielomianów p
k
, k = 0, 1, 2, . . ., nazywamy cią-
giem wielomianów ortogonalnych w przestrzeni
L
2,ρ
(a, b) jeśli
(i) wielomian p
k
jest stopnia dokładnie k,
deg p
k
= k,
∀k ≥ 0,
(ii) wielomiany te są wzajemnie ortogonalne w przestrzeni
L
2,ρ
(a, b),
tzn.
hp
i
, p
j
i =
Z
b
a
p
i
(x)p
j
(x)ρ(x) dx = 0,
i
6= j.
Pokażemy, że ta definicja ma sens.
Lemat 10.2 Ciąg wielomianów ortogonalnych
{p
k
}
k≥0
w przestrzeni
unitarnej
L
2,ρ
(a, b) istnieje. Jeśli dodatkowo założymy, że p
k
(x) = x
k
+
. . ., tzn. współczynnik przy najwyższej potędzie wielomianu p
k
wynosi
1, to ciąg taki jest wyznaczony jednoznacznie.
Dowód Wielomiany p
k
można skonstruować stosując proces ortogo-
nalizacji Grama-Schmidta, tzn. ortogonalizując dowolny ciąg wielomia-
nów {w
k
}
k≥0
spełniający deg w
k
= k. Rzeczywiście, weźmy np. w
k
(x) =
x
k
. Jeśli położymy p
0
= w
0
i dalej indukcyjnie
p
k
= w
k
−
k−1
X
j=0
hw
k
, p
j
i
hp
j
, p
j
i
p
j
,
k
≥ 1,
to, jak łatwo bezpośrednio sprawdzić, {p
k
}
k≥0
będzie ciągiem wielomia-
nów ortogonalnych i p
k
(x) = x
k
+ . . ..
Aby pokazać jednoznaczność załóżmy, że istnieje inny ciąg {q
k
}
k≥0
wielomianów ortogonalnych, w którym współczynniki przy najwyższych

10.2. CIĄGI WIELOMIANÓW ORTOGONALNYCH
121
potęgach wynoszą 1. Ponieważ deg p
k
= k, ∀k, wielomiany p
0
, p
1
, . . . , p
k
tworzą bazę ortogonalną w Π
k
(ze względu na iloczyn skalarny h·, ·i), a
stąd
q
k
=
k
X
j=0
hq
k
, p
j
i
hp
j
, p
j
i
p
j
.
Z drugiej strony, dla 0 ≤ j ≤ k−1, mamy hq
k
, p
j
i = 0, bo ortogonalność
q
k
do wielomianów bazowych q
j
, 0 ≤ j ≤ k − 1, jest równoważna
ortogonalności do całej przestrzeni Π
k−1
, a w szczególności do p
j
. Stąd
q
k
= h
q
k
, p
k
i
hp
k
, p
k
i
p
k
,
a ponieważ współczynniki przy x
k
w wielomianach q
k
i p
k
są takie same,
to q
k
= p
k
. To kończy dowód.
2
Pokazaliśmy, że ciąg wielomianów ortogonalnych jest wyznaczony
jednoznacznie z dokładnością do współczynników przy najwyższych po-
tęgach x
k
. Podamy teraz kilka przykładów takich ciągów.
Wielomiany Legendre’a L
k
.
Jest to najbardziej naturalnie zdefiniowany ciąg wielomianów ortogo-
nalnych, bowiem w tym przypadku [a, b] = [−1, 1] i waga jest jednost-
kowa, ρ ≡ 1. Mamy
L
k
(x) =
1
2
k
k
!
d
k
dx
k
(x
2
− 1)
k
,
albo
L
0
(x) = 1,
L
1
(x) = x,
L
k
(x) =
2k − 1
k
xL
k−1
(x) −
k
− 1
k
L
k−2
(x),
k
≥ 2.
Wielomiany Czebyszewa T
k
.
Ten ciąg wielomianów poznaliśmy już w Rozdziale 7.2. Są one ortogo-
nalne w przedziale [−1, 1] z wagą ρ(x) = (1 − x
2
)
−1/2
. Przypomnijmy,
że T
k
(x) = cos(k arccos(x)) albo
T
0
(x) = 1,
T
1
(x) = x,
T
k
(x) = 2xT
k−1
(x) − T
k−2
(x),
k
≥ 2.

122
ROZDZIAŁ 10. CAŁKOWANIE A APROKSYMACJA
Wielomiany Hermite’a H
k
.
Jest to przykład wielomianów ortogonalnych na całej prostej rzeczywi-
stej, a więc (a, b) = (−∞, +∞), przy czym waga ρ(x) = e
−x
2
. Wielo-
miany Hermite’a dane są wzorami
H
k
(x) = (−1)
k
e
x
2
d
k
dx
k
e
−x
2
,
albo
H
0
(x) = 1,
H
1
(x) = 2x,
H
k
(x) = 2xH
k−1
(x) − (2k − 2)H
k−2
(x),
k
≥ 2.
Zauważmy, że we wszystkich tych przykładach kolejny wielomian
ortogonalny zależał tylko od dwóch poprzednich. Nie jest to przypadek,
ale ogólna reguła. Wielomiany ortogonalne spełniają bowiem formułę
trójczłonową, zob. U. 10.1.
Ciągi wielomianów ortogonalnych mają również szereg innych cie-
kawych własności, co powoduje, że często używane są jako narzędzie
do aproksymacji funkcji wielomianami, zob. U. 10.2. Teraz pokażemy
tylko jedną bardzo ważną ich własność, a dokładniej, własność zer tych
wielomianów, która będzie nam potrzebna do rozwiązania problemu
kwadratur maksymalnego rzędu.
Lemat 10.3 Wielomian ortogonalny p
k
ma dokładnie k pojedynczych
i różnych zer w przedziale otwartym (a, b).
Dowód Niech y
1
, y
2
, . . . , y
s
będą wszystkimi punktami z przedziału
(a, b), w których wielomian p
k
zmienia znak. Gdyby lemat nie był praw-
dziwy to mielibyśmy s < k. Wtedy, kładąc
w
(x) = (x − y
1
)(x − y
2
) · · · (x − y
s
),
mamy hw, p
k
i = 0, bo w ∈ Π
s
i s < k. Z drugiej strony,
hw, p
k
i =
Z
b
a
w
(x)p
k
(x)ρ(x) dx 6= 0,
bo funkcja podcałkowa jest albo stale dodatnia, albo stale ujemna (z
wyjątkiem zbioru miary zero). Ta sprzeczność kończy dowód.
2

10.3. KWADRATURY GAUSSA
123
10.3 Kwadratury Gaussa
Dla dowolnej n, niech x
∗
0
, x
∗
1
, . . . , x
∗
n
będą (różnymi) zerami (n+1)-szego
wielomianu p
n+1
w ciągu wielomianów ortogonalnych w przestrzeni uni-
tarnej L
2,ρ
(a, b), tzn.
p
n+1
(x) = (x − x
∗
0
)(x − x
∗
1
) · · · (x − x
∗
n
).
(10.1)
Ponieważ x
∗
j
leżą w przedziale (a, b), możemy mówić o kwadraturze
interpolacyjnej opartej na tych węzłach.
Definicja 10.3 Kwadraturę interpolacyjną Q
GS
n
opartą na zerach wie-
lomianu ortogonalnego p
n+1
nazywamy kwadraturą Gaussa.
Okazuje się, że właśnie kwadratury Gaussa mają najwyższy rząd.
Dokładniej, mamy następujące twierdzenie.
Twierdzenie 10.2 Kwadratura Gaussa Q
GS
n
ma najwyższy rząd spo-
śród wszystkich kwadratur opartych na węzłach o łącznej krotności n+1,
oraz
rz(Q
GS
n
) = 2n + 2.
Dowód Wobec Lematu 10.1(ii) wystarczy pokazać, że kwadratura Q
GS
n
jest dokładna dla każdego wielomianu stopnia nie większego niż 2n + 1.
Niech f ∈ Π
2n+1
. Niech w
f
∈ Π
n
będzie wielomianem interpolującym
f
w węzłach-zerach x
∗
0
, . . . , x
∗
n
wielomianu p
n+1
. Jeśli deg f ≤ n to
oczywiście w
f
= f i Q
GS
n
(f) = S
ρ
(w
f
) = S
ρ
(f). Jeśli zaś
n
+ 1 ≤ deg f ≤ 2n + 1,
to f − w
f
jest wielomianem stopnia tego samego co f i zeruje się w x
∗
j
,
0 ≤ j ≤ n. Stąd
f
(x) − w
f
(x) = (x − x
∗
0
)(x − x
∗
1
) · · · (x − x
∗
n
)g(x),
gdzie g jest wielomianem,
deg g = deg f − (n + 1) ≤ (2n + 1) − (n + 1) = n.

124
ROZDZIAŁ 10. CAŁKOWANIE A APROKSYMACJA
Korzystając z (10.1) i faktu, że p
n+1
jest prostopadły do Π
n
, ostatecznie
otrzymujemy
S
ρ
(f) − Q
GS
n
(f) =
Z
b
a
(f(x) − w
f
(x))ρ(x) dx
=
Z
b
a
(x − x
∗
0
) · · · (x − x
∗
n
)g(x)ρ(x) dx
=
Z
b
a
p
n+1
(x)g(x)ρ(x) = hp
n+1
, g
i = 0,
co kończy dowód.
2
Zajmiemy się teraz błędem kwadratur Gaussa. Pokażemy, że również
ze względu na błąd mają one dobre własności.
Twierdzenie 10.3 Jeśli f
∈ C
2n+2
([a, b]) to błąd kwadratury Gaussa
Q
GS
n
wyraża się wzorem
S
ρ
(f) − Q
GS
n
(f) = kp
n+1
k
2
f
(2n+2)
(ξ)
(2n + 2)!
,
gdzie ξ
∈ [a, b]. Stąd, w szczególności,
max
f ∈F
2
n+1
M
([a,b])
|S
ρ
(f) − Q
GS
n
(f)| =
M
kp
n+1
k
2
(2n + 2)!
.
Dowód Niech w
f
∈ Π
n
będzie wielomianem interpolującym f w zerach
x
∗
j
wielomianu p
n+1
. Niech ˜
w
f
∈ Π
2n+1
będzie z kolei wielomianem
(Hermite’a) interpolującym f w dwukrotnych węzłach x
∗
j
, tzn. takim,
że ˜
w
f
(x
∗
j
) = f(x
∗
j
) i ˜
w
′
f
(x
∗
j
) = f
′
(x
∗
j
), 0 ≤ j ≤ n. Ponieważ rz(Q
GS
n
) =
2n + 2 to Q
GS
n
( ˜
w
f
) = S
ρ
( ˜
w
f
), a stąd i ze wzoru na błąd interpolacji
Hermite’a mamy
S
ρ
(f) − Q
GS
n
(f) = S
ρ
(f) − Q
GS
n
(w
f
) = S
ρ
(f) − Q
GS
n
( ˜
w
f
)
= S
ρ
(f) − S
ρ
( ˜
w
f
) =
Z
b
a
(f(x) − ˜
w
f
(x))ρ(x) dx
=
Z
b
a
(x − x
∗
0
)
2
· · · (x − x
∗
n
)
2
f
(x
∗
0
, . . . , x
∗
n
, x
)ρ(x) dx
=
Z
b
a
p
2
n+1
(x)ρ(x)f(x
∗
0
, . . . , x
∗
n
, x
) dx.

10.3. KWADRATURY GAUSSA
125
Ponieważ funkcja p
2
n+1
(x)ρ(x) jest prawie wszędzie dodatnia, możemy
teraz zastosować twierdzenie o wartości średniej, aby ostatecznie otrzy-
mać
S
ρ
(f) − Q
GS
n
(f) =
f
(2n+2)
(ξ)
(2n + 2)!
Z
b
a
p
2
n+1
(x)ρ(x) dx
=
f
(2n+2)
(ξ)
(2n + 2)! k
p
n+1
k
2
,
co kończy dowód.
2
Na końcu, zwrócimy jeszcze uwagę na inną, bardzo ważną własność
kwadratur Gaussa, a mianowicie, że ich współczynniki są dodatnie.
Rzeczywiście, zapisując
Q
GS
n
(f) =
n
X
j=0
a
j
f
(x
j
)
i podstawiając
f
j
(x) = (x − x
∗
0
)
2
· · · (x − x
∗
j−1
)
2
(x − x
∗
j+1
)
2
· · · (x − x
∗
n
)
2
mamy, że f
j
∈ Π
2n
i f
j
jest prawie wszędzie dodatnia. Stąd
0 < S
ρ
(f
j
) = Q
GS
n
(f
j
) = a
j
f
j
(x
∗
j
)
i a
j
>
0, bo f
j
(x
∗
j
) > 0. Przypomnijmy, że dodatniość współczynni-
ków kwadratury ma duże znaczenie przy numerycznym ich obliczaniu,
zwłaszcza gdy funkcja podcałkowa f ma stały znak, zob. Rozdział 2.5.2.
Mimo niewątpliwych zalet kwadratur Gaussa, ich stosowalność ogra-
niczają trudności w wyliczeniu pierwiastków wielomianów ortogonal-
nych, gdy stopień wielomianu jest duży. Wyjątkiem są tutaj kwadra-
tury interpolacyjne oparte na zerach wielomianów Czebyszewa, zob. U.
10.3.
Uwagi i uzupełnienia
U. 10.1 Pokażemy teraz, że wielomiany ortogonalne {p
k
}
k≥0
w danej prze-
strzeni L
2,ρ
(a, b) spełniają następującą formulę trójczłonową. Załóżmy dla

126
ROZDZIAŁ 10. CAŁKOWANIE A APROKSYMACJA
uproszczenia, że współczynnik przy x
k
w wielomianie p
k
jest dla każdego k
jednością. Wtedy istnieją liczby β
k
(dla k ≥ 1) i γ
k
> 0 (dla k
≥ 2) takie, że
p
0
(x) = 1,
p
1
(x) = (x − β
1
),
(10.2)
p
k
(x) = (x − β
k
)p
k−1
(x) − γ
k
p
k−2
(x),
k
≥ 2.
Aby to pokazać zauważmy, że p
k
można dla k ≥ 1 przedstawić w postaci
rozwinięcia
p
k
(x) = (x − c
k−1
)p
k−1
(x) +
k−2
X
j=0
c
j
p
j
(x).
Mnożąc skalarnie obie strony tego równania przez p
s
dla 0 ≤ s ≤ k − 3,
otrzymujemy
0 = hp
k
(x), p
s
(x)i = h(x − c
k−1
)p
k−1
(x), p
s
(x)i + c
s
hp
s
(x), p
s
(x)i.
Wobec tego, że (x−c
k−1
)p
s
(x) jest wielomianem stopnia mniejszego niż k−1,
mamy
h(x − c
k−1
)p
k−1
(x), p
s
(x)i = hp
k−1
(x), (x − c
k−1
)p
s
(x)i = 0,
a stąd c
s
hp
s
(x), p
s
(x)i = 0 i c
s
= 0. Możemy więc napisać, że dla k = 1
mamy p
1
(x) = (x − β
1
), a dla k ≥ 2,
p
k
(x) = (x − β
k
)p
k−1
(x) − γ
k
p
k−2
(x),
(10.3)
gdzie β
k
= c
k−1
i γ
k
= c
k−2
. Aby jawnie wyznaczyć β
k
i γ
k
, pomnożymy
skalarnie obie strony równania (10.3) kolejno przez p
k−1
i p
k−2
. Otrzymujemy
0 = hp
k
(x), p
k−1
i
= h(x − β
k
)p
k−1
(x), p
k−1
(x)i − γ
k
hp
k−2
(x), p
k−1
(x)i
= hxp
k−1
(x), p
k−1
(x)i − β
k
hp
k−1
(x), p
k−1
(x)i,
czyli
β
k
= h
xp
k−1
(x), p
k−1
(x)i
hp
k−1
(x), p
k−1
(x)i
,
oraz
0 = hp
k
(x), p
k−2
(x)i
= h(x − β
k
)p
k−1
(x), p
k−2
(x)i − γ
k
hp
k−2
(x), p
k−2
(x)i
= hp
k−1
(x), xp
k−2
(x)i − γ
k
hp
k−2
(x), p
k−2
(x)i,

10.3. KWADRATURY GAUSSA
127
a stąd i z równości hp
k−1
(x), xp
k−2
(x)i = hp
k−1
(x), p
k−1
(x)i,
γ
k
= h
p
k−1
(x), p
k−1
(x)i
hp
k−2
(x), p
k−2
(x)i
.
Zauważmy, że z formuły trójczłonowej wynika w szczególności algorytm
wyznaczenia ciągu wielomianów ortogonalnych. Wystarczy bowiem wyzna-
czać kolejne współczynniki β
k
i γ
k
(obliczając odpowiednie iloczyny skalarne
hxp
k
(x), p
k
(x)i i hp
k
(x), p
k
(x)i) i stosować wzór rekurencyjny (10.2). Do-
dajmy jeszcze, że w obliczeniach numerycznych najlepiej jest przechowywać
informację o ciągu {p
k
}
k≥0
po prostu w postaci liczb β
k
i γ
k
.
U. 10.2 Wygodnie jest posłużyć się wielomianami ortogonalnymi w przy-
padku, gdy chcemy znaleźć najlepszą aproksymację danej funkcji f wielomia-
nem ustalonego stopnia n, i błąd mierzymy w normie przestrzeni L
2,ρ
(a, b).
Rzeczywiście, jak wiadomo, najlepszą aproksymacją dla f w przestrzeni Π
n
jest jej rzut prostopadły na Π
n
. Ponieważ n + 1 początkowych wielomianów
ortogonalnych p
k
, 0 ≤ k ≤ n, tworzy bazę w Π
n
, rzut ten wyraża się wzorem
w
∗
f
=
n
X
k=0
hf, p
k
i
hp
k
, p
k
i
p
k
.
U. 10.3 Zachodzi następujące twierdzenie Łuzina. Niech przedział [a, b] bę-
dzie skończony. Niech Q
n
(f) =
P
n
j=0
a
(n)
j
f (x
(n)
j
) będzie takim ciągiem kwa-
dratur, że:
(i) wszystkie współczynniki a
(n)
j
są dodatnie,
(ii) rząd kwadratur Q
n
rośnie do nieskończoności gdy n → ∞.
Wtedy ciąg Q
n
(f) zbiega do
R
b
a
f (x)dx dla każdej funkcji ciągłej f .
Zauważmy, że twierdzenie to stosuje się do ciągu kwadratur Gaussa Q
GS
n
,
ale nie do ciągu kwadratur Newtona-Cotesa Q
N C
m
, ponieważ w tych ostatnich
pojawiają się dla dużych n współczynniki ujemne.
W praktyce, najczęściej stosuje się ciąg kwadratur interpolacyjnych opar-
tych na zerach kolejnych wielomianów Czebyszewa, ponieważ zera te dane są
jawnie i “zagęszczają się”, tzn. zera wielomianu Czebyszewa T
k
są też zerami
wielomianu T
2k
. Powstające w ten sposób kwadratury noszą nazwę formuł
Clanshow-Curtis’a. Są one w pewnym sensie uniwersalne, bowiem posiadają
optymalną szybkość zbieżności n
−(r+1)
w klasach F
r
M
([a, b]) dla dowolnych
r i M .

128
ROZDZIAŁ 10. CAŁKOWANIE A APROKSYMACJA
U. 10.4 Jeśli przedział całkowania jest skończony i waga jest jednostkowa
to kwadratury Gaussa (a dokładniej kwadratury Legendre’a) można użyć
do tworzenia kwadratur złożonych ¯
Q
GS
r,k
, gdzie k oznacza liczbę podprzedzia-
łów. Łatwo widać, że dla f ∈ F
2r+1
M
([a, b]), błąd takiej kwadratury można
oszacować przez
|S(f) − ¯
Q
GS
r,k
| ≤
M (b
− a)
2r+3
(2r + 2)!
1
k
2r+2
,
czyli jest on porównywalny do błędu “zwykłej” złożonej kwadratury interpo-
lacyjnej. Jednak złożona kwadratura Legendre’a korzysta z dwa razy mniej-
szej liczby węzłów.
U. 10.5 Błąd złożonej kwadratury Legendre’a w klasie F
2r+1
M
([a, b]) można
podać dokładnie. Wystarczy wykorzystać wzory z Ćw. 10.4 i 10.5, aby otrzy-
mać
max
f ∈F
2
r+1
M
([a,b])
|S(f) − ¯
Q
GS
r,k
| = C
1
n
2r+2
,
gdzie
C =
M 2
2r+3
(r + 1)
2r+2
(2r + 3)!
(r + 2) · · · (2r + 2)
1 · 2 · · · (r + 1)
2
i n = k(r + 1) jest ogólną liczbą węzłów na [a, b].
Ćwiczenia
Ćw. 10.1 Uzasadnić, że:
(a) jeśli kwadratura jest dokładna dla dowolnych n + 1 wielomianów tworzą-
cych bazę w Π
n
, to jest ona rzędu co najmniej n + 1, oraz
(b) jeśli kwadratura jest rzędu n + 1 to jest ona niedokładna dla każdego
wielomianu stopnia dokładnie n + 1.
Ćw. 10.2 Uzasadnić, że kwadratura prostokątów jest kwadraturą Legen-
dre’a, natomiast żadna z kwadratur Newtona-Cotesa Q
N C
n
nie jest kwadra-
turą Gaussa.
Ćw. 10.3 Załóżmy, że dane są liczby β
k
i γ
k
definiujące ciąg wielomia-
nów ortogonalnych przez formułę trójczłonową. Zaproponować ekonomiczny
(tzn. o koszcie proporcjonalnym do n) algorytm obliczania wartości n-tego
wielomianu ortogonalnego w danym punkcie x, wykorzystujący formułę trój-
członową.

10.3. KWADRATURY GAUSSA
129
Ćw. 10.4 Niech x
j
, 0 ≤ j ≤ n, będą zerami (n + 1)-szego wielomianu
Legendre’a. Pokazać, że
Z
1
−1
(x − x
0
)
2
(x − x
1
)
2
· · · (x − x
n
)
2
dx
=
2
2n+3
2n + 3
1 · 2 · · · n · (n + 1)
(n + 2)(n + 3) · · · (2n + 2)
2
.
Wskazówka. Wykorzystać fakt, że dla n-tego wielomianu Legendre’a mamy
R
1
−1
L
2
n
(x)dx = (2n + 1)
−1
.
Ćw. 10.5 Niech
Q
GS
n
(f) =
n
X
j=0
a
j
f (x
j
)
będzie kwadraturą interpolacyjną opartą na zerach (n+1)-ezego wielomianu
Legendre’a. Niech −∞ < a < b < ∞. Pokazać, że wtedy kwadratura
˜
Q
GS
n
(f) =
b
− a
2
n
X
j=0
f
a +
x
j
+ 1
2
(b − a)
jest kwadraturą Gaussa opartą na n + 1 węzłach, dla całki na przedziale
(a, b) z wagą jednostkową. Ponadto, jeśli f ∈ C
(2n+2
)([a, b]), to
Z
b
a
f (x) dx
− ˜
Q
GS
n
(f) =
b
− a
2
2n+3
1 · 2 · · · (n + 1)
(n + 2) · · · (2n + 2)
2
f
(2n+2)
(ξ)
(2n + 3)!
.
Ćw. 10.6 Niech ρ ≡ 1 i −∞ < a < b < +∞. Pokazać, że jeśli kwadratura
Q oparta na n + 1 węzłach jest rzędu r
≥ n + 1, to odpowiadająca jej
kwadratura złożona ¯
Q
k
ma następującą własność. Jeśli f ∈ C
(r)
([a, b]) to
|S(f) − ¯
Q
k
(f)| ≤
1
k
r−1
(b − a)
r
r!
kf
(r)
k
C
([a,b])
.
Ćw. 10.7 Niech x
j
, 0 ≤ j ≤ n, będą zerami (n + 1)-szego wielomianu
ortogonalnego Legendre’a (tzn. na przedziale [−1, 1] z wagą 1). Niech dla
0 ≤ j ≤ n,
w
j
=
Z
1
−1
(x − x
0
) · · · (x − x
j−1
)(x − x
j+1
) · · · (x − x
n
)
(x
j
− x
0
) · · · (x
j
− x
j−1
)(x
j
− x
j+1
) · · · (x
j
− x
n
)
dx.
Pokazać, że jeśli f i g są wielomianami stopnia nie większego niż n, to ich
iloczyn skalarny w L
2,1
(−1, 1),
hf, gi =
Z
1
−1
f (x)g(x) dx =
n
X
j=0
w
j
f (x
j
)g(x
j
).

130
ROZDZIAŁ 10. CAŁKOWANIE A APROKSYMACJA

Rozdział 11
Iteracje dla równań
liniowych
Algorytmy rozwiązywania układów równań liniowych postaci
A~x
= ~b,
gdzie A jest nieosobliwą macierzą rzeczywistą n × n, a ~b jest wektorem
rzeczywistym w R
n
, które rozpatrywaliśmy w Rozdziałach 3, 4 i 5, na-
leżą do grupy algorytmów dokładnych albo bezpośrednich. To znaczy, że
po wykonaniu skończonej liczby dopuszczalnych operacji elementarnych
dostajemy w arytmetyce idealnej dokładne rozwiązanie
~x
∗
= A
−1
~b.
W tym rozdziale zajmiemy się algorytmami iteracyjnymi rozwiązy-
wania układów równań liniowych. Polegają one na tym, że, startując
z pewnego przybliżenia początkowego ~x
0
, konstruuje się ciąg kolejnych
przybliżeń
~x
k
= Φ
k
(A,~b; ~x
0
),
k
= 1, 2, . . . ,
które w granicy osiągają rozwiązanie dokładne,
lim
k→∞
~x
k
= ~x
∗
.
131

132
ROZDZIAŁ 11. ITERACJE DLA RÓWNAŃ LINIOWYCH
11.1 Kiedy stosujemy iteracje?
Jasne jest, że algorytmy iteracyjne stosujemy wtedy, gdy są one konku-
rencyjne w stosunku do algorytmów bezpośrednich. Dlatego przekształ-
cenia Φ
k
należy wybierać tak, aby kolejne przybliżenia można było ła-
two obliczać i jednocześnie kolejne błędy k~x
k
− ~x
∗
k szybko zbiegały do
zera.
Zwykle zakłada się również, że dokładne rozwiązanie ~x
∗
jest punk-
tem stałym przekształcenia Φ
k
(A,~b; ·). Wtedy kolejne błędy spełniają
zależność
~x
k
− ~x
∗
= Φ
k
(A,~b; ~x
0
) − Φ
k
(A,~b; ~x
∗
).
Jeśli teraz Φ
k
(A,~b; ·) są lipschitzowskie ze stałymi m
k
<
+∞, tzn. dla
pewnej normy wektorowej k · k mamy
kΦ
k
(~x) − Φ
k
(~y)k ≤ m
k
k~x − ~yk,
∀~x, ~y,
to
k~x
k
− ~x
∗
k ≤ m
k
k~x
0
− ~x
∗
k.
Warunek lim
k→∞
m
k
= 0 jest więc dostateczny na to, aby metoda była
zbieżna dla dowolnego przybliżenia początkowego ~x
0
, przy czym szyb-
kość zbieżności zależy od tego, jak szybko m
k
maleją do zera. Dla więk-
szości stosowanych metod Φ
k
jest funkcją liniową błędu początkowego,
tzn.
Φ
k
(A,~b; ~x
0
− ~x
∗
) = M
k
(~x
0
− ~x
∗
),
gdzie M
k
jest pewną macierzą. Wtedy jako m
k
można przyjąć normę
tej macierzy,
m
k
= kM
k
k = sup
k~
xk=1
kM
k
~x
k.
Dla ilustracji, rozpatrzmy ogólną metodę iteracji prostej, w której
~x
k
= B~x
k−1
+ ~c,
(11.1)
dla pewnej macierzy B wymiaru n × n i wektora ~c ∈ R
n
. W tym
przypadku
~x
k
− ~x
∗
= B
k
(~x
0
− ~x
∗
),

11.1. KIEDY STOSUJEMY ITERACJE?
133
a stąd i z nierówności kB
k
k ≤ kBk
k
, mamy
k~x
k
− ~x
∗
k ≤ kBk
k
k~x
0
− ~x
∗
k.
Warunkiem dostatecznym zbieżności iteracji prostych jest więc kBk <
1. Mówimy, że metoda jest zbieżna liniowo z ilorazem kBk.
Przykład 11.1 Rozkładając macierz A = (a
i,j
)
n
i,j=1
na sumę
A
= D + C,
gdzie D jest macierzą diagonalną składającą się z wyrazów stojących
na głównej przekątnej macierzy A, układ A~x = ~b jest równoważny
układowi
D~x
= −C~x + ~b,
a stąd (o ile na przekątnej macierzy A nie mamy zera) otrzymujemy
metodę iteracyjną
~x
k
= B~x
k−1
+ ~c,
gdzie B = −D
−1
C
i ~c = D
−1
~b, zwaną metodą Jacobiego.
W metodzie Jacobiego warunek dostateczny zbieżności, kBk < 1,
jest spełniony wtedy, gdy macierz A ma dominującą przekątną, tzn.
gdy
2|a
i,i
| >
n
X
j=1
|a
i,j
|,
1 ≤ i ≤ n.
(11.2)
Rzeczywiście, ponieważ wyraz (i, j) macierzy D
−1
C
wynosi 0 dla i = j
i a
i,j
/a
i,i
dla i 6= j, to
kD
−1
C
k
∞
= max
1≤i≤n
n
X
j=1,j6=i
|a
i,j
|/|a
i,i
|
= max
1≤i≤n
n
X
j=1
|a
i,j
|/|a
i,i
| − 1 < 1,
przy czym ostatnia nierówność wynika z (11.2).
Inne przykłady iteracji prostych podane są w U. 11.3 i Ćw. 11.2.
Zastanówmy się teraz nad złożonością metod iteracyjnych. Ponieważ
możemy jedynie znaleźć pewne przybliżenie rozwiązania dokładnego ~x
∗
,

134
ROZDZIAŁ 11. ITERACJE DLA RÓWNAŃ LINIOWYCH
przez złożoność metody będziemy rozumieli koszt kombinatoryczny ob-
liczenia ~x
k
z zadaną dokładnością ε > 0. Dla uproszczenia założymy, że
medoda jest zbieżna liniowo z ilorazem m. Zauważmy, że aby zreduko-
wać błąd początkowy do ε > 0, wystarczy wykonać k = k(ε) iteracji,
gdzie k spełnia
m
k
k~x
0
− ~x
∗
k ≤ ε,
czyli
k
≥
log(1/ε) − log(1/k~x
0
− ~x
∗
k)
log(1/m)
.
Liczba ta zależy więc w istotny sposób od błędu początkowego i (przede
wszystkim) od stałej Lipschitza m, natomiast zależność od dokładności
ε
i wymiaru n układu jest dużo mniej istotna. Zakładając, że koszt jed-
nej iteracji wynosi c = c(n) (zwykle c(n) jest tym mniejszy, im mniejsza
jest liczba niezerowych elementów macierzy A), złożoność metody jest
proporcjonalna do
c
(n)
log(1/ε)
log(1/m)
.
Stąd oczywisty wniosek, że metody iteracyjne warto stosować zamiast
metod bezpośrednich w przypadku gdy
• wymiar n układu A~x = ~b jest “duży”, oraz
• macierz A układu jest “rozrzedzona”, tzn. ma stosunkowo nie-
wielką liczbę elementów niezerowych, np. proporcjonalną do n.
Układy o tych własnościach powstają często przy numerycznym roz-
wiązywaniu równań różniczkowych cząstkowych.
Zaletą metod iteracyjnych jest również ich prostota, przez co są one
łatwe do zaprogramowania.
11.2 Metoda Czebyszewa
Zauważyliśmy, że ze względu na szybkość zbieżności metody iteracyjnej
ważne jest, aby stałe lipschitzowskie m
k
odwzorowań Φ
k
malały jak
najszybciej. Metoda Czebyszewa, którą przedstawimy w tym rozdziale,
jest właśnie próbą minimalizacji tych stałych.

11.2. METODA CZEBYSZEWA
135
Przy opisie metody będziemy korzystać z następujących dwóch fak-
tów, które sformułujemy jako lematy.
Lemat 11.1 Jeśli macierz A jest symetryczna, to istnieje ortonor-
malna w R
n
baza jej wektorów własnych ~
ξ
j
, 1
≤ j ≤ n, tzn.
h~ξ
i
, ~
ξ
j
i
2
= ~ξ
T
i
~
ξ
j
=
(
0
i
6= j,
1
i
= j,
a odpowiadające im wartości własne λ
j
, A~
ξ
j
= λ
j
~
ξ
j
, są rzeczywiste.
Jeśli ponadto A jest dodatnio określona to λ
j
są dodatnie.
Lemat 11.2 Niech macierz A będzie symetryczna i niech
|λ
1
| ≥ |λ
2
| ≥ · · · ≥ |λ
n
|
będą jej wartościami własnymi. Wtedy
kAk
2
= sup
~
x6=~0
kA~xk
2
k~xk
2
= |λ
1
|.
Jeśli ponadto A jest nieosobliwa, tzn.
|λ
n
| > 0, to
kA
−1
k
2
=
1
|λ
n
|
.
Lemat 11.1 jest znanym faktem z algebry liniowej, więc dowód po-
miniemy. Dowód Lematu 11.2 podany jest w U. 11.1.
Zakładamy, że macierz A wyjściowego układu równań jest syme-
tryczna i dodatnio określona.
A
= A
T
>
0,
a jej wartości własne λ
j
leżą w znanym przedziale [a, b],
0 < a ≤ λ
n
≤ · · · ≤ λ
1
= kAk
2
≤ b < ∞.
W metodzie Czebyszewa kolejne przybliżenia ~x
k
konstruujemy tak,
aby była spełniona równość
(~x
k
− ~x
∗
) = W
k
(A)(~x
0
− ~x
∗
),
(11.3)

136
ROZDZIAŁ 11. ITERACJE DLA RÓWNAŃ LINIOWYCH
gdzie W
k
(A) jest macierzą, która wielomianowo zależy od A,
W
k
(A) =
k
X
j=0
a
(k)
j
A
k
,
i ma możliwie małą normę. (Dalej będziemy również używać tego sa-
mego symbolu W
k
do oznaczenia wielomianu zmiennej rzeczywistej,
tzn. dla t ∈ R mamy W
k
(t) =
P
k
j=0
a
(k)
j
t
k
.) Możemy więc napisać, że
~x
k
= W
k
(A)~x
0
+ (I − W
k
(A))~x
∗
.
Aby zapewnić konstruowalność przybliżenia ~x
k
, musimy umieć obliczać
(I − W
k
(A))~x
∗
. Ponieważ
(I − W
k
(A))~x
∗
= −
k
X
j=1
a
(k)
j
A
j
~x
∗
+ (1 − a
(k)
0
)~x
∗
= −
k−1
X
j=0
a
(k)
j+1
A
j
~b + (1 − a
(k)
0
)~x
∗
,
dla konstruowalności ~x
k
wystarczy założyć, że a
(k)
0
= 1, co odpowiada
warunkowi
W
k
(0) = 1,
∀k.
(11.4)
Z nierówności (11.3) mamy
k~x
k
− ~x
∗
k
2
≤ kW
k
(A)k
2
k~x
0
− ~x
∗
k
2
.
Idea metody polega teraz na wyborze wielomianów W
k
tak, aby miały
one jak najmniejszą normę kW
k
(A)k
2
. W tym celu zauważmy, że ma-
cierz W
k
(A) jest symetryczna, a jej wartości własne wynoszą W
k
(λ
j
),
gdzie λ
j
są wartościami własnymi macierzy A, zob. Ćw. 11.1. Stąd
kW
k
(A)k
2
≤ max
a≤t≤b
|W
k
(t)| = kW
k
k
C
([a,b])
.
Rozwiązanie problemu minimalizacji ostatniego maksimum ze względu
na wszystkie wielomiany W
k
∈ Π
k
takie, że W
k
(0) = 1, jest podane
w Rozdziale 7 (zob. Ćw. 7.8). Przypomnijmy, że optymalny wielomian
dany jest wzorem
W
∗
k
(t) =
T
k
(h(t))
T
k
(h(0))
,

11.2. METODA CZEBYSZEWA
137
gdzie T
k
jest k-tym wielomianem Czebyszewa, a
h
(t) =
2t − (b + a)
b
− a
.
Przypomnijmy również, że wielomiany Czebyszewa spełniają formułę
trójczłonową, T
0
(t) = 1, T
1
(t) = t, oraz T
k
(t) = 2tT
k−1
(t)−T
k−2
dla k ≥
2. Pozwala to na rekurencyjną konstrukcję kolejnych ~x
k
w zależności od
~x
k−1
i ~x
k−2
. Dokładniej, dla pierwszego przybliżenia mamy
W
∗
1
(A) =
T
1
(h(A))
T
1
(h(0))
=
2A−(b+a)I
b−a
−
b+a
b−a
= I −
2
b
+ a
A,
a stąd
~x
1
= W
∗
1
(A)~x
0
+ (I − W
1
(A))~x
∗
= ~x
0
+
2
b
+ a
(~b − A~x
0
)
= ~x
0
+
2
b
+ a
~r
0
,
gdzie ~r
0
= ~b − A~x
0
jest początkowym residuum.
Dla k ≥ 2 wykorzystamy formułę rekurencyjną dla wielomianów
Czebyszewa. Oznaczając t
j
= T
j
(h(0)), j ≥ 0, mamy
W
∗
k
(A) =
T
k
(h(A))
t
k
=
2h(A)T
k−1
(h(A)) − T
k−2
(h(A))
t
k
= 2
t
k−1
t
k
h
(A)
T
k−1
(h(A))
t
k−1
−
t
k−2
t
k
T
k−2
(h(A))
t
k−2
= 2
t
k−1
t
k
h
(A)W
∗
k−1
(A) −
t
k−2
t
k
W
∗
k−2
(A).
Stąd
~x
k
− ~x
∗
= W
∗
k
(A)(~x
0
− ~x
∗
)
= 2
t
k−1
t
k
h
(A)W
∗
k−1
(~x
0
− ~x
∗
) −
t
k−2
t
k
W
∗
k−2
(A)(~x
0
− ~x
∗
)
= 2
t
k−1
t
k
h
(A)(~x
k−1
− ~x
∗
) −
t
k−2
t
k
(~x
k−2
− ~x
∗
)

138
ROZDZIAŁ 11. ITERACJE DLA RÓWNAŃ LINIOWYCH
= 2
t
k−1
t
k
2
b
− a
A
−
b
+ a
b
− a
I
(~x
k−1
− ~x
∗
) −
t
k−2
t
k
(~x
k−2
− ~x
∗
)
= −
4
b
− a
t
k−1
t
k
~r
k−1
− 2
t
k−1
t
k
b
+ a
b
− a
~x
k−1
−
t
k−2
t
k
~x
k−2
+
2
t
k−1
t
k
b
+ a
b
− a
+
t
k−2
t
k
~x
∗
.
Wykorzystując wynikającą z formuły trójczłonowej równość
t
k
= −2
b
− a
b
+ a
t
k−1
− t
k−2
otrzymujemy ostatecznie
~x
k
= (1 + α
k
)~x
k−1
− α
k
~x
k−2
− β
k
~r
k−1
,
gdzie α
k
= t
k−2
/t
k
i β
k
= (4t
k−1
)/(t
k
(b + a)). Algorytm wynikający z
metody Czebyszewa można więc zapisać następująco.
~x
0
:= {dowolne};
~r
0
:= ~b − A~x
0
;
~x
1
:= ~x
0
+ 2~r
0
/
(b + a);
~r
1
:= ~b − A~x
1
;
t
0
:= 1;
t
1
:= −(b + a)/(b − a);
β
:= −4/(b − a);
for j = 2, 3, . . .
do
begin
t
k
:= 2t
1
t
k−1
− t
k−2
;
α
k
:= t
k−2
/t
k
;
~x
k
:= (1 + α
k
)~x
k−1
− α
k
~x
k−2
+ β(t
k−1
/t
k
)~r
k−1
;
~r
k
:= ~b − A~x
k
end.
Zauważmy, że opisana metoda Czebyszewa jest metodą dwupunktową,
bowiem do konstrukcji kolejnego przybliżenia ~x
k
wykorzystuje się dwa
poprzednie przybliżenia ~x
k−1
i ~x
k−2
.
Zastanowimy się jeszcze nad szybkością zbieżności metody Czeby-
szewa. Wobec
kW
k
(A)k
2
= k
T
k
(h(·))k
C
([a,b])
|T
k
(h(0))|
=
1
T
k
b+a
b−a
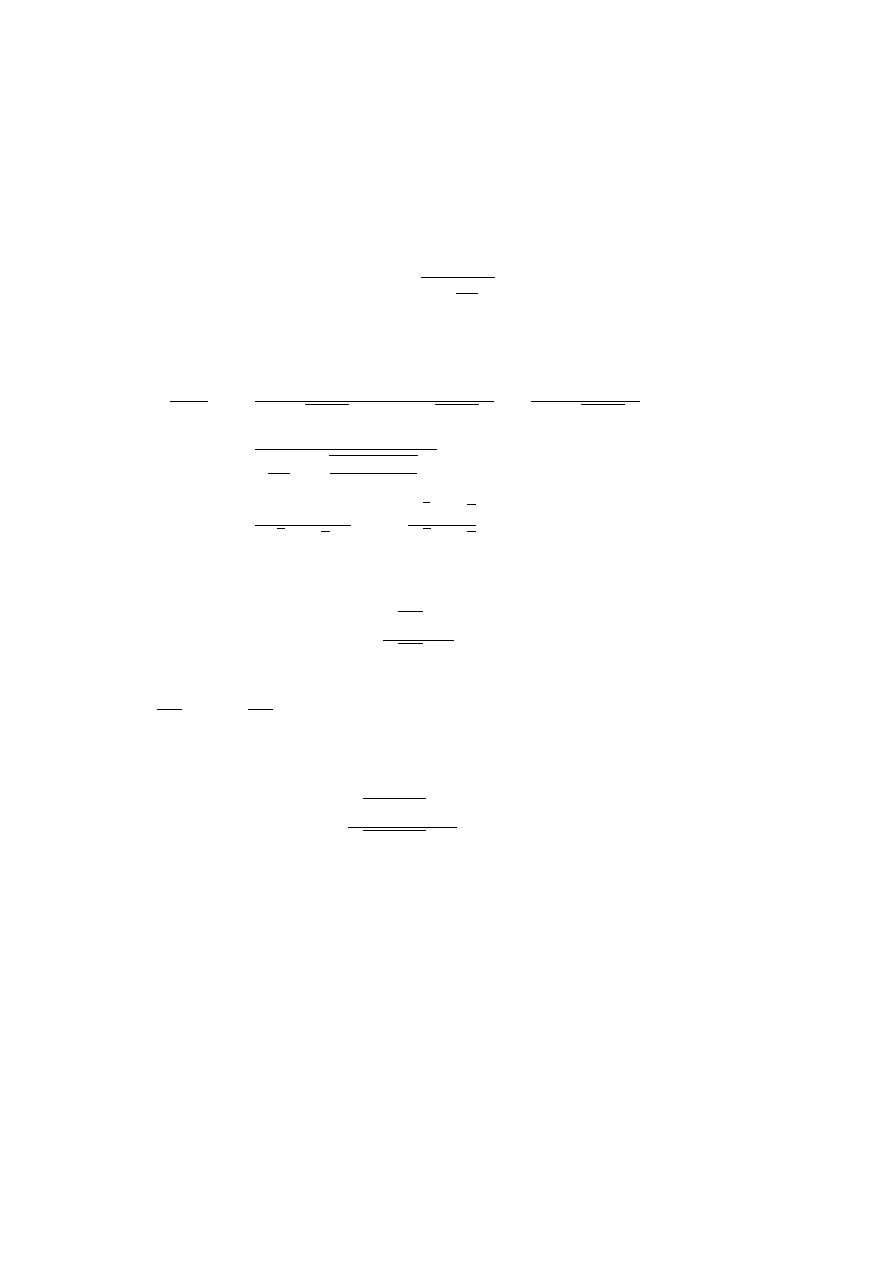
11.3. METODA NAJSZYBSZEGO SPADKU
139
mamy
k~x
k
− ~x
∗
k
2
≤
k~x
0
− ~x
∗
k
T
k
b+a
b−a
.
Aby oszacować T
−1
k
((b + a)/(b − a)), wykorzystamy jawną formułę na
T
k
(t) z Ćw. 7.2. Oznaczając t = (b + a)/(b − a) mamy dla dużych k
1
T
k
(t)
=
2
(t +
√
t
2
− 1)
k
+ (t −
√
t
2
− 1)
k
≈
2
(t +
√
t
2
− 1)
k
=
2
b−a
b+a
+
r
(b+a)
2
−(b−a)
2
(b−a)
2
k
=
2(b − a)
k
(
√
b
+ √a)
2k
= 2
√
b
−
√
a
√
b
+ √a
!
k
,
a stąd w przybliżeniu
k~x
k
− ~x
∗
k
2
≤ 2
q
b/a
− 1
q
b/a
+ 1
k
k~x
0
− ~x
∗
k
2
.
Metoda Czebyszewa jest więc zbieżna co najmniej liniowo z ilorazem
(
q
b/a
− 1)/(
q
b/a
+ 1). Zauważmy jeszcze, że jeśli a i b są odpowiednio
najmniejszą i największą wartością własną macierzy A, to b = kAk
2
,
1/a = kA
−1
k
2
, a stąd b/a = kAk
2
kA
−1
k
2
= cond(A) i metoda jest
zbieżna z ilorazem
q
cond(A) − 1
q
cond(A) + 1
.
Po raz kolejny widzimy tu ważną rolę uwarunkowania macierzy. Im
uwarunkowanie jest gorsze tym gorsza zbieżność metody Czebyszewa.
11.3 Metoda najszybszego spadku
Tak jak poprzednio, będziemy zakładać, że macierz A układu jest sy-
metryczna i dodatnio określona. Wtedy zachodzi następujący fakt.

140
ROZDZIAŁ 11. ITERACJE DLA RÓWNAŃ LINIOWYCH
Lemat 11.3 Rozwiązanie ~x
∗
układu A~x = ~b jest jedynym wektorem
minimalizującym formę kwadratową
Q
(~x) =
1
2
~x
T
A~x
− ~x
T
~b.
Dowód Zauważmy, że dla dowolnych ~x i ~z mamy
Q
(~x + ~z) =
1
2
(~x
T
+ ~z
T
)A(~x + ~z) − (~x
T
+ ~z
T
)~b
=
1
2
~x
T
A~x
− ~x
T
~b +
1
2
(~z
T
A~x
+ ~x
T
A~z
) − ~z
T
~b +
1
2
~z
T
A~z
= Q(~x) − z
T
(~b − ~
A~x
) +
1
2
~z
T
A~z,
przy czym w ostatniej równości wykorzystaliśmy symetrię macierzy A.
Stąd dla ~x = ~x
∗
i ~z 6= ~0 dostajemy
Q
(~x
∗
+ ~z) = Q(~x
∗
) +
1
2
~z
T
A~z > Q
(~x
∗
),
co z kolei wynika z dodatniej określoności A.
2
W metodzie najszybszego spadku konstruuje się kolejne przybliżenie
~x
k
przesuwając się od ~x
k−1
w kierunku przeciwnym do gradientu formy
Q
tak długo jak długo wartość tej formy maleje. (Przypomnijmy, że
minus gradient wyznacza kierunek lokalnie najszybszego spadku.) Po-
nieważ gradient Q w punkcie ~x
k−1
wynosi
∂Q
∂x
i
(~x
k−1
)
!
n
i=1
= A~x
k−1
−~b = −~r
k−1
,
metoda ma postać
~x
k
= ~x
k−1
+ γ
k
~r
k−1
,
(11.5)
gdzie γ
k
jest dobrane tak, aby zminimalizować Q(~x
k
). Jak łatwo się
przekonać,
Q
(~x
k
) = Q(~x
k−1
+ γ~r
k−1
)
= Q(~x
k−1
) +
1
2
γ
2
~r
T
k−1
A~r
k−1
+ γ~r
T
k−1
A~x
k−1
− γ~r
T
k−1
~b
= Q(x
k−1
) +
1
2
γ
2
~r
T
k−1
A~r
k−1
− γ~r
T
k−1
~r
k−1

11.3. METODA NAJSZYBSZEGO SPADKU
141
jest jako funkcja γ parabolą, która przyjmuje minimum w
γ
k
=
~r
T
k−1
~r
k−1
~r
T
k−1
A~r
k−1
.
(11.6)
Wzory (11.5) i (11.6) definiują już w pełni metodę najszybszego spadku.
Pokażemy jeszcze zbieżność metody. W tym celu zauważmy, że
Q
(~x
k
) = Q(~x
k−1
) −
1
2
(~r
T
k−1
~r
k−1
)
2
~r
k−1
A~r
k−1
≤ Q(~x
k−1
).
Ciąg Q(~x
k
) jest nierosnący i ograniczony z dołu przez Q(~x
∗
), a więc
jest zbieżny. To wymusza
lim
k→∞
(~r
T
k−1
~r
k−1
)
2
~r
k−1
A~r
k−1
= 0,
co z kolei oznacza, że ~r
k
= ~b − A~x
k
zbiega do zera i w konsekwencji
lim
k→∞
~x
k
= ~x
∗
.
Uwagi i uzupełnienia
U. 11.1 (Dowód Lematu 11.2) Jeśli (~ξ
j
)
n
j=1
jest ortonormalną bazą wek-
torów własnych macierzy A, to dla dowolnego wektora ~x =
P
n
j=1
α
j
~
ξ
j
mamy
kA~xk
2
2
= hA~x, A~xi
2
=
*
n
X
i=1
α
i
A(~
ξ
i
),
n
X
j=1
α
j
A(~
ξ
j
)
+
2
=
*
n
X
i=1
α
i
λ
i
~
ξ
i
,
n
X
j=1
α
j
λ
j
~
ξ
j
+
2
=
n
X
j=1
α
2
j
λ
2
j
≤ λ
2
1
n
X
j=1
α
2
j
= λ
2
1
k~xk
2
2
,
a stąd kA~xk
2
≤ |λ
1
|k~xk
2
. Z drugiej strony,
kA~ξ
1
k
2
= kλ
1
~
ξ
1
k
2
= |λ
1
|k~ξ
1
k
2
= |λ
1
|,
a więc kAk
2
= |λ
1
|.
Aby pokazać drugą część lematu zauważmy, że macierz A
−1
jest też sy-
metryczna. Ma ona te same wektory własne co A, a wartości własne wynoszą
1/λ
j
, przy czym |1/λ
n
| ≥ · · · ≥ |1/λ
1
|. Stąd kA
−1
k
2
= |1/λ
n
|.

142
ROZDZIAŁ 11. ITERACJE DLA RÓWNAŃ LINIOWYCH
U. 11.2 Pokazaliśmy, że warunkiem dostatecznym zbieżności metody ite-
racji prostej ~x
k
= B~x
k−1
+ ~c jest kBk < 1. Okazuje się, że można podać
warunek konieczny i dostateczny. Metoda iteracji prostej jest zbieżna dla
dowolnego przybliżenia początkowego ~x
0
wtedy i tylko wtedy, gdy promień
spektralny macierzy B jest nie większy od jedności, tzn.
ρ(A) = max
|λ| < 1,
gdzie maksimum wzięte jest po wszystkich wartościach własnych macierzy
A.
U. 11.3 Przedstawiając macierz A w postaci A = L + U, gdzie L jest ma-
cierzą trójkątną dolną elementów występujących na i pod główną przekątną
A, układ równań A~x = ~b jest równoważny układowi L~x =
−U~x + ~b. Stąd
wynika metoda iteracji prostej
~x
k
= −L
−1
U~x
k−1
+ L
−1
~b,
zwana metodą Seidla. Można pokazać, że metoda ta jest zbieżna gdy macierz
A jest symetryczna i dodatnio określona.
U. 11.4 Pokazana metoda Czebyszewa dla macierzy A = A
T
> 0 o war-
tościach własnych z przedziału [a, b], 0 < a < b < ∞, jest metodą dwu-
punktową. Rozpatruje się też jednopunktowe, cykliczne metody Czebyszewa
postaci
~x
k
= ~x
k−1
+ α
k
~r
k−1
,
gdzie parametry α
k
są wybierane cyklicznie, α
j+m
= α
j
dla wszystkich j i
pewnej ustalonej m, oraz tak, aby zminimalizować normę macierzy przejścia
w każdym cyklu. Dokładniej, mamy ~x
k
− ~x
∗
= (I − α
k
A)(~x
k−1
− ~x
∗
), a stąd
~x
m
− ~x
∗
= W
m
(A)(~x
0
− ~x
∗
),
gdzie
W
m
(A) = (I − α
m
A)(I
− α
m−1
A)
· · · (I − α
1
A).
Wielomian W
m
(t) jest więc stopnia m, a jego pierwiastki wynoszą t
j
= 1/α
j
,
1 ≤ j ≤ m. Ponadto W
m
(0) = 1. Jak już wiemy, norma macierzy kW
m
(A)k
2
jest minimalna gdy W
m
(t) = W
∗
m
(t) = T
m
(h(t))/T
m
(h(0)), gdzie h(t) =
(2x − (a + b))/(b − a). Stąd parametry α
j+m
najlepiej jest wybrać tak, aby
α
j
były odwrotnościami pierwiastków W
∗
m
(t), czyli
α
j
=
b + a
2
−
b
− a
2
cos
2j − 1
2j
π
−1
,
1 ≤ j ≤ m.

11.3. METODA NAJSZYBSZEGO SPADKU
143
U. 11.5 Metoda najszybszego spadku należy do rodziny metod gradiento-
wych postaci
~x
k
= ~x
k−1
+ α
k
~r
k−1
,
gdzie parametr α
k
wybiera się tak, aby zminimalizować normę
k~x
k
− ~x
∗
k
B
=
q
(~x
k
− ~x
∗
)
T
B(~x
k
− ~x
∗
),
a B jest pewną macierzą, B = B
T
> 0. Zwykle przyjmuje się B = A
p
. Jak
łatwo się przekonać, metodę najszybszego spadku otrzymujemy w przypadku
p = 1, czyli B = A.
Można pokazać, że dla metod gradientowych
k~x
k
− ~x
∗
k
B
≤
cond(A) − 1
cond(A) + 1
k
k~x
0
− ~x
∗
k
B
.
Ćwiczenia
Ćw. 11.1 Niech A będzie macierzą symetryczną o wartościach własnych
λ
j
, 1 ≤ j ≤ n. Pokazać, że dla dowolnego wielomianu W (t) =
P
k
j=0
a
j
t
j
,
macierz
W (A) =
n
X
j=1
a
j
A
j
jest też symetryczna. Ponadto wektory własne A i W (A) są takie same, a
wartości własne W (A) wynoszą W (λ
j
) dla 1 ≤ j ≤ n.
Ćw. 11.2 Niech A = A
T
> 0. Rozpatrzmy metodę Richardsona postaci
~x
k
= (I − αA)~x
k−1
+ α~b.
gdzie α dobieramy tak, aby zminimalizować normę macierzy kI − αAk
2
.
Zauważyć, że jest to metoda iteracji prostej, ale równocześnie jednopunktowa
metoda Czebyszewa z U. 11.4 przy m = 1. Pokazać, że optymalne α wyraża
się wzorem
α
opt
=
2
λ
1
+ λ
n
,
gdzie λ
1
i λ
n
są odpowiednio największą i najmniejszą wartością własną A.
Ponadto
kI − α
opt
A
k
2
=
λ
1
− λ
n
λ
1
+ λ
n
=
cond(A) − 1
cond(A) + 1
,
gdzie cond(A) = kAk
2
kA
−1
k
2
.

144
ROZDZIAŁ 11. ITERACJE DLA RÓWNAŃ LINIOWYCH
Ćw. 11.3 Pokazać, że warunkiem koniecznym i dostatecznym zbieżności
metody Richardsona z Ćw. 11.2, dla dowolnego przybliżenia początkowego
~x
0
, jest
0 < α <
2
kAk
2
.
(11.7)
Ponadto dla α spełniającego (11.7) iloraz zbieżności wynosi
kI − αAk
2
=
(
αλ
1
− 1
α
opt
< 2/λ
1
,
1 − αλ
n
0 < α ≤ α
opt
,
gdzie α
opt
= 2/(λ
1
+ λ
n
).
Ćw. 11.4 Wykazać, że m-cykliczna jednopunktowa metoda Czebyszewa z
U. 11.4 jest zbieżna liniowo z ilorazem równym (b − a)/(b + a) dla m = 1 i
dążącym do (
√
b
−
√
a)/(
√
b +
√
a), gdy m
→ ∞.
Ćw. 11.5 Niech A = A
T
> 0 i niech
Q(~x) =
1
2
~x
T
A~x + ~x
T
~b.
Pokazać, że zbiór
{ ~x ∈ R
n
: Q(~x) = const. }
tworzy hiperelipsoidę w R
n
o środku A
−1
~b i osiach w kierunkach wektorów
własnych macierzy A o długościach proporcjonalnych do 1/
p
λ
j
, gdzie λ
j
są
wartościami własnymi A.
Wskazówka. Wykorzystać Lemat 11.1.

Rozdział 12
Iteracje dla równań
nieliniowych
W Rozdziale 11 analizowaliśmy metody iteracyjne dla rozwiązywania
równań liniowych A~x = ~b. Teraz zajmiemy się równaniami nielinio-
wymi, w których zamiast operatora liniowego (macierzy) A mamy od-
wzorowanie nieliniowe f : D → R
n
, gdzie D jest podzbiorem w R
n
. Dla
uproszczenia będziemy zakładać, że ~b = ~0, gdyż w przeciwnym przy-
padku możemy zastąpić f funkcją f
1
(~x) = f(~x) −~b. Będziemy również
zakładać, że f należy do pewnej znanej klasy F funkcji przekształcają-
cych D w R
n
i mających co najmniej jedno zero w D. Zadanie polega
więc na znalezieniu rozwiązania ~x
∗
= ~x
∗
(f) równania nieliniowego
f
(~x) = ~0,
dla
f
∈ F.
(12.1)
Jak zwykle w przypadku, gdy danymi są funkcje zakładamy, że jedyną
informacją “a priori” o f jest, że f ∈ F . Dodatkową informację mo-
żemy zdobyć przez obliczanie wartości, a niekiedy i pochodnych f (o
ile istnieją) w wybranych punktach. Zauważmy, że metody iteracyjne
Czebyszewa i najszybszego spadku z Rozdziału 11 dla równań linio-
wych korzystały właśnie z takiej (częściowej) informacji o macierzy A,
chociaż formalnie zakładaliśmy, że dostępna jest pełna informacja o jej
współczynnikach. Dla równań nieliniowych możliwość obliczenia jedy-
nie informacji częściowej jest założeniem modelowym, a to wymusza
już fakt, że każda metoda rozwiązywania równania (12.1) może dawać
co najwyżej wynik przybliżony.
145

146 ROZDZIAŁ 12. ITERACJE DLA RÓWNAŃ NIELINIOWYCH
12.1 Bisekcja
Metoda bisekcji, czyli połowienia, jest dość naturalną metodą obliczania
zer skalarnych funkcji ciągłych określonych na danym przedziale [a, b] i
zmieniających znak. Dokładniej, rozpatrzmy klasę funkcji
F
= { f ∈ C([a, b]) : f(a) < 0 < f(b) }.
(12.2)
Oczywiście, każda funkcja f ∈ F ma co najmniej jedno zero w [a, b].
Startując z przedziału [a, b], w kolejnych krokach metody bisekcji obli-
czamy informację o wartości f w środku przedziału, co pozwala nam,
w zależności od znaku obliczonej wartości, zmniejszyć o połowę prze-
dział, w którym na pewno znajduje się zero funkcji. Bisekcję realizuje
następujący ciąg poleceń, po wykonaniu którego x jest przybliżeniem
zera funkcji f z zadaną dokładnością ε.
xl
:= a; xr := b;
x
:= (a + b)/2; e := (b − a)/2;
while (e > ε) do
begin
if
(f(x) < 0) then xr := x else xl := x;
x
= (xl + xr)/2; e := e/2
end.
Z konstrukcji metody łatwo wynika, że po wykonaniu k iteracji (albo
po obliczeniu k wartości funkcji) otrzymujemy x = x
k
, które odległe jest
od pewnego rozwiązania x
∗
o co najwyżej
|x
k
− x
∗
| ≤
1
2
k
b
− a
2
.
(12.3)
Metoda bisekcji jest więc zbieżna liniowo z ilorazem 1/2. Choć ta zbież-
ność nie jest imponująca, bisekcja ma kilka istotnych zalet. Oprócz jej
prostoty, należy podkreślić fakt, że bisekcja jest w pewnym sensie uni-
wersalna. Dla jej zbieżności wystarcza bowiem jedynie ciągłośc funkcji.
Poza tym możemy łatwo kontrolować jej błąd. Konsekwencją (12.3) jest
bowiem następujący wniosek.

12.2. ITERACJE PROSTE
147
Wniosek 12.1 Dla znalezienia zera z dokładnością ε > 0, wystarczy
obliczyć w metodzie bisekcji
k
= k(ε) =
l
log
2
(b − a)
ε
m
− 1
wartości funkcji.
Dodajmy jeszcze, że bisekcja minimalizuje błąd najgorszy w klasie
F
zdefiniowanej przez (12.2), wśród wszystkich algorytmów korzysta-
jących z określonej liczby obliczeń wartości funkcji, zob U. 12.1.
12.2 Iteracje proste
Przedstawimy teraz metodę iteracji prostych dla rozwiązywania rów-
nań nieliniowych, którą można traktować jako uogólnienie iteracji pro-
stych dla równań liniowych. Najpierw równanie (12.1) przekształcamy
do równania równoważnego (tzn. mającego te same rozwiązania)
~x
= φ(~x).
(12.4)
Następnie, startując z pewnego przybliżenia początkowego ~x
0
, konstru-
ujemy ciąg kolejnych przybliżeń ~x
k
według wzoru
~x
k
= φ(~x
k−1
),
k
≥ 1.
Twierdzenie 12.1 Niech D
0
będzie domkniętym podzbiorem dziedziny
D,
D
0
= D
0
⊂ D,
w którym φ jest odwzorowaniem zwężającym. To znaczy, φ(D
0
) ⊂ D
0
,
oraz istnieje stała 0
≤ L < 1 taka, że
kφ(~x) − φ(~y)k ≤ L k~x − ~yk,
∀~x, ~y ∈ D
0
.
Wtedy równanie (12.4) ma dokładnie jedno rozwiązanie ~x
∗
, oraz
~x
∗
= lim
k→∞
~x
k
,
dla dowolnego przybliżenia początkowego ~x
0
∈ D
0
.

148 ROZDZIAŁ 12. ITERACJE DLA RÓWNAŃ NIELINIOWYCH
Dowód Wobec
k~x
k
− ~x
k−1
k = kφ(~x
k−1
) − φ(~x
k−2
)k ≤ L k~x
k−1
− ~x
k−2
k
≤ · · · ≤ L
k−1
k~x
1
− ~x
0
k,
dla k ≥ s mamy
k~x
k
− ~x
s
k ≤
k
X
j=s+1
k~x
j
− ~x
j−1
k ≤
k
X
j=s+1
L
j−1
k~x
1
− ~x
0
k
= L
s
(1 + L + · · · + L
k−s−1
)k~x
1
− ~x
0
k ≤
L
s
1 − L
k~x
1
− ~x
0
k.
Ciąg {~x
k
}
k
jest więc ciągiem Couchy’ego. Stąd istnieje granica ~α =
lim
k→∞
~x
k
, która należy do D
0
, wobec domkniętości tego zbioru. Po-
nieważ lipschitzowskość φ implikuje jej ciągłość, mamy też
φ
(~α) = φ
lim
k→∞
~x
k
= lim
k→∞
φ
(~x
k
) = lim
k→∞
~x
k
= ~α,
tzn. ~α jest punktem stałym odwzorowania φ. Dla jednoznaczności za-
uważmy, że jeśliby istniał drugi, różny od ~α, punkt stały ~β, to mieliby-
śmy
k~α − ~βk = kφ(~α) − φ(~β)k ≤ L k~α − ~βk.
Stąd 1 < L, co jest sprzeczne z założeniem, że φ jest zwężająca.
2
Z powyższych rozważań otrzymujemy natychmiastowy wniosek do-
tyczący zbieżności iteracji prostych.
Wniosek 12.2 Przy założeniach twierdzenia 12.1, metoda iteracji pro-
stych jest zbieżna co najmniej liniowo z ilorazem L, tzn.
k~x
k
− ~x
∗
k ≤ L
k
k~x
0
− ~x
∗
k.
Dla ilustracji, rozpatrzmy natępujące proste równanie skalarne:
x
= cos(x),
dla
x
∈ D = R.
(12.5)
W tym przypadku φ(x) = cos(x). Zauważamy, że w przedziale [0, 1]
funkcja φ jest zwężająca ze stałą
L
= max
0≤x≤1
| cos
′
(x)| = sin(1) < 1.

12.3. METODY INTERPOLACYJNE
149
Stąd istnieje dokładnie jedno rozwiązanie równania (12.5) w przedziale
[0, 1]. Rozwiązanie to może być aproksymowane z dowolnie małym błę-
dem przy pomocy iteracji prostych, startując z dowolnego przybliżenia
początkowego ~x
0
∈ [0, 1].
Zaletą iteracji prostych jest fakt, że zbieżność nie zależy od wymiaru
n
zadania, ale tylko od stałej Lipschitza L. Ma ona szczególne zastoso-
wanie w przypadku, gdy funkcja φ jest zwężająca na całym zbiorze D,
tzn. D
0
= D. Jeśli ponadto D ma skończoną średnicę diam(D), to dla
osiągnięcia ε-sproksymacji zera funkcji f wystarczy wykonać
k
= k(ε) =
l
log(k~x
0
− ~x
∗
k/ε)
log(1/L)
m
=
l
log(diam(D)/ε)
log(1/L)
m
iteracji, niezależnie od x
0
. Metody zbieżne dla dowolnego przybliżenia
początkowego, nazywamy zbieżnymi globalnie.
12.3 Metody interpolacyjne
Metody iterpolacyjne dla równań nieliniowych powstają podobnie jak
kwadratury interpolacyjne dla całkowania. Najpierw daną funkcję in-
terpolujemy wielomianem Lagrange’a albo Hermite’a ustalonego stop-
nia, a następnie jako przybliżenie zera bierzemy zero tego wielomianu
iterpolacyjnego. Proces taki można iterować (powtarzać) wymieniając
za każdym razem jeden z punktów interpolacyjnych na punkt nowo
obliczony. Zauważmy, że w ogólności takie metody muszą korzystać w
kolejnych iteracjach nie tylko z ostatniego przybliżenia x
k−1
, ale również
z kilku poprzednich, tzn.
x
k
= φ(x
k−1
, . . . , x
k−s
).
Wymagają one również podania nie jednego, ale s przybliżeń począt-
kowych x
0
, . . . , x
s−1
.
W praktyce stosuje się jednak tylko interpolację wielomianami ni-
skich stopni, np. wielomianami liniowymi lub najwyżej kwadratowymi,
których zera można łatwo obliczyć korzystając z bezpośrednich formuł.
Jak się przekonamy, metody interpolacyjne należą do grupy metod
zbieżnych lokalnie. Znaczy to, że zbieżność ciągu
{x
k
}
k
do zera danej

150 ROZDZIAŁ 12. ITERACJE DLA RÓWNAŃ NIELINIOWYCH
funkcji f jest zapewniona jedynie wtedy, gdy przybliżenia początkowe
zostały wybrane dostatecznie blisko x
∗
.
W dalszych rozważaniach będziemy zakładać dla uproszczenia, że
dziedzina D = R.
W przypadku, gdy wielomianem interpolacyjnym jest wielomian li-
niowy Hermite’a, mówimy o metodzie Newtona, albo stycznych. Star-
tując z pewnego przybliżenia początkowego x
0
, w kolejnych krokach
metody, k-te przybliżenie x
k
jest punktem przecięcia stycznej do wy-
kresu f w punkcie x
k−1
. Ponieważ równanie stycznej wynosi y(x) =
f
(x
k−1
) + f
′
(x
k−1
)(x − x
k−1
), otrzymujemy wzór
x
k
= x
k−1
−
f
(x
k−1
)
f
′
(x
k−1
)
.
Oczywiście, aby metoda Newtona była dobrze zdefiniowana, musimy
założyć, że f
′
(x
k−1
) istnieje i nie jest zerem.
Zauważmy, że metodę Newtona można traktować jako szczególny
przypadek iteracji prostych, gdzie
φ
(x) = x −
f
(x)
f
′
(x)
.
Widać też, że nie jest ona zbieżna globalnie. Nawet jeśli pochodna w
x
k−1
się nie zeruje, ciąg {x
k
}
k
może nie zbiegać do zera funkcji f, zob.
Ćw. 12.2. Okazuje się jednak, że jeśli wystartujemy dostatecznie blisko
rozwiązania x
∗
, to metoda Newtona jest zbieżna. Dokładniej, załóżmy
najpierw, że f(x
∗
) = 0 oraz
f
′
(x
∗
) 6= 0.
Ponadto załóżmy, że f jest dwukrotnie różniczkowalna w sposób ciągły,
f
∈ C
2
(D). Rozwijając φ w szereg Taylora w punkcie x
∗
otrzymujemy
x
k
− x
∗
= φ(x
k−1
) − φ(x
∗
) = (x
k−1
− x
∗
)φ
′
(x
∗
) + (x
k−1
− x
∗
)
2
φ
′′
(ξ
k
)/2,
gdzie min(x
∗
, x
k−1
) ≤ ξ
k
≤ max(x
∗
, x
k−1
). Wobec tego, że φ
′
(x
∗
) =
f
(x)f
′′
(x)/(f
′
(x))
2
= 0 i φ
′′
(ξ
k
) = f
′′
(ξ
k
)/f
′
(ξ
k
), mamy
x
k
− x
∗
= (x
k−1
− x
∗
)
2
f
′′
(ξ
k
)
2f
′
(ξ
k
)
.
(12.6)

12.3. METODY INTERPOLACYJNE
151
Zdefiniujmy liczbę
R
f
= sup
r≥0
sup
{x:|x−x
∗
|≤r}
2(x − x
∗
)f
′′
(x)
f
′
(x)
<
1.
Oczywiście R
f
>
0. Dla x
k−1
spełniającego |x
k−1
− x
∗
| ≤ R < R
f
,
mamy z równości (12.6)
|x
k
− x
∗
| ≤ q |x
k−1
− x
∗
|,
gdzie q < 1 i q zależy tylko od R.
Niech teraz x
∗
będzie zerem m-krotnym,
f
(x
∗
) = f
′
(x
∗
) = · · · = f
(m−1)
(x
∗
) = 0 6= f
(m)
(x
∗
),
gdzie m ≥ 2, oraz niech f będzie m-krotnie różniczkowalna w sposób
ciągły. Wtedy
x
k
− x
∗
= (x
k−1
− x
∗
) −
(x
k−1
− x
∗
)
m
f
(m)
(η
(1)
k
)/m!
(x
k−1
− x
∗
)
m−1
f
(m−1)
(η
(2)
k
)/(m − 1)!
= (x
k−1
− x
∗
)
1 −
1
m
f
(m)
(η
(1)
k
)
f
(m)
(η
(2)
k
)
≈ (x
k−1
− x
∗
)
1 −
1
m
,
(12.7)
o ile x
k−1
jest “blisko” x
∗
.
Metoda Newtona jest więc zbieżna lokalnie. Z (12.6) i (12.7) można
też wywnioskować, jaki jest charakter zbieżności metody Newtona. Dla
zera jednokrotnego x
∗
oraz f
′′
(x
∗
) 6= 0 mamy bowiem
(x
k
− x
∗
) ≈ (x − x
k−1
)
2
f
′′
(x
∗
)
2f
′
(x
∗
)
.
Mówimy, że zbieżność jest kwadratowa. Jeśli zaś f
′′
(x
∗
) = 0 to zbieżnośc
jest nawet szybsza. Z kolei dla zera m-krotnego zbieżność jest liniowa
z ilorazem (1 − 1/m).
Metoda Newtona jest pierwszą poznaną tutaj metodą iteracyjną,
która jest (dla zer jednokrotnych) zbieżna szybciej niż liniowo. Dla ta-
kich metod wprowadza się pojęcie wykładnika zbieżności, który jest
zdefiniowany następująco.

152 ROZDZIAŁ 12. ITERACJE DLA RÓWNAŃ NIELINIOWYCH
Powiemy, że metoda iteracyjna φ jest w klasie funkcji F rzędu co
najmniej p ≥ 1, gdy spełniony jest następujący warunek. Niech f ∈
F
i f(x
∗
) = 0. Wtedy istnieje stała C < ∞ taka, że dla dowolnych
przybliżeń początkowych x
0
, . . . , x
s−1
dostatecznie bliskich x
∗
, kolejne
przybliżenia x
k
= φ(x
k−1
, . . . , x
k−s
) generowane tą metodą spełniają
|x
k
− x
∗
| ≤ C |x
k−1
− x
∗
|
p
.
Ponadto, jeśli p = 1 to dodatkowo żąda się, aby C < 1.
Definicja 12.1 Wykładnikiem zbieżności metody iteracyjnej φ w klasie
F nazywamy liczbę p
∗
zdefiniowaną równością
p
∗
= sup { p ≥ 1 : φ jest rzędu co najmniej p }.
Możemy teraz sformułować następujące twierdzenie, które natych-
miast wynika z poprzednich rozważań.
Twierdzenie 12.2 Wykładnik zbieżności metody Newtona (stycznych)
wynosi p
∗
= 2 w klasie funkcji o zerach jednokrotnych, oraz p
∗
= 1 w
klasie funkcji o zerach wielokrotnych.
Inną znaną i często używaną metodą interpolacyjną jest metoda
siecznych, w której stosuje się liniowy wielomian interpolacyjny La-
grange’a. Metoda ta wykorzystuje więc do konstrukcji x
k
przybliżenia
x
k−1
i x
k−2
. Musimy również wybrać dwa różne punkty startowe x
0
i
x
1
. Ponieważ prosta interpolująca f w x
k−1
i x
k−2
ma wzór
y
(x) =
x
− x
k−2
x
k−1
− x
k−2
f
(x
k−1
) +
x
− x
k−1
x
k−2
− x
k−1
f
(x
k−2
),
otrzymujemy
x
k
= x
k−1
−
x
k−1
− x
k−2
f
(x
k−1
) − f(x
k−2
)
f
(x
k−1
).
Zauważmy, że jeśli x
k−1
i x
k−2
są blisko siebie, to x
k
jest podobny do
tego z metody Newtona, bowiem wtedy iloraz różnicowy (f(x
k−1
) −

12.4. OBLICZANIE ZER WIELOMIANÓW
153
f
(x
k−2
))/(x
k−1
− x
k−2
) dobrze przybliża pochodną f
′
(x
k−1
). Nie wy-
starcza to jednak, aby osiągnąć zbieżność z wykładnikiem 2. Dokład-
niej, można pokazać, że wykładnik zbieżności metody siecznych dla zer
jednokrotnych wynosi p
∗
= (1 +
√
5)/2 = 1.618 . . ., zob. U. 12.3.
Niewątpliwą zaletą metody siecznych jest jednak to, że nie wymaga
ona obliczania pochodnej funkcji (co w praktyce jest często bardzo
trudne, a niekiedy nawet niemożliwe), a tylko jej wartości.
12.4 Obliczanie zer wielomianów
Obliczanie zer w przypadku, gdy funkcja f jest wielomianem jest wła-
ściwie osobnym zadaniem–my tylko dotkniemy tego tematu.
Załóżmy, że wielomian w : R → R jest dany poprzez jego współ-
czynniki a
j
w bazie potęgowej,
w
(x) =
n
X
j=0
a
j
x
j
(a
n
6= 0), i zastosujmy metodę Newtona dla znalezienia największego
zera tego wielomianu. Jedna iteracja metody Newtona jest wtedy sto-
sunkowo prosta, gdyż obliczenie wartości i pochodnej wielomianu w ko-
lejnym pukcie ξ = x
k−1
polega po prostu na dwukrotnym zastosowaniu
schematu Hornera. Rzeczywiście, przypomnijmy, że schemat Hornera
oblicza nie tylko wartość w(ξ), ale również współczynniki w bazie potę-
gowej ilorazu w
1
(x) przy dzieleniu w(x) przez jednomian (x − ξ), zob.
Ćw. 6.2. Zauważmy dalej, że równość
w
(x) = (x − ξ)w
1
(x) + w(ξ)
implikuje w
′
(ξ) = w
1
(ξ). Stąd schemat obliczania jednocześnie w(ξ) i
w
′
(ξ) wygląda następująco.
w
0 := w1 := a
n
;
for j := n
− 1 downto 1 do
begin
w
0 := w0 ∗ ξ + a
j
;
w
1 := w1 ∗ ξ + w0
end;
w
0 := w0 + a
0
.

154 ROZDZIAŁ 12. ITERACJE DLA RÓWNAŃ NIELINIOWYCH
Po wykonaniu tych poleceń mamy w0 = w(ξ) i w1 = w
′
(ξ).
Twierdzenie 12.3 Załóżmy, że wielomian w(x) =
P
n
j=0
a
j
x
j
ma zera
rzeczywiste
ξ
1
≥ ξ
2
≥ · · · ≥ ξ
n
.
Jeśli tylko przybliżenie początkowe x
0
> ξ
1
, to ciąg x
k
generowany me-
todą Newtona jest ściśle malejący i zbieżny do ξ
1
.
Dowód Wielomian w można przedstawić w postaci
w
(x) = (x − ξ
1
)w
1
(x),
gdzie w
1
(x) = a
n
(x − ξ
2
) · · · (x − ξ
n
). Wtedy
w
′
(x) = w
1
(x) + (x − ξ
1
)w
′
1
(x),
a stąd
x
k
− ξ
1
= (x
k−1
− ξ
1
) −
w
(x
k−1
)
w
′
(x
k−1
)
(12.8)
= (x
k−1
− ξ
1
)
1 −
w
1
(x
k−1
)
w
1
(x
k−1
) + (x
k−1
− ξ
1
)w
′
1
(x
k−1
)
!
.
Zauważmy teraz, że wielomiany w
1
(x) i w
′
1
(x) mają stały znak dla
x > ξ
1
, który równy jest znakowi a
n
. Rzeczywiście, ponieważ w
1
(x)
ma wszystkie n − 1 pierwiastków w przedziale (−∞, ξ
1
], to w
′
1
(x) ma
również wszystkie n − 2 pierwiastki w tym samym przedziale. Stąd oba
wielomiany mają ten sam znak na (ξ
1
,
+∞) równy znakowi współczyn-
nika przy najwyższych potęgach tych wielomianów. Wspłczynnik ten
jest w obu przypadkach równy a
n
.
Z rozważań tych wynika, że mnożnik przy (x
k−1
− ξ
1
) w prawej
stronie równania (12.8) jest dla x
k−1
> ξ
1
dodatni i mniejszy od 1,
a stąd, że ciąg x
k
jest malejący i ograniczony z dołu przez ξ
1
. Niech
g
= lim
k→∞
x
k
≥ ξ
1
. Biorąc granicę obu stron (12.8) przy k → ∞
otrzymujemy
g
− ξ
1
= (g − ξ
1
)
1 −
w
1
(g)
w
1
(g) + (g − ξ
1
)w
′
1
(g)
!
,
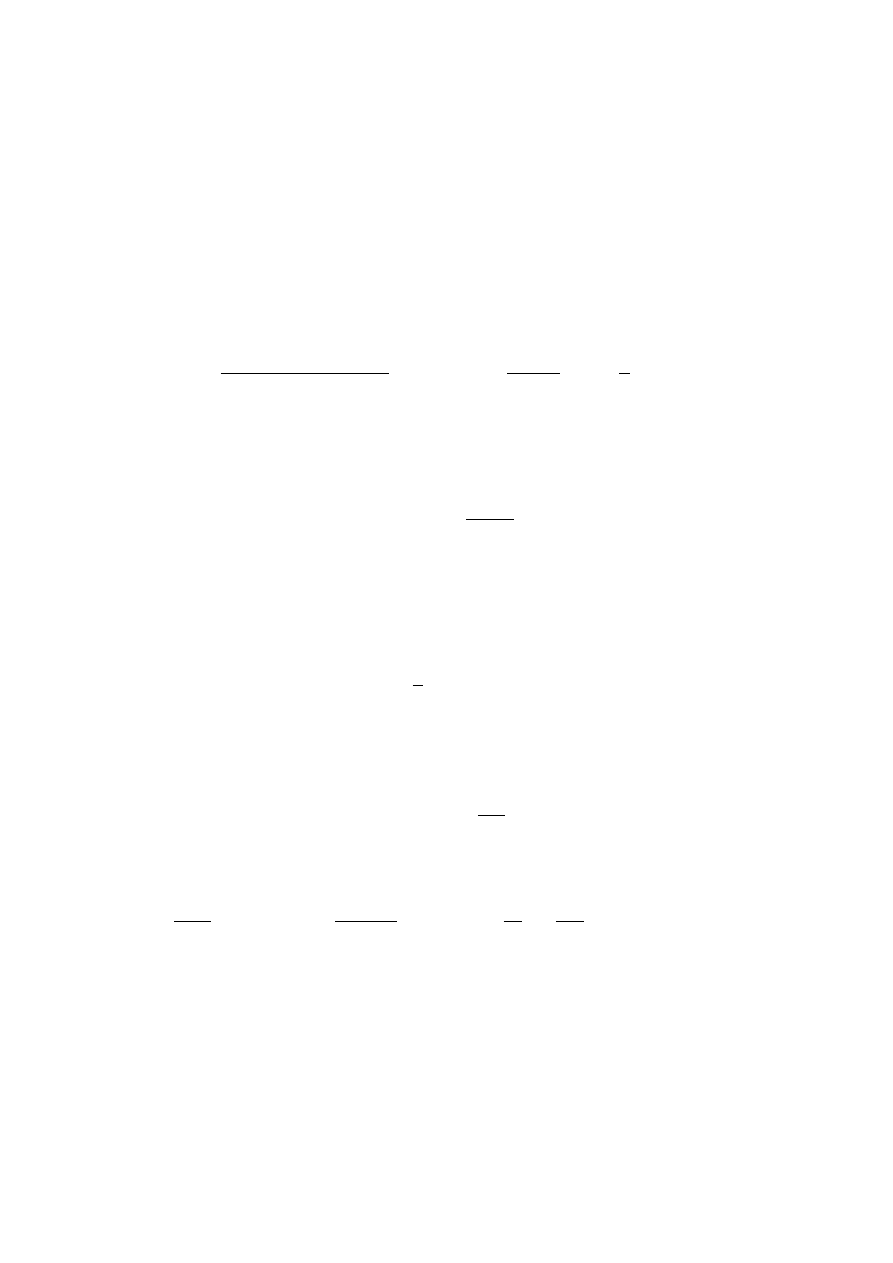
12.4. OBLICZANIE ZER WIELOMIANÓW
155
co wymusza g = ξ
1
, kończąc dowód.
2
Dodajmy, że jeśli zero ξ
1
jest jednokrotne, ξ
1
> ξ
2
, to mamy zbież-
ność kwadratową. Należy jednak podkreślić, że zbieżność kwadratową
uzyskujemy dopiero pod koniec procesu iteracyjnego. Mamy bowiem
lim
x→+∞
w
1
(x)
w
1
(x) + (x − ξ
1
)w
′
1
(x)
= lim
x→+∞
1 +
xw
′
1
(x)
w
1
(x)
−1
=
1
n
.
Jeśli więc wystartujemy z x
0
≫ ξ
1
to początkowo zaobserwujemy zbież-
ność tylko liniową z ilorazem 1−1/n. W miarę zbliżania się do ξ
1
zbież-
ność będzie rosła, aż osiągnie w końcu poziom zbieżności kwadratowej,
x
k
− ξ
1
≈ (x
k−1
− ξ
1
)
2
w
′
1
(ξ
1
)
w
1
(ξ
1
)
,
Dla zera wielokrotnego, ξ
1
= · · · = ξ
m
> ξ
m+1
, m < n, zbieżność pozo-
stanie jednak cały czas na poziomie liniowym, przy czym iloraz zbież-
ności wzrośnie do 1 − 1/m. W końcu, jeśli ξ
1
jest zerem o maksymalnej
krotności n, to łatwo zauważyć, że
x
k
− ξ
1
=
1 −
1
n
(x
k−1
− ξ
1
).
Pozostaje jeszcze problem znalezienia przybliżenia x
0
> ξ
1
. Można
to zrobić na kilka sposobów. Na przykład, zauważmy, że dla
x > M
= max
1,
n−1
X
j=0
|a
j
|
|a
n
|
mamy
w
(x)
a
n
≥ x
n
1 −
n−1
X
j=0
|a
j
|
|a
n
x
n−j
|
≥ x
n
1 −
1
M
n−1
X
j=0
|a
j
|
|a
n
|
>
0.
Stąd w(x) ma stały znak na (M, +∞), a to oznacza, że ξ
1
≤ M. Jako
x
0
można więc wziąć dowolną liczbę większą od M.

156 ROZDZIAŁ 12. ITERACJE DLA RÓWNAŃ NIELINIOWYCH
Uwagi i uzupełnienia
U. 12.1 Metoda bisekcji jest optymalna w następującym sensie. Niech A :
F
→ R będzie dowolną metodą (algorytmem) aproksymującą zero x
∗
(f)
funkcji f z klasy F zdefiniowanej w (12.2), korzystającą jedynie z obliczeń
(informacji o) f w k punktach. Wtedy dla dowolnego γ > 0 istnieje funkcja
f
γ
∈ F mająca tylko jedno zero x
∗
(f
γ
) w [a, b] i taka, że
|A(f
γ
) − x
∗
(f
γ
)| ≥
1
2
k
b
− a
2
+ γ.
Co więcej, można pokazać, że fakt ten zachodzi też w węższej klasie F
1
funkcji f ∈ F , które są dowolnie wiele razy różniczkowalne. Oczywiście,
nie wyklucza to istnienia metod iteracyjnych (takich jak metoda Newtona),
które dla f ∈ F
1
są zbieżne szybciej niż liniowo.
U. 12.2 Wszystkie metody iteracyjne opisane w tym rozdziale należą do
grupy metod adaptacyjnych. Są to metody, które obliczają kolejną wartość
(ew. pochodną) funkcji f w punkcie x
k
, którego wybór istotnie zależy od po-
przednio obliczonych wartości f, tzn. x
k
= x
k
(f(x
0
), . . . , f(x
k−1
)). Okazuje
się, że metody nieadaptacyjne są dużo gorsze przy rozwiązywaniu równań
nieliniowych. Na przykład, najlepsza metoda korzystająca z k wartości funk-
cji wybranych nieadaptacyjnie ma w klasie (12.2) błąd najgorszy równy tylko
(b − a)/(2k + 2).
Zauważmy jeszcze, że dla zadania całkowania z Rozdziałów 9 i 10, opty-
malne metody okazały się nieadaptacyjne.
U. 12.3 Uzasadnimy teraz, że dla zer jednokrotnych wykładnik zbieżności
metody siecznych wynosi p
∗
= (1 +
√
5)/2.
Niech f ∈ C
2
(D). Wykorzystując ilorazy różnicowe otrzymujemy
x
k
− x
∗
= (x
k−1
− x
∗
) −
f (x
k−1
)
f (x
k−2
, x
k−1
)
= (x
k−1
− x
∗
)
1 −
f (x
k−1
, x
∗
)
f (x
k−2
, x
k−1
)
= (x
k−1
− x
∗
)(x
k−2
− x
∗
)
f (x
k−2
, x
k−1
, x
∗
)
f (x
k−2
, x
k−1
)
= (x
k−1
− x
∗
)(x
k−2
− x
∗
)
f
′′
(ξ
(1)
k
)
2f
′
(ξ
(2)
k
)
.

12.4. OBLICZANIE ZER WIELOMIANÓW
157
Stąd widać, że dla x
k−2
i x
k−1
dostatecznie bliskich x
∗
, ciąg x
k
zbiega do x
∗
.
Aby znaleźć wykładnik zbieżności, załóżmy bez zmniejszenia ogólności, że
f
′′
(x
∗
) 6= 0 (w przeciwnym przypadku zbieżność jest jeszcze szybsza). Wtedy
x
k
− x
∗
≈ C(x
k−1
− x
∗
)(x
k−2
− x
∗
),
(12.9)
gdzie C = f
′′
(x
∗
)/(2f
′
(x
∗
)). Stąd, po podstawieniu z
j
= ln(|C(x
j
− x
∗
)|),
dostajemy
z
k
≈ z
k−1
+ z
k−2
.
Ostatnie równanie jest równaniem różnicowym, którego rozwiązaniem jest
z
k
≈ q
k
, gdzie q = (1 +
√
5)/2 jest dominującym pierwiastkiem równania
z
2
= z + 1. Ostatecznie więc |x
k
− x
∗
| ≈ |C
−1
e
q
k
|, czyli
|x
k
− x
∗
| ≈ |C|
q−1
|C
−1
e
q
k−1
q
≈ |C|
q−1
|x
k−1
− x
∗
|
q
.
U. 12.4 Dla znalezienia zera funkcji f : R
n
→ R
n
można zastosować wielo-
wymiarową metodę Newtona. Jest ona zdefiniowana następującym wzorem
rekurencyjnym:
~x
k
= ~x
k−1
− (f
′
(~x
k−1
))
−1
f (~x
k−1
),
gdzie f
′
(~ξ) jest macierzą–Jacobianem funkcji f wziętym w punkcie ~ξ, tzn.
f
′
(~ξ) =
∂f
1
∂x
1
(~ξ) · · ·
∂f
1
∂x
n
(~ξ)
...
...
∂f
n
∂x
1
(~ξ) · · ·
∂f
n
∂x
n
(~ξ)
,
f (~
ξ) =
f
1
(~ξ)
...
f
n
(~ξ)
,
~
ξ =
ξ
1
...
ξ
n
.
W praktyce metodę tą realizuje się rozwiązując w każdym kroku iteracyjnym
układ równań liniowych n × n. Dokładniej,
~x
k
= ~x
k−1
− ~y
k−1
,
gdzie ~y
k−1
jest rozwiązaniem układu
f
′
(~x
k−1
)~y
k−1
= f(~x
k−1
).
Tak jak w przypadku jednowymiarowym, wielowymiarowa metoda Newtona
jest zbieżna lokalnie do zera ~x
∗
z wykładnikiem 2, o ile Jacobian w punkcie
~x
∗
jest nieosobliwy, tzn. det(f
′
(~x
∗
)) 6= 0.

158 ROZDZIAŁ 12. ITERACJE DLA RÓWNAŃ NIELINIOWYCH
Ćwiczenia
Ćw. 12.1 Uzasadnić, że metoda iteracji prostych x
k
= cos(x
k−1
) jest zbie-
żna do jedynego rozwiązania równnania x = cos(x) dla dowolnego przybli-
żenia początkowego x
0
∈ R.
Ćw. 12.2 Podać przykład funkcji f i przybliżenia początkowego x
0
takich,
że ciąg generowany metodą Newtona oscyluje, tzn. x
2s
= x
0
i x
2s+1
= x
1
,
dla wszystkich s.
Ćw. 12.3 Jeśli w modelu obliczeniowym liczenie pierwiastka kwadratowego
√
a (a > 0) nie jest dopuszczalne, to możemy go przybliżyć stosując wzór
rekurencyjny
x
k
=
1
2
x
k−1
+
a
x
k−1
,
który powstaje przez zastosowanie metody Newtona do równania f(x) =
x
2
−a = 0. Pokazać, że ciąg x
k
jest zbieżny do √a dla dowolnego przybliżenia
początkowego x
0
> 0. Scharakteryzować szybkość zbieżności.
Ćw. 12.4 Zaproponować metodę iteracyjną obliczania 1/a dla a > 0 nie
używającą dzielenia. Jak wybrać przybliżenie początkowe aby metoda była
zbieżna? Jaki jest wykładnik zbieżności?
Wskazówka. Zastosować metodę Newtona do funkcji f(x) = 1/x − a.
Ćw. 12.5 Rozpatrzmy metodę iteracyjną
x
k
= x
k−1
−
x
k−1
− a
f (x
k−1
) − f(a)
f (x
k−1
),
gdzie a jest pewnym parametrem. Pokazać, że metoda ta jest zbieżna liniowo,
o ile a jest dostatecznie blisko zera x
∗
.
Ćw. 12.6 Pokazać, że metoda Steffensena
x
k
= x
k−1
−
f
2
(x
k−1
)
f (x
k−1
+ f(x
k−1
)) − f(x
k−1
)
jest zbieżna lokalnie z wykładnikiem 2.
Ćw. 12.7 Rozpatrzmy metodę iteracyjną daną wzorem
x
k
= x
k−1
− m
f (x
k−1
)
f
′
(x
k−1
)
.
Pokazać, że jeśli f ma m-krotne zero x
∗
to metoda ta jest lokalnie zbieżna
do x
∗
z wykładnikiem 2.
Wyszukiwarka
Podobne podstrony:
Marcinkowski L Zadania do wykładu z matematyki obliczeniowej
Matematyka Obliczeniowa Wyklad 2
Matematyka Obliczeniowa Wyklad 1
Matematyka Obliczeniowa Wyklad 2
Wyklady z matematyki V sciaga
Ochrona wlasnosci intelektualnej wyklad 1, Matematyka studia, Ochrona Własności Intelektualnej
wykladnicza, Matematyka, Liceum
wyklad3(1), matematyka, 0, httpmath.uni.lodz.pl~kowalcr, Topologia 1
Wyklady z matematyki II sciaga, MATMA, matematyka, Matma, Matma, Stare, I semestr
Wyklady z matematyki I sciaga
Algorytmy wyklady, Złożoność obliczeniowa algorytmów
notacja wykładnicza, Matematyka, Liceum
Wyklady z matematyki II sciaga
Matematyka obliczeniowa ćwiczenia
funkcja wykładnicza, Matematyka, Liceum
21 04 07 wykład matematyka
Wyklady z Matematyki czesc VI, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc VI, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
więcej podobnych podstron