Funkcje trygonometryczne

Funkcje sinx oraz cosx są określone na całej osi rzeczywistej R i odwzorowujące R na przedział <-1;1>. Funkcja
jest określona na zbiorze x=R\A gdzie
funkcja
jest określona na zbiorze X=R\B gdzie
. Przeciwdziedzina funkcji tgx i ctgx jest y=R.

Odwrotności funkcji sinx oraz cosx oznaczamy następująco:
(„sekans” x)
(„kosekans” x). Funkcja secx jest określona na zbiorze x=R\A gdzie
. Funkcja cscx jest określona na zbiorze x=R\B gdzie
. Przeciwdziedziną funkcji secx i cscx jest zbiór
.

Funkcje cyklometryczne.

Funkcje odwrotne do funkcji trygonometrycznych rozważane w odpowiednio zawężonych dziedzinach:

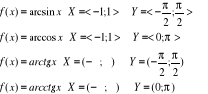
f(x)=arcsinx

arcsin(-1)=y siny=-1 dla

arccos(-1)=y cosy₀=-1 dla y=π

arccos(0)=ycosy=0 dla

arctg(0)=y₀tgy₀=0 dla y₀=0 f(x)=arctgx

arcctg(0)=y₀ctgy=0 dla

Fukcja wykładnicza

Funkcję f nazywamy funkcję wykładniczą jeżeli
, gdzie a<0. Dziedziną funkcji f jest zbiór X=R. Przeciwdziedziną funkcji f jest zbiór Y=(0;∞) gdy a≠1 lub zbiór Y={1}, gdy a=1

Funkcja logarytmiczna

Ponieważ funkcja wykładnicza
jest dla a>0 a≠1 rosnąca lub malejąca więc jest to wtedy funkcja wzajemnie jednoznaczna. Zatem istnieje wówczas funkcja odwrotna do f, która odwzorowuje przedział (0;∞) na zbiór liczb rzeczywistych R. Funkcję f_-1 nazywamy funkcją (logarytmiczną) logarytmem o podstawie a i oznaczamy symbolem m. f_-1x=log_ax.

Dla a>0, a≠1, b>0, b≠1, x,y>0 zachodzą równości:

log_a(x*y)=log_ax+log_ay

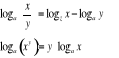
log_a1=0

log_aa=1

Podstawiając w ostatniej równości x=a otrzymujemy:
czyli
,

czyli:
.

Logarytmem naturalnym nazywamy funkcję logarytmiczną o podstawie a=e, gdzie

Przyjmujemy oznaczenia:

związek między logarytmem naturalnym oraz logarytmem o dowolnej podstawie b>0 i b≠1 jest następująca.

Funkcje hiperboliczne.

Funkcje hiperboliczne są to funkcje postaci.

(sinus hiperboliczny)

(cosinus hiperboliczny)

Funkcje sinhx, coshx, tghx są określone dla każdego xεR natomiast ctghx jest określony dla xεR\{0}
Przeciwdziedzina funkcji hiperbolicznych

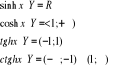
Wartość bezwzględna liczby rzeczywistej lub modułem liczby rzeczywistej xεR nazywamy liczbę nieujemną |x|, przy czym :

Własności:

1. Nierówność |x|≤a jest równoważna z nierównością podwójną -a≤x≤a

Dowód.

2.

Ponieważ x≤|x|; y≤|y| więc, -|x|≤x≤|x|, -|y|≤y≤|y| dodając stronami otrzymujemy.

-(|x|+|y|)≤x+y≤|x|+|y|

z własności 1 otrzymujemy :

|x+y|≤|x|+|y|

3. |x-y|≤|x|+|y|

Dowód.

|x-y|=|x+(-y)| ≤|x|+|-y|=|x|+|y|

4. |x+y|≥|x|-|y|

x-(x+y)-y,

|x|=|x+(y-y)| ≤|x+y|+|y|

|x|-|y|≤|x+y|

5. |x-y|≥|x|-|y|

6. |x-y|≥||x|-|y||

Dowód: 5

Otrzymujemy: |x-y|≥|x|-|y|

Ponadto można napisać:

|x-y|=|-(y-x)|=|y-x|≥|y|-|x|=-(|x|-|y|)

Zatem: |x-y|≥||x|-|y||

Funkcje złożone.

Niech g będzie funkcją odwzorowującą funkcję X na zbiór Y, a f niech będzie funkcją odwzorowującą zbiór Y w zbiór Z.

f°g=f(g)

Złożeniem lub superpozycją funkcji f oraz g nazywamy funkcję (f°g)(x)=f(g(x)) odwzorować x w zbiór z. Oznacza to, że superpozycja

Własności superpozycji funkcji:

1. f•(g•h)=(f•g) •h - łączność

2. f•g≠g•f - nieprzemienność

3. Jeżeli f odwzorowuje wzajemnie jednoznacznie X na Y, f_-1 jest funkcją odwrotną do f, to zachodzi:
   

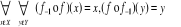
W superpozycji funkcji f•g to znaczy funkcji (f•g)(x)=f(g(x)) funkcję g nazywamy funkcją wewnętrzną, a f funkcją zewnętrzną.

Np. Funkcja h(x)=
jest funkcją złożoną z funkcji wewnętrznej u=g(x)=
oraz funkcji zewnętrznej f(u)=sinu

Przyjmujemy oznaczenia.

R=(-∞;∞) cała oś rzeczywista, zbiór liczb rzeczywistych.

N={1,2,...} zbiór liczb naturalnych

C={0,±1, ±2,....} zbiór liczb całkowitych

W={
mεC, nεN} zbiór liczb wymiernych.

5

---