§10. Szeregi potęgowe.
Dane są funkcje rzeczywiste f1,f2, ..................f określone na niepustym zbiorze ΩεR. Mówimy, że ciąg funkcyjny (fn(x)), xεΩ, jest zbieżny punktowo do funkcji granicznej f jeżeli: ![]()
.
Definicja: Mówimy, że ciąg funkcyjny (f1(x)) xεΩ jest zbieżny jednostajnie względem xεΩ do funkcji granicznej f jeżeli ![]()
Definicja: Szereg funkcyjny ![]()
jest zbieżny punktowo do sumy f(x), xεΩ jeżeli ![]()
Szereg funkcyjny ![]()
, jest zbieżny jednostajnie do sumy f(x) xεΩ jeżeli ciąg sum częściowych 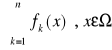
jest zbieżny jednostajnie względem xεΩ do f(x) tzn. 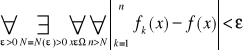
Twierdzenie 1. (Kryterium Weierstrassa)
Jeżeli dla szeregu funkcyjnego ![]()
zachodzą nierówności ![]()
dla każdego xεΩ oraz szereg liczbowy ![]()
jest zbieżny, to szereg ![]()
jest zbieżny jednostajnie względem xεΩ.
Szeregi funkcyjne postaci ![]()
gdzie a0, xεR nazywamy szeregiem potęgowym.
Twierdzenie 2:
a) Jeżeli szereg ![]()
jest zbieżny, gdzie ![]()
to szereg potęgowy ![]()
jest zbieżny dla każdego x takiego, że |x|<|x0| przy czym dla każdego ε ε(0,|x0|) szereg ten jest zbieżny jednostajnie w zbiorze tych x, które spełniają nierówność ![]()
Jeżeli szereg
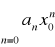
jest rozbieżny to szereg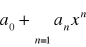
jest rozbieżny dla x takich, że |x|>|x0|
Promieniem zbieżności szeregu ![]()
nazywamy kres górny, czyli supremum R zbioru tych |x| dla których szereg ![]()
jest zbieżny. Jeżeli zbiór ten jest nieograniczony, to przyjmujemy ![]()
. Przedział (skończony lub nieskończony) (-R,R) nazywamy przedziałem zbieżności szeregu ![]()
o promieniu zbieżności R.
Twierdzenie 3: (Twierdzenie Cauchyego -Hadamarda)
Niech ![]()
wtedy promień zbieżności szeregu ![]()
jest równy ![]()
gdy ![]()
przy czym gdy ![]()
przyjmujemy ![]()
gdy ![]()
przyjmujemy R=0.
Twierdzenie 4:
Jeżeli ![]()
dla n=1,2,3,........ oraz ciąg 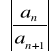
posiada granicę g (skończoną lub nieskończoną) to promień zbieżności szeregu ![]()
jest równy g. Jeżeli we wzorze Taylora ![]()
przyjąć x0=0 ε ε<a,b>, to otrzymamy tzw. wzór Maclaurina w postaci ![]()
Twierdzenie 5: (O rozwijaniu funkcji w szereg Taylora lub szereg Maclaurina)![]()
Jeżeli:
funkcja f ma pochodne wszystkich rzędów w przedziale <a,b>
reszta w postaci Schlomilcha
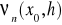
dąży do zera przy
to dla x0, x0+h, ε <a,b> mamy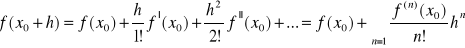
Jeżeli podstawimy h=x-x0 to otrzymujemy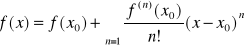
jest to tzw. szereg taylora dla funkcji f. W przypadku gdy x0=0 otrzymujemy tzw. szereg Maclaurina w funkcji f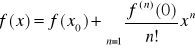
Przykłady:
Rozwinąć w szereg potęgowy funkcję f(x)=ex, xεR
Rozwinąć w szereg Maclaurina funkcje trygonometryczne sinx, cosx, xεR
Rozwinąć w szereg Maclaurina funkcję f(x)=ln(1+x) dla xε(-1,1>
§ 11. WYZNACZANIE WYRAŻEŃ NIEOZNACZONYCH PRZY
POMOCY POCHODNYCH.
WYRAŻENIA NIEOZNACZONE TYPU ![]()
TWIERDZENIE 1:
Jeżeli:
Funkcje f, g są określone na przedziale
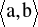
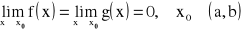
istnieje skończona pochodna
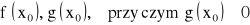
to: ![]()
.
DOWÓD:
Ponieważ istnieją skończone pochodne ![]()
więc funkcje f, g są ciągłe w x0.
Zatem:
![]()
Ponieważ ![]()
więc ze wzoru, Taylora wynika, że istnieje taki otoczenie ![]()
Stąd dla![]()
mamy: 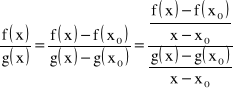
.
Przy ![]()
otrzymujemy: ![]()
Zachodzi również twierdzenie ogólniejsze:
TWIERDZENIE 2:
Jeżeli:
funkcje f, g są określone na przedziale
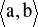
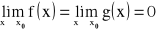
na przedziale
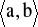
istnieje skończona pochodna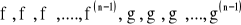
, przy czym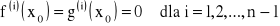
istnieje skończona pochodna
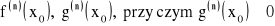
to: 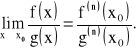
TWIERDZENIE 3:
Jeżeli:
funkcje f, g są określone na przedziale
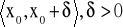
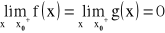
na przedziale
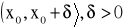
istnieje skończona pochodna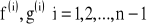
, przy czym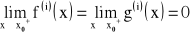
na przedziale
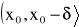
istnieją skończone pochodne n-tego rzędu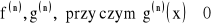
oraz istnieje granica właściwa lub niewłaściwa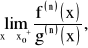
to: 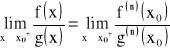
.
W twierdzeniu powyższym można również rozważać lewostronne otoczenie punktu x0.
W przypadku, gdy ![]()
stosujemy:
TWIERDZENIE 4:
Jeżeli:
funkcje f, g są określone na przedziale
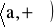
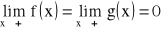

na przedziale
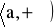
istnieje skończona pochodna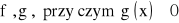
oraz istnieje granica skończona lub nieskończona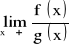
,
to: ![]()
.
Do badania wyrażeń nieoznaczonych typu ![]()
stosujemy:
TWIERDZENIE 5:
Jeżeli:
funkcje f, g są określone na przedziale
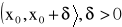
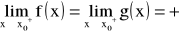
na przedziale
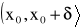
istnieje skończona pochodna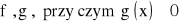
oraz istnieje granica właściwa lub niewłaściwa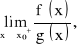
to: ![]()
.
Twierdzenie 5 można sformułować również w przypadku lewostronnego otoczenia x0 oraz gdy ![]()
.
UWAGA!!!
Jeżeli funkcje f, g dążą do ![]()
, to zamiast badać wyrażenie typu ![]()
można badać wyrażenie typu ![]()
, pisząc tożsamość 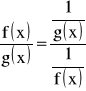
.
Powyższe twierdzenia należą do G.F de l'Hospitala i J. Bernoulliego. Twierdzenia te można nazwać regułami e l'Hospitala potrzebnymi do obliczenia wyrażeń nieoznaczonych.
WYRAŻENIA NIEOZNACZONE TYPU ![]()
Wyrażenie typu
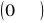
można sprowadzić do postaci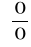
lub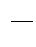
pisząc tożsamość. Jeżeli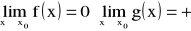
to można napisać :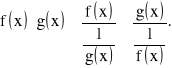
Jeżeli
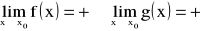
, to badając wyrażenie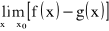
, można napisać tożsamość: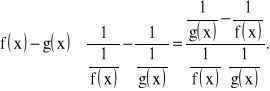
Jeżeli funkcja
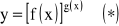
jest przy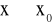
wyrażeniem nieoznaczonym typu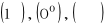
to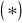
logarytmujemy obustronnie: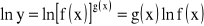
.Jeżeli
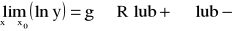
, to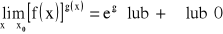
.
PRZYKŁADY:
Znaleźć:
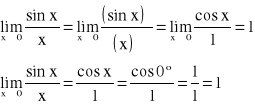
Znaleźć:
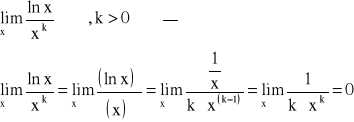
Znaleźć:
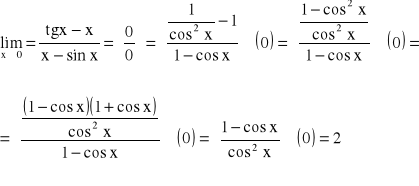
Znaleźć:
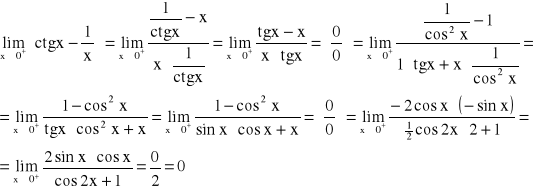
§ 12. CAŁKA NIEOZNACZONA
DEFINICJA: Funkcję F nazywamy funkcją pierwotną funkcji rzeczywistej f, określonej na przedziale otwartym (skończonym lub nieskończonym) X przyjmującej wartości rzeczywiste, jeżeli:
![]()
.
Jeżeli funkcja f jest określona na przedziale domkniętym ![]()
, to funkcję F nazywamy funkcją pierwotną funkcji f, jeżeli:
![]()
,
gdzie ![]()
- pochodna prawostronna
![]()
- pochodna lewostronna
Niech C1 oznacza dowolną stałą. Jeżeli F jest funkcją pierwotną funkcji f to zwg na to, że ![]()
, funkcja G, gdzie ![]()
, jest również funkcją pierwotną funkcji f.
Na odwrót, jeżeli ![]()
są funkcjami pierwotnymi funkcji f, to ![]()
, czyli na podstawie twierdzenia o wartości średniej: ![]()
, gdzie ![]()
jest odpowiednio dobraną stałą.
![]()
Zatem wyrażenie ![]()
, gdzie C jest dowolnie ustaloną stałą oraz ![]()
dla ![]()
jest ogólną postacią funkcji pierwotnej dla funkcji f.
DEFINICJA: Rodziną wszystkich funkcji pierwotnych funkcji f nazywamy całką nieoznaczoną z f i oznaczamy przy pomocy symbolu:![]()
.
Jeżeli funkcja f posiada całkę nieoznaczoną dla ![]()
, to mówimy, że f jest całkowalna dla ![]()
.
Zatem:
![]()
,
gdzie ![]()
dla każdego ![]()
, c-dowolne, ustalona stała.
Wtedy funkcję f nazywamy funkcją podcałkową. Obliczanie całek nieoznaczonych nazywamy całkowaniem:
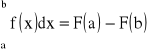
.
TWIERDZENIE 1:
Jeżeli funkcja f posiada funkcję pierwotną na przedziale ![]()
to dla każdego punktu ![]()
, gdzie![]()
istnieje dokładnie jedna funkcja pierwotna F, taka, że:![]()
.TWIERDZENIE 2:
Jeżeli funkcja f jest ciągła na przedziale ![]()
to posiada na tym przedziale funkcje pierwotną.
TWIERDZENIE 3:
Jeżeli funkcje f, g są całkowalne dla ![]()
to:
![]()
,
gdzie ![]()
-stałe.
DOWÓD:
Ponieważ:
![]()
więc dla ![]()
![]()
.
UWAGA!:
Wzór z tezy twierdzenia 3 należy rozumieć następująco:
Dla dowolnych, ustalonych stałych cf, cg odpowiadających całkom:
![]()
,
można dobrać stałą ![]()
odpowiadającą całce:![]()
tak by zachodziła równość:
![]()
.
PODSTAWOWE METODY CAŁKOWANIA:
całkowanie przez podstawianie:
TWIERDZENIE 4:
Jeżeli:
funkcja f jest ciągła na przedziale
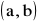
funkcja
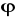
ma ciągłą pochodną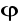
na przedziale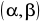
,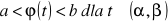
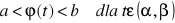
to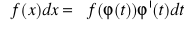
gdzie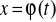
dla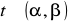
DOWÓD:
Niech:
![]()
a więc
![]()
Funkcja złożona ![]()
jest określona dla ![]()
. Z twierdzenia o pochodnej funkcji złożonej otrzymujemy:
![]()
stąd
![]()
.
Przyjmując ![]()
mamy:
![]()
.
całkowanie przez części („per partes”)
TWIERDZENIE 5:
Jeżeli funkcje ![]()
posiadają skończone pochodne ![]()
na przedziale ![]()
to dla każdego ![]()
zachodzi równość:
![]()
przy założeniu istnienia obu całek>
DOWÓD:
Dla ![]()
zachodzi równość
![]()
,
czyli
![]()
stąd po obustronnym scałkowaniu otrzymujemy:
![]()
.
PRZYKŁADY:
Znaleźć:
![]()
.
Rozwiązanie: Stosujemy wzór na całkowanie przez części, przyjmując:
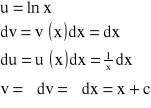
Zatem
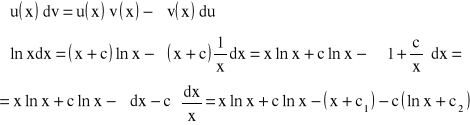
c,c1,c2-dowolne wzajemnie niezależne stałe.
![]()
,
gdzie c3 dowolna stała.
Zatem:
![]()
.
Znaleźć:
![]()
.
Rozwiązanie:
Niech x>0. Wtedy:
![]()
.
Niech x<0. Wtedy podstawiając x=-t, gdzie t>0 otrzymujemy:
![]()
oraz ![]()
.
Zatem dla ![]()
mamy:
![]()
.
Znaleźć:
![]()
,
gdzie f jest ciągła wraz z pochodną ![]()
na przedziale ![]()
oraz ![]()
.
Rozwiązanie:
Podstawiamy ![]()
, po obustronnym zróżniczkowaniu otrzymujemy:
![]()
.
Zatem:
![]()
Znaleźć:
![]()
.
Rozwiązanie:
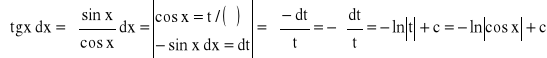
![]()
Całkujemy przez części:
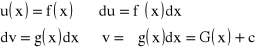
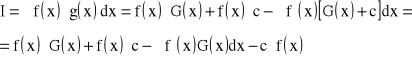
Znaleźć:
![]()
.
Rozwiązanie:
Zastosujemy dwukrotne całkowanie przez części:
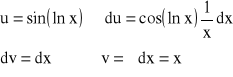
![]()
Obliczamy całkę:
![]()
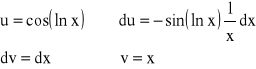
![]()
Zatem otrzymujemy następujące równanie funkcyjne:
![]()
czyli:
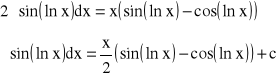
.
CAŁKI NIEOZNACZONE FUNKCJI ELEMENTARNEJ:
Funkcja f: |
Całka nieoznaczona
|
Uwagi; |
a-stałe |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lnx |
|
|
sinx |
|
|
cosx |
|
|
tgx |
|
|
ctgx |
|
|
PRZYKŁADY:
Znaleźć:
![]()
.
Stosujemy całkowanie przez części:
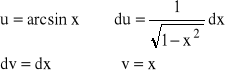
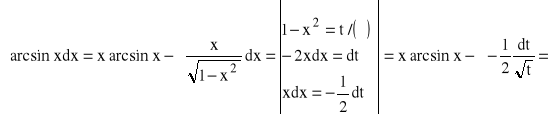
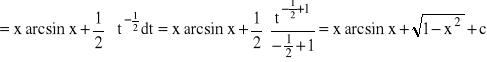
Znaleźć:
![]()
.
Całkujemy przez części:
![]()
:
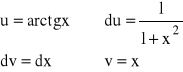
![]()
.
WZORY REKURENCYJNE:
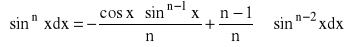
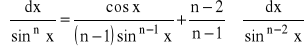
dla n=2,3,...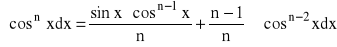
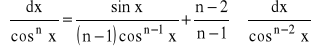
dla n=2,3,...
PRZYKŁADY:
Znaleźć:
![]()
Rozwiązanie:
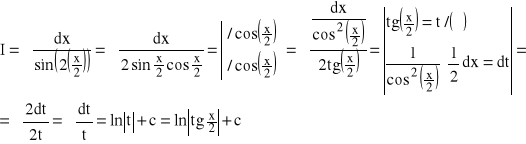
Znaleźć:
![]()
Rozwiązanie:
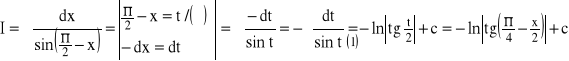
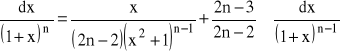
dla n=2,3,..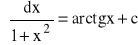
CAŁKOWANIE FUNKCJI WYMIERNYCH:
Jeżeli funkcja podcałkowa jest funkcją wymierną tzn. ma postać ![]()
, gdzie P, Q są wielomianami algebraicznymi, to w przypadku, gdy stopień wielomianu P jest większy lub równy stopniowi wielomianu Q, wykonujemy dzielenie ![]()
. Otrzymujemy wielomian R(x) oraz resztę postaci ![]()
, przy czym stopień ![]()
jest większy niż stopień ![]()
.
Funkcją wymierną, dla której stopień licznika jest niższy od stopnia mianownika nazywamy ułamkiem właściwym.
Niech funkcja podcałkowa będzie ułamkiem właściwym ![]()
.
Jeżeli wielomian Q ma pierwiastki rzeczywiste ![]()
odpowiednio rzędów ![]()
oraz pierwiastki zespolone ![]()
odpowiednio rzędów ![]()
to wielomian Q ma postać:
![]()
,
gdzie ![]()
jest liczbą sprzężoną do ![]()
.
Ponieważ:
![]()
,
gdzie ![]()
oraz ![]()
więc:
![]()
Funkcje wymierne postaci:
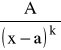
, 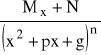
,
gdzie ![]()
nazywamy ułamkiem prostym.
TWIERDZENIE 6:
Każda funkcja wymierna ![]()
, gdzie stopień wielomianu P jest mniejszy niż stopień wielomianu Q oraz wielomian Q ma postać (1), rozkłada się jednoznacznie na sumę ułamków prostych:
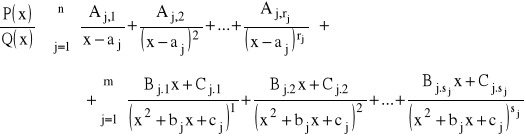
PRZYKŁAD:
Znaleźć całkę:
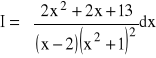
Rozwiązanie:
Funkcja podcałkowa jest ułamkiem właściwym. Rozłóżmy ją na ułamki proste stosując tzw. metodę współczynników nieoznaczonych.
Dla ![]()
możemy napisać:
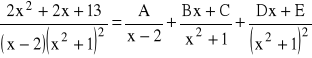
przy czym współczynniki A-E wyznaczamy z tożsamości:
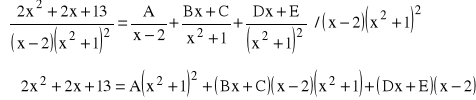
Po uporządkowaniu prawej strony powyższej tożsamości według potęg zmiennej x, otrzymujemy porównując współczynniki przy tych samych potęgach x w odniesieniu do wielomianów z lewej i prawej strony.
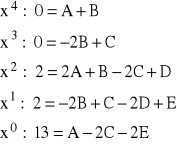
stąd:
![]()
.
Zatem dla ![]()
mamy:
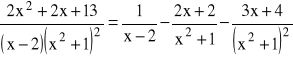
.
Stąd:
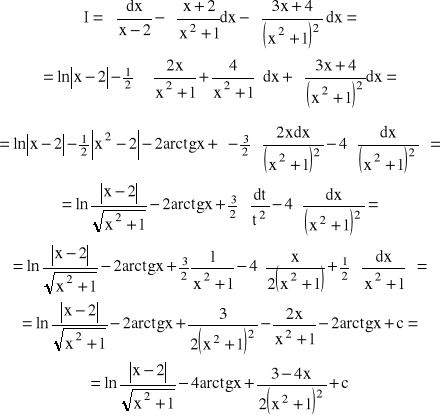
Całki ułamków prostych obliczamy w następujący sposób:
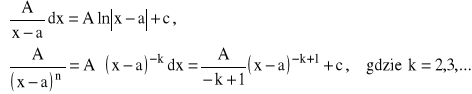
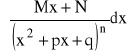
zakładamy, że ![]()
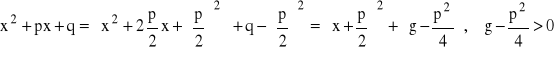
Podstawiamy:
![]()
Wtedy:
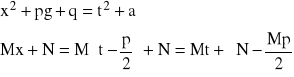
Zatem:
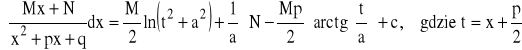
Podobnie podstawiając obliczamy całkę:
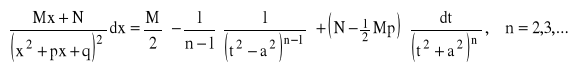
W dalszym ciągu stosujemy wzór rekurencyjny e):
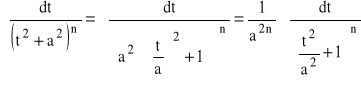
.
CAŁKOWANIE PEWNYCH FUNKCJI NIEWYMIERNYCH:
Podstawienia Eulera
Niech W=W(x,y) będzie funkcją wymierną dwóch zmiennych tzn. ![]()
, gdzie P, Q są wielomianami algebraicznymi zmiennych x, y.
Rozważmy całkę:
![]()
.
Przy pomocy tzw. podstawień Eulera można zawsze sprowadzić wyrażenie:
![]()
do postaci funkcji wymiernej.
Jeżeli a>0 to podstawiamy:
![]()
lub
![]()
Wtedy otrzymujemy:
![]()
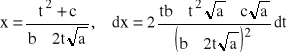
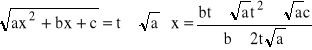
Jeżeli c>0 to podstawiamy:
![]()
wtedy:
![]()
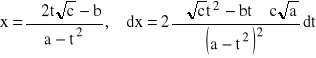
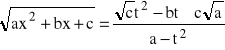
Jeżeli trójmian kwadratowy
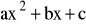
posiada dwa różne pierwiastki x1, x2 tzn.:
![]()
to podstawiamy:
![]()
, gdzie i=1 lub i=2.
Wtedy np. przy i=1 otrzymujemy:
![]()
![]()
![]()
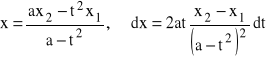
Niech
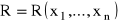
będzie iloczynem sum skończonych postaci:
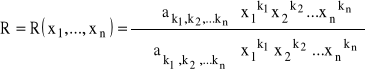
,
gdzie ![]()
-liczby całkowite nieujemne,
![]()
-stałe rzeczywiste.
Całkowanie wyrażeń:
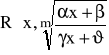
gdzie m-liczba naturalna, -stałe rzeczywiste.
Podstawiamy:
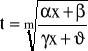
otrzymujemy:
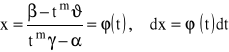
gdzie ![]()
jest funkcją wymierną.
W przypadku całki postaci:
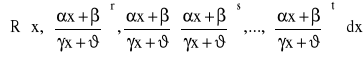
gdzie r,s,...t są liczbami dodatnimi. Wykładniki r,s,...,t sprowadzamy do wspólnego mianownika: m i podstawiamy:
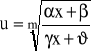
.
Całkowanie różniczek dwuwymiernych.
Różniczką dwuwymierną nazywamy wyrażenie:
![]()
gdzie m,n,p są liczbami wymiernymi ![]()
.
Całkę różniczki dwuwymiernej:
![]()
gdzie ![]()
,
można sprowadzić do całki z funkcji wymiernej wtedy, gdy co najmniej jedna z liczb:
![]()
jest całkowita.
Jeżeli p-liczba całkowita, to podstawiamy:
![]()
gdzie ![]()
najmniejsza wspólna wielokrotność mianowników liczb wymiernych m,n.
Jeżeli
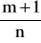
-liczba całkowita, to podstawiamy:
![]()
gdzie ![]()
-mianownik liczby wymiernej p.
Jeżeli
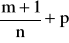
-liczba całkowita, to podstawiamy:
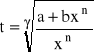
gdzie ![]()
mianownik liczby wymiernej p.
CAŁKOWANIE WYRAŻEŃ ZAWIERAJĄCYCH FUNKCJE TRYGONOMETRYCZNE:
Podstawienie uniwersalne:
Różniczka postaci:
![]()
,
gdzie funkcja dwóch zmiennych ![]()
jest określona wcześniej, można sprowadzić do funkcji wymiernej stosując podstawienie
![]()
wtedy:
![]()
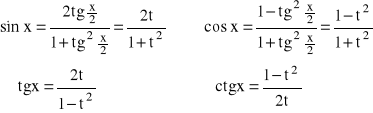
Jeżeli:
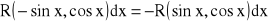
to podstawiamy: ![]()
.
Jeżeli: ![]()
to podstawiamy: ![]()
.
Jeżeli: ![]()
to podstawiamy: ![]()
.
Jeżeli wyrażenie podcałkowe ma postać:
![]()
gdzie ![]()
liczby wymierne ![]()
, to podstawiamy: ![]()
.
Wtedy:
![]()
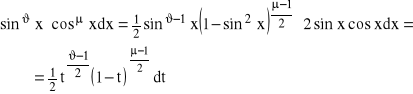
PRZYKŁAD:
Znaleźć:
![]()
Rozwiązanie:
Stosujemy podstawienie uniwersalne: ![]()
.
Wtedy:
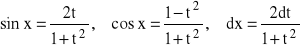
.
Otrzymujemy:
![]()
.
to:
![]()
, gdzie ![]()
.
38
(x0,y0)
a
b
![]()
Warunek brzegowy dla funkcji pierwotnej F
Wyszukiwarka
Podobne podstrony:
Wyklady z Matematyki czesc III, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc VI, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc VI, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc IV, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc V, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc II, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc I, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc VII do mdruku, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykład
Wyklady z Matematyki czesc V, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc IV, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
czesc III zarzadzanie ryzykiem bankowym, STUDIA UE Katowice, semestr I mgr, ZARZĄDZANIE INSTYTUCJAMI
Stat FiR TEORIA III (estymacja, sggw - finanse i rachunkowość, studia, II semestr, Statystyka ĆW
Wyklady z matematyki II sciaga, MATMA, matematyka, Matma, Matma, Stare, I semestr
Wyklady z matematyki IV sciaga, MATMA, matematyka, Matma, Matma, Stare, I semestr
Jak pomóc w przezwyciężaniu trudności w uczeniu się matematyki – Cześć III
Jak pomóc w przezwyciężaniu trudności w uczeniu się matematyki – Cześć III
Z Wykład 15.03.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Wykład z dnia 10.05.2008, Zajęcia, II semestr 2008, Matematyka dyskretna i logika
Z Wykład 19.04.2008, Zajęcia, II semestr 2008, Analiza matematyczna
więcej podobnych podstron