§ 14. Całki niewłaściwe
Całki niewłaściwe to całki o granicach nieskończonych lub funkcji nieograniczonych.
14.1 Całki o granicach nieskończonych
Niech funkcja f będzie określona na przedziale nieskończonym ![]()
oraz całkowana w sensie Riemanna na każdym przedziale skończonym <a,A>, gdzie ![]()
Definicja: Całkę funkcji f o granicach a, +∞ nazywamy wielkość postaci: 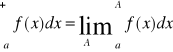
(1) gdy przy założeniu, że powyższa granica jest skończona lub nieskończona w przypadku gdy granice (1) jest skończona mówimy, że całka (1) jest zbieżna, z funkcja f całkowana na przedziale <a, ∞). Jeżeli granica (1) jest nieskończona to mówimy, że całka (1) jest rozbieżna.
Podobnie definiujemy całki:
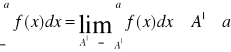
określa się też całkę 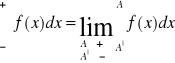
gdzie A nie zależy od A| .
Przykłady:
Znaleźć
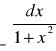
Zbadać zbieżność całki
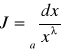
gdzie a>0,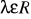
Znaleźć V i pole powierzchni bocznej bryły otrzymanej przez obrót hiperboli x*y=1 dookoła osi OX, gdzie

Twierdzenie 1 - Na to by całka 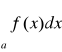
gdzie f(x)≥0 dla x≥a, była zbieżna potrzeba i wystarcza by był spełniony warunek 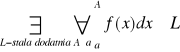
Twierdzenie 2 (kryterium porównawcze)
Jeżeli dla x≥A≥a zachodzą nierówności 0≤f(x) ≤g(x) wynika zbieżność całki 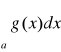
wynika zbieżność całki 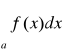
a, z rozbieżności całki 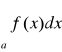
wynika rozbieżność całki 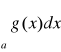
.
Dowód: Ponieważ na rozbieżność całki 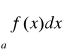
nie ma wpływu całka c więc wystarczy badać zbieżność całki 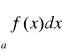
. Ponieważ dla x≥A≥a mamy 0≤f(x) ≤g(x) więc korzystając z własności całki Riemana otrzymujemy: 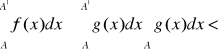
gdy ![]()
. Zatem przechodząc do granicy przy ![]()
otrzymujemy 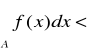
. Jeżeli założymy, że całka 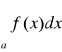
jest rozbieżna z nierówności 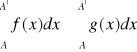
przy dowolnym ![]()
wynika, że całka 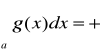
(jest rozbieżna)
Twierdzenie 3.
Jeżeli istnieje granica ![]()
dla ![]()
, g(x)>0 przy ![]()
to ze zbieżności całki 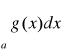
wynika zbieżność 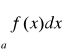
, gdy k<∞ a z rozbieżności całki 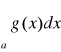
przy k>∞ wynika rozbieżność całki 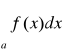
Dowód:
niech k<∞ zakładamy, że całki
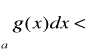
(zbieżna) Ponieważ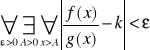
więc dla x>A mamy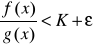
=>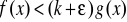
Stąd na podstawie twierdzenia w całka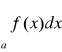
jest zbieżnaniech k>0 oraz
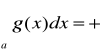
Ponieważ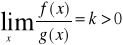
więc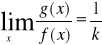
Podobnie jak w a. otrzymujemy oszacowanie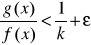
lub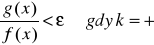
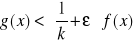
dla x≥A| z twierdzenia 2 wynika więc rozbieżność całki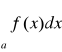
Badając zbieżność 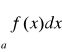
gdzie f(x)≥0 jest nieujemne dla x≥a można obrać konkretną funkcje ![]()
, która jest całkowana gdy a>0, ![]()
oraz nie jest całkowana, gdy a>0, ![]()
i stosować kryterium porównawcze.
Twierdzenie 4 (Cauchy)
Niech funkcja f ma dla dostatecznie dużych X postać ![]()
, ![]()
Wtedy:
jeżeli

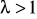
oraz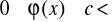
to całka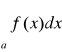
jest rozbieżnajeżeli
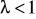
oraz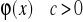
to całka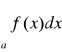
jest rozbieżna
W przypadku gdy funkcja podcałkowa zmienia znak stosujemy następujące twierdzenie 5.
Twierdzenie 5 (Cauchy)
Na to by całka 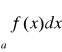
była zbieżna potrzeba i wystarcza by był spełniony warunek 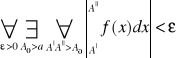
Jeżeli zbieżna jest całka 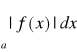
, to całka 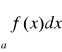
nazywa się bezwzględnie zbieżna
Z twierdzenia 5 wynika, że jeżeli zbieżna jest całka 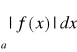
to zbieżna jest całka 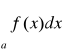
. Istnieją całki zbieżne, które nie są bezwzględnie zbieżne. np. 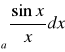
Całkę 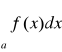
nazywamy warunkowo zbieżną gdy jest zbieżna, ale nie jest bezwzględnie zbieżna.
Twierdzenie 6. (Kryterium Abela)
Niech funkcje f,g będą określone na przedziale <a, ∞), jeżeli:
funkcja f jest całkowalna na <a, ∞)
funkcja g jest monotoniczna i ograniczona
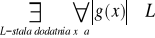
to całka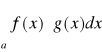
jest zbieżna
Twierdzenie 7. (Kryterium Dirichleta)
Niech funkcje f,g będą określone na przedziale <a, ∞) jeżeli
funkcja f jest całkowalna na każdym przedziale skończonym <a,A> oraz
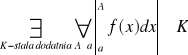
funkcja g jest ograniczona i zbieżna monotonicznie do zera przy

, to całka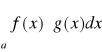
jest zbieżna
Przykład : Zbadać zbieżność całki 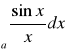
, a>0
14.2 Całki niewłaściwe z funkcji nieograniczonych.
Niech funkcja f będzie ograniczona i całkowana w sensie Riemanna na każdym przedziale ![]()
gdzie ![]()
oraz nieograniczona w każdym przedziale ![]()
. Wtedy punkt b nazywamy punktem osobliwym funkcji f np. funkcje: 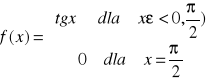
ma punkt osobliwy ![]()
. Całką funkcji f w granicach a, b a<b nazywamy wielkość
(1) 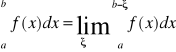
przy założeniu, że granica ta jest skończona lub nieskończona. W przypadku,, gdy granica (1) jest skończona mówimy, że całka (1) jest zbieżna, a funkcja f jest całkowalna na przedziale <a,b>
Jeżeli granica (1) jest nieskończona, to mówimy że całka (1) jest rozbieżna. Analogicznie określamy całkę 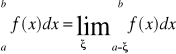
gdy funkcja ma punkt osobliwy x=a.
Ogólnie można rozważać przypadek, gdy funkcja f ma w przedziale <a,b> skończoną liczbę punktów osobliwych: c0,c1,....cn w otoczeniu których f jest nieograniczona oraz f jest ograniczona i całkowalna w każdym przedziale, który nie zawiera punktów osobliwych. Np. Dla ![]()
mamy: 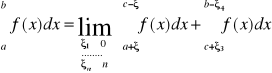
przy czym ![]()
są wzajemnie niezależne.
Podobnie jak w przypadku całek w przedziałach nieskończonych wykazujemy następujące twierdzenia. Zakładamy, że x0=b jest punktem osobliwym funkcji f.
Twierdzenie 8.
Na to by zbieżna była całka niewłaściwa (1) z funkcji nieujemnej f potrzeba i wystarcza by był spełniony warunek. 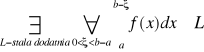
Twierdzenie 9. (Kryterium porównawcze)
Jeżeli dla ![]()
zachodzi nierówność 0≤f(x) ≤g(x) to ze zbieżności całki 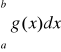
wynika zbieżności całki 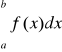
a z rozbieżności całki 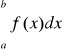
wynika rozbieżność całki 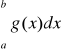
.
Przykład zbadać zbieżność całki 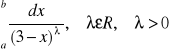
Twierdzenie 10.
Jeżeli 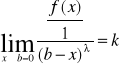
gdzie f(x)≥0 dla xε<a,b> 0≤k≤∞ to przy ![]()
gdzie 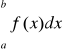
jest zbieżna, gdy k<∞ oraz całka 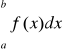
jest rozbieżna przy ![]()
oraz K>0
Twierdzenie 11. (Cauchy)
Niech funkcja f ma dla x dostatecznie ........... (granicy górnej) b postać ![]()
wtedy:
Jeżeli
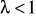
oraz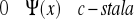
to całka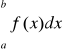
jest zbieżnaJeżeli
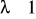
oraz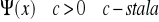
to całka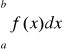
jest rozbieżna
Dla funkcji f zmieniającej znak na przedziale <a,b> stosujemy:
Twierdzenie 12. (Cauchy)
Na to by całka 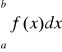
, gdzie ... jest punktem osobliwym, była zbieżna potrzeba i wystarcza by był spełniony warunek: 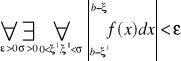
z twierdzenia 12 wynika, że jeżeli jest zbieżna całka 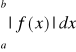
to jest zbieżna całka 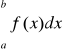
. Mówimy wtedy, że całka bezwzględnie zbieżna jest zbieżna.
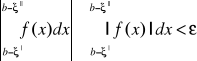
. Niech na przedziale <a,b> będzie określona funkcja f mająca dokładnie jeden punkt osobliwy ![]()
oraz całkowana w sensie Riemanna w każdym podprzedziale przedziału <a,b>, który nie zawiera punktu osobliwego c.
Wtedy 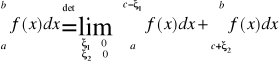
przy założeniu istnienia granicy właściwej lub niewłaściwej. Wartością główną całki niewłaściwej 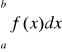
nazywamy wyrażenie 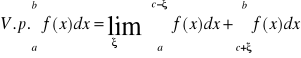
przy założeniu istnienia granicy w sensie właściwym lub niewłaściwym. (V.p. -„Valeur pricipale”)
Mówimy wtedy, że całka 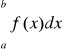
istnieje w sensie wartości głównej.
Jeżeli całka 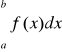
istnieje jako całka niewłaściwa to zawsze istnieje jej wartość główna. Twierdzenie odwrotne nie zachodzi.
14.3 Kryterium całkowania zbieżności szeregów liczbowych.
Twierdzenie 13.
Dany jest szereg liczb ![]()
niech f jest funkcją określoną na przedziale <1,∞), ciągłą, dodatnią, malejącą. Szereg ![]()
jest zbieżny wtedy i tylko wtedy gdy zbieżna jest całka niewłaściwa 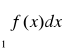
Dowód: Niech F będzie funkcją pierwotną funkcji f. Z twierdzenia Lagrange'a o wartości średniej wynika, że dla n=1,2,..... ![]()
Z monotoniczności f wynika, że ![]()
Z kryterium porównawczego zbieżności szeregów wynika, że szereg ![]()
jest zbieżny wtedy i tylko wtedy gdy zbieżny jest szereg ![]()
Ponieważ ![]()
![]()
Więc 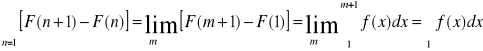
Przykład: Zbadać zbieżność szeregu harmonicznego ![]()
Rozwiązanie: ![]()
, Ponieważ całka ![]()
jest zbieżna, gdy ![]()
oraz rozbieżna gdy ![]()
więc szereg harmoniczny ![]()
jest zbieżny wtedy i tylko wtedy gdy ![]()
.
ROZDZIAŁ IV MACIERZE, WYZNACZNIKI, UKŁADY RÓWNAŃ LINIOWYCH
MACIERZE, WYZNACZNIKI
Macierzą prostokątną o wymiarze ![]()
lub o m wierszach i n kolumnach nazywamy funkcję dwóch zmiennych postaci:
![]()
=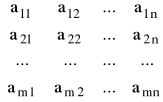
,
przyporządkowującą każdej uporządkowanej parze (j;k), gdzie ![]()
![]()
, liczbę zespoloną ajk.
Macierz nazywamy kwadratową, jeżeli![]()
. Wtedy liczbę n nazywamy stopniem macierzy. Jeżeli w macierzy ![]()
zamienimy wiersze na kolumny to otrzymujemy tzw. macierz transponowaną: ![]()
.
Elementy a11, a22,..., anm tworzą tzw. przekątną główną.
Macierz kwadratową nazywamy diagonalną, jeżeli ![]()
, czyli poza przekątną główną występuje tylko 0. W szczególności, jeżeli w macierzy diagonalnej ![]()
, dla każdego j = 1,2,...,n, to macierz taką nazywamy jednostkową i oznaczamy przez I, czyli
I = 
.
DZIAŁANIA NA MACIERZACH:
Dodawanie macierzy:
Dwie macierze A, B można dodać, gdy są tego samego wymiaru. Wtedy, jeżeli:
![]()
to:
![]()
.
Mnożenie macierzy przez liczbę:
Jeżeli ![]()
- liczba rzeczywista lub zespolona, to: ![]()
.
Mnożenie macierzy przez macierz:
Macierz A można pomnożyć przez macierz B wtedy i tylko wtedy, gdy liczba kolumn macierzy A jest równa liczbie wierszy macierzy B.
Jeżeli: ![]()
to iloczynem macierzy A i B nazywamy macierz:
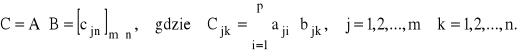
Dodawanie macierzy jest przemienne, tzn. A+B=B+A.
Mnożenie macierzy nie jest przemienne tzn. ![]()
Zachodzą następujące nierówności:
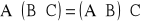
- łączność mnożenia macierzy.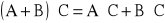
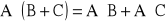
WYZNACZNIKI:
Niech a1, a2, ..., an będzie dowolnym ciągiem liczb rzeczywistych różnych między sobą. Mówimy, że para wyznaczników tego ciągu ![]()
tworzy inwersję, jeżeli: ![]()
.
DEFINICJA WYZNACZNIKA:
Dana jest macierz kwadratowa:
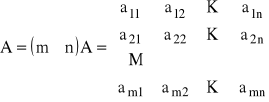
Tworzymy dowolną permutację ![]()
liczb naturalnych: 1,2,3,...,n. Niech ![]()
oznacza ilość inwersji w permutacji f.
Wyznacznikiem macierzy ![]()
nazywamy liczbę:
det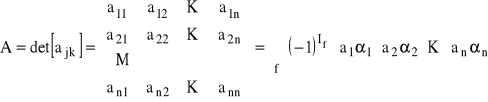
,
przy czym przyjmujemy ze względu na wszystkie permutacje liczb naturalnych: 1,2,...
Stopniem wyznacznika detA nazywamy stopień macierzy.
Bezpośrednio z definicji wyznacznika macierzy kwadratowej otrzymujemy:
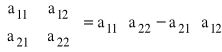

Wyznacznik trzeciego stopnia można wyliczyć stosując tzw. schemat Sarrusa:
WŁASNOŚCI WYZNACZNIKÓW:
Rozwinięcie Laplace'a
Minorem macierzy prostokątnej A nazywamy wyznacznik detM macierzy M, która powstała przez skreślenie w macierzy A pewnej liczby wierszy i kolumn tak, aby elementy nie skreślone tworzyły macierz kwadratową M.
Jeżeli w macierzy kwadratowej A stopnia n skreślimy j-ty wiersz oraz k-tą kolumnę to otrzymany minor będziemy oznaczać: ![]()
.
Dopełnieniem algebraicznym elementu ![]()
macierzy kwadratowej A nazywamy liczbę:![]()
.
TWIERDZENIE 1:
Dla wyznacznika macierzy kwadratowej:
A=
Ma miejsce następujące rozwinięcie Laplace'a:
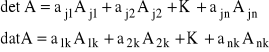
,
gdzie ![]()
, ![]()
.
Wyznacznik, w którym jeden wiersz lub jedna kolumna składa się z samych zer, równa się zero.
Wyznacznik macierzy kwadratowej A jest równy wyznacznikowi jej macierzy przestawionej
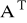
tzn.:
![]()
.
Jeżeli macierz B stopnia

z powstaje z macierzy A przez zamianę dwóch kolumn lub wierszy, to wyznacznik:
![]()
.
Jeżeli w macierzy A dwie kolumny lub dwa wiersze są jednakowe to:
![]()
Jeżeli macierz B powstaje z macierzy A przez pomnożenie wszystkich elementów danego wiersza lub kolumny przez stałą c, to:
![]()
.
Wyznacznik nie zmienia wartości, gdy do elementów danej kolumny (lub wiersza) dodać odpowiednie elementy innej kolumny (lub wiersza) pomnożone przez dowolną ustaloną stałą.
WZORY CRAMERA
Układ n równań liniowych o n niewiadomych ![]()
postaci:
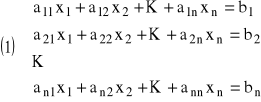
,
gdzie ![]()
, są liczbami rzeczywistymi, nazywamy układem Cramera, jeżeli:
![]()
.
Macierz ![]()
nazywamy macierzą układu (1), a detA wyznacznikiem układu (1).
Macierzą kwadratową A taką, że ![]()
nazywamy macierzą nieosobliwą.
Rozwinięciem układu (1) nazywamy każdy układ liczb ![]()
spełniający (1).
TWIERDZENIE 1 (tw. Cramera):
Układ Cramera ma dokładnie jedno rozwiązanie. Rozwiązanie to ma postać: ![]()
,
gdzie ![]()
jest macierzą, która powstaje z macierzy A przez zastąpienie k-tej kolumny przez liczby ![]()
.
UWAGA!
Jeżeli układ równań liniowych ma postać:
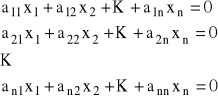
,
to układ Cramera ma tylko rozwiązanie zerowe, tzn.:
![]()
.
OGÓLNY UKŁAD RÓWNAŃ LINIOWYCH
Dana jest macierz prostokątna:
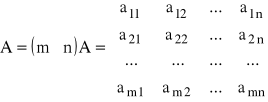
o wymiarach ![]()
.
DEFINICJA: Rzędem macierzy nazywamy najwyższy ze stopni tych jej minorów, które są różne od zera. Liczbę tą oznaczamy symbolem: rzA.
Dany jest układ m równań liniowych o n niewiadomych:
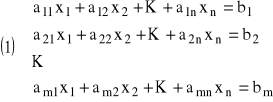
,
gdzie ![]()
, są liczbami rzeczywistymi.
Dla układu (1) budujemy dwie macierze:
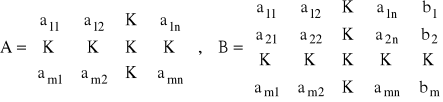
.
Rozwiązaniem układu (1) nazywamy każdy układ liczb ![]()
spełniający (1).
TWIERDZENIE 1 (Kromecker-Cepelli):
Na to, by układ (1) miał rozwiązanie należące do zbioru R, potrzeba i wystarcza, by:
![]()
.
TWIERDZENIE 2:
Na to, by układ (1) miał dokładnie jedno rozwiązanie, potrzeba i wystarcza, by:
![]()
,
n - ilość zmiennych.
Dwa układy równań liniowych nazywamy układami równoważnymi, jeżeli każde rozwiązanie jednego z nich jest rozwiązaniem drugiego i na odwrót.
Niech układ (1) posiada rozwiązanie oraz niech ![]()
. Zakładamy, że M jest minorem stopnia r macierzy A różnym od zera.
Jeżeli z układu (1) skreślimy te równania, których współczynniki nie wchodzą w skład minora M, to można wykazać, że otrzymany w ten sposób układ jest równoważny układowi (1).
Niech macierz A ze współczynników przy niewiadomych układu postaci:
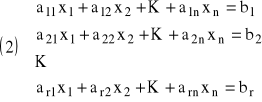
, ma rząd ![]()
.
Wówczas wszystkie rozwiązania układu (2) otrzymamy przyjmując dla (n-r) niewiadomych dowolne wartości, a pozostałe niewiadome obliczając ze wzorów Cramera.
Kilka ogólnych uwag o skrypcie.
W niektórych paragrafach 10, 13, 14 brakuje przykładów ilustrujących ważne twierdzenia i definicje - no cóż brakło czasu
Z góry przepraszamy za wszystkie gafy powstałe przy przepisywaniu wykładów, mamy nadzieję, iż będą to tylko literówki i nie spowodują żadnych błędów merytorycznych
Chcielibyśmy podziękować Łukaszowi Markowskiemu za udostępnienie wzorowo prowadzonych notatek - dzięki Luk !
Wierzymy, że wszyscy razem spotkamy się w III semestrze.
64
- rozdzielność mnożenia względem dodawania
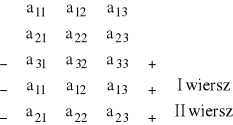
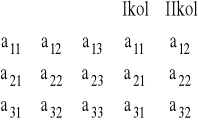
![]()
Wyszukiwarka
Podobne podstrony:
Wyklady z Matematyki czesc VI, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc VI, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc IV, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc V, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc II, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc I, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc III, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc III, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc VII do mdruku, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykład
Wyklady z Matematyki czesc IV, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
czesc odp zespol 2, Prywatne, Uczelnia, Budownictwo, II Semestr, Materiały Budowlane, materiały budo
Wyklady z matematyki II sciaga, MATMA, matematyka, Matma, Matma, Stare, I semestr
Wyklady z matematyki IV sciaga, MATMA, matematyka, Matma, Matma, Stare, I semestr
Z Wykład 15.03.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Wykład z dnia 10.05.2008, Zajęcia, II semestr 2008, Matematyka dyskretna i logika
Z Wykład 19.04.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Wykład 23.02.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Przykładowe egzaminy, Studia - Chemia kosmetyczna UŁ, I rok, II semestr, MATEMATYKA wykłady
Z Wykład 29.03.2008, Zajęcia, II semestr 2008, Matematyka dyskretna i logika
więcej podobnych podstron