§ 2. PRZESTRZEŃ LICZB ZESPOLONYCH

Definicja: Liczbami zespolonymi nazywamy uporządkowaną parę liczb rzeczywistych: a, b
. Oznaczamy je symbolem (a, b).

W zbiorze liczb zespolonych określamy w następujący sposób: dodawanie i mnożenie:

Def. Niech x = (a, b) ; y = (c, d), gdzie a, b, c, d
, wtedy:

x = y

x +y =

x

Twierdzenie 1.

Operację dodawania oraz mnożenia w postaci (*) w zbiorze liczb zespolonych są przemienne, łączne oraz mnożenie jest rozdzielne względem dodawania, tzn. : dla dowolnych liczb zespolonych x, y, z zachodzą równości:

Dla dowolnej liczby zespolonej x zachodzą równości:

Twierdzenie 2.

Dla dowolnej liczby zespolonej x istnieje dokładnie jedna liczba zespolona y, taka, że :

DOWÓD

Niech
wtedy
spełnia równanie

*Jeśli istniałoby
takie, że
to:

czyli
sprzeczność dowodzi jednoznaczności określana
.

*Jeżeli
to
. Zatem różnicę liczb rzeczywistych
przyjmując:

Def. Niech
. Wartością bezwzględną lub modułem liczby zespolonej x nieujemną liczbę rzeczywistą

Twierdzenie 2

Niech x, y, z będą dowolnymi liczbami zespolonymi, wtedy:

1. jeżeli
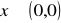
   , to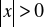
   ,
   

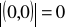
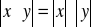
2. 
   

3. jeżeli
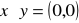
   , to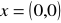
   , lub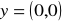
   , lub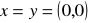
   

jeżeli
oraz
,

DOWÓD b)

Niech

wtedy:

Twierdzenie 4

Dla dowolnej liczby zespolonej
istnieje dokładnie jedna liczba zespolona y, taka, że:

Piszemy wtedy

DOWÓD

Jednoznaczność wynika z twierdzenia 3d)

Niech
wtedy y określamy następująco:

gdyż:

Jeżeli liczba zespolona
, to dla dowolnej liczby zespolonej istnieje dokładnie jedna liczba zespolona z taka, że
Oznaczamy ją symbolem:

Ponieważ dla dowolnych liczb rzeczywistych a, b zachodzą równości:

, gdzie

więc liczby zespolone postaci
można utożsamić z liczbami rzeczywistymi: a.

Zatem zbiór liczb rzeczywistych
można traktować jako podzbiór właściwy zbioru liczb zespolonych.

Def.

Jednostką urojoną nazywamy liczbę zespoloną postaci:

zauważmy, że:

czyli:

PRZYKŁAD

Rozwiązywanie równania:

(*)
gdzie
,

Rozwiązanie: Pierwiastkami równania (*) są liczby zespolone

Jeżeli a, b są liczbami rzeczywistymi to liczba zespolona

gdyż

Jeżeli liczba zespolona ma postać

to "a" nazywamy częścią rzeczywistą liczby, a "b" częścią urojoną liczby "z"

Re z = a ("realis")

Im z = b ("imaginalis")

Twierdzenie 5

Jeżeli x, y są liczbami zespolonymi to zachodzi nierówność:

Def.

Liczbą sprzężoną do liczby zespolonej

nazywamy liczbę

Twierdzenie 6

Jeżeli x, y nazywamy liczbami zespolonymi, to:

1. 
   

2. 
   

3. 
   

4. 
   

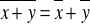
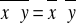
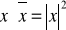
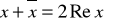
5. jeżeli
   , to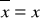
   

DOWÓD b)

Niech
,

Wtedy:

czyli

UWAGA !!!

Twierdzenie 7

Jeżeli a­­₁,...,a_n, b₁,....,b_n są liczbami zespolonymi to zachodzi nierówność Schwarza:

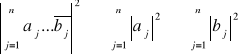
Liczbie zespolonej
odpowiada wzajemnie jednoznacznie na płaszczyźnie prostokątnego układu współrzędnych OXY punkt P=(a,b). Płaszczyznę C, Której punktom zostały przyporządkowane dowolne liczby zespolone
;
nazywamy płaszczyzną liczbową.

Punktom osi OX odpowiadają liczby zespolone postaci

, tzn. liczby rzeczywiste.

Punktom osi OY odpowiadają liczby zespolone postaci
, tzn. liczby urojone.

Płaszczyzna liczbowa C

Def.Argumentem liczby zespolonej

nazywamy liczbę rzeczywistą
określoną równościami:

oraz

Piszemy:

Każda liczba zespolona
posiada nieskończenie wiele argumentów. Jeżeli
,
to każdy inny argument liczby "z" ma postać
;

Argument liczby zespolonej
spełniającej nierówności:

nazywamy argumentem głównym liczby "z". Oznaczamy symbolem:

Arg z

Argumentem liczby zespolonej
nazywamy każdą liczbę rzeczywistą.

Jeżeli
to ze względu na to, że
,

Możemy napisać

czyli

Jest to postać trygonometryczna liczby

Na odwrót, jeżeli
gdzie
, to
,

Dwie liczby zespolone, różne od zera są równe wtedy i tylko wtedy, gdy są równe ich moduły, a argumenty różnią się o całkowitą wielokrotność 2*.

Jeżeli liczba zespolona:

czyli

to

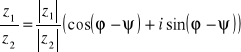
Zatem:

(*)

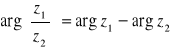
Powyższe równości rozumiemy następująco:

Dla dowolnych argumentów
,
istnieje argument iloczynu
oraz argument ilorazu
takie, że zachodzą równości (*).

Twierdzenie 8

Dla każdej liczby rzeczywistej
zachodzi równość:

1. 
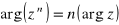
   przy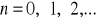
   

DOWÓD

1. dla
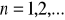
   równość (1) dowodzimy stosując indukcję zupełną

2. Dla
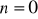
   mamy:

,

Ponieważ dla dowolnego
istnieje
(przy k=0) więc zachodzi równość (1), gdyż dla dowolnego

, gdzie
dowolny argument "z".

c) Dla
podstawiamy
przy

wtedy

Biorąc arg1=0 otrzymujemy:

dla

Wniosek

Zachodzi wzór de Moivre'a

dla

DOWÓD

Dla
mamy:

zatem dla
otrzymujemy:

stąd

czyli

Z drugiej strony mamy:

czyli

dla

Dla

ta potęga liczby zespolonej

ma postać:

Każdą liczbę zespoloną "w" spełniającą równanie

gdzie
nazywamy pierwiastkiem n-tego stopnia lub n-tym pierwiastkiem liczby zespolonej "z", oznaczamy symbolem:

Twierdzenie 9

Jeżeli
to istnieje dokładni n różnych pierwiastków w_k , k=0,1,2,...,n-1, gdzie
oznacza pierwiastek arytmetyczny tj. liczbę nieujemną, a n-ta potęga równa się

Płaszczyzna rozszerzona

Niech będzie dana płaszczyzna czysta
zbiór liczb zespolonych, wyznaczona przez układ prostokątny OXY

Sfera S o dowolnym promieniu dodatnim
jest styczna do płaszczyzny C w punkcie (0,0). Prosta prostopadła do płaszczyzny C w punkcie (0,0) przecina sferę S w punkcie

Przyporządkowujemy każdemu punktowi
punkt
,
przy czym z' jest punktem przecięcia prostej przechodzącej przez z oraz N ze sferą S. Otrzymaliśmy odwzorowanie płaszczyzny C na sferę S, ale bez punktu N. Jest to tzw. rzut stereograficzny na sferę.

Odwzorowanie odwrotne do punktu stereograficznego przyporządkowuje punktom sfery S bez punktu N punkty płaszczyzny C.

Uzupełnimy płaszczyznę C nowym punktem, któremu przy rzucie stereograficznym odpowiada punkt N sfery S. Ten nowy punkt nazywamy punktem nieskończoności i oznaczamy symbolem:

∞

Prosta C uzupełniona punktem w nieskończoności nazywa się płaszczyzną domkniętą lub rozszerzoną. Oznaczmy ją przez:

Między skończonymi liczbami zespolonymi a punktem nieskończoności definiujemy następujące działania:

gdy

gdy

dla

W zbiorze liczb zespolonych C określamy następująco metrykę:

Dla dowolnych

Funkcjonał
spełnia akcjometry metryki, gdy:

1. 
   

2. 
   

3. 
   

Jeżeli

To

Między skończonymi liczbami zespolonymi a punktem nieskończoności definiujemy następujące działania:

gdy

gdy

dla

W zbiorze liczb zespolonych C określamy następująco metrykę:

Dla dowolnych

Funkcjonał
spełnia akcjometry metryki, gdy:

4. 
   

5. 
   

6. 
   

Jeżeli

To

ROZDZIAŁ III

Rachunek różniczkowy i całkowy funkcji rzeczywistych jednej zmiennej

§ 1. CIĄG LICZB RZECZYWISTYCH

Będziemy sprawdzać ciągi o wyrazach rzeczywistych.

PRZYKŁAD

1. Ciąg arytmetyczny
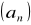
   gdzie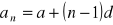
   ,
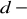
   różnica,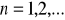
   

2. Ciąg geometryczny
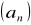
   , gdzie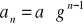
   ,
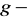
   iloraz,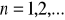
   

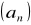
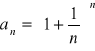
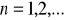
3. 
   ,
   ,
   

Def.

Mówimy, że
jest granicą ciągów
gdzie

jeżeli dla dowolnie małej

,

tzn. dla dowolnie małej liczby dodatniej *>0 istnieje taka liczba dodatnia N>0, że dla każdej liczby naturalnej n>N zachodzi nierówność

Piszemy wtedy:

lub

przy

Interpretacja geometryczna granicy ciągu

,
,

Zatem wyrazy
o wskaźnikach
należą do otoczenia liczby g

Def.

Mówimy, że ciąg
ma granicę
,
jeżeli:

M - dowolnie duże

Piszemy wtedy:

Ciąg posiadający granicę skończoną nazywamy zbieżnym.

Ciąg, który nie jest zbieżny, czyli ma granicę nieskończoną lub nie posiada granicy skończonej, ani nieskończonej nazywamy rozbieżnym.

Granicą właściwą nazywamy granicę skończoną. Natomiast:
to granice niewłaściwe.

Ciąg
nazywamy ograniczonym jeżeli istnieje taka stała dodatnia M

WŁASNOŚCI CIĄGÓW ZBIEŻNYCH

1. Jeżeli ciąg
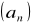
   jest zbieżny, to jest ograniczony.

DOWÓD

Zakładamy, że
to znaczy

czyli dla
przy czym N można obrać równe liczbie rzeczywistej, mamy:

Zatem oznaczając

otrzymujemy

zatem ciąg
jest ograniczony.

Na odwrót nie każdy ciąg ograniczony jest zbieżny.

Np. Ciąg
jest ograniczony, ale nie posiada granicy skończonej ani

nieskończonej.

2. Ciąg
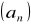
   posiada co najmniej jedną granicę.

DOWÓD

Przypuśćmy, że
oraz
, przy czym
. Istnieje liczba rzeczywista r taka, że
. Biorąc
otrzymujemy

dla

oraz

dla

stąd dla
mamy

czyli

oraz

sprzeczność.

3. Jeżeli ciągi
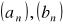
   są zbieżne odpowiednio do granic a, b to suma, iloczyn i różnica tych ciągów są także zbieżne oraz:

Jeżeli ponadto
dla

to

DOWÓD

Ponieważ
,
więc

oraz

gdzie
jest stałą tak dobraną, że

,
,

Stąd dla
mamy:

czyli

Ćwiczenie

Wykazać, że

Z twierdzenia o granicy iloczynu wynika wniosek:

Jeżeli ciąg
jest zbieżny, to

gdzie c - stała

PRZYKŁAD

Znaleźć granicę ciągu
gdzie

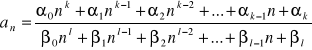
gdzie

k, l - ustalone liczby naturalne,

Rozwiązanie

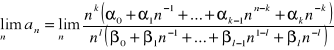
Rozważmy następujące możliwe przypadki:

1. k = l

2. k > l

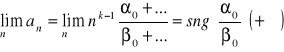
3. k < l

Twierdzenie 1 (Twierdzenie o trzech ciągach)

Jeżeli ciągi
są zbieżne, przy czym
oraz

to

DOWÓD

Ponieważ
więc

oraz

Zatem dla
zachodzą nierówności:

czyli

a więc

PRZYKŁAD

Znaleźć

przy
wyrazy ciągu prowadzą do wyrażenia nieoznaczonego typu

Zachodzą następujące oszacowania:

Z twierdzenia o trzech ciągach wynika, że granica równa się 5.

4. ciąg
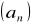
   jest zbieżny do granicy g wtedy i t6ylko wtedy, gdy każde otoczenie punktu g zawiera prawie wszystkie wyrazy ciągu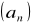
   tzn. wszystkie wyrazy z wyjątkiem w najwyżej skończonej ilości.

WŁASNOŚCI CIĄGÓW MAJĄCYCH GRANICE NIEWŁAŚCIWE

Jeżeli ciąg
posiada granicę niewłaściwą, to ciąg ten jest nieograniczony. Twierdzenie odwrotne nie jest prawdziwe Np. ciąg
, gdzie
jest nieograniczony
oraz nie posiada granicy ani właściwej (skończonej), ani niewłaściwej.

Dla ciągów mających granice niewłaściwe - ∞ lub +∞ zachodzi twierdzenie o jednoznaczności.

Przy formułowaniu twierdzeń o działaniach arytmetycznych, dla granic niewłaściwych należy wykluczyć wyrażenia nieoznaczone.

Np.Jeżeli ciągi
posiada granicę oraz nie zachodzi

to ciągi
mają granicę oraz

1. Jeżeli ciąg
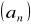
   ma granicę niewłaściwą oraz
   dla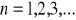
   

to:

DOWÓD

Jeżeli
to dla każdego
istnieje
taki, że

dla

Jeżeli
to dla każdego
istnieje
taki, że

dla

w każdym przypadku mamy:

dla
gdzie

czyli dla

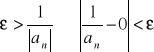
więc

2. Jeżeli
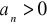
   dla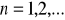
   oraz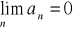
   , to

a jeżeli
dla
oraz
, to

DOWÓD

Jeżeli
oraz
, to

oznacza to, że:

dla

czyli

Twierdzenie o trzech ciągach przenosi się na przykłady granic nieskończonych.

Badając granice: sumy, różnicy, iloczynu lub ilorazu ciągów mających granice:
otrzymujemy tzw. wyrażenia nieoznaczone:

,
,
,
,
,

W tych przypadkach szukając granicy należy uwzględnić własności wyrazów ciągu: przez odpowiednie przekształcenia usunąć nieoznaczoność.

35

---