Para uporządkowana

Bardzo często będziemy chcieli mieć do czynienia ze zbiorem, który niesie w sobie informację o dwóch innych zbiorach, informację tak trafnie zakodowaną,
aby można było odzyskać z niej każdą z jego składowych. Do tego celu wprowadzimy zbiór nazywany parą uporządkowaną dwóch innych zbiorów.

D

EFINICJA

1.1.

Niech oraz

będą zbiorami. Przez parę uporządkowaną

rozumiemy zbiór

Parę uporządkowaną można zdefiniować inaczej na wiele sposobów. Chodzi jednak o to, aby ze zbioru, który jest parą, można było odzyskać jednoznacznie
każdą z jego składowych. Tak więc moglibyśmy zaakceptować każdą

inn

ą inną definicję pod warunkiem, że będzie spełnione następujące twierdzenie:

T

WIERDZENIE

1.2.

Dla dowolnych zbiorów

zachodzi:

D

OWÓD

Dowód przeprowadzimy tylko ze

strony

lewej do prawej, bo w odwrotnym kierunku jest to fakt oczywisty. Niech zatem dwie pary

i

będą równe.

Ponieważ

, więc

. Mamy zatem

lub

. W pierwszym przypadku

,

ale

w drugim również jest

tak, mamy bowiem, że

. Pierwszą część twierdzenia mamy za sobą, bo już wiemy, że pierwsze współrzędne równych par są równe.

Następnie przeprowadzamy dowód przez przypadki. Jeżeli jest tak, że

, to

. Zatem

, co daje,

że

, a zatem

. W przeciwnym przypadku, gdy

mamy, że

. Daje to dwie

możliwoś

ci

albo

, co nie może mieć miejsca, bo mielibyśmy, że

albo zaś

. To drugie prowadzi do naszej

tezy

.

Ć

WICZENIE

1.3

Dla każdej pary

udowodnij, że

R

OZWIĄZANIE

Rozważymy dwa przypadki.

1.

Jeśli

, to

i wtedy

.

2.

Jeśli

, to

a więc

skąd otrzymujemy

Ć

WICZENIE

1.4

Udowodnij, że dla dowolnej pary uporządkowanej zbiór

jest pusty, gdy współrzędne par są różne, a w przeciwnym przypadku jest zbiorem jednoelementowym zawierającym współrzędną pary .

R

OZWIĄZANIE

Jeśli jest parą, to istnieją zbiory

takie, że

.

1. Przypuśćmy, że

. Wtedy

i

. Ponieważ

to

, a wtedy

gdyż przecinany zbiór zawiera elementy rozłączne

. Wobec tego również

2. W przypadku, gdy

, otrzymujemy

, a więc

i wtedy

skąd otrzymujemy

Ć

WICZENIE

1.5

Poka

ż, że z każdej pary można otrzymać jej drugą współrzędną, posługując się jedynie parą , mnogościowymi operacjami

oraz

stałą .
W

SKAZÓWKA

1.

Rozważ najpierw pary różnych elementów.

2.

Wykorzystaj zbiór z Ćwiczenia 1.4 (patrz

ćwiczenie 1.4

) .

R

OZWIĄZANIE

Rozważmy najpierw przypadek, gdy para ma różne elementy. Zobaczymy, że dla każdej takiej pary

, mamy

Ponieważ

, to

i wtedy

Zobaczmy teraz, jak proponowany wzór działa na parach o równych współrzędnych. Jeśli

, to

i wtedy

Musimy więc jeszcze trochę popracować. Wykorzystajmy ćwiczenie 1.4 (patrz

ćwiczenie 1.4

), niech nowy wzór będzie postaci

Dla par o różnych elementach dodana część wzoru jest zbiorem pustym, więc ta sytuacja jest analogiczna do 1.1, skąd otrzymujemy, że tak zdefiniowany
zbiór jest równy .

Dla par o równych elementach pierwsza część zbioru jest zbiorem pustym. W ćwiczeniu 1.4 (patrz

ćwiczenie 1.4

) pokazaliśmy, że w takim przypadku

mamy

, jeśli jest współrzędną pary . Wobec tego

Iloczyn kartezjański

Zanim wprowadzimy definicję zbioru wszystkich par uporządkowanych elementów dwóch zbiorów (zwanego dalej iloczynem kartezjańskim), należy nam się

krótkie wprowadzenie. Otóż niech

oraz

. Łatwo zauważyć, że zarówno

, jak i

są podzbiorami

.

Zatem

oraz

. Więc

, co daje,

że

.

Istnienie i konstrukcja iloczynu kartezjańskiego zostało dokładnie omówione w dodatkowym rozdziale

"Iloczyn kartezjański i aksjomat wyróżniania"

.

Proponuję przestudiowanie dodatkowego rozdziału dopiero po zapoznaniu się z rozdziałami wcześniejszymi, pomimo braku precyzji w następnej definicji.

D

EFINICJA

2.1.

Niech

będą zbiorami. Iloczynem kartezjańskim (produktem)

nazywamy zbiór

Będziemy używać specjalnej notacji

na zbiór

.

Ć

WICZENIE

2.2

Pokaż następujące elementarne własności iloczynu kartezjańskiego:

R

OZWIĄZANIE

[

SCHOWAJ

]

Z definicji iloczynu kartezjańskiego oraz twierdzenia 1.2 (patrz

twierdzenie 1.2.

) w sposób oczywisty wynika

następujący fakt, który wykorzystamy w dowodach. Dla dowolnych zbiorów

zachodzi

1.

Ponieważ

jest zawsze fałszem, to powyższy zbiór jest pusty.

2. Ponieważ obydwa zbiory są zbiorami par, więc wykażemy, że dowolna para należy do jednego

wtedy i tylko wtedy, gdy należy do drugiego. Weźmy dowolną parę

, wtedy

3. A

nalogicznie do poprzedniego punktu, weźmy dowolną parę

, wtedy

4. Analogicznie do poprzednich punktów, weźmy dowolną parę

, wtedy

Ć

WICZENIE

2.3

Produkt kartezjań

ski

jest monotoniczny ze względu na każdą współrzędną osobno, to znaczy:

R

OZWIĄZANIE

[

SCHOWAJ

]

1.

Niech

będą dowolnymi zbiorami takimi, że

. Wtedy dla dowolnej pary

mamy

Stąd

.

1.

Dla dowolnych zbiorów

mamy

. Z poprzedniego

ćwiczenia otrzymujemy

(Metoda z poprzedniego punktu podziała równie dobrze.)

Ć

WICZENIE

2.4

Sprawdź, czy dla dowolnych zbiorów

, prawdziwa jest następująca implikacja:

R

OZWIĄZANIE

[

SCHOWAJ

]

Nie. Na przykład, gdy

, to dla dowolnych zbiorów

mamy

Biorąc różne zbiory

, otrzymamy kon

trprzykład dla badanej implikacji.

Relacje

D

EFINICJA

3.1.

Relacją nazywamy każdy podzbiór iloczynu

.

[

Edytuj

]

Operacje na relacjach:

D

EFINICJA

3.2.

Niech

oraz

.

Ć

WICZENIE

3.3

Niech relacja

oraz

. Pokazać elementarne własności operacji na relacjach:

R

OZWIĄZANIE

[

SCHOWAJ

]

1.

2.

3.

4.

5. Dowód

jest analogiczny do poprzedniego.

6.

Ć

WICZENIE

3.4

Niech relacja

oraz

. Pokaż własności:

R

OZWIĄZANIE

[

SCHOWAJ

]

W poniższych punktach (1-4) pokażemy, że dowolna para należy do zbioru po lewej

stronie odpowiedniej równości wtedy i tylko wtedy, gdy należy do prawej. W punkcie 5, pokazujemy jedynie implikację w prawą stronę, gdyż mamy udowodnić
inkluzję.

1.

2. Dowód drugiej równości jest analogiczny do dowodu pierwszej, wystarczy użyć

w miejsce

oraz

w miejsce

.

3.

4.

5.

Ć

WICZENIE

3.5

Podaj przykład relacji, dla których poniższa równość nie jest prawdziwa.

R

OZWIĄZANIE

[

SCHOWAJ

]

Niech

, wtedy

1.

, więc

.

2.

i

, a więc

Ć

WICZENIE

3.6

Udowodnij, że zbiór

jest relacją wtedy i tylko wtedy, gdy

R

OZWIĄZANIE

[

SCHOWAJ

]

Pokażemy najpierw, że dla każdej relacji

mamy

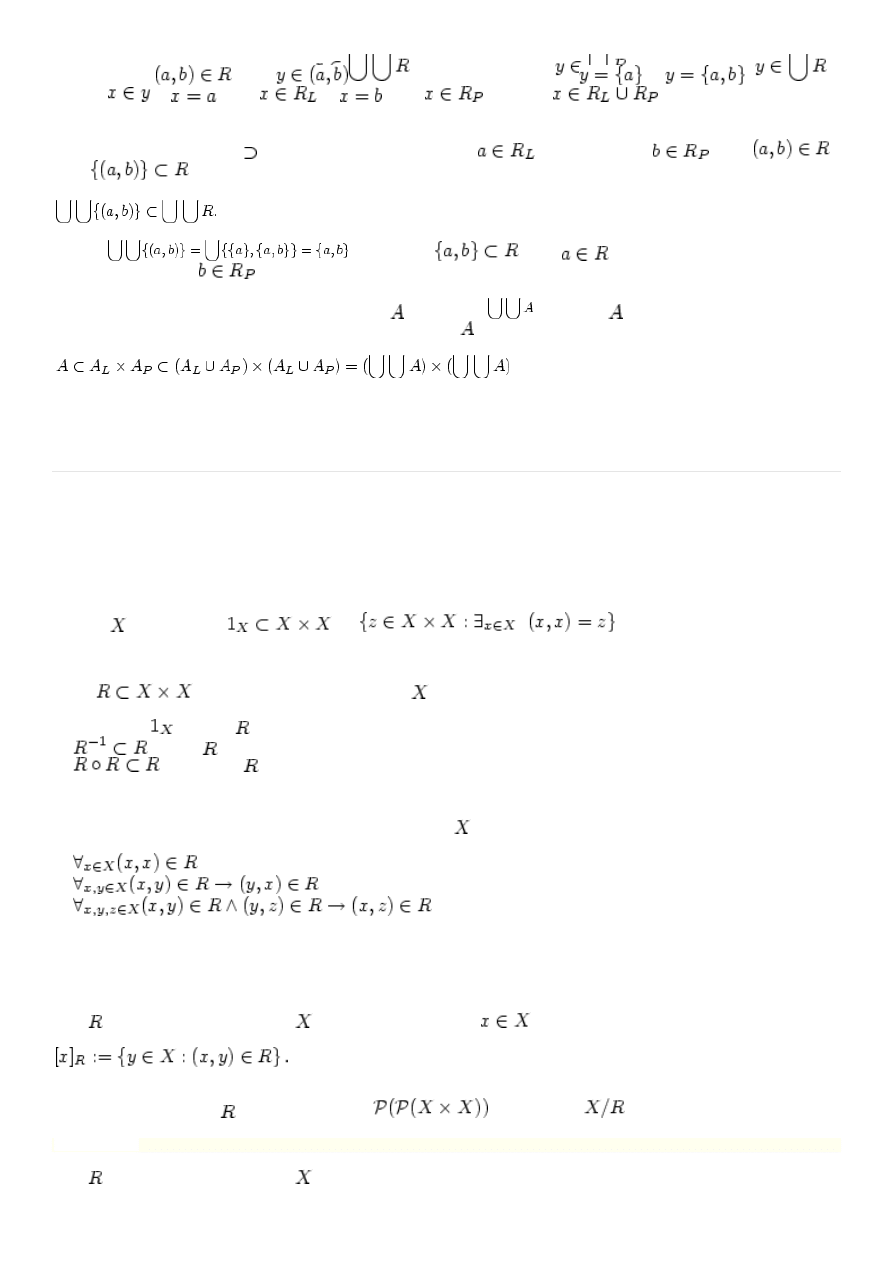
Zaczniemy od inkluzji

. Weźmy dowolny element

, wtedy musi istnieć element

taki, że

. Skoro

,

to musi istnieć para

taka, że

. Wobec tego z definicji pary uporządkowanej

lub

.

Poniew

aż

, to

i wtedy

lub

i wtedy

. Wobec tego

.

Pokażemy teraz prawdziwość inkluzji

w równaniu 3.12. Weźmy dowolny element

wtedy istnieje element

taki, że

,

a więc

. Stąd otrzymujemy

Ponieważ

, to otrzymujemy

, a więc

. Analogiczne rozumow

anie można

przeprowadzić dla elementu

. Zakończyliśmy więc dowód równości 3.12.

W temacie ćwiczenia implikacja w lewą stronę jest oczywista. Jeśli

jest zbiorem, to

jest zbiorem i

jest podzbiorem iloczynu kartezjańskiego

dwóch zbiorów, więc musi być relacją. Dla implikacji w prawą stronę załóżmy, że

jest relacją, wtedy

Relacje równoważności

W tym podrozdziale poznamy ważną klasę (zbiór) relacji zwaną klasą relacji równoważności(w innych podręcznikach mogą się państwo spotkać z nazwą
r

elacja abstrakcji). Relacje takie będą służyły do definiowania pojęć abstrakcyjnych, o czym przekonamy się w wielu miejscach tego i innych wykładów.

Bardzo dobrym ćwiczeniem pokazującym abstrakcyjne metody definiowania pojęć będzie

wykład 8

, w którym zaprzęgniemy relacje abstrakcji do definiowania

liczb.

Rozpoczynamy rozdział od koniecznej definicji.

D

EFINICJA

4.1.

Dla zbioru

definiujemy relację

jako

.

D

EFINICJA

4.2.

Relację

nazywamy relacją równoważnością o polu

, jeżeli:



zawiera relacje

(zwrotność

),



(symetria

),



(przechodniość

).

Ć

WICZENIE

4.3

Pokazać, że definicje zwrotności, symetryczności i przechodniości relacji o polu

są odpowiednio równoważne następującym własnościom:



,



,



.

R

OZWIĄZANIE

[

SCHOWAJ

]

Ćwiczenie jest elementarne.

D

EFINICJA

4.4.

Niech

będzie relacją równoważności o polu

. Klasą równoważności elementu

jest zbiór

D

EFINICJA

4.5.

Zbiór klas równoważności relacji

będący elementem zbioru

oznaczamy przez

.

T

WIERDZENIE

4.6.

Niech

będzie relacją równoważności o polu

. Następujące warunki są równoważne:

1.

,

2.

,

3.

.

D

OWÓD

Pokażemy, że

. Niech wspólny element dwóch klas

oraz

nazywa się . Ze względu na pełną symetrię tezy wystarczy pokazać,

że

. Niech zatem

. Mamy więc

. Z założenia jest również

oraz

. Z symetrii

otrzymujemy

. Zatem

i

i

. Natychmiast z przechodniości otrzymujemy, że

.

Pokażemy, że

. Ze zwrotności mamy, że

, co z założenia

daje

, a to tłumaczy się na

.

Pokażemy, że

. Wystarczy pokazać, że wspólnym elementem klas

oraz

jest

. Dla pierwszej z nich wynika to z założenia

,

a dla drugiej ze zwrotności

.

W nas

tępnym twierdzeniu zobaczymy, jak rodzina relacji równoważności jest odporna na przecinanie. Pokażemy mianowicie, że przecięcie dowolnej liczby

relacji równoważności jest nadal relacją równoważności.

T

WIERDZENIE

4.7.

Niech

będzie pewną rodziną (zbiorem) relacji równoważności o tym samym polu

. Mamy że:

1.

jest relacją równoważności o polu

,

2.

.

D

OWÓD

Zwrotność

jest oczywista, ponieważ

zawiera się w każdej relacji rodziny . Symetria. Weźmy

. Dla każdej

relacji

jest

. Z symetrii każdej

jest więc

, co daje

. Przechodniość.

Niech

oraz

. Dla każdej relacji

jest więc

i

. Z przechodniości każdej

relacji

mamy, że

, co daje

.

Niech

. Mamy zatem, że

, co daje

dla każdej relacji

. To zaś daje, że

dla

każdej

, co jest równoważne z

.

W szczególności przecięcie wszystkich relacji równoważności o polu

daje

. Jest ona najsilniejszą relacją równoważności. Najsłabszą jest

.

Rozkłady zbiorów

D

EFINICJA

4.8.

Niech

. Rodzinę

nazywamy rozkładem zbioru

, gdy:

1.

,

2.

,

3.

.

L

EMAT

4.9.

Dla

relacji równoważności

o polu

zbiór

jest rozkładem

.

D

OWÓD

Każda klasa jest niepusta, bo zawiera element, który ją wyznacza.

, bo każda klasa jest podzbiorem

. Odwrotnie

każdy

.

Dwie klasy, gdy są różne, muszą być rozłączne co udowodniliśmy w twierdzeniu 4.6 (patrz

twierdzenie 4.6.

).

D

EFINICJA

4.10.

Niech

będzie rozkładem zbioru

. Definiujemy relacje

następująco:

wtw

L

EMAT

4.11.

Dla rozkładu

relacja

jest:

1.

równoważnością,

2.

D

OWÓD

Relacja

jest zwrotna, każdy bowiem

musi leżeć w pewnym zbiorze

rozkładu . Symetria

nie wymaga dowodu.

Przechodniość

. Niech

i

. Istnieją zatem dwa zbiory

i

rozkładu takie, że

oraz

.

Przeci

ęcie

i

jest więc niepuste, zatem

, co daje tezę

.

Inkluzja w prawo

. Niech

. Klasa

jest zatem wyznaczona przez pewien element

taki, że

. Niech

będzie zbiorem rozkładu , do którego należy . Łatwo wykazać, że

. Inkluzja w lewo

. Niech

.

jest niepusty, więc

istnieje

. Klasa

.

Ć

WICZENIE

4.12

Niech

będzie niepustym zbiorem oraz niech

. Zdefiniujemy relację

następująco: dla dowolnych

zbiorów

mamy

(

oznacza różnicę symetryczną zbiorów, czyli

). Udowodnij, że relacja

jest rel

acją równoważności.

W

SKAZÓWKA

[

SCHOWAJ

]

Najtrudniej jest pokazać przechodniość. Udowodnij, że

. Dobrym punktem wyjścia jest naszkicowanie wszystkich

przecięć zbiorów

.

R

OZWIĄZANIE

[

SCHOWAJ

]

Pokażemy po kolei zwrotność, przechodniość i symetryczność.

1.

Dla każdego

mamy

, a więc relacja

jest zwrotna.

2.

Ponieważ dla dowolnych zbiorów

, to

wtedy i tylko wtedy, gdy

. Wobec tego

relacja

jest symetryczna.

3.

Weźmy zbiory

, takie

że

. Wtedy

Ponieważ z definicji relacji

mamy

oraz

, to ich suma też jest podzbiorem

i w konsekwencji

również

. Oznacza to, że

, a więc relacja

jest przechodnia.

Ć

WICZENIE

4.13

Udowodnij, że dla relacji równoważności

na zbiorze

, relacja

jest relacją równoważności wtedy i tylko wtedy, gdy

Podaj przykłady relacji równoważności

takich, że

jest relacją równoważności oraz

i

.

W

SKAZÓWKA

[

SCHOWAJ

]

Przyjrzyj się dokładnie rodzinie zbiorów

.

R

OZWI

ĄZANIE

[

SCHOWAJ

]

Zaczniemy od pokazania, że formuła 4.1 implikuje, iż relacja

jest relacją równoważności. Pokażemy, że

rodzina

tworzy rozkład zbioru

. Oczywiście, dla każdego elementu

mamy

oraz

. Wystarczy

więc pokazać, że zbiory w rodzinie

są rozłączne. Weźmy dowolne dwa elementy rodziny

i przypuśćmy, że

ich przecięcie jest niepuste. Niech to będą zbiory odpowiadające elementom

, a więc

oraz

. Skoro te zbiory

mają niepuste przecięcie, to istnieje

.

Ponieważ

, to

,

co jest równoważne

. Podobne rozumowanie dla

daje

. Wobec czego

dostajemy

, ponieważ jednak zgodnie z formułą 4.1 jedna z tych klas jest nadzbiorem drugiej, to

lub

. W przypadku, gdy

, dostajemy również z 4.1.

oraz

, wobec

czego otrzymujemy

. Drugi przypadek jest analogiczny. Wobec czego rodzina

jest rozkładem

zbioru

. Wystarczy teraz przekonać się, że

wtedy i tylko wtedy, gdy

, aby udowodnić, że jest to rzeczywiście

rozkład generowany przez relację

. Weźmy dowolne

, wtedy

Pokażemy teraz, że jeśli

jest relacją równoważności, to musi być spełniona formuła 4.1. Dla dowodu niewprost przypuśćmy, że nie jest spełniona.

Oznacza to, że istnieje element

, dla którego

oraz

. Wobec tego istnieje

oraz

. Oznacza to, że

oraz

. Skoro

jest relacją równoważności,

to

. Przypuśćmy, że

. Wtedy

, wobec czego

, co jest sprzeczne z tym,

że

, ponieważ relacja

jest symetryczna. Analogiczną sprzeczność otrzymujemy dla

. Obie możliwości prowadzą do

sprzeczności, a więc formuła 4.1 musi być spełniona.

Na koniec podajemy przykład relacji równoważności, równoważności

takich, że

jest relacją równoważności oraz

i

.

Polem relacji będzie zbiór

. Relacje

określimy poprzez wyznaczane przez nie rozkłady odpowiednio

:

Łatwo sprawdzić, że

i

, gdyż

oraz

. Z rozkładów

w prosty sposób wynika, że formuła

4.1 jest prawdziwa dla tych relacji, wobec czego

jest relacją równoważności. Wyznaczany przez nią rozkład to

.

Domykanie relacji

W praktyce matematycznej często potrzebne jest rozważanie domknięć relacji ze względu na wiele przeróżnych własności. W podrozdziale tym dokonamy
charakteryzacji domknięć. Pokażemy między innymi, kiedy takie domykanie jest możliwe.

D

EFINICJA

4.14.

Niech

będzie rodziną relacji o polu

, czyli niech

. Rodzina

jest zamknięta na przecięcia, gdy:

1.

2.

jeżeli

to

Poniżej podamy definicję domknięcia relacji w pewnej klasie (zbiorze) relacji. Definiujemy intuicyjnie najmniejszą relację zawierającą daną należącą do klasy.

D

EFINICJA

4.15.

Relacja

jest domknięciem relacji

w klasie (zbiorze) relacji

gdy:

1.

2.

3.

dla każdej relacji

jeżeli

oraz

to

L

EMAT

4.16.

Domknięcie relacji (w dowolnej klasie), jeżeli istnieje, to jest jedyne.

D

OWÓD

Gdyby istniały dwa domknięcia pewnej relacji, to ze względu na warunek

wzajemnie by się zawierały.

T

WIERDZENIE

4.17.

Następujące warunki są równoważne:

1.

Klasa relacji

jest domknięta na przecięcia.

2.

Każda relacja ma domknięcie w klasie relacji

.

D

OWÓD

. Niech

będzie relacją. Utwórzmy zbiór relacji

jako

. Takie

nie jest puste, bowiem

relacja totalna

należy do

. Pokażmy, że

jest domknięciem

w

. Istotnie

. Z założenia mamy też

.

Minimalność

stwierdzamy przez: niech

takie że

. Takie

musi leżeć w zbiorze

, jest więc

.

. Po pierwsze

leży w zbiorze

, bo wystarczy domknąć

. Niech

będzie niepustym podzbiorem

. Niech

będzie

domknięciem

w

. Wiemy, że dla dowolnej relacji

, o ile

i

to

. Połóżmy za

dowolny element z

.

Założenia implikacji pozostają automatycznie spełnione, jest więc tak, że

dla dowolnej

wyjętej z

. W takim razie

.

Ponieważ mamy też

, bo

było domknięciem, jest więc

, a to oznacza, że

.

Ć

WICZENIE

4.18

Pokazać jak wyglądają domknięcia w klasie relacji, zwrotnych, symetrycznych i przechodnich.

Pokaz

ać, stosując twierdzenie 4.17 (patrz

twierdzenie 4.17.

), że nie istnieje domknięcie spójne ani antysymetryczne. (Relacja

jest spójna,

gdy

. Relacja

jest antysymetryczna, gdy z faktu, że

oraz

, da się pokazać,

że

).

R

OZWIĄZANIE

[

SCHOWAJ

]

1. Pokażemy, że dla każdej relacji

jej domknięcie w klasie relacji zwrotnych na

to

. Pokażemy po kolei, że spełnia warunki

domknięcia:

(a)

(b)

, a więc jest zwrotna,

(c) weźmy dowolną zwrotną relację

. Ponieważ

jest zwrotna to

, a więc

.

2. Pokażemy, że dla każdej relacji

jej domknięcie w klasie relacji symetrycznych na

to

. Pokażemy po kolei, że spełnia

warunki domknięcia:

(a)

(b)

, a więc jest symetryczna ,

(c) weźmy dowolną symetryczną relację

. Ponieważ

jest symetryczna to

. Skoro

to

.

Ponieważ

, to

.

3 Posługując się intuicyjnym pojęciem liczb naturalnych, przedstawimy szkic konstrukcji przechodniego domknięcia, pomimo że konstrukcja ta wyprzedza

prezentowany mate

riał. Dla dowolnej liczby

przez

będziemy oznaczać

-

krotne złożenie relacji

z sobą (czyli

oraz

dla

). Zdefiniujmy rodzinę

jako zbiór wszystkich skończonych wielokrotnych złożeń relacji

z sobą,

czyli

. Do formalnego zdefiniowania rodziny

p

otrzebne są pojęcia liczb naturalnych,

funkcji oraz definiowania przez indukcje, które zostaną przedstawione w następnych rozdziałach. Pokażemy teraz, że domknięcie relacji

w klasie relacji

przechodnich na

to relacja

. Pokażemy po kolei, że spełnia warunki domknięcia:

(a)

(b) Aby pokazać, że relacja

jest przechodnia, weźmy dowolne dwie pary

. Wtedy muszą istnieć

liczby

takie, że

oraz

. Wobec tego

. Z łączności składania relacji

wynika, że

. Wobec tego

.

(c) Weźmy dowolną przechodnią relację

taką, że

, pokażemy indukcyjnie, że dla każdego

mamy

.

i. Baza indukcji. Dla

mamy

, a więc z założenia

.

ii. Krok indukcyjny. Weźmy dowolne

i przypuśćmy, że dla każdego

zachodzi

. Weźmy

dowolną parę

. Ponieważ

, to

. Oznacza to, że istnieje element

taki,

że

oraz

. Z założenia indukcyjnego wynika, że

oraz

. Ponieważ

jest

przechodnia to

. Wobec dowolności wyboru pary

otrzymujemy

.

Skoro dla każdego

mamy

, to również

.

Pokażemy teraz, że istnieje zbiór

taki, że klasa relacji spójnych na zbiorze

i

klasa relacji symetrycznych na zbiorze

nie są domknięte na przecięcia. W obliczu Twierdzenia 4.17 (patrz

Twierdzenie 4.17.

) będzie to oznaczało, że nie

wszystkie relacje mają domknięcia w tych klasach. Niech

.

1.

Relacje

są spójne na

, a ich przecięcie, czyli

zbiór

, nie jest.

2.

Relacja

nie jest antysymetryczna, a więc klasa relacji antysymetrycznych na

nie jest domknięta na przecięcia.

Ć

WICZENIE

4.19

Dla relacji

niech

,

,

oznaczają odpowiednio zwrotne, symetryczne, przechodnie domknięcie relacji

. Czy prawdą jest, że:

1.

dla dowolnej relacji

relacja

jest relacją równoważności,

2.

dla dowolnej relacji

zachodzi

W każdym z powyższych przypadków proszę podać dowód lub kontrprzykład.

R

OZ

WIĄZANIE

[

SCHOWAJ

]

1. Zaczniemy od pokazania, że dowolne domknięcie relacji zwrotnej jest zwrotne. Rozważamy relacje na zbiorze

. Z definicji zwrotności mamy,

jest

zwrotna wtedy i tylko wtedy gdy

. W definicji do

mknięcia 4.15 (patrz

Definicja 4.15.

) punkt pierwszy mówi, że jeśli

jest domknięciem

to

. Wobec tego konieczne jest, aby

. Zwróćmy uwagę, że powyższy argument działa dla dowolnych klas rodzin relacji domkniętych na

przecięcia. Stąd otrzymujemy, że symetryczne domknięcie relacji zwrotnej jest zwrotne, i przechodnie domknięcie relacji zwrotnej jest zwrotne. Ponieważ

relacja

jest zwrotna, to również zwrotna musi być

. Pokażemy teraz, że przechodnie domknięcie relacji symetrycznej jest symetryczne.

Wykorzystamy charakteryzację domknięcia przechodniego z ćwiczenia 4.18 (patrz

ćwiczenie 4.18.

). Można łatwo pokazać indukcyjnie, że dla

dowolnego

mamy

. Dla relacji symetrycznych dostajemy więc

. Wobec tego mamy:

a więc przechodnie domknięcie relacji symetrycznej jest symetryczne. Oznacza to, że relacja

jest symetryczna. Wcześniej pokazaliśmy, że

jest zwrotna. Ponieważ jest przechodnim domknięciem, to jest też przechodnia. Wobec tego jest relacją równoważności. 2. Pokażemy relację

, dla której

relacja

nie jest przechodnia. Ponieważ relacja

jest przechodnia, będzie to oznaczało, że te relacje są różne.

Niech

oraz

. Relacja

jest przechodnia, więc

; jej symetryczne domknięcie

to

. I po zwr

otnym domknięciu

otrzymujemy

. Łatwo zauważyć, że otrzymana relacja nie jest

przechodnia, gdyż

, podczas gdy

.