1
Prawie wszystkie dziedziny nauki posługują się metodami statystycznymi w celu wydobycia
wiedzy z dużych zbiorów informacji. Zarówno informatyka, jako nauka zajmująca się m.in.
zbieraniem i przetwarzaniem informacji, jak i fizyka, wykorzystują osiągnięcia statystyki i
rachunek prawdopodobieństwa. Fizyka doświadczalna dostarcza nam pewnego zasobu
danych będących wynikiem eksperymentów – czyli informacji, na podstawie których można
uzyskać ogólny opis materii, zjawisk fizycznych, praw nimi rządzących – czyli wiedzę.
Możemy podzielić ten proces na dwa etapy:
1.
zbieranie danych,
2.
wyciąganie wniosków.
Oba etapy wymagają użycia odpowiednich metod opartych na statystyce
i rachunku prawdopodobieństwa.
1. ELEMENTY STATYSTYKI I RACHUNKU PRAWDOPODOBIEŃSTWA.
Załóżmy, że mamy do wykonania jakieś doświadczenie, np. rzut kostką
do gry. W rezultacie otrzymujemy różne wyniki (oczywiście ilość możliwych wyników jest
w tym wypadku ograniczona i wynosi 6). Nie możemy z całą pewnością przewidzieć wyniku,
ponadto wynik następnego rzutu nie zależy od wyniku poprzedniego. Jeśli powtórzymy nasz
eksperyment dostateczną ilość razy (tu oczywiście powstaje problem co to znaczy
„dostateczną”) a kostka nie była oszukana możemy zauważyć, że każda liczba oczek
występuje w przybliżeniu równie często. Przez częstość bezwzględną (oznaczmy ją
x
n )
rozumieć będziemy ilość wystąpień określonej liczby oczek
x
w całym eksperymencie, czyli
w
N
rzutach (np. ilość „trójek” oznaczymy
3
n , bo
3
=
x
), natomiast częstość względna (
x
f )
równa jest stosunkowi częstości bezwzględnej do całkowitej liczby rzutów, czyli
N
n
f
x
x
=
.
( 1)
Spróbujmy
opisać to zdarzenie losowe w sposób teoretyczny używając
podstawowych pojęć. Niech ilość rzutów
N
dąży do nieskończoności
∞
→
N
. Wynikiem
pojedynczego rzutu może być tylko jedna z sześciu liczb: 1, 2, 3, 4, 5, 6. Mówimy,
że zmienna losowa
x
przyjmuje takie właśnie wartości. Są to tylko określone wartości – w
tym wypadku sześć liczb całkowitych. Taką zmienną losową nazywamy dyskretną
(skokową). Wcześniej mówiliśmy o częstości występowania określonej liczby oczek. Gdy
ilość rzutów dąży do nieskończoności, częstość względna dąży do prawdopodobieństwa:
N
n
P
x
x
=
, gdzie
∞
→
N
( 2)
Jeśli kostka nie jest oszukana, prawdopodobieństwo przyjęcia przez zmienną losową każdej
2
z sześciu wartości jest jednakowe. Możemy zilustrować to przy pomocy wykresu:
0
1
2
3
4
5
6
7
x
P(x)
1/6
Rys. 1. Rzut kostką do gry. Rozkład prawdopodobieństwa.
Taki sposób opisu zmiennej losowej przy pomocy prawdopodobieństw nazywamy
rozkładem zmiennej losowej. Zauważmy, że powyższy rozkład jest unormowany do
jedynki, tzn. suma prawdopodobieństw wszystkich możliwych rezultatów, czyli
prawdopodobieństwo, że w wyniku rzutu kostką otrzymamy liczbę oczek równą liczbie
całkowitej od 1 do 6, jest równe „jedności”, co w języku rachunku prawdopodobieństwa
oznacza „pewność” (pomijamy możliwość rozpadnięcia się kości, rezultat interesujący raczej
dla osób badających historię amnestii, pozwalał on bowiem ujść skazańcowi z życiem).
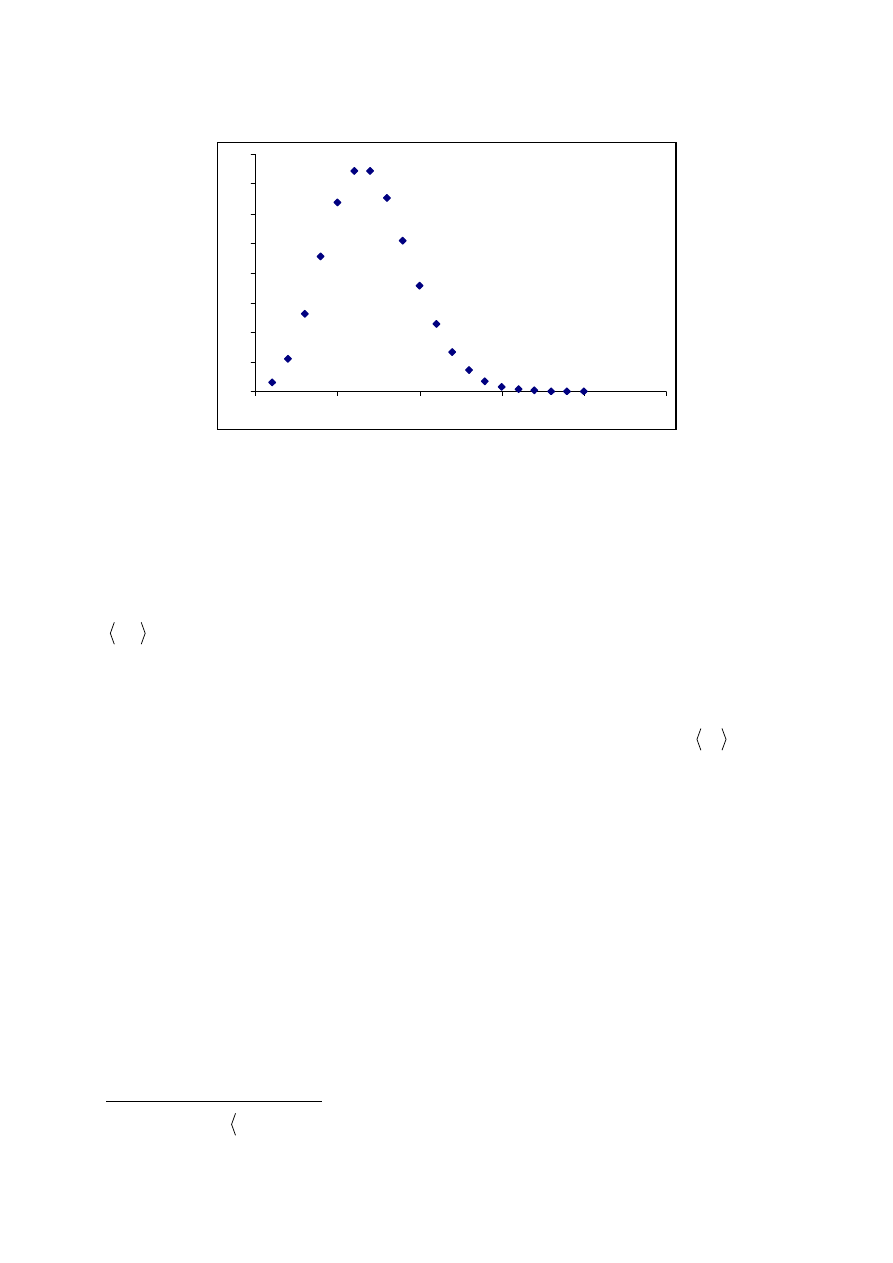
Przykładem rozkładu zmiennej losowej dyskretnej, w którym prawdopodobieństwo
przyjęcia przez zmienną określonej wartości z dozwolonego przedziału (dodatnie liczby
całkowite) nie jest dla wszystkich wartości zmiennej jednakowe jest rozkład Poissona
(czyt. „płasona”).
Rozkład ten czasami nazywany jest rozkładem zdarzeń rzadkich, ponieważ mamy
z nim do czynienia wtedy, gdy niezależnie występujące zdarzenia losowe są bardzo mało
prawdopodobne. Rozkładem tym opisywano np. liczbę zgonów żołnierzy na skutek kopnięcia
konia w pruskiej armii, ale podlega mu również np. liczba rozpadów jąder w próbce
promieniotwórczej na jednostkę czasu. Znane są również przykłady wnioskowania
odwrotnego. Fakt, że liczba cząstek powstałych w wyniku eksperymentów akceleratorowych
nie daje się opisać rozkładem Poissona, który opisuje zdarzenia niezależne, pozwolił na
wysnucie wniosku, że cząstki te nie są produkowane w sposób niezależny. Podobnie jest
z wyszukiwaniem słów kluczowych w tekście. Słowa związane z tematem tekstu nie
pojawiają się w nim przypadkowo i nie powinny dać się opisać rozkładem Poissona.
3
x
P
x
Rys. 2. Przykładowy rozkład Poissona.
W omawianych wyżej przykładach zmienna losowa mogła przyjmować tylko wartości
dyskretne. Jeśli zmienna losowa może być dowolną liczbą rzeczywistą z dozwolonego
przedziału nazywamy ją ciągłą zmienną losową. W przypadku, gdy prawdopodobieństwo
przyjęcia przez zmienną losową dowolnej wartości rzeczywistej z określonego przedziału
b
a;
1
jest jednakowe mamy do czynienia z tzw. rozkładem równomiernym.
Generator liczb losowych (w rzeczywistości pseudolosowych) daje liczby z takiego
właśnie rozkładu (przy czym
1
,
0
=
= b
a
), tzn. że losując kolejną liczbę z jednakowym
prawdopodobieństwem otrzymamy dowolną liczbę rzeczywistą z przedziału
1
;
0
(osoby
grające w gry losowe powinny zwrócić uwagę, że prawdopodobieństwo otrzymania takiej
samej liczby co poprzednio jest takie samo jak każdej innej ponieważ zdarzenia są
niezależne!).
1
Nawias trójkątny „
” oznacza, że wartość należy do przedziału, nawias okrągły „
(
”, że jest z niego
wyłączona.
4
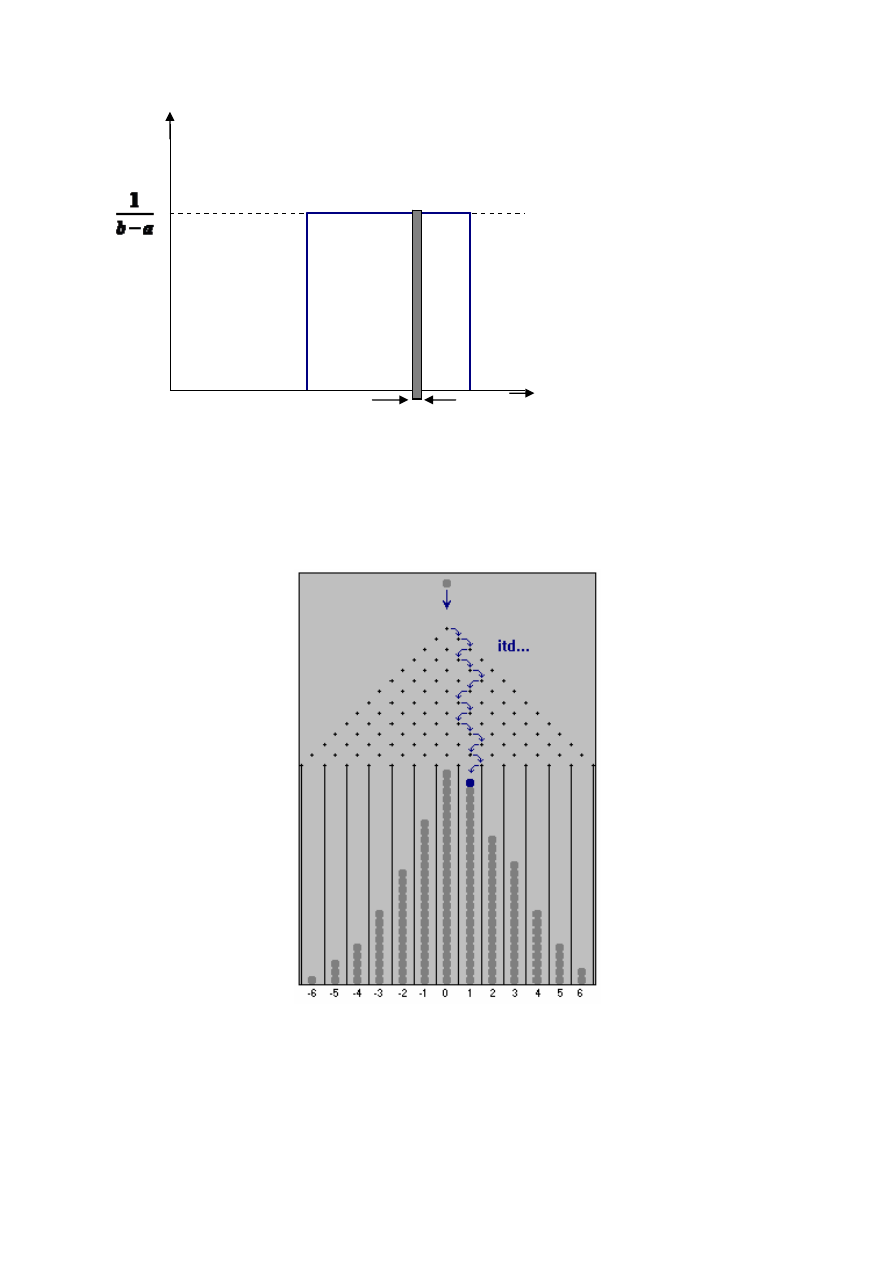
Rys. 3. Rozkład równomierny.
Wyobraźmy sobie teraz następujące doświadczenie. Do pionowej płyty
przymocowano cienkie pręty tak, jak przedstawia to rys. 4. Jest to tzw. tablica Galtona.
Rys. 4. Tablica Galtona
Doświadczenie polega na przepuszczeniu przez taki tor przeszkód dużej ilości kulek
i zbadaniu w jaki sposób rozłożą się w przegrodach w najniższym rzędzie. Jeśli odstępy
pomiędzy prętami są dobrane do wielkości kulek tak, że prawdopodobieństwo odchylenia
x
f(x)
a
b
Δx
5
kulki w obie strony jest równe (tzn. są niewiele większe od średnicy kulek tak, żeby zderzenia
z prętami były centralne), najwięcej kulek wpadnie do środkowych przegród (gdyby kulki
miały tendencje do odchylania się raczej w lewo, najwięcej wpadło by do przegród
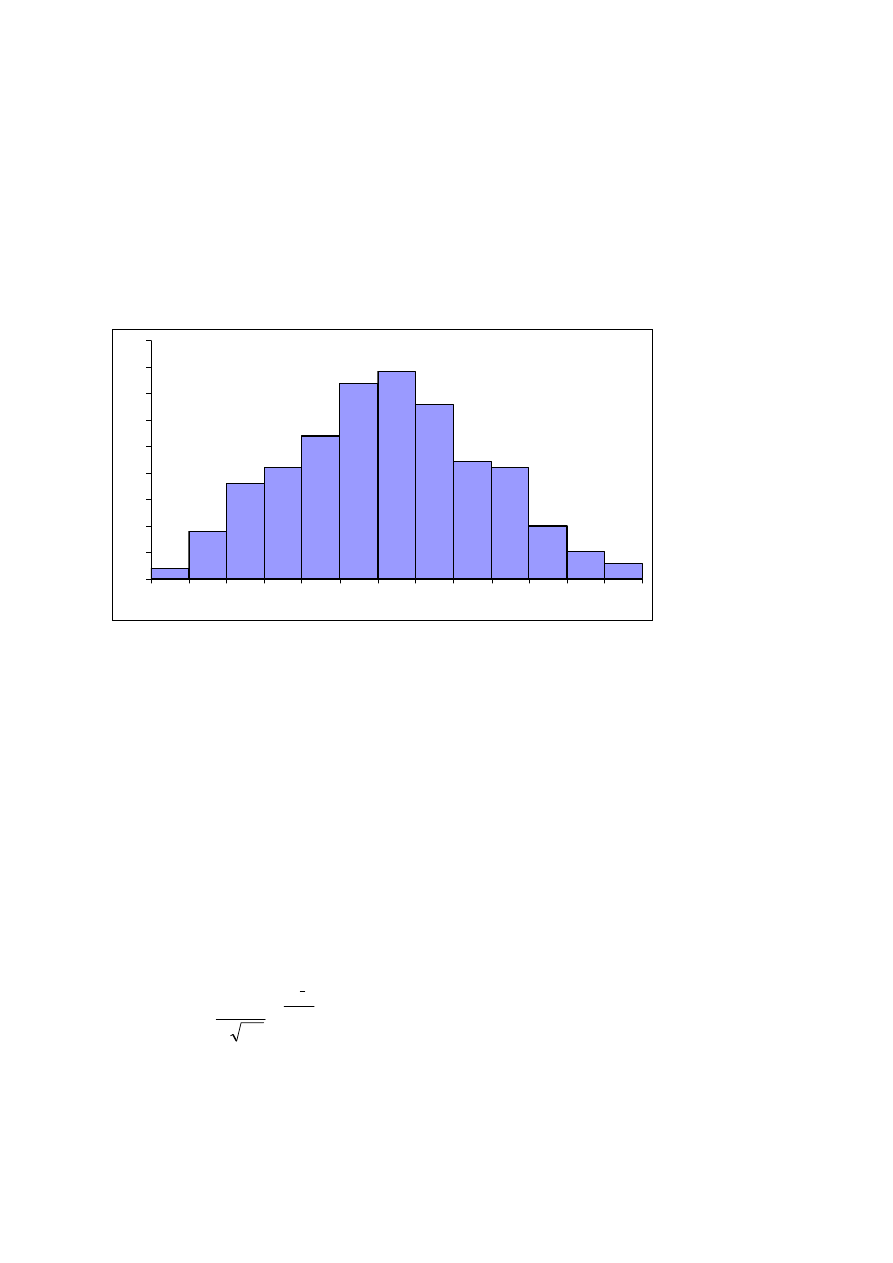
położonych na lewo od środka, itd.). Ilościowo możemy zilustrować wyniki doświadczenia w
postaci tzw. histogramu. Na osi X odkładamy numer przegrody (i), na osi Y liczbę kulek,
które do niej wpadły (czyli częstość bezwzględną) lub też stosunek tej liczby do wszystkich
kulek użytych w eksperymencie (czyli częstość względną).
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
i
n
i
Rys. 5. Przykładowy histogram.
Przedstawiony histogram jest oczywiście histogramem przykładowym, ponieważ
powtarzając doświadczenie w tych samych warunkach za każdym razem możemy uzyskać
trochę inne wyniki. Są to wyniki doświadczalne będące rezultatem procesu losowego.
Aby uzyskać opis teoretyczny musimy znaleźć wzór funkcji, której wykres przechodzi przez
środki słupków histogramu w matematycznie wyidealizowanej sytuacji gdy liczba kulek dąży
do nieskończoności, natomiast średnice kulek, odległości między prętami i szerokości
przegród dążą do zera. Częstości względne przechodzą wtedy w prawdopodobieństwa,
a numery przedziałów możemy zastąpić wartościami ciągłej zmiennej losowej. Okazuje się,
że w takim wyidealizowanym, granicznym przypadku linia przechodząca przez środki
słupków (których szerokości dążą do zera) dąży do wykresu funkcji:
( )
2
2
2
2
1
)
(
σ
π
σ
x
x
e
x
f
−
−
=
( 3)
Jest to funkcja gęstości prawdopodobieństwa rozkładu Gaussa, zwanego inaczej
rozkładem normalnym
.
Zauważmy, że w odniesieniu do prawdopodobieństwa zostało tutaj użyte słowo
6
„gęstość”. W przypadku skokowej zmiennej losowej mogliśmy mówić
o prawdopodobieństwie przyjęcia przez zmienną danej wartości (np. w rzucie kostką
prawdopodobieństwo, że wypadnie liczba oczek
4
=
x
wynosi 1/6, czyli
6
1
4
=
P
lub
( )
6
1
4
=
P
). Gdy mamy do czynienia ze zmienną ciągłą przyjmującą wartości liczb
rzeczywistych, prawdopodobieństwo to odnosi się raczej do przedziału liczbowego
(
)
x
x
x
Δ
+
,
. Jeśli szerokość przedziału
x
Δ
dąży do zera odpowiada mu wartość gęstości
prawdopodobieństwa
)
(x
f
, a prawdopodobieństwo przyjęcia przez zmienną losową wartości
z przedziału
(
)
x
x
x
Δ
+
,
jest równe
(
)
x
x
f
x
x
x
P
Δ
⋅
=
Δ
+
)
(
,
.
( 4)
Użycie określenia „gęstość” powinno teraz wydawać się bardziej uzasadnione, kiedy bardziej
widoczna staje się analogia do znanej z lekcji fizyki w szkole gęstości ciał
ρ
(
V
m
⋅
=
ρ
,
gdzie
m
– masa,
V
- objętość).
Przyjrzyjmy
się jeszcze raz rysunkowi 3. Zaznaczono na nim przykładowy przedział
o szerokości
x
Δ
. Ze wzoru 4 wynika, że prawdopodobieństwu odpowiada pole powierzchni
(wysokość zaciemnionego prostokąta pomnożona przez jego szerokość) pod wykresem
funkcji gęstości ograniczone krańcami przedziału (lewy kraniec przedziału jest równy
x
,
prawy:
x
x
Δ
+
). Całemu dozwolonemu przedziałowi
b
a
,
powinno odpowiadać zdarzenie
pewne, czyli – jeśli rozkład jest unormowany - prawdopodobieństwo równe jedności.
Rzeczywiście łatwo można obliczyć, że pole powierzchni pod całym wykresem
z rys. 3 jest równe 1. Również rozkład Gaussa opisany wzorem 3 jest unormowany
do jedności. Przyjrzyjmy się bliżej temu wzorowi. Występują w nim dwa parametry:
x
- wartość średnia (liczba rzeczywista),
σ - odchylenie standardowe (dodatnia liczba rzeczywista).
Od wartości średniej zależy położenie wykresu względem osi X,
σ odpowiada natomiast za
jego szerokość. Im odchylenie standardowe jest mniejsze, wykres staje się węższy ale
jednocześnie wyższy tak, aby pole pod wykresem pozostało niezmienione. W odróżnieniu od
rozkładu równomiernego, w przypadku rozkładu Gaussa wykres funkcji nie przecina nigdy
osi X, zbliża się tylko do niej asymptotycznie (
0
)
(
→
x
f
gdy
±∞
→
x
). Oznacza to, że cały
dozwolony przedział to
(
)
+∞
∞
− ,
, czyli wszystkie liczby rzeczywiste. Jeśli zmienna losowa
podlega rozkładowi normalnemu, możemy powiedzieć zatem, że pewne jest tylko to, że
przyjmie jakąś wartość rzeczywistą
7
(
)
1
,
=
+∞
∞
−
P
.
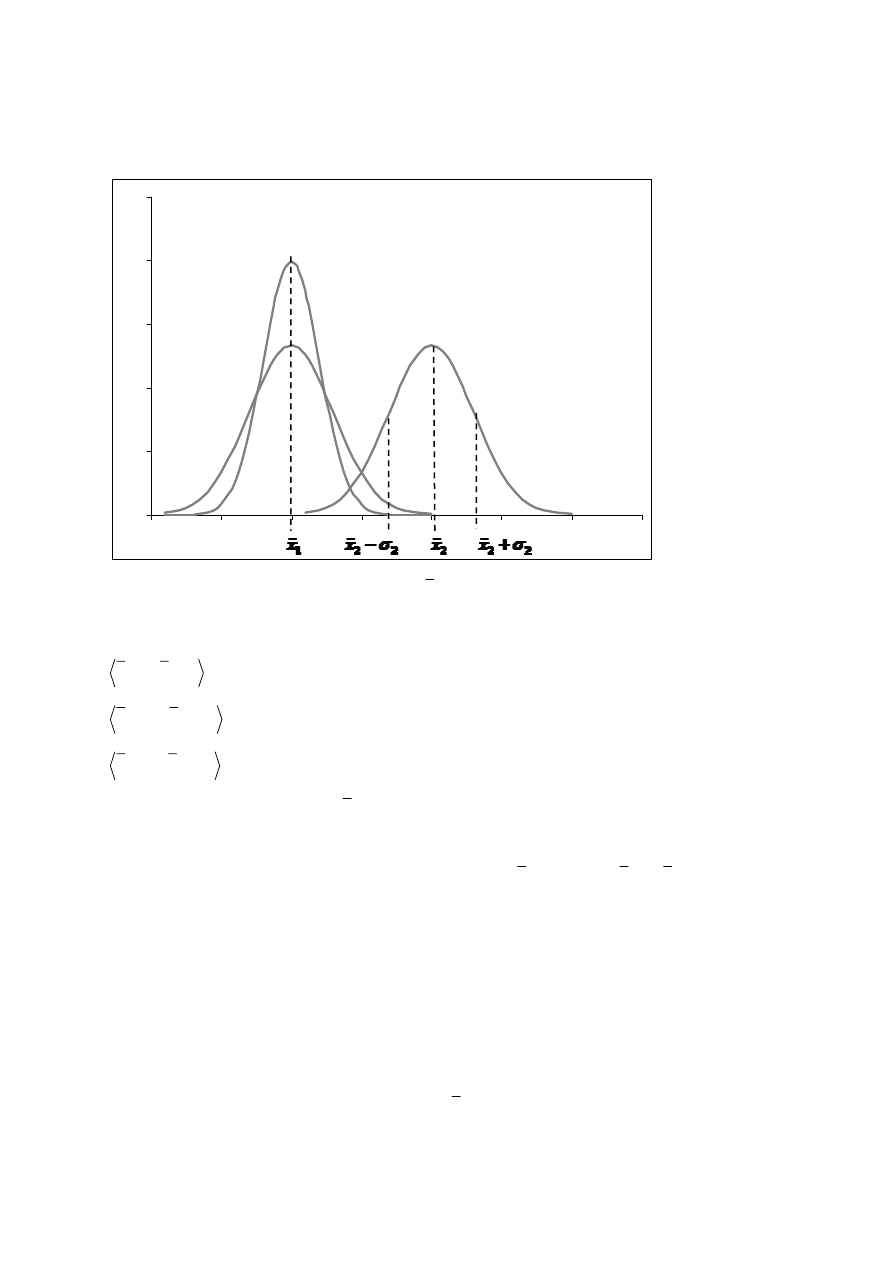
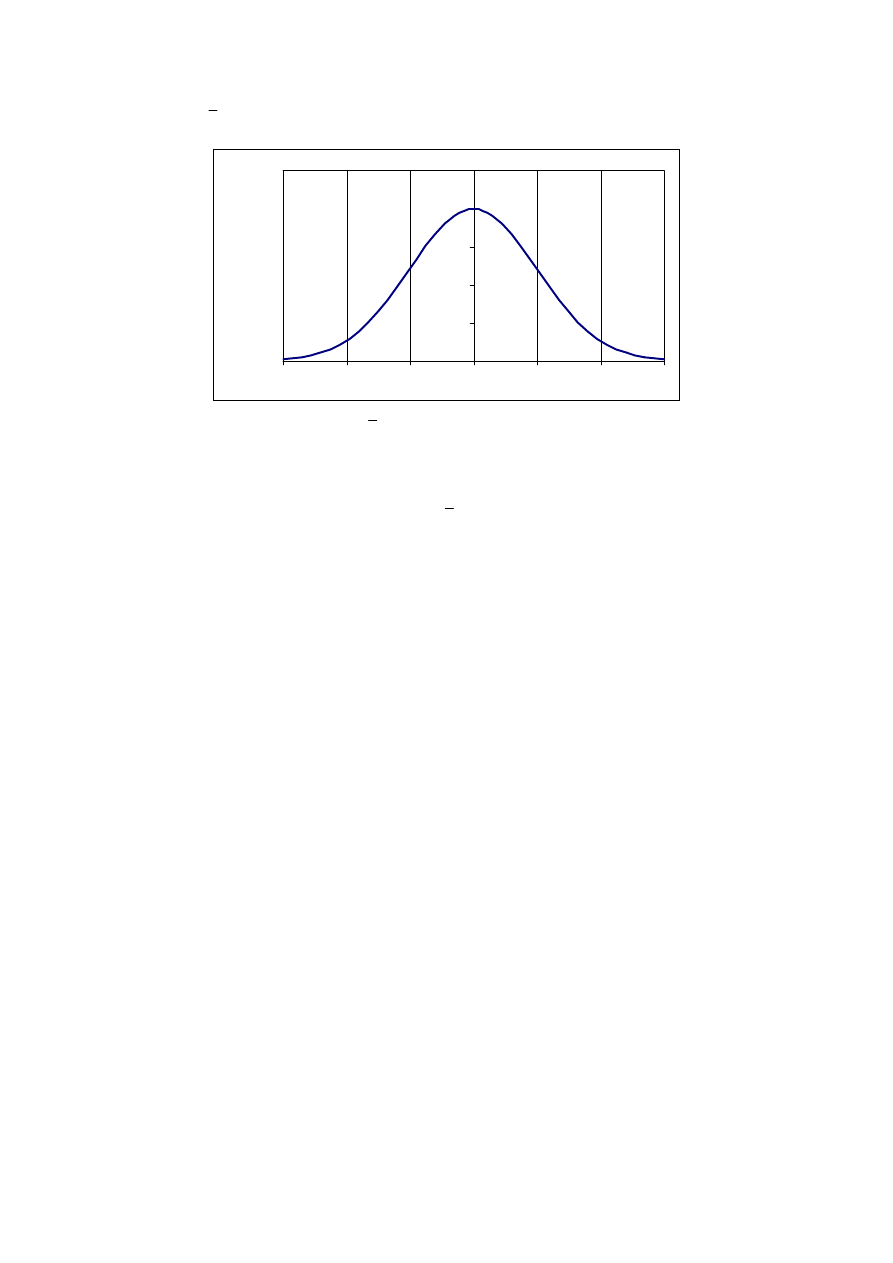
Rys. 6. Rozkład Gaussa dla różnych parametrów
x
i
σ
.
2
1
σ
σ
<
.
Prawdopodobieństwo, że wartość ta znajdzie się w przedziale
σ
σ
+
−
x
x
,
wynosi w przybliżeniu 0.6826, czyli 68.26%,
σ
σ
2
,
2
+
−
x
x
- 0.9545, czyli 95.45%,
σ
σ
3
,
3
+
−
x
x
- 0.9973, czyli 99.73%.
Wartości parametrów
x
i
σ
można odczytać z wykresu funkcji gęstości
prawdopodobieństwa. Wartość
zmiennej losowej
x
, dla której gęstość prawdopodobieństwa
)
(
x
f
jest największa odpowiada wartości średniej
x
, wartości
σ
σ
+
−
x
x
,
na osi X
natomiast wyznaczają tzw. punkty przegięcia. Są to charakterystyczne punkty na krzywej, w
których krzywa zmienia kształt z wklęsłego na wypukły lub odwrotnie. Ponieważ we wzorze
3 występuje funkcja eksponencjalna (
( )
exp
), szczególny przypadek funkcji wykładniczej
o podstawie
e
(
72
.
2
≈
e
tzw. liczba Nepera lub Eulera), mająca w wykładniku zmienną
podniesioną do kwadratu, krzywa Gaussa (zwana również krzywą dzwonową) posiada dwa
takie punkty.
Rozkład normalny o wartości średniej
x
i odchyleniu standardowym
σ
oznaczamy
x
f(x)
σ
1
σ
2
σ
2
8
symbolem
( )
σ
,
x
N
. Rozkład
( )
1
,
0
N
nazywamy standardowym rozkładem normalnym.
0,00
0,10
0,20
0,30
0,40
0,50
-3
-2
-1
0
1
2
3
x
f(x)
Rys. 7. Standardowy rozkład normalny.
0
=
x
,
1
=
σ
.
Rozkład o dowolnych parametrach można poprzez odpowiednie przekształcenia
sprowadzić do standardowej postaci i odwrotnie, ze standardowego rozkładu można łatwo
otrzymać rozkład o dowolnych parametrach
x
i
σ . Jest to użyteczne, ponieważ pola pod
krzywą Gaussa nie można obliczyć analitycznie tak, jak w przypadku np. rozkładu
równomiernego, gdzie mamy do czynienia z polami prostokątów. Numerycznie policzone i
zawarte w odpowiednich tablicach wartości pól odnoszące się do rozkładu standardowego
pozwalają na nieskomplikowane analityczne obliczanie pól dla rozkładu o dowolnych
parametrach.
Zastanówmy
się jakie zmienne losowe mogą podlegać rozkładowi normalnemu.
Tablica Galtona jest ilustracją pewnego procesu, w którym na ostateczny wynik wpływ ma
wiele niezależnych czynników (każdemu z nich odpowiada jeden rząd w tablicy Galtona).
Ogólnie taki sam wynik dostajemy, gdy badamy zmienną losową będącą sumą wielu
niezależnych zmiennych o takich samych rozkładach. W praktyce okazuje się jednak,
że wielkości, na które ma wpływ wiele niezależnych czynników, których liczby i charakteru
wpływu nawet nie znamy, dają się z dobrym przybliżeniem opisać rozkładem Gaussa.
Przykładem takich wielkości mogą być wzrost czy długość stopy dorosłego człowieka.
Nie z tego powodu jednak poświęciliśmy rozkładowi normalnemu tyle uwagi.
W laboratorium będziemy zajmować się pomiarami różnych wielkości fizycznych. Pomiar
jest złożonym procesem, w którym na ostateczny wynik wpływ ma wiele czynników.
W rezultacie mierząc daną wielkość w tych samych warunkach za każdym razem możemy
otrzymać trochę inną wartość. Jeśli powtórzymy nasz pomiar dostatecznie dużo razy
i przyjrzymy się sporządzonemu z wyników histogramowi, okaże się, że obwiednia
histogramu przypomina krzywą Gaussa. Jeśli tak jednak nie jest mamy podstawy
9
przypuszczać, że popełniliśmy błędy, których można uniknąć. Posługując się mechanicznym
modelem rozkładu normalnego jakim jest tablica Galtona, wyobraźmy sobie, że jeden rząd
prętów jest uszkodzony tak, że kulki nie odchylają się z jednakowym prawdopodobieństwem
w prawo i w lewo. Spowoduje to zaburzenie sytuacji z jaką mieliśmy do czynienia w
przypadku prawidłowo skonstruowanej tablicy, gdzie średnio biorąc – mówiąc już językiem
potocznym i odwołując się do intuicji – odchyleń w prawo i w lewo jest tyle samo i „w końcu
wychodzi na zero”. (Wskazówka dla osób chcących rozważyć to ściśle: Ile dróg prowadzi do
każdej z przegród? Do których przegród prowadzi tylko jedna droga, a do której najwięcej
dróg? Co to jest częstość względna i prawdopodobieństwo?). Błędami, z którymi mamy do
czynienia w procesie pomiarowym zajmiemy się w dalszej części naszych rozważań.
2. Błędy pomiarowe w pomiarach bezpośrednich
Celem pomiaru wielkości fizycznej jest poznanie jej wartości rzeczywistej (
R
x
).
W praktyce jest to jednak niemożliwe. Niemożliwe jest bowiem dokonanie pomiaru nie
obarczonego błędem. Różnicę pomiędzy wartością rzeczywistą a zmierzoną (
x
) nazywać
będziemy błędem bezwzględnym (
x
x
R
−
), błąd względny natomiast określa jaką część
wartości rzeczywistej stanowi błąd bezwzględny:
R
R
x
x
x
x
−
=
δ
(5)
Błąd względny można również wyrazić w procentach mnożąc powyższy wzór przez
%
100
.
Nie znając wartości rzeczywistej
R
x
nie jesteśmy w stanie określić dokładnej wartości
błędów. Możemy natomiast dokonać ich oceny i wyeliminować te błędy, których przyczyny
powstania i charakter wpływu jest nam znany. Są jednak błędy, których nie jesteśmy w stanie
skorygować. Musimy zatem dokonać oceny wartości rzeczywistej oraz oceny błędu z jakim
została wyznaczona. Dopiero te dwie wartości stanowią prawidłową odpowiedź w fizyce
doświadczalnej.
Metody oceny wartości opierają się na statystyce i rachunku prawdopodobieństwa.
Konieczne jest więc zebranie dużej liczby danych. Możemy zrealizować to na przykład
poprzez wielokrotne powtórzenie pomiaru w tych samych warunkach pomiarowych.
Od liczby pomiarów oraz prawidłowego ich opracowania zależy dokładność wyniku naszego
eksperymentu.
Już na pierwszym etapie opracowania danych pomiarowych należy pozbyć się
10
wpływu na ostateczny wynik tzw. błędów grubych. Przyczyną ich powstania może być
np. pomyłka eksperymentatora przy odczytywaniu wyniku. W rezultacie otrzymujemy
wynik, który znacznie odbiega od innych wyników. Prawdopodobieństwo popełnienia
takiego błędu jest małe, zatem jeśli przyglądając się dużej liczbie zebranych danych
pomiarowych zauważymy kilka wartości znacznie odbiegających od reszty, możemy
pominąć je w opracowaniu. Mówimy, że odrzucamy pomiary obarczone błędem grubym. Są
one odpowiedzialne za powstawanie peryferyjnych części histogramu (słupków daleko
położonych od środka).
Drugim rodzajem dających się wyeliminować błędów są tzw. błędy systematyczne.
Mogą one być spowodowane nieuwzględnieniem pewnych poprawek (np. siły wyporu
powietrza przy bardzo dokładnym ważeniu), czy też wadami urządzeń pomiarowych
(przykładem może być źle wyskalowany przyrząd). W efekcie tego rodzaju błędy powodują
przesunięcie całego histogramu wzdłuż osi X (każdy pomiar obarczony jest dodatkowo
błędem o takiej samej wartości). Trudniejsze do skorygowania są błędy systematyczne
charakteryzujące się nie stałą, lecz zmieniającą się według określonego prawa wartością.
Wyobraźmy sobie na przykład, że dokonujemy bardzo dokładnego pomiaru długości
metalowego pręta. Jeśli w trakcie pomiaru, na skutek różnych czynników, temperatura
wzrasta na tyle, że zjawisko termicznej rozszerzalności metali staje się nie do pominięcia,
otrzymywać będziemy coraz to większe wartości długości pręta. Znając jednak zależność
długości od temperatury i przebieg zmian tego czynnika zewnętrznego możemy dokonać
odpowiednich poprawek.
Po pozbyciu się błędów grubych i systematycznych pozostaje nam zająć się
niemożliwymi do wyeliminowania błędami statystycznymi (przypadkowymi). Są one
wynikiem działania wielu czynników, których wpływ na rezultat pomiaru ma charakter
fluktuacji i powodują, że wyniki wielokrotnego pomiaru tej samej wartości w warunkach,
które uważamy za jednakowe układają się w krzywą Gaussa.
Wróćmy do mechanicznego modelu rozkładu normalnego jakim jest tablica Galtona.
Każdy rząd prętów umocowanych na tablicy odpowiada jednemu czynnikowi, który ma
wpływ na wartość pomiaru. Przykładem mogą być warunki zewnętrzne (takie jak
temperatura, ciśnienie powietrza, wahania napięcia zasilania itp.), czy też niedokładność
odczytu. Jak już mówiliśmy w poprzednim rozdziale nie znamy i nie musimy nawet znać ich
liczby. Jednakowe prawdopodobieństwo odchylenia kulki w prawą i lewą stronę ilustruje
fluktuacyjny wpływ czynników. Oznacza to, że dana wartość (np. napięcia zasilania) może
odbiegać nieznacznie od pewnej wartości, którą przybiera najczęściej raz w jedną raz
11
w drugą stronę. Zmiany te mają charakter losowy. Losowy charakter zatem mają same
wyniki pomiaru. Jednakowe prawdopodobieństwo z jakim kulka znajdzie się
w odpowiednich przegrodach po zderzeniu z prętem powoduje, że najwięcej kulek wpadnie
do przegrody znajdującej się pod szczeliną, w której kulki zaczynają swoją drogę. Podobnie
jest w procesie pomiarowym. Jeśli zmiany czynników pomiarowych nie są jednokierunkowe
(co może być przyczyną błędów systematycznych), a mają tylko charakter fluktuacji,
powstałe w ich wyniku błędy powinny się wzajemnie znosić. Posługując się dalej analogią
do tablicy Galtona, mamy prawo przypuszczać, że środkowej przegrodzie (w której
położenie kulki względem osi X jest nie odchylone) odpowiada wartość rzeczywista
mierzonej wielkości. Jednocześnie środkowej przegrodzie tablicy odpowiada parametr
x
(wartość średnia) rozkładu normalnego. Wynika z tego, że jeśli wyniki wielokrotnego
pomiaru danej wielkości fizycznej przeprowadzone w takich samych warunkach dają się
opisać rozkładem Gaussa, najlepszą oceną rzeczywistej wartości tej wielkości jest wartość
średnia
x
.
Najlepszą oceną tego parametru jest średnia arytmetyczna:
N
x
x
x
x
x
N
+
+
+
+
=
...
3
2
1
,
(6)
gdzie:
...
,
2
1
x
x
-
oznaczają pojedyncze pomiary,
N
- liczbę wszystkich pomiarów.
Zapiszmy ten wzór używając bardziej zaawansowanych symboli:
N
x
x
N
i
i
∑
=
=
1
,
(7)
gdzie:
indeks
N
i
,...
3
,
2
,
1
=
.
Parametr
σ , który jest miarą rozmycia rozkładu Gaussa, a co za tym idzie miarą rozrzutu
naszych wyników wokół wartości średniej możemy ocenić przy pomocy wzoru:
(
)
1
1
2
−
−
=
∑
=
N
x
x
N
i
i
x
σ
.
(8)
Korzystając z wiadomości zawartych w rozdziale 1. możemy powiedzieć, że jeśli
skądinąd (mówimy „a priori”, co oznacza „z założenia”) wiemy, że pomiary podlegają
rozkładowi Gaussa o parametrach
x
i
x
σ
(co zapisujemy w postaci
( )
x
x
N
x
σ
,
~
)
12
i dokonujemy pojedynczego pomiaru, na 68% zmierzona wartość
x
znajdzie się
w przedziale
(
)
x
x
x
x
σ
σ
+
−
,
.
Jest to zarazem prawdopodobieństwo, że wartość średnia
x
znajduje się w przedziale
(
)
x
x
x
x
σ
σ
+
−
,
(zrozumienie tego może ułatwić wyobrażenie sobie wykresu
przedstawiającego dwa rozkłady Gaussa:
( )
x
x
N
σ
,
i rozkładu o wartości średniej równej
x
,
czyli
(
)
x
x
N
σ
,
). Mimo tego, że nie jest to zbyt duża szansa, wartość
x
σ
podaje się jako błąd
pojedynczego pomiaru (dokładnie określamy go mianem średniego błędu kwadratowego
pojedynczego pomiaru
)
x
x
s
σ
=
.
(9)
Wybór taki podyktowany jest koniecznością pogodzenia dwóch sprzecznych interesów:
chcemy mieć możliwie jak najmniejszy błąd i możliwie jak największe
prawdopodobieństwo, że wartość średnia (będąca najlepszą oceną wartości rzeczywistej)
zawarta jest w przedziale
x
s
x
± .
Udowodnijmy zasadność wyboru na ogólnym przykładzie rozkładu normalnego
o parametrach
μ
(wartość średnia) i
σ (odchylenie standardowe). Jak już wiemy
z poprzedniego rozdziału, miarą prawdopodobieństwa w rozkładach gęstości
prawdopodobieństwa jest pole pod wykresem funkcji gęstości. Zwiększanie pola, czyli
prawdopodobieństwa (tzw. poziomu ufności) wiąże się z poszerzaniem przedziału, który mu
odpowiada (tzw. przedziału ufności). Ponieważ krańce przedziału
(
)
σ
μ
σ
μ
+
− ,
wyznaczone są przez punkty przegięcia, stosunkowo małe zawężenie przedziału ufności
powoduje stosunkowo duże zmniejszenie pola (w tym obszarze krzywa Gaussa jest
wypukła), poszerzanie przedziału zaś jest mało opłacalne (na zewnątrz przedziału
(
)
σ
μ
±
krzywa dzwonowa jest wklęsła i pole pod nią daje już mały wkład do poziomu ufności,
porównaj przedziały i odpowiadające im wartości prawdopodobieństwa podane w rozdz. 1
).
Wybór 5 można uznać więc za optymalny.
Ostatecznie, zgodnie z zasadą, że podanie wyniku pomiaru wymaga określenia błędu
z jakim był wyznaczony, rezultat pojedynczego pomiaru przedstawiamy w formie:
x
s
x
±
.
( 50)
Podobnie podanie wartości średniej jako najbardziej zbliżonej do wartości
rzeczywistej mierzonej wielkości fizycznej wymaga określenia niepewności jej znajomości.
Wartość średnia obliczona przy pomocy wzoru 7 z danych doświadczalnych podlega również
rozkładowi normalnemu (jest zmienną losową o rozkładzie Gaussa). Gdybyśmy powtórzyli
13
wielokrotnie eksperyment polegający na wykonaniu
N
pomiarów tej samej wielkości, z
każdej serii
N
pomiarów obliczyli wartość średnią i usypali z tych wartości histogram
okazałoby się, że daje się on również opisać krzywą Gaussa. Parametr
x
σ
tej krzywej byłby
jednak znacznie mniejszy niż odchylenie standardowe serii składającej się z
N
pomiarów.
Można udowodnić, że związek pomiędzy tymi wartościami jest następujący:
N
x
x
σ
σ
=
.
(11)
Rozkład wartości średniej jest więc N -krotnie węższy od rozkładu wyników pomiaru.
Jak
już wykazaliśmy wcześniej, przyjęcie za błąd odchylenia standardowego jest
wyborem optymalnym. Jako niepewność znajomości wartości średniej zatem należy podać
wartość obliczoną ze wzoru:
(
)
(
)
1
1
2
−
⋅
−
=
∑
=
N
N
x
x
s
N
i
i
x
(12)
gdzie:
x
s nazywamy średnim błędem kwadratowym wartości średniej.
Ostatecznie wynik pomiaru wielkości fizycznej
X , której wartości rzeczywistej nie znamy,
zapisujemy jako:
(
)
x
s
x
X
±
=
,
(13)
co oznacza tylko tyle, że prawdopodobieństwo, że wartość rzeczywista znajduje się
w przedziale
(
)
x
x
s
x
s
x
+
− ,
wynosi 68%.
Ze wzoru 12 wynika, że im więcej pomiarów wykonamy tym błąd wyznaczenia
wartości średniej jest mniejszy, węższy jest więc przedział, w którym
z prawdopodobieństwem 68% znajduje się wartość rzeczywista, co oznacza, że wynik jest
dokładniejszy. W praktyce jednak zwiększanie liczby pomiarów wiąże się z wydłużaniem
czasu trwania eksperymentu, co zwiększa prawdopodobieństwo jednokierunkowej zmiany
warunków zewnętrznych. Należy zatem uważać by nie spowodować powstania błędów
systematycznych.
Interpretacja zapisu 13 opiera się na założeniu, że wyniki pomiarów podlegają
rozkładowi normalnemu. Faktycznie jest to tylko hipoteza, czyli przypuszczenie podlegające
weryfikacji. Weryfikacja, która polega na sprawdzeniu prawdziwości, może zostać dokonana
przy pomocy testów zgodności. Jednym z takich testów używanych do porównywania
rozkładów doświadczalnych z teoretycznymi jest test χ
2
(chi-kwadrat).
14
3. Testowanie hipotezy przy pomocy testu χ
2
przedstawione na
wybranym przykładzie.
Nauczmy
się posługiwać testem χ
2
na wybranym przykładzie. Jak wiadomo jednym
z warunków prawidłowego działania łożyska jest to, aby kulki użyte do jego produkcji miały
takie same średnice. Określenie „takie same” jest jednak czysto teoretyczne, ponieważ
w praktyce niemożliwe jest wyprodukowanie takich kulek. Jest to spowodowane
nieuniknionymi błędami w procesie produkcji. Błędy te (spowodowane np. fluktuacjami
warunków zewnętrznych) mają taki sam charakter jak błędy pomiarowe. Proces kontroli
jakości ma za zadanie odrzucenie elementów o średnicach znacznie (to, co rozumiemy pod
pojęciem „znacznie” jest oczywiście ilościowo dokładnie określone i podane przez
producenta) odbiegających od wartości nominalnej (zwróćmy uwagę na analogię do błędów
grubych omawianych w poprzednim rozdziale). Wiedząc już jakie skutki wywołują błędy
statystyczne, przypuszczamy, że rzeczywiste wartości średnic kulek podlegają rozkładowi
normalnemu. Jednokierunkowa zmiana warunków w trakcie trwania produkcji może jednak
być powodem wystąpienia błędów systematycznych. Jeśli wpływ takich błędów na wartości
średnic jest na tyle mały, że kulki nie zostaną odrzucone podczas kontroli jakości
uwzględnienie ich w rozkładzie może spowodować jego deformację. Błędy systematyczne
o stałej wartości spowodują tylko przesunięcie wartości średniej względem wartości
nominalnej, nie są one odpowiedzialne za zmianę kształtu rozkładu .
Z
wcześniejszych rozważań zawartych w tym opracowaniu wynika, że zbadanie
rozkładu wartości rzeczywistych jest w praktyce nie do zrealizowania ze względu na
występowanie nieuniknionych statystycznych błędów pomiarowych. Mamy prawo jednak
przypuszczać, że wyniki pojedynczych pomiarów średnicy serii
N
kulek podlegają również
rozkładowi Gaussa. Podstawą tego przypuszczenia jest twierdzenie, że zmienna losowa
x
będąca sumą zmiennych losowych o rozkładach normalnych podlega również rozkładowi
normalnemu.
Stawiamy zatem hipotezę, że zmienna losowa
x
podlega rozkładowi Gaussa
o parametrach
x
i
x
σ
, co zapisujemy symbolicznie w postaci:
( )
x
x
N
x
H
σ
,
~
:
0
.
Aby ją zweryfikować w pierwszej kolejności dokonujemy oceny parametrów założonego
rozkładu korzystając ze wzorów 7 i 8.
15
Jakościowo możemy porównać rozkład doświadczalny z teoretycznym (założonym)
przedstawiając wyniki pomiarów w postaci histogramu i nanosząc odpowiednią krzywą
teoretyczną. W tym celu musimy cały zakres pomiarowy (oznaczmy go literą
r ) podzielić na
odpowiednią liczbę przedziałów (
k
), przy czym
min
max
x
x
r
−
=
,
(14)
gdzie:
max
x
oznacza największą zmierzoną wartość,
min
x
odpowiednio najmniejszą.
Niestety wynik testu zależy od liczby przedziałów
k
, wyborem której nie rządzą żadne
dające się teoretycznie uzasadnić zasady. Otrzymamy w ten sposób jakby
k
„szufladek”,
do których posortujmy nasze pomiary. Szerokość każdego przedziału jest taka sama i równa
k
r
x
=
Δ
.
( 15)
Histogram jest słupkowym wykresem, w którym na osi X odkładamy numery przedziałów
lub wartości zmiennej losowej
x
(zaznaczenie tylko wartości odpowiadających krańcom
przedziałów czyni wykres bardziej czytelnym). Na osi Y natomiast, dla każdego przedziału,
którego numer możemy oznaczyć indeksem
l
(
k
l
...
1
=
) zaznaczamy liczbę pomiarów (
l
n ),
które „wpadają” do tego przedziału. Mówimy, że pomiar „wpada” do danego przedziału,
jeśli jego wartość jest większa od wartości lewego krańca przedziału i jednocześnie mniejsza
od wartości prawego krańca. W tym miejscu nasuwa się pytanie co zrobić gdy pomiar ma
wartość równą któremuś krańcowi. Oczywiście nie możemy takiego pomiaru zaliczyć do
dwóch przedziałów jednocześnie, nie możemy również pominąć go w ogóle. Z tych
względów przedziały muszą być jednostronnie domknięte (mówiliśmy już co to oznacza przy
okazji rozkładu równomiernego). Wybór pomiędzy lewostronnie i prawostronnie
domkniętymi przedziałami jest dowolny, obowiązuje nas jednak konsekwencja w całym
opracowaniu. Symbolicznie zapisujemy to w postaci:
)
l
P
l
L
x
x ,
lub
(
l
P
l
L
x
x ,
,
gdzie:
l
L
x symbolizuje lewy kraniec
l
-tego przedziału, a
l
P
x jego prawy kraniec.
Wyjątek od tej reguły stanowią lewy kraniec pierwszego przedziału
1
L
x i prawy kraniec
ostatniego przedziału
k
P
x , które muszą być zawsze domknięte. Dzięki temu
max
x
i
min
x
nie
zostaną pominięte w opracowaniu. Za
1
L
x bowiem przyjmujemy najmniejszą zmierzoną
wartość (
min
1
x
x
L
=
),
k
P
x natomiast powinno odpowiadać wartości największej (
max
x
x
k
P
=
).
16
Ogólnie prawy kraniec przedziału powstaje przez dodanie do lewego krańca wartości
szerokości przedziału, czyli dla dowolnego przedziału o numerze
l
mamy:
x
x
x
l
L
l
P
Δ
+
=
.
(16)
Prawy kraniec poprzedniego przedziału jest jednocześnie lewym krańcem następnego:
1
+
=
l
L
l
P
x
x
.
(17)
Krańce (granice) przedziałów obliczamy zatem korzystając ze wzorów:
x
l
x
x
l
L
Δ
⋅
−
+
=
)
1
(
min
x
l
x
x
l
P
Δ
⋅
+
=
min
.
(18)
Rzeczywiście po dokonaniu prawidłowych obliczeń
k
P
x powinien odpowiadać największej
zmierzonej wartości:
(
)
max
min
max
min
min
min
x
x
x
x
k
r
k
x
x
k
x
x
k
P
=
−
+
=
⋅
+
=
Δ
⋅
+
=
.
(19)
Naniesienie na gotowy histogram krzywej teoretycznej wymaga policzenia
teoretycznych wartości
l
n (oznaczmy je
t
l
n ). Określają one jakiej wartości
l
n spodziewamy
się średnio
2
przypuszczając, że zmienna losowa
x
podlega rozkładowi Gaussa o parametrach
x
i
x
σ
.
Z
wiadomości zawartych w rozdz. 1. wynika, że prawdopodobieństwo znalezienia się
wyniku pomiaru w danym przedziale jest równe polu pod krzywą ograniczonemu krańcami
tego przedziału. Pozwólmy sobie na zastosowanie przybliżenia tego pola polem prostokąta,
tzn. niech
x
x
f
x
x
P
l
C
l
P
l
L
Δ
⋅
=
)
(
)
,
(
,
(20)
gdzie
l
C
x oznacza środek
l
-tego przedziału:
2
l
P
l
L
l
C
x
x
x
+
=
,
(21)
a )
(
l
C
x
f
wartość funkcji gęstości prawdopodobieństwa określoną wzorem 3.
Doświadczalnym wartościom
l
n odpowiadają prawdopodobieństwa )
,
(
l
P
l
L
x
x
P
określone wzorem 20. Aby jednak porównać te wartości musimy oba rozkłady
(doświadczalny i teoretyczny) unormować do tej samej wartości (pola pod rozkładami muszą
być równe). Jeśli na osi Y histogramu odkładamy liczbę (spośród
N
pomiarów) wyników,
które wpadają do danego przedziału, czyli częstości bezwzględne
l
n , odpowiadają im
wartości teoretyczne, które należy obliczyć jako:
2
l
n
jest bowiem również zmienną losową (podlega fluktuacjom), jest to jednak zmienna losowa dyskretna.
17
N
x
x
f
N
x
x
P
n
l
C
l
P
l
L
t
l
⋅
Δ
⋅
=
⋅
=
)
(
)
,
(
.
(22)
Warto zwrócić uwagę, że są to liczby rzeczywiste. Porównywanie ich z naturalnymi
wartościami
l
n
nie wymaga jednak zaokrąglania. Jest to wręcz niewskazane, gdyż powoduje
wprowadzenie niepotrzebnego błędu, co ma szczególne znaczenie przy ilościowym
porównywaniu rozkładu doświadczalnego z teoretycznym.
Jakościowe porównanie polegające na określeniu stopnia zgodności bez zastosowania
liczbowej miary pozwala nam tylko powiedzieć, że „naszym zdaniem rozkłady są podobne
lub nie”. Jest to jednak odpowiedź niewystarczająca w ścisłej dziedzinie nauki jaką jest
fizyka. Hipoteza
0
H
wymaga weryfikacji, która jest ściśle określoną procedurą opartą na
statystyce i rachunku prawdopodobieństwa. Stosując taki sposób badania prawdziwości
przypuszczenia dokonujemy porównania ilościowego. Jedną z metod jest test
χ
2
.
Z przyczyn, które pozostawiamy dociekliwemu czytelnikowi do samodzielnego
studiowania, wartość
χ
2
należy obliczyć z następującego wzoru:
(
)
∑
∑
=
=
−
=
=
'
1
2
'
1
2
'
'
'
k
l
t
l
t
l
l
k
l
l
n
n
n
m
χ
.
(23)
Użyliśmy w nim znanych z dotychczasowych rozważań oznaczeń opatrzonych jednak
dodatkowo znaczkiem „’ „. Znaczek ten symbolizuje tutaj odpowiednie wartości po
dokonaniu pewnego zabiegu. Zabieg ten jest podyktowany koniecznością spełnienia
warunku, że częstość bezwzględna
l
n
nie może być zbyt mała jeśli chcemy porównywać
rozkład doświadczalny (histogram) z rozkładem teoretycznym przy pomocy testu
χ
2
.
Zwykło się przyjmować, że
l
n
musi być większa od pięciu:
5
>
l
n
.
(24)
Warunek 24 w praktyce nie zawsze jest jednak spełniony, musimy więc dokonać pewnego
oszustwa. Polega ono na łączeniu sąsiednich przedziałów tak aby nierówność 24 była
prawdziwa (jeśli histogram sugeruje, że dane podlegają rozkładowi Gaussa, problem dotyczy
tylko peryferyjnych części histogramu, czyli słupków położonych daleko od środka). Jest to
potrzebne tylko do prawidłowego policzenia wartości
χ
2
, wystarczy zatem obliczyć wartości
opatrzone znaczkiem „’ „ występujące we wzorze 23 (rysowanie „oszukanego histogramu”
nie ma sensu). Dokonujemy tego poprzez zwykłe dodatnie liczebności doświadczalnych
sąsiednich przedziałów tylko tam gdzie jest to konieczne. Pozostałe przedziały
pozostawiamy bez zmian. Sens porównania wymaga dodania wartości
t
l
n
w sposób
analogiczny, czyli np. jeśli połączyliśmy pierwszy, drugi i trzeci przedział histogramu
18
(mówimy, że zsypaliśmy te przedziały), tzn. obliczyliśmy nową wartość
3
2
1
1
'
n
n
n
n
+
+
=
,
możemy porównać ją tylko z wartością '
1
t
n
obliczoną jako:
t
t
t
t
n
n
n
n
3
2
1
1
'
+
+
=
.
Liczba przedziałów
k
zmniejszy się więc do
'
k
(chyba że częstości wszystkich przedziałów
są większe od 5, wtedy wszystkie wartości „primowane” są równe wartościom bez znaczka
„’ „).
Przyglądając się wzorowi 23 widzimy, że występują w nim kwadraty różnic pomiędzy
odpowiednimi wartościami częstości doświadczalnych i teoretycznych:
(
)
2
'
'
t
l
l
n
n
−
.
Możemy zatem powiedzieć, że
χ
2
, zbudowane jako suma takich kwadratów (podniesienie
różnicy do kwadratu daje nam zawsze dodatnią wartość dzięki czemu nie występuje znane
nam z rozważań na temat rozkładu normalnego zjawisko znoszenia się odchyłek), jest miarą
rozbieżności rozkładów doświadczalnego i teoretycznego. Im większe różnice pomiędzy
rozkładami tym
χ
2
ma większą wartość. Musimy zatem wybrać graniczną wartość
χ
2
, do
której przyjmujemy hipotezę (uznajemy ją za prawdziwą), że dane pomiarowe podlegają
rozkładowi teoretycznemu, tzn. uznajemy rozbieżności pomiędzy rozkładami za fluktuacje
statystyczne. Otrzymanie wyniku większego od wartości granicznej pozwala na odrzucenie
hipotezy (uznanie jej za fałszywą). Należy jednak zwrócić uwagę, że
χ
2
jest również zmienną
losową i podlega rozkładowi prawdopodobieństwa (rozkład
χ
2
). Istnieje zatem różne od zera
prawdopodobieństwo, że wyniki pomiarów podlegają założonemu rozkładowi,
ale w rezultacie eksperymentu otrzymaliśmy akurat wartość
χ
2
większą od wartości
granicznej (inaczej mówiąc krytycznej). Prawdopodobieństwo to nazywamy poziomem
istotności
i oznaczamy najczęściej literą
α. Jest ono równe polu pod rozkładem χ
2
odpowiadającemu przedziałowi
(
)
+∞
,
2
,
α
χ
K
(przez
2
,
α
χ
K
oznaczyliśmy wartość krytyczną
χ
2
).
Jak widać zależy ona od dwóch parametrów: K i
α. W przypadku testowania rozkładu
normalnego
3
'
−
= k
K
.
(25)
Ogólnie jednak, w przypadku testowania innych rozkładów liczba przedziałów po zsypaniu
'
k
może być pomniejszana o inną niż 3 wartość.
Ostatecznie jeśli w wyniku eksperymentu otrzymaliśmy wartość
χ
2
taką, że:
19
•
2
,
2
α
χ
χ
K
>
hipotezę
0
H należy odrzucić, przy czym prawdopodobieństwo
odrzucenia w rzeczywistości prawdziwej hipotezy (popełnienia błędu I
rodzaju
) wynosi
α;
•
2
,
2
α
χ
χ
K
≤
nie ma podstaw do odrzucenia hipotezy
0
H .
Z dotychczasowych rozważań wynika, że przyjmując mniejsze wartości
α
zmniejszamy prawdopodobieństwo popełnienia błędu I rodzaju, skutkuje to jednak
wybieraniem większych wartości krytycznych
2
,
α
χ
K
, a co za tym idzie zwiększaniem
przyjęcia hipotezy fałszywej (błąd II rodzaju).
Po
obliczeniu
K ze wzoru 25 i wybraniu wartości poziomu istotności
α, wartość
krytyczną
2
,
α
χ
K
należy odnaleźć w tablicach statystycznych (można również skorzystać
z funkcji statystycznych dostępnych np. w programie Excel).