 | Pobierz cały dokument przyklad.rozwiazania.tarczy.mes.wersja.2.pdf Rozmiar 57 KB |
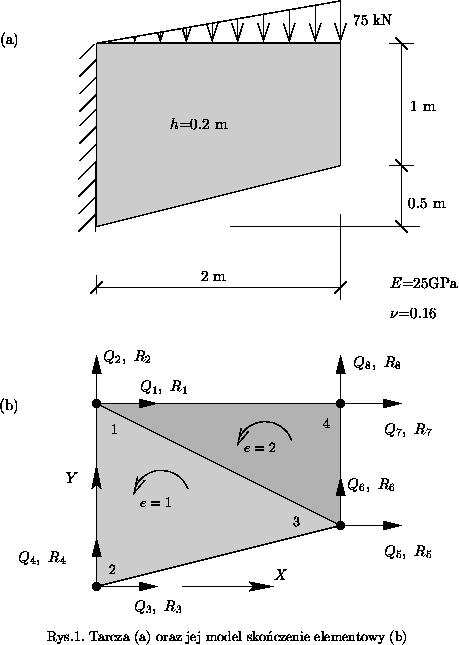
Przykład rozwi zania tarczy MES
1
ORIGIN
1
Stałe materiałowe Wzór na obliczenie pola elementów E
25e6
v
0.16
h
0.2
0 1.5
wsp
wsp
wsp
top
,
top
,
top
,
e,
1
1
e,
1
2
e,
1
3
0
0
1 2 3
1
wsp
top
A( e )
. wsp
wsp
wsp
top
,
top
,
top
,
2 0.5
1 3 4
2
e,
2
1
e,
2
2
e,
2
3
2 1.5
1
1
1
Obliczenie modułu spr ysto ci
1 v
0
7
6
2.566.10
4.105.10
0
E
v 1
0
D
.
D
6
7
= 4.105.10 2.566.10
0
2
1
v
1
v
0 0
7
.
2
0
0
1.078 10
2007-05-17
Opracowanie: P. Pluci ski, IMKwIL, PK
Przykład rozwi zania tarczy MES
2
Funkcje kształtu
x
y
Nd1( e, x, y)
wsp
.
wsp
.
top
,
wsp top
,
top
,
wsp top
,
e,
2
2
e,
2
3
2 .A( e )
e,
1
3
e,
1
2
2 .A( e )
wsp
.
wsp
.
top
, wsp top
,
top
, wsp top
,
e,
1
2
e,
2
3
e,
1
3
e,
2
2
N1( e , x, y)
Nd1( e , x, y)
2 .A( e )
x
y
Nd2( e, x, y)
wsp
.
wsp
.
top
,
wsp top
,
top
,
wsp top
,
e,
2
3
e,
2
1
2 .A( e )
e,
1
1
e,
1
3
2 .A( e )
wsp
.
wsp
.
top
, wsp top
,
top
, wsp top
,
e,
1
3
e,
2
1
e,
1
1
e,
2
3
N2( e , x, y)
Nd2( e , x, y)
2 .A( e )
x
y
Nd3( e, x, y)
wsp
.
wsp
.
top
,
wsp top
,
top
,
wsp top
,
e,
2
1
e,
2
2
2 .A( e )
e,
1
2
e,
1
1
2 .A( e )
wsp
.
wsp
.
top
, wsp top
,
top
, wsp top
,
e,
1
1
e,
2
2
e,
1
2
e,
2
1
N3( e , x, y)
Nd3( e , x, y)
2 .A( e )
element 1
N1( 1 , x, y)
.16666666666666666667.x
.66666666666666666666.y N2( 1 , x, y)
.33333333333333333333.x
.66666666666666666666.y 1.0000000000000000000
N3( 1 , x, y)
.50000000000000000000.x element 2
N1( 2 , x, y)
.50000000000000000000.x 1.0000000000000000000
N2( 2 , x, y)
1.0000000000000000000.y 1.5000000000000000000
N3( 2 , x, y)
.50000000000000000000.x 1.0000000000000000000.y 1.5000000000000000000
Macierz funkcji kształtu N1( e , x, y)
0
N2( e , x, y)
0
N3( e , x, y)
0
N( e , x, y)
0
N1( e , x, y)
0
N2( e, x, y)
0
N3( e , x, y)
Macierz pochodnych funkcji kształtu d
d
d
N1( e , x, y)
0
N2( e, x, y)
0
N3( e , x, y)
0
d x
d x
d x
d
d
d
B( e , x, y)
0
N1( e , x, y)
0
N2( e , x, y)
0
N3( e , x, y)
d y
d y
d y
d
d
d
d
d
d
N1( e , x, y)
N1( e , x, y)
N2( e, x, y)
N2( e , x, y)
N3( e , x, y)
N3( e , x, y)
d y
d x
d y
d x
d y
d x
A( 1 ) = 1.5
A( 2 ) = 1
0.167
0
0.333
0
0.5
0
0.5
0
0
0
0.5
0
B( 1 , 0 , 0 ) =
0
0.667
0
0.667
0
0
B( 2 , 0 , 0 ) =
0
0
0
1
0
1
0.667
0.167
0.667
0.333
0
0.5
0
0.5
1
0
1
0.5
2007-05-17
Opracowanie: P. Pluci ski, IMKwIL, PK
Przykład rozwi zania tarczy MES
3
Macierze sztywno ci
T
K( e )
B( e , 0 , 0 ) .D.B( e, 0 , 0 ) .h .A( e) 6
5
6
5
5
6
1.651.10
4.96 .10
1.009.10
5.816.10
6.414.10
1.078.10
5
6
4
6
5
5
4.96 .10
3.511.10
8.552.10
3.241.10
4.105.10
2.694.10
6
4
6
5
6
6
1.009.10
8.552.10
2.292.10
9.921.10
1.283.10
1.078.10
K( 1 ) =
5
6
5
6
5
5
5.816.10
3.241.10
9.921.10
3.78 .10
4.105.10
5.388.10
5
5
6
5
6
6.414.10
4.105.10
1.283.10
4.105.10
1.924.10
0
6
5
6
5
5
1.078.10
2.694.10
1.078.10
5.388.10
0
8.082.10
6
5
6
5
1.283.10
0
0
4.105.10
1.283.10
4.105.10
5
6
6
5
0
5.388.10
1.078.10
0
1.078.10
5.388.10
6
6
6
6
0
1.078.10
2.155.10
0
2.155.10
1.078.10
K( 2 ) =
5
6
5
6
4.105.10
0
0
 | Pobierz cały dokument przyklad.rozwiazania.tarczy.mes.wersja.2.pdf rozmiar 57 KB |
