SPIS TREŚCI
1. Czym jest kryptografia?
Na samym początku, warto zastanowić się czym w ogóle jest sama kryptografia.
Otóż jest to dziedzina zajmująca się praktycznym zastosowaniem wiedzy matematycznej
w celu ochrony danych przechowywanych w komputerach, podczas przesyłu informacji
przez sieci, w których występują dane w postaci cyfrowej. Ma ona ogromne znaczenie
w ochronie danych komputerowych. Nie jest to oczywiście pełny opis, ponieważ kryptografia zajmowała się ochroną danych ogólnie, nie tylko komputerowych, jednak w dzisiejszych czasach ma to już raczej tylko znaczenie historyczne.
Początki kryptografii sięgają czasów starożytnych. Już starożytni Egipcjanie szyfrowali swoje hieroglify (przypuszcza się, że symbol chrabąszcza oznaczał papirus) a starożytni Hebrajczycy - niektóre ważniejsze słowa w swoich skryptach. Stosowane metody
były dawniej zazwyczaj dość prymitywne i pozwalały na złamanie szyfrów dostatecznie zdeterminowanemu przeciwnikowi. W pierwszej połowie dwudziestego wieku sytuacja
ta uległa zmianie. Zbudowano wtedy wiele systemów szyfrowania za pomocą urządzeń mechanicznych, systemy te wykorzystywano podczas drugiej wojny światowej.
Część z nich została skutecznie złamana jak na przykład niemiecki system Enigma,
który to w łatach trzydziestych i czterdziestych dwudziestego wieku spędzał sen z powiek generalicji państw Ententy oraz szefom sztabów wojsk alianckich. Balsamem na ich skołatane serca okazała się grupa polskich matematyków - Marian Rejewski, Jerzy Różycki i Henryk Zygalski - którzy to ogromnym nakładem sił doprowadzili do złamania szyfru tej groźnej machiny.
Rozwój kryptografii od swych początków był bardzo silnie związany z celami wojskowymi. W dzisiejszych czasach też wykorzystuje się kryptografię w bankowości internetowej, gdzie wszystkie transakcje odbywają się w tak zwanym bezpiecznym połączeniu, a dodatkowo każda operacja jest zatwierdzana przy użyciu klucza prywatnego.
2. Podstawowe definicje
Tekst jawny
Tekst w postaci pierwotnej, zrozumiałej dla nadawcy i odbiorcy, który zostanie poddany procesowi szyfrowania. Taki tekst może być również odczytany przez osobę trzecią, nieupoważnioną do tego.
Szyfrogram
Tekst zakodowany, w postaci niezrozumiałej dla nadawcy i odbiorcy, który wymaga odszyfrowania.
Szyfrowanie (kodowanie)
Proces przekształcania tekstu jawnego w szyfrogram tak, że zostaje ukryta jego zawartość przed osobami postronnymi. Do przekształcenia używa się algorytmu szyfrującego.
Deszyfrowanie (dekodowanie)
Proces przekształcania szyfrogramu w tekst jawny tak, że jego zawartość zostaje ponownie odkryta. Do przekształcenia używa się algorytmu deszyfrującego.
Algorytm szyfrujący
Sposób zapisu informacji w formie niemożliwej lub skrajnie trudnej do odczytania
przez osobę nieposiadającą dodatkowej informacji, czyli tzw. klucza.
Jest to zatem zdeterminowany zbiór metod postępowania, który prowadzi do zaszyfrowania tekstu jawnego w szyfrogram.
Algorytm deszyfrujący
Zbiór metod służących do przekształcenia szyfrogramu w tekst jawny.
3. Kod ASCII
ASCII (American Standard Codę for Information Interchange) to standardowy sposób przypisania liczb do znaków pisarskich. Jest kodem specjalnym, w którym wszystkim małym i dużym literom, cyfrom, znakom interpunkcyjnym oraz znakom specjalnym zostały przypisane liczby z przedziału od 0 do 127. Dla komputera IBM-PC i jemu kompatybilnych liczby kodu należą do przedziału od 0 do 255. Kod ASCII rozszerzono o liczby z przedziału od 128 do 255 dla oznaczenia symboli matematycznych, prostych symboli graficznych
i kilku znaków specjalnych.
Kod ASCII pierwotnie przeznaczony był dla telefaksów, lecz koniec końców zyskał szerokie zastosowanie w komputerach osobistych. Po raz pierwszy o kodzie ASCII świat usłyszał za sprawa Boba Bemera w maju 1961 roku. Bemer zaproponował wtedy bardziej uniwersalny standard, dzięki któremu komputery są dziś w stanie łatwiej się ze sobą porozumiewać. Pierwsze komputery wiedziały tylko „0" i „1". Ludzie nie chcieli czytać cyfr
i po jakimś czasie powstał pierwszy zestaw znaków. Nazwano go ASCII
(127 kodów znaków). W 1963 roku powstał standard ASCII, dzięki któremu możliwa stała się wymiana danych pomiędzy maszynami zbudowanymi przez różnych producentów. Każdy znak ASCII to 16-bitowa informacja (128 bitów), w której zakodowano litery alfabetu łacińskiego, cyfry arabskie oraz znaki interpunkcyjne, symbole i znaki funkcyjne (np. enter). Z biegiem lat standard poszerzono o znaki narodowe. Siedmiobitowy ASCII jest sercem wszystkich kodów komputerowych, włączając HTML.
Poniżej została umieszczona tabela podstawowych znaków ASCII (od 32 do 127):
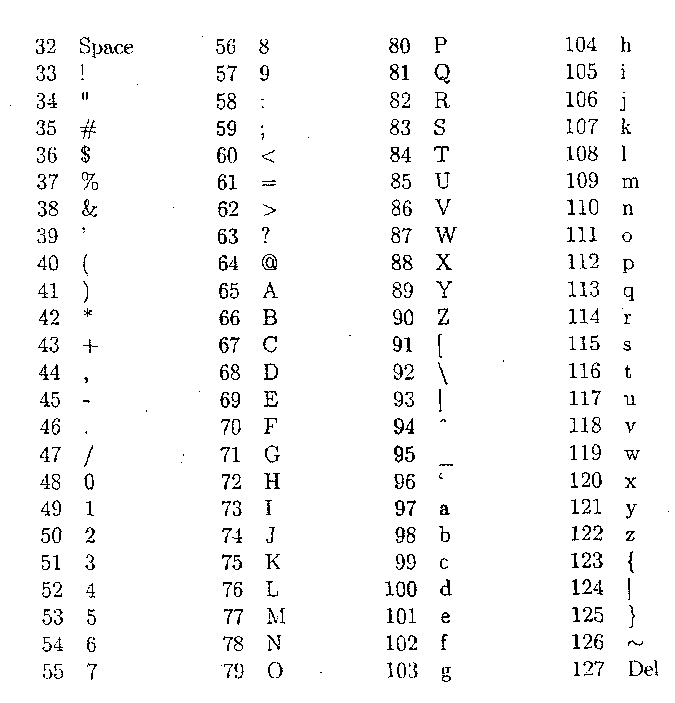
4. Niezbędne twierdzenia
Do skutecznego użytkowania Algorytmu Rabina niezbędna jest znajomość
trzech twierdzeń z arytmetyki modularnej oraz Algorytmu Euklidesa (znajdowania elementu odwrotnego w Zp).
Twierdzenie 1
![]()
Jeżeli p ≡3 (mod4) oraz a jest residuum kwadratowym (modp) (to znaczy: istnieje b: b2≡a (modp)), wówczas
Twierdzenie 2
Jeśli p jest liczbą pierwszą i![]()
wówczas a mamy co najwyżej dwa pierwiastki kwadratowe.
Lemat (chiński)
Jeżeli ![]()
, NWD(m,n) = 1, to układ równań
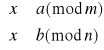
ma dokładnie jedno rozwiązanie (mod![]()
) (w ![]()
).
5. Kim jest Michael Oser Rabin?
Michael Oser Rabin to wybitny matematyk znany przede wszystkim ze swych prac nad teorią i zastosowaniem algorytmów komputerowych. Szczególną uwagę poświęca
on elektronicznemu bezpieczeństwu oraz zastosowaniom metod generowania liczb pseudolosowych.
Michael Rabin urodził się we Wrocławiu (ówczesnym Breslau) w 1931 roku.
Jego ojciec pochodził z Rosji. Kultywując rodzinną tradycję był Rabinem.
Wobec rosnącego w siłę faszyzmu w Niemczech rodzina Rabinów w 1935 roku podjęła decyzję o wyjeździe do Palestyny. Michael Rabin pobierał tam nauki w szkole o charakterze religijnym, gdzie początkowo poświęcił się mikrobiologii by z czasem diametralnie zmienić swe zainteresowania i poświęcić się w pełni „Królowej Nauk" - Matematyce.
Nie zważając na kategoryczne sprzeciwy ojca, którego marzeniem był syn podtrzymujący rodzinną religijną tradycję, Michael kontynuował naukę w szkole o profilu ściśle naukowym. Po szkole rozpoczął studia na Hebrajskim Uniwersytecie w Jerozolimie, gdzie studiował
i w 1953 roku po długiej, wieloletniej i ciężkiej pracy zdobył tytuł Magistra Algebry.
W czasie studiów, po przeczytaniu pracy Alana Turinga, Rabin zafascynował się techniką komputerową, która w tamtych czasach była jeszcze bardzo słabo rozwinięta, można by rzec — w powijakach. W związku z tym, że w Jerozolimie nie było komputerów,
Rabin podjął poważną decyzję, mającą zmienić jego dalsze życie — zdecydował się wyjechać do Stanów Zjednoczonych Ameryki Północnej. W USA Rabin zapoczątkował kolejny etap swojego życia na Stanowym Uniwersytecie w Pensylwanii, co wkrótce otworzyło mu drogę ku studiom doktoranckim z logiki na Uniwersytecie w Princeton.
Praca doktorska Rabina dowiodła, że wiele problemów związanych z teorią grup nie może być rozwiązanych przy pomocy maszyn cyfrowych. W 1957 roku, kiedy Rabin pracował
nad swoją pracą doktorską otrzymał ofertę współpracy z działem Nowych Technologii korporacji IBM (International Business Machines Corporation). Ponieważ IBM zaufało mu
w 100%, Rabin miał „wolną rękę" w doborze kierunku badań którymi chciał się zajmować. Po zrobieniu doktoratu Rabin postanowił kontynuować pracę w firmie IBM, która oferowała mu szerokie spektrum rozwoju naukowego. W tym okresie rozpoczął rozważania nad ideą funkcji jednostronnej - a więc funkcji, której wartość obliczyć jest bardzo łatwo,
podczas gdy znalezienie argumentu dla danej wartości jest ekstremalnie trudne,
wręcz niewykonalne. Badania te dały podstawy całej współczesnej kryptografii.
W 1974 roku Rabin powrócił do prac nad zastosowaniem liczb losowych dla przyspieszenia znajdowania rozwiązań. Techniki te dawały w rezultacie pewną niedokładność, jednakże Rabin zwrócił uwagę na fakt, że przyrost prędkości przyćmiewa ten problem.
W 1975 roku Rabin napotkał publikację Gary'ego Miller'a o Hipotezie Riemanna,
która doprowadziła mistrza do wynalezienia najszybszego znanego algorytmu, który pozwala nam sprawdzić, czy dana liczba naturalna jest liczbą pierwszą.
W 2001 roku Michael O. Rabin zdobył tytuł profesora (Thomas J. Watson Sr. Pro-fessor of Computer Science Harvard Unwersity). Posiada on również tytuł - Albert Einstein Professor of Mathematics and Computer Science at the Hebrew Unwersity in Jerusalem.
W swojej misji ku zwiększeniu elektronicznego bezpieczeństwa Rabin używa złożonych algorytmów, aby bronić dostępu do danych. Rabin i jego student - D. Tygar wprowadzili ITOSS (Itegrated Toolkitfor Operating System Security) - co tłumaczymy,
jako Zintegrowany Zestaw Narzędzi dla Bezpieczeństwa Systemu Operacyjnego.
Rabin jest również deweloperem IDA (Information Dispersal Algorithm) — algorytmu używanego do rozpowszechniania informacji wewnątrz sieci a także w tablicach dysków
(RAID - Redundand Array of Independent Disks).
Rabin pracuje również nad systemem MCB - środowiskiem programowym pozwalającym dużym procesom być obsługiwanym przez wiele połączonych w sieć stacji roboczych. MCB pozwala na użytkowanie szeregu komputerów jako jedną maszynę,
co znacznie zwiększa możliwości obliczeniowe i daje przewagę dzięki zwiększonej tolerancji błędu.
W 1976 roku wspólnie z Daną S. Scott dzięki ich wspólnej pracy zostali laureatami 11-tej nagrody ACM Turing Award. Ta prestiżowa nagroda jest w dziedzinie informatyki odpowiednikiem Nagrody Nobla. Obecnie fundatorem nagrody w wysokości 100 000 dolarów jest korporacja Intel.
Obecnie Michael Rabin spędza pół roku mieszkając w Stanach Zjednoczonych Ameryki Północnej i pracując na Uniwersytecie Harvardzkim, natomiast pozostałą część roku pracuje na Jerozolimskim Hebrajskim Uniwersytecie.
6. Metoda Rabina
Metoda Rabina jest pierwszym kryptosystemem asymetrycznym, która podobnie
jak RSA oparta jest na trudności rozkładu „dużych" liczb na czynniki pierwsze.
Opublikowana w styczniu 1979 roku przez Michaela Rabina. Był to pierwszy kryptosystem, którego bezpieczeństwo zostało udowodnione na drodze matematycznego dowodu,
przy założeniu, że problem szybkiego rozkładu jest nierozwiązywalny. Dowód taki do dziś nie powstał dla algorytmu RSA. Minusem Metody Rabina jest niejednoznaczny wynik dekodowania - za każdym razem zwracane są co najwyżej cztery możliwe rozwiązania,
co w konsekwencji wymaga zastosowania większej złożoności danych wejściowych
(na przykład duplikowanie ostatniego baj tu informacji).
Mechanizm działania Metody Rabina zilustruje poniższy przykład.
Przykład
Na tym przykładzie pokażemy jak wygląda szyfrowanie i deszyfrowanie trzech literek WMS przy pomocy Algorytmu Rabina, używając funkcji szyfrującej -![]()
; (![]()
). Na samym początku przyporządkowujemy literom W, M i S jakieś liczby.
W naszym przypadku niech to będą liczby: 87, 77, 83 - zgodnie ze standardowym
Kodem ASCII.
Szyfrowanie (przez Basię) polega na znalezieniu wartości funkcji szyfrującej dla zadanych argumentów(dla nas 87, 77, 83).
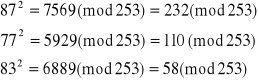
Po wykonaniu tej operacji osoba kodująca, Basia, przesyła otrzymany wynik (232,110,58) osobie deszyfrującej, Kubie. Można powiedzieć, że jedyną i wystarczającą „przewagą” osoby deszyfrującej nad wszystkimi innymi osobami jest znajomość faktoryzacji „liczby modulo”
(u nas jest to liczba ![]()
).
W celu rozszyfrowania wiadomości osoba deszyfrująca wykonuje kolejne operacje:
1) Liczba 232
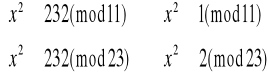
![]()
Następnie korzystając z Twierdzenia 1 i powyższego układu równań można wyliczyć x:
![]()
Czyli również jest możliwe:
![]()
![]()
Czyli również jest możliwe:
![]()
Rozpatrujemy zatem cztery układy równań:
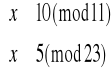


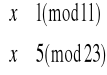
Zajmijmy się układem pierwszym:
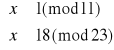
Z pierwszego równania zapisujemy x jako:
![]()
A następnie porównujemy x z obydwu równań z układu:
![]()
![]()
Wyliczamy k z powyższego równania mnożąc obydwie strony przez ![]()
czyli 21 w ![]()
![]()
![]()
Po czym podstawiamy wyliczone k do pierwszej równości i wyliczmy x:
![]()
A co za tym idzie - drugim rozwiązaniem może być również:
![]()
Znaleźliśmy dwa rozwiązania. Jednak rozwiązania te nie spełniają warunków naszego zadania.
Zatem rozwiązujemy układ drugi:
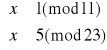
Z pierwszego równania zapisujemy x jako:
![]()
A następnie porównujemy x z obydwu równań z układu:
![]()
![]()
Wyliczamy k z powyższego równania mnożąc obydwie strony przez ![]()
czyli 21 w ![]()
![]()
![]()
Po czym podstawiamy wyliczone k do pierwszej równości i wyliczmy x:
![]()
A co za tym idzie - drugim rozwiązaniem może być również:
![]()
Na tym zakończymy przykład. Znaleźliśmy dwa różne rozwiązania. Z pozostałych dwóch układów znajdziemy jeszcze co najwyżej 4 rozwiązań, jednak będą się one powtarzały. Wybieramy teraz jedno „logiczne” spośród otrzymanych. W naszym przypadku jest to,
rzecz jasna, liczba 87 odpowiadająca literze W.
2) Liczba 110
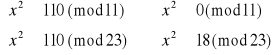
Następnie korzystając z Twierdzenia 1 i powyższego układu równań można wyliczyć x:
![]()
Czyli również jest możliwe:
![]()
![]()
Czyli również jest możliwe:
![]()
Rozpatrujemy zatem tylko dwa układy równań:
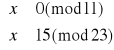
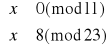
Wystarczy rozwiązać tylko jeden układ, gdyż drugi będzie analogiczny do pierwszego. Zatem zajmijmy się układem pierwszym:
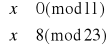
Z pierwszego równania zapisujemy x jako:
![]()
A następnie porównujemy x z obydwu równań z układu:
![]()
Wyliczamy k z powyższego równania mnożąc obydwie strony przez ![]()
czyli 21 w ![]()
![]()
![]()
Po czym podstawiamy wyliczone k do pierwszej równości i wyliczmy x:
![]()
A co za tym idzie - drugim rozwiązaniem może być również:
![]()
Znaleźliśmy dwa różne rozwiązania. Wybieramy teraz jedno „logiczne” spośród otrzymanych. W naszym przypadku jest to, rzecz jasna, liczba 77 odpowiadająca literze M.
3) Liczba 58
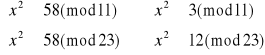
Następnie korzystając z Twierdzenia 1 i powyższego układu równań można wyliczyć x:
![]()
Czyli również jest możliwe:
![]()
![]()
Czyli również jest możliwe:
![]()
Rozpatrujemy zatem cztery układy równań:
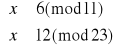

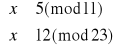

Zajmijmy się układem pierwszym:
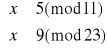
Z pierwszego równania zapisujemy x jako:
![]()
A następnie porównujemy x z obydwu równań z układu:
![]()
![]()
Wyliczamy k z powyższego równania mnożąc obydwie strony przez ![]()
czyli 21 w ![]()
![]()
![]()
Po czym podstawiamy wyliczone k do pierwszej równości i wyliczmy x:
![]()
A co za tym idzie - drugim rozwiązaniem może być również:
![]()
Na tym zakończymy przykład. Znaleźliśmy dwa różne rozwiązania. Z pozostałych trzech układów znajdziemy jeszcze co najwyżej 6 rozwiązań, jednak będą się one powtarzały. Wybieramy teraz jedno „logiczne” spośród otrzymanych. W naszym przypadku jest to, rzecz jasna, liczba 83 odpowiadająca literze S.
Zadanie
Basia i Kuba ustalili kod, w którym liczby odpowiadają symbolom w sposób przedstawiony w poniższej tabelce:
NA |
MA |
LE |
WDY |
KAŻ |
KI |
PRA |
ILE |
DEJ |
JEST |
11 |
12 |
13 |
14 |
15 |
16 |
10 |
18 |
19 |
21 |
22 |
24 |
25 |
26 |
27 |
28 |
31 |
33 |
34 |
35 |
W |
CZY |
NIEJ |
UCE |
TY |
TE |
KA |
ONI |
NIE |
BO |
Wiedząc że funkcja kodująca k(l) = l2(mod 77), odkoduj poniższe hasło wiedząc, że 77=7∙11:
22, 71, 53, 44, 60, 36, 15, 56, 23, 42, 16, 22, 9,56, 67, 14,67, 25
Rozwiązanie:
Dekodujemy liczbę 22:
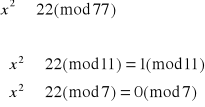
![]()
![]()
![]()
![]()
Otrzymujemy więc dwa równoważne układy równań:

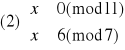
Rozwiązujemy układ (1):
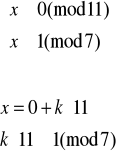
Elementem odwrotnym do 11 w Z7 jest 2 (obliczamy to korzystając z algorytmu Euklidesa), więc:

Mamy więc pierwsze z szukanych rozwiązań x1≡22(mod77). Wiadomo, że element przeciwny do x1 będzie także rozwiązaniem i będzie ono odpowiadało układowi (2), dlatego też nie ma potrzeby rozwiązywania go. Mamy zatem x2≡55(mod77). Jednak spośród otrzymanych rozwiązań jedynym możliwym jest x1≡22(mod77).
Dekodujemy liczbę 71:

![]()
![]()
![]()
![]()
Otrzymujemy więc cztery równoważne układy równań:

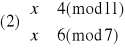
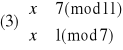
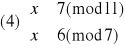
Rozwiązujemy układ (1):
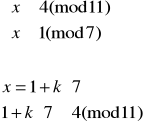
![]()
Elementem odwrotnym do 7 z Z11 jest 8 (obliczamy to korzystając z algorytmu Euklidesa), więc:
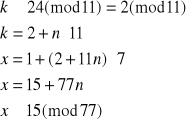
Mamy więc pierwsze z szukanych rozwiązań x1≡15(mod77). Wiadomo, że element przeciwny do x1 będzie także rozwiązaniem i będzie ono odpowiadało układowi (2), dlatego też nie ma potrzeby rozwiązywania go. Mamy zatem x2≡60(mod77).
Rozwiązujemy układ (3):
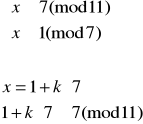
![]()
Elementem odwrotnym do 7 z Z11 jest 8 (obliczamy to korzystając z algorytmu Euklidesa), więc:

Czyli x3≡29(mod 77) oraz x4≡48(mod77). Jednak spośród otrzymanych rozwiązań jedynym możliwym jest x1≡15(mod77).
Dekodujemy liczbę 53:
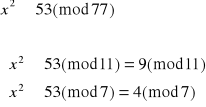
![]()
![]()
![]()
![]()
Otrzymujemy więc cztery równoważne układy równań:

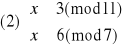

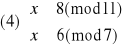
Rozwiązujemy układ (1):
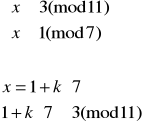
![]()
Elementem odwrotnym do 7 z Z11 jest 8 (obliczamy to korzystając z algorytmu Euklidesa), więc:
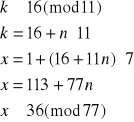
Czyli x1≡36(mod 77) oraz x2≡41(mod77). Jednak nie są poszukiwanym naszym rozwiązaniem.
Zatem rozwiązujemy układ (2):
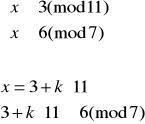
![]()
Elementem odwrotnym do 11 z Z7 jest 2 (obliczamy to korzystając z algorytmu Euklidesa), więc:
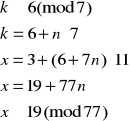
Mamy więc kolejne z szukanych rozwiązań x3≡19(mod77). Wiadomo, że element przeciwny do x1 będzie także rozwiązaniem i będzie ono odpowiadało układowi (3), dlatego też nie ma potrzeby rozwiązywania go. Mamy zatem x4≡58(mod77).
Dekodujemy liczbę 44:
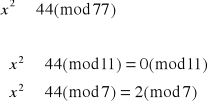
![]()
![]()
![]()
![]()
Otrzymujemy więc dwa równoważne układy równań:
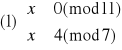

Rozwiązujemy układ (1):

Elementem odwrotnym do 11 z Z7 jest 2 (obliczamy to korzystając z algorytmu Euklidesa), więc:

Mamy więc pierwsze z szukanych rozwiązań x1≡11(mod77). Wiadomo, że element przeciwny do x1 będzie także rozwiązaniem i będzie ono odpowiadało układowi (2), dlatego też nie ma potrzeby rozwiązywania go. Mamy zatem x2≡66(mod77).
Dekodujemy liczbę 23:
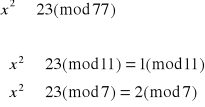
![]()
![]()
![]()
![]()
Otrzymujemy więc cztery równoważne układy równań:
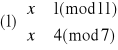

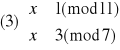
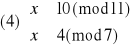
Rozwiązujemy układ (1):
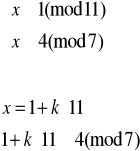
![]()
Elementem odwrotnym do 11 z Z7 jest 2 (obliczamy to korzystając z algorytmu Euklidesa), więc:

Mamy więc pierwsze z szukanych rozwiązań x1≡67(mod77). Wiadomo, że element przeciwny do x1 będzie także rozwiązaniem i będzie ono odpowiadało układowi (2), dlatego też nie ma potrzeby rozwiązywania go. Mamy zatem x2≡10(mod77).
Rozwiązujemy układ (3):


Czyli x3≡45(mod 77) oraz x4≡32(mod77). Jednak spośród otrzymanych rozwiązań jedynym możliwym jest x2≡10(mod77).
Dekodujemy liczbę 42:

![]()
![]()
![]()
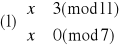
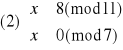
Rozwiązanie układu (1):
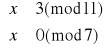

Mamy więc rozwiązania: x1≡14(mod77) oraz x2≡63(mod77).
Drugi układ będzie miał to samo rozwiązanie. Jedynym możliwym rozwiązaniem jest x1≡14(mod77).
Dekodujemy liczbę 16:
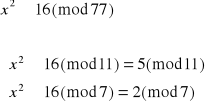
![]()
![]()
![]()
![]()
Otrzymujemy więc cztery równoważne układy równań:
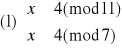

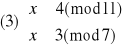
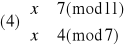
Rozwiązujemy układ (1):
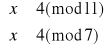
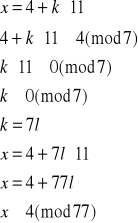
Mamy więc rozwiązania: x1≡4(mod77) oraz x2≡73(mod77).
Rozwiązujemy układ (3):
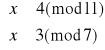

Mamy więc rozwiązania: x3≡59(mod77) oraz x4≡18(mod77).
Jedynym możliwym rozwiązaniem jest x4≡18(mod77).
Dekodujemy liczbę 9:
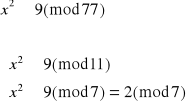
![]()
![]()
![]()
![]()
Otrzymujemy więc cztery równoważne układy równań:
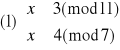
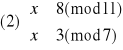
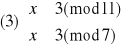

Rozwiązujemy układ (1):

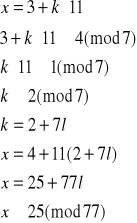
Mamy więc rozwiązania: x1≡25(mod77) oraz x2≡52(mod77).
Rozwiązujemy układ (3):
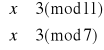
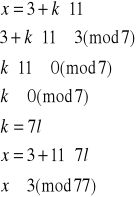
Mamy więc rozwiązania: x3≡3(mod77) oraz x4≡74(mod77).
Jedynym możliwym rozwiązaniem jest x1≡25(mod77).
Dekodujemy liczbę 25:
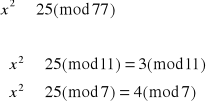
![]()
![]()
![]()
![]()
Otrzymujemy więc cztery równoważne układy równań:
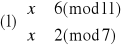
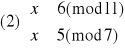
(3) 

Rozwiązujemy układ (1):
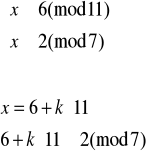
![]()
Elementem odwrotnym do 11 z Z7 jest 2 (obliczamy to korzystając z algorytmu Euklidesa), więc:
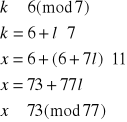
Mamy więc pierwsze z szukanych rozwiązań x1≡73(mod77). Wiadomo, że element przeciwny do x1 będzie także rozwiązaniem i będzie ono odpowiadało układowi (2), dlatego też nie ma potrzeby rozwiązywania go. Mamy zatem x2≡4(mod77).
Rozwiązujemy układ (2):
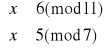
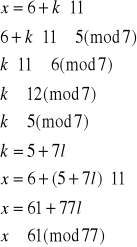
Czyli x3≡61(mod 77) oraz x4≡16(mod77). Jednak spośród otrzymanych rozwiązań jedynym możliwym jest x2≡16(mod77).
Dekodujemy liczbę 67:
![]()
![]()
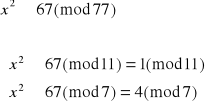
![]()
![]()
![]()
![]()
Otrzymujemy więc cztery równoważne układy równań:


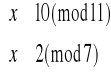

Rozwiązujemy układ (1):
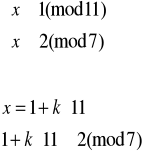
![]()
Elementem odwrotnym do 11 z Z7 jest 2 (obliczamy to korzystając z algorytmu Euklidesa), więc:

Mamy więc pierwsze z szukanych rozwiązań x1≡23(mod77). Wiadomo, że element przeciwny do x1 będzie także rozwiązaniem i będzie ono odpowiadało układowi (2), dlatego też nie ma potrzeby rozwiązywania go. Mamy zatem x2≡54(mod77).
Rozwiązujemy układ (2):
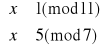
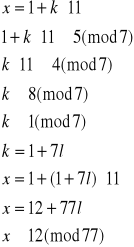
Czyli x3≡12(mod 77) oraz x4≡65(mod77). Jednak spośród otrzymanych rozwiązań jedynym możliwym jest x2≡12(mod77).
Dekodujemy liczbę 14:
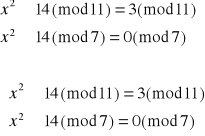
![]()
![]()
![]()
![]()
Otrzymujemy więc dwa równoważne układy równań:

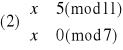
Rozwiązujemy układ (1):

Elementem odwrotnym do 11 z Z11 jest 8 (obliczamy to korzystając z algorytmu Euklidesa), więc:

Mamy więc pierwsze z szukanych rozwiązań x1≡28(mod77). Wiadomo, że element przeciwny do x1 będzie także rozwiązaniem i będzie ono odpowiadało układowi (2), dlatego też nie ma potrzeby rozwiązywania go. Mamy zatem x2≡49(mod77).
Dekodujemy liczbę 15:
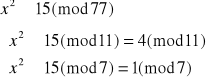
![]()
![]()
![]()
![]()
Otrzymujemy więc cztery równoważne układy równań:
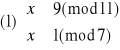

(3) 

Rozwiązujemy układ (1):
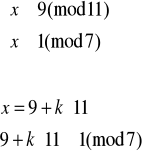
![]()
Elementem odwrotnym do 11 z Z7 jest 2 (obliczamy to korzystając z algorytmu Euklidesa), więc:

Mamy więc pierwsze z szukanych rozwiązań x1≡64(mod77). Wiadomo, że element przeciwny do x1 będzie także rozwiązaniem i będzie ono odpowiadało układowi (4), dlatego też nie ma potrzeby rozwiązywania go. Mamy zatem x2≡13(mod77).
Rozwiązujemy układ (3):
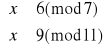

Czyli x3≡20(mod 77) oraz x4≡57(mod77). Jednak spośród otrzymanych rozwiązań jedynym możliwym jest x2≡13(mod77).
Dekodujemy liczbę 36:

![]()
![]()
![]()
![]()
Otrzymujemy więc cztery równoważne układy równań:
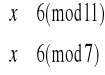
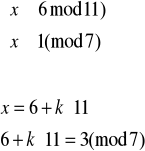

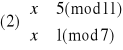
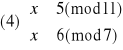
Rozwiązujemy układ (1):
![]()
Elementem odwrotnym do 7 z Z2 jest 2 (obliczamy to korzystając z algorytmu Euklidesa), więc:
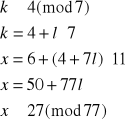
Mamy więc pierwsze z szukanych rozwiązań x1≡27(mod77). Wiadomo, że element przeciwny do x1 będzie także rozwiązaniem i będzie ono odpowiadało układowi (2), dlatego też nie ma potrzeby rozwiązywania go. Mamy zatem x2≡50(mod77).
Rozwiązujemy układ (2):


Czyli x3≡6(mod 77) oraz x4≡71(mod77). Jednak spośród otrzymanych rozwiązań jedynym możliwym jest x2≡27(mod77).
Dekodujemy liczbę 60:
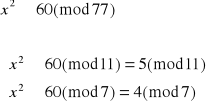
![]()
![]()
![]()
![]()
Otrzymujemy więc cztery równoważne układy równań:
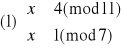



Rozwiązujemy układ (1):
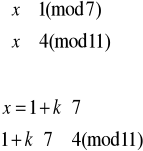
![]()
Elementem odwrotnym do 11 z Z11 jest 2 (obliczamy to korzystając z algorytmu Euklidesa), więc:
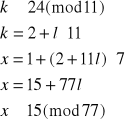
Mamy więc pierwsze z szukanych rozwiązań x1≡15(mod77). Wiadomo, że element przeciwny do x1 będzie także rozwiązaniem i będzie ono odpowiadało układowi (2),
dlatego też nie ma potrzeby rozwiązywania go. Mamy zatem x2≡62(mod77).
Rozwiązujemy układ (2):

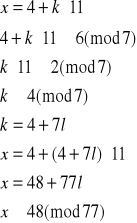
Czyli x3≡48(mod 77) oraz x4≡29(mod77). Jednak spośród otrzymanych rozwiązań jedynym możliwym jest x2≡15(mod77).
Dekodujemy liczbę 56:
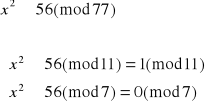
![]()
![]()
![]()
![]()
Otrzymujemy więc dwa równoważne układy równań:


Rozwiązujemy układ (1):
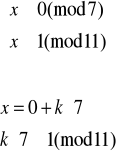
Elementem odwrotnym do 11 w Z11 jest 8 (obliczamy to korzystając z algorytmu Euklidesa), więc:

Mamy więc pierwsze z szukanych rozwiązań x1≡56(mod77). Wiadomo, że element przeciwny do x1 będzie także rozwiązaniem i będzie ono odpowiadało układowi (2),
dlatego też nie ma potrzeby rozwiązywania go. Mamy zatem x2≡21(mod77).
Jednak spośród otrzymanych rozwiązań jedynym możliwym jest x1≡21(mod77).
7. Uogólniona metoda Rabina
Uogólniona metoda Rabina nie różni się znacznie od „zwykłej" Metody Rabina. Główną różnicą jest postać funkcji szyfrującej, która wygląda następująco: ![]()
, gdzie ![]()
, natomiast c jest iloczynem dwóch liczb pierwszych. Różnica w zastosowaniu trudna jest do wyjaśnienia „słownego", więc uważamy, że dobrze zilustruje ją poniższy przykład.
Przykład
Przykład ten przedstawia szyfrowanie i rozszyfrowanie litery W za pomocą uogólnionej metody Rabina. Szyfrowanie odbędzie się za pomocą funkcji szyfrującej k(l) =l2+7l(mod253). Przy deszyfrowaniu pomoże nam rozkład liczby 253 na iloczyn dwóch liczb pierwszych, których reszty z dzielenia przez 4 wynoszą 3 (253=11∙23).
Przyporządkowujemy literze W liczbę 87 zgodnie ze standardowym Kodem ASCII.
Szukamy wartości funkcji szyfrującej dla zadanego argumentu, czyli dla naszej liczby 87:
![]()
Tak, więc po zaszyfrowaniu otrzymaliśmy liczbę 82.
Teraz pokażemy jak ją rozszyfrować:
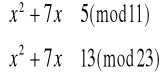

![]()
![]()
Spełnione są więc równania:
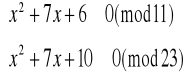
Znajdziemy najpierw pierwiastki równania pierwszego:
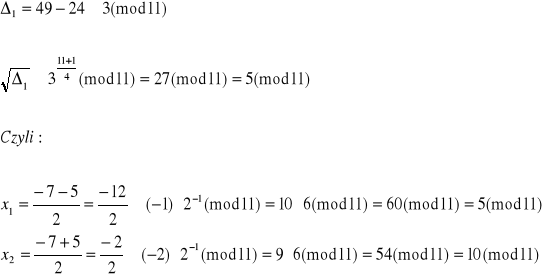
Dla ![]()
otrzymujemy te same pierwiastki.
Szukamy pierwiastków równania drugiego:

Dla ![]()
otrzymujemy te same pierwiastki.
Otrzymujemy, więc cztery układy równań:
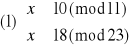


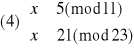
Rozwiązujemy układ (1):
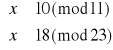
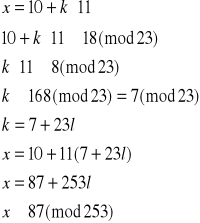
Mamy więc rozwiązania: x1≡87(mod253) oraz x2≡166(mod253).
Rozwiązujemy układ (2):
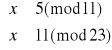
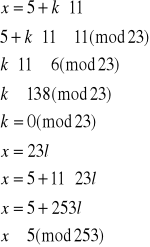
Mamy więc rozwiązania: x3≡5(mod253) oraz x4≡248(mod253).
Zatem otrzymaliśmy szukane rozwiązanie, którym jest x1≡87(mod253).
8. Dodatkowe zadania domowe
Zadanie 1.
Basia chciała żeby Kuba odgadł, jaką bajkę lubiła w dzieciństwie. Podała mu funkcję kodującą k(l) = l 2(mod 437), (437=19∙23). Basia zakodowała swoją informację i posłała Kubie ciąg liczb: 277, 188, 381 oraz poniższą tabelkę. Jaką bajkę zakodowała Basia, wiedząc że kodowała tylko liczby dwucyfrowe podzielne przez 5?
305 |
45 |
25 |
95 |
15 |
65 |
44 |
55 |
75 |
35 |
GU |
MI |
CIU |
MU |
KOP |
MIN |
REK |
SIE |
SZEK |
KI |
Zadanie 2. (Uogólniona metoda Rabina)
Kuba stworzył sobie funkcję kodującą ![]()
. Tylko on zna rozkład liczby 21 na czynniki pierwsze ![]()
i to takie, że ![]()
i ![]()
, co ułatwi jemu rozkodowanie wiadomości. Wcześniej z Basią ustalił jakie litery odpowiadającą poszczególnym wartością liczbowym:
50 |
13 |
225 |
121 |
63 |
38 |
20 |
A |
K |
Ń |
O |
P |
L |
R |
Kuba podaje Basi swoją funkcję kodującą, aby ta mogła jemu przesłać wiadomość. Basia podaje Kubie następujące wartości: 6, 20, 15, 0, 8, 17.
Rozszyfruj wiadomość, jaką Basia chce przekazać Kubie.
7
![]()



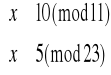
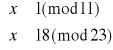


![]()
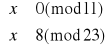

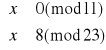
![]()
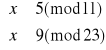

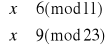
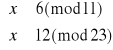

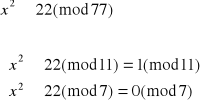
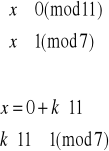
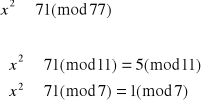
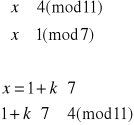
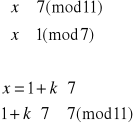


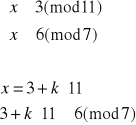

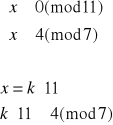

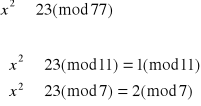
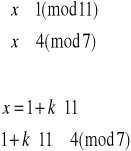



![]()
![]()

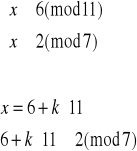
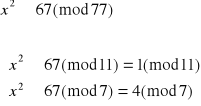
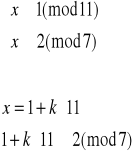


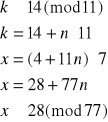
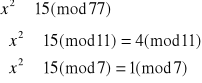
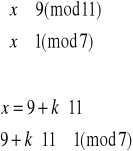

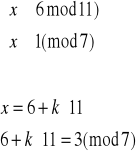
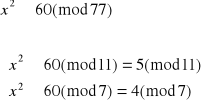
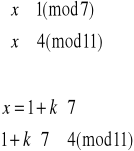

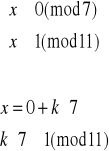

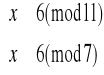



![]()
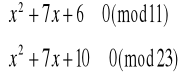
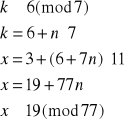
Wyszukiwarka
Podobne podstrony:
Dezynfekcja metody, stosowane preparaty, mechanizm działania, badanie ich aktywności; Promieniowani
Mechanizmy działania antybiotyków, materiały farmacja, Materiały 4 rok, farmacja 4 rok part 2, farma
Toksykologia - Wykład 3 - Mechanizmy działania, szkoła bhp, Toksykologia
Mechanizmy Działania Rynku Finansowego UE z ubieglego roku takie same
Jaki jest mechanizm działania zabiegów na rozstępy
Zbrodnia doskonała Mechanizm działania przemocy emocjonalnej podejście poznawczo behawioralnex
Mechanizm działania leku
Mechanizmy działania toksycznego
Mechanizmy działania toksycznego
MECHANIZM DZIAŁANIA BODŹCÓW FIZYKOTERAPEUTYCZNYCH, MEDYCYNA, Fizykoterapia, FIZYKOTERAPIA
Wojna, Mechanizmy i skutki działania systemu totalitarnego, Mechanizmy i skutki działania systemu to
Metodyczne działanie, Metodyczne działanie -„wola działania”, wziąć z własnej woli w czy
Wojna, Mechanizmy i skutki działania systemu totalitarnego, Mechanizmy i skutki działania systemu to
Metodyczne działanie, Metodyczne działanie -„wola działania”, wziąć z własnej woli w czy
RODZAJE I MECHANIZMY DZIAŁANIA ŚRODKÓW ODKAŻAJĄCYCH I ANTYSEPTYCZNYCH
Molekularne mechanizmy działania różnych rzeczy (2)
Indywidualne Plany Dzialania metody
działalnosc metody, Studia, Pedagogika
więcej podobnych podstron