XVIII Przestrzenie liniowe. Liniowa niezależność układów. Baza i wymiar p-ni liniowej. Suma prosta p-ni liniowych.

Definicja

Niech V będzie dowolnym zbiorem niepustym i F dowolnym ciałem. Uporządkowaną czwórkę
nazywamy p-nią liniową (wektorową) nad ciałem F jeżeli:

1). (V,+) jest grupa abelową, tzn.

a).

b).

c).

d).

e).

f).

2).

3).

4).

5).

6).
.

Definicja

Niech V będzie PL nad ciałem F i
. Jeżeli
jest PL to nazywamy ją podprzestrzenią p-ni
.

Twierdzenie

Niech V będzie PL nad ciałem F i
. Na to by
była podp-nią p-ni
potrzeba i wystarcza, by

1).

2).

3).
.

Przykład

P-niami są

Twierdzenie

Niech
będzie PL. Wówczas

a). dla dowolnych
i dowolnego

(*)
co będziemy też zapisywać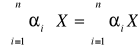

b). dla dowolnego
i dowolnych

(**)
co będziemy zapisywać
.

TWIERDZENIA DOTYCZĄCE WŁASNOŚCI DZIAŁAŃ

Twierdzenie

Niech
będzie p-nią liniową. Wówczas
.

Twierdzenie

Niech
będzie PL. Wówczas
.

Twierdzenie

Niech
będzie PL. Wówczas
.

Definicja

Niech v będzie PL nad ciałem F. Niech
oraz
. Element

(*)
nazywamy kombinacją liniową wektorów
o współczynnikach
. Zbiór wszystkich kombinacji liniowych wektorów
oznaczamy symbolem
i nazywamy zbiorem generowanym prze układ
.

Definicja

Układ wektorów
PL V nad ciałem F nazywamy lnz jeżeli

Układ wektorów
PL V nad cialem F nazywamy lz jeżeli nie jest on lnz czyli

.

Przykład

Przykład p-ni z wymiarem bazy
np. p-ń ciągów.

Definicja

Niech V będzie PL nad ciałem F. Zbiór
nazywamy bazą p-ni V jeżeli

1). B jest lnz

2). V=C[B] (zbiór b generuje p-ń V)

czyli baza p-ni liniowej, to generujący ją podzbiór liniowo niezależny.

Twierdzenie

Niech V będzie PL nad ciałem F. Jeżeli p-ń V generowana jest przez układ n-wektorów, to każdy układ (n+1)-wektorów tej p-ni jest lz.

Twierdzenie

Niech V będzie PL nad ciałem F.

1). Jeżeli p-ń V posiada n-elementową bazę, to każda baza tej p-ni złożona jest z n-elementów

2). Jeżeli p-ń V posiada nieskończoną bazę, to każda baza tej p-ni jest zbiorem nieskończonym.

Twierdzenie

Każda nietrywialna p-ń liniowa posiada bazę.

Definicja

Wymiarem nietrywialnej PL nazywamy ilość wektorów bazy tej p-ni, gdy ta jest skończona i przyjmujemy nieskończoność w przeciwnym wypadku. Wymiar p-ni liniowej V oznaczać będziemy symbolem dimV: mamy więc

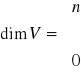
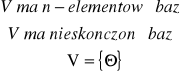
Definicja

P-ń liniową V nad ciałem F nazywamy skończenie wymiarową jeżeli
.

Definicja

Niech U i W będą podp-niami liniowymi PL V nad ciałem F. Powiemy, że p-ń V jest sumą algebraiczną swych podp-ni U i W jeżeli

(*)

Fakt, że V jest sumą algebraiczną swych podp-ni U i W zapisujemy V=U+W. Mamy więc

(*)

Powiemy, że p-ń Vjest sumą prostą swych podp-ni U i W jeżeli

(**)

Fakt, że V jest sumą prostą swych podp-ni U i W zapisujemy
. Mamy więc

(**)

oczywiście, jeżeli
, to V=U+W.

Twierdzenie

Niech U i W będą podp-niami liniowymi PL V nad ciałem F. Wówczas

.

Twierdzenie

Niech U i W będą podp-niami liniowymi skończenie wymiarowymi PL V nad ciałem F. Wówczas

.

Twierdzenie

Niech U i W będą podp-niami liniowymi skończenie wymiarowymi PL V nad ciałem F. Wówczas

.

Twierdzenie

Niech V będzie skończenie wymiarową PL nad ciałem F. Wówczas dla dowolnej podp-ni U

p-ni V istnieje taka podp-ń W p-ni V, że
.

Przykład