Ekonomia matematyczna II

Prowadzący ćwiczenia

mgr inż. Piotr Betlej

Funkcja produkcji Cobba-Douglasa

Produkcja

Produkcja jest procesem, w którym poprzez kombinację pracy ludzkiej, środków i przedmiotów pracy oraz przy użyciu właściwej technologii powstają nowe dobra, czyli produkty i usługi.

Rodzaje produkcji

Produkcja wymagająca dużych nakładów rzeczowych składników majątkowych (maszyn, urządzeń) nazywana jest produkcją kapitałochłonną.

Niektóre rodzaje produkcji wymagają zużycia dużej ilości materiału co wyraża się znacznym udziałem kosztów materiałowych w koszty wyrobu np. przemysł metalurgiczny, spożywczy itp. Produkcję taką nazywamy materiałochłonną.

Jeżeli w produkcji przeważają nakłady pracy ludzkie, mówimy o produkcji pracochłonnej.(np. przemysł precyzyjny)

Produkcja jednorodna występuje w przedsiębiorstwach wytwarzających jeden rodzaj wyrobu np. w cementowni itp.

Produkcja różnorodna w przedsiębiorstwach wykonujących różne wyroby np. fabryka wykonująca obrabiarki. Zestaw wyrobów wytwarzanych przez przedsiębiorstwo przemysłowe i wykaz świadczonych przez nie usług nosi nazwę asortymentu produkcji.

Proces produkcyjny

W procesie produkcji zużywane są czynniki produkcji nabywane na rynku bądż zdobyte inną drogą, poza rynkową, są to: ziemia, praca, kapitał, przedsiębiorczość, postęp technologiczny.

Funkcja produkcji

Obrazuje zależność między wielkością poniesionych nakładów (ilością czynników produkcji) na produkcję dóbr a osiągniętymi wynikami (ilość wytworzonego produktu).

W kontekście funkcji produkcji mówi się o tzw. efektywności technicznej produkcji, czyli sytuacji, w której producent maksymalizując efekt produkcji nie będzie wkładał do produkcji więcej czynników aniżeli jest to konieczne dla osiągnięcia tego poziomu efektu.

Funkcja produkcji wskazuje technicznie (a nie ekonomicznie) możliwą wielkość produkcji. Po włączeniu kosztów czynników produkcji do analizy możliwości producenta uzyskamy rzeczywistą wielkość produkcji, jaką może on wytworzyć przy danym poziomie kosztów. Wówczas będziemy mówili o efektywności ekonomicznej produkcji, czyli sytuacji polegającej na takim wykorzystaniu nakładów czynników produkcji, aby koszt wytworzenia jednostki produktu był minimalny. Efektywność ekonomiczna oznacza wybór w oparciu o zasadę najmniejszego kosztu produkcji.

Funkcja produkcji Cobba-Douglasa

Jedną z rodzajów funkcji produkcji jest funkcja Cobba-Douglasa. Jej ogólny wzór jest następujacy:

Q ( K , L ) = aK ^b1 L ^b2

gdzie:

Q - produkcja

K - nakład kapitału

L - nakład pracy

a, b1, b2 - parametry modelu

W funkcji Cobba-Douglasa zakładamy, iż możliwa jest w pewnym stopniu substytucja pomiędzy nakładami. Przykładowo, aby zachować ten samo poziom produkcji, możemy zrezygnować z pewnego ilości kapitału zastępując go pracą i na odwrót, aczkolwiek nie mamy tutaj doczynienia z substytucją doskonałą.

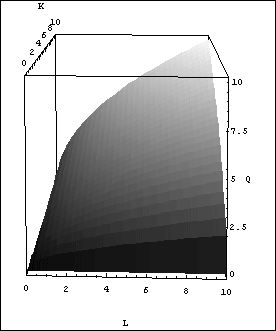
Ilustracja funkcji produkcji Cobba-Douglasa

Funkcja produkcji Cobba-Douglasa jest funkcją dwóch zmiennych - możliwe jest sporządzenie jej ilustracji graficznej. Można sporządzić wykres 3d, w którym osie poziome można oznaczyć L i K, natomiast oś pionową jako Q. Wówczas wykresem tej funkcji będzie płaszczyzna.

Można wykonać inne uproszczone podejście przy konstrukcji wykresu, zakłada się pewien ustalony poziom produkcji, np. Q = 200, a następnie rysuje się wykres na prostokątnym układzie współrzędnych, w którym na osi poziomej nanosimy pracę (L) a na osi pionowej kapitał (K).

Omawiając funkcję produkcji Cobba-Douglasa pokazane zostanie sposób w jaki może zostać zastosowany gradient przy ustalaniu zmian w nakładach czynników produkcji - optymalnego przyrostu nakładów pracy i kapitału, aby rezultat (produkcja) wzrosła możliwie najszybciej (abstrahujemy od kosztów czynników produkcji oraz ograniczeniach budżetowych).

Gradient w danym punkcie określa szybkość i kierunek największego wzrostu funkcji w tym punkcie. Z tego względu pełni niezwykle istotną rolę w optymalizacji funkcji wielu zmiennych.

Naszym zadaniem jest znalezienie kierunku, w którym wartość tej funkcji rośnie najszybciej. Posługujemy się gradientem - wyznaczamy w tym celu pochodne cząstkowe względem pracy oraz kapitału:

Funkcja Q ( L, K ) = K ^0,5 L ^0,5

Q' _L = 0,5 K ^0,5 L ^{0,5 - 1}

Q' _K = 0,5 K ^{0,5 - 1} L ^0,5

Kierunek ustalamy jako wektor złożony z tych pochodnych cząstkowych:


f = [ 0,5 K_o^0,5 L_o^{0,5 - 1} , 0,5 K_o^{0,5 - 1} L_o^0,5 ]

gdzie:

L_o, K_o - wartości początkowe nakładów pracy i kapitału

Zakładając, iż dane są wartości początkowe jesteśmy w stanie odnaleźć przy pomocy gradientu, optymalną kombinację tych nakładów dla której wartość produkcji będzie rosła najszybciej. W poniższej tabelce znajduje się przykład wyznaczania nowych wartości nakładów pracy i kapitału.

Zadanie 1

Dana jest funkcja F ( x, y) = x ² y + y ³ x

a) wyznacz wartość funkcji F ( 1, 2)
b) wyznacz
F = (1, 2)
c) wyznacz wartość funkcji dla punktu (1, 2) przesuniętego o wyznaczony wektor
d) dla punktu wyznaczonego w podpunkcie c wyznacz nowy gradient


Zadanie 2

Jaki jest kierunek najszybszego wzrostu funkcji użyteczności:
u (x, y) = x ² y ⁵, gdy x = 1, y = 2?

Zadanie 3

Dana jest funkcja produkcji Cobba-Douglasa:

F ( K , L ) = 2 K ^0,4 L ^0,6

niech Ko = 10 oraz Lo = 5

a) ile wynosi wartość produkcji
b) o ile zmieni się wartość produkcji jeżeli kapitał wzrośnie o jednostkę?
c) o ile zmieni się wartość produkcji jeżeli praca wzrośnie o jeden procent?
d) wyznacz gradient dla tego punktu
e) ustal dowolną wartość dla mnożnika
f) pomnóż wektor z ustalonym mnożnikiem
g) wyznacz punkty K1 oraz L1
h) dla nowo wyznaczonych punktów wyznacz ponownie gradient


Zadanie 4

Dana jest następująca funkcja produkcji, której wartość jest zależna od trzech rodzajów nakładów (x, y, z):

F ( x , y, z ) = 2 x ^0,4 y ^0,6 z ^0,4

niech xo = 7, yo = 8 oraz zo = 5

a) ile wynosi wartość produkcji
b) o ile zmieni się wartość produkcji jeżeli x wzrośnie o jednostkę?
c) o ile zmieni się wartość produkcji jeżeli z wzrośnie o jeden procent?
d) wyznacz gradient dla tego punktu
e) ustal dowolną wartość dla mnożnika
f) pomnóż wektor z ustalonym mnożnikiem
g) wyznacz nową kombinację czynników produkcji
h) dla nowo wyznaczonych punktów wyznacz ponownie gradient

Gradient

Zagadnienie gradientu oraz jego przykładowe zastosowania. Gradient funkcji n-zmiennych jest to wektor złożony z n-pochodnych cząstkowych stopnia pierwszego tej funkcji.

Załóżmy, iż dla funkcji f ( x ₁, x ₂, ..., x _n) możemy wyznaczyć n pochodnych cząstkowych pierwszego stopnia, które możemy zapisać w następujący sposób:

f _x1, f _x2, ..., f _xn

Gradient, który możemy oznaczyć symbolem
jest wektorem złożonym z tych pochodnych cząstkowych i może zostać zapisany jako:

f = [ f _x1, f _x2, ..., f _xn]

Na przykład dla funkcji f ( x, y) = x ² + xy - y ² gradientem jest:

f =

Gradient w danym punkcie określa szybkość i kierunek największego wzrostu funkcji w tym punkcie. Z tego względu pełni niezwykle istotną rolę w optymalizacji funkcji wielu zmiennych.

Ekonomia matematyczna II mgr inż. Piotr Betlej

Strona 1/5

---