PODSTAWY METOD NUMERYCZNYCH

nauka

metody numeryczne (MN)

sztuka

MN jako nauka: badanie sposobów rozwiązania zadania matematycznego za pomocą działań arytmetycznych.

MN jako sztuka: wybór procedury rozwiązania która jest “najlepiej” dostosowana do danego zadania.

ŹRÓDŁA BŁĘDÓW PRZY ROZWIĄZYWANIU PROBLEMU:

Powstają w dwóch obszarach:

1. Przy matematycznym formułowaniu zadania.

2. Podczas wykonywania obliczeń:

• błędy grube lub pomyłki;

• błąd metody lub obcięcia;

• błąd zaokrąglenia.

Błędy grube ⇐ stosowanie komputerów w obliczeniach zmniejszyło prawdopodobieństwo ich występowania.

Błąd metody lub obcięcia ⇐ rozwiązywanie problemu w postaci przybliżonej, mogącej się różnić od postaci pierwotnej.

Błąd zaokrąglenia ⇐ nieskończone rozwinięcia dziesiętne (lub dwójkowe w komputerze) trzeba zaokrąglać.

DEFINICJE BŁĘDÓW:

Pojęcie pierwotne ⇒ wartość dokładna (WD)

1. Wartość przybliżona (WP) :

wart. dokładna = wart. przybliżona + błąd bezwzględny

WD = WP + BB

2. Błąd względny (BW):
   

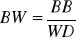
Prosty przykład:

WD =
; przybliżenie dziesiętne: WP = 0.333

BB = WD - WP =
- 0.333 =

BW =
=

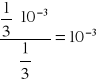
RERGUŁA ZAOKRĄGLEŃ:

Liczba x jest poprawnie zaokrąglona na d-tej pozycji do liczby x^(d) jeżeli błąd zaokrąglenia ε jest taki, że

Jeżeli
⇒ można wybrać zaokrąglenie “w dół” lub “w górę”.

Przykład:

niech WD

wtedy: WP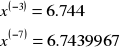

oraz niech WD x = 0.27755000.....

wtedy WP :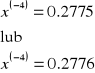

CYFRY ZNACZĄCE:

wartość dokładna: x

wartość przybliżona: y

k-ta cyfra dziesiętna liczby y jest znacząca wtedy gdy:

Przykład:

WD x = 6.74399.......

WP y = 6.7427 ⇐ tylko pierwsze trzy cyfry są znaczące.

KOLEJNOŚĆ OBLICZEŃ A BŁĄD:

Kolejność wykonywania działań i zaokrągleń ma wpływ na błąd wyniku obliczeń.

Przykład:

• obliczenia dokładne (bez błędu zaokrągleń):
  

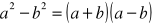
bez względu na wartości a i b.

• obliczenia przybliżone (z błędem zaokrągleń) :

wynik działań
może być różny od wyniku działań
szczególnie, jeżeli a i b są dużymi liczbami mało różniącymi się od siebie.

BŁĄD WARTOŚCI FUNKCJI:

Funkcja wielu zmiennych:
⇐ WD

WD x_i ; WP y_i = x_i - ε_i ; ε_i ⇐ BB zmiennej x_i.

WP funkcji

BB funkcji =
-

BB funkcji =
-
=

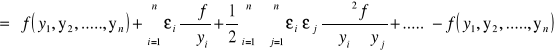
BB funkcji =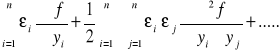

Ostatecznie: BB funkcji

Przykład: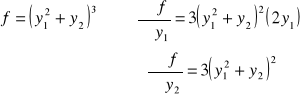

(BB)_f

Niech:

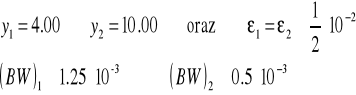
To:

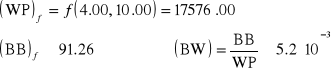
TEORIA STATYSTYCZNA BŁĘDU ZAOKRĄGLENIA:

Rozkład sumy n wzajemnie niezależnych błędów, przy n→
, dąży do rozkładu normalnego.

Przy obliczeniach, w których występuje n działań: max. błąd bezwzględny (BB)_max jest proporcjonalny do n; błąd prawdopodobny BP jest proporcjonalny do
.

ALBEBRA MACIERZY

Określenie macierzy:

Uporządkowany zbiór m x n liczb rozmieszczonych w postaci prostokątnej tabeli o m wierszach i n kolumnach nazywamy macierzą.

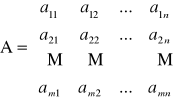
a_ij (i=1,2,...,m ; j=1,2,....,n) - elementy macierzy

A = [ a_ij] - Jest to macierz typu m x n inaczej dim A = m x n

• m = n → macierz kwadratowa

• 
  → macierz prostokątna

• m = 1, n >1 → macierz (lub wektor) wierszowy

• m > 1, n = 1→ macierz (lub wektor) kolumnowy

m = n → macierz kwadratowa

→ macierz prostokątna

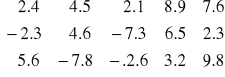
m = 1, n >1 → macierz (lub wektor) wierszowy

m > 1, n = 1→ macierz (lub wektor) kolumnowy

Ważne macierze:

• macierz przekątniowa (lub diagonalna) - macierz kwadratowa m x n o własności: a_ii ≠ 0 , a_ij = 0 dla i ≠ j

A =

• macierz jednostkowa I - jeżeli
  

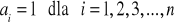
I =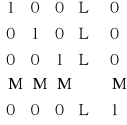

symbol Kroneckera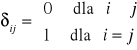
⇒ I = [δ_ij]

• macierz zerowa 0 - jeżeli wszystkie elementy macierzy a_ij = 0

0 =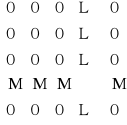

• macierz symetryczna - macierz kwadratowa o własności: a_ij = a_ji

• macierz asymetryczna - macierz kwadratowa o własności: a_ij = -a_ji

Podstawowe działania na macierzach:

1. Równość macierzy: dim A = dim B

A = B → a_ij = b_ij

=

2. Dodawanie dwóch macierzy: dim A = dim B = dim C

C = A + B → c_ij = a_ij + b_ij

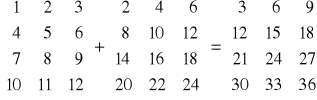
Własności:

1. A + B = B + A

2. A + 0 = A

3. A + ( B + C ) = ( A + B ) + C

3. Odejmowanie dwóch macierzy: dim A = dim B = dim C

C = A - B → c_ij = a_ij - b_ij

A - B = A + (-B)

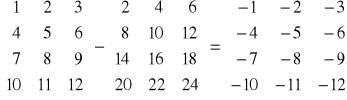
4. Mnożenie macierzy przez liczbę: dim B = dim A

B = αA = Aα → b_ij =α a_ij

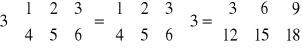
Własności:

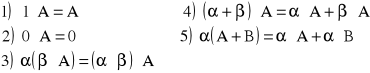
5. Mnożenie macierzy przez macierz:

Dane: dim A = m x n dim B = n x q

tzn. liczba kolumn A = liczbie wierszy B

Określamy macierz C, taką, że dim C = m x q, której współczynniki

określone są wzorem:

wtedy:
← macierz C jest iloczynem macierzy A i B.

Własności: (A, B, C - macierze; α - skalar (liczba)

1. 
   

2. 
   

3. 
   

4. 
   

5. 
   

6. 
   

Ad. 1

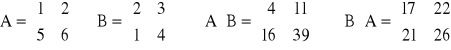
ale
nie ma sensu

6. Transpozycja macierzy:

A → A^T

Macierz transponowana powstaje z macierzy wyjściowej przez zamianę wierszy z kolumnami.

B = A^T → b_ij = a_ji

dim A = m x n → dim B = dim A^T= n x m.

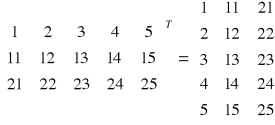
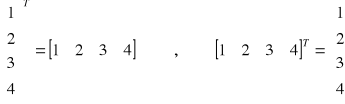
Własności:

1. (A^T)^T = A

2. (A + B)^T = A^T + B^T

3. 
   

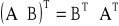
Wniosek: Macierz identyczna ze swoją macierzą transponowaną jest macierzą symetryczną. A^T = A → a_ij = a_ji czyli: macierz symetryczna jest macierzą kwadratową, której elementy są symetryczne względem przekątnej głównej.

Twierdzenie: Iloczyn macierzy i jej macierzy transponowanej jest macierzą symetryczną,
.

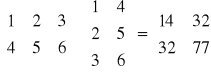
7. Wyznacznik macierzy kwadratowej

A_{n x n} = [ a_ij] =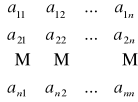

←

Tej tablicy przypisujemy pewną liczbę W obliczana wg ściśle określonych reguł i zwaną wyznacznikiem:

W = det A =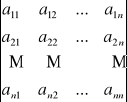
=

SPOSÓB OBLICZANIA WYZNACZNIKA:

Krok 1: Z kolejnych wierszy macierzy wybieramy po jednym elemencie, każdy leżący w innej kolumnie.

Wybieramy wszystkie możliwe kombinacje.

Np. dla macierzy 3 x 3:

Możliwosci Permutacje t

wyboru drugich indeksów

A =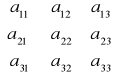

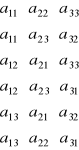
1 2 3 0 +

1 3 2 1 -

2 1 3 1 -

2 3 1 2 +

3 1 2 2 +

3 2 1 3 -

Krok 2: Dla każdej możliwości określa się najmniejszą liczbę przestawień t odpowiedniej permutacji, przywracającą naturalny porządek 1,2, 3, . . . , n.

Np.

Reguła obliczania liczby przestawień:

Idąc w danej permutacji od lewej doprawej strony sumuje się ilość cyfr po prawej stronie kolejnej cyfry, które są od niej mniejsze.

Permutacje: 3 2 1 2 3 1 5 3 1 2 4

↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓

t = 2+1 = 3 1+1 = 2 4+2+0+0 = 6

Krok 3: Tworzy się sumę iloczynów elementów wybranych w kroku 1 opatrzonych znakiem “+” gdy ilość przestawień stowarzyszonej permu-tacji wyznaczona w kroku 2 jest parzysta lub znakiem “-“ jeżeli jest nie-parzysta.

Dla rozpatrywanego przykładu:

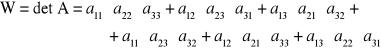
Ogólnie: dla macierzy A_{n x n}

gdzie sumowanie jest rozciągniete na wszystkie możliwe permutacje j₁, j₂, j₃, . . ., j_n ciągu liczb 1, 2, 3, . . ., n zaś t jest liczbą przestawień.

Wyznacznik macierzy diagonalnej:

A =
→ det A =

Wyznacznik macierzy 2 x 2:

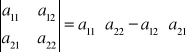
Wyznacznik macierzy 3 x 3:

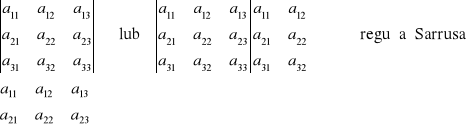
Własności wyznacznika:

1. Zamiana dwóch wierszy macierzy zmienia znak wyznacznika.

2. Pomnożenie wiersza przez liczbę powoduje pomnożenie wyznacznika przez tą samą liczbę.

3. Jeżeli dwa wiersze w macierzy są identyczne to wyznacznik jest równy zero.

4. Dodanie do jednego wiersza innego wiersza pomnożonego przez dowolną liczbę nie zmienia wartości wyznacznika.

5. Wyznacznik macierzy transponowanej jest taki sam jak macierzy oryginalnej.

Uwaga: Własności 1 ÷ 4 dotyczą również kolumn macierzy ← konsek-wencja własności 5 (det A^T = det A ).

Definicja: Macierz, której wyznacznik jest równy zeru nazywamy macierzą osobliwą.

Numeryczne wyznaczanie wartości wyznacznika:

Korzystając z własności 4, wyznacznik macierzy oryginalnej przekształcamy do wyznacznika macierzy diagonalnej.

Przykład 1: det A =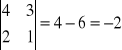

det A =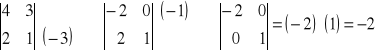

Przykład 2: det A =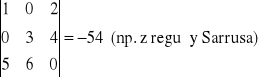

det A=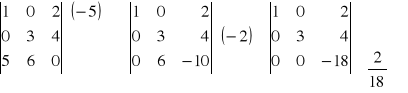

INNA METODA WYZNACZANIA WARTOŚCI WYZNACZNIKA MACIERZY

Dana jest macierz kwadratowa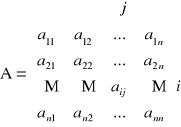

Usuwamy z A i - ty wiersz i j - tą kolumnę → macierz A^ij dim A^ij =(n-1) ×(n-1)

Podwyznacznik macierzy A odpowiadający elementowi a_ij:

minor (a_ij) = (-1)^i+j det A^ij

Wtedy zachodzi:

Przykład: det A =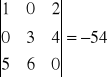

Wybieramy pierwszy wiersz do rozwinięcia: n = 3, i = 1, j = 1, 2, 3

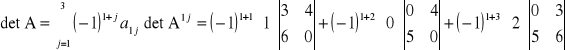
ROZKŁAD MACIERZY NA SKŁADOWĄ SYMETRYCZNĄ I ASYMETRYCZNĄ

Dana jest A = [a_ij]

Można napisać: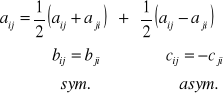

czyli A = B + C

gdzie:

Przykład:

MACIERZ TRÓJKĄTNA

Macierz kwadratowa, której elementy położone ponad (lub pod) główną przekątną są równe zeru.

Dolna macierz trójkątna:

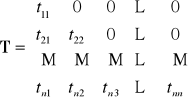
T = [t_ij] t_ij= 0 dla j>i

Górna macierz trójkątna:

T = [t_ij] t_ij= 0 dla i>j

Wyznacznik macierzy trójkątnej:

ROZKŁAD MACIERZY KWADRATOWEJ NA ILOCZYN DWÓCH MACIERZY TRÓJKĄTNYCH

Dana jest nieosobliwa macierz A_{n x n} (det A ≠0)

wtedy:

L = [l_ij] - dolna macierz trójkątna

U = [u_ij] - górna macierz trójkątna

taka, że u_ii = 1

Inny rozkład:

= [l_ij] - dolna macierz trójkątna taka, że l_ii = 1

= [u_ij] - górna macierz trójkątna

Ogólnie:

Jeżeli macierz A jest symetryczna, to zachodzi A^T = A

Wtedy:

Ale równocześnie:

Zatem (z porównania):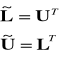
jeżeli A jest symetryczne.

NORMA MACIERZY KWADRATOWEJ

Norma - to miara “wielkości” macierzy.

Największa suma w bezwzględnych wartości elementów w kolumnie.

Norma Euklidesowa: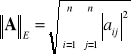

MACIERZ ODWROTNA DO DANEJ MACIERZY

Dana jest macierz kwadratowa A_{n x n} nieosobliwa. Macierzą odwrotną do macierzy A jest macierz B spełniająca

warunek:

tzn.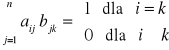

Macierz odwrotną B oznacza się najczęściej przez A^-1 , tzn.

A
A^-1 = I

Własności:

1. (A^T)^-1=(A^-1)^T

2. Jeżeli A jest symetryczna, to A^-1 jest również symetryczna.

3. (A
   B)^-1 = B^-1
   A^-1

4. (A^-1)^-1 = A

METODY WYZNACZANIA MACIERZY ODWROTNEJ

Metoda 1: Wykorzystując definicję podwyznacznika (minora) macierzy A:

B = A^-1 →

Metoda 2: Korzystając z rozkładu macierzy A na iloczyn macierzy trójkątnych.

Niech:

Wtedy:

WARTOŚCI WŁASNE MACIERZY KWADRATOWEJ

Wartościami własnymi kwadratowej macierzy A są liczby λ_i będące rozwiązaniami równania wyznacznikowego:

To równanie nazywamy równaniem charakterystycznym i ma ono postać:

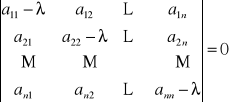
Wyznaczanie największej co do wartości bezwzględnej wartości własnej:

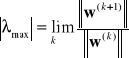
gdzie:

- dowolny niezerowy wektor początkowy

- norma wektora - wart. bezwzględna max. składowej.

UKŁADY LINIOWYCH RÓWNAŃ ALGEBRAICZNYCH

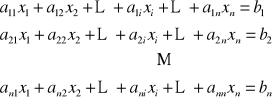
m - liczba równań

n - liczba niewiadomych

1. m > n - brak rozwiązań

2. m < n - nieskończenie wiele rozwiązań n-m zmiennych można przyjąć dowolnie

3. m = n - jedno rozwiązanie (jeżeli det A ≠0)

Typy zagadnień:

1. Macierze pełne ale nieduże (n<30) - metody dokładne eliminacji.

2. Macierze rzadkie ale być może duże (n>100) - metody iteracyjne.

Złe uwarunkowanie macierzy:

Niech: x_d - rozwiązanie dokładne

x₀ - rozwiązanie przybliżone

Zatem: b - Ax_d = 0 oraz b - Ax₀ = r ←wektor reszt

r = A(x_d - x₀) i stąd x_d - x₀ = A^-1r

Jeżeli niektóre elementy A^-1 są bardzo duże, to x₀ może znacznie się różnić od x_d nawet gdy wektor reszt r jest mały.

To zachodzi gdy detA jest bliski zeru - macierz A jest źle uwarunkowana.

Źródła błędów:

1. Błędy współczynników A i b.

2. Błędy zaokrągleń w czasie obliczeń.

3. Błąd metody.

Metody rozwiązania:

• dokładne:
  

• metody iteracyjne:
  

METODA WYZNACZNIKÓW

A x = b → A_{n x n}= [a_ij] b_{n x 1}= {b_i} x_{n x 1}= {x_i}

Wyznacznik główny macierzy A: D = det A

Wyznacznik macierzy A_j powstałej z A przez zastąpienie

j -tej kolumny kolumną wyrazów wolnych b: D_j = det A_j

Wzory Cramera:

Analiza rozwiązań:

D ≠ 0 - układ oznaczony, jedno rozwiązanie.

D = 0 , D_j ≠ 0 - układ sprzeczny, brak rozwiązań.

D = 0 , D_j = 0 - układ jednorodny, wiele rozwiązań.

METODA ELIMINACJI GAUSSA

A x = b det A ≠ 0

Kolumnę b potraktujemy jako dodatkową kolumnę macierzy A.

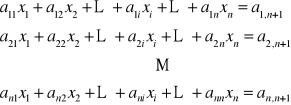
Idea metody:

Etap redukcji:

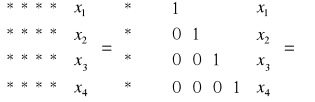
Etap postępowania odwrotnego:

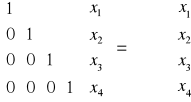
Wariant eliminacji Gaussa - redukcja Gaussa-Jordana

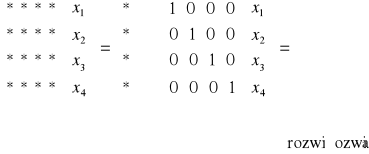
Algorytm redukcji Gaussa-Jordana

⇓

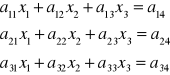
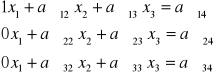
c = a₁₁

a₁₁ = c-1

k=2,4

d = a_1k/c

j=1,3

a_jk=a_jk-d⋅a_j1

c=a₁₁

a₁₁=c-1

d=a₁₂/c d=a₁₃/c d=a₁₄/c

a₁₂=a₁₂-d a₁₁ a₁₃=a₁₃-d a₁₁ a₁₄=a₁₄-d a₁₁

a₂₂=a₂₂-d a₂₁ a₂₃=a₂₃-d a₂₁ a₂₄=a₂₄-d a₂₁

a₃₂=a₃₂-d a₃₁ a₃₃=a₃₃-d a₃₁ a₃₄=a₃₄-d a₃₁

⇓

⇓

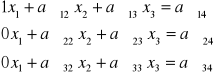
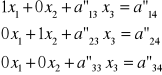
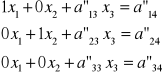
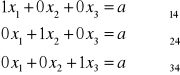
c = a₂₂

a₂₂ = c-1

k=3,4

d = a_2k/c

j=1,3

a_jk=a_jk-d⋅a_j2

c = a₃₃

a₃₃ = c-1

k=4,4

d = a_3k/c

j=1,3

a_jk=a_jk-d⋅a_j3

i=1,3

c = a_ii

a_ii = c-1

k=i+1,4

d = a_ik/c

j=1,3

a_jk=a_jk-d⋅a_ji

Algorytm ogólny:

i=1,n

c = a_ii

a_ii = c-1

k=i+1,m

d = a_ik/c

j=1,n

a_jk=a_jk-d⋅a_ji

METODA
ROZWIĄZANIA UKŁADU RÓWNAŃ

A x = b det A ≠ 0

A =

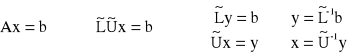
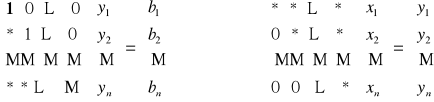
PRZYKŁAD:

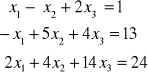
Metoda redukcji Gaussa-Jordana:

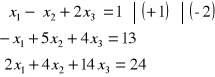
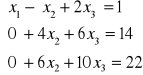
| : 4

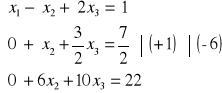
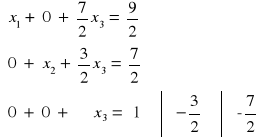
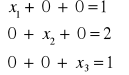
Metoda
:

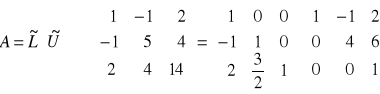
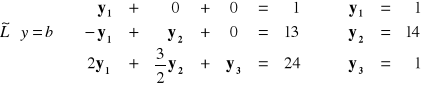
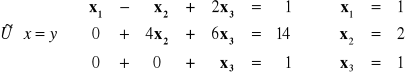
METODY ITERACYJNE

x⁽⁰⁾ - przybliżenie początkowe

x^(k+1) = F_k(x^(k),x^(k-1),. . . . . .,x^(k-l))

F_k - funkcja iteracyjna

Zalety:

1. Mogą być lepsze od metod dokładnych pod względem czasu obliczeń;

2. Są bardziej ekonomiczne pod względem wykorzystania pamięci komputera;

3. Nie przekształca się oryginalnych równań - mniejsze błędy zaokrągleń.

Dany jest układ równań:

stąd:

To sugeruje wzór iteracyjny postaci:

Metoda iteracji prostej (Jacobiego):

gdzie C = I - A

tzn.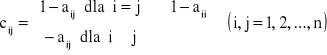

Warunki zbieżności procesu iteracyjnego:

lub

Warunek zakończenia procesu iteracyjnego:

- założona dokładność

Iteracja prosta Gaussa:

Z równania “i” wyznaczamy x_i: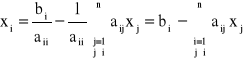

To sugeruje następujący wzór iteracyjny:

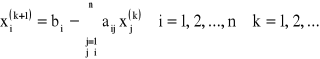
Algorytm:

Krok 1: Zakładamy x⁽⁰⁾ i dokładność obliczeń
, k=0.

Krok 2: Obliczamy nowe przybliżenie x^(k+1) według wzoru:

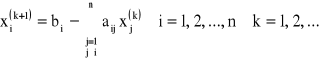
Krok 3: Sprawdzamy kryterium zatrzymania algorytmu:

?

Jeżeli TAK to koniec algorytmu, inaczej: k=k+1, x^(k) = x^(k+1), idź do kroku 2.

Warunek zbieżności algorytmu: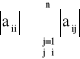
i=1, 2, . . ., n

METODA ITERACJI SEIDLA:

Algorytm:

Krok 1: Zakładamy x⁽⁰⁾ i dokładność obliczeń
, k=0.

Krok 2: Obliczamy nowe przybliżenie x^(k+1) według wzoru:

Krok 3: Sprawdzamy kryterium zatrzymania algorytmu:

?

Jeżeli TAK to koniec algorytmu, inaczej: k=k+1, x^(k) = x^(k+1), idź do kroku 2.

PRZYKŁAD:

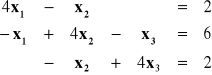
Po przekształceniu: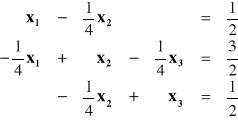

Stąd: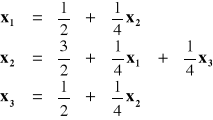

Metoda iteracji prostej: Metoda iteracji Seidla:

METODA NADRELAKSACJI:

Stąd:

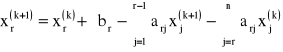
Wprowadzamy wzór zmodyfikowany:

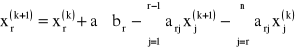
gdzie
- współczynnik nadrelaksacji z zakresu <1,2
1,45.

WIELOMIANY

Wielomian potęgowy

Obliczanie wartości wielomianu dla zadanej wartości zmiennej x
schemat Hornera:

Przykład:

Algorytm obliczania wartości wielomianu
:

i=1,n

Obliczanie kolejnych pochodnych wielomianu:

i.t.d.

Algorytm obliczania kolejnych pochodnych i wartości funkcji:

i=1,n

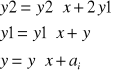
Przykład:

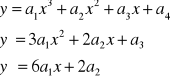
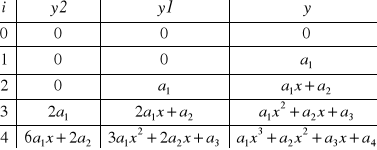
Znajdowanie wielomianu (n-1) stopnia który w punktach
przyjmuje wartości
.

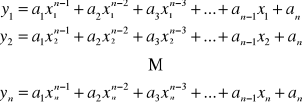
Jest to liniowy układ n równań z n niewiadomymi
.

gdzie

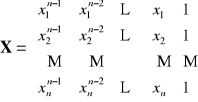
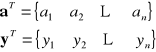
Zatem:

współczynniki poszukiwanego wielomianu.

Przykład: Znaleźć wielomian przechodzący przez 3 punkty (n = 3)

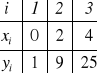
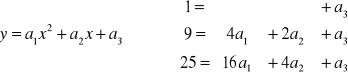
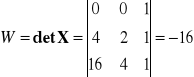
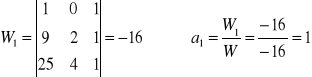
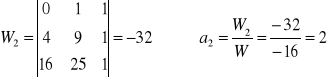
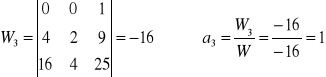
Wielomiany Lagrange'a

Dany jest ciąg wartości: x₁ , x₂ , x₃ , . . . . . , x_i , . . . . , x_n.

Na tym ciągu tworzy się ciąg wielomianów Lagrange'a , tzn, wielomianów

potęgowych stopnia (n-1) L₁(x) , L₂(x), . . . , L_n(x) o własności:

Postać wielomianu Lagrange'a:

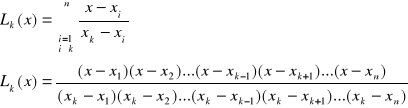
Przykład:

n = 3 , x₁ , x₂ , x₃

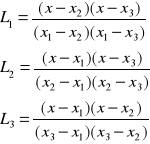
Inna postać wielomianu L_k(x) :

Współczynniki a_ki można obliczyć wykorzystując własność:

Wektor współczynników k-tego wielomianu:

Macierz współczynników:

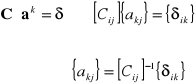
Obliczanie wartości wielomianu L_k(x) w punkcie x = h:

y = L_k(x)

y=0 d=x_k

i=1,n

TAK NIE

i=k ?

y=y(h-x_i)/(d-x_i)

Zastosowanie wielomianów Lagrange'a:

Wielomian , który w zadanych punktach x_k osiąga zadane wartości y_k (k=1,2, . . . ,n).

Przykład:

Dane: (x₁,y₁) , (x₂,y₂) , (x₃,y₃)

Wielomiany Hermite'a:

Dany jest ciąg punktów: x₁, x₂, x₃, . . . . . ., x_n.

Wielomian Hermite'a - wielomian potęgowy stopnia (nm-1) spełniający warunki:

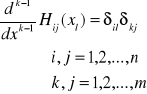
• (k-1) pochodna wielomianu H_lk w punkcie x = x_l przyjmuje wartość 1 , a w pozostałych punktach wartość 0.

• Wszystkie pozostałe pochodne we wszystkich punktach przyjmują wartość 0.

UWAGA: pochodna rzędu zerowego = sama funkcja.

Jeżeli m = 1 tzn. najwyższa pochodna = pochodna zerowa, czyli sama funkcja, to wielomian Hermite'a = wielomian Lagrange'a.

Zwykle ograniczamy się do m = 2
ograniczamy się do wartości funkcji i jej pierwszej pochodnej.

m = 2

k = 1

k = 2

czyli

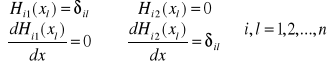
Wielomiany i szeregi Czebyszewa

Wielomian Czebyszewa k-tego stopnia:

Wzór rekurencyjny na tworzenie wielomianów:

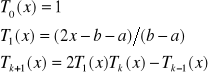
Szereg Czebyszewa: rozwinięcie funkcji w szereg względem wielomianów Czebyszewa :

Pierwsza pochodna rozwinięcia funkcji w szereg Czebyszewa:

Pochodne wielomianów Czebyszewa
różniczkowanie wzorów rekurencyjnych określających te wielomiany.

Obliczanie wartości szeregu Czebyszewa i jego pochodnej w punkcie x.

Dane: współczynniki a_i ,

granice przedziału a , b

wartość zmiennej niezależnej x

Algorytm:

p=4/(b-a) p=2 dT₁/dx

z=2*(2*x-(b+a)/(b-a) z=2T₁

v,v1,w,w1= 0

i=1,n

u1=v1

v1=w1

w1=w1*z-u1+p*w

u=v

v=w

w=w*z-u+a_i

y1=w1-(v1*z+v*p)/2

y=w-v*z/2

INTERPOLACJA FUNKCJI

Nie jest znana postać funkcji
ale znamy jej wartości
w wybranych punktach
i=1,2, . . .,n.

- interpolacja

- extrapolacja

• Interpolacja liniowa

W przedziale
zawierającym x funkcję
aproksymujemy prostą
.

• Interpolacja kwadratowa

W przedziale
zawierającym x funkcję
aproksymujemy wielomianem 2 stopnia (parabolą)

Przykład: (dla funkcji y = e^x )

Dane są 4 punkty:

i x_i y_i

1 0 1.0

2 0.25 1.28403

3 0.50 1.64875

4 0.75 2.11700

Znaleźć y dla x = 0.4 (wart. dokł. 1.49182)

Interpolacja liniowa na podstawie punktów 2 i 3 y = 1.50284 (BW=0.738%)

Interpolacja kwadratowa na podstawie punktów 2, 3 i 4 y = 1.49044 (BW=-0.093%)

Interpolacja kwadratowa na podstawie punktów 1, 2 i 3 y = 1.49318 (BW=0.091%)

METODA KOLOKACJI

Dany jest ciąg punktów

Poszukiwaną funkcję
przybliżymy w postaci:

• 
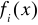
  - znane, przyjęte przez nas dowolnie funkcje, które intuicyjnie najlepiej odwzorowują charakter poszukiwanej funkcji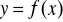
  

Na przykład, można przyjąć:

• 
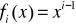
  - wielomian potęgowy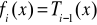

• 
  - szereg Czebyszewa

Współczynniki a_i wyznaczymy żądając aby poszukiwana funkcja przeszła dokładnie przez wszystkie dane punkty, tzn. aby był spełniony warunek:

Zatem

Oznaczając

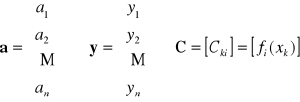
otrzymujemy układ równań liniowych względem a o postaci

i współczynniki a_i wielomianu są określone.

Inny sposób postępowania:

Bezpośrednie wykorzystanie wielomianów Lagrange'a:

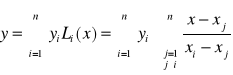
METODA NAJMNIEJSZYCH KWADRATÓW

Dany jest ciąg punktów

Poszukiwaną funkcję
przybliżymy w postaci:

• 
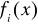
  - znane, przyjęte przez nas dowolnie funkcje, które intuicyjnie najlepiej odwzorowują charakter poszukiwanej funkcji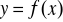
  

Nie można zastosować metody kolokacji do wyznaczenia a_i , gdyż liczba związków typu
jest większa od liczby niewiadomych.

Przy założonych a_i błąd spełnienia k-tego warunku:

czyli

Współczynniki a_i trzeba dobrać tak, aby sumaryczna miara błędu była

najmniejsza.

Błąd sumaryczny (wariancja):

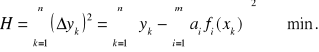
Warunek konieczny minimum:

Wszystkie pochodne cząstkowe
są równe zeru w punkcie minimalnym.

Czyli: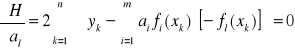

Oznaczmy: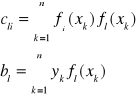

Wtedy: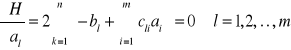

Co prowadzi do układu równań:

Miara błędu niezależna od liczby punktów:

Odchylenie standardowe

Przykład:

Regresja liniowa

Stąd:

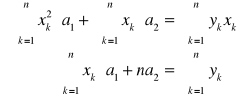
Z tego układu wyznaczamy a₁ i a₂.

RÓŻNICZKOWANIE NUMERYCZNE

Powody:

1. Zbyt skomplikowana analityczna postać funkcji.

1. Wartość funkcji znana tylko w punktach.

Metoda I: Przybliżamy daną funkcję wielomianem interpolacyjnym, a następnie wielomian ten różniczkujemy.

Metoda II: Pochodną funkcji zastępujemy ilorazem różnicowym:

,

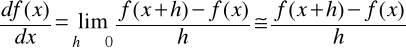
lub inaczej:

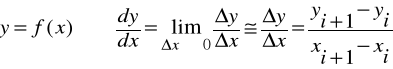
Rodzaje ilorazów różnicowych:

1. Iloraz zwykły:
   

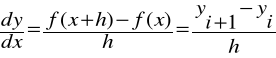
2. Iloraz wsteczny:
   

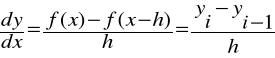
3. Iloraz centralny:
   

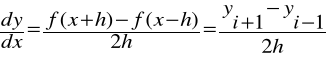
Inaczej:

Ad. 1 f(x) zastępujemy prostą y = a x + b poprowadzoną przez x i x + h.

Ad. 2 f(x) zastępujemy prostą y = a x + b poprowadzoną przez x-h i x.

Ad. 3 f(x) zastępujemy parabolą y = a x² + b x +c poprowadzoną przez x-h , x i x+h.

Pochodne wyższych rzędów:

Iloraz zwykły:

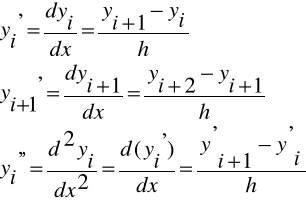
Zatem:

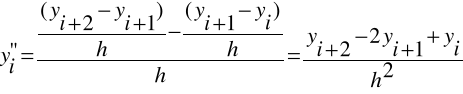
Podobnie: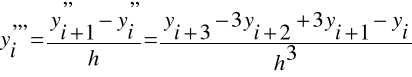
itd.

Identycznie obliczamy wyższe pochodne korzystając z ilorazów wstecznych i ilorazów centralnych.

CAŁKOWANIE NUMERYCZNE

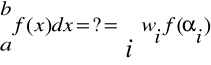
w_i - wagi

- punkty z przedziału <a,b>

Funkcję f(x) aproksymujemy (przybliżamy) wielomianem P(x).

• Można przybliżać jednym wielomianem w całym przedziale <a,b> - wzór kwadratur Gaussa.

• Można przedział <a,b> podzielić na podprzedziały i w każdym podprzedziale przybliżać różnymi wielomianami tego samego (niskiego) stopnia - wzór trapezów, wzór Simpsona.

Wzór trapezów:

Przedział <a,b> dzielimy na n równych podprzedziałów o długości

h = (b - a)/n.

W każdym podprzedziale f(x) zastępujemy prostą a x + b.

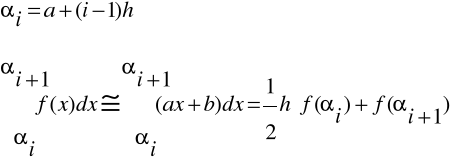
Zatem: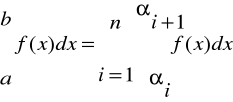

• Stąd:
  

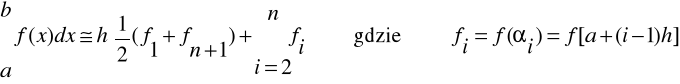
Wzór Simpsona:

Przedział <a,b> dzielimy na n równych podprzedziałów o długości

h = (b - a)/n.

W każdym podprzedziale f(x) zastępujemy parabolą a x² + b x + c.

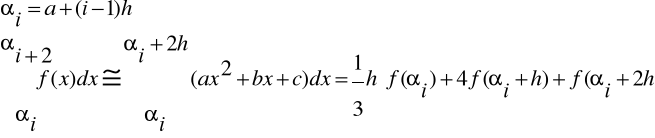
Niech

Zatem: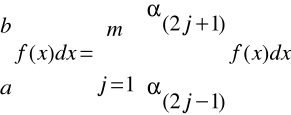

• Stąd:
  

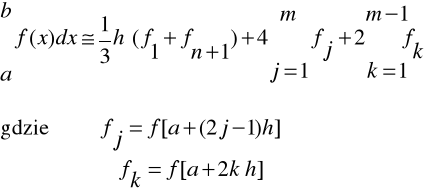
7

---