1. RÓWNANIA RÓŻNICZKOWE RZĘDU PIERWSZEGO

1.1 POJĘCIA WSTĘPNE

Def. 1.1.1 (równanie różniczkowe zwyczajne pierwszego rzędu)

Równaniem różniczkowym zwyczajnym rzędu pierwszego nazywamy równanie postaci:

(R)
.

Uwaga. Będziemy się również posługiwali tzw. formą różniczkową równania różniczkowego, czyli równaniem postaci

.

Jednak najogólniejszą formą równania różniczkowego rzędu pierwszego jest równanie postaci

.

Inaczej mówiąc równanie różniczkowe rzędu pierwszego jest zależnością między funkcją niewiadomą, zmienną niezależną i pierwszą pochodną funkcji niewiadomej.

Def. 1.1.2 (rozwiązanie równania różniczkowego)

Funkcję y(t) nazywamy rozwiązaniem równania różniczkowego (R) na przedziale (a,b), jeżeli jest ona różniczkowalna na tym przedziale oraz zamienia to równanie w tożsamość

,

prawdziwą dla wszystkich t ∈ (a,b). Wykres (rys. 1) rozwiązania równania różniczkowego nazywamy jego krzywą całkową.

Rys. 1 Krzywa całkowa

Uwaga. Analogicznie określamy rozwiązania na przedziałach postaci: [a,b), (a,b], [a,b], (-∞,b), (-∞,b], [a,∞), (-∞,∞). Przy czym w przypadku, gdy rozwiązanie określone jest na przedziale domkniętym z jednego lub obu końców, przez jego pochodną na końcu przedziału rozumiemy odpowiednią pochodną jednostronną. Rozwiązanie równania różniczkowego zadane w postaci uwikłanej

nazywamy całką tego równania. Ponieważ każde rozwiązanie jest całką (niekoniecznie odwrotnie), więc często w odniesieniu do rozwiązań używa się także terminu całka. Stąd mówimy zwyczajowo scałkować równanie różniczkowe, zamiast rozwiązać równanie.

Def. 1.1.3 (zagadnienie początkowe)

Równanie różniczkowe (R) oraz warunek

(W)

nazywamy zagadnieniem początkowym lub zagadnieniem Cauchy'ego.

Uwaga. Zagadnienie początkowe będziemy zapisywali krótko

(RW)

Przy czym liczby t₀ i y₀ nazywamy wartościami początkowymi, a warunek (W) nazywamy warunkiem początkowym.

Def. 1.1.4 (rozwiązanie zagadnienia początkowego)

Funkcja y(t) jest rozwiązaniem zagadnienia początkowego (RW), jeżeli jest rozwiązaniem równania (R) na pewnym przedziale zawierającym t₀ i spełnia warunek (W).

Rys. 2

Uwaga. W interpretacji geometrycznej, rozwiązanie zagadnienia początkowego, polega na znalezieniu wśród wszystkich krzywych całkowych równania (R) tej, która przechodzi przez punkt (t₀,y₀) (rys.2). Jednak zagadnienie to niekoniecznie musi mieć jednoznaczne rozwiązanie. Może istnieć więcej niż jedno rozwiązanie danego zagadnienia początkowego. Istnienie rozwiązań zagadnienia początkowego oraz ich jednoznaczność jest jednym z głównych problemów teorii równań różniczkowych zwyczajnych.

Tw. 1.1.5 (o istnieniu i jednoznaczności rozwiązań równania (R))

Niech funkcja f(t,y) oraz jej pochodna cząstkowa
będą określone i ciągłe na obszarze domkniętym D ⊂ R². Wtedy dla każdego punktu (t₀,y₀) ∈ D, zagadnienie początkowe (RW) ma dokładnie jedno rozwiązanie.

Uwaga. Inaczej mówiąc przy dowolnych wartościach początkowych wybranych z obszaru D istnieje zawsze rozwiązanie zagadnienia początkowego (RW). Co więcej, jeżeli dane są dwa rozwiązania o tych samych wartościach początkowych (W), przy czym każde z rozwiązań określone jest na pewnym przedziale zawierającym punkt t₀, to rozwiązania te pokrywają się na wspólnej części rozważanych przedziałów.

Def. 1.1.6 (rozwiązanie ogólne i szczególne równania różniczkowego)

Rodzinę funkcji

,

zależnych od parametru rzeczywistego C, nazywamy rozwiązaniem ogólnym równania (R), jeżeli:

1. każda funkcja tej rodziny jest jego rozwiązaniem,

2. dla każdego warunku początkowego
, dla którego rozwiązanie istnieje i jest jednoznaczne można dobrać stałą C tak, aby
.

Każdą funkcję otrzymaną z rozwiązania ogólnego równania (R) przy ustalonej wartości parametru C nazywamy rozwiązaniem szczególnym tego równania.

Uwaga. Rozwiązanie zagadnienia początkowego, jeżeli istnieje i jest jednoznaczne, jest rozwiązaniem szczególnym. W praktyce znajomość rozwiązania ogólnego jest bardzo dogodna, gdyż przez odpowiedni dobór parametru C można otrzymać rozwiązanie zagadnienia początkowego. Rozwiązanie ogólne równania różniczkowego, określone w postaci uwikłanej

,

nazywamy całką ogólną tego równania.

1.2 RÓWNANIA RÓŻNICZKOWE O ZMIENNYCH ROZDZIELONYCH

Def. 1.2.1 (równanie różniczkowe o zmiennych rozdzielonych)

Równaniem różniczkowym o zmiennych rozdzielonych nazywamy równanie postaci

(S)
.

Uwaga. Zauważmy, że jeżeli h(y₀) = 0 dla pewnego y₀, to funkcja y(t) ≡ y₀ jest jednym z rozwiązań powyższego równania. W formie różniczkowej o zmiennych rozdzielonych przyjmuje postać

.

Fakt 1.2.2 (całka ogólna równania (S))

Niech funkcje g(t) i h(y) będą ciągłe odpowiednio na przedziałach (a,b) i (c,d), przy czym h(y) ≠ 0 dla każdego y ∈ (c,d). Wtedy całka ogólna równania różniczkowego o zmiennych rozdzielonych (S) dana jest wzorem

Uwaga. Całki w powyższym wzorze rozumiane są jako dowolne, lecz ustalone funkcje pierwotne.

Tw. 1.2.3 (o istnieniu i jednoznaczności rozwiązań równania (S))

Niech funkcje g(t) i h(y) będą ciągłe odpowiednio na przedziałach (a,b) i (c,d), przy czym h(y) ≠ 0 dla każdego y ∈ (c,d). Wtedy dla każdego punktu (t₀,y₀), gdzie t₀ ∈ (a,b), y₀ ∈ (c,d), zagadnienie początkowe

ma dokładnie jedno rozwiązanie.

Uwaga. Inaczej mówiąc, przez każdy punkt (t₀,y₀) prostokąta (a,b)×(c,d) przechodzi dokładnie jedna krzywa całkowa (rys.3) równania y' = g(t)h(y).

Rys. 3

1.3 RÓWNANIA RÓŻNICZKOWE JEDNORODNE

Def. 1.3.1 (równanie różniczkowe jednorodne)

Równaniem różniczkowym jednorodnym nazywamy równanie postaci

(J)
.

Uwaga. Jeżeli f(u) ≡ u, to równanie jednorodne przyjmuje postać
i całkuje się przy pomocy metody rozdzielonych zmiennych. Jego rozwiązanie ogólne dane jest wtedy wzorem y(t) = Ct, gdzie C ∈ R. jeżeli f(u₀) = u₀ dla pewnego u₀, to jedynym rozwiązaniem równania (J) jest funkcja y(t) = u₀t.

Fakt 1.3.2 (o zamianie zmiennych w równaniu jednorodnym)

Równanie jednorodne (J) przez zamianę zmiennych

y=ut

sprowadza się do równania o zmiennych rozdzielonych postaci

tu' = f(u) - u.

Tw. 1.3.3 (o istnieniu i jednoznaczności rozwiązań równania (J))

Niech funkcja f(u) będzie ciągła na przedziale (a,b) i niech spełnia na nim warunek f(u) ≠ u. Wtedy dla każdego punktu (t₀,y₀) takiego, że
zagadnienie początkowe

ma dokładnie jedno rozwiązanie.

Rys. 4

Uwaga. Inaczej mówiąc, przez każdy punkt (t₀,y₀) obszaru

,

przechodzi dokładnie jedna krzywa całkowa (rys. 4) równania (J).

1.4 RÓWNANIA RÓŻNICZKOWE LINIOWE

Def. 1.4.1 (równanie różniczkowe liniowe)

Równaniem różniczkowym liniowym pierwszego rzędu nazywamy równanie postaci

(L)
.

Jeżeli q(t) ≠ 0, to równanie nazywamy niejednorodnym. W przypadku przeciwnym nazywamy je jednorodnym.

Uwaga. Równanie różniczkowe liniowe jednorodne jest szczególnym przypadkiem równania różniczkowego o zmiennych rozdzielonych y'=g(t)h(y), w którym przyjęto g(t) = - p(t), h(y) = y.

Tw. 1.4.2 (o istnieniu i jednoznaczności rozwiązań równania (L))

Niech funkcje p(t) i q(t) będą ciągłe na przedziale (a,b), gdzie -∞ ≤ a < b ≤ ∞. Wtedy dla każdego punktu (t₀,y₀), gdzie t₀ ∈ (a,b) oraz y₀ ∈ R, zagadnienie początkowe

ma dokładnie jedno rozwiązanie. Rozwiązanie to jest określone na przedziale (a,b).

Rys. 5

Uwaga. Inaczej mówiąc, przez każdy punkt pasa (a,b) × R przechodzi dokładnie jedna krzywa całkowa (rys. 5) równania różniczkowego liniowego.

1.5 RÓWNANIE RÓŻNICZKOWE BERNOULLIEGO

Def. 1.5.1 (równanie różniczkowe Bernoulliego)

Równaniem różniczkowym Bernoulliego nazywamy równanie postaci

,

gdzie r∈R-{0,1}.

Uwaga. Gdyby dopuścić r = 0, to równanie Bernoulliego byłoby równaniem różniczkowym liniowym niejednorodnym. Natomiast dla r = 1, równanie to byłoby równaniem różniczkowym liniowym jednorodnym. Zauważmy jeszcze, że dla r > 0 funkcja y(t) ≡ 0 jest zawsze jednym z rozwiązań równania Bernoilliego.

Fakt 1.5.2 (sprowadzanie równania Bernoulliego do równania liniowego)

Równanie Bernoulliego

,

gdzie r ≠ 0, 1, przez zamianę zmiennych
sprowadza się do równania liniowego niejednorodnego postaci

.

1. 6 KRZYWE ORTOGONALNE

Def. 1.6.1 (równanie rodziny krzywych)

Jeżeli równanie

dla każdej wartości parametru C z pewnego przedziału określa krzywą, to nazywamy je równaniem rodziny krzywych (rys. 6).

Def. 1.6.1 (rodzina krzywych ortogonalnych)

Mówimy, że rodziny krzywych (t,y,C) = 0, (t,y,C) = 0 są ortogonalne, jeżeli w każdym punkcie przecięcia krzywych z obu rodzin, krzywe te tworzą między sobą kąt prosty (rys. 7).

Rys. 6	Rys. 7

Fakt 1.6.2 (równanie różniczkowe rodziny krzywych ortogonalnych)

Jeżeli F(t,y,y') = 0 jest równaniem różniczkowym rodziny krzywych, to równanie różniczkowe rodziny krzywych ortogonal­nych ma postać

.

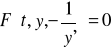
1.7 POJĘCIA WSTĘPNE DLA RÓWNAŃ RÓŻNICZKOWYCH WYŻSZYCH RZĘDÓW

Def. 1.7.1 (równanie różniczkowe zwyczajne n-tego rzędu)

Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie postaci

(R)
.

Uwaga. Najogólniejszą formą równania różniczkowego rzędu n jest wyrażenie postaci
.

Def. 1.7.2 (rozwiązanie równania różniczkowego n-tego rzędu)

Funkcję y(t), różniczkowalną n-krotnie na przedziale otwartym (a,b), nazywamy rozwiązaniem równania różniczkowego (R) na tym przedziale, jeżeli zamienia to równanie w tożsamość

prawdziwą dla wszystkich t należących do przedziału t ∈ (a,b). Wykres rozwiązania równania różniczkowego nazywamy jego krzywą całkową.

Def. 1.7.3 (zagadnienie początkowe)

Równanie różniczkowe (R) oraz warunki

(W)
,

nazywamy zagadnieniem początkowym lub zagadnieniem Cauchy'ego.

Uwaga. Zagadnienie początkowe będziemy zapisywali krótko

(RW)
,

przy czym liczby t₀ i y₀, y₁, ..., y_n-1 nazywamy wartościami początkowymi, a warunek (W) nazywamy warunkiem początkowym.

Def. 1.7.4 (rozwiązanie zagadnienia początkowego)

Funkcja y(t) jest rozwiązaniem zagadnienia początkowego (RW) jeżeli jest rozwiązaniem równania (R) na przedziale zawierającym punkt t₀ i jeżeli spełnia warunki (W).

Def. 1.7.5 (rozwiązanie ogólne i szczególne równania różniczkowego)

Rodzinę funkcji

zależnych od n rzeczywistych parametrów C₁, C₂, ..., C_n nazywamy rozwiązaniem ogólnym równania
, jeżeli:

1. każda funkcja tej rodziny jest rozwiązaniem tego równania,

2. dla każdego układu warunków początkowych
,
, ...,
, dla którego rozwiązanie istnieje i jest jednoznaczne, można dobrać stałe C₁, C₂, ..., C_n tak, aby

.

Każdą funkcję otrzymaną z rozwiązania ogólnego równania (R) przy ustalonych wartościach parametrów C₁, C₂, ..., C_n nazywamy rozwiązaniem szczególnym tego równania.

Uwaga. Rozwiązanie zagadnienia początkowego, jeżeli istnieje i jest jednoznaczne, jest rozwiązaniem szczególnym. W praktyce znajomość rozwiązania ogólnego jest bardzo dogodna, gdyż przez odpowiedni dobór parametrów C₁, C₂, ..., C_n można otrzymać rozwiązanie zagadnienia początkowego.

1.8 RÓWNANIA RZĘDU DRUGIEGO SPROWADZALNE DO RÓWNAŃ RZĘDU PIERWSZEGO

Fakt 1.8.1 (równanie różniczkowe postaci y'' = f(t,y'))

Równanie różniczkowe drugiego rzędu postaci

przez podstawienie y' = u sprowadza się do równania różniczkowego rzędu pierwszego postaci

.

Fakt 1.8.2 (równanie różniczkowe postaci y'' = f(y,y'))

Równanie różniczkowe drugiego rzędu postaci

przez podstawienie y = q(y) sprowadza się do równania różniczkowego rzędu pierwszego postaci

.

2. RÓWNANIA RÓŻNICZKOWE LINIOWE WYŻSZYCH RZĘDÓW

2.1 POJĘCIA WSTĘPNE

Def. 2.1.1 (Równanie różniczkowe liniowe rzędu n)

Równaniem różniczkowym liniowym rzędu n nazywamy równanie postaci

(L_n)
.

Uwaga. Jeżeli n = 2, to będziemy pisali p(t) i q(t) zamiast odpowiednio p₁(t) i p₂(t). Równanie różniczkowe liniowe rzędu drugiego ma wtedy postać

(L₂)
.

Tw. 2.1.2 (o istnieniu i jednoznaczności rozwiązań dla równania (L_n))

Niech funkcje p₁(t), p₂(t), ..., p_n(t) i h(t) będą ciągłe na przedziale (a,b). Wtedy dla każdego punktu (t₀, y₀, y₁, ..., y_n-1) ∈ (a,b) × Rⁿ zagadnienie początkowe

,

ma dokładnie jedno rozwiązanie. Rozwiązanie to jest określone na przedziale (a,b).

2.2 RÓWNANIA RÓŻNICZKOWE LINIOWE JEDNORODNE

Def. 2.2.1 (równanie różniczkowe liniowe jednorodne)

Równaniem różniczkowym jednorodnym rzędu n nazywamy równanie postaci

(LJ_n)
.

Uwaga. Dla równania drugiego rzędu w tym przypadku (LJ₂) piszemy p(t) i q(t) zamiast odpowiednio p₁(t) i p₂(t), czyli

(LJ₂)
.

Fakt 2.2.2 (o kombinacji liniowej rozwiązań równania jednorodnego)

Niech ϕ(t), (t) będą rozwiązaniami równania jednorodnego (LJ_n). Wtedy dla dowolnych stałych ,  funkcja
jest także rozwiązaniem tego równania.

Uwaga. Inaczej mówiąc, dowolna kombinacja liniowa rozwiązań równania różniczkowego liniowego jednorodnego jest również rozwiązaniem tego równania.

Def. 2.2.3 (układ fundamentalny równania (LJ_n))

Układ n rozwiązań (y₁(t), y₂(t), ..., y_n(t)) równania jednorodnego (LJ_n) określonych na przedziale (a,b) nazywamy układem fundamentalnym tego równania na tym przedziale, jeżeli dla każdego t ∈ (a,b) spełniony jest warunek

.

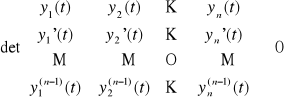
Uwaga. Powyższy wyznacznik oznaczamy przez W(y₁(t), y₂(t), ..., y_n(t)) i nazywamy wrońskianem układu funkcji (y₁(t), y₂(t), ..., y_n(t)).

Fakt 2.2.4 (Wzór Liouville'a)

Niech (y₁(t), y₂(t), ..., y_n(t)) będzie układem n rozwiązań równania jednorodnego (LJ_n) określonych na przedziale (a,b). Wtedy ich wrońskian W(t) = W(y₁(t), y₂(t), ..., y_n(t)) spełnia warunek

,

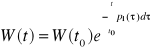
gdzie t₀ jest dowolnym punktem z przedziału (a,b).

Fakt 2.2.5 (o postaci rozwiązania ogólnego równania liniowego jednorodnego)

Niech (y₁(t), y₂(t), ..., y_n(t)) będzie układem fundamentalnym równania jednorodnego (LJ_n). Wtedy rozwiązanie ogólne tego równania dane jest wzorem

,

gdzie C₁, C₂, ..., C_n są dowolnymi stałymi rzeczywistymi.

Uwaga. Przypominamy, że z rozwiązania ogólnego przez odpowiedni dobór stałych C₁, C₂, ..., C_n można otrzymać rozwiązanie każdego zagadnienia początkowego. Rozwiązanie ogólne równania liniowego jednorodnego będziemy oznaczali symbolem y_RORLJ.

Fakt 2.2.6 (o obniżaniu rzędu równania liniowego jednorodnego)

Niech ϕ(t) będzie różnym od zera rozwiązaniem równania różniczkowego liniowego jednorodnego rzędu n. Wtedy przez podstawienie

równanie to sprowadza się do równania liniowego jednorodnego rzędu n - 1 (względem nowej zmiennej z).

Uwaga. Jeżeli znamy jedno rozwiązanie równania liniowego jednorodnego rzędu drugiego, to znalezienie rozwiązania ogólnego tego równania sprowadza się do rozwiązania, otrzymanego przez podstawienie, równania liniowego jednorodnego rzędu pierwszego.

2.3 RÓWNANIA RÓŻNICZKOWE LINIOWE O STAŁYCH WSPÓŁCZYNNIKACH

Def. 2.3.1 (równania różniczkowe liniowe o stałych współczynnikach)

Równaniem różniczkowym liniowym jednorodnym rzędu n o stałych współczynnikach nazywamy równanie postaci

(LS_n)
,

gdzie p₁, p₂, ..., p_n ∈ R.

Uwaga. Każde rozwiązanie równania różniczkowego liniowego o stałych współczynnikach (LS_n) jest określone na R. Przypominamy, że zgodnie z poprzednią umową równanie różniczkowe jednorodne rzędu drugiego o stałych współczynnikach ma postać

(LS₂)
.

Def. 2.3.2 (wielomian i równanie charakterystyczne)

Równanie postaci

nazywamy równaniem charakterystycznym równania różniczkowego liniowego o stałych współczynnikach (LS_n). Natomiast wielomian

nazywamy wielomianem charakterystycznym tego równania.

Fakt 2.3.3 (o postaci układu fundamentalnego równania (LS_n))

Niech ₁, ..., _s będą rzeczywistymi pierwiastkami o krotnościach odpowiednio k₁, ..., k_s i niech
, gdzie
będą zespolonymi pierwiastkami o krotnościach odpowiednio l₁, ..., l_m wielomianu charakterystycznego w() równania liniowego o stałych współczynnikach (LS_n), przy czym k₁+...+k_s+2(l₁+...+l_m) = n. Wtedy układ fundamentalny tego równania tworzą funkcje:

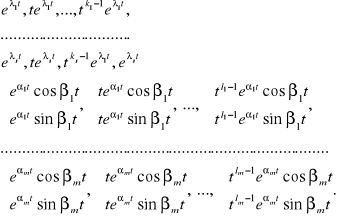
Uwaga. W tym zestawieniu:

1. pierwiastkowi rzeczywistemu jednokrotnemu  odpowiada funkcja
   ;

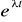
2. pierwiastkowi rzeczywistemu k-krotnemu  odpowiada k funkcji
   ;

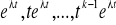
3. parze jednokrotnych sprzężonych ze sobą pierwiastków zespolonych
   ,
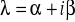
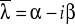
   odpowiada para funkcji

;

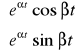
4. parze l-krotnych sprzężonych ze sobą pierwiastków zespolonych
   ,
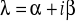
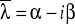
   odpowiada l par funkcji

.

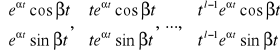
Fakt 2.3.4 (algorytm rozwiązywania równań o stałych współczynnikach)

Równanie jednorodne o stałych współczynnikach (LSn)

Równanie charakterystyczne

Pierwiastki równania charakterystycznego

Układ fundamentalny równania (LSn)

Rozwiązanie ogólne równania (LSn)

2.4 RÓWNANIE EULERA

Def. 2.4.1 (równanie Eulera)

Równaniem różniczkowym Eulera rzędu n nazywamy równanie postaci

(E_n)
,

gdzie p₁, p₂, ..., p_n ∈ R.

Uwaga. Do równania Eulera (E_n) sprowadza się równanie różniczkowe postaci

.

Aby tego dokonać należy podstawić
.

Fakt 2.4.2 (o sprowadzaniu równania Eulera do równania liniowego)

Podstawienie
przy t > 0 lub
przy t < 0 sprowadza równanie Eulera do równania różniczkowego liniowego jednorodnego o stałych współczynnikach.

2.5 RÓWNANIA RÓŻNICZKOWE LINIOWE NIEJEDNORODNE

Def. 2.5.1 (równanie różniczkowe liniowe niejednorodne)

Równaniem różniczkowym liniowym niejednorodnym rzędu n nazywamy równanie postaci

(LN_n)

gdzie h(t)≠0.

Uwaga. Przypominamy, że zgodnie z poprzednią umową równanie różniczkowe liniowe niejednorodne rzędu drugiego ma postać

(LN₂)
.

Fakt 2.5.2 (o postaci rozwiązania ogólnego równania niejednorodnego)

Niech (y₁(t), y₂(t), ..., y_n(t)) będzie układem fundamentalnym równania jednorodnego (LJ_n) i niech ϕ(t) będzie dowolnym rozwiązaniem równania niejednorodnego (LN_n). Wtedy rozwiązanie ogólne równania niejednorodnego dane jest wzorem

,

gdzie C₁, C₂, ..., C_n są dowolnymi stałymi rzeczywistymi.

Uwaga. Rozwiązanie ogólne równania niejednorodnego (LN_n) będziemy oznaczali symbolerm y_RORLN. Zauważmy, że rozwiązanie to jest sumą rozwiązania ogólnego y_RORLJ równania jednorodnego i dowolnego rozwiązania ϕ równania niejednorodnego, co można zapisać w postaci

y_RORLN = y_RORLJ + ϕ.

Każde rozwiązanie równania liniowego jest rozwiązaniem szczególnym tego równania.

2.6 METODA UZMIENNIANIA STAŁYCH

Fakt 2.6.1 (metoda uzmienniania stałych)

Niech (y₁(t), y₂(t), ..., y_n(t)) będzie układem fundamentalnym równania jednorodnego (LJ_n). Wtedy funkcja

,

gdzie c₁(t), c₂(t), ...,c_n(t) są dowolnymi rozwiązaniami układu równań

,

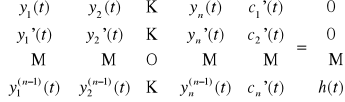
jest rozwiązaniem szczególnym równania niejednorodnego (LN_n).

Uwaga. Powyższy układ równań względem niewiadomych c₁'(t), c₂'(t), ...,c_n'(t) ma jednoznaczne rozwiązanie, gdyż jego wyznacznik jest wrońskianem układu fundamentalnego (y₁(t), y₂(t), ..., y_n(t)) równania jednorodnego (LJ_n), który jest różny od zera.

2.7 METODA WSPÓŁCZYNNIKÓW NIEOZNACZONYCH - METODA PRZEWIDYWANIA

Def. 2.7.1 (stała kontrolna)

Niech funkcja h(t) ma postać

.

Stałą kontrolną tej funkcji nazywamy liczbę
.

Fakt 2.7.2 (o rozwiązaniach szczególnych równania liniowego niejednorodnego)

Niech prawa strona równania liniowego niejednorodnego o stałych współczynnikach

ma postać

i niech w() będzie wielomianem charakterystycznym tego równania, a
stałą kontrolną funkcji h(t). Wtedy

1. jeżeli σ nie jest pierwiastkiem wielomianu w(), to funkcja postaci

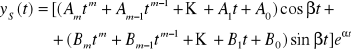
2. jeżeli σ jest s-krotnym pierwiastkiem wielomianu w(), to funkcja postaci

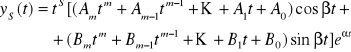
gdzie m = max{k,l}, a A₁, ..., A_m, B₁, ..., B_m są odpowiednio dobranymi współczynnikami rzeczywistymi, jest rozwiązaniem szczególnym tego równania.

Fakt 2.7.3 (o superpozycji rozwiązań)

Niech funkcje ψ(t) i ϕ(t) będą rozwiązaniami odpowiednio równań

.

Wtedy ich suma ψ(t) + ϕ(t) jest rozwiązaniem równania

.

3. UKŁADY RÓWNAŃ RÓŻNICZKOWYCH

3.1 POJĘCIA WSTĘPNE

Def. 3.1.1 (układ równań różniczkowych)

Układem równań różniczkowych rzędu pierwszego nazywamy układ równań postaci

(U)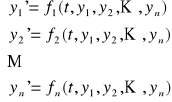
.

Uwaga. Jeżeli n = 2, to będziemy pisali x, y zamiast y₁, y₂ oraz f, g w miejsce f₁, f₂. Podobnie, jeżeli n = 3, to będziemy pisali x, y, z zamiast y₁, y₂, y₃ oraz f, g, h w miejsce f₁, f₂, f₃.

Def. 3.1.2 (rozwiązanie układu równań)

Ciąg funkcji (y₁(t), y₂(t), ..., y_n(t)) określonych i różniczkowalnych na przedziale (a,b) nazywamy rozwiązaniem układu równań (U) na tym przedziale, jeżeli zamienia on wszystkie równania tego układu w tożsamości

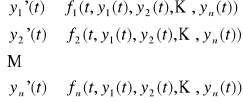
na przedziale (a,b).

Uwaga. W notacji wektorowej układ równań różniczkowych (U) można zapisać w postaci

,

gdzie

,
,
.

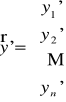
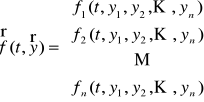
Wtedy rozwiązanie układu równań (U) jest funkcją wektorową

.

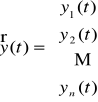
Def. 3.1.3 (zagadnienie początkowe dla układu równań)

Układ równań różniczkowych (U) oraz układ warunków

(W)
,

nazywamy zagadnieniem początkowym lub zagadnieniem Cauchy'ego.

Uwaga. Liczby
i
nazywamy wartościami początkowymi, a warunek (W) nazywamy warunkiem początkowym. Używając notacji wektorowej zagadnienie początkowe można zapisać w postaci

(UW)
.

Def. 3.1.4 (rozwiązanie zagadnienia początkowego)

Ciąg funkcji (y₁(t), y₂(t), ..., y_n(t)) jest rozwiązaniem zagadnienia początkowego (UW), jeżeli jest rozwiązaniem układu równań (U) na pewnym przedziale zawierającym punkt t₀ i spełnia warunki (W).

Tw. 3.1.5 (o istnieniu i jednoznaczności rozwiązań układu (U))

Niech funkcje f_i(t,y₁,y₂,...,y_n), gdzie 1 ≤ i ≤ n, wraz ze swoimi pochodnymi cząstkowymi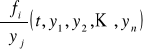
, gdzie 1 ≤ i, j ≤ n, będą określone i ciągłe na obszarze D ⊂ Rⁿ⁺¹. Wtedy dla dowolnego punktu
zagadnienie początkowe (UW) ma dokładnie jedno rozwiązanie. Rozwiązanie to jest określone na pewnym otoczeniu punktu t₀.

Def. 3.1.6 (rozwiązania ogólne i szczególne układu równań)

Rodzinę funkcji wektorowych

,

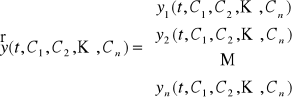
zależnych od parametrów rzeczywistych C₁, C₂, ..., C_n nazywamy rozwiązaniem ogólnym układu równań (U) jeżeli:

1. każda funkcja wektorowa z tej rodziny jest rozwiązaniem układu,

2. dla każdego układu warunków początkowych
, dla którego rozwiązanie istnieje i jest jednoznaczne, można dobrać stałe C₁, C₂, ..., C_n tak, aby
.

Każdą funkcję wektorową otrzymaną z rozwiązania ogólnego układu (U) przy ustalonych wartościach parametrów C₁, C₂, ..., C_n nazywamy rozwiązaniem szczególnym tego układu.

Uwaga. Rozwiązanie zagadnienia początkowego, jeżeli istnieje i jest jednoznaczne, jest rozwiązaniem szczególnym. W praktyce znajomość rozwiązania ogólnego jest bardzo dogodna, gdyż przez odpowiedni dobór parametrów C₁, C₂, ..., C_n można otrzymać rozwiązanie zagadnienia początkowego.

3.2 UKŁADY RÓWNAŃ RÓŻNICZKOWYCH LINIOWYCH

Def. 3.2.1 (układ równań różniczkowych liniowych)

Układem równań różniczkowych liniowych rzędu pierwszego nazywamy układ równań postaci

(UL)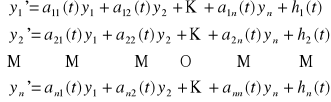
.

Uwaga. W notacji wektorowej układ równań (UL) przyjmuje postać

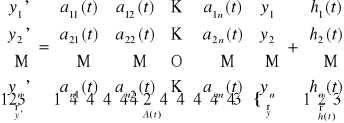
lub krótko

.

Tw. 3.2.2 (o istnieniu i jednoznaczności rozwiązań dla układu (UL))

Niech funkcje a_ij(t), gdzie i,j = 1, 2, ..., n, oraz h_i(t), gdzie i = 1, 2, ..., n, będą ciągłe na przedziale (a,b). Wtedy dla każdego punktu
zagadnienie początkowe

,

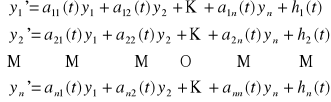
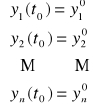
ma dokładnie jedno rozwiązanie. Rozwiązanie to określone jest na przedziale (a,b).

3.3 UKŁADY JEDNORODNE RÓWNAŃ RÓŻNICZKOWYCH LINIOWYCH

Def. 3.3.1 (układ jednorodny równań różniczkowych jednorodnych)

Układem jednorodnym równań różniczkowych liniowych rzędu pierwszego nazywamy układ równań postaci

(UJ)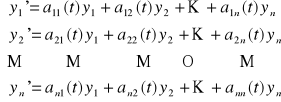

Uwaga. W notacji wektorowej układ jednorodny (UJ) przyjmuje postać

.

Fakt 3.3.2 (o kombinacji liniowej rozwiązań układu jednorodnego)

Niech
,
będą rozwiązaniami układu jednorodnego (UJ). Wtedy dla dowolnych stałych α,β ∈ R funkcja wektorowa

jest również rozwiązaniem tego układu.

Def. 3.3.3 (układ fundamentalny układu jednorodnego (UJ))

Układ rozwiązań
układu jednorodnego (UJ) określonych na przedziale (a,b) nazywamy układem fundamentalnym tego układu na tym przedziale, jeżeli dla każdego t ∈ (a,b) spełniony jest warunek

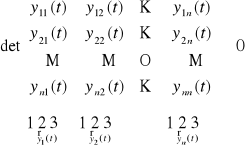
Uwaga. Powyższy wyznacznik oznaczamy przez
i nazywamy wrońskianem układu funkcji wektorowych
.

Fakt 3.3.4 (o postaci rozwiązania ogólnego układu jednorodnego)

Niech
będzie układem fundamentalnym układu jednorodnego równań różniczkowych (UJ). Wtedy rozwiązanie ogólne tego układu równań dane jest wzorem

gdzie C₁, C₂, ..., C_n są dowolnymi stałymi rzeczywistymi.

Uwaga. Przypomnijmy, że z rozwiązania ogólnego przez odpowiedni dobór stałych C₁, C₂, ..., C_n można otrzymać rozwiązanie każdego zagadnienia początkowego. Rozwiązanie ogólne układu jednorodnego (UJ) będziemy oznaczali symbolem
.

3.4 UKŁADY RÓWNAŃ RÓŻNICZKOWYCH LINIOWYCH O STAŁYCH WSPÓŁCZYNNIKACH

Def. 3.4.1 (układ jednorodny równań liniowych o stałych współczynnikach)

Układem jednorodnym równań różniczkowych liniowych o stałych współczynnikach nazywamy układ równań postaci

(US)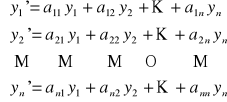
,

gdzie a_ij ∈ R dla 1 ≤ i, j ≤ n.

Uwaga. W notacji wektorowej układ jednorodny równań różniczkowych liniowych o stałych współczynnikach (US) przyjmuje postać

.

Każde rozwiązanie układu (US) określone jest na R. Układy (US) można rozwiązywać metodą eliminacji.

Def. 3.4.2 (wielomian i równanie charakterystyczne macierzy)

Niech
będzie macierzą kwadratową stopnia n. Wielomianem charakterystycznym macierzy A nazywamy wielomian

,

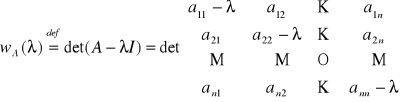
gdzie I oznacza macierz jednostkową stopnia n. Równaniem charakterystycznym macierzy A nazywamy równanie

.

Def. 3.4.3 (wartości własne i wektory własne macierzy)

Niech
będzie rzeczywistą macierzą kwadratową stopnia n. Wartością własną macierzy A nazywamy każdy (rzeczywisty lub zespolony) pierwiastek wielomianu charakterystycznego tej macierzy, tj. liczbę λ spełniającą równanie

.

Niezerowy wektor
(o rzeczywistych lub zespolonych współrzędnych) nazywamy wektorem własnym macierzy A odpowiadającym wartości własnej λ (rzeczywistej lub zespolonej) tej macierzy, jeżeli spełnia warunek

.

Uwaga. Ostatnią równość można zapisać w postaci układu równań

.

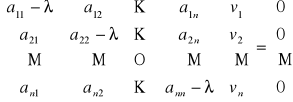
Fakt 3.4.4 (o postaci układu fundamentalnego układu (US) - metoda Eulera I)

Jeżeli macierz A układu jednorodnego równań o stałych współczynnikach (US) ma n różnych rzeczywistych wartości własnych λ₁, λ₂, ..., λ_n, to jego układ fundamentalny składa się z funkcji wektorowych:

,
, ...,
,

gdzie
są wektorami własnymi odpowiadającymi wartościom własnym λ₁, λ₂, ..., λ_n.

Fakt 3.4.5 (o postaci układu fundamentalnego układu (US) - metoda Eulera II)

Jeżeli macierz A układu jednorodnego równań o stałych współczynnikach (US) ma 2k=n parami różnych zespolonych wartości własnych
,
,
,
, …,
,
, gdzie β_j≠0 dla 1 ≤ j ≤ k, to jego układ fundamentalny składa się z funkcji wektorowych:

,
,
,

, ...,
,
,

gdzie
oznaczają wektory własne odpowiadające wartościom własnym λ₁, λ₂, ..., λ_n.

Fakt 3.4.6 (o postaci układu fundamentalnego układu (US) - metoda Eulera III)

Jeżeli macierz A układu jednorodnego równań o stałych współczynnikach (US) ma s parami różnych zespolonych wartości własnych λ₁, λ₂, ..., λ_s oraz 2k parami różnych zespolonych wartości własnych
,
,
,
, …,
,
, gdzie s + 2k = n, β_j ≠ 0 dla 1 ≤ j ≤ k, to jego układ fundamentalny składa się z funkcji wektorowych:

,
, …,
,

,
,

…,
,
,

gdzie
oznaczają wektory własne odpowiadające rzeczywistym wartościom własnym λ₁, λ₂, ..., λ_s, a
oznaczają wektory własne odpowiadające zespolonym wartościom własnym λ_s+1, λ_s+2, ..., λ_s+k.

3.5 UKŁADY NIEJEDNORODNE RÓWNAŃ RÓŻNICZKOWYCH LINIOWYCH

Def. 3.5.1 (układ niejednorodny równań różniczkowych liniowych)

Układem niejednorodnym równań różniczkowych liniowych pierwszego rzędu nazywamy układ równań postaci

(UN)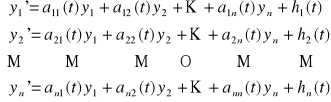
,

gdzie h_i(t) ≠ 0 dla pewnego 1 ≤ i ≤ n.

Uwaga. W notacji wektorowej układ niejednorodny (UN) przyjmuje postać

.

Fakt 3.5.2 (o postaci rozwiązania ogólnego układu niejednorodnego)

Niech
będzie układem fundamentalnym układu jednorodnego (UJ) i niech
będzie dowolnym rozwiązaniem układu niejednorodnego (UN). Wtedy rozwiązanie ogólne układu niejednorodnego dane jest wzorem

,

gdzie C₁, C₂, ..., C_n są dowolnymi stałymi rzeczywistymi.

Uwaga. Przypomnijmy, że z rozwiązania ogólnego przez odpowiedni dobór stałych C₁, C₂, ..., C_n można otrzymać rozwiązanie każdego zagadnienia początkowego. Rozwiązanie ogólne układu niejednorodnego (UN) będziemy oznaczali symbolem
. Rozwiązanie to ma taką samą postać jak rozwiązanie ogólne równania liniowego niejednorodnego (LN)

.

3.6 METODA UZMIENNIANIA STAŁYCH

Def. 3.6.1 (metoda uzmienniania stałych)

Niech dany będzie układ fundamentalny

,
, ...,
,

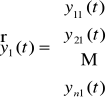
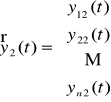
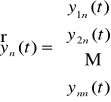
układu jednorodnego (UJ). Wtedy funkcja wektorowa

,

gdzie c₁(t), c₂(t), ..., c_n(t) są dowolnymi rozwiązaniami układu równań

,

jest rozwiązaniem szczególnym układu niejednorodnego (UN).

Uwaga. Powyższy układ równań względem niewiadomych
ma jednoznaczne rozwiązanie, gdyż jego wyznacznik jest wrońskianem układu fundamentalnego
układu (UJ), który jest różny od zera.

4. ELEMENTY RACHUNKU OPERATOROWEGO

4.1 PRZEKSZTAŁCENIE LAPLACE'A

Def. 4.1.1 (transformata Laplace'a)

Niech funkcja f będzie określona na przedziale [0,∞). Transformatę Laplace'a funkcji f oznaczamy symbolem F(s) lub L{f(t)} i definiujemy wzorem

L{f(t)}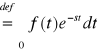
,

gdzie s jest zmienną rzeczywistą. Funkcję F(s) nazywamy także L-transformatą lub obrazem funkcji f(t).

Fakt 4.1.2 (transformaty ważniejszych funkcji)

Funkcja	Transformata
1

Fakt 4.1.3 (warunki wystarczające istnienia transformaty Laplace'a)

Niech

1. funkcja
ma skończoną liczbę punktów nieciągłości pierwszego rodzaju na każdym przedziale [0,T], gdzie T > 0;

2.
.

Wtedy transformata Laplace'a L{f(t)} istnieje dla s > C.

Uwaga. Funkcję f spełniającą warunki 1. i 2. powyższego faktu będziemy nazywali oryginałem.

Fakt 4.1.4 (o liniowości przekształcenia Laplace'a)

Jeżeli istnieją transformaty Laplace'a funkcji f i g oraz c ∈ R, to

1. istnieje transformata Laplace'a funkcji f + g oraz

L{f(t)+g(t)} = L{f(t)} + L{g(t)};

2. istnieje transformata Laplace'a funkcji cf oraz

L{cf(t)} = cL{f(t)}.

Fakt 4.1.5 (o jednoznaczności transformaty Laplace'a)

Jeżeli funkcje ciągłe
mają takie same transformaty Laplace'a: F(s) = G(s), to są równe na przedziale [0,∞).

4.2 METODA OPERATOROWA ROZWIĄZYWANIA RÓWNAŃ RÓŻNICZKOWYCH

Fakt 4.2.1 (transformata n-tej pochodnej)

Jeżeli funkcja f(t) oraz jej pochodne f'(t), f''(t), ..., f^(n-1)(t) są oryginałami, a ponadto funkcja ta ma na przedziale (0,∞) ciągłą n-tą pochodną, to istnieje transformata L{f(t)} oraz

L{f⁽ⁿ⁾(t)} =

= sⁿL{f(t)} - s^n-1f(0⁺) - s^n-2f'(0⁺) + ... - sf^(n-2)(0⁺) - f^(n-1)(0⁺) =

= sⁿF(s) - s^n-1f(0⁺) - s^n-2f'(0⁺) + ... - sf^(n-2)(0⁺) - f^(n-1)(0⁺),

gdzie F(s) = L{f(t)},
,
, ...,
.

Uwaga. Jeżeli funkcje f(t), f'(t), ..., f^(n-1)(t) są ciągłe prawostronnie w punkcie t₀ = 0, to f(0⁺) = f(0), f'(0⁺) = f'(0), ..., f^(n-1)(0⁺) = f^(n-1)(0).

4.3 WŁASNOŚCI PRZEKSZTAŁCENIA LAPLACE'A

Fakt 4.3.1 (zmiana skali)

Jeżeli funkcja f(t) jest oryginałem, to dla dowolnej stałej α > 0

L{f(αt)} =
,

gdzie F(s) oznacza obraz funkcji f(t).

Fakt 4.3.2 (o różniczkowaniu obrazu)

Jeżeli funkcja f(t) jest oryginałem, to

L{tⁿf(t)} =(-1)ⁿF⁽ⁿ⁾(s),

gdzie F(s) oznacza obraz funkcji f(t).

Fakt 4.3.3 (o przesunięciu argumentów obrazu)

Jeżeli funkcja f(t) jest oryginałem, to dla dowolnej stałej a ∈ R

L{e^αtf(t)} = F(s - a),

gdzie F(s) oznacza obraz funkcji f(t).

Fakt 4.3.4 (o przesunięciu argumentów oryginału)

Jeżeli funkcja f(t) jest oryginałem, to dla dowolnej stałej τ > 0

L{1(t - τ)f(t - τ)} = e^-sτF(s),

gdzie F(s) oznacza obraz funkcji f(t).

Fakt 4.3.4 (o całkowaniu oryginału)

Jeżeli funkcja f(t) jest oryginałem, to

L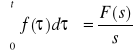
,

gdzie F(s) oznacza obraz funkcji f(t).

Fakt 4.3.5 (transformaty ważniejszych funkcji c.d.)

Funkcja	Transformata
shαt
chαt
t^ne^α^t
e^α^tsinβt
e^α^tcosβt

4.4 SPLOT FUNKCJI

Def. 4.4.1 (splot funkcji)

Niech funkcje f(t) i g(t) będą całkowalne na każdym przedziale [0,T], gdzie T > 0. Splot funkcji f(t) i g(t) oznaczamy symbolem
i określamy wzorem

.

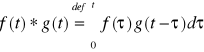
Fakt 4.4.2 (własności splotu funkcji)

Niech funkcje f(t), g(t), h(t) będą całkowalne na każdym przedziale [0,T], gdzie T > 0 i niech c ∈ R. Wtedy

1.
;

2.
;

3.
;

4.
.

Tw. 4.4.3 (wzór Borela)

Jeżeli funkcje f(t) i g(t) są oryginałami, to istniej transformata Laplace'a ich splotu oraz

L{
} = L{f(t)}⋅ L{g(t)}.

---