0286

288

XI. Szeregi nieskończone o wyrazach stałych

Na szeregi podwójne przenoszą się łatwo twierdzenia [364, 3° i 4°] o mnożeniu wyrazów szeregu zbieżnego przez stałą i o dodawaniu i odejmowaniu szeregów wyraz za wyrazem, pozostawiamy czytelnikowi przeprowadzenie odpowiedniego rozumowania.

Tak samo, na to by szereg podwójny był zbieżny, potrzeba, by wyraz ogólny dążył do zera:

lim a\^k) = 0

ł-¹oo

k-oo

[porównaj 364, 5°]. Widać to od razu z wzoru

_<¹) _    a<¹) Aik)

Ol — A_t —Ai-i—Aj +A(-i

Naturalne jest żestawienie szeregu podwójnego (10) z szeregami iterowanymi (3) i (4) rozpatrzonymi wyżej. Ponieważ

<(»)

-SIS""’}.

*-i i-i więc przechodząc do granicy przy ustalonym n i m -» oo otrzymujemy (przy założeniu, że szeregi utworzone z wierszy są zbieżne)

lim A™

lr=1

Teraz jest jasne, że suma szeregu iterowanego (3) nie jest niczym innym jak granicą iterowaną

lim lim A™.

n—oo m~+<x>

Zagadnienie równości sum szeregów iterowanych (3) i (4) jest przypadkiem szczególnym zagadnienia równości dwóch granic iterowanych.

Stosując w rozpatrywanym przypadku ogólne twierdzenie z ustępu 168 o granicy podwójnej i granicach iterowanych (¹) otrzymujemy następujący wynik:

Twierdzenie 4. Jeżeli: 1) jest zbieżny szereg podwójny (10) i 2) są zbieżne wszystkie szeregi utworzone z wierszy, to jest także zbieżny szereg iterowany (3) i ma tę samą sumę, co szereg podwójny:

OO 00    CO

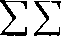
a\^k) = A =

*= 1 (-1    I. k=l

Analogiczne twierdzenie zachodzi dla szeregu iterowanego (4).

Zagadnienie zbieżności szeregu (10) rozwiązuje się prosto w przypadku szeregu dodatniego, tzn. szeregu o wyrazach nieujemnych: a/² > 0.

1

Tutaj m i n odgrywają rolę zmiennych niezależnych, a suma częściowa A_m rolę funkcji tych

2

zmiennych.