Str099

194 S. Liczby pierwsze i rozkład na czynnik

redukłowi, w którym d_M, zastąpimy przez 1 /,v₍. Zatem z twierdzenia 5.4. l(_a\ (w którym zastąpimy i przez i -ł I oraz a,.,, przez l/x,) otrzymujemy

+ Vi_ ₌ ^bt ± ^xi^bt-i

cJ*i    +

a ten ułamek jest zawarty między Ó,_₁/c,_₁ i bjc,. (Aby się o tym przekonać, popatrzmy na dwa wektory u = (b,_t ej i u = (b,„_lf Ł) w tej samej ćwiartce płaszczyzny; zauważmy następnie, że nachylenie wektora u + x,v jest zawarte między nachyleniem wektora u i wektora o). Zatem ciąg bjc, oscyluje wokół x, skąd wynika, że jest zbieżny do x.

Ułamki łańcuchowe mają wiele własności, które powodują, że pojawiają się one w różnych działach matematyki. Na przykład dają one metodę tworzenia „najlepszych możliwych” przybliżeń wymiernych liczb rzeczywistych (o-znacza to, że każda liczba wymierna leżąca bliżej x niż bjc, musi mieć mianownik większy od ej. Inna własność jest analogiczna do tej własności liczb rzeczywistych, która mówi, że rozwinięcie dziesiętne (lub przy podstawie b) liczby jc jest okresowe wtedy i tylko wtedy, gdy liczba x jest wymierna. Rozwinięcie na ułamek łańcuchowy liczby x jest skończone wtedy i tylko wtedy, gdy liczba x jest wymierna. Można pokazać, że dąg liczb całkowitych a, jest okresowy wtedy i tylko wtedy, gdy liczba x jest liczbą postaci x_l -f x₂Jn, przy czym ą i x₂ są liczbami wymiernymi, a liczba całkowita n nie jest pełnym kwadratem. Ta własność jest znana jako twierdzenie Lagrange’a.

Przykład 1. Jeżeli zaczniemy rozwijać ^3 na ułamek łańcuchowy, to otrzymamy

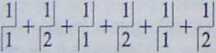
73 =1 +

W tym momencie możemy już podejrzewać, że wyrazy ciągu a, przyjmują na przemian wartości 1 i 2. Aby tego dowieść, weźmy liczbę x równą nieskończonemu ułamkowi łańcuchowemu po prawej stronie, z występującymi na przemian liczbami 1 i 2. Wtedy oczywiście x = 1 + ———— ---, o czym mo-

1 + (1/(1 + x))

żerny się przekonać, podstawiając w miejsce x po prawej stronie jego rozwinięcie łańcuchowe. Upraszczając wyrażenie wymierne po prawej stronie i mnożąc obie strony przez 2 + x, otrzymujemy: 2x + x² = 3 + 2x, czyli x = 71 •

Twierdzenie 5.4.2. Niech x > 1 będzie liczbą rzeczywistą, której rozwinięcie na ułamek łańcuchowy ma redukty bjc,. Wtedy dla wszystkich i zachodzi nierówność 11| - x²cf\ < 2x.

5.4. Fakłoryzacja iz pomoc* ułamków łańcuchowych 195

.j ponieważ liczba x jest zawarta między bjc_l i b_nllc_l+_l oraz wartość P°^v olcdna różnicy tych dwóch kolejnych reduktów wynosi 1/^,+ , (por. jedzenie 5.4. l(c)), mamy

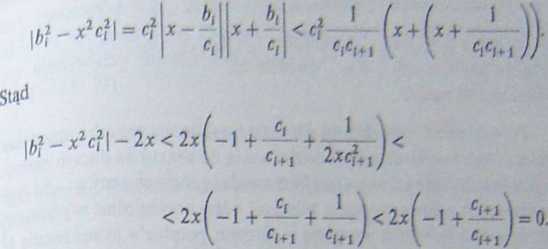
To kończy dowód twierdzenia.

'Twierdzenie 5.4.3. Niech n będzie liczbą całkowitą dodatnią, nie będącą pełnym kwadratem. Niech bjc_l będą reduktarm rozwinięcia łańcuchowego Jn. Wtedy bezwzględna reszta z dzielenia bf przez n (tzn. zawarta między -n/2 i nl2) jest mniejsza odljn.

powód. Skorzystajmy z twierdzenia 5.4.2 dla x = <Jn. Wtedy óf = *l-nc} (mod n) i liczba po prawej stronie kongruencji ma wartość bezwzględną mniejszą od 2 \[n.

Twierdzenie 5.4.3 ma zasadnicze znaczenie dla algorytmu faktoryzacji, w którym korzysta się z ułamków łańcuchowych. Mówi ono, że możemy znaleźć ciąg liczb b_lf których kwadraty dają małe reszty przy dzieleniu przez Ti, biorąc liczniki kolejnych reduktów rozwinięcia n na ułamek łańcuchowy. Zauważmy, że nie musimy obliczać całego reduktu: wystarczy znaleźć jego licznik b_lt a dokładniej, resztę z dzielenia tego licznika przez ?i. Zatem nie musimy przejmować się tym, że liczniki i mianowniki kolejnych reduktów szybko stają się bardzo duże. Przez cały czas będziemy mieć bowiem do czynienia tylko z liczbami mniejszymi od n² (gdyż będziemy mnożyć liczby całkowite modulo n).

Opiszemy teraz kolejne kroki algorytmu, w którym korzysta się z ułamków łańcuchowych. Będzie to dokładnie algorytm używający baz rozkładu, opisany w podrozdziale 5.3, z tym tylko, że skorzystamy z twierdzenia 5.4.3, zamiast wybierać losowo liczby %

Algorytm faktoryzacji korzystający z ułamków łańcuchowych. Niech n będzie liczbą całkowitą, którą chcemy rozłożyć na czynniki. Wszystkie obliczenia będą wykonywane modulo n, tzn. sumy i iloczyny liczb całkowitych