1.Hipoteza badawcza i jej definicja.
Hipoteza badawcza to zdanie twierdzące, dotyczące przewidywanego wyniku eksperymentu, przeprowadzonego aby odpowiedzieć na pytanie badawcze. (wyklady)
Zwana także przypuszczeniem, jest propozycją odpowiedzi na pytania zawarte w problemach badawczych. Jest to jednak oczywiście odpowiedź wstępna, przypuszczalna, której prawdziwość ma być potwierdzona w podejmowanym badaniu. Hipoteza nie różni się więc kształtem gramatycznym od zdania obserwacyjnego, na którego to treść składa się opis faktu naukowego. Jedyna różnica jest jedynie to iż nie wiemy czy jest to prawda czy fałsz. Obecność dokładnie sformułowanych hipotez odróżnia poznanie naukowe od poznania potocznego, stąd uznanie koniecznej obecności w badaniach naukowych. Hipoteza ukierunkowuje nam badania na problemy ważne. Jednak żeby hipoteza mogła tę barierę ochronną stanowić, musi spełnić następujące warunki:
-tłumaczyć w sposób dostateczny znane fakty
-musi być możliwa do zweryfikowania przez konsekwencje, które z niej wynikają
-musi dotyczyć istotnych dla danej nauki zdarzeń i ma moc teoriotwórczą
-musi być zdaniem wysoce prawdopodobnym, którego słuszność wstępna polega na tym, że jest zdaniem niesprzecznym z udowodnionymi już twierdzeniami danej dyscypliny naukowej.
Rola hipotez w badaniach naukowych jest nie oceniona, gdyż dzięki niej wyznaczamy sobie nowe cele w różnych badaniach jak np.: Musimy zbadać małe dziecko gdyż podejrzewa się u niego chorobę psychiczną. Stawiamy sobie wtedy hipotezy takie jak: czy dziecko się normalnie zachowuje, czy dziecko normalnie rozwija się prawidłowo (czy mówi normalnie, czy czyta, czy pisze itp.), itp. A jeżeli byśmy zastosowali tutaj tekze zamiast hipotezy nie było by co badać gdyż z gory byśmy coś zakładali np.: dziecko nie rozwija się prawidłowo ponieważ jest chore psychicznie. Krótko mówiąc hipoteza daje nam pytania na dany temat na które musimy poprzez badania odpowiedzieć.
2.Przykłady problemów klasyfikacyjnych w chemii.
3.Przykłady problemów kalibracyjnych w chemii.
4.Modele kalibracyjne i ich zastosowanie.
5.Czym zajmuje się statystyka?
STATYSTYKA- służy do oszacowania nieznanego momentu lub wprost nieznanego parametru zmiennej losowej. Posługuje się eksperymentem do potwierdzania swoich teorii. Statystyka zajmuje się badaniem zjawisk masowych, co pozwala na poznanie natury zjawiska (cechy) i praw nim rządzących. Celem badania statystycznego jest najczęściej poznanie rozkładu danej cechy i oszacowanie charakterystyk tego rozkładu.
6. Rodzaje zmiennych eksperymentalnych; zmienne ciągłe i zmienne dyskretne
Zmienna - to badana cecha obiektów populacji, czyli obiektów interesujących nas w danym doświadczeniu, eksperymencie. Zmienne dzielimy na:
zmienne liczbowe (ilościowe) - określa liczbowo próbę np. wartość pH buforu, temperatura powietrza
zmienne jakościowe - określa nie liczbowo cechę próbki np. kolor, smak, pochodzenie, poglądy polityczne
zmienne zależne
zmienne niezależne
Zmienne liczbowe dzielimy na:
ciągłe lub dyskretne
skalarne lub wektorowe
Zmienne jakościowe dzielimy na:
uporządkowane lub nieuporządkowane
Zmienne liczbowe skalarne to takie, które są określone przez liczbę np. wcześniej wymieniona temperatura powietrza. Zmienne liczbowe wektorowe to takie, które można wyrazić za pomocą wektora przesunięcia np. prędkość samochodu.
Zmienne liczbowe dyskretne lub inaczej zwane skokowe to takie zmienne losowe, które skończony lub przeliczalny zbiór wartości np. ocena uzyskiwana przez studenta na egzaminie z wybranego przedmiotu lub liczba urodzeń w danym kraju. Zmienna ciągła to taka zmienna losowa, która może przybierać dowolne wartości liczbowe z pewnego przedziału liczbowego np. wzrost, waga człowieka lub badanie oporu elektrycznego. Na chłopski rozum zmienna ciągła wtedy, gdy zmienne tworzą na wykresie funkcję ciągłą, zmienna dyskretna, gdy jest wykres albo punktowy albo skokowy
Rozkład zmiennej losowej dyskretnej:
Rozkładem skokowej (dyskretnej) zmiennej losowej X nazywamy prawdopodobieństwo tego, że zmienna losowa X przybiera wartości xi, gdzie (i=1,2,3…).
Rozkład zmiennej losowej ciągłej:
Zakładając, że wartości x przyjmowane są przez zmienną otrzymujemy X zmieniające się w sposób ciągły w przedziale <a, b> otrzymujemy granicę danej funkcji, która nazywa się funkcja gęstości prawdopodobieństwa zmiennej losowej.
7. Populacja, a próba
8. Rozkład normalny i rozkład `t'
Rozkład normalny jest jednym z najważniejszych rozkładów prawdopodobieństwa. Odgrywa ważną rolę w statystycznym opisie zagadnień przyrodniczych, przemysłowych, medycznych, socjalnych itp.
Przyczyną jest jego popularność w naturze. Jeśli jakaś wielkość jest sumą lub średnią bardzo wielu drobnych losowych czynników, to niezależnie od rozkładu każdego z tych czynników, jej rozkład będzie zbliżony do normalnego.
Jest to rozkład teoretyczny, charakteryzujący się określonymi właściwościami. Jest on rozkładem
symetrycznym (czyli liczebności odpowiadające wartościom zmiennej rozkładają się symetrycznie
wokół liczebności największej). Każdy rozkład normalny jest rozkładem symetrycznym, ale nie każdy rozkład symetryczny jest rozkładem normalnym.
Kolejną właściwością tego rozkładu jest jedno maksimum oraz ściśle określona kurtoza
(czyli koncentracja wartości zmiennej wokół średniej arytmetycznej)
Wykres rozkładu normalnego ma postać krzywej w kształcie dzwonu. W punkcie centralnym
rozkładu znajduje się średnia arytmetyczna, a także dominanta i mediana.
Z tego wynika, że średnia arytmetyczna jest wartością cechy najczęściej spotykaną
w badanej zbiorowości.
Wielokrotne powtarzanie tego samego pomiaru daje wyniki rozrzucone wokół określonej wartości. Jeśli wyeliminujemy wszystkie większe przyczyny błędów, zakłada się, że pozostałe mniejsze błędy muszą być rezultatem dodawania się do siebie dużej liczby niezależnych czynników, co daje w efekcie rozkład normalny. Odchylenia od rozkładu normalnego rozumiane są jako wskazówka, że zostały pominięte błędy systematyczne. To stwierdzenie jest centralnym założeniem teorii błędów.
Krzywa rozkładu normalnego
Jeżeli liczba pomiarów zbliży się do nieskończoności , wówczas wartości stają się ciągłe, a krzywa nazywa się krzywą rozkładu Gaussa.
Funkcja gęstości rozkładu normalnego ze średnią μ i odchyleniem standardowym σ (równoważnie: wariancją σ2) jest przykładem funkcji Gaussa. Dana jest ona wzorem:
Rozkład Studenta - (rozkład t lub rozkład t-Studenta) ciągły rozkład prawdopodobieństwa stosowany często w statystyce w procedurach testowania hipotez statystycznych i przy ocenie błędów pomiaru. Przy opracowaniu wyników pomiarów często powstaje zagadnienie oszacowania przedziału, w którym leży, z określonym prawdopodobieństwem, rzeczywista wartość mierzona, jeśli dysponujemy tylko wynikami n pomiarów, dla których możemy wyznaczyć takie parametry, jak średnia
i odchylenie standardowe
lub wariancja
(„z próby”), nie znamy natomiast odch. standardowego
w populacji.
Rozkład normalny a rozkład t Studenta
W przeciwieństwie do rozkładu t Studenta, kształt rozkładu normalnego nie zależy od stopni swobody. Im mniejsza jest liczba stopni swobody, tym większa jest różnica między rozkładem normalnym a t Studenta i odwrotnie.
9. Rozkład Gaussa - postać krzywej i interpretacja
10.Zmienna standardyzowana i zmienna centrowana
Co to są zmienne? Zmienne są to wielkości, które mierzymy, kontrolujemy lub którymi manipulujemy w jakiś sposób w trakcie badań. Zmienne mogą mieć różne właściwości, zwłaszcza ze względu na rolę, jaką pełnią w naszych badaniach, jak też ze względu na to, jaki rodzaj miary można do nich zastosować.
Mówimy, że zmienna losowa ciągła X ma rozkład normalny o wartości oczekiwanej μ i odchyleniu standardowym σ

W celu obliczenia prawdopodobieństwa zmiennej X w rozkładzie normalnym o dowolnej wartości oczekiwanej μ i odchyleniu standardowym σ dokonuje się standaryzacji
Standaryzacja polega na sprowadzeniu dowolnego rozkładu normalnego o danych parametrach i σ do rozkładu standaryzowanego (modelowego) o wartości oczekiwanej = 0 i odchyleniu standardowym σ = 1.
Zmienną losową X zastępujemy zmienną standaryzowaną U, która ma rozkład N(0,1)
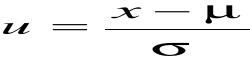
gdzie:
x - zmienna standaryzowana
σ - odchylenie standardowe populacji
μ - średnia z populacji.
11. Miary opisujące położenie rozkładu
Średnia - miara tendencji centralnej danej zmiennej, która niesie szczególnie dużo informacji, jeśli jest podawana wraz ze swoim przedziałem ufności. Charakteryzują ona populację. Im większa jest liczność próby tym bardziej niezawodna jest średnia. Z kolei wraz ze wzrostem wariancji danych średnia staje się mniej pewna.
Średnia = (∑xi)/n , gdzie n oznacza liczność próby.
Mediana - miara tendencji centralnej, dla której połowa obserwacji (50%) leży powyżej, a druga połowa poniżej jej wartości. Jeśli liczba obserwacji w próbie jest parzysta, wówczas mediana jest obliczana jako średnia z dwóch wartości leżących pośrodku.
Aby obliczyć medianę ze zbioru n obserwacji, sortujemy je w kolejności od najmniejszej do największej i numerujemy od 1 do n. Następnie, jeśli n jest nieparzyste, medianą jest wartość obserwacji w środku (czyli obserwacji numer n+1/2). Jeśli natomiast n jest parzyste, wynikiem jest średnia arytmetyczna między dwiema środkowymi obserwacjami, czyli obserwacją numer n/2 i obserwacją numer (n/2) +1.
Moda - miara tendencji centralnej, oznacza wartość, która występuje w próbie najczęściej
(z największym prawdopodobieństwem)
12. Miary opisujące rozrzut wyników :odchylenie standardowe i wariancja
13. Prawdopodobieństwo- podstawowe aksjomaty
14.Poziom ufności, a poziom istotności.
Przedział ufności- zakres ufności, których z określoną ufnością możemy być pewni. Pewna wartość leży w przedziale, którego zakres determinuje:
- precyzja danej metody;
- ilość powtórzeń;
O przedziale ufności decyduje stopień ufności (im większy stopień ufności tym przedział jest większy);
Dla dużej wartości pomiarów przedział ma ufność:
Xśr +- Z(sigma/pierwiastek z n)
Im mniej próbek tym sigma jest mniej dokładnie wyznaczone.
Poziom ufności:
-przyjmując, że przedział ufności obejmuje 95% rozkładu, to 5% znajduje się poza przedziałem(poziom ufności=95%)
-te 5% które znajdują się poza przedziałem zwane jest poziomem istotności =>
=> błąd I rodzaju zw. błędem alfa
=> jest to prawdopodobieństwo popełnienia błędu związane z odrzuceniem Ho,
podczas gdy jest ona prawdziwa.
15. Błąd I rodzaju (błąd α)
Przyjmując, że przedział ufności obejmuje 95% rozkładu to 5% znajduje się poza przedziałem (po 2,5 z każdej strony, gdy test dwustronny lub 5% z jednej strony gdy test jednostronny) Te 5% zwane jest poziomem istotności - zwane inaczej błędem I rodzaju lub błędem α. Jest to prawdopodobieństwo popełnienia błędu związanego z odrzuceniem hipotezy Ho, podczas gdy jest ona prawdziwa. Innymi słowy jest to błąd polegający na tym, że na podstawie wyników testu statystycznego twierdzimy, że jakiś fakt jest statystycznie istotny, natomiast w rzeczywistości jest on dziełem przypadku. Inaczej może nazwać ten błąd α mocą testu.
16. Idea testowania hipotez statystycznych
17. Hipoteza zerowa i hipoteza alternatywna
Hipoteza zerowa (H0) - Jest to hipoteza poddana procedurze weryfikacyjnej, w której zakładamy, że różnica między analizowanymi parametrami lub rozkładami wynosi zero. Przykładowo wnioskując o parametrach hipotezę zerową zapiszemy jako:
Np. H0: średnia μ zbioru jest równa wartości μ0
H0 : μ = μ0
Hipoteza alternatywna (H1) - hipoteza przeciwstawna do weryfikowanej. Możemy ją zapisać na trzy sposoby w zależności od sformułowania badanego problemu:
Np. H1: średnia μ zbioru jest różna od wartości μ0
H1 : μ ≠ μ0
18. test jednostronny i test dwustronny
19. konstrukcja przedziału ufności wokół wartości średniej lub innej statystyki
Przedział ufności dla średniej. Przedziały ufności dla średniej określają zakres wartości wokół średniej, w którym, przy danym poziomie pewności, spodziewać się możemy "prawdziwej" średniej W niektórych pakietach statystycznych (np. w STATISTICA) możemy obliczać przedziały ufności dla dowolnych poziomów p; na przykład, jeśli średnia w naszej próbie wynosi 23, a dolna i górna granica przedziału ufności przy p=0,05 wynosi odpowiednio 19 i 27, to możemy wyciągnąć wniosek, że z prawdopodobieństwem 95% średnia w populacji jest większa od 19 i mniejsza od 27.
Jeśli wybierzemy mniejsze p, to przedział będzie szerszy, a tym samym zwiększy się pewność estymatora i vice versa; jak wiadomo z prognoz pogody, im bardziej nieokreślone przewidywanie (tzn. szerszy przedział ufności), tym bardziej prawdopodobne, że się spełni. Zauważmy, że szerokość przedziału ufności zależy od wielkości próby i od zmienności danych. Obliczanie przedziałów ufności opiera się na założeniu, że zmienna ma rozkład normalny. W przeciwnym wypadku ocena może być niepoprawna, chyba, że próba jest liczna, powiedzmy n=100 lub więcej.
20. Precyzja a dokładność metody analitycznej
Precyzja metody pomiaru - stopień zgodności między wynikami uzyskanymi w określonych warunkach z wielokrotnych pomiarów tej samej wielkości.
Dokładność metody pomiaru - stopień zgodności wartości rzeczywistej ze średnią arytmetyczną wyników uzyskanych dla oznaczanej wielkości. Im dokładniejsza metoda pomiaru, tym uzyskiwane wyniki są bliższe wartości prawdziwej. W serii pomiarów o dużej dokładności tej samej wielkości fizycznej lub chemicznej większość wyników będzie zbliżona do wartości prawdziwej, a wyniki obarczone błędem przypadkowym będą rozrzucone po obu stronach wartości prawdziwej.
Dokładność i precyzja metody pomiaru są parametrami niezależnymi od siebie nawzajem. Metoda może być mało precyzyjna, gdy uzyskane wyniki mają duży rozrzut, ale mimo to dokładna, jeżeli średnia tych wyników odpowiada wartości prawdziwej. Z kolei, gdy rozrzut wyników jest nieduży, ale ich średnia jest odległa od wartości prawdziwej, metoda jest precyzyjna, ale niedokładna.
21. Przykłady porównania zbioru wartości eksperymentalnych z wartością deklarowaną
22. Idea porównania wartości średnich i przykład zastosowania
23.Porównanie dwóch wariancji
=>do porównania dwóch wariancji stosujemy test F,
=>wyraża on stosunek dwóch wariancji, a więc i odchyleń standardowych,
F=sigma1(kwadrat)/sigma2(kwadrat)
=>W liczniku F umieszczamy tzw. wariancję międzygrupową, na której maksymalizacji nam zależy. Jest to zróżnicowanie wyników zmiennej zależnej wyjaśniane przez wpływ zmiennej niezależnej. W mianowniku znajduje się tzw. wariancja wewnątrzgrupowa, czyli ważona średnia wariancji w poszczególnych grupach. Nazywana jest często wariancją błędu. Wielkość tej wariancji chcielibyśmy z kolei minimalizować, ponieważ jest to ta część całkowitej wariancji zmiennej zależnej, której nie jesteśmy w stanie wyjaśnić efektem wpływu zmiennej niezależnej.
F = wariancja międzygrupowa / wariancja wewnątrzgrupowa
Ho: sigma1(kwadrat)=sigma2(kwadrat)
H1:
-.> hipoteza alternatywna
Założenie: wariancje obu populacji są równe => hipoteza zerowa jest prawdziwa
F < Fkr => Ho jest prawdziwa
F> Fkr => wariancje obu próbek różnią się istotnie, Ho odrzucona
24. Zmienne zależne i zmienne niezależne
Zmienne, które badacz chce wyjaśnić nazywamy zmienną zależną. Są nimi bezpośrednie lub pośrednie skutki oddziaływania zmiennych niezależnych. Są to zjawiska, które badacz wyjaśnia a jednocześnie tymi wartościami, których badacz poszukuje.
Zmienna, za pomocą, której badacz chce wyjaśnić zmiany w wartościach zmiennej zależnej nazywamy zmienną niezależną. Zmienną niezależną jest ta, „która wyjaśnia badane zjawisko i która powoduje zmiany w wartościach zmiennych zależnych”. Jest zakładaną przyczyną zmian wartości zmiennej zależnej. Uchodzi za przyczynę zmiennej zależnej, która jest jej skutkiem.
Czyli na chłopski rozum zmienna niezależna jest przyczyną danych wartości zmiennej, a skutkiem są zmienne zależne, które wyjaśniamy i poszukujemy ich.
25. Regresja jednoparametrowa, a regresja wieloraka
Regresja liniowa - w statystyce, metoda estymowania wartości oczekiwanej zmiennej y przy znanych wartościach innej zmiennej lub zmiennych x. Szukana zmienna y jest tradycyjnie nazywana zmienną objaśnianą, lub zależną. Inne zmienne x nazywa się zmiennymi objaśniającymi lub niezależnymi. Zarówno zmienne objaśniane, jak i objaśniające, mogą być wielkościami skalarnymi lub wektorami.
Regresja w ogólności to problem estymacji warunkowej wartości oczekiwanej. Regresja liniowa jest nazywana liniową, gdyż zakładanym modelem zależności między zmiennymi zależnymi, a niezależnymi, jest funkcja liniowa.
Prosta regresji
Dla jednej zmiennej objaśniającej zagadnienie polega na poprowadzeniu prostej
Prostą regresji obliczamy za pomocą współczynnika kierunkowego (tu wzór z zajęc)
b=yśr+a*ośr.
Reszta od modelu - jest to odległość od wyznaczonej prostej równaniem liniowym do punktu przez który ta prosta nie przechodzi. Mają rozkład normalny. Wartości przewidywane a wartości resztowe. Linia regresji wyraża najlepszą predykcję zmiennej zależnej (Y) przy danych zmiennych niezależnych (X). Jednakże natura rzadko (jeśli w ogóle) bywa przewidywalna doskonale i zazwyczaj mamy do czynienia z odchyleniami punktów pomiarowych od linii regresji (jak można się było przekonać na wykresie rozrzutu). Odchylenie danego punktu na wykresie od linii regresji (czyli od jego wartości przewidywanej) nosi nazwę wartości resztowej.
e=y-y(e)
S^2=suma e^2/n-2 jest wariancją reszt i jest związana z błędem eksperymentalnym.
RMS= suma* e^2/n pod pierwiastek wartość średniego błędu kwadratowego.
Regresja wieloraka - Ogólnym celem regresji wielorakiej (termin ten został po raz pierwszy użyty przez Pearsona w 1908 roku) jest ilościowe ujęcie związków pomiędzy wieloma zmiennymi niezależnymi (objaśniającymi) a zmienną zależną (kryterialną, objaśnianą)
y1 1 x11 x12 x13 b0
y2 1 x21 x22 x23 b1
y3 1 x31 x32 x33 b2
y1=b01+b1x1+b2x2
X^Ty=X^TXb
b(X^TX)^-1X^Ty
y^= Xb=X(X^TX)^-1X^Ty+e
Tutaj używamy również do obliczeń RMS.
R^2=1-(suma (y-y^)^2)/(suma (y-yśr)^2 Współczynnik determinacji
Zmienne X są skorelowane. Liczba zmiennych niezależnych jest większa niż liczba próbek (szeroka macierz) nie można wyznaczyć macierzy odwrotnej
b= (X^TX)^-1X^Ty
Macierz możliwa do wyznaczenia musi posiadać więcej wierszy niż kolumn, ponieważ macierz z większa ilością kolumn nie można wyznaczyć współczynnika korelacji.
26. Miary oceny dopasowania modelu regresji do danych eksperymentalnych
Współczynnik determinacji R2 - jedna z podstawowych miar jakości dopasowania modelu. Powiązany z tym współczynnikiem jest współczynnik zbieżności.
Informuje o tym, jaka część zmienności zmiennej objaśnianej została wyjaśniona przez model. Jest on więc miarą stopnia, w jakim model wyjaśnia kształtowanie się zmiennej objaśnianej. Można również powiedzieć, że współczynnik determinacji opisuje tę część zmienności objaśnianej, która wynika z jej zależności od uwzględnionych w modelu zmiennych objaśniających. Współczynnik determinacji przyjmuje wartości z przedziału [0;1]. Jego wartości najczęściej są wyrażane w procentach. Dopasowanie modelu jest tym lepsze, im wartość R2 jest bliższa jedności. Wyraża się on wzorem:
,
gdzie:
- rzeczywista wartość zmiennej Y w momencie t,
- wartość teoretyczna zmiennej objaśnianej (na podstawie modelu),
- średnia arytmetyczna empirycznych wartości zmiennej objaśnianej.
Współczynnik zbieżności
określa, jaka część zmienności zmiennej objaśnianej nie została wyjaśniona przez model. Można również powiedzieć, że współczynnik zbieżności opisuje tę część zmienności zmiennej objaśnianej, która wynika z jej zależności od innych czynników niż uwzględnione w modelu. Współczynnik zbieżności przyjmuje wartości z przedziału [0;1]; wartości te najczęściej są wyrażane w procentach. Dopasowanie modelu jest tym lepsze, im wartość
jest bliższa zeru. Wyraża się on wzorem:
,
27. Przykłady zastosowań równań regresji jednoparametrowej w chemii
28. wyznaczanie współczynników regresji metodą najmniejszych kwadratów
-Wprowadzona przez Legendre'a i Gaussa, jest najczęściej stosowaną w praktyce metodą statystyczną
-
Jej istota jest następująca:
Wynik kolejnego pomiaru yi można przedstawić jako sumę (nieznanej) wielkości mierzonej y oraz błędu pomiarowego i ,
-Od wielkości oczekujemy, aby suma kwadratów była jak najmniejsza:
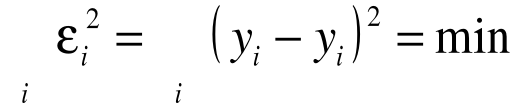
-Zasadniczy cel analizy regresji polega na ocenie nieznanych parametrów modelu regresji. Ocena ta jest dokonywana za pomocą metody najmniejszych kwadratów (MNK).
-MNK sprowadza się do minimalizacji sum kwadratów odchyleń wartości teoretycznych od wartości rzeczywistych (czyli tzw. reszt modelu).
-Dopasowany model regresji prostej, który daje punktową ocenę średniej wartości y dla określonej wartości x przyjmuje postać:
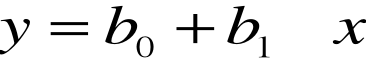
![]()
gdzie oznacza teoretyczną wartość zmiennej zależnej, a
-b 0 i b1 odpowiednio oceny wyrazu wolnego i współczynnika kierunkowego, uzyskane na podstawie wyników z próby.
29.
Założenia klasycznej metody najmniejszych kwadratów (KMNK).
Najlepiej znaną i najczęściej stosowaną w praktyce metodą estymacji nieznanych parametrów strukturalnych α modelu y = αX + ε jest metoda najmniejszych kwadratów (MNK). Przyjmujemy następujące założenia dotyczące stosowalności MNK do szacowania wektora α w modelu
y = αX + ε :
(Z1) zmienne objaśniające Xj są nielosowe i nieskorelowane ze składnikiem losowym ε,
(Z2) rz(x)=k+1≤n,
(Z3) E(ε)=0,
(Z4) D2 (ε) = E (εεT) = σ2 l , przy czym σ2 < ∞
Niekiedy przyjmuje się dodatkowe założenie (Z5), rozszerzające założenia (Z3) i (Z4) , mianowicie
(Z5) εt: N(0,σ2) dla t=1,2,...,n
Założenie (Z5) oznacza, że składnik losowy w każdym z okresów ma rozkład normalny o wartości oczekiwanej 0 i skończonej, stałej wariancji σ2. Zasadność założenia (Z2) ma charakter algebraiczny i zostanie wyjaśniona poniżej. Założenia (Z3) i (Z4) warunkują korzystne własności estymatora a wektora parametrów α wymienione w podanym dalej twierdzeniu Gaussa-Markowa. Symbol D2 (ε) użyty w twierdzeniu Z4 oznacza macierz wariancji i kowariancji wektora składników losowych.
30.Macierz odwrotna, wyznacznik macierzy, rząd macierzy
31. Obiekty odległe i ich wpływ na wyznaczanie współczynników równania regresji
32.Wizualizacja modelu i wizualizacja reszt od modelu
33. Model liniowy i model nieliniowy
Model liniowy to taki model wizualizacyjny, w którym możemy wyznaczyć linie trendu (regresje liniową), czyli wtedy, gdy współczynnik korelacji jest bliski 1 lub -1. Oprócz regresji liniowej może być także regresja wieloraka, ale są jej pewne ograniczenia:
- zmienne X są skorelowane
- liczba zmiennych niezależnych jest większa niż liczba próbek
Do metody regresji liniowej możemy stosować model najmniejszych kwadratów, czyli ten co był na lekcji i ostatnim kolokwium. Obowiązują wzory na a i funkcję opisującą krzywą regresji y = ax + b.
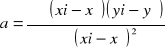
przy regresji wielorakiej stosujemy macierze (na egzaminie pewnie nie będzie, ale wzory można pamiętać) ![]()
Jeżeli współczynnik korelacji jest bliski 0 to nie możemy wyznaczyć regresji i mamy model nieliniowy. Znalazłem bardzo dużo równań opisujących modele nieliniowe, ale są zbyt długie i skomplikowane żeby je wypisywać. Również czasem przy użyciu regresji wielorakiej występuje model nieliniowy, ale nie wiem, w jaki sposób to wyjaśnić (tak gdzieś w necie pisało). Jeżeli ktoś uważa, że jest za mało to na własny koszt szuka w różnych źródłach.
34. Współczynnik korelacji Pearsona - własności i zastosowania.
Współczynnik korelacji liniowej Pearsona określa poziom zależności liniowej między zmiennymi losowymi. Niech x i y będą zmiennymi losowymi o ciągłych rozkładach. xi,yi oznaczają wartości prób losowych tych zmiennych (i = 1,2,...,n), natomiast
- wartości średnie z tych prób, tj.
Wówczas estymator współczynnika korelacji liniowej definiuje się następująco:
Ogólnie współczynnik korelacji liniowej dwóch zmiennych jest ilorazem kowariancji i iloczynu odchyleń standardowych tych zmiennych:
Współczynnik korelacji posiada następujące własności:
-1<= q <=1
q=-1 <==> Y=aX+b dla pewnego a<0
q=1 <==> Y=aX+b dla pewnego a>0
q(X,Y) = q(aX+b,cY+d) gdy ac>0
q(X,Y) = -q(aX+b,cY+d) gdy ac<0
Z powyższych własnosci wynika wniosek, że współczynnik korelacji jest miarą liniowej zależności zmiennych X i Y.
W konkretnym doświadczeniu statystycznym uzyskujemy próbę (X1,Y1),(X2 ,Y2),...,(Xn,Yn), na podstawie której estymujemy parametry rozważanych zmiennych losowych.
35. Na czym polega planowanie eksperymentu.
36. Kroki planowania eksperymentów
37. Do czego służą plany eksploracyjne?
38. Plany kompletne (plany czynnikowe) - używane są do badania zależności pomiędzy wynikiem eksperymentu i wartościami wpływającymi na ten wynik. Pełne plany czynnikowe są najużyteczniejsze, kiedy liczba czynników jest stosunkowo niewielka. Należy określić jak wiele czynników jest przedmiotem zainteresowania eksperymentatora i na ilu poziomach czynniki te będą badane. Dla m czynników przyjmujących wartości na K poziomach pełne plany czynnikowe wymagają przeprowadzenia Km eksperymentów. To jakiego planu używa się w eksperymencie zależy od charakteru badanego zjawiska. Najprostszym modelem, jaki może opisywać badaną zależność jest model liniowy będący wielomianem pierwszego stopnia postaci:
F(x1,x2,...,xk) = αo + α1x1 + α2x2 + … + αkxk
Gdzie F(x1,x2,...,xk) to odpowiedź wyznaczana w wyniku eksperymentu, αo - oszacowanie wyrazu wolnego, a α1 do αk to szacowane współczynniki regresji. Plany czynnikowe służą do szacowania współczynnika regresji równania.
39. Czynniki i poziomy czynników
40. Efekt czynnika, wpływ kombinacji efektów
41.Optymalizacja jedno, a wieloczynnikowa.
42. Metoda optymalizacji „simpleks”
Istota tej metody polega na badaniu rozwiązań bazowych programu kanonicznego w taki sposób, że znajdujemy wyjściowe rozwiązanie bazowe programu liniowego. Mając rozwiązanie bazowe sprawdzamy czy jest ono optymalne czy nie. Jeżeli dane rozwiązanie nie jest optymalne budujemy kolejne aż do momentu znalezienia rozwiązania optymalnego. Zadanie programowanie liniowego z dowolną liczbą zmiennych można rozwiązać wyznaczając wszystkie wierzchołki wielościanu, a następnie porównując wartości funkcji w punktach wierzchołkowych. W metodzie sympleks dla układu równań Akx=bk w postaci kanonicznej istnieje tablica sympleksowa Yk o wymiarach (m+1)x(n+1) w postaci:
Przykładem tej metody może być określenie wyrobu, jaki musi być produkowany przez przedsiębiorstwo w określonej ilości, aby nie przekroczyć zasobów produkcji oraz maksymalizować zysk ze sprzedaży.
43.Funkcja optymalizacji, płaszczyzna odpowiedzi
44. Przykłady zastosowań metod optymalizacyjnych w chemii.
45. ANOVA
![]()
Wyszukiwarka
Podobne podstrony:
matiematyka dla junolhu Klaldia ZAGADNIENIA Z MATEMATYKI
zagadnienia matematyczne, Ściągi dla studentów, Matematyka
Zagadnienia z matematyki ZROBIONE
1 PLAN WYNIKOWY DLA KLASY III GIMNAZJUM, Matematyka, Gimnazjum kl 3, Plany Rozkłady PSO
Scenariusz zajęcia dla dzieci trzyletnich z zakresu?ukacji matematycznej w oparciu o metodę Ex
cyfra 1, dla dzieci, Pomoce edukacyjne, Matematyka
Program koła matematycznego dla klas IV-VI (Matematyka), Szkoła
Zadania dla TRZECIEJ KLASY(1), szkoła, Matematyka, klasa III, zadania
zagadnienia matematyczne, INNE KIERUNKI, matematyka
Zagadnienia Matematyka2, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semest
Materialy dla uczestnikow wykladu ZAGADNIENIA PRAWNE A CHOROBY PSYCHICZNE
Zajęcie otwarte dla rodziców z zakresu edukacji matematycznejw oparciu o metodę E, wychowanie przeds
Zabawa matematyczna pokarm dla kaczuszek, scenariusze, edukacja matematyczna
zagadnienia matematyka stosowana 2012-2013
3 ROZKŁAD MATERIAŁU DLA KLASY III GIMNAZJUM, Matematyka, Gimnazjum kl 3, Plany Rozkłady PSO
AKSJOMATY DLA LICZB NATURALNYCH, Edukacja matematyczna
czynniki dla kaitalizmu, Opracowane zagadnienia
więcej podobnych podstron