7090996911

W. Guzicki: Zadania z kombinatoryki 15

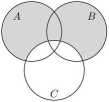
Następnie z zacieniowanego zbioru usuwamy tę część, która jest zawarta w zbiorze C. W ten sposób otrzymamy graficzną ilustrację zbioru L = (A U B) \ C, stojącego po lewej stronie naszej tożsamości:

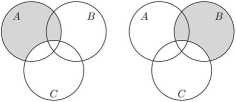
Teraz zajmiemy się zbiorem po prawej stronie dowodzonej tożsamości. Zaczynamy od narysowania zbiorów A\C oraz B\C. Oto one na następujących dwóch rysunkach (zbiór i\Cna rysunku po lewej stronie oraz zbiór B\C na rysunku po prawej stronie):

Teraz widzimy, że suma tych zbiorów, czyli zbiór P = {A \ C) U (B \ C) jest zacieniowany w następujący sposób:

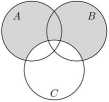
Zbiory L i P są zacieniowane tak samo, a więc są równe. To kończy dowód tożsamości.

Niektórzy nauczyciele protestują, że nie jest to dowód ogólny, a tylko ilustracja na jednym przykładzie. Otóż nie. Można udowodnić twierdzenie, które mówi, że jeśli jakaś tożsamość rachunku zbiorów (równość lub inkluzja) jest prawdziwa dla jednej tzw. niezależnej rodziny zbiorów (niezależność oznacza tu, że wszystkie składowe są niepuste), to jest prawdziwa dla dowolnej rodziny zbiorów. Skoro udowodniliśmy naszą tożsamość dla jednej niezależnej rodziny zbiorów {A, B, C}, to ta tożsamość jest też prawdziwa dla dowolnych zbiorów A, B i C. Tak więc ilustracja tożsamości za pomocą diagramów Venna jest w istocie dowodem. Jest to przy tym ten rodzaj dowodu, który polecałbym w szkole — o ile w ogóle musimy dowodzić jakiejkolwiek tożsamości rachunku zbiorów.

Jeśli jednak decydujemy się na użycie diagramów Venna, to nie widzę wielkiego sensu w tym, by najpierw użyć diagramów Venna do dowodu tych tożsamości, które są następnie potrzebne do dowodu zasady włączeń i wyłączeń, zamiast od razu użyć diagramów Venna do rozwiązania zadań kombinatorycznych. Zasada włączeń i wyłączeń jest oczywiście ważna w rachunku prawdopodobieństwa, ale wolałbym tylko podać ją uczniom, bez dowodu.

Na zakończenie rozdziału o regule dodawania popatrzmy jeszcze na kilka zadań dotyczących podzielności. W rozwiązaniach tych zadań skorzystamy z reguły dodawania oraz z zasady włączeń i wyłączeń. Oczywiście te zadania można także rozwiązać graficznie za pomocą diagramów Venna. Takie rozwiązania pozostawię jako ćwiczenie.

Warszawa, 19-20 października 2013 r.