Akademia Techniczno-Humanistyczna

w Bielsku - Białej

Wydział Nauk o Materiałach i Środowisku

Ochrona Środowiska

Rok I semestr 2

Grupa:101

Ćwiczenie nr 61

Wyznaczanie natężenia pola elektrycznego metodą sondy płomykowej

Wykonała:

Patrycja Skawska

1. Natężenie i potencjał pola elektrycznego

Ładunki działają na siebie wzajemnie. Wynika stąd, że wokół każdego ładunku występuje obszar, w którym działają siły elektrostatyczne. Obszar ten nazywamy polem elektrycznym. Pole elektryczne stałe w czasie nazywamy polem elektrostatycznym. Podobnie, jak w polu grawitacyjnym, tak i tu pole obrazują linie pola, czyli linie, do których wektor natężenia pola w każdym punkcie jest styczny.
Natężeniem pola elektrostatycznego nazywamy wielkość fizyczną, której miarą jest iloraz siły działającej na ładunek próbny umieszczony w danym punkcie pola, do wartości tego ładunku próbnego.

Od czego zależy natężenie pola elektrostatycznego w polu pojedynczego ładunku punktowego - w polu centralnym?

W danym punkcie pola P występującego wokół ładunku Q umieszczamy ładunek próbny q₀. Na ładunek ten działa siła:

Liczymy więc natężenie pola E:

Natężenie nie zależy od ładunku próbnego.
Jeżeli kilka punktowych ładunków elektrycznych wytwarza w przestrzeni pole elektrostatyczne, to natężenie w danym punkcie pola jest sumą wektorową natężeń pól wytwarzanych przez każdy z tych ładunków niezależnie.
Jest to treść zasady superpozycji.

Potencjałem elektrycznym
dowolnego punktu P, pola nazywa się stosunek pracy W wykonanej przez siłę elektryczną przy przenoszeniu ładunku q z tego punktu do nieskończoności, do wartości tego ładunku:

.

Jednostką potencjału jest 1 V (wolt) równy 1 J / 1 C.Związek między natężeniem pola elektrycznego
a potencjałem
wyraża się wzorem:

,

wobec czego:

lub inaczej:

przy przeniesieniu ładunku elektrycznego z punktu P do punktu R. Wówczas wzór ten określa napięcie elektryczne pomiędzy tymi dwoma punktami.

2.Związek między wartością natężenia pola E i potencjałem V

Powyższa zależność określa wartość natężenia pola elektrostatycznego jako stosunek spadku potencjału
na niewielkim odcinku prostopadłym do powierzchni ekwipotencjalnej

(powierzchnia równego potencjału) do długości
tego odcinka.

Znak „ - ” wynika stąd, że zwrot wektora
jest przeciwny do spadku potencjału.

3. Gęstość powierzchniowa ładunku i jej związek z natężeniem pola

Wszystkie ładunki znajdujące się na powierzchni jakiegoś naładowanego przewodnika rozmieszczone są z różną gęstością powierzchniową. Gęstość powierzchniową ładunku określamy jako:

gdzie:

- gęstość powierzchniowa

Δq - ładunek elektryczny znajdujący się elementarnej powierzchni

ΔS - elementarna powierzchnia

Za pomocą związku między gęstością powierzchniową ładunku a natężeniem pola możemy obliczyć gęstość powierzchniową na podstawie znajomości natężenie pola.

Dla kondensatora gęstość powierzchniowa wyrażać się będzie wzorem:

gdzie:

- gęstość powierzchniowa

V₁ - wartość potencjału na pierwszej płytce kondensatora

V₂ - wartość potencjału na drugiej płytce kondensatora

d - odległość okładek kondensatora od siebie

E - natężenie pola elektrycznego

= 8,85·10^-12 [F/m] - przenikalność elektryczna próżni

Tabela.1

Tabela wyników pomiarowych

d1=40 mm		d2=80 mm		d3=120 mm
U	l	U	l	U	l
[V]	[mm]	[V]	[mm]	[V]	[mm]
600	10	600	21	600	39
810	12	700	24	700	42
1000	14	800	27	760	45
1300	16	910	30	840	48
1515	18	1020	33	900	52
1585	20	1160	36	980	57
1780	22	1280	39	1040	60
1970	24	1400	42	1120	63
1980	26	1540	45	1200	66
2380	28	1680	48	1280	69
2520	30	1800	51	1360	71
		1950	54	1420	74
		2100	57	1500	77
		2240	60	1600	80
		2380	63	1700	83
		2540	66	1820	86
		2680	69	1940	89
		2820	72	2020	92
				2140	95
				2250	98
				2390	101
				2440	104
				2560	107
				2660	110
				2820	113
				2940	116

Na podstawie wyników pomiarów z tab.1 sporządziłyśmy trzy wykresy zależności U=f(l). Współczynnik kierunkowy a jest równy natężeniu pola elektrycznego Ed.

Za pomocą programu komputerowego obliczyłyśmy współczynnik a, ∆a, b i ∆b. Współczynnik kierunkowy a jest równy natężeniu pola elektrycznego Ed.

	Parametry prostej regresji
Odległość płytek - d		a =Ed	a	b [V]	b [V]
d1=40 mm		96,3	2,5	-316,8	53,4
d1=80 mm		50,6	1,4	-798,5	8,8
d1=120 mm		38,0	2,6	-1488,0	28,0

Zgodnie ze wzorem:

obliczyłyśmy teoretyczne wartości natężenia pola elektrycznego E_t dla poszczególnych wartości d i zadanego napięcia między okładkami. Wartość napięcia odczytałyśmy z zasilacza WN: U=3000 V.

Otrzymałyśmy następujące wyniki dla:

d₁=40 mm E_t=3000/40 = 75 [V/mm]

d₁=80 mm E_t= 3000/80 = 37,5 [V/mm]

d₁=120 mm 3000/120 = 25 [V/mm]

Obliczyłyśmy względne odchylenia δ wartości doświadczalnych natężenia pola elektrycznego E_d od wartości teoretycznych E_t.

Korzystając ze wzoru:

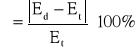
otrzymałyśmy następujące wyniki dla poszczególnych odległości d_x:

• d₁=40 mm δ= 96,3 - 75 / 75 * 100% = 28,4%

• d₁=40 mm δ= 50,6 - 37,5 / 37,5 * 100% = 34,9%

• d₁=40 mm δ= 38,0 - 25 / 25 * 100% = 52,0%

Tabela 2.

Wyniki obliczeń:

d1=40 mm			d2=80 mm			d3=120 mm
Ed [V/mm]	Et [V/mm]	δ [%]	Ed [V/mm]	Et [V/mm]	δ [%]		Ed [V/mm]	Et [V/mm]	δ [%]
96,3	75	28,4	50,6	37,5	34,9		38,0	25	52,0

Obliczyłyśmy gęstość powierzchniową ładunku σ_d na wewnętrznej powierzchni jednej z płytek.

Dla pierwszego doświadczenia (d₁=40 mm), które tworzy liniową zależność U=f(l) obliczyłyśmy gęstość powierzchniową ze wzoru:

σ = ε₀ ^. E_d

gdzie:

σ - gęstość powierzchniowa

ε₀ =8,85^.10^-12[F/mm] - przenikalność elektryczna próżni

•dla d₁=40 mm σ = 8,85 * 10^-12 * 96,3 [V/mm * F/m]= 8,85 * 10^-15 * 96,3 [V/mm * F/mm]= 773.5 *10^-15 [C/mm²]= 852,3 *10^-9 [μC/mm²]

W doświadczeniu 2 i 3 (dla d₂=80mm i d₃=120 mm) wykres zależności U=f(l) odbiega od linii prostej. W celu obliczenie gęstości wyznaczyliśmy parametry prostej regresji dopasowanej do ostatnich 6-ciu punktów pomiarowych. Parametr „a” określa nam lokalne natężenie pola elektrycznego E_dl.

Gęstość powierzchniowa wynosić będzie:

•dla d₂ =80mm σ = 8,85 * 10^-12 * 50,6= 447,8 * 10^-9[μC/mm²]

•dla d₃ =120mm σ = 8,85 * 10^-12 * 38,0= 336,3 * 10^-9[μC/mm²]

Tabela 3

Wyniki obliczeń natężenia pola elektrycznego, gęstości powierzchniowej ładunku oraz liczba elektronów dla poszczególnych odległości:

d1=40 mm			d2=80 mm			d3=120 mm
Ed [V/mm]	σ x10^-7[μC /mm^2 ]	Le [1/mm^2]	Ed [V/mm]	σ x10^-7[μC /mm^2 ]	Le [1/mm^2]	Edl [V/mm]	σ x10^-7[μC /mm^2 ]	Le [1/mm^2]
96,3	8,5	5,3 * 10^6	50,6	4,4	2,8* 10^6	38,0	3,3	2,1[μC/mm^2] * 10^6

Liczba elektronów:

d₁=40mm

L_e= σ/e= 8,5*10^-7/1,602 * 10^-13[μC/mm²*μC]= 5,305 * 10⁶[1/mm²]

d₂= 80mm

L_e=4,410^-7/1,602 * 10^-13[μC/mm²*μC]= 2,746 * 10⁶[1/mm²]

d₃ =120mm

L_e=3,310^-7/1,602 * 10^-13[μC/mm²*μC]= 2,059* 10⁶[1/mm²]

---