POLITECHNIKA ŚWIĘTOKRZYSKA
LABORATORIUM ELEKTROTECHNIKI TEORETYCZNEJ
Numer ćwiczenia: 2	Temat ćwiczenia: Metody analizy układów w stanie ustalonym (metoda oczkowa i potencjałów węzłowych).	Zespół: Zuchowicz Marcin Stępień Grzegorz
Data wykonania: 25.03.1998	Data oddania do sprawdzenia: 1.04.1998	Ocena:

Schemat pomiarowy układu :

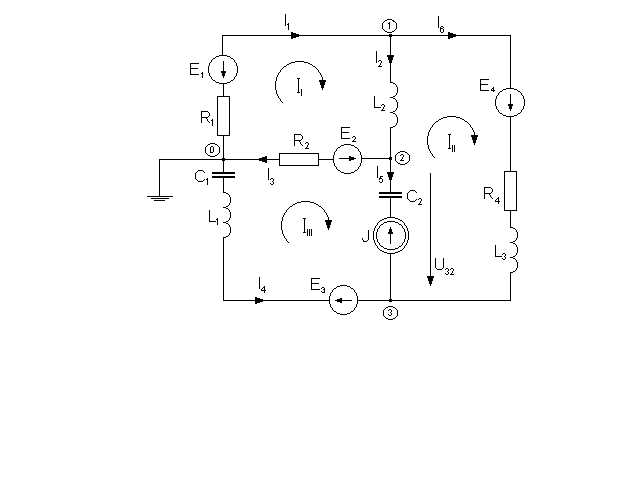
Układy równań (metoda potencjałów węzłowych) :

Układy równań (prądy oczkowe) :

DEKLARACJE

» R1 = 20, » R2 = 12, » R4 = 20, » XL4 = 12, » XL2 = 30, » XC2 = 30, » XL1 = 16, » XC1 = 24,

» E1 = 1.6180e+002- 1.1756e+002i, » E2 = 70.7107 +70.7107i, » E3 = 70.7107 +70.7107i, » E4 = 1.6180e+002- 1.1756e+002i

» JZ = 4.6985 + 1.7101i

POTENCJAŁY WĘZŁOWE

0. ELEMENTY MACIERZY ADMITANCYJNEJ

» y11=1/R1+1/(j*XL2)+1/(R4+j*XL4), y11 = 0.0868 - 0.0554i,

» y12=-1/(j*XL2), y12 = 0 + 0.0333i,

» y13=-1/(R4+j*XL4), y13 = -0.0368 + 0.0221i,

» y21=-1/(j*XL2), y21 = 0 + 0.0333i,

» y22=1/R2+1/(j*XL2), y22 = 0.0833 - 0.0333i,

» y23=0, y23 = 0,

» y31=-1/(R4+j*XL4), y31 = -0.0368 + 0.0221i,

» y32=0, y32 = 0,

» y33=1/(j*XL1-j*XC1)+1/(R4+j*XL4), y33 = 0.0368 + 0.1029i,

0. MACIERZ IMPEDANCYJNA

» Y=[y11 y12 y13 ; y21 y22 y23 ; y31 y32 y33],

Y =

0.0868 - 0.0554i 0 + 0.0333i -0.0368 + 0.0221i

0 + 0.0333i 0.0833 - 0.0333i 0

-0.0368 + 0.0221i 0 0.0368 + 0.1029i

0. ELEMENTY MACIERZY PRADOW ŻRÓDŁOWYCH

» iw1=-E1/R1-E4/(R4+j*XL4), iw1 = -11.4457 +13.7690i,

» iw2=E2/R2+JZ, iw2 = 10.5910 + 7.6027i,

» iw3=-E3/(j*XL1-j*XC1)-JZ+E4/(R4+j*XL4), iw3 = 7.4959 -18.4401i,

0. MACIERZ PRADOW ŻRÓDŁOWYCH

» IW=[iw1;iw2;iw3],

IW =

-11.4457 +13.7690i

10.5910 + 7.6027i

7.4959 -18.4401i

0. MACIERZ POTENCJAŁÓW

» V=Y^(-1)*IW,

V = 1.0e+002 *

-1.4982 + 0.3610i

0.6988 + 1.7912i

-1.1040 - 0.6647i

» v1=1.0e+002*(-1.4982+j*0.3610), v1 = -1.4982e+002+ 3.6100e+001i,

» v2=1.0e+002*(0.6988+j*1.7912), v2 = 6.9880e+001+ 1.7912e+002i,

» v3=1.0e+002*(-1.1040-j*0.6647), v3 = -1.1040e+002- 6.6470e+001i,

0. PRADY GAŁĘZIOWE OBLICZONE METODA WĘZŁOWA

» IW1=(v1+E1)/(-R1), IW1 = -0.5992 + 4.0729i, » IW2=(v1-v2)/(j*XL2), IW2 = -4.7673 + 7.3233i,

» IW3=(v2-E2)/R2, IW3 = -0.0692 + 9.0341i, » IW4=(v3+E3)/(j*XC1-j*XL1), IW4 = 0.5301 + 4.9612i,

» IW5=-JZ, IW5 = -4.6985 - 1.7101i, » IW6=(v3-v1-E4)/(-R4-j*XL4), IW6 = 4.1688 - 3.2506i

METODA PRADÓW OCZKOWYCH

0. ELEMENTY MACIERZY WSPÓŁCZYNNIKÓW

» z11=R1+R2+j*XL2, z11 = 32.0000 +30.0000i, » z12=-j*XL2, z12 = 0 -30.0000i, » z13=-R2, z13 = -12,

» z14=0, z14 = 0, » z21=-j*XL2, z21 = 0 -30.0000i, » z22=j*XL2+j*XL4+R4, z22 = 20.0000 +42.0000i,

» z23=0, z23 = 0, » z24=1, z24 = 1, » z31=-R2, z31 = -12, » z32=0, z32 = 0,

» z33=R2+j*XL1-j*XC1, z33 = 12.0000 - 8.0000i, » z34=-1, z34 = -1, » z41=0, z41 = 0, » z42=1, z42 = 1,

» z43= -1, z43 = -1, » z44=0, z44 = 0

0. MACIERZ WSPÓŁCZYNNIKÓW

» Z=[z11 z12 z13 z14 ; z21 z22 z23 z24 ; z31 z32 z33 z34 ; z41 z42 z43 z44],

Z =

32.0000 +30.0000i 0 -30.0000i -12.0000 0

0 -30.0000i 20.0000 +42.0000i 0 1.0000

-12.0000 0 12.0000 - 8.0000i -1.0000

0 1.0000 -1.0000 0

0. ELEMENTY MACIERZY ŻRÓDŁOWEJ

» e1=-E1-E2, e1 =-2.3251e+002+ 4.6846e+001i, » e2=E1, e2 = 1.6180e+002- 1.1756e+002i,

» e3=E2+E3, e3 = 1.4142e+002+ 1.4142e+002i, » e4=JZ, e4 = 4.6985 + 1.7101i,

» E=[e1;e2;e3;e4],

0. MACIERZ ŻRÓDŁOWA

E = 1.0e+002 *

-2.3251 + 0.4685i

1.6180 - 1.1756i

1.4142 + 1.4142i

0.0470 + 0.0171i

0. MACIERZ NIEWIADOMYCH ( PRADÓW OCKOWYCH I NAPIĘCIA NA ŻRÓDLE PRADU )

» IO=Z^(-1)*E,

IO = 1.0e+002 *

-0.0060 + 0.0407i

0.0417 - 0.0325i

-0.0053 - 0.0496i

-1.8028 - 2.4559i

» i1=1.0e+002*(-0.0060+j*0.0407), i1 = -0.6000 + 4.0700i, » i2=1.0e+002*(0.0417-j*0.0325), i2 = 4.1700 - 3.2500i,

» i3=1.0e+002*(-0.0053-j*0.0496), i3 = -0.5300 - 4.9600i, » uz=1.0e+002*(-1.8028-j*2.4559), uz = -1.8028e+002- 2.4559e+002i

0. PRADY GAŁĘZIOWE OBLICZONE METODA PRADÓW OCZKOWYCH

» IO1=i1, IO1 = -0.6000 + 4.0700i, » IO2=i1-i2, IO2 = -4.7700 + 7.3200i, » IO3=i1-i3, IO3 = -0.0700 + 9.0300i,

» IO4=-i3, IO4 = 0.5300 + 4.9600i, » IO5=-JZ, IO5 = -4.6985 - 1.7101i, » IO6=i2, IO6 = 4.1700 - 3.2500i

0. PORÓWNANIE WYNIKÓW OTRZYMANYCH METODA WĘZŁOWA I OCZKOWA

» IW1-IO1 ans = 0.0008 + 0.0029i

» IW2-IO2 ans = 0.0027 + 0.0033i

» IW3-IO3 ans = 0.0008 + 0.0041i

» IW4-IO4 ans = 0.0001 + 0.0012i

» IW5-IO5 ans = 0

» IW6-IO6 ans = -0.0012 - 0.0006i

WNIOSKI :

Na podstawie wyników obliczeń zauważamy , że różnice w wynikach pomiędzy obliczeniami metodą oczkową a metodą potencjałów węzłowych są minimalne co świadczy o tym, że nie popełniliśmy błędów przy doborze odpowiednich równań do poszczególnych metod.

---