POLITECHNIKA RADOMSKA im. Kazimierza Pułaskiego WYDZIAŁ TRANSPORTU		LABORATORIUM MIERNICTWA				Data:
Wykonali:		Grupa:		Zespół:		Rok akademicki:
Temat:	Pomiary oscyloskopowe			Nr ćwiczenia		Ocena i podpis prowadzącego:

1. Cel ćwiczenia:

Celem ćwiczenia jest poznanie budowy, zasady działania i obsługi oscyloskopu elektronicznego oraz obserwacja przebiegów jednokrotnych i innych przebiegów na ekranie oscyloskopu, a także zapoznanie się z możliwością wykonania za pomocą oscyloskopu pomiarów takich wielkości fizycznych, jak okres badanego przebiegu, częstotliwość, kąt przesunięcia fazowego.

2. Przebieg ćwiczenia:

2.1 Pomiar amplitudy, częstotliwości i okresu badanego przebiegu za pomocą oscyloskopu elektronicznego typu 3502

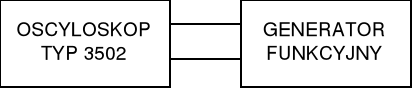
Rys.1 Układ połączeń oscyloskopu z generatorem funkcyjnym

Tabela pomiarowa

Lp.	Amplituda A	Okres T	Częstotliwość f	Uwagi
	[V]	[s]	[Hz]
1a	0.8	960 μs	1041,667	1 kHz, sinusoida
1b	0.8	340 μs	2941,176	3 kHz, sinusoida
2a	0.8	100 μs	10000	10 kHz, trójkąt
2b	0.8	10 μs	100000	100 kHz, trójkąt
3a	0.8	5.2 μs	192307,7	200 kHz, prostokąt
3b	0.8	20 μs	50000	50 kHz, prostokąt

Przykładowe obliczenia:

Hz

2.2 Pomiar kąta przesunięcia fazowego

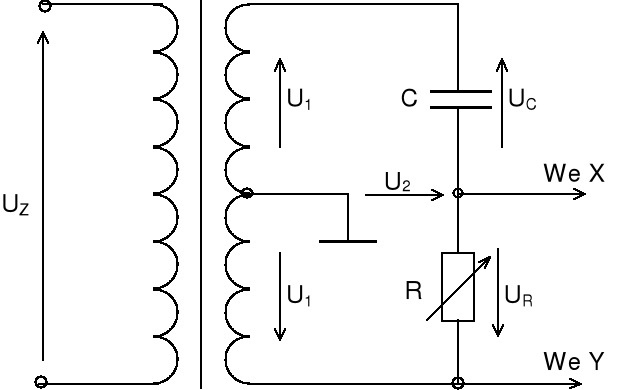
Rys.3 Schemat przesuwnika fazowego

Tabela pomiarowa dla pomiaru kąta przesunięcia fazowego

Lp.	R	ϕosc	ϕ=360-ϕosc	xo/x	asin(xo/x)	ϕobl	Δϕ	δϕ
	[kΩ]	[°]	[°]		[°]	[°]	[°]	[%]
1	2	329,7	30,3	0,5176	31,2	31,2	0,9	2,97
2	5	293	67	0,931	68,6	68,6	1,6	2,388
3	10	254,5	105,5	0,9749	77,1	102,9	2,6	2,465
4	15	232	128	0,8352	56,6	123,4	4,6	3,594
5	20	219,4	140,6	0,7805	51,3	128,7	11,9	8,464
6	23	216	144	0,5756	35,1	144,9	0,9	0,625
7	40	201,7	158,3	0,4092	24,2	155,8	2,5	1,579

Uwaga: Kąt w rubryce ϕ_osc jest przesunięciem fazowym odczytanym z oscyloskopu, ϕ=360-ϕ_osc to przesunięcie między sygnałami wejściowym a wejściowym.

Przykładowe obliczenia:

°

°

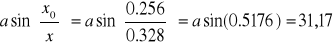
° , ponieważ kąt w pierwszej ćwiartce układu współrzędnych;

°

%

2.3 Badanie i obserwacje przebiegów jednokrotnych

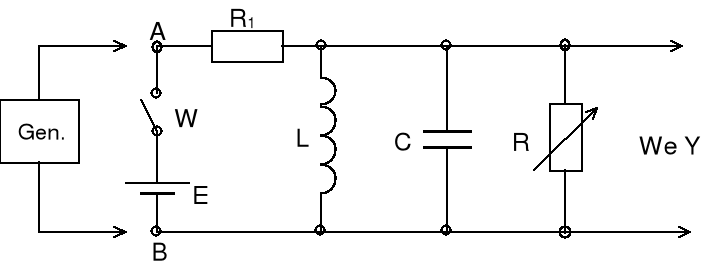
Rys.4 Schemat układu do badania przebiegów jednokrotnych

Tabela pomiarowa dla wyników obserwacji przebiegów jednokrotnych

Lp.	R	T	f	fobl	Δf	δf	Q
	[kΩ]	[μs]	[Hz]	[Hz]	[Hz]	[%]
1	32	30	33333	39888	6555	16.43	8 π
2	20	32	31250	39888	8638	21.66	4 π
3	60	32	31250	39888	8638	21.66	11 π

Przykładowe obliczenia:

Hz

Hz

Hz

%

3. Wnioski:

W pierwszej części ćwiczenia zbadaliśmy możliwości oscyloskopu w dziedzinie pomiarów amplitudy, częstotliwości i okresu badanego przebiegu. Jak się okazało, można dokonać pomiarów przybliżonych wartości tych wielkości, jednak ich dokładność jest znacznie ograniczona. Duży wpływ na dokładność odczytu okresu badanego sygnału ma właściwy dobór podstawy czasu. Należy tak ustawić parametry podstawy czasu, by na lampie oscyloskopowej oglądać jeden pełny okres badanego przebiegu. Nasze pomiary są na tyle dokładne, na ile pozwala na to podziałka na lampie oscyloskopowej. W praktyce błędy nie przekraczały kilku procent.

Dzięki najnowszej technologii cyfrowej, pomiary stają się dokładniejsze, ponieważ mamy możliwość bezpośredniego odczytu mierzonej wartości w postaci liczbowej. Skorzystaliśmy z tych dogodności przy pomiarze kąta przesunięcia fazowego w drugiej części ćwiczenia. Najpierw odczytywaliśmy bezpośrednio przesunięcie między sygnałami badanymi, następnie czyniliśmy to za pomocą metody figur Lissajous. Przy porównaniu wyników pomiarów okazało się, że przy określaniu kąta przesunięcia fazowego należy wziąć pod uwagę zachowanie się funkcji arcus sinus dla różnych wartości jej argumentów:

asin(x) = asin(180 - x)

Biorąc pod uwagę powyższą zależność, określiliśmy badane przesunięcia fazowe i porównaliśmy je z uzysaknymi pierwszą metodą. W jednym wypadku błąd bezwzględny sięgał 12%, co może być spowodowane błędem grubym przy odczycie z ekranu oscyloskopu. W pozostałych wypadkach błąd ten nie przekraczał 4%.

Technika cyfrowa daje także możliwość obserwacji przebiegów jednokrotnych. Istnieje możliwość zapamiętania takiego przebiegu i późniejszej jego analizy. Naszym zadaniem była obserwacja drgań gasnących obwodu rezonansowego i ustalenie podstawowych parametrów tego obwodu : dobroci Q i częstotliwości drgań własnych. Jak wykazały nasze obserwacje, dobroć jest wprost proporcjonalna do rezystancji szeregowej przyłączonej równolegle do obwodu rezonansowego. Przy ustalaniu częstotliwości drgań własnych badanego obwodu błąd bezwzględny przekroczył 20% w stosunku do wartości teoretycznej, obliczonej na podstawie parametrów zastosowanych elementów. Wynikać to może z niedokładności odczytu z oscyloskopu.

1

---