POLITECHNIKA LUBELSKA w LUBLINIE LABORATORIUM PODSTAW ELEKTROTECHNIKI Ćwicz. nr 7 TEMAT: ANALIZATORY HARMONICZNYCHDATA: 1996.11.20 WYKONAŁ: DUDA GRZEGORZSZUBA KRZYSZTOFOSIŃSKI ANDRZEJ GRUPA: ED 3.5OCENA: Część teoretyczna: Przykładowe obliczenia dla prostowania bez wygładzania napięcia:gdzie a,b,c,b,e,f,g są stosunkami % względem wartości pierwszej harmonicznej.Dla sygnału prostokątnego szereg Fouriera przyjmie postać: Część wykonawcza:1. Pomiar udziału harmonicznych w prądzie magnesującym transformatora.rys.1 Układ pomiarowy do punktu 1Tabela nr 1P.OMIARY OB L I C Z EN I A Lp.UII2/I1I3/I1I4/I1I5/I1I6/I1I1I2I3I4I5I6VA%%%%%AAAAAA2500,116363280,0883540,0053010,0318070,0026510,0017670,0070682250,086333280,0648890,0038930,0214130,0019470,0012980,0051912000,066303280,0491540,0029490,0147460,0014750,0009830,0039321750,055272180,0418120,0020910,0112890,0008360,0004180,0033451500,041,5710,540,0374630,0005620,0026220,0003750,0001870,0014991250,021,5610,540,0188140,0002820,0011290,0001889,41E-050,000753
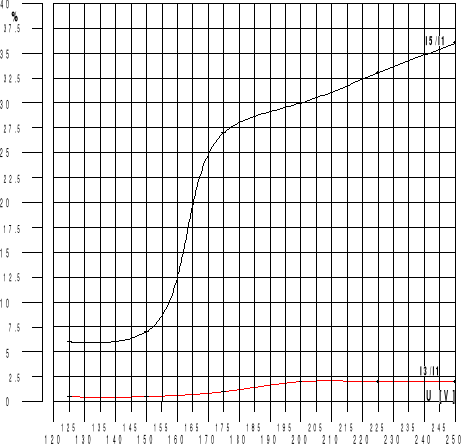
Wyk.1 Charakterystyka I3/I1=f(U) ; I5/I1
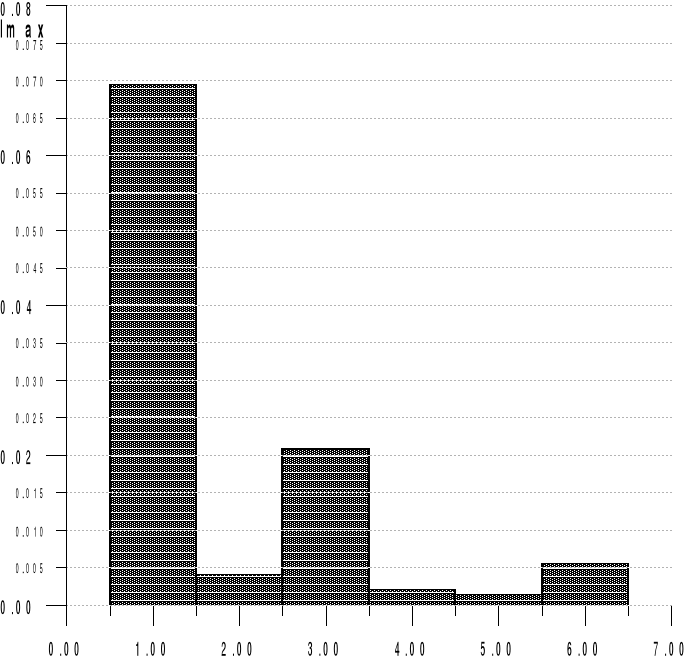
Wyk.2 Widmo harmonicznych prądu dla napięcia 200V.
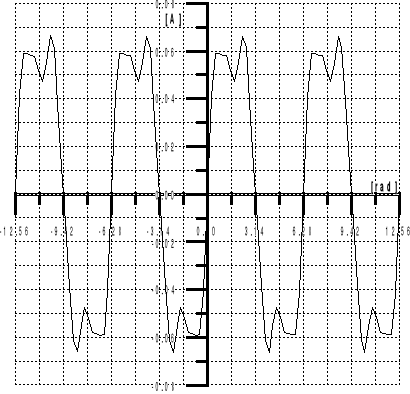
Wyk.3 Wypadkowy wykres prądu przy napięciu U=200V2. Pomiar udziału harmonicznych w napięciu na wyjściu ukladu do prostowania jednopołówkowego. PO MIARY O BL I C Z EN I ALpUIUIICU0/U1U2/U1U3/U1U4/U1U5/U1U6/U1U0U1U2U3U4U5U6VVμF%%%%%%VVVVVVV208,502172002,5003,99121,83930,367900,046002012,5123,74,21652110,2434635,79670,92750,28980,11590,0580,0582012,51204,318621,810,2371395,51490,99270,33090,11030,09930,055120121105,24311431,80,2061753,96491,70490,43610,15860,11890,07142010904,84610430,50,1715383,57371,64390,35740,14290,10720,0179209,5604,156943,500,1353853,30211,84920,29720,13210,11560
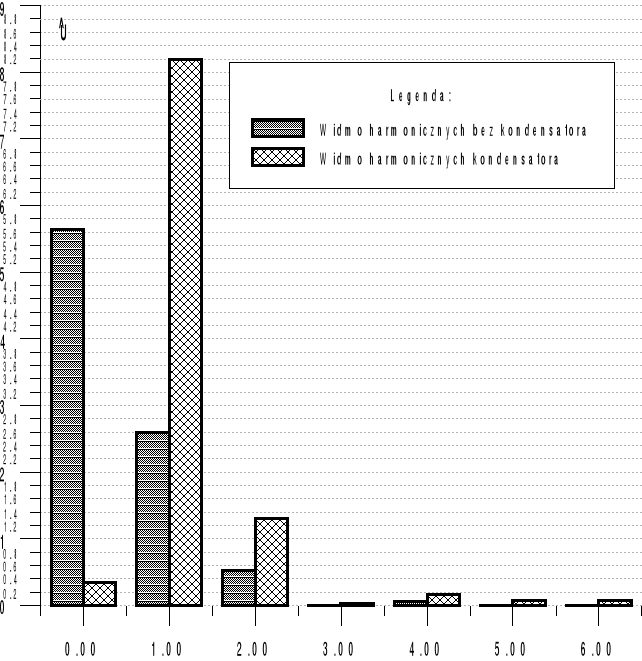
Wyk.4 Widmo harmonicznych mierzonych przebiegów3.Pomiar udziału harmonicznych w przebiegu prostokątnym i trójkątnym. POMIARYOBLICZENIAL.p.U2/U1U3/U1U5/U1U7/U1U9/U1U2/U1U3/U1U5/U1U7/U1U9/U1sygnał%%%%%%%%%%123216106-33.32014.311.11prost.610421-11.113.992.0351.237trójk.n=1 ; n=3

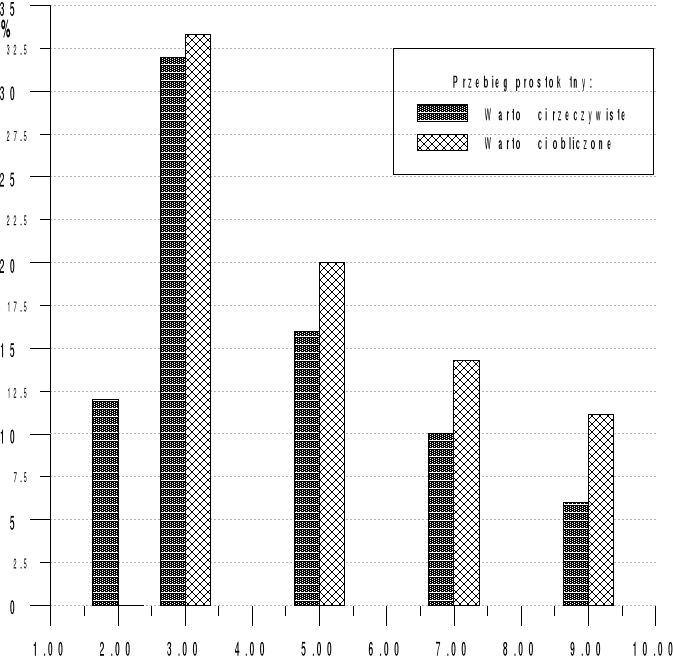
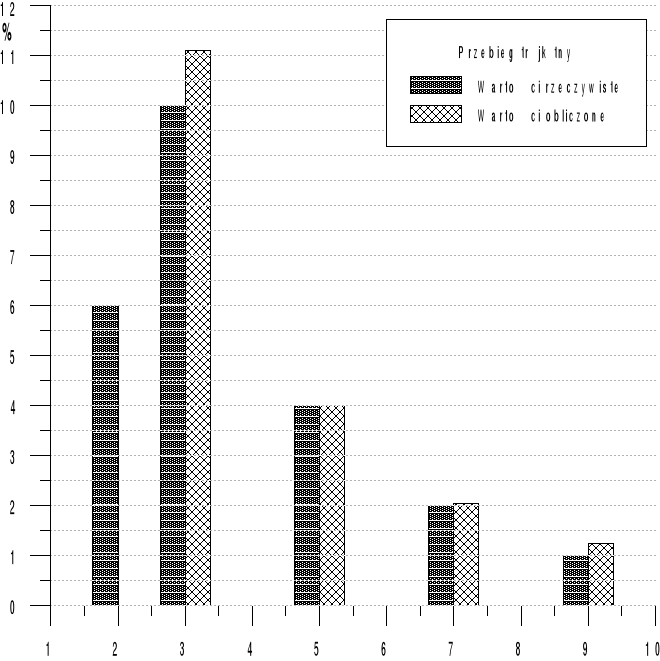
Ponieważ przebieg prostokątny jest : okresowy, nieparzysty, asymetryczny to wiemy, że w rozwinięciu Fouriera szereg nie będzie posiadał części składającej się z rozwinięcia cosinusowego oraz nie wystąpi w nim składowa stała ani też składowe parzyste.WNIOSKI I SPOSTRZEŻENIA:Przy przebiegach prostokątnych wystąpiło pewne przekłamanie dotyczące składowych parzystych. Polegające na tym że w idealnym przebiegu prostokątnym nie powinno być składowych parzystych. Jego powodem mogło być złe zestrojenie filtru lub niedokładności pomiarów. Być może na takie wyniki miały wpływ inne czynniki, które doprowadziły do zakłóceń w obwodzie. Ale jest to układ rzeczywisty, a nie idealny.

---