LABORATORIUM FIZYKI
Ćwiczenie nr: 8
Temat: Badanie zjawisk galwanomagnetycznych w ciałach stałych.
Grupa T-41
Sekcja 6
Bednarz Krzysztof
Kopecki Marcin
Wstęp teoretyczny
Zjawisko Halla
Zjawiska galwanomagnetyczne występujące w ciałach stałych są związane z działaniem siły Lorentza na nośniki ładunku elektrycznego poruszające się w polach elektrycznym i magnetycznym. Załóżmy, iż próbka w kształcie prostopadłościanu znajduje się w polu magnetycznym o wektorze indukcji B prostopadłym do największej jej ściany. Pod wpływem zewnętrznego pola magnetycznego B nośniki ładunku tworzące prąd elektryczny zostają odchylone w kierunku jednej ze ścian bocznych próbki. W wyniku powyższego procesu następuje gromadzenie się części nośników ładunku przy danej ścianie, a tym samym powstaje asymetria obsadzenia nośnikami. Pociąga to za sobą powstanie mierzalnej poprzecznej różnicy potencjałów pola elektrycznego, zwanej napięciem Halla „U".
Wartość napięcia Halla ustala się samoczynnie w wyniku wytworzenia stanu równowagi dynamicznej pomiędzy siła Lorentza a siła pochodząca od powstającego poprzecznego pola elektrycznego.
Pole magnetyczne prowadzi nie tylko do wytworzenia napięcia Halla, lecz wpływa również na przewodnictwo elektryczne materiału, który w nim się znajduje. Bez pola magnetycznego cząstka porusza się prostoliniowo i pomiędzy dwoma zderzeniami w czasie z przebywa wzdłuż pola elektrycznego Ez drogę równa długości drogi swobodnej.
W próbce znajdującej się w polu magnetycznym tor ruchu cząstki jest zakrzywiony. Zakrzywienie toru powoduje skrócenie drogi przebytej przez cząstkę wzdłuż pola elektrycznego w czasie. Jest to równoznaczne ze zmniejszeniem wartości tzw. prędkości unoszenia lub ruchliwości nośników ładunku. Tym samym maleje przewodnictwo elektryczne materiału umieszczonego w polu magnetycznym, a jego rezystywność wzrasta.
Schemat układu pomiarowego
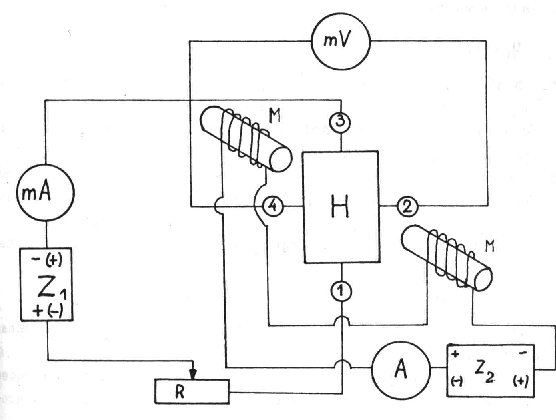
Schemat stanowiska pomiarowego do badania zjawiska Halla składa się z:
A, mA - amperomierze, Z1 i Z2 - zasilacze, H - badana próbka, R - regulowany opornik,
mV -woltomierz, M- elektromagnesy
Opracowanie wyników
A6. Niepewności wszystkich uzyskanych wyników pomiaru.
Dla Is Dla I
I=20 [mA] k=1 k=0,2
I=0,02 [A] z=10 z=0,03
![]()
![]()
A7. Wykres zależności B=f(Is).
Is [A] |
0,1 |
0,5 |
1,1 |
1,5 |
2,1 |
2,5 |
3,1 |
3,5 |
4,1 |
4,5 |
5,1 |
B [mT] |
0,37 |
17,5 |
31,4 |
45,2 |
59,1 |
72,9 |
86,7 |
101 |
114 |
128 |
142 |
B [T] |
0,00037 |
0,0175 |
0,0314 |
0,0452 |
0,0591 |
0,0729 |
0,0867 |
0,1010 |
0,1140 |
0,1280 |
0,1420 |
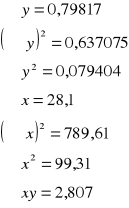
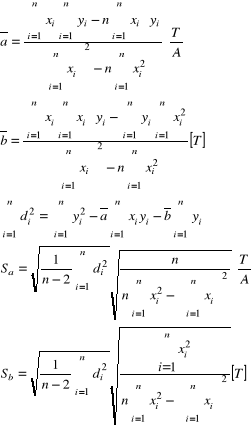
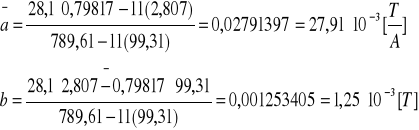
![]()

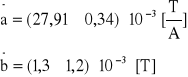
A8. Aproksymacja B=f(Is).
A9. Obliczyć wartości indukcji pola magnetycznego B, dla których badano zjawisko Halla.
![]()
Is [A] |
B [T] |
0,1 |
0,0040448 |
0,5 |
0,0152104 |
1,1 |
0,0319588 |
1,5 |
0,0431244 |
2,1 |
0,0598727 |
2,5 |
0,0710383 |
3,1 |
0,0877867 |
3,5 |
0,0989523 |
4,1 |
0,1157007 |
4,5 |
0,1268663 |
5,1 |
0,1436146 |
A10. Niepewność B - metodą różniczki zupełnej.
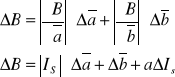
Is [A] |
Δ B [T] |
0,1 |
0,001241 |
0,5 |
0,001401 |
1,1 |
0,001641 |
1,5 |
0,001801 |
2,1 |
0,002041 |
2,5 |
0,002200 |
3,1 |
0,002440 |
3,5 |
0,002600 |
4,1 |
0,002840 |
4,5 |
0,003000 |
5,1 |
0,003240 |
A11. Obliczyć napięcie Halla ze wzoru 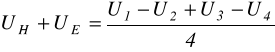
.
I[A] |
Uh[V] |
||
0 |
0,043 |
||
0,0025 |
0,092 |
||
0,0050 |
0,138 |
||
0,0075 |
0,176 |
||
0,0100 |
0,217 |
||
0,0125 |
0,253 |
||
0,0150 |
0,290 |
||
0,0175 |
0,333 |
||
0,0200 |
0,368 |
||
Is [A] |
UH [V] |
||
1,5 |
0,166 |
||
2,1 |
0,168 |
||
2,5 |
0,230 |
||
3,1 |
0,238 |
||
3,5 |
0,298 |
||
4,1 |
0,306 |
||
4,5 |
0,359 |
||
5,1 |
0,368 |
||
A12. Dla wyników w pkt. A2 i A3 sporządzić wykres UH=f(B).
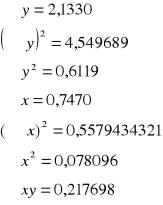

![]()


A13. Aproksymować wyniki przedstawione na wykresie UH=f(B).
A14. Korzystając z równania prostej aproksymującej obliczyć wartość stałej Halla R.
d = 10-5 m=0,00001
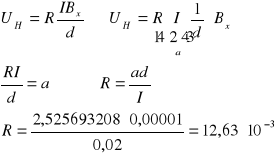
A15. Wyznaczyć niepewność stałej R.

A16. Dla wyników w pkt. A4 i A5 sporządzić wykres zależności UH=f(I).
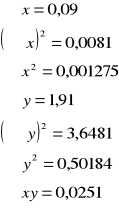
![]()
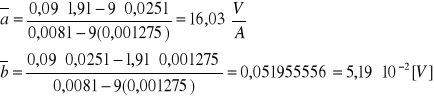
![]()
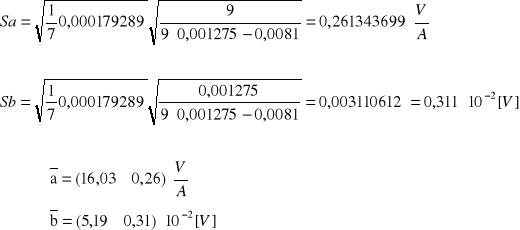
A17. Metodą najmniejszych kwadratów aproksymować wyniki wykresu UH=f(I).
A18. Korzystając z równania prostej aproksymującej w pkt A17 oraz równania
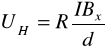
obliczyć stałą Halla R. d = 10-5 m.
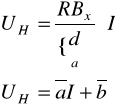
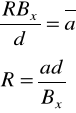
![]()
A19. Niepewność stałej R.
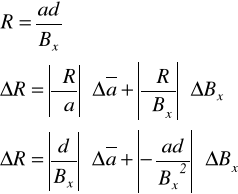
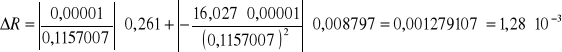
R = (13,9±1,3)10-3![]()
A20. Porównać wartości stałej R z pkt. A14 i A15 z punktami A18 i A19.
![]()
![]()
R = (13,9 ± 1,3)10-3![]()
A21. Korzystając ze wzoru 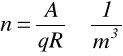
i z dokładniej wyznaczonej wartości stałej R obliczyć koncentrację n nośników ładunku w próbce (jako wartość współczynnika korygującego przyjąć A=1,0)
q=1,6·10-19[C]
![]()
A22. Metodą różniczki zupełnej obliczyć niepewność n.
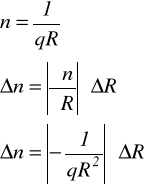
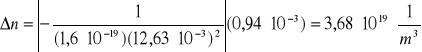
n= (4,94 ± 0,37 )1020[1/m3]
A23. Na podstawie znaku stałej Halla określić typ przewodnictwa w badanej próbce.
Na podstawie wyznaczonego znaku stałej Halla R możemy wywnioskować iż mamy do czynienia z materiałem o dziurowym typie przewodnictwa ponieważ ma wartość dodatnią .
Wnioski
1.W ćwiczeniu badaliśmy próbkę o grubości 10-5 [m]. Wartości indukcji magnetycznej Halla zmienia się liniowo wraz ze wzrostem prądu IS.
2.Korzystając z równania prostej aproksymującej wykresu UH=f(B) oraz równania 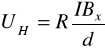
wyznaczyliśmy wartość stałej Halla ![]()
![]()
,którą porównaliśmy z wartością stałej Halla wyznaczoną na bazie równania prostej aproksymującej wykresu UH=f(I)
R = (13,9 ± 1,3)10-3![]()
.
3.Koncentracja n nośników ładunku w badanej próbce po uwzględnieniu współczynnika korygującego oraz wzięciu pod uwagę wartości stałej R, która została wyznaczona z większą dokładnością tj. ![]()
![]()
wynosi n = (4,94 ± 0,37 )1020![]()
.
4. Na podstawie wyznaczonego znaku stałej Halla R możemy wywnioskować iż mamy
do czynienia z materiałem o dziurowym typie przewodnictwa ponieważ ma wartość
dodatnią .
5.Badanie zjawiska Halla w półprzewodnikach ma szczególnie duże znaczenie ze
względu na możliwość wyznaczenia wartości przerwy energetycznej oraz energii
poziomów lokalnych elektronów
10
10
Badanie zjawisk galwanomagnetycznych w ciałach stałych
3
Badanie zjawisk galwanomagnetycznych w ciałach stałych
Wyszukiwarka
Podobne podstrony:
Zjawiska galwanomagnetyczne moje
Moje 12, Wykonały : Klimach Justyna
Badanie zjawisk galwanomagnetycznych, Badanie zjawisk galwanomagnetycznych
Badanie zjawisk galwanomagnetycznych, Badanie zjawisk galwanomagnetycznych
Analiza struktury zjawisk - zadania, Statystyka - ćwiczenia - Rumiana Górska
Galwanizacja i Jonoforeza, ĆWICZENIE 1
moje cwiczenie, BIOTECHNOLOGIA POLITECHNIKA ŁÓDZKA, CHEMIA FIZYCZNA
aSDVF, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, MOJE CWICzeNIA
galwanotechnika II, ĆWICZENIE NR 5, Pojęcie „metalizowanie” oznacza powllekanie powierz
asdadfsada, sprawozdania, Fizyka - Labolatoria, MOJE CWICzeNIA PK
cwiczeni nr 24, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, MOJE C
pierwsza strona sprawozdania, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labol
obliczeniawwdd, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, MOJE C
ćw 2, gik, semestr 3, Geodezja wyższa, moje ćwiczenia
15. Wychowanie - 3 sposoby rozumienia zjawiska, st. Pedagogika ćwiczenia, pedagogika U P tematy do
Sprawozdanie z Ćwicznia 4, Politechnika Warszawska Wydział Transportu, Semestr VI, Systemy Łączności
więcej podobnych podstron