1 pomiar strumienia objętości
-przepływomierz pływakowy (rotometr) przepływ płynu odbywa się ku górze. Pomiar strumienia objętości rotometru sprowadza się do określenia położenia pływaka w kanale.
Vz=√[(2Δp)/ρ] - z równ. Bernoulliego
Δp - różnica ciśnień dla dolnej i górnej powierzchni pływaka.
ΔpF + Vρy = Vyp - w stanie ustalonym
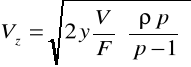
0 = Vz - F0
V - objętość pływaka
ρ - gęstość płynu
F - pole pow. pływaka
F0 - swobodny przekrój szczeliny między pływakiem a ścianką kanału
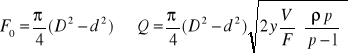
, gdy ρ=const Q=(π/4)*(D²-d²).
-przepływ krzywakowy
pomiar strumienia objętości za pomocą tego przyrządu polega na pomiarze różnicy ciśnień między strumieniami płynu opływowego. Wypukłą i wklęsłą stronę zakrywa przewód. Przy przepływie płynu przez zakrzywiony przewód na skutek działania siły dośrodkowej następuje wzrost ciśnienia w kierunku odśrodkowym. Różnica ciśnień po stronie wklęsłej i wypukłej krzywaka jest większa, im większy jest strumień m objętości przepływu krzywaka, jakościowo zbliżony jest do ruchu płynu idealnego, w którym moment prędkości M jest stały dla wszystkich elementów.
R - promień krzywizny linii środkowej.
r1=R-a r2=R+a {promienie zewnętrzne i wewnętrzne krzywaka}
p2 - p1=[(V12-V22)/2]*ρ V1=μ/r1 ; V2=μ/r2
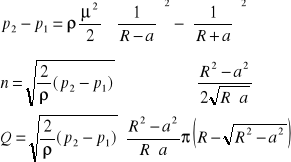
-przepływomierz końcowy (gazometr)
W obudowie przepływomierza znajdują się dwa ruchome przewody z części komory zaworowej na stałą przegrodę dzielące przewód na dwie identyczne części. Przy otwartych zaworach wlotowych i zamkniętych wylotowych następuje napełnienie komór powietrzem. Wielkością pomiarową gazomierza jest wielkość skokowa komór.
2 płyty nieprzesuwne - wzór Naviera - Stokesa
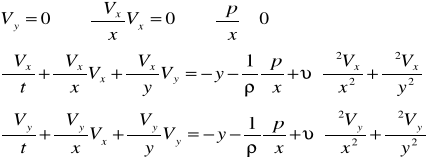
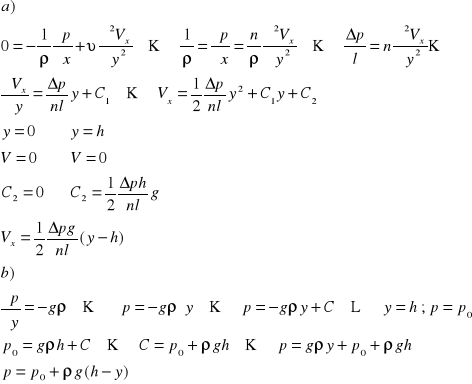
3 równanie ciągłości - ruch nieustalony płynu ściśliwego
Przy przepływie przestrzennym, gdzie wyznaczamy składowe prędkości Vx,Vy,Vz ciśnienie p i ρ jako funkcję współrzędnych x, y, z równania ciągłości wyprowadza się z równania masy płynu, która wypływa z elementarnego sześcianu o krawędziach dx, dy, dz .
☺- ![]()
Nieustawny przepływ płynu ściśliwego gdzie gęstość ρ(x, y, z, t)=0. W czasie dt w kierunku osi x wpływa do elementu przez lewą ścianę o powierzchni dydz masa płynu ρVxdzdydt. Przez przeciwległą ściankę w tym samym czasie wypływa masa płynu.
![]()
przyrost masy w czasie dt w kierunku osi x ![]()
Analogicznie przyrost masy przy przepływie w kierunku y i z wynoszą:
![]()
Suma przyrostów mas w elemencie płynu w kierunku wszystkich osi:
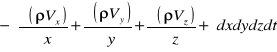
Równocześnie jednak mamy gęstość ρ która w czasie t wynosiła ρ(x,y,z,t), więc w czasie t+dt gęstość ρ(x,y,z,t+dt)=ρ+(لρ/لt)*dt
W czasie dt masa płynu wewnątrz elementu zmieni się od wartości ρ(dxdydz) do [ρ(لρ/لt)*dt]dxdydz. Stąd przyrost masy -ρdxdydz+[ρ+(لρ/لt)*dt]dxdydz = (لρ/لt)dxdydzdt. Porównując przyrosty otrzymujemy:
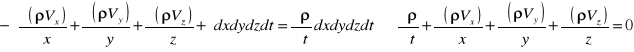
{różnicowe równanie ciągłości ruchu nieustalonego płynu ściśliwego.
lub : 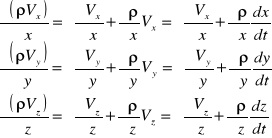
Podstawiając do równania ciągłości :
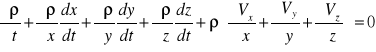
![]()
→ równanie ciągłości ruchu nieustalonego płynu ściśliwego.
4. Dysza zwężka Venturiego
Dysza Venturiego jest to dysza z długim dyfuzorem, czyli takim, gdzie większa średnica dyfuzora równa jest średnicy przewodu a otwory impulsowe znajdują się po stronie dopływu w obudowie dyszy a po stronie odpływu w cylindrycznym przewężeniu.
Jeżeli zastosujemy zwężkę w rurociągu to spowoduje ona zmniejszenie przekroju poprzecznego a co za tym idzie wzrost średniej prędkości przepływu i energii kinetycznej oraz spadek ciśnienia statycznego. Jeżeli płyn ma gęstość stałą i porusza się w kierunku poziomym rurociągu to równanie Bernoulliego będzie miało postać :
V1²/2 + p1/ρ = V2²/2 + p2/ρ
Stopień rozwarcia modułu zwężki „m”=(d/Δ)² a stopień przewężenia strumienia m=(d/Δ)². Z równania ciągłości wynika V1=V2=F2/F1 → V2=μm.
Prędkość przepływu płynu idealnego wynosi :
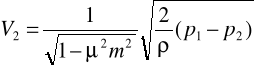
W przepływie rzeczywistym ρ<<1
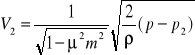
Strumień objętości wynosi :
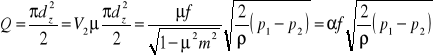
Gdzie : 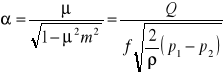
α - liczba przepływu zwężki, f - pole powierzchni przekroju zwężki.
5 prawo Darcy'ego
Prawo Darcy'ego łączy w liniową zależność wydatek strumienia filtracyjnego Q z powierzchnią jego przekroju poprzecznego F i spadkiem hydraulicznym J.
Q = kf*F*J , gdzie kf - wsp. filtracji , l - długość drogi przepływu.
∆=∆h/l (∆h=∆p/γ)
Ponieważ Vf (prędkość filtracji) = Q/F, otrzymujemy Vf = kf*J
Dla małych prędkości przepływ ma charakter laminarny i podlega liniowemu prawu Darcy'ego. Gdy prędkość wzrasta, siły pulsacji powodują zmianę ruchu cząsteczek. Chaotyczny wsp. filtracji kf nie zależy jedynie od własności skały porowatej, ale również od własności płynu takich jak lepkość oraz ciężar właściwy. Można to opisać tak :
Kf = k/μ = -kf/υ , gdzie:
k - współ. przepuszczalności
υ - kinetyczny współ. lepkości
μ - dynamiczny współ. lepkości
Podstawiając powyższą zależność do wzoru Darcy'ego mamy :
![]()
przy małych długościach rdzenia pśr = (p1-p2)/2 ,
gdzie p1 i p2 to ciśnienie gazu na wlocie i wylocie ![]()
.
Przy zał., że proces wznoszenia się gazu w rdzeniu jest izotermiczny. ![]()
Q0 - wydatek gazu w warunkach atmosferycznych jest izotermiczny
p0 - ciśnienie barometryczne
czyli współ. przepuszczalności ma postać: ![]()
6 płyty ruchome
v=c≠e ![]()
ruch ustalony
x - składowa pozioma jedn. sił masowych
y = -y - składowa pionowa sił masowych
![]()
z założenia ruchu
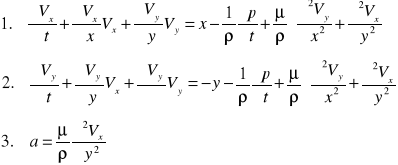
Całkujemy wobec tego μ/ρ≠0 oraz ![]()
dla y=0→Vx=0 ; y=h→Vx=VB
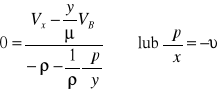
p=xy+c dla y=h
p0=-υh+c → c=p0+υh, ostatecznie : p=υ(h-y+p0) dla y=0 ; pB=υh+p0
7 wyprowadzić układ ciśnienia wzdłuż długiego rurociągu
Równanie ruchu płynu lepkiego:
![]()
gdzie υ=μ/ρ - liniowy współczynnik lepkości
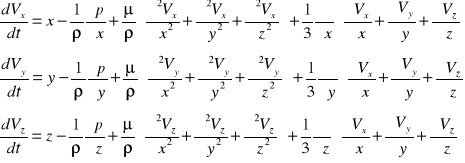
Rozwiązania te są rozwiązaniami ruchu płynów lepkich i ściśliwych przy założeniu, że μ=const. Dla płynu nieściśliwego ![]()
Równanie ruchu płynu nieściśliwego i lepkiego można przedstawić w jednej postaci po rozwiązaniu wyrażenia na przyśpieszenie całkowite.
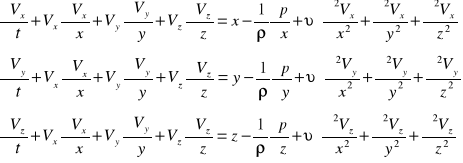
8 równanie Eulera dla płynu nieściśliwego
ρ=const - płyn nieściśliwy
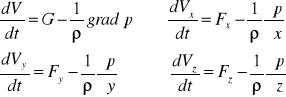
z równania statyki otrzymujemy
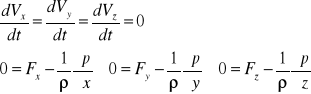
siły działające na osi x=y=0 z=-y
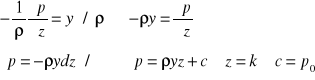
p(V)=Vk+p0
![]()
Jest to równanie na ciśnienie w stanie statycznym dla cieczy ρ=const (nieściśliwej)
9 równanie ruchu płynu lepkiego
W przepływie laminarnym w którym wektor prędkości elementu płynu są względem siebie równoległe, zgodnie z hipotezą Newtona, dynamiczny współczynnik lepkości μ jest równy:
μ=σ/(∂v/∂u) σ-naprężenie sztywne, v-prędkość przepływu
∂v/∂u - składowa gradientu prędkości w kierunkach prostopadłych do V
Kinetyczny współczynnik lepkości jest równy ilorazowi dynamicznego wsp. lepkości płynu μ i jego gęstości ρ υ=μ/ρ.
Do pomiaru lepkości służą wiskozymetry, lepkościomierze wykorzystujące różnice zjawiska fizycznego o przebiegu zbliżonym do zjawiska lepkości. Są to lepkościomierze kapilarne, rotacyjne, ultradźwiękowe.
Lepkościomierz Eulera - pomiar lepkości oparty jest na prawie Hagena. Zgodnie z tym prawem strumień objętości cieczy w przepływie laminarnym przez kapilarę jest równy.
![]()
∆p - różnica ciśnień między końcami kapilary
l, d - długość i średnica kapiary
μ - dynamiczny współczynnik lepkości cieczy
Lepkościomierz Höplera - pomiar oparty na prawie Stokena. Kula a gęstości ρk opada z prędkością v w cieczy o ρc wypełniającej cylinder lepkościomierza poddana jest oddziaływaniu sił:
- ciężkości G=(π/6)d3y ρk
- wyporu W=(π/6)d3y ρc
- oporu ośrodka ![]()
Współczynnik lepkości względnej ε = T/(kγ) ; T-czas wypływu, γ-stała wypływu
Gdy wypadowa tych sił jest równa zero, kulka upada ze stałą prędkością v=const.
Dla G=W+P wynosi 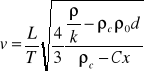
Dla Re < Q2 siła wyporu wynosi W=P - 3πμvd
Dla ruchu laminarnego Cx=24/Re Re=(V0dρc)/μ
![]()
Dla zmniejszenia błędu systematycznego wykorzystuje się zależność μ=(ρk-ρc)kHT
T - czas opadania kuli ; kH - stała przyrządu
10 Równanie Eulera dla płynu rzeczywistego
Występują siły:
-grawitacyjna ![]()
-wymuszająca ruch ![]()
-tarcie ρ=τ dv
![]()
![]()
równanie przepływu jedn. płynu rzeczywistego, gdy
![]()
dla potencjalnego gazociągu, który nie powoduje zmian prędkości :
![]()
dla płynu idealnego Fτ=0
![]()
gdy dv/dt=0 (v grad) v=σ - (1/ρ)grad p
v=const to σ - (1/ρ)grad p =0
v=0 to σ - (1/ρ)grad p =0
11 Bezwymiarowy współczynnik strat λ
Korzystając z prawa Hagena-Poiseuille
Q=πΔpR4/(8μl)
Q=vśr*F vśr=Q/F F=π* R2
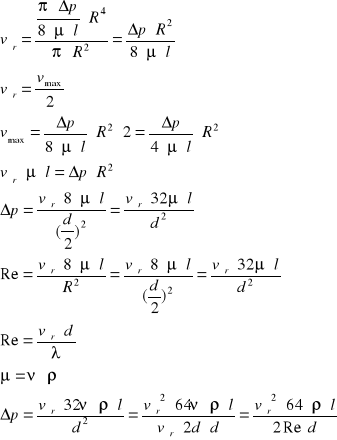
Porównując ten wzór ze wzorem na straty Darcy'ego
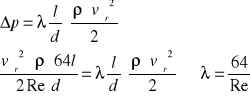
12 Całka Eulera dla płynu
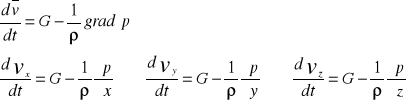
Z równania statyki otrzymujemy
![]()
=![]()
=![]()
=0
0=![]()
0=![]()
0=![]()
Działające sily wzdłuż osi x=y=0 z= - g
0= - g ![]()
![]()
=g /*![]()
![]()
![]()
Dp= - ![]()
gdz
Z równania Clapyrona 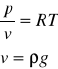
![]()
dp= - v dz = -![]()
![]()
ln p = - ![]()
założenia p = ![]()
z = ![]()
ln p = - ![]()
c=ln ![]()
ln pn= - ![]()
+![]()
ln po = ![]()
![]()
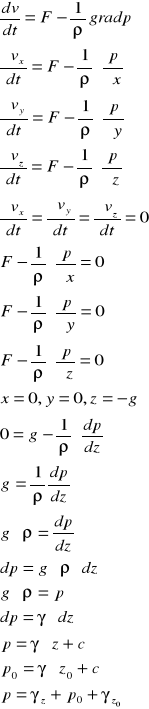
13. Całka i równane Eulera dla cieczy.
14. Cisnieniomierze (sonda Prandta)
Ciśnieniomierz tego typu pozwala na pomiar roznicy cisnienia całkowitego i statycznego. Różnica ta jest cisnieniem dynamicznym.
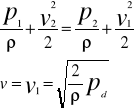
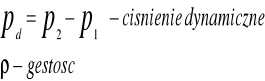
Manometr naczyniowy z rurka pochyła służy do pomiaru małych wartości roznic cisnienia stosuje się miedzy innymi mikromanometry cieczowe z rurka pochyla, protekcyjne , mikrometr Betza
Na podstawie wychylenia cieczy manometrycznej l i kata pochylenia rurki alfa można określić miarowo przez manometr roznicy cisnien![]()
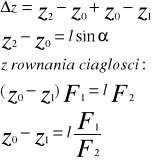
Różnica ciśnień: ![]()
sin![]()
)=![]()
ln g
Manometr z U-rurka
Manometr Aslavia słuzy do pomiaru pod i nadcisnien w zakresie do 2006 Re
15 Czas wypływu
v(z) = ![]()
dv = F0![]()
dt
dv = F(z)dz
- F(z)dz = μ0F0 ![]()
dt
- F(z)dz = μF0 ![]()
dt
dt=-![]()
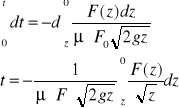
Prawo Pascala.
Jeżeli dv/dt=0 to Fx=1/ro*dp/dx; Fy=1/ro*dp/dy; Fz=1/ro*dp/dz
Fxdx+Fydy+Fzdz= 1/ro*(dp/dx*dx+dp/dy*dy+dp/dz*dz)
Fxdx+Fydy+Fzdz=1/ro*dp
Prawa strona równania to pochodna zupełna i aby był warunek równania spełniony musi i lewa strona być pochodna zupełną.
wektorF=grad mi gdzie mi to potencjał wektora F(potencjał jednostkowy sil masowych)
Fx=dmi/dx; Fy=dmi/dy; Fz=dmi/dz.
Warunki równania płynu doskonałego dmi=1/ro*dp, ro=const.
Mi=1/ro*p+cosalfa
Zapis wektorowy radmi=1/ro gadp
Jeżeli F=0 grad mi=0 to 1/rogradp=0 - Prawo Pascala.16 Gęstość
Gęstość jest wielkością fizyczną charakteryzującą wszystkie zależne od masy i objętości. Gęstość średnia to stosunek masy i objętości: ρśr=m/V
Gęstość w punkcie: ρ=dm/dv= lim Δm/ΔV
ΔV→Ve
Pomiar gęstości wilgotnego powietrza:
Powietrze zawiera w swym składzie parę wodną. Ilość pary wodnej i jej sprężystośc zależy tylko od jej temperatury. Wilgotnością bezwzględną nazywa się ilośc pary wodnej w jednostkach masy zawartej w jednostce powietrza [kg/m3]
Parametry mieszaniny spełniają zatem równanie Clapeyrona p/ρ =RT gdzie:
p-ciśnienie wilgotnego powietrza
ps-ciśnienie suchego powietrza
oraz prawo Daltona b=ePs+ePw gdzie ePw-ciśnienie pary wodnej w powietrzu wilgotnym
ps-ciśnienie suchego powietrza
Gęstość powietrza wilgotnego zależy od temperatury, ciśnienia, wilgotnośći, która wyrażona jest przez sprężystość pary wodnej. Gęstość cieczy - pomiar polega na wyrażeniu masy i objętości cieczy znajdującej się w piktometrze. Pomiar masy wyznacza się na wadze analitycznej, objętość wyznacza się pośrednio poprzez ważenie wody analitycznej o znanej gęstości
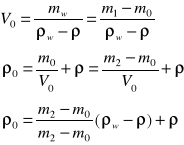
V0-objętość cieczy w pikometrze ![]()
-gęstość badanej cieczy
Gęstość materiału ziarnistego wyznacza się przy pomocy pikometru. Należy zważyć dwukrotnie pikometr z próbką ciała rozdrobnionego oraz pikometr z tą samą próbką ciała dopełnionego cieczą o znacznej gęstości
ms=m0+mp-V0*ρ
mw=m0+mp-(V0- Vp) ρw - V0*ρ
ρ-gęstość; V0- objętość cieczy w pikometrze; m0,mp-masypikometru pustego, ciała rozdrobnionego; ρwgęstość rozdrobnionych ziaren
Vp- objętość rozdrobnionych ziaren
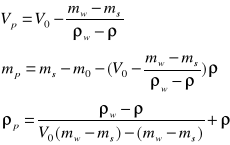
![]()
- gęstość materiału z którego zbudowane są ziarna ciała rozdrobnionego
17 Kryza zwężka
Celem jest wyznaczenie zależności liczy przepływu od liczy Reynoldsa (Re) dla zwęzki. Wykres α= α(Re) umożliwia wyznaczenie strumienia objętości pynu na podstawie pomiaru różnicy ciśnień na kryzie lub dyszy. Zwężka zabudowana w rurociągu powoduje zmniejszenie przekroju poprzecznego a tym samym wzrost średniej prędkości przepływu i energii kinetycznej oraz spadek ciśnienia.
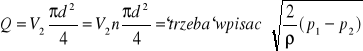
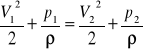
- równanie Bernoulliego ![]()
= const
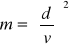
- moduł zwężki
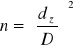
- stopień przewężenia strumienia
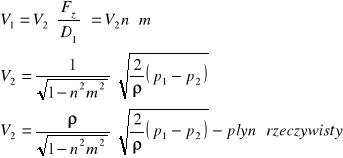
- płyn idealny
18 Magistrala dla cieczy
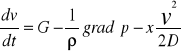
Założenia:
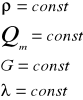
![]()
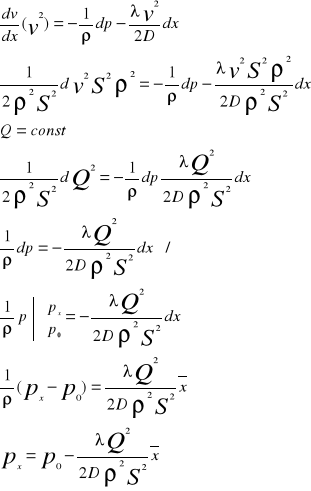
19 Paradoks de'Alamberta
Przy ruchu ciała w płynie doskonały nie powstają żadne siły reakcji. W płynach rzeczywistych występują składowa reakcji px││v a w przypadku ciała niesymetrycznego występują obie składowe
px││v py ┴ v
py-siła nośna
vy=2vosinφ
z równania Bernouliego
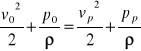
/ρ
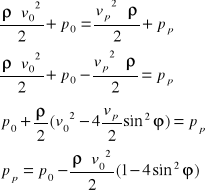
20 Porównanie przepływu gazu przez ośrodki porowate.
Prędkość filtracji zgodnie z prawem Darcy (przy przepływie laminarnym) jest proporcjonalna do gradientu ciśnienia ![]()
.
k- współczynnik charakteryzujący przepuszczalność ośrodka porowatego, zależy od materiału i płynu.
µ- dynamiczny współczynnik lepkości gazu.
Podczas badania współczynnika filtracji cylindrycznej próbki mnożne różnice ciśnienia na zewnątrz i wewnątrz odcinka przewodu porowatego o długości l. Jedna część rury jest zamknięta a do drugiej jest podłączony wentylator. Na skutek podciśnienia następuje filtracja powietrza przez rurkę porowatą. Bezwzględna prędkość filtracji jest więc równa V=k/mi*dp/dt.
Strumień objętości powietrza przepływającego przez powierzchnię zewnętrzną rurki o polu jest równy: ![]()
gdzie ![]()
- wektor prędkości, n - wersom normalny.
Q= k/mi*dp/dv*2pi*l*r.
W celu wyznaczenia p=(p(r)) należy rozwiązać otrzymane równanie różniczkowe gdy Q=const.
dv/dr= 2pi*l*k/mi*Q*dp
lnr= 2pi*l*k/(mi*Q)*p+c
Równanie musi być spełnione dla wszystkich punktów cylindra porowatego w szczególności gdy leżące na powierzchni r=rz
lnrz=(2pi*l*k/mi*Q)*b+c gdzie b-ciśnienie barometryczne.
Funkcja p(r)ma postać p(r)=b-(mi*Q/2pi*l*k)*ln(rz/r).
Wewnątrz rurki (r=rw) a cieśninie wynosi pw. p(rw)=b-(mi*Q/2pi*l*k)*ln(rz/r)= pw
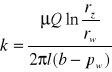
21 Równanie równowagi płynu
Równanie równowagi uwzględnia równowagę sił masowych i sił powierzchniowych. A więc
![]()
FM -siły masowe; np- siły powierzchniowe
Przekształcamy całkę powierzchniową na objętościową korzystając z twierdzenia GAUSSA-OSTROGRADSKIEGO:
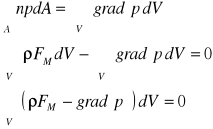
Ze względu na dowolność obszaru całkowania V można zapisać:
![]()
Jest to równanie równowagi płynu w formie różniczkowej. A w układzie współrzędnych kartezjańskich ma ono postać.
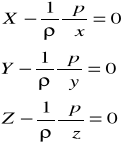
x,y,z - to składowe siły masowej FM w kierunkach osi x,y,z
Równanie równowagi wyprowadzone z różniczkowego sześcianu dxdydz. Rozpatrzona zostanie równowaga w kierunku osi x, gdzie siła powierzchniowa będąca iloczynem ciśnienia i powierzchni na odcinku dx rośnie o wielkość pdzdy do ![]()
dV=dxdydz
Element płynu dV =dxdydz jest w równowadze jeżeli rzuty sił na osi x są równe 0
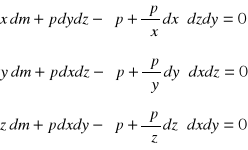
Korzystając z faktu że ![]()
dodając stronami trzy składowe można naoisać
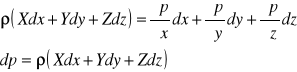
PRAWO PASCALA
Gdy na płyn nie działają siły masowe lub gdy są one zaniedbywanie małe w stosunku do sił powierzchniowych można zapisać warunek FM=0 ; a więc i składowe X=Y=Z=0 ZATEM z równania EULERA w postaci różniczkowej wynika że grad p = 0 czyli dp = 0 a więc p=const jest to matematyczny zapis prawa PASCALA, mówiący że ciśnienie jest stałe w całej objętości
22 Prędkość przepływu termoanometru
Prędkość przepływu określa się za pomocą termoanometru. Poszczególne punkty pomiarowe wybiera się na przecięciu okręgów o promieniu ru i prostopadłych względem siebie średnic:
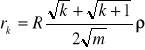
m - liczba pierścieni
k - kolejny numer punktu pomiarowego
R - promień
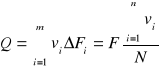
![]()
N - liczba punktów pomiarowych
F - pole przekroju poprzecznego F = пR2
ΔFi - powierzchnia części przekroju poprzecznego, której odpowiednia prędkość odpowiada prędkości vi
Przy przepływie osiowosymetrycznym, gdy v nie zalezy od kąta kierunkowego
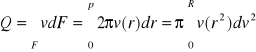
Można także obliczyć energię kinetyczną płynu przypadającego na jednostkę czasu, w którym płyn przepływa przez przewód
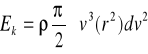
Współczynnik Coriolisa (α) to stosunek rzeczywisty energii kinetycznej strumienia płynu i energii, jaką miałby strumień płynu gdyby prędkość jego była w calymprzekroju równa vśr
Ek=mvśr/2 = ρvśrv/2 = ρFvśr3
α = Ek/ Ek*
α = Ek/ Ek**1/( vśr3R2)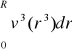
23 Rownanie Bernoulliego dla plynu idealnego.
Płyn idealny v=0 ; ![]()
rot![]()
=0 ruch ustalony
Równanie Eullera dla tego płynu ![]()
= G -![]()
grad p
![]()
=>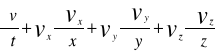
Czyli
v(x,y,z) grad (![]()
;![]()
;![]()
)
v(grad v)= G -![]()
grad p
v(grad v)= ![]()
![]()
= G -![]()
grad p
![]()
- G - G -![]()
grad p =0
G=grad v - potencjał sil masowych
![]()
grad p=grad p - cisnienie p = ![]()
grad 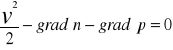
grad(![]()
+ n +p)= 0 n= -gz p= const
![]()
+ n +p= const
![]()
+ gz+ ![]()
-- - dla gazu
![]()
+ gz+ ![]()
= const --- dla cieczy
Dla cieczy rzeczywistej
![]()
+ gz+ ![]()
+![]()
Gdzie:
![]()
=![]()
24 Rownanie Eulera dla plynu doskonałego
x,y,z-skladowe Si masowych przypadających na jednostke masy w kierunku osi współrzędnych
dm=![]()
dm—masa elementarnego prostopadłościanu
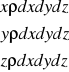
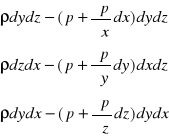
Mnożę siłe składowa z masy elementu z „-`'
![]()
![]()
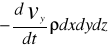
![]()
Gdy układ sil jest w równowadze to zgodnie z zasada De'Alamberta suma rzutow sil = 0
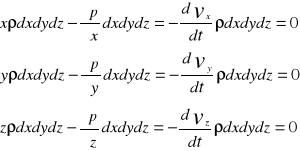
25 Równanie Bernouliego dla jednowymiarowego stacjonarnego przepływu strugi.
dv/dt+v*dv/ds=GS-(1/ro)*dp/ds+(lambda*g*v2/2D)
Pole grawitacyjne:
v*dv/ds-GS+1/ro*dp/ds+(lambda*g*v2/2D)=0
½*dv2/ds+g*dz/ds+(lambda*g*v2/2D)=0 /*ds.
½ * dv2+gdz+dp/ro+( lambda*g*v2/2D)*ds=0
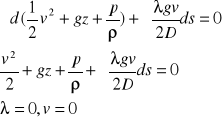
v2/2+p/ro+gz=const
dla cieczy rzeczywistej
v2/2+p/ro+gz+(lambda*g*v2/2D)+(ε*v2*g/2)=const
dla gazu
v2/2+g*dp/ro+gz=const
pv=(z)RT; v=1/ro
p/ro=RT(z)
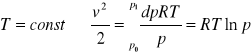
I=p/RT
p=IRT(z)
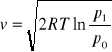
26 Równanie Bernouliego dla płynu idealnego.
V=0
dv/dt=0 - przyśpieszenie lokalne
rotv =0
dv/dt=g=1/ro*▼p
dv/dt=(v*▼)*v=g-(1/ro)* ▼p
Z analizy matematycznej:
(v*▼)=1/2*▼*v2+v *rotv
½*▼*v2-g-(1/ro) * ▼p=0 g=-▼n
½*▼*v2+vn+▼p=0 1/ro▼=▼p
ro=const 1/ro▼p=▼p/ro
v2/2+n+p=const
v2/2+n+ p/ro=const
n=gz
v2/2+gz+ p/ro=const
Równanie Bernouliego - przemiana gazowa
R - indywidualna stała gazowa
pV=nRT
p/ρ=RT/μ z tego ρ=pμ/RT
V=-m/ρ ; n=m/μ ; R=R*M
pm/ρ=m R*μT/μ
p/ρ= R*T
ρ=p/ R*T / ∫
∫dp/ρ + v2 = const
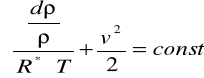
R*T ∫dp/ρ + v2/2 = const
R*T ln│p│+v2/2 = const
27 Równanie ruch płynu doskonałego (równanie Eulera) wyprowadzone z równowagi sił
Równanie ruchu płynu doskonałego wynika z zasady zachowania pędu, gdzie pochodna płynu zawartego wewnątrz obszaru V względem czasu jest równa sumie sił zewnętrznych czyli:
![]()
Stosując twierdzenie GAUSSA-OSTROGRADSKIEGO i pamiętając, że pA=-n*p otrzymujemy:
![]()
dV=0
![]()
Ze względu na dowolność obszaru całkowania V dla każdego elementu dv funkcja podcałkowa musi się zerować. Otrzymujemy więc:
![]()
![]()
Równanie płynu doskonałego lub równanie Eulera okresla zasadę zachowania pędu gdyż wystarczy rozdzielić różniczki dV/dt i pomnożyć je przez masę a otrzymam równanie pędu w klasycznej postaci. Równanie to można przedstawić w zapisie skalarnym w następujący sposób:![]()
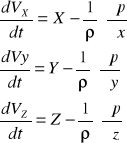
28 Równanie Bernouliego wyprowadzone z równania Eulera
W celu wyprowadzenia równania Bernouliego z całki równania Eulera zależy uzyskać związek algebraiczny pomiędzy prędkością przepływu płynu, a jego ciśnieniem. Jest to możliwe w przypadku ruchu ustalonego, potencjalnego dla płynu o stałej gęstości ![]()
.
Należy przekształcić całkę Eulera do postaci w której wystąpi rotacja prędkości (rot v). rozważamy składowe substancjalne dla kierunku X
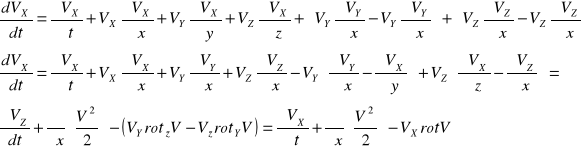
Ostatnią część powyższych obliczeń można zapisać dla kierunków Y i Z w taki sam sposób. Można więc zapisać równanie wektorowe
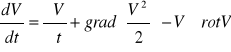
Po podstawieniu otrzymamy
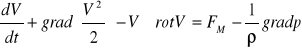
![]()
Jest to równanie w formie Lambra-Gromek
29 Równanie Bernoulliego dla płynu ściśliwego (dwuwymiarowego).
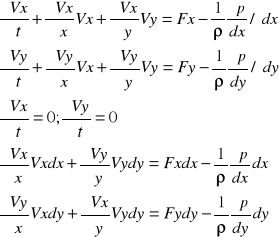
Przepływ stacjonarny- przepływ po liniach prędkości
Vxdy=Vydx
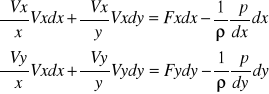
Po dodaniu stronami tych dwóch równań otrzymujemy:
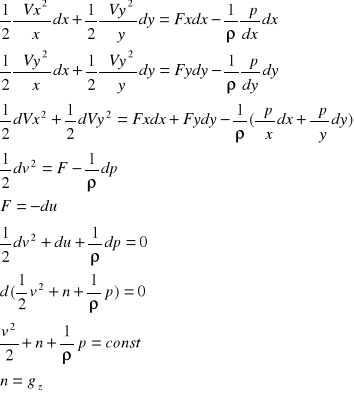
Poprzez powyższe przekształcenia dochodzimy do równania Bernoulliego mającego w tym przypadku postac:
![]()
30 Równ. Bernoulliego dla przepływu stacjonarnego płynu nieściśliwego.
ρ =const
![]()
-równanie Eulera
![]()
= (ΰ*▼)*ΰ= G - ![]()
![]()
=0 ![]()
=▼p
(ΰ*▼)*ΰ=1/2▼V2 + V x rot ΰ
rot ΰ = 0
przepływ bezwymiarowy
1/2▼V2 = G - 1/![]()
▼p
G = -g2
1/2▼V2 = ▼V - 1/![]()
▼p
V2/2 = - 1/![]()
p - g2
V2/2 + gz +p/![]()
/:![]()
gV2/2 + gz + p/V = const
![]()
=G-1/![]()
gradp
![]()
=G-1/![]()
![]()
![]()
=(ΰ*▼)*ΰ=G-1/![]()
![]()
![]()
=0 ![]()
=▼p
(ΰ*▼)*ΰ=1/2▼V2 + V x rot ΰ
rot ΰ = 0
1/2▼V2 = G - 1/![]()
▼p
G-gzG=▼V
▼V2/2 = ▼V-1/![]()
▼p
▼V2/2=▼(V-1/![]()
p)
V2/2 V-p/![]()
☻☻☻
31 Równanie Bernoulliego -przeniana adiabatyczna
Przyjmujemy związek miedzy cisnieniem i gęstością dla przemiany adiabatycznej odpowiadającej z dostatecznym przybliżeniem niektórym zjawiskom zachodzącym przy przepływie gazow
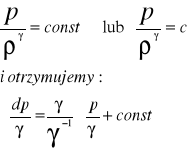
Po podstawieniu do równania Bernoulliego otrzymujemy równanie w przemianie adiabatycznej wzdłuż strumienia :
![]()
![]()
![]()
= const
![]()
![]()
![]()
= const
Rozwiązując strumien gazu można napisac row. Bernoulliego dla dwoch przekrojow w postaci
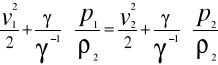
32 Równanie Eulera dla płynu ściśliwego
Siły ściskające pochodzą od pozostałych części płynu.
Założenia:
1) zasada de'Alamberta εFi=0; Fc=F+G
2) G0 τ 0
![]()
wiadomo, że
pn= cos(sinx)p+jcos(n,y)p+kcos(u,ε)p
z tw. Gaussa:
lim![]()
τ0
![]()
Równanie ma postać
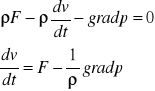
ruch płynu doskonałego
Równanie Eulera dla trzech osi (x,y,z)
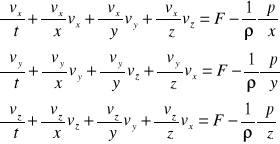
Fx,Fy,Fz - jednostkowe siły masowe działające wzdłuż osi x,y,z
Równanie Eulera dla płynu doskonałego
![]()
33 Równanie przepływu dla strugi
Struga jest to zespol lini pradu wypełniający rurke
S- droga plynu , v—droga prędkości przepływu , F - pole przekroju poprzecznego
v(s,t)=![]()
vdF=dv / *![]()
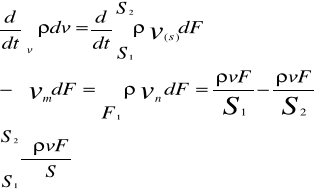
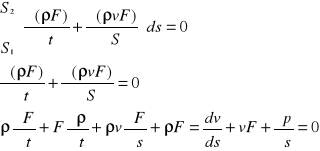
34 Równanie równowagi płyny:
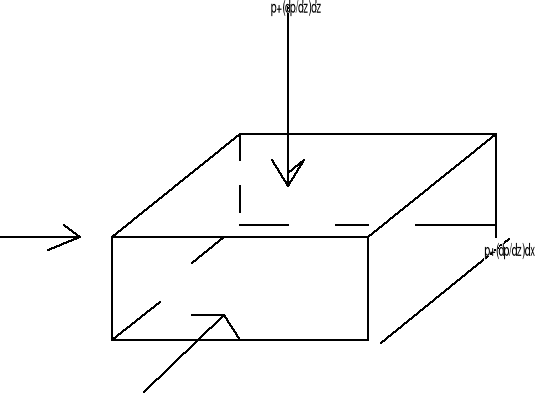
W cieczy znajdującej się w spoczynku wyznaczamy sześcian o krawędziach dx, dy, dz równoległych do odpowiednich osi układu współrzędnych. Na sześcian działają następujące siły:
- powierzchniowe normalne;
- masowe;
Ciśnienie p znajduje się w punkcie M będącym środkiem sześcianach prostopadłych do osi x odległych o -1/2dx i 1/2dx wynoszą:
![]()
i ![]()
Natomiast siły powierzchniowe wynoszą:
![]()
![]()
Siły masowe działające na sześcian otrzymujemy przez przemnożenie jednostkowej siły masowej x, y, z przez masę elementu.
dFx = ρxdxdydz
dFy = ρydxdydz
dFz = ρzdxdydz
Z warunków równowagi wynika, że suma sił działających na element (powierzchniowych powierzchniowych masowych) na dowolnie wybrany kierunek musi być równa zero. Wyprowadzenie jest takie samo na każdą oś x, y, z.
Wyprowadzenie na oś x:
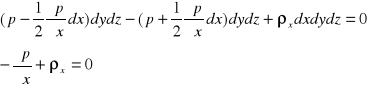
Wyliczamy analogicznie równanie na osi y i z
![]()
i ![]()
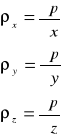
układ równania różniczkowego Eulera
Po przemnożeniu przez dx, dy, dz i dodając
![]()
różniczka zupełna ciśnienia
![]()
równanie równowagi płynu
35 Równ. różniczkowe ciągłości dla ruchu płynu ścisliwego - równanie Eulera dla gazu
ρ(x,y,z,t)![]()
0
![]()
W kierunku osi x wpływa w czasie dt do elementarnego sześcianu masa płynu ![]()
. Dla tego przypadku czas lub przyrost czasu równy jest:
![]()
![]()
![]()
Całkowity przyrost masy płynu w danym elemencie wynosi:
![]()
jeżeli dana gęstość ρ(x,y,z,t) tyle wynosiła w czasie t0, a w czasie t+dt gęstość będzie równa
ρ(x,y,z,t+dt)= ρ+dp/dt
Masa płynu też ulegnie zmianie od p dx dy dz dt do wartości ![]()
W czasie t+dt przyrost masy będzie wynosił ![]()
Wobec tego: ![]()
albo
![]()
36 Różniczkowe równanie ruchu Eulera
Aby wyznaczyć równanie obieramy powierzchnie kontrolną S obejmującą V płynu na taką powierzchnie działaja siły zewnętrzne masowe i powierzchniowe z których wyznaczamy równanie. Siły powierzchniowe to siły wywierane z zewnątrz przez płyn otaczający powierzchnie kontrolną S. Siły ściskające:
![]()
n - normalna zewnętrzna siły o zwrocie”+”
Siły masowe są to siły równomiernie rozłożone w płynie jednorodnym
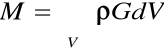
G - jednostkowa siła masowa
Prąd elementarny masowy dm wynosi ![]()
Prąd całkowity układu wynosi![]()
Z II zasady dynamiki Netona, która mówi, że pochodna pędu układu względem czasu równa jest wektorowi głównemu sił zewnętrznych działających na układ
Fzew=M+N
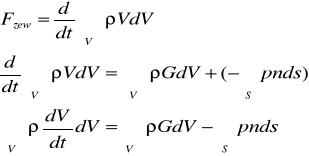
Z tw. Gaussa zmieniamy całkę powierzchniową na objętościową
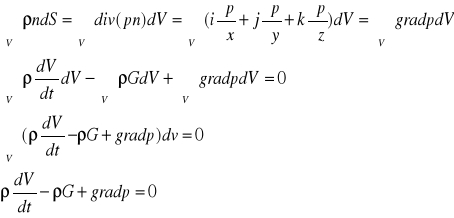
Równanie Eulera w kierunku osi x,y,z
![]()
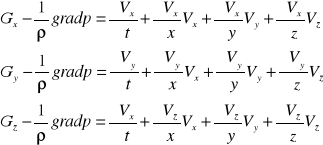
Równanie Eulera dla płynu doskonałegow przepływie nieustalonym
37 Srumień objetości powietrza. Wyznaczenie współczynnika Corriolosa.
Określenie rozkładu prędkości polega na przyporządkowaniu wartości prędkości każdemu punktowi tego przekroju. W przewodzie o przekroju kołowym poszczególne punkty można wybrać na pięciu okręgach o promieniu rk i prostopadłych względem siebie średnic. Strumień objętość przepływu wynosi.![]()
![]()
n- liczba punktów powłokowych
Vi - prędkość zmienna w tej części przekroju ;![]()
Fi - powierzchnia przekroju
Przy przepływie osiowo symetrycznym gdy prędkość przepływu nie zależy od kata kierunkowego pomiaru prędkości upraszcza się, strumień objętości wynosi:
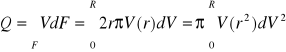
Elementarna energia kinetyczna płynu o stałej gęstości ρ przepływającego w jednostce czasu przez przekrój przewodu o powierzchni F jest równa: ![]()
Gdzie : dm - elementarna masa ; dV - elementarna objętość płynu przepływającego przez powierzchnię dF w jednostce czasu.
Skąd : ![]()
dla przekroju kołowego: ![]()
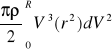
Współczynnik Corriolliossa ![]()
nazywamy stosunek energii kinetycznej strumienia płynu do energii jaką miałby ten strumień gdyby jego prędkość w całym przekroju była równa prędkości średniej ![]()
. Energia kinetyczna płynu pomniejszającego się w całym przekroju z prędkością vŚr przypadając na jednostke czasu jest równa:
![]()
dlatego dla przewodu kołowego: 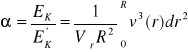
38 Stosunek prędkości średniej do max.
Cel ćwiczenia określa Vśr/Vmax przy przepływie płynu przez przewód w zależności od liczby Reynoldsa. W ćwiczeniu bada się przepływ powietrza przez przewód o przekroju kołowym. Założenia: płyn lepki nieściśliwy, przepływ ustalony, przewód kołowy o średnicy D. Układ współrzędnych taki, że pokrywa się z osią przewodu. Równanie Novera-Stokesa dla ruchu laminarnego: 1/ro*dp/dt=ni*(d2v/dr2+1/r*dv/dt) gdzie p-ciśnienie, ro- gęstość, ni- kinematyczny współczynnik lepkości. dp/dz = -deltap/l=const. Delta p- różnica ciśnień miedzy przekrojami odległymi od siebie o l.
-1/ro*deltap/l=ni(d2v/dr2+1/r*dv/dr)
-1/ro*deltap/l=ni*1/r*dv/dr*(r*dv/dr)+1
Po scałkowaniu mamy: 3. -1/ro*deltap/l*r2/4=ni(v(r)+c1*r+c2) gdy v=R- v=0 -prędkość na powierzchni kontaktu z ciałem stałym.
v(r)= delta*R2/4*(1-(r2/R2)) z czego wynika że vmax=v(r=0)=(delta*R2)/4mi
Q=całka vd*F=2pi*calka v(r)dr=pi/8*(lambda*p*k4)/(mi*l) gdzie mi to dynamiczny współczynnik lepkośći.
Vśr=Q/F=(deltap*R2)/(8mi*l), Vśr= ½*vmax - w ruchu.
W przepływie turbulentnym prędkość nieznacznie maleje w podstawowym rdzeniu strumienia płynu i szybko maleje przy ścianach.
39 Współczynnik oporu liniowego
Podczas przepływu płynu przez występują straty ciśnienia na oporach zwanych lokalnymi, poprzez co występują zmiany kierunków oraz modułów wektorów prędkości. Występujące zawirowania powodują większe straty od strat występujących podczas przepływu przez odcinek prostoliniowy. Występują one na skutek nagłego zwężenia i rozszerzenia przewodu o stałej średnicy, zakrzywienia przewodu, konfuzora (stożkowy). Strat na oporze liniowym
![]()
![]()
![]()
-bezwzględny współ. oporu odniesiony do prędkości za przeszkoda zależy od kształtu elementu wywierającego opór, prędkość przepływu gęstości, lepkości płynu. W przepływie laminarnym ρ maleje ze wzrostem Re. Natomiast przy przepływie turbulentnym ξ jest wartością stałą.
Stała ciśnienia przy oporze
-liniowym ![]()
-lokalnym ![]()
Zmiana ciśnienia związana jest także ze zmiany energi
![]()
[Pa] ![]()
- współczynniki Coriollosa
v1 v2 - średnie prędkości
40 Wzór Hagena Passenielle'a.
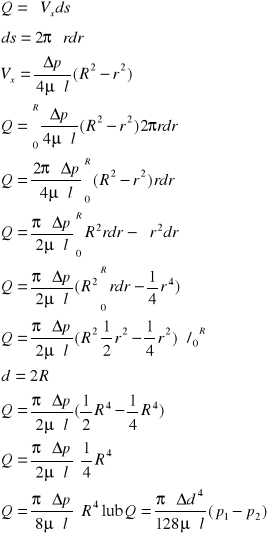
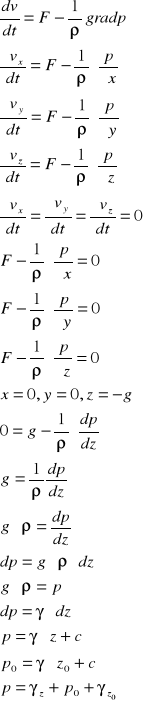
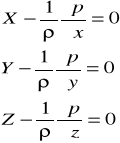
![]()
Wyszukiwarka
Podobne podstrony:
10 pomiar strumienia objetosciid 11010
10 pomiar strumienia objetosci
10 pomiar strumienia objętości, mechanika plynów
Ćw 1 Pomiar strumienia objętości i masy płynu przy użyciu rurek spiętrzających
Pomiar strumienia objętości gazu i masy
Pomiar strumienia objętości przepływu gazu gazomierzami zwężkowymi
Ćw 1 Pomiar strumienia objętości i masy płynu przy użyciu rurek spiętrzających
Pomiar strumienia objętości gazu i masy
nowaczewski,Podstawy Metrologii i Technik Eksperymentu L, system do pomiaru strumienia objętości wod
Metrologia-lab-Pomiar strumienia magnetycznego oraz indukcji magnetycznej, Strumień1SPR, POLITECHNIK
10 Pomiary szczegolow sytuacyjnych
więcej podobnych podstron