Rachunek zbiorów - ciąg dalszy

• działania na zbiorach:

1. suma zbiorów A i B to zbiór wszystkich elementów, które należą do A lub należą do B
   
   
   

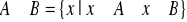
2. iloczyn zbiorów A i B to zbiór wszystkich elementów, które należą do A i należą do B
   
   
   

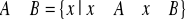
3. różnica zbiorów A i B to zbiór wszystkich elementów, które należą do A i nie należą do B
   
   
   
   
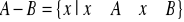
   Szczególnym rodzajem różnicy zbiorów jest dopełnienie zbioru: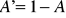
   
   
   , gdzie 1 znaczy „uniwersum”

• podstawowe tautologie rachunku zbiorów:

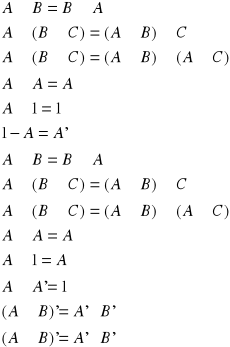
• klasyczne zdania kategoryczne:

1. zdanie ogólno-twierdzące (SaP) - każde A jest B
   
   
   

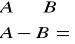
2. zdanie ogólno-przeczące (SeP) - żadne A nie jest B
   
   
   

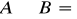
3. zdanie szczegółowo-twierdzące (SiP) - niektóre A są B
   
   
   

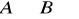
4. zdanie szczegółowo-przeczące (SoP) - niektóre A nie są B
   
   
   

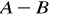
Każdy wieloryb (A) jest ssakiem (B), a żaden ssak (B) nie oddycha skrzelami (C), więc żaden wieloryb (A) nie oddycha skrzelami (C).

<kolorem czarnym oznaczono zbiory puste>

Z diagramu wynika, że jeśli spełnione zostaną warunki zawarte w poprzedniku, spełniony jest także warunek zawarty w następniku (po zamalowaniu części pustych okazuje się, że nie ma wspólnej części A i C). Powyższy schemat jest więc tautologią rachunku zbiorów.

Każda definicja (A) jest zdaniem (B), a niektóre zdania (B) są fałszywe (C), więc i niektóre definicje (A) są fałszywe (C).

W tym przypadku należy rozważyć trzy możliwości - to, że iloczyn zbiorów B i C jest nie pusty, nie jest jednoznaczne - jak widać na diagramie. Mamy udowodnić, że przy spełnieniu warunków zawartych w poprzedniku, spełniony będzie warunek następnika - iloczyn A i C ma być niepusty. Warunek ten nie jest spełniony w przypadku jednej z możliwości (środkowy diagram), w związku z czym powyższy schemat nie jest tautologią rachunku zdań.

LOGIKA