LABORATORIUM MECHANIKI PŁYNÓW

Ćwiczenie N 14

KAWITACJA

1. Cel ćwiczenia

Doświadczalne wyznaczenie ciśnienia i strumienia objętości kawitacji oraz

charakterystyki przepływu zwężki, w której powstaje kawitacja.

2. Podstawy teoretyczne:

Analizując równanie Bernoulliego, nietrudno zauważyć, że wzrost prędkości strugi

powoduje spadek ciśnienia. W ustalonej temperaturze ciecz wrze przy określonym ciśnieniu
p

w

– zwanym ciśnieniem parowania.

W miejscach, gdzie ciśnienie osiągnie wartość mniejszą od p

w

pojawiają się

pęcherzyki par cieczy. Znikają one gwałtownie po przejściu w obszar wyższego ciśnienia i
powodują mikrouderzenia cieczy o ścianę. Zjawisko to nazywa się kawitacją, a powoduje
niszczenie materiału rury (tzw. korozja kawitacyjna) na skutek wielkiej częstości uderzeń i
dużej ich energii jednostkowej. Objawia się ono również intensywnym charakterystycznym
dźwiękiem.

Ocenę możliwości powstania kawitacji w poziomej rurze z przewężeniem umożliwia

równanie Bernoulliego, uzupełnione członem reprezentującym straty energetyczne wzdłuż
strugi cieczy lepkiej. Równanie to, dla przekroju 1 i 2 (rys. 1) i poziomu porównawczego na
wysokości przewężenia, jest następujące

s

D

D

b

h

g

h

g

p

g

g

p

12

2

2

2

2

∆

+

+

+

=

+

υ

α

ρ

υ

α

ρ

(1)

gdzie:
p, p

b

– ciśnienie odpowiednio w przewężeniu i przekroju 2,

υ

,

υ

D

– prędkość w przewężeniu i przekroju 2,

α

,

α

D

– współczynnik Coriolisa uwzględniający wpływ rozkładu prędkości na wartość energii

kinetycznej w przewężeniu i przekroju 2,

∆

h

s

12

– wysokość strat energetycznych na odcinku 1-2, które składają się e strat liniowych i

miejscowych.

Straty energetyczne można przedstawić jako

g

g

D

l

h

D

D

s

2

2

2

2

12

υ

ζ

υ

λ

+

=

∆

(2)

gdzie:

λ

- współczynnik oporu liniowego rury o średnicy D i długości l,

ζ

- suma współczynników oporów miejscowych na odcinku 1-2.

Wśród oporów miejscowych znajduje się zawór regulacyjny R

x

, którego współczynnik oporu

ζ

x

jest zmienny (nastawialny), natomiast suma pozostałych współczynników oporu wynosi

ζ

D

. Wówczas

D

x

ζ

ζ

ζ

+

=

(3)

Równanie ciągłości przepływu jest następujące

D

V

D

d

q

υ

π

υ

π

4

4

2

2

=

=

(4)

gdzie
q

V

– strumień objętości,

d – średnica przewężenia.

Po uporządkowaniu równania (1) i uwzględnieniu wzorów (2) – (4) możńa obliczyć

wysokość ciśnienia w przewężeniu

(

)

2

*

2

*

*

V

d

V

X

D

b

q

R

q

R

R

h

g

p

g

p

−

+

+













+

=

ρ

ρ

(5)

gdzie stałe

*

*

*

,

,

d

X

D

R

R

R

, zwane

opornościami hydraulicznymi, są następujące:

4

2

*

8

D

g

D

l

R

D

D

D

π

ζ

λ

α













+

+

=

4

2

*

8

D

g

R

X

π

α

=

(6)

4

2

*

8

d

g

R

d

π

α

=

Kawitacja wystąpi tylko wtedy, gdy

0

*

*

*

<

−

+

d

X

D

R

R

R

(7)

tzn. gdy ze wzrostem q

V

maleje p, osiągając przy pewnym q

V

=q

V_cr

wartość p=p

w

. Natomiast

dla

0

*

*

*

≥

−

+

d

X

D

R

R

R

(8)

Kawitacja w ogóle nie wystąpi, gdyż ciśnienie p w przewężeniu nie maleje ze

wzrostem strumienia przepływu q

V

. Nie każde zatem przewężenie rury może spowodować

kawitację. Mianowicie z (7) – po uwzględnieniu (3) i (6) – wynika, że kawitacja może
wystąpić, gdy

4

ζ

λ

ζ

α

+

+

<

D

l

D

d

D

(9)

Natomiast jeśli kawitacja w przewężeniu występuje, to można ją zlikwidować, umieszczając
za przewężeniem opór hydrauliczny taki, że spełniony będzie warunek (8), tzn.













+

+

−













≥

D

D

X

D

l

d

D

ζ

λ

α

α

ζ

4

(10)

Należy przy tym pamiętać, że zwiększenie oporności hydraulicznej zazwyczaj odbywa

się przez umieszczenie w rurociągu zaworów regulacyjnych (oporność zmienna) lub kryz
dławiących (oporność stała). Elementy takie zwężają strugę i mogą także wywołać kawitacje.
Dlatego powinny one być odpowiednio dobrane i umieszczone.

Ze wzoru (5) wynika, że ciśnienie p w przewężeniu, przy ustalonym współczynniku

ζ

x

zależy tylko od strumienia przepływu q

V

. Zadając różne wartości

ζ

xi

można doświadczalnie

wyznaczyć rodzinę krzywych (charakterystyk)

( )

V

i

q

f

g

p

=

ρ

/

praz punkty (q

V_cri

, p

wr

)

oznaczające zaobserwowany początek kawitacji. Krzywe

( )

V

i

q

f

g

p

=

ρ

/

leżą pod prostą

h

g

p

g

p

b

+

=

ρ

ρ

/

/

.

Znalezione doświadczalnie wartości p

wr

ciśnienia kawitacji różnią się od wartości

wziętych z tablic własności fizycznych cieczy. Mierzone ciśnienie p

wr

jest większe od

ciśnienia p

w

z tablic, bo pomiarowi podlega ciśnienie mieszaniny gazów (prawo Daltona),

składających się z par cieczy i gazów, które zwykle są rozpuszczalne w cieczach. W tablicach
podawane są wartości p

w

cieczy specjalnie odgazowanych.

Kawitacja jest zjawiskiem bardzo złożonym i zależy od parametrów cieczy i ruchu, w

jakim ta ciecz się znajduje. Jak dotąd, nie udało się stworzyć zwartej teorii zjawiska kawitacji,
uwzględniającej wszystkie własności cieczy. Przeanalizowano jedynie uproszczone
przypadki, które dają pogląd na przebieg tego zjawiska i wpływ podstawowych czynników
(ciśnienia, temperatury, prędkości). W technice kawitacja zmniejsza sprawność maszyn i
urządzeń, powodując erozje kawitacyjną, w medycynie ujemnie działa na mięsień sercowy i
układ krążenia, w biologii powoduje rozkład czerwonych ciałek krwi i bakterii. Zjawisko to
jest niekiedy wykorzystywane w niektórych procesach technologicznych, np. mieszania i
odgazowania.

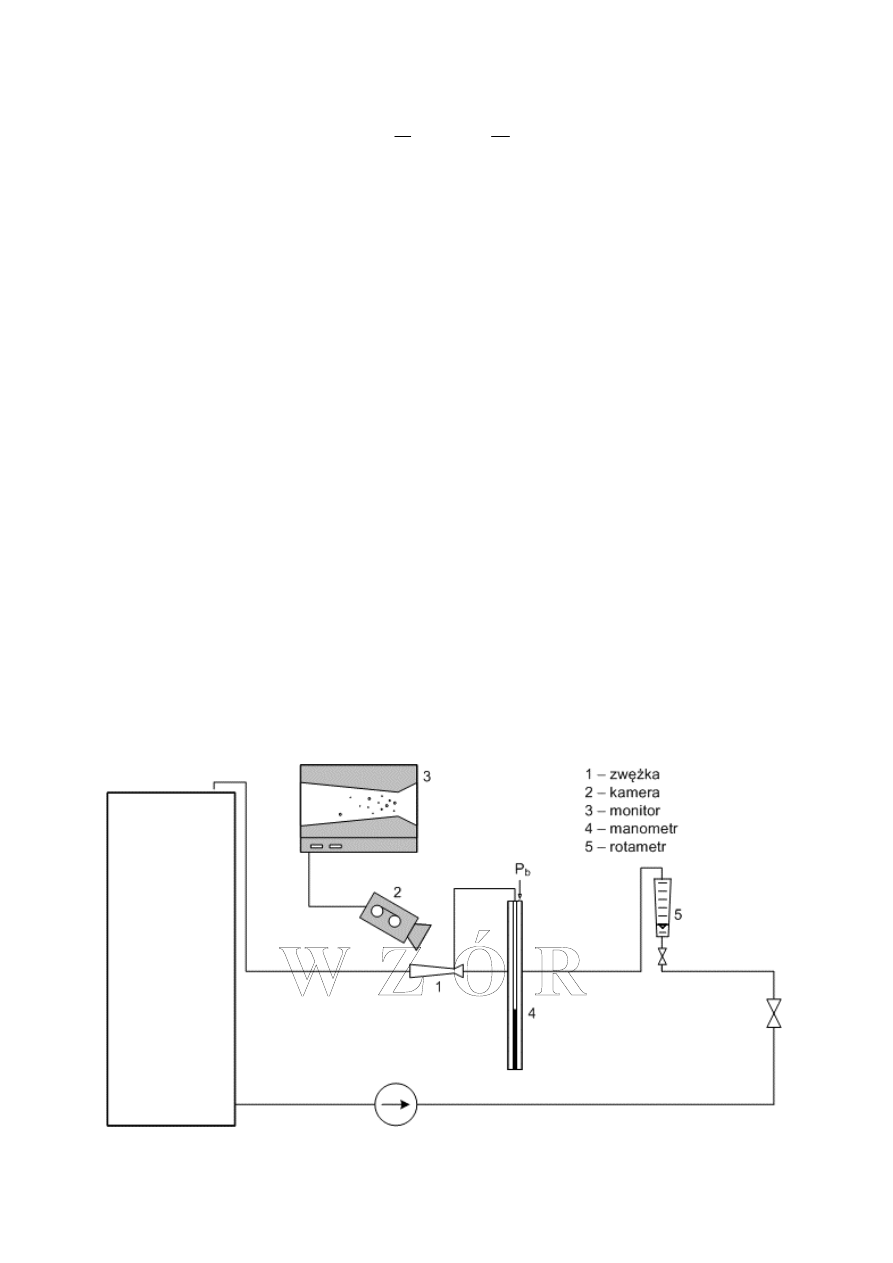
3. Stanowisko pomiarowe

Schemat stanowiska przedstawiono na rys. 1.

Rys.1. Schemat stanowiska pomiarowego

4. Przebieg i program ćwiczenia:

Sprawdzić czy zawór regulacyjny jest zamknięty.
Włączyć pompę i powolnym, płynnym ruchem otwierać zawór regulacyjnym aż do uzyskania
na rotametrze przepływu 300. Odczytać wysokość słupa cieczy manometrycznej w
manometrze rtęciowym oraz temperaturę cieczy.
Następne pomiary wykonać dla strumieni objętości: 350, 400, 450, 500, 550, 600, 650, 700,
750, 780, 800, 820, 840, 860, 880, 900, 920, 940, 960, 980, 1000.

Zadanie polega na wykonaniu pomiarów potrzebnych do doświadczalnego

wyznaczenia zależności ciśnienia

g

p

ρ

/

od strumienia objętości wody

V

q . Pomiary należy

przeprowadzić dla

(

)

max

_

,

0

V

V

q

q

∈

zadając kilka wartości

ζ

xi

przy czym należy określić

wartość q

V_cri

.

Wyniki

pomiarów

posłużą

do

wykreślenia

rodziny

krzywych

( )

(

)

n

i

q

f

g

p

V

i

,...,

1

/

=

=

ρ

i określenia przedziałów

(

)

cri

V

q

_

,

0

wolnych od kawitacji. Po

odczytaniu wartości p

w

ciśnienia parowania, dla zmierzonej temperatury cieczy, można

znaleźć przedziały

(

)

(

)

n

i

q

crthi

V

,...,

1

,

0

_

=

teoretycznie wolne od kawitacji.

5. Przykładowe obliczenia

Tabela pomiarowa

Wielkość

q

v

z

t

Jednostka

L.p.

1

2

Wzory do obliczenia ciśnienia panującego w przewężeniu:

−

−

−

+

=

gz

gH

gH

p

p

w

Hg

w

b

ρ

ρ

ρ

Pa

p

100787

34

,

0

81

,

9

1

,

999

027

,

0

81

,

9

13600

747

,

0

81

,

9

1

,

999

100400

=

⋅

⋅

−

⋅

⋅

−

⋅

⋅

+

=

+

−

−

+

=

gz

gH

gH

p

p

w

Hg

w

b

ρ

ρ

ρ

Pa

p

29829

22

,

0

81

,

9

1

,

999

027

,

0

81

,

9

13600

747

,

0

81

,

9

1

,

999

100400

=

⋅

⋅

−

⋅

⋅

−

⋅

⋅

+

=

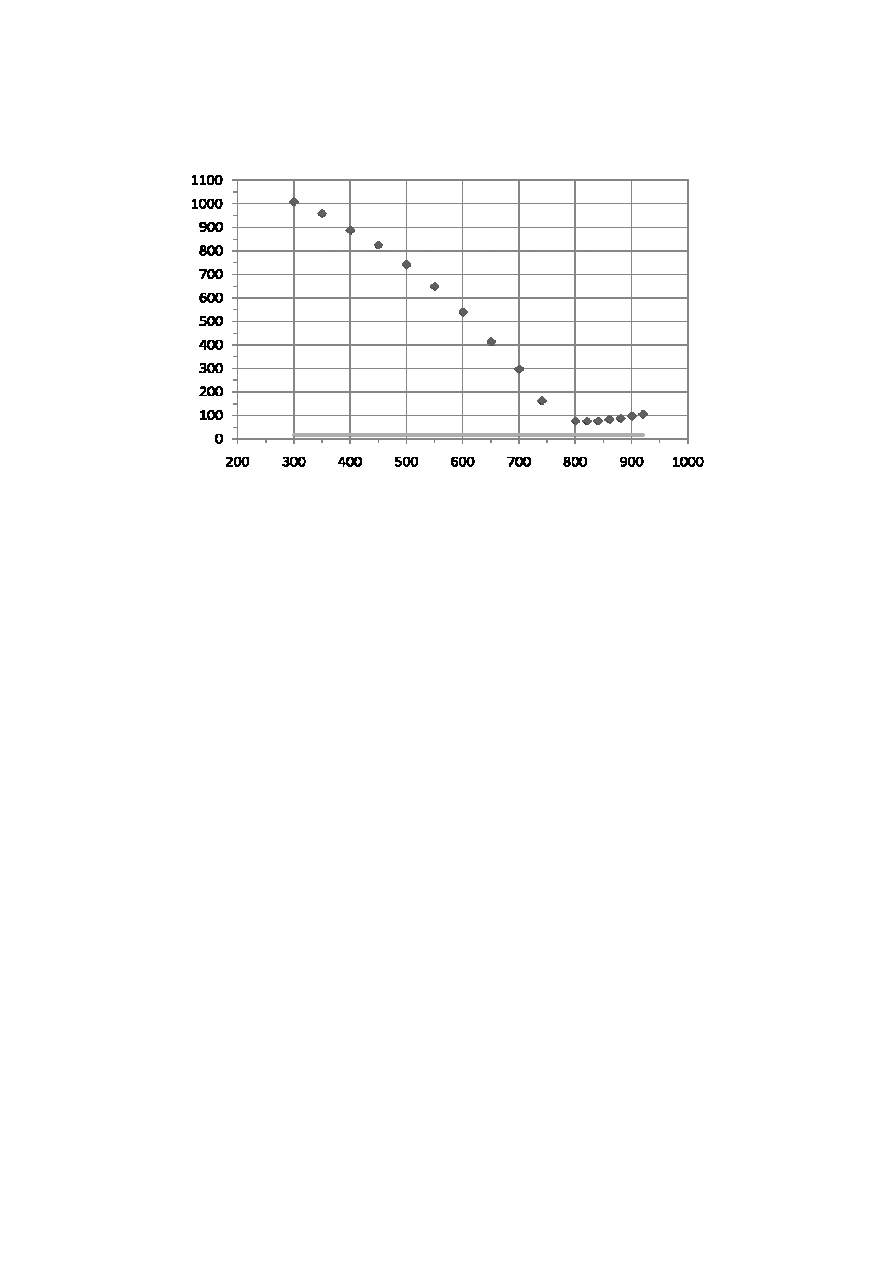
Wykres