Pracownia Miernictwa Komputerowego

1.

Cel dwiczenia:

Celem dwiczenia jest zapoznanie się z pomiarem nieznanej wartości rezystancji przy użyciu metody
mostkowej. Wszystkie wykonane pomiary są pomiarami pochodzącymi z zastosowania tejże metody,
która pozwala wyznaczyd charakterystykę prądowo - napięciową badanego elementu bądź układu.

2.

Układ pomiarowy:

Karta RBR przeznaczona jest do pomiarów oporności w zakresie od 1Ω do 100 MΩ w sześciu
podzakresach o centrach 100Ω, 1kΩ, 10kΩ, 100kΩ, 1MΩ, 10MΩ. Pomiar jest realizowany przez
pośredni pomiar napięcia nierównowagi mostka oporowego - mierzona opornośd umieszczona
jest w jednej z gałęzi mostka. Karta nie jest urządzeniem samodzielnym. Do pracy wymaga
sterownika Eurodriver - do sterowania zakresami i wzmocnieniem oraz woltomierza o zakresie
pomiarowym od -5V do 5V - do pomiaru napięcia nierównowagi mostka (-15V do +15V jeśli
planowana jest praca ze wzmocnieniem napięcia niezrównoważenia innym niż 1). W celu
automatyzacji pomiaru woltomierz zastępuje się przetwornikiem analogowo-cyfrowym
umieszczonym w kasecie EURO np. kartą ADC-2 lub TRM1. Wartośd oporności można obliczyd
znając wartości napięcia zasilania mostka, napięcia nierównowagi oraz pozostałych oporności w
gałęziach mostka.

3.

Kalibracja układu pomiarowego:

a. Przed rozpoczęciem właściwej procedury pomiarowej należało wykalibrowad przetwornik

A/C. Przetwornik analogowo-cyfrowy przetwarzający napięcie na liczbę, która odczytywana
jest przez program sterujący eksperymentem. Zależnośd pomiędzy napięciem wyrażonym w
jednostkach przetwornika i napięciem w Voltach jest liniowa i przeliczenie następuje w
programie po obliczeniu i wpisaniu współczynników kalibracji A

p

i B

p

.

b. Zależnośd ta opisana jest wzorem:

U

RBR

[V] = u[j.p.] * A

p

+ B

p

gdzie:



u[j.p.] - napięcie w jednostkach przetwornika



A

p

, B

p

– współczynniki kalibracji

Nazwisko i Imię:

Samczyoski Ariel

Nr ćwiczenia:

11

Temat ćwiczenia

Pomiar oporności metodą mostkową

Data wykonania ćwiczenia:

11.10.2011

Data oddania raportu:

17.10.2011

Ocena raportu

Podczas kalibracji przetwornika wykorzystaliśmy następujące fakty:
Napięcie nierównowagi mostka:

U

n

= U

R

R

R

x

x

z















1
2

.

Na podstawie tego wzoru można wyciągnąd następujące wnioski:

R

x





(R

x

>> R

z

) U

n

= 0,5U (czyli +5V)

R

x



0 (R

x

<< R

z

) U

n

= - 0,5U (czyli -5V)

U

n

nie jest liniową funkcją R

x

Przekształcając ten wzór tak, aby uzyskad zależnośd R

x

= f(U

n

) otrzymamy ostatecznie wzór, za

pomocą którego obliczymy wartośd mierzonej rezystancji.

z

n

n

R

U

U

U

U









2

2

R

x

W ten sposób dokonując pomiaru (bezpośrednio z programu rvt dla współczynników A

p

=1 i B

p

=0)

przy zwartych i rozwartych wejściach RBR mogliśmy obliczyd współczynniki kalibracji A

p

i B

p

.

Wyznaczyliśmy je z układu równao:

5V = A

p

*u[j.p.]

rozw

+ B

p

-5V = A

p

*u[j.p.]

zwar

+ B

p

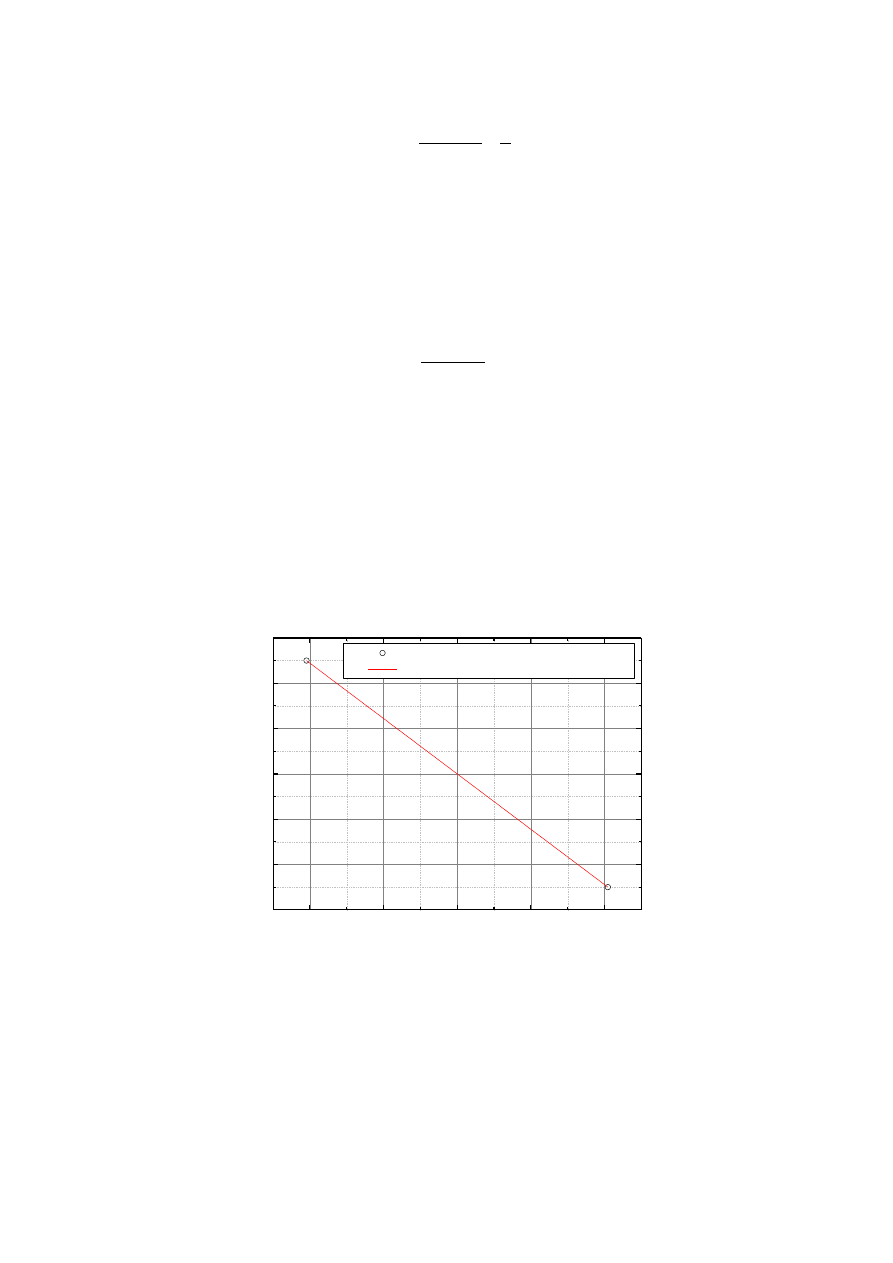
Po wprowadzeniu danych do programu ORGIN i dopasowaniu prostej otrzymaliśmy następujące
wyniki:
A

p

= - 0,00244 V/j.p.

B

p

= -7,73535E-17 V

-2000

-1000

0

1000

2000

-6

-4

-2

0

2

4

6

dane eksperymentalne
dopasowanie prostej typu Y=A + B*X

N

a

p

ie

ci

e

[V]

Napiecie [j. A D C]

Rysunek 1 - dane eksperymentalne uzyskane podczas kalibracji oraz dopasowana do nich prosta

4.

Sprawdzenie poprawności kalibracji układu pomiarowego:

a. W tej części dwiczenia należało wykreślid histogram oraz porównad zmierzone wartości z

wartością nominalną opornika, oraz sprawdzenie czy wszystkie oporniki mieszczą się w
zadanej tolerancji. Dokonałem pomiaru wartości niezrównoważenia mostka dla 90 oporników,
następnie obliczyłem wartośd ich rezystancji. Dane wykorzystane w obliczeniach:



Rz=10 kΩ,



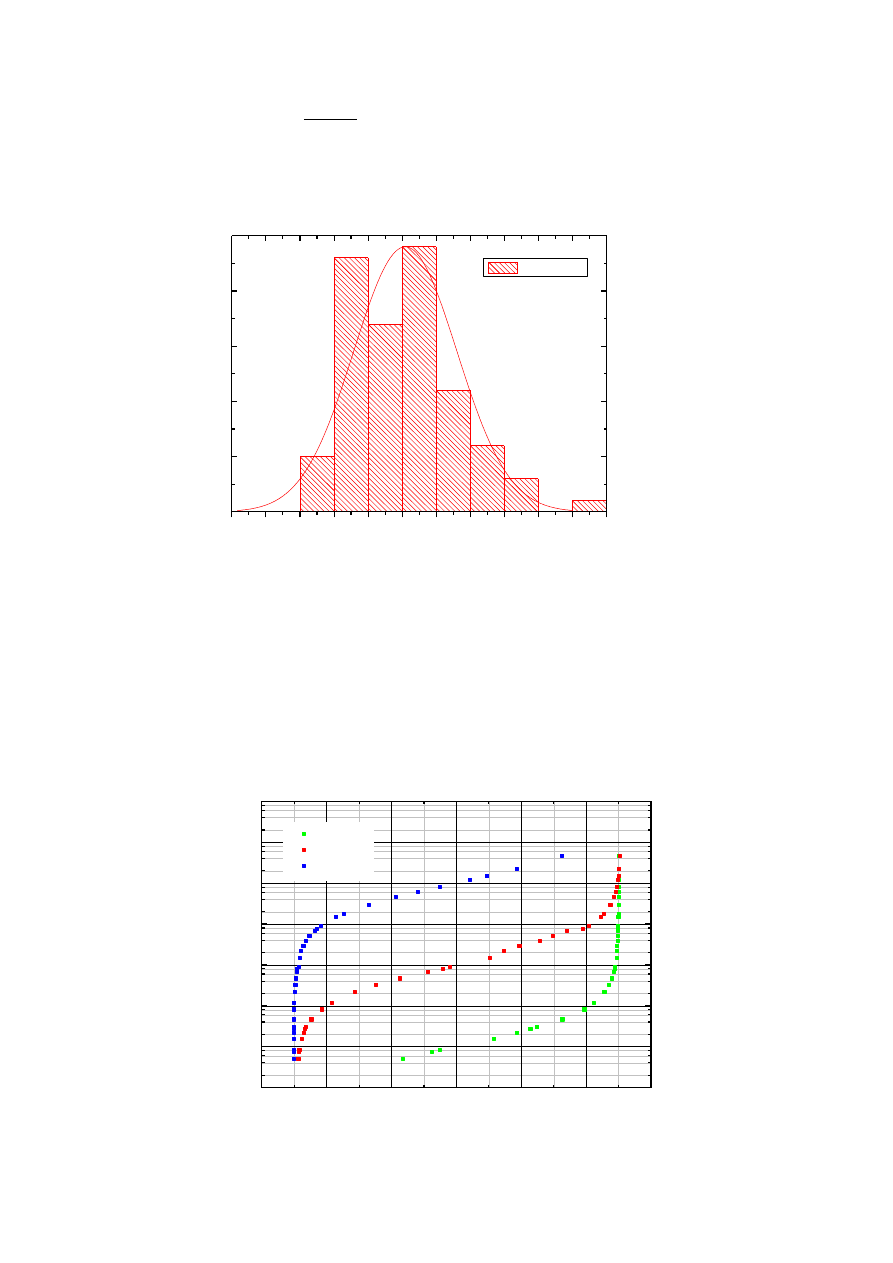
U=10 V,



z

n

n

R

U

U

U

U









2

2

R

x

.

b. Po wprowadzeniu uzyskanych danych do programu Origin sporządziłem histogram

5,04

5,06

5,08

5,10

5,12

5,14

5,16

5,18

5,20

5,22

5,24

5,26

0

5

10

15

20

25

L

icze

b

n

o

sc

p

rze

d

zi

a

lu

R [kOhm]

Liczebosc

Rysunek 2 - Histogram rozrzutu wartości oporu dla oporników o tej samej wartościu nominalnej i tolerancji.

5.

Wyznaczenie charakterystyki U

n

= f(R

x

):

a. W tym celu zmierzyłem wartości napięcia nierównowagi mostka dla znanych wartości

rezystorów. Dokonałem trzech serii pomiarów U

n

przy użyciu 34 rezystorów. W kolejnych

seriach użyłem opornika zakresowego 100 Ω, 10 kΩ i 1 MΩ.

b.

Otrzymane zależności przedstawione są na wykresie:

-6

-4

-2

0

2

4

6

10

100

1k

10k

100k

1M

10M

100M

R

z

= 100



R

z

= 10 k



R

z

= 1 M



R

x

[



]

U

n

[V]

Rysunek 3 - Wykres rezystancji w funkcji napięcia niezrównoważenia mostka Wheatstona dla serii rezystorów. Dane

zmierzono dla trzech różnych rezystorów zakresowych.

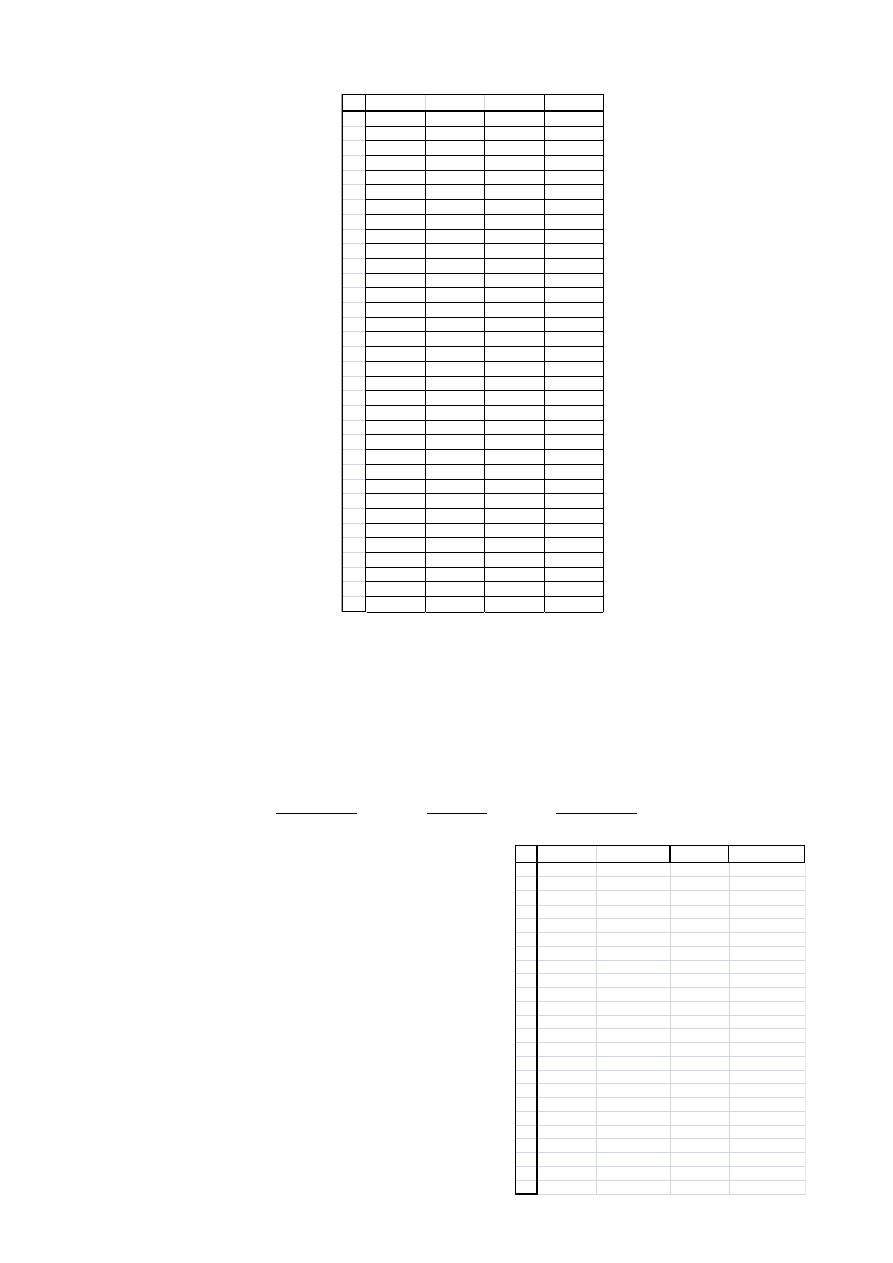
c. dane pomiarowe na postawie, których został utworzony wykres zamieszczam w tableli:

Lp.

100

Ω

10

kΩ

1

MΩ

R [k

Ω]

1

-1,647

-4,873

-5,011

0,051

2

-0,768

-4,851

-5,012

0,074

3

-0,517

-4,842

-5,011

0,082

4

1,161

-4,766

-5,011

0,16

5

1,876

-4,71

-5,011

0,22

6

2,282

-4,663

-5,011

0,27

7

2,488

-4,637

-5,009

0,3

8

3,262

-4,473

-5,009

0,47

9

3,945

-4,144

-5,004

0,82

10

4,238

-3,844

-5,001

1,21

11

4,562

-3,134

-4,992

2,2

12

4,702

-2,477

-4,967

3,3

13

4,792

-1,738

-4,945

4,7

14

4,855

-0,869

-4,931

6,8

15

4,88

-0,411

-4,923

8,2

16

4,889

-0,211

-4,867

9,1

17

4,933

1,022

-4,838

15

18

4,946

1,473

-4,799

22

19

4,955

1,941

-4,721

30

20

4,968

2,573

-4,65

39

21

4,975

2,974

-4,533

51

22

4,98

3,41

-4,374

68

23

4,985

3,891

-4,316

75

24

4,987

4,072

-4,181

91

25

4,989

4,44

-3,708

150

26

4,994

4,54

-3,484

180

27

4,997

4,743

-2,705

300

28

4,999

4,853

-1,879

470

29

4,999

4,904

-1,19

620

30

4,999

4,943

-0,505

820

31

4,999

4,98

0,423

1200

32

4,999

4,996

0,95

1500

33

4,999

5,018

1,862

2200

34

4,999

5,043

3,258

4700

Tabela 1 - Wartośd napięcia nierównowagi mostka dla znanych wartości rezystorów w trzech zakresach

6.

Ocena błędu pomiarowego:

a. Obliczam błąd wyznaczenia R

x

dla 90 rezystorów o oporze znamionowym 5,1 kΩ. Błąd

obliczyłem za pomocą różniczki zupełnej.
Wzór:

Gdzie:

- ΔU

n

= 4,9 mV, wzmocnienie = 1

- ΔU = 5 mV
-

Δ

R

z

= 0,1% R

z

b. Wartośd błędów dla zakresu 10 kΩ:

c. średnia wartośd oporu R

x

= 5141,84 Ω ze średnim

błędem ΔR

z

= 18,22 Ω.

Lp. U

n

R

x

[?]

ΔR

x

[?]

powtórzenia

1

-1,626

5092,06

18,10

2

2

-1,623

5098,90

18,12

3

3

-1,621

5103,46

18,13

8

4

-1,618

5110,31

18,15

4

5

-1,616

5114,87

18,16

3

6

-1,614

5119,44

18,17

8

7

-1,611

5126,30

18,18

3

8

-1,609

5130,88

18,19

8

9

-1,606

5137,75

18,21

6

10

-1,604

5142,34

18,22

7

11

-1,603

5144,63

18,22

1

12

-1,601

5149,22

18,23

5

13

-1,599

5153,81

18,24

4

14

-1,597

5158,41

18,25

7

15

-1,595

5163,00

18,26

1

16

-1,594

5165,30

18,27

3

17

-1,592

5169,90

18,28

6

18

-1,591

5172,20

18,28

1

19

-1,587

5181,42

18,30

2

20

-1,584

5188,34

18,32

1

21

-1,582

5192,95

18,33

1

22

-1,579

5199,88

18,34

2

23

-1,577

5204,50

18,35

3

24

-1,56

5243,90

18,44

1

Tabela 2 - Wartości błędów

7.

Wnioski

Podsumowując, kalibracja karty RBR została wykonana jak najbardziej prawidłowo, gdyż po tym zabiegu i

wprowadzeniu współczynników prostej do programu wskazywał on -5V dla zwartej karty a dla rozwartej +5V. Z
histogramu można odczytad, iż wartości oporników najczęściej wahają się miedzy 5,10 a 5,16 kΩ. Mimo tego
mieszczą się w granicy tolerancji 5,10 ±5% kΩ.

Aby wynik pomiaru rezystancji był w miarę dokładny należy dobierad zakres

pomiarowy jak najbliżej wartości rezystora. Największe błędy występowały, kiedy wartości
wykorzystywanych oporników odbiegały od wykorzystywanego zakresu.