1
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
1
Dynamika cieplna
przegród budowlanych
Wprowadzenie do symulacji energetycznej
budynków
Piotr Narowski, dr inż.
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
2
Jak obliczyć dostarczaną moc
cieplną lub temperaturę
wewnętrzną?
W warunkach ustalonych – projektowanie obciążenia
cieplnego lub chłodniczego
W warunkach nieustalonych – symulacja energetyczna
Q = ?
t
w
= ?

2
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
3
Oddziaływanie środowiska na
zjawiska cieplne w budynku
Promieniowanie
długofalowe
Promieniowanie słoneczne
całkowite i rozproszone
Kierunek i prędkość
wiatru
otoczenie
atmosfera
nieboskłon
opad
Azymut i wysokość
Słońca
Zachmurzenie
ogólne
Temperatura i
wilgotność
powietrza
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
4
Środowisko wewnętrzne
Temperatura powietrza wewnętrznego
Temperatura powierzchni wewnętrznych przegród
Strumień powietrza wentylacyjnego
Wewnętrzne zyski ciepła – ludzie, oświetlenie, urządzenia
Dostarczana moc cieplna
t
i
t
si
Q
z
Q
g
3
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
5
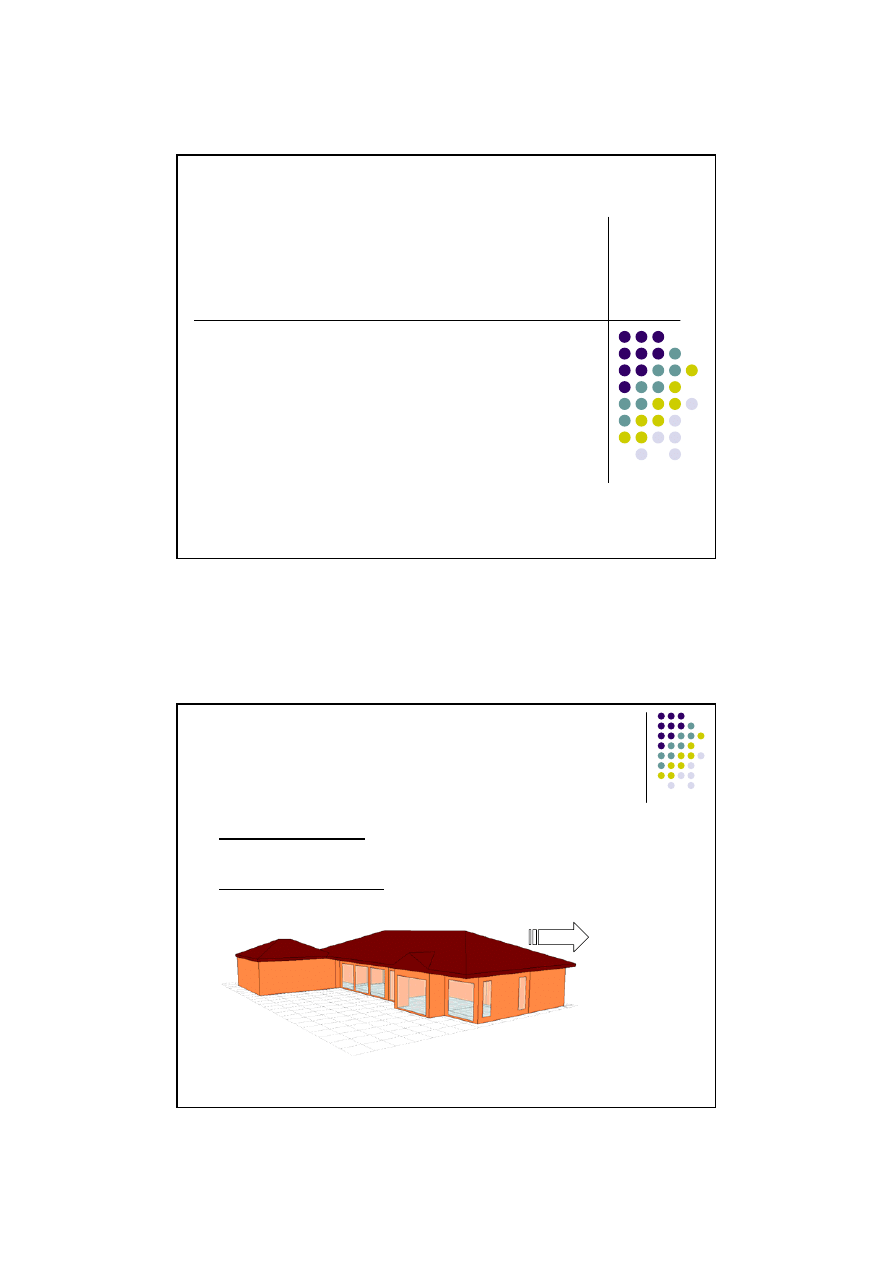
Model dynamiki procesów
cieplnych w budynku
Dane
geograficzne
GEO
Dane o
konstrukcji i
geometrii
budynku
KONST
t
v
w
d
w
cc
ϕ
I
t
τ
METEO
POZS
RNPS
NPSB
NPSR
NPD
KPZ
BCPZ
CTF
BCPW
BCPS
T
RNS
DNPS
NPKS
HWZC
KRSO
ISOW
INF
KPW
BMAT
STPD
t
I 2
...
t
I n
t
I 1
Temp.
przegród
t
i 2
...
t
i n
t
i 1
Temp.
powietrza
MSOW
MODEL DYNAMIKI CIEPLNEJ BUDYNKU
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
6
Model dynamiki procesów
cieplnych w budynku
godzinowe wartości temperatury powietrza strefach budynku
T. pow.
biblioteka właściwości fizycznych materiałów budowlanych
BMAT
godzinowe wartości temperatury powierzchni przegród budynku
T. prz.
model infiltracji powietrza do budynku
INF
model krzywej regulacji systemu ogrzewania lub wentylacji
KRSO
model transmisji promieniowania słonecznego przez przegrody
zewnętrzne
TRNS
instalacja ogrzewania i /lub wentylacji
ISOW
bilans ciepła powierzchni zewnętrznych przegród budynku
BCPZ
model systemu ogrzewania i /lub wentylacji
MSOW
model przejmowania ciepła na powierzchniach zewnętrznych
przegród
KPZ
bilans ciepła powietrza strefach budynku
BCPS
model bezpośredniego natężenia promieniowania słonecznego
NPSB
harmonogramy wewnętrznych zysków ciepła
HWZC
model rozproszonego natężenia promieniowania słonecznego
NPSR
model konwekcji ciepła na powierzchniach wewnętrznych
przegród
KPW
model natężenia promieniowania długofalowego środowiska
zewnętrznego
NPD
natężenie promieniowania krótkofalowego wytworzonego
wewnątrz stref
NPKS
pozycja Słońca na nieboskłonie
POZS
bilans ciepła powierzchni wewnętrznych przegród budynku
BCPW
model podziału natężenia promieniowania słonecznego
RPNS
model promieniowania długofalowego strefie budynku (MRT)
STPD
dane geometryczne konstrukcyjne budynku
KONST
model dystrybucji natężenia promieniowania krótkofalowego
wewnątrz stref budynku
DNPS
dane lokalizacji orientacji budynku
GEO
moduł funkcji CTF dynamiki przewodzenia ciepła przegród
wielowarstwowych
CTF
godzinowe dane meteorologiczne
METEO
4
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
7
Jak obliczyć strumień ciepła
przenikający przez przegrodę przy
zmiennej temperaturze
zewnętrznej i wewnętrznej?
t
i
(
τ)
q
i
(
τ)
q
e
(
τ)
t
e
(
τ)
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
8
Równanie Fouriera – 3W
*)
Model matematyczny przewodnictwa
cieplnego
z
x
y
dx
dy
dz
dV
x
q
r
dx
x
q
q
x
x
⋅
∂
∂
+
r
r
y
q
r
dy
y
q
q
y
y
⋅
∂
∂
+
r
r
z
q
r
dz
z
q
q
z
z
⋅
∂
∂
+
r
r
x
dA
y
dA
z
dA
gdzie:
s
m
2
ρ
λ
⋅
=
p
c
a
Przy braku wewnętrznego źródła ciepła
g
v
=0
T
a
T
a
t
T
z
T
y
T
x
T
a
t
T
∆
=
∇
=
∂
∂
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
⋅
=
∂
∂
2
2
2
2
2
2
2
Równanie dyfuzji cieplnej zwane równaniem Fouriera
to współczynnik dyfuzji cieplnej lub współczynnik wyrównania temperatury.
*) – patrz wykład nr 3.
Oznaczenia: T =T(x,y,z,t)– temperatura; x,y,z –
zmienne geometryczne; t - czas
5
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
9
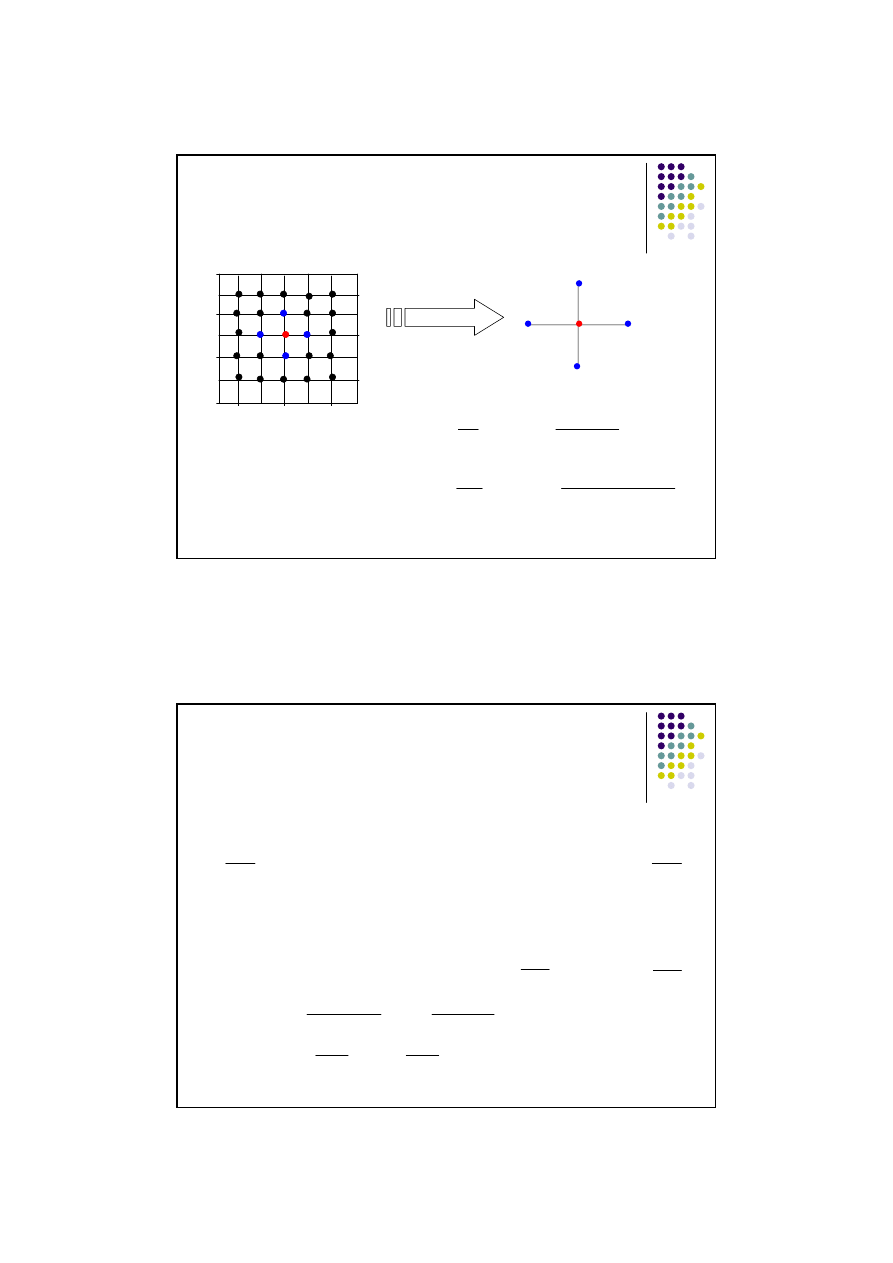
Metoda różnic skończonych
Zatem dla schematu różnicowego jednowymiarowego pola temperatury w
stanie nieustalonym otrzymujemy tzw gwiazdę pięciopunktową:
T
ij
T
i-1j
T
i+1j
T
ij+1
T
ij-1
x
i
x
i-1
x
i-2
x
i+1
x
i+2
t
j
t
j+1
t
j+2
t
j-1
t
j-2
∆t
∆x
Podstawiając za f(x) funkcję
temperatury T(x,t) otrzymamy
:
Druga pochodna cząstkowa temperatury w
punkcie i,j względem zmiennej
geometrycznej x
2
,
1
,
,
1
,
''
,
2
2
2
x
T
T
T
T
x
T
j
i
j
i
j
i
j
i
j
i
∆
+
−
≈
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
−
T
i,j
T
i+1,j
T
i-1,j
T
i,j+1
T
i,j-1
t
T
T
T
t
T
j
i
j
i
j
i
j
i
∆
−
≈
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−1
,
,
,
'
,
Pierwsza pochodna cząstkowa temperatury
w punkcie i,j względem czasu t
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
10
Metoda różnic skończonych
4
4 3
4
4 2
1
M
3
2
1
M
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
3
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
2
1
L
L
M
M
O
O
O
M
M
L
L
B
X
A
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⋅
+
⋅
+
=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
×
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
−
−
+
+
−
−
+
+
−
−
+
+
−
−
+
+
−
+
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
j
z
z
z
j
n
j
n
j
j
j
w
w
w
j
n
j
n
j
n
j
j
j
z
n
n
n
n
n
n
n
n
w
T
Bi
Bi
T
T
T
T
T
Bi
Bi
T
T
T
T
T
T
Bi
k
k
h
h
k
k
h
h
k
k
h
h
k
k
h
h
Bi
,
1
,
1
1
,
2
1
,
2
1
,
1
,
,
,
1
,
2
,
2
,
1
,
0
1
1
1
1
2
2
2
2
2
2
2
2
1
1
1
1
1
1
1
1
1
0
1
1
1
1
0
1
1
1
Układ równań dla przegrody wielowarstwowej z nierównomiernym
podziałem na warstwy elementarne i III warunkiem brzegowym
przyjmuje następującą postać:
gdzie:
n
n
z
z
w
w
i
i
i
p
i
i
i
i
i
i
p
i
i
x
Bi
x
Bi
n
i
x
c
t
k
x
x
c
t
h
λ
α
λ
α
ρ
λ
ρ
λ
∆
=
∆
=
−
=
∆
⋅
∆
=
∆
∆
⋅
∆
=
+
+
+
i
1
,
,
2
,
1
dla
i
1
1
2
1
1
1
K
6
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
11
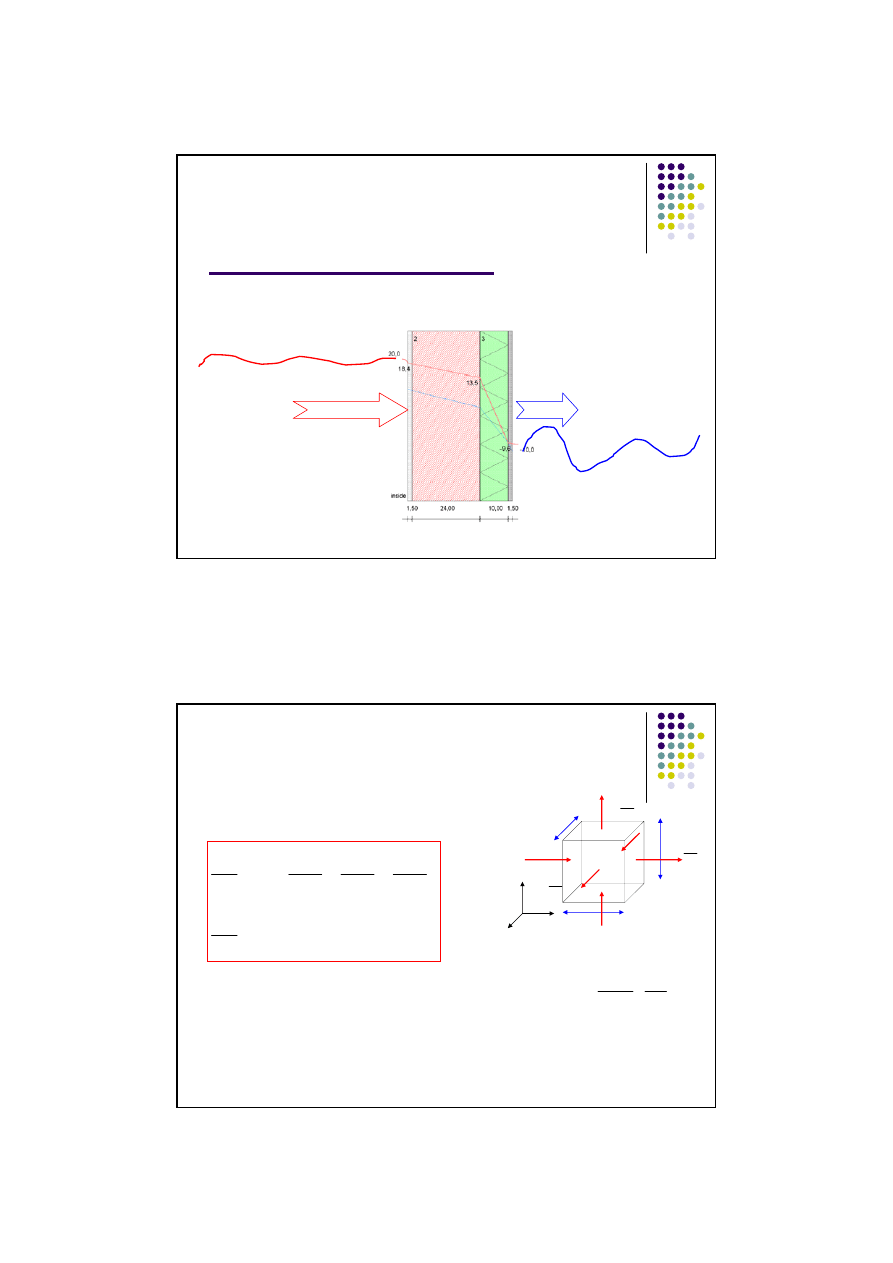
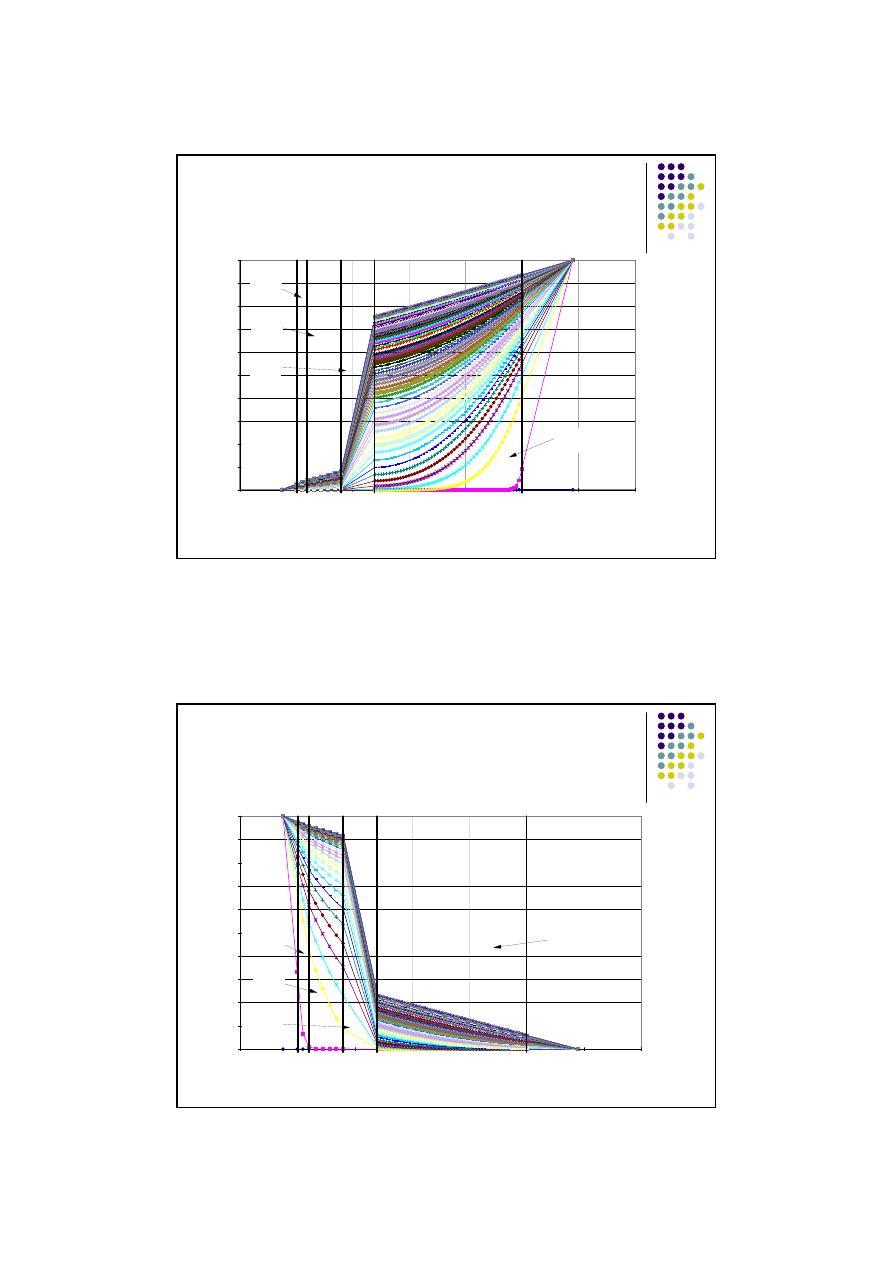
Pole temperatury w ścianie
Wykres zmian temperatury w przegrodzie w wyniku skoku temperatury
powietrza po
stronie wewnętrznej
o 1 K.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
Warstwy [m]
T
emp
eratu
ra [C]
Beton -
keramzyt
1200
Beton -
keramzyt
1400
Wełna
mineralna
Beton -
keramzyt
1400
T
z
(t)
T
w
(t)
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
12
Pole temperatury w ścianie
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
Warstwy [m]
T
e
m
p
er
atu
ra [C]
Beton -
keramzyt
1200
Beton -
keramzyt
1400
Wełna
mineralna
Beton -
keramzyt
1400
Wykres zmian temperatury w przegrodzie w wyniku skoku temperatury
powietrza po
stronie zewnętrznej
o 1 K.
T
z
(t)
T
w
(t)
7
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
13
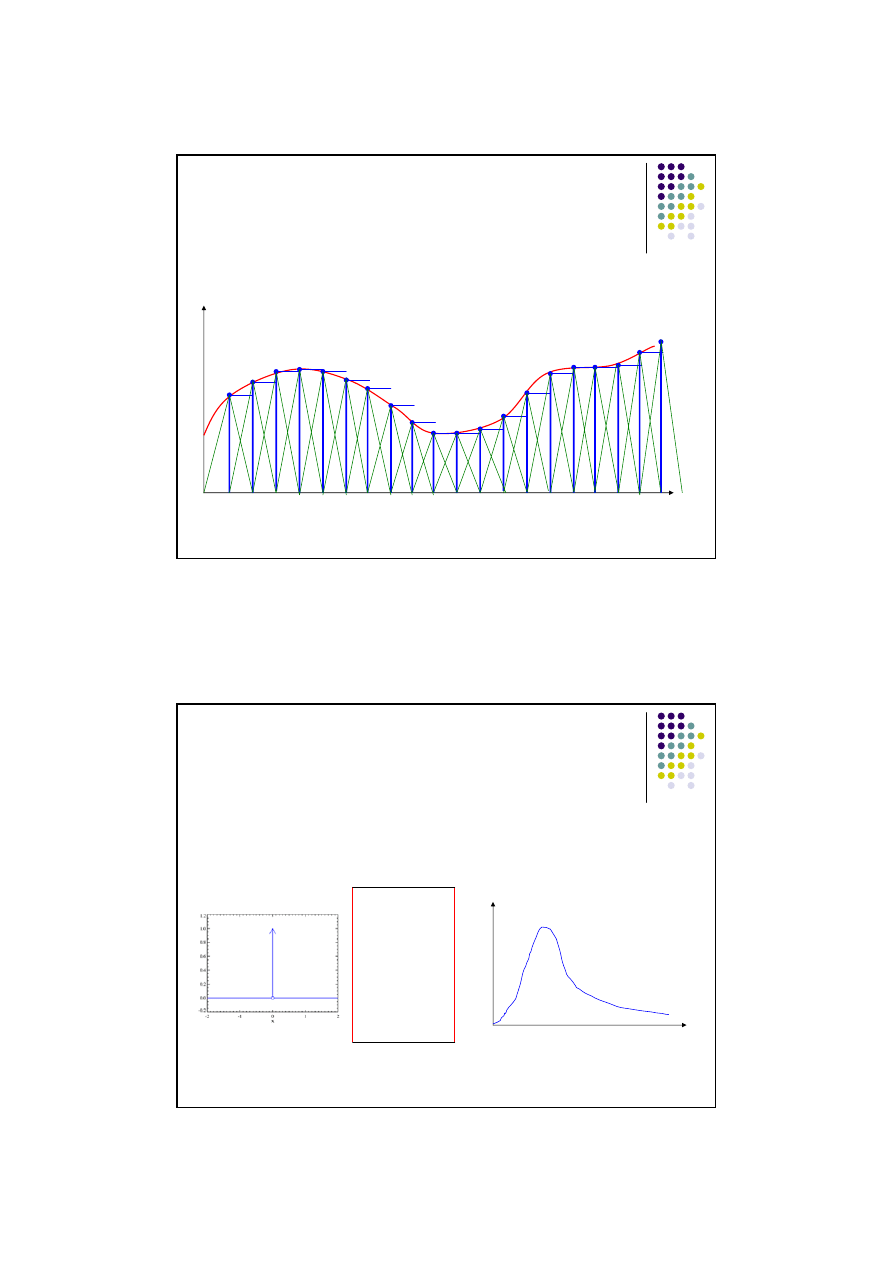
Funkcje odpowiedzi przegrody
Każdą funkcję ciągłą f(t) można przedstawić w postaci szeregu
impulsów o wartości odpowiadających wartości funkcji w punkcie.
t
T
T(t)
∆t
Dla
∆t -> 0 funkcja dyskretna dąży do funkcji ciągłej.
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
14
Funkcje odpowiedzi przegrody
Jeżeli poznamy odpowiedź przegrody na wymuszenie impulsowe
wówczas odpowiedź na dowolne wymuszenie termiczne będzie sumą
odpowiedzi serię impulsów.
Odpowiedź na impuls
Wymuszenie impulsowe
8
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
15
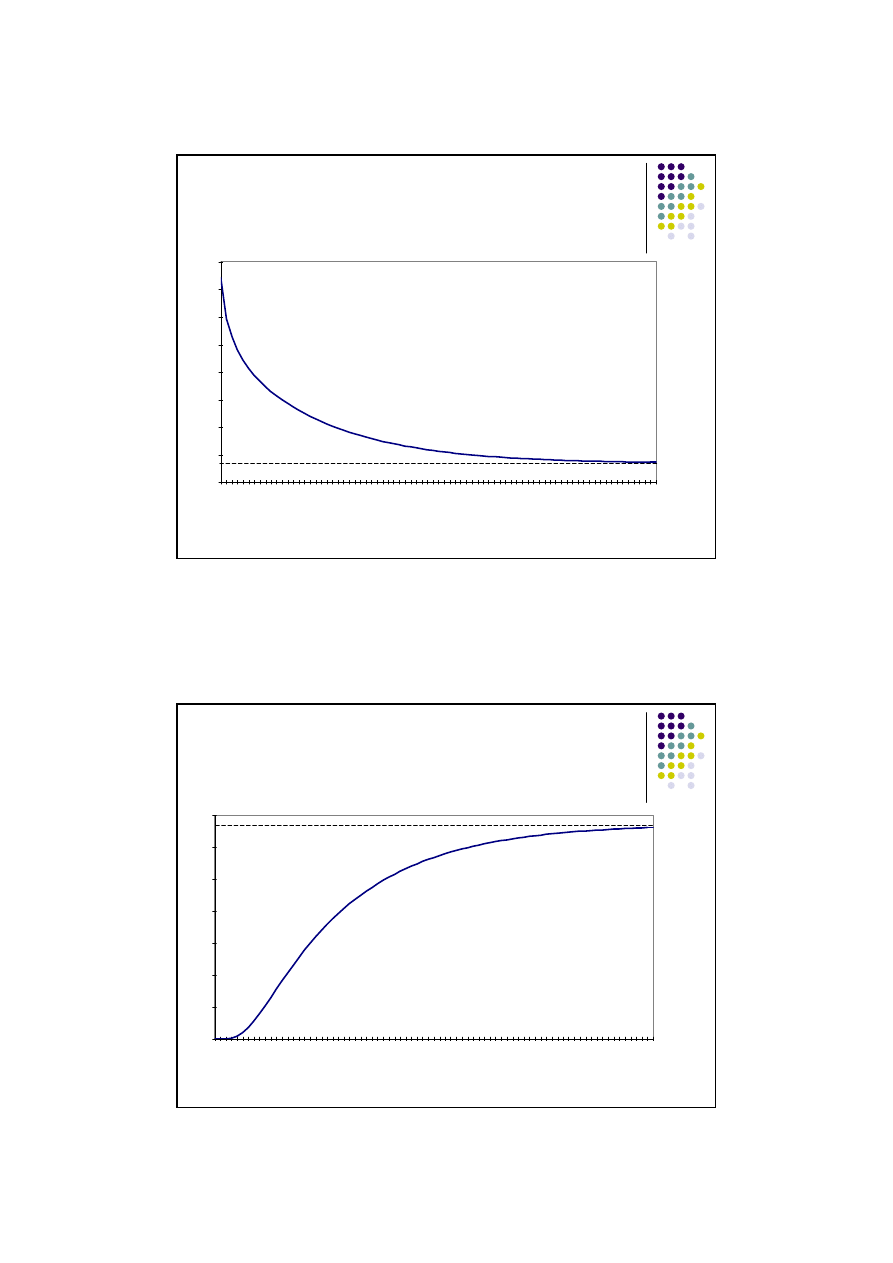
Funkcje odpowiedzi przegrody
0
1
2
3
4
5
6
7
8
2
5
8
11
14
17
20
23
26
29
32
35
38
41
44
47
50
53
56
59
62
65
68
71
74
77
80
t [h]
h
w
(t)
α
w
Odpowiedź przegrody (gęstość strumienia ciepła) na
powierzchni przy której wystąpił skok temperatury.
Dla t->0 wartość funkcji h
w
(t) wynosi
α
w
ponieważ,
q
w
=
α
w
(1-0), natomiast dla t->
∞ h
w
(t) dąży do wartości
współczynnika przenikania ciepła U, ponieważ w
stanie ustalonym q
w
=U*(T
w
-T
z
) = U*(1-0).
q [W/m
2
]
U
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
16
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
2
5
8
11
14
17
20
23
26
29
32
35
38
41
44
47
50
53
56
59
62
65
68
71
74
77
80
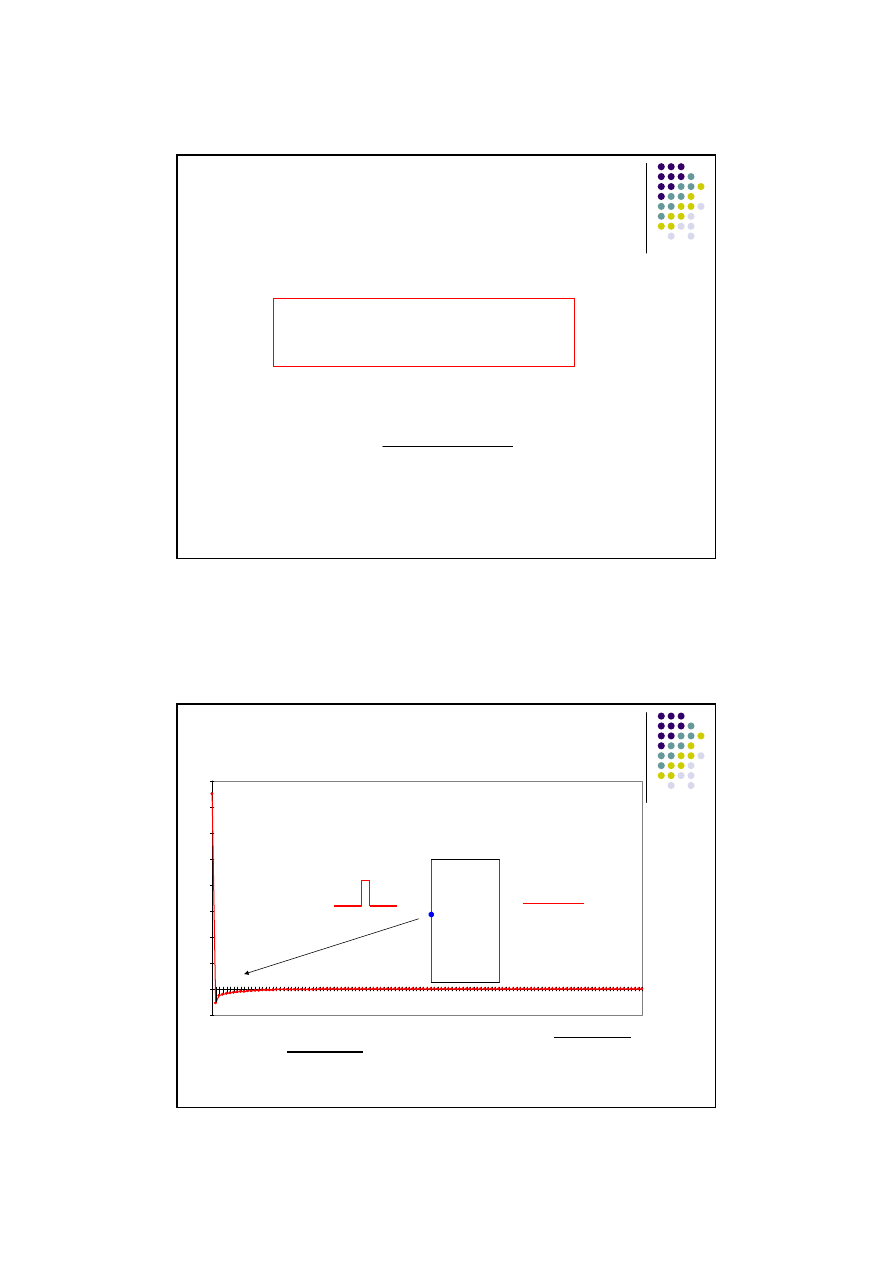
Funkcje odpowiedzi przegrody
t [h]
h
z
(t)
Odpowiedź przegrody (gęstość
strumienia ciepła) na przeciwległej
powierzchni niż ta przy której wystąpił
skok temperatury.
Dla t->0 wartość funkcji h
z
(t) wynosi 0
ponieważ, q
z
=
α
z
(0-0), natomiast dla t->
∞ h
z
(t)
dąży do wartości współczynnika przenikania
ciepła U, ponieważ w stanie ustalonym
q
z
=U*(T
w
-T
z
) = U*(1-0).
q [W/m
2
]
U
9
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
17
Odpowiedź przegrody na
wymuszenie impulsowe
W celu określenia odpowiedzi przegrody budowlanej na pojedynczy
impuls temperatury należy określić wartości funkcji podanej poniżej
dla zakresu t należącego do przedziału <0, +
∞):
( ) ( ) ( )
(
) ( )
∫
−
+
⋅
=
+
τ
τ
τ
τ
0
'
0
d
h
t
T
h
t
T
t
q
W funkcji tej mamy pochodną odpowiedzi na skok temperatury, którą
można wyznaczyć poprzez numeryczne różniczkowanie funkcji h(t):
( )
τ
τ
∆
−
∆
+
≅
)
(
)
(
'
t
h
t
h
t
h
Oraz funkcję temperatury w postaci jednostkowego
impulsu:
( )
)
(t
t
T
δ
=
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
18
-2
0
2
4
6
8
10
12
14
16
0
4
8
12
16
20
24
28
32
36
40
44
48
52
56
60
64
68
72
76
80
84
88
92
96 10
0
10
4
10
8
11
2
11
6
12
0
Odpowiedź przegrody na
wymuszenie impulsowe
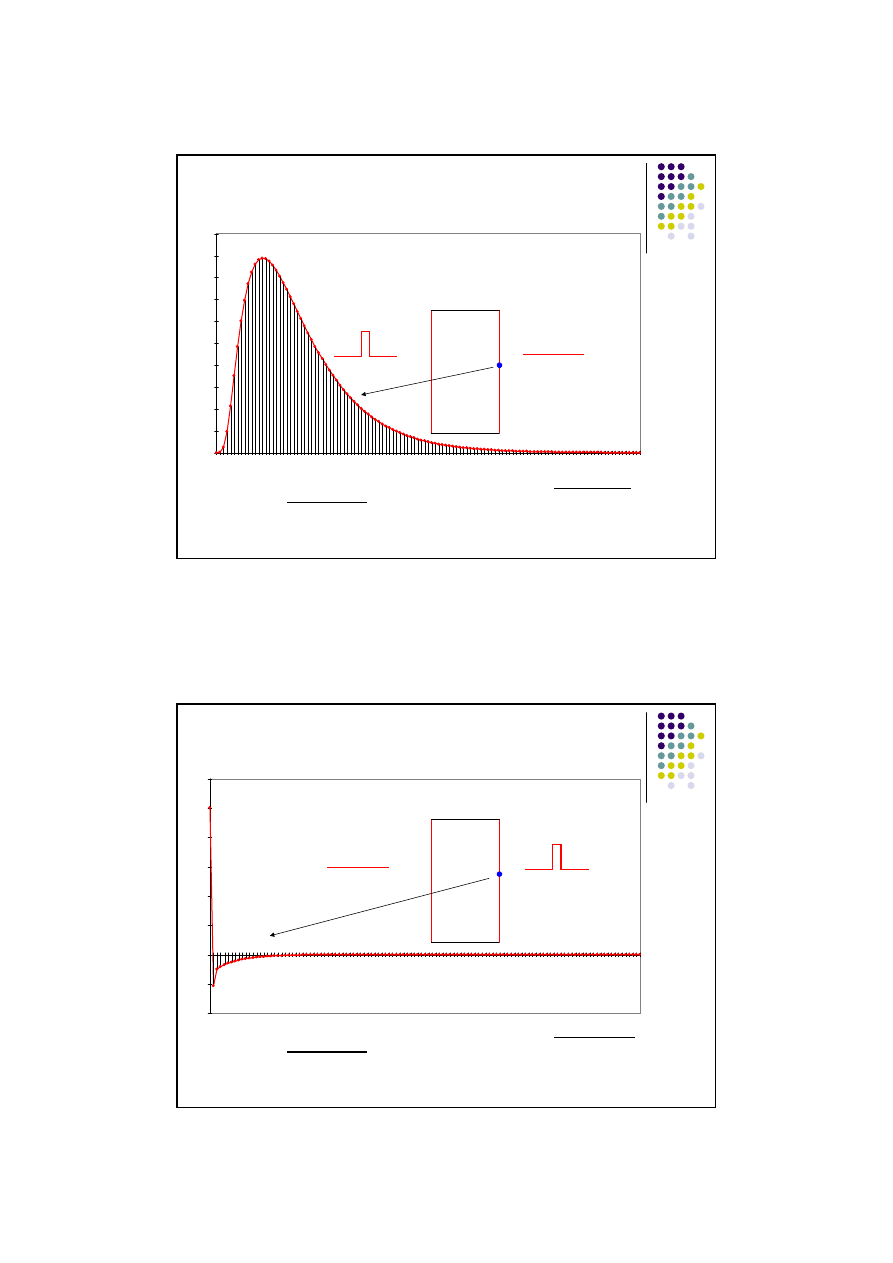
Funkcja odpowiedzi przegrody na impuls temperatury zewnętrznej dla
powierzchni zewnętrznej przegrody.
t
g
zz
(t)
T
z
T
w
z
α
z
10
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
19
0
0,002
0,004
0,006
0,008
0,01
0,012
0,014
0,016
0,018
0,02
0
4
8
12
16
20
24
28
32
36
40
44
48
52
56
60
64
68
72
76
80
84
88
92
96 10
0
10
4
10
8
11
2
11
6
12
0
Odpowiedź przegrody na
wymuszenie impulsowe
Funkcja odpowiedzi przegrody na impuls temperatury zewnętrznej dla
powierzchni wewnętrznej przegrody.
t
g
wz
(t)
T
z
T
w
w
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
20
-2
-1
0
1
2
3
4
5
6
0
4
8
12
16
20
24
28
32
36
40
44
48
52
56
60
64
68
72
76
80
84
88
92
96 10
0
10
4
10
8
112 116 12
0
Odpowiedź przegrody na
wymuszenie impulsowe
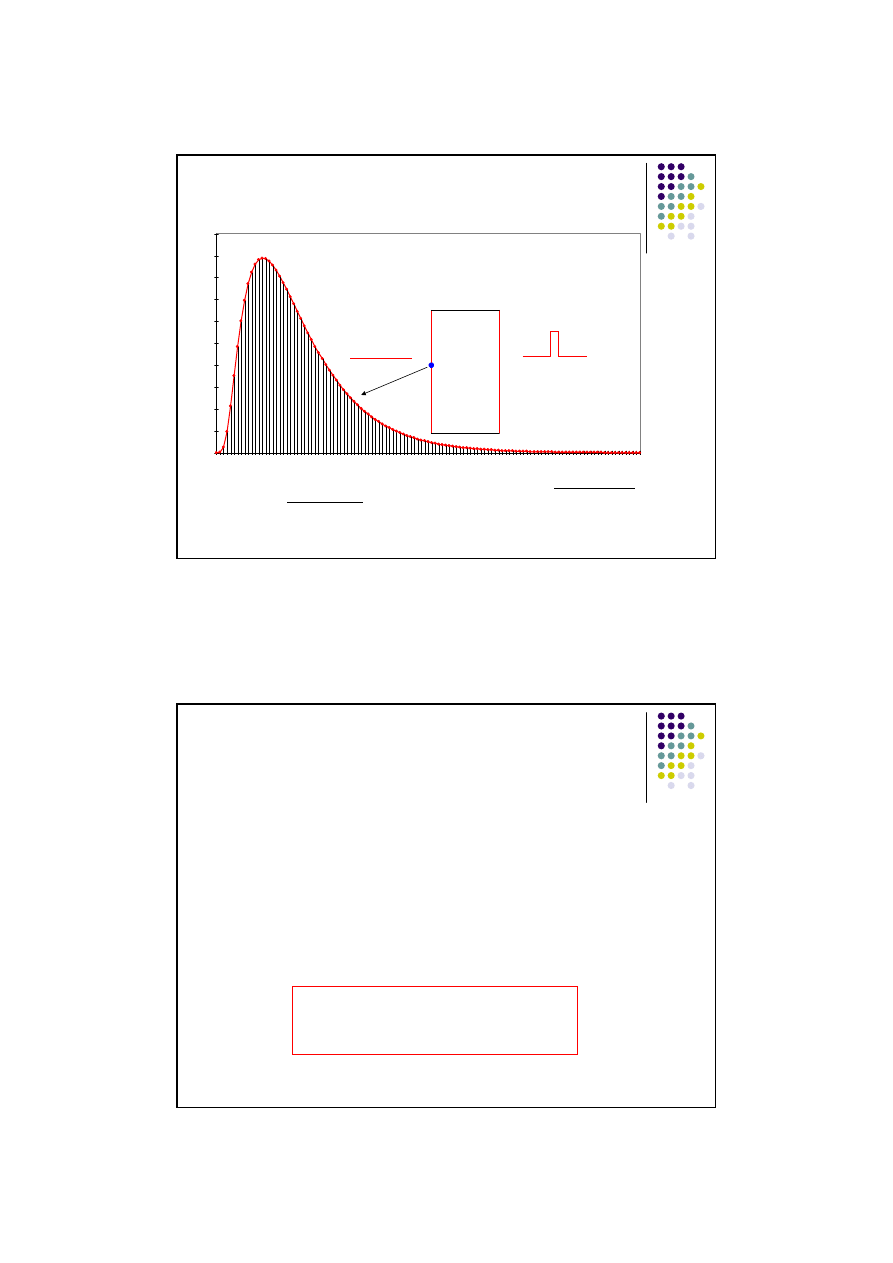
Funkcja odpowiedzi przegrody na impuls temperatury wewnętrznej dla
powierzchni wewnętrznej przegrody.
t
g
ww
(t)
T
z
T
w
w
α
w
11
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
21
0
0,002
0,004
0,006
0,008
0,01
0,012
0,014
0,016
0,018
0,02
0
4
8
12
16
20
24
28
32
36
40
44
48
52
56
60
64
68
72
76
80
84
88
92
96 10
0
10
4
10
8
11
2
11
6
12
0
Odpowiedź przegrody na
wymuszenie impulsowe
Funkcja odpowiedzi przegrody na impuls temperatury wewnętrznej dla
powierzchni zewnętrznej przegrody.
t
g
zw
(t)
T
w
z
T
z
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
22
Splot funkcji
Dla
∆τ dążącego do zera suma dąży do całki, którą można zapisać:
g
f
d
g
t
f
t
y
g
f
d
t
g
f
t
y
∗
=
⋅
⋅
−
=
∗
=
⋅
−
⋅
=
∫
∫
∞
∞
τ
τ
τ
τ
τ
τ
0
0
)
(
)
(
)
(
)
(
)
(
)
(
Splot funkcji f i g:
Zamieniając argumenty funkcji f i g
otrzymujemy identyczną wartość splotu
:
g
T
d
g
t
T
t
q
∗
=
⋅
⋅
−
=
∫
∞
τ
τ
τ
0
)
(
)
(
)
(
Podstawiając za funkcję f funkcję temperatury w czasie T(t) otrzymujemy splot temperatury i
odpowiedzi na impuls temperatury czyli funkcję gęstości strumienia ciepła na powierzchni
przegrody q(t)
:
12
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
23
Splot funkcji
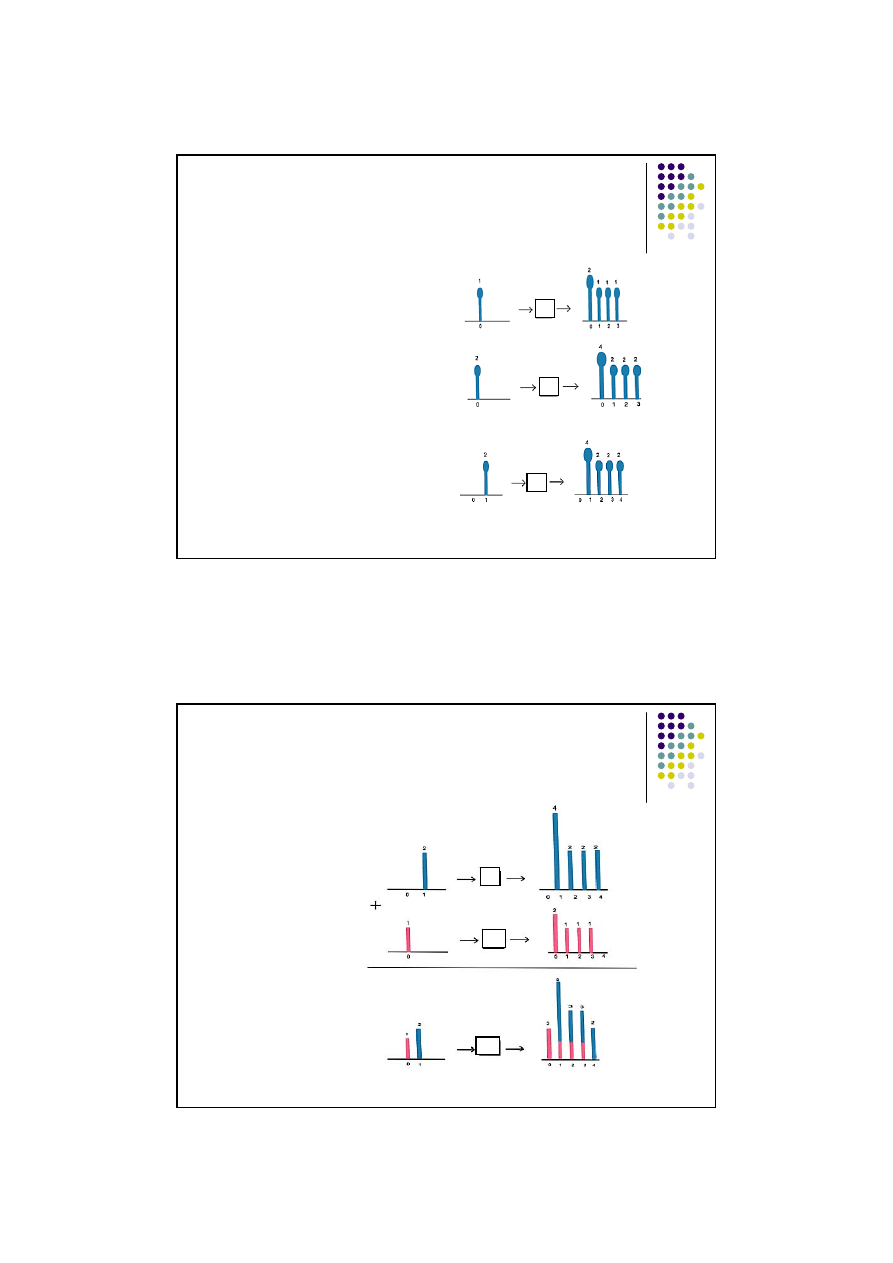
W przypadku funkcji dyskretnych splot funkcji można zobrazować
następująco:
g
g
Odpowiedź na przeskalowany
impuls:
Odpowiedź na przeskalowany i
przesunięty w czasie impuls:
g
Odpowiedź na impuls
jednostkowy:
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
24
Splot funkcji
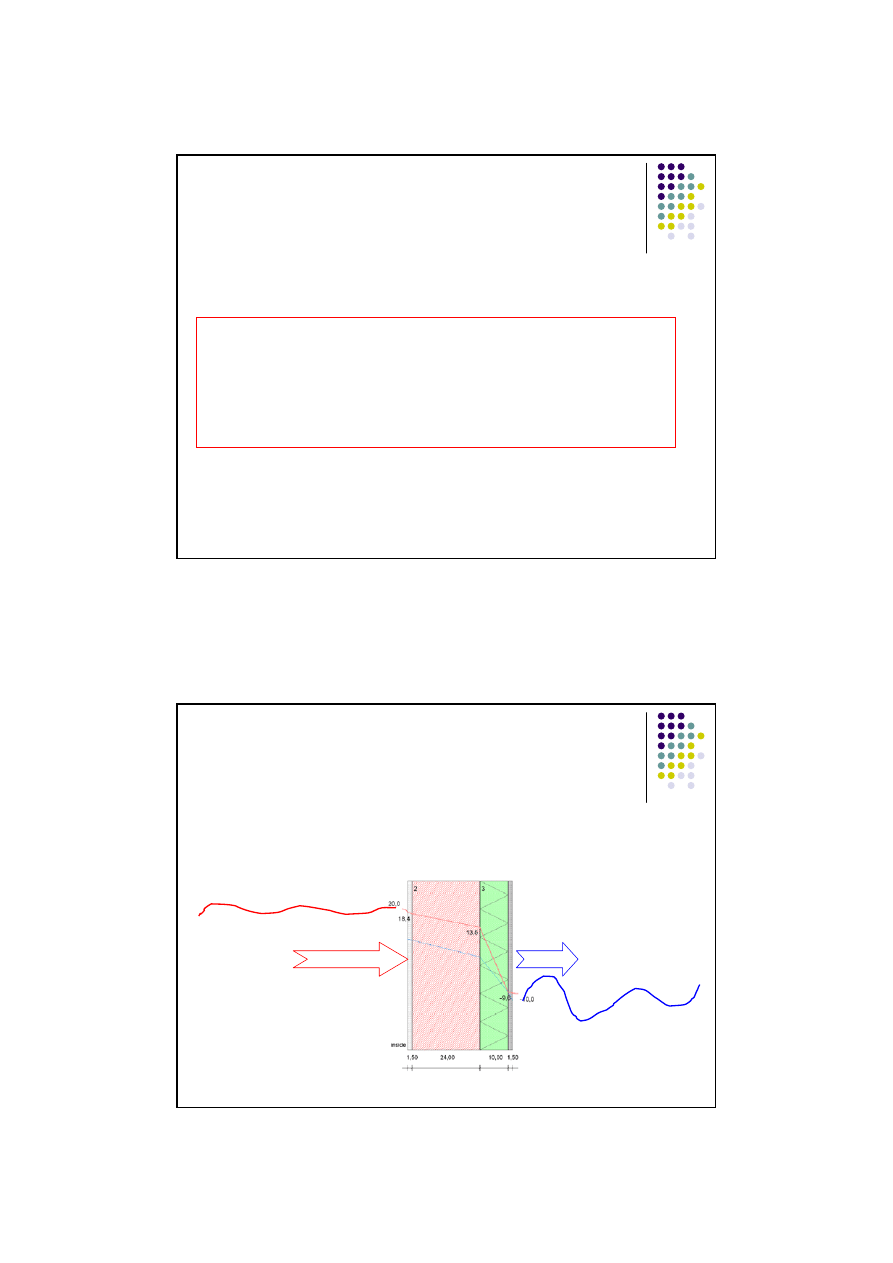
W przypadku funkcji dyskretnych splot funkcji można zobrazować
następująco:
g
g
g
Superpozycja dwóch
odpowiedzi
impulsowych:
13
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
25
Odpowiedź przegrody na
wymuszenie impulsowe
Wykorzystując powyższe rozważania gęstości strumieni ciepła na
powierzchni wewnętrznej q
w
i powierzchni zewnętrznej q
z
przegrody w odpowiedzi na zmienne w czasie temperatury
powietrza po stronie wewnętrznej T
w
i stronie zewnętrznej T
z
w
dowolnej chwili czasu i można zapisać w postaci równań:
τ
τ
τ
τ
∆
⋅
−
⋅
−
∆
⋅
−
⋅
=
∆
⋅
−
⋅
−
∆
⋅
−
⋅
=
∑
∑
∑
∑
=
=
=
=
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
0
0
0
0
j
i
T
j
g
j
i
T
j
g
i
q
j
i
T
j
g
j
i
T
j
g
i
q
z
n
j
zz
w
n
j
zw
z
z
n
j
wz
w
n
j
ww
w
W powyższych równaniach za dodatni przyjęto kierunek przepływu
ciepła od powierzchni wewnętrznej przegrody do jej powierzchni
zewnętrznej.
11/29/2007
Dynamika cieplna przegród budowlanych - Piotr
Narowski
26
Umiemy zatem obliczyć strumień
ciepła przenikający przez
przegrodę przy zmiennej
temperaturze zewnętrznej i
wewnętrznej
t
i
(t)
q
i
(t)
q
e
(t)
t
e
(t)
Wyszukiwarka
Podobne podstrony:
METODY OBLICZE CIEPLNYCH PRZEGR D BUDOWLANYCH
METODY OBLICZEŃ CIEPLNYCH PRZEGRÓD BUDOWLANYCH
PRZEGR 1, Sprawdzi˙ pod wzgl˙dem cieplno-wilgotno˙ciowym przegrod˙ budowlan˙ pionow˙ o nast˙puj˙cym
BUD PRZEGRODA, Sprawdzi˙ pod wzgl˙dem cieplno-wilgotno˙ciowym przegrod˙ budowlan˙ pionow˙ o nast˙puj
IZOLACYJNOŚĆ TERMICZNA WIELOWARSTWOWYCH PRZEGRÓD BUDOWLANYCH
certyfikacja przegrody budowlane
Izolacyjność termiczna wielowarstwowych przegród budowlanych, budownictwo ogólne
49 Odporność ogniowa przegród budowlanych w budynkach mieszkalnych
Efektywne docieplanie przegród budowlanych
8 stateczność cieplna przegród i pomieszczeń, budownictwo
W jaki sposób oszacować opór cieplny przegród zewnętrznych
Izolacyjność termiczna wielowarstwowych przegród budowlanych (1)
Stateczność cieplna, Fizyka Budowli - WSTiP
Efektywne ieplanie przegród budowlanych, sanbud, Audyty Energetyczne
Odporność ogniowa przegród budowlanych w budynkach mieszkalnych
ZAGADNIENIA WYMIANY CIEP A W PRZEGRODACH BUDOWLANYCH
więcej podobnych podstron