POPRAWA II

1. Do jakiego typu metod rozwiązywania układów równań liniowych zaliczamy metodę opartą

o rozkład QR?

Odp.: Do dokładnych

2. Kiedy mówimy o aproksymacji integralnej?

Odp.: Przypadek ciągły (aproksymacja integralna) oznacza, że przy wyliczaniu błędu

aproksymacji możemy korzystać z informacji o funkcji aproksymowanej w całej dziedzinie.

3. Wyznacz ilorazy różnicowe dla funkcji podanej w postaci punktów: (0;1),(1;2),(3,1).

Odp.: używamy wzoru

oraz

Następnie wyliczmy:

2 − 1
1 − 0

= 1,

1 − 2
3 − 1

= −

1
2

,

−

1

2 − 1

3 − 0

= −

1
2

4. Dana jest dyskretna funkcja f(x) określona na zbiorze punktów 𝒙

𝟏

, 𝒙

𝟐

, … , 𝒙

𝒏

. Jaki

maksymalny stopień będzie miał wielomian interpolacyjny przybliżający tę funkcję?

Odp.: n-1

5. W pewnej kwadratowej macierzy A element 𝒂

𝟏𝟏

= 𝟎 . Co należy zrobić, aby możliwe stało

się użycie metody eliminacji Gaussa do rozwiazywania układu Ax=b.

Odp.: NIE WIEM

6. Zapisz równanie różniczkowe, którego model przedstawiony jest na schemacie. Jako

zmienną przyjmij literę ‘y’.

Odp.: NIE MAM POJĘCIA

1. Zbieżny proces ma cechę samopoprawności. Wyjaśnij co to oznacza:

Chodzi o to, że w kolejnym kroku korzysta z wyników obliczonych w poprzednim kroku. To
znaczy ze przy małym kroku występują błędy a on z każdym kolejnym obiegiem sam je
naprawia bo nie korzysta z poprzedniego wyniku tylko jakby liczy od nowa czyli dokładnie.
W skrócie: poprawia błędy.

2. Błąd całkowity to suma trzech rodzajów błędów. Wymień dwa z nich.

błąd całkowity to błąd wejścia + błąd metody + błąd zaokrąglenia

3. Jak można zwiększyć dokładność aproksymacji

Dokładność aproksymacji możemy zwiększyć poprzez zmianę liczby m (większa liczba –
mniejszy błąd). Wtedy błąd aproksymacji optymalnej nie przekracza podanej liczby
dodatniej epsilon postaci 10^(-m), gdzie m jest liczbą dodatnią.

4. Kiedy w obliczeniach numerycznych mówimy o NADMIARZE?

W obliczeniach numerycznych mówimy o nadmiarze wtedy, gdy wynik działania ma zbyt
dużą cechę.

5. Jaka jest różnica pomiędzy metodą jednokrokową a wielokrokową rozwiązywania równań

różniczkowych?

jednokrokowa - przechodząc z x do x+h, musimy znać wartość rozwiązania tylko w jednym
punkcie, wielokrokowa - wartość funkcji w nowym punkcie wyrażamy przez jej wartości w
kilku punktach

6. Zilustruj twierdzenie Bolzano. Podpisz elementy rysunku.

Pierwszy termin/I poprawa

1. Pytanie o interpolacja/ekstrapolacja/aproksymacja, 1g-inter 2g-extra

jak coś z przedziału to inter, spoza extra.

2. Wzór newtona:

sqrt(3)z c lub sqrt(4) z c, przyrównujemy do x, uzyskujemy funkcje, liczymy pochodną i

tworzymy wzór
3. Co jest potrzebne do rozwiązania równania metodą eulera:



Zakres x



wartosc poczatkowa dla wszystkich pochodnych (n-1 kropek)



Wartość początkową dla y(0)



Krok(h)

4. - przebieg funkcji interpolacyjnej (prosta po punktach) i aproksymacyjnej(prosta po środkowym
punkcie pozioma) 0 stopnia
5. - metoda rozwiazywania układu równań różniczkowych -> całkowanie
6. pytania brzmiało że masz 1000 czegoś tam i jaka metoda będzie najlepsza : metoda iteracji
7. -Zjawisko Rungego

8. *przekształcić wyrażenie żeby uniknąć problemu kasowania dla małych x
-wzór taylora

-sprzężenie

9.* Wersja2: 1,6 binarnie i dziesiętnie (znak mantysa cecha) 5 bitowe słowo, 1bit znak, 2 bit cecha, 2
bit
-przybliżenie:
1,5
-binarnie:
001,10
10. * Wersja1: 1,6 binarnie i dziesietnie (mantysa cecha znak) 5 bitowe słowo, , 2 bit cecha, 2 bit, 1bit
znak
-przybliżenie:
1,5
-binarnie:
01,100
11.
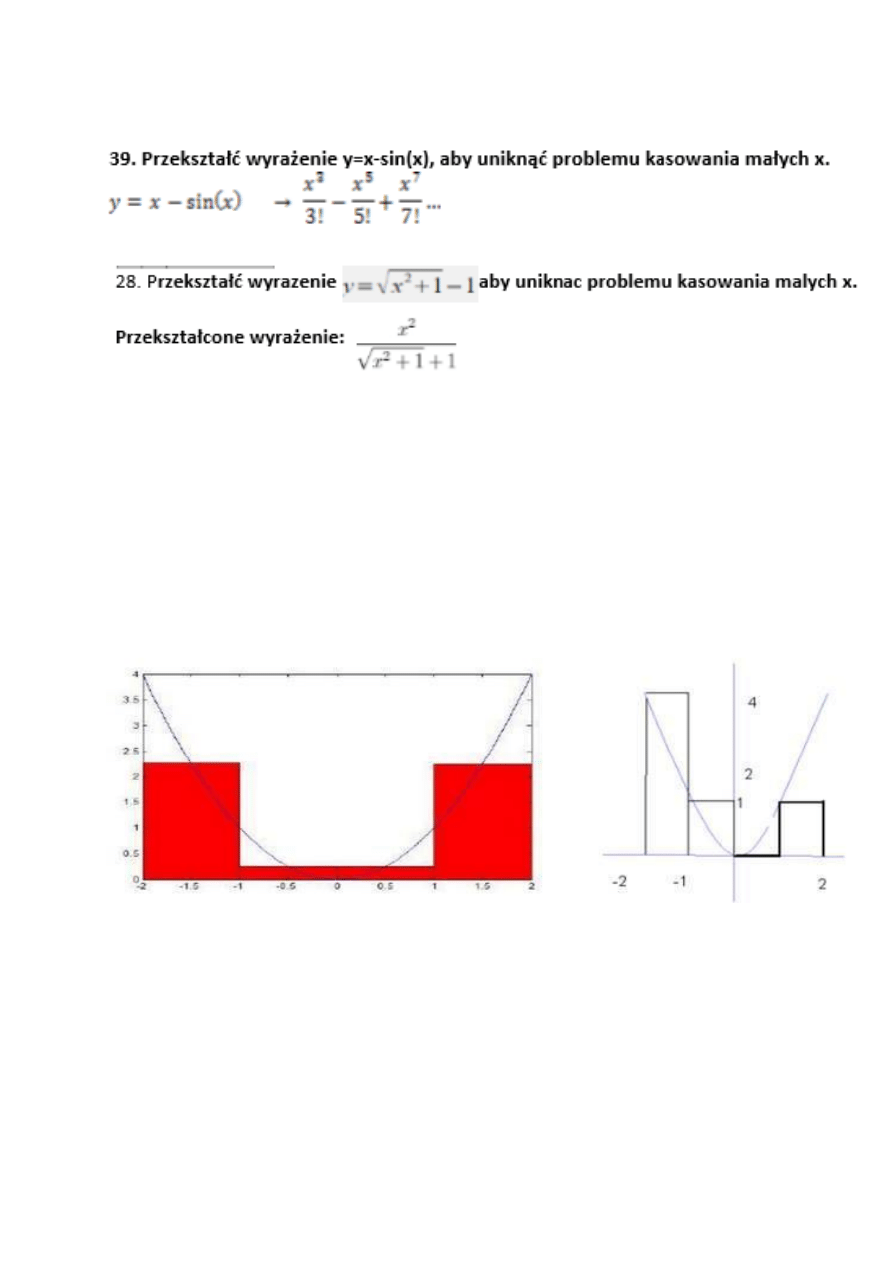
a) * metoda prostokątów (całki) - x^2 (3 metody)

b)* metoda prostokątów (całki) - abs(x) - adekwatnie( abs= wart bezwzgledna) (3metody)

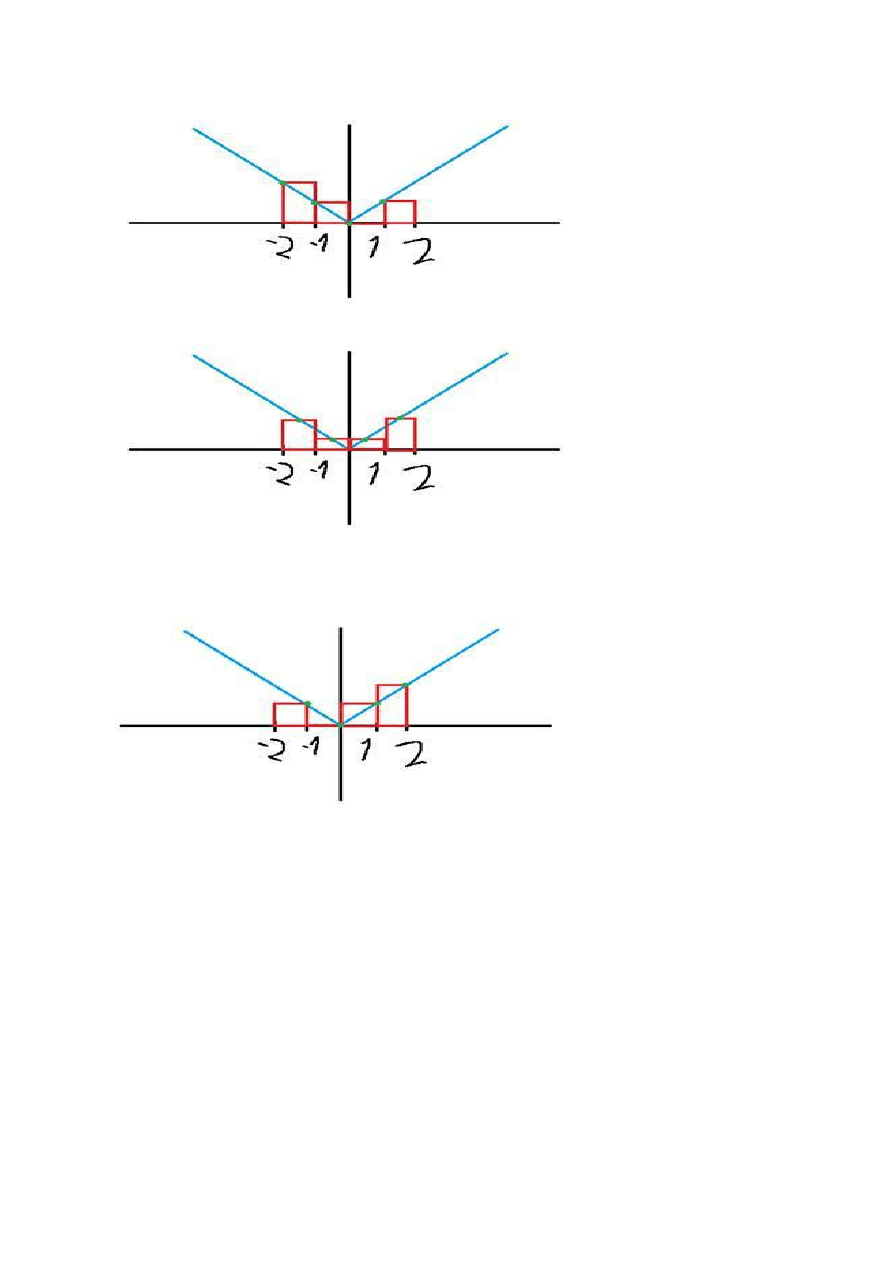
12.* dlaczego nie można robić kroku 0.2 w jakiejs tam metodzie dyskretyzującej czy jakos tak
13. *dlaczego nie można zrobić kroku 0.1 w różniczkowaniu
krok 0.1 czy też 0.2 nie jest preferowany w obliczeniach numerycznych, ponieważ nie jest on liczbą
maszynową i przy konwersji na liczbę binarną wychodzi ułamek okresowy, a więc niezbędne są
zaokrąglenia
14. * nawiasy w macierzach były
-uzyskać jak najmniejszą macierz na końcu

15. * Macierz Vandermonde'a
wiersze są kolejnymi potęgami X

16. *Uniknąć Odwracania macierzy
-metoda QR

17. Napisz układ równań potrzebny do znalezienia funkcji aproksymującej I stopnia, mając 4 węzły