Teoria sterowania i technika regulacji, II rok

14.04.2014

KEiASPE

, AGH Kraków

dr inż. Andrzej Firlit

1

Program ćwiczenia laboratoryjnego – O

PIS

UAR

W PRZESTRZENI STANU

Dany jest układ dynamiczny III rzędu, opisany transmitancją operatorową oraz równaniem stanu
wraz z równaniem wyjścia w przestrzeni stanu:

 

2

3

2

2

8

8 2

18 4

12

s

G s

s

, s

, s











1.

Dokonaj transformacji:

a. z opisu transmitancyjnego układu do opisu w przestrzeni stanu

tf2ss()

oraz

b. z opisu układu w przestrzeni stanu do opisu transmitancyjnego

ss2tf()

.

2.

Wyznacz zera i bieguny układu, wartości własne i wektory własne macierzy stanu A, porównaj
zbiór wartości własnych ze zbiorem biegunów transmitancji G(s) –

ss2zp(), [Mw,Ad]=eig()

.

3.

Wyznacz opis układu w postaci równań algebraiczno-różniczkowych oraz w przestrzeni stanu w
postaci macierzowej

(A, B, C, D)

– forma kanonicza sterowalna (zmiennych fazowych).

u

x

x

x

x

x

x































































































1

0

0

2

,

8

4

,

18

12

1

0

0

0

1

0

3

2

1

3

2

1



































3

2

1

2

0

8

x

x

x

y

)

(

)

(

)

(

t

t

t

u

B

x

A

x











)

(

)

(

)

(

t

t

t

u

D

x

C

y









4.

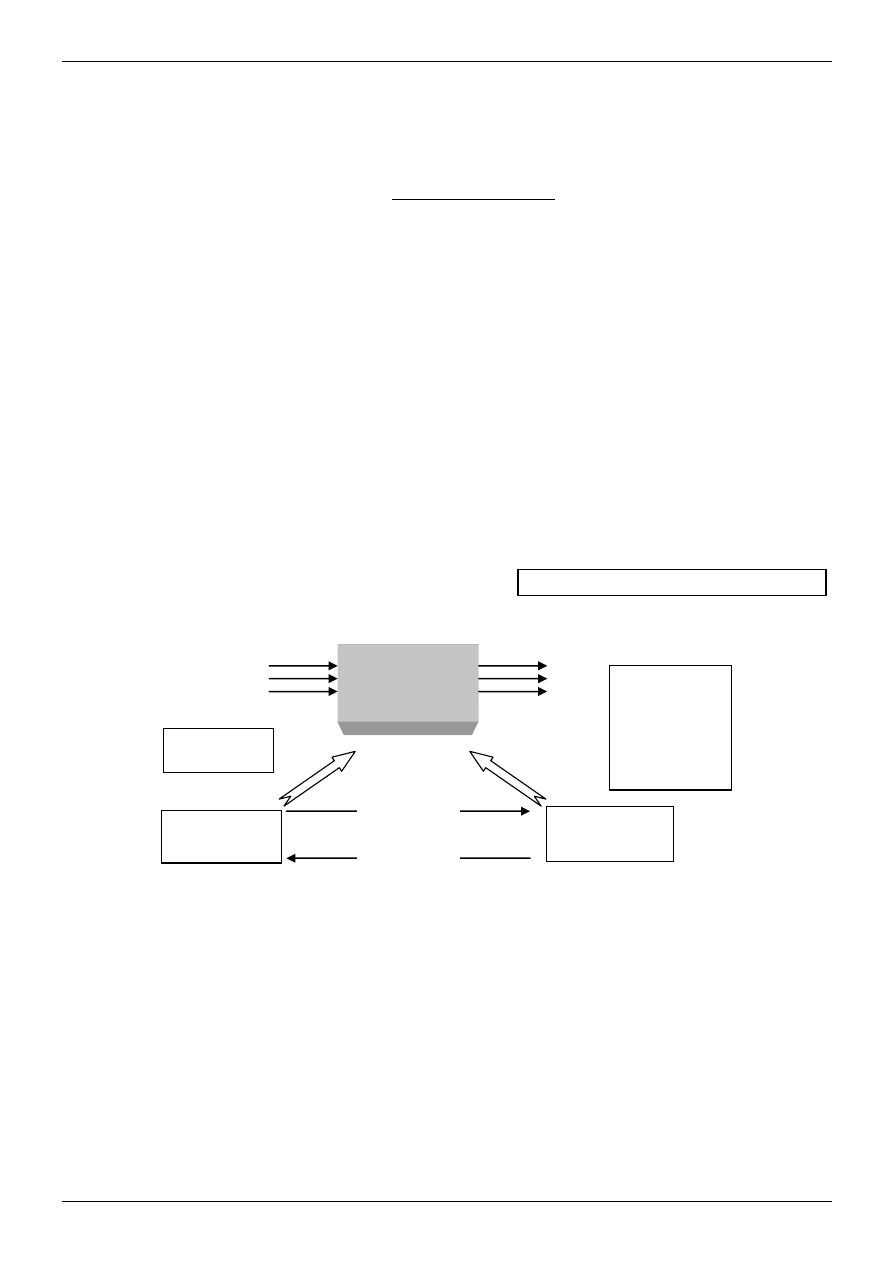
Narysuj schemat blokowy dla opisu w przestrzeni stanu.

5.

Wyznacz charakterystyki dynamiczne układu sterowania w odpowiedzi na skok jednostkowy
dla zerowych x

0

= [0, 0, 0]

T

i niezerowych warunków początkowych, np. x

0

= [0.5, 0, 1]

T

.

6.

Wyznacz opis układu w przestrzeni stanu w różnych (równoważnych) postaciach:

[Am,Bm,Cm,Dm,Tm]=canon(A,B,C,D,'modal'),
[An,Bn,Cn,Dn,Tn]=canon(A,B,C,D,'companion')

.

7.

Wyznacz opis układu w nowym układzie współrzędnych po zastosowaniu liniowej transformacji
w postaci:

8.

Zbadaj sterowalność i obserwowalność układu.

Listing m-pliku

echo on,
clc, clear, close all
%-------------------------------------
% transmitancja G(s) - wektory współczynników
numG = [2, 0, 8];
denG = [1, 8.2, 18.4, 12];
sysG = tf(numG,denG) %printsys(numG,denG)
pause
%-------------------------------------
% funkcja tf2ss() => forma sterowalna
[Ac,Bc,Cc,Dc] = tf2ss(numG,denG)
pause
%-------------------------------------
% funkcja ss2tf()
[numGc,denGc] = ss2tf(Ac,Bc,Cc,Dc),
pause
%-------------------------------------
sysGc = tf(numGc,denGc) %printsys(numG,denG)
pause
%-------------------------------------

% ZAOKRĄGLENIE
% numGc=roundaf(numGc); denGc=roundaf(denGc)
% sysGc = tf(numGc,denGc), pause
%-------------------------------------
% model przestrzeni stanu
sysc = ss(Ac,Bc,Cc,Dc), pause
%-------------------------------------
% funkcja eig() - wartości własne macierzy A
eigAc = eig(Ac)
[Mww,Mdiag] = eig(Ac) % Ac*Mww = Mww*Mdiag
pause
%-------------------------------------
% funkcja tf2zp() - zera, bieguny
[z,b,w] = tf2zp(numG,denG)
[zGc,bGc,wGc] = tf2zp(numGc,denGc), pause
%-------------------------------------
% funkcja ss2zp() - zera, bieguny
[zss,bss,wss] = ss2zp(Ac,Bc,Cc,Dc), pause
%-------------------------------------

D

D

P

C

C

B

P

B

P

A

P

A

z

z

1

z

1

z





















obiekt

sterowania

y

i

u

i

u

D

x

C

y

u

B

x

A

x



















u

D

z

C

y

u

B

z

A

z

z

z

z

z



















z

P

x

x

P

z

1











1





P

T

Tm, Tn – MACIERZE TRANSFORMACJI