
1
Wykład 8
Ruch harmoniczny
Ruch harmoniczny
Wrocław University of Technology
07-I-2012
2
Spr
ęż
ysto
ść
Ruch harmoniczny
07.I.2012
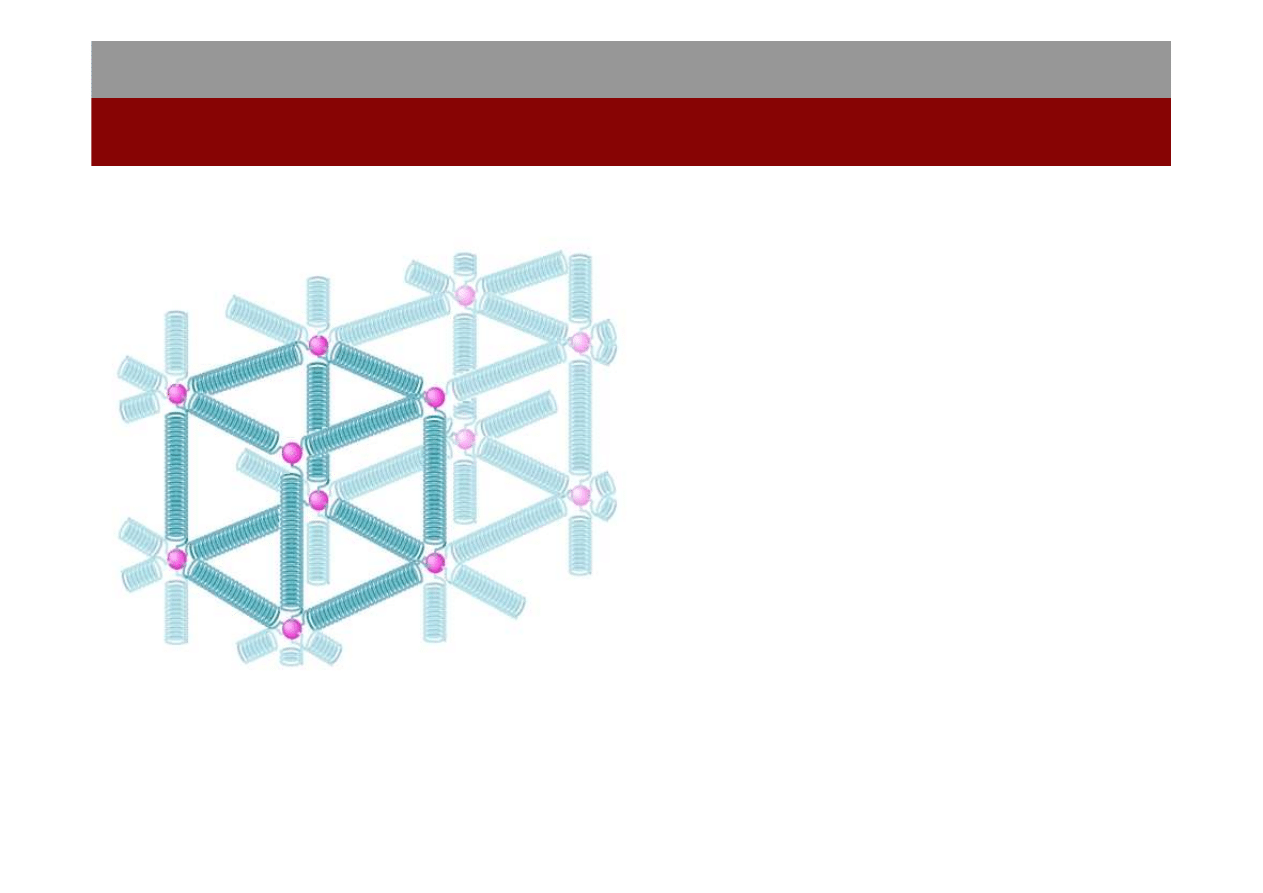
Gdy duża liczba atomów znajduje się
bardzo blisko siebie, atomy zajmują
położenia równowagi w trójwymiarowej
sieci. Atomy znajdują się blisko siebie
dzięki występującym między nimi siłom
międzyatomowym. Działają one tak, jak
gdyby atomy połączone były małymi
sprężynkami, jak na rysunku obok. Sieć
jest niezwykle sztywna, co oznacza,
ż
e te „międzyatomowe sprężynki" są
bardzo mocne.
3
Spr
ęż
ysto
ść
Ruch harmoniczny
07.I.2012
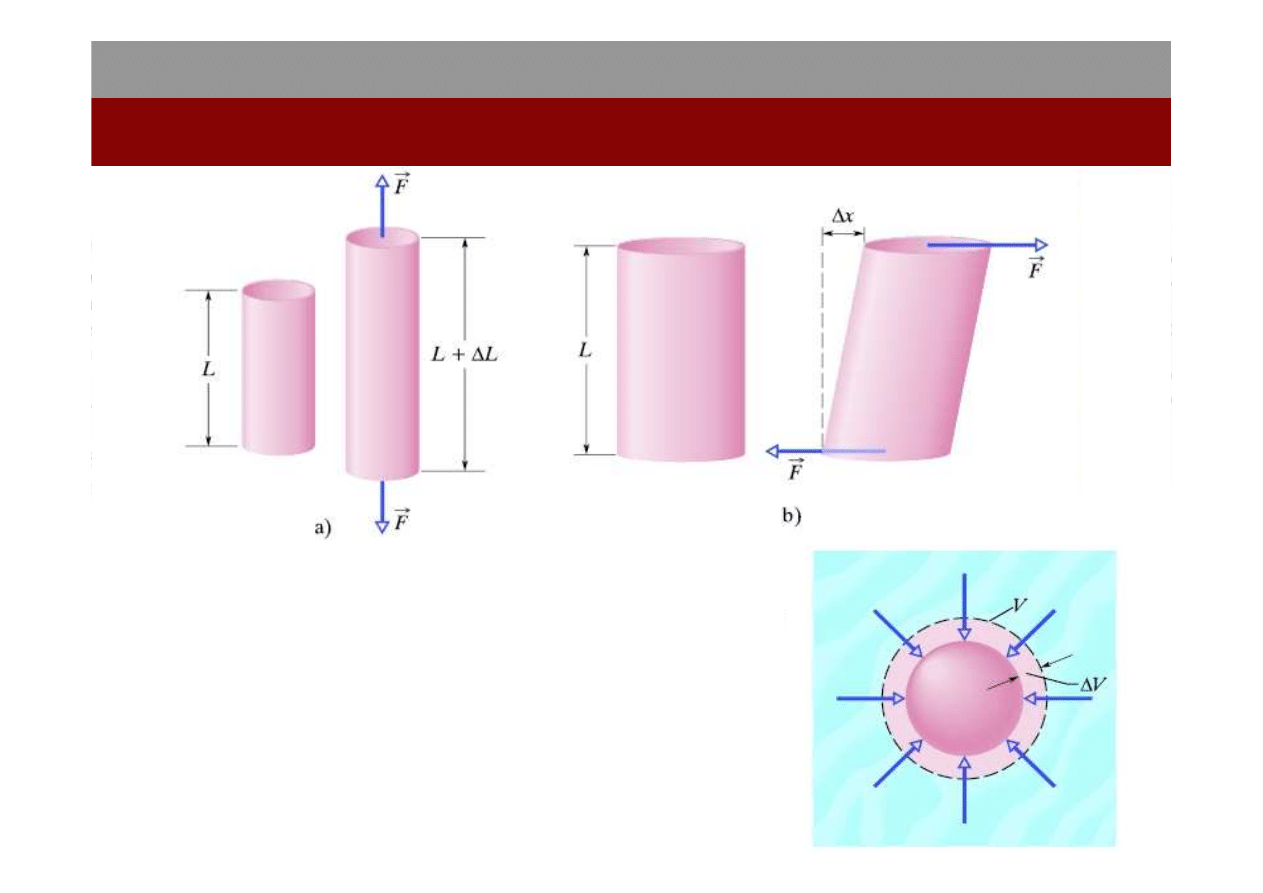
Wszystkie rzeczywiste ciała „sztywne" są w
jakimś stopniu sprężyste, co oznacza, że
można nieznacznie zmienić ich rozmiary,
rozciągając je, ściskając lub skręcając.
4
Prawo Hooke’a
Ruch harmoniczny
07.I.2012
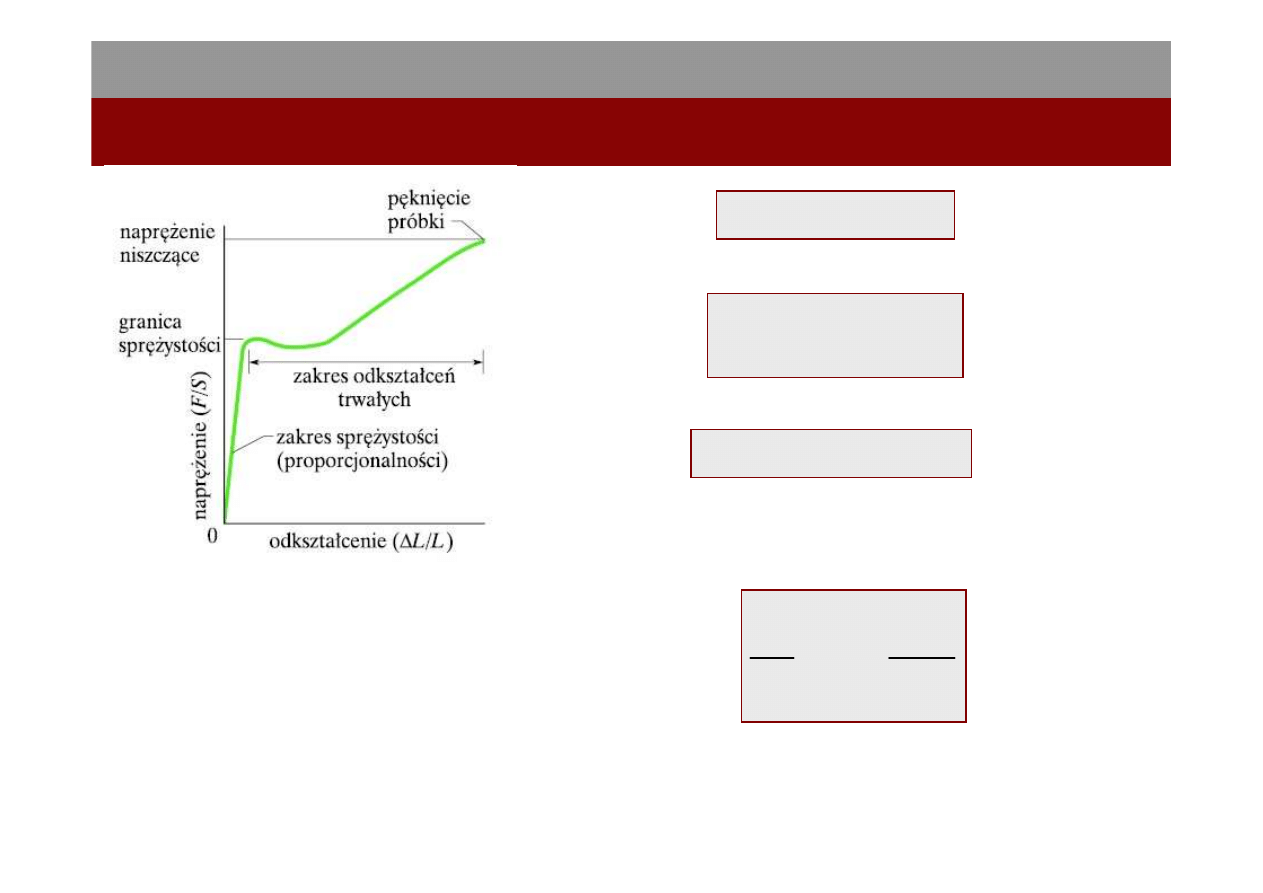
Zależność odkształcenia od naprężenia dla
próbki ze stali. Próbka ulega odkształceniu
trwałemu po przekroczeniu przez naprężenie
granicy sprężystości materiału. Próbka pęka
po osiągnięciu przez naprężenie wartości
odpowiadającej naprężeniu niszczącemu dla
badanego materiału.
NAPRĘśENIE
=
MODUŁ
SPRĘśYSTOŚCI
x
ODKSZTAŁCENIE
L
L
E
S
F
∆
=
5
Ruch harmoniczny
Ruch harmoniczny
07.I.2012
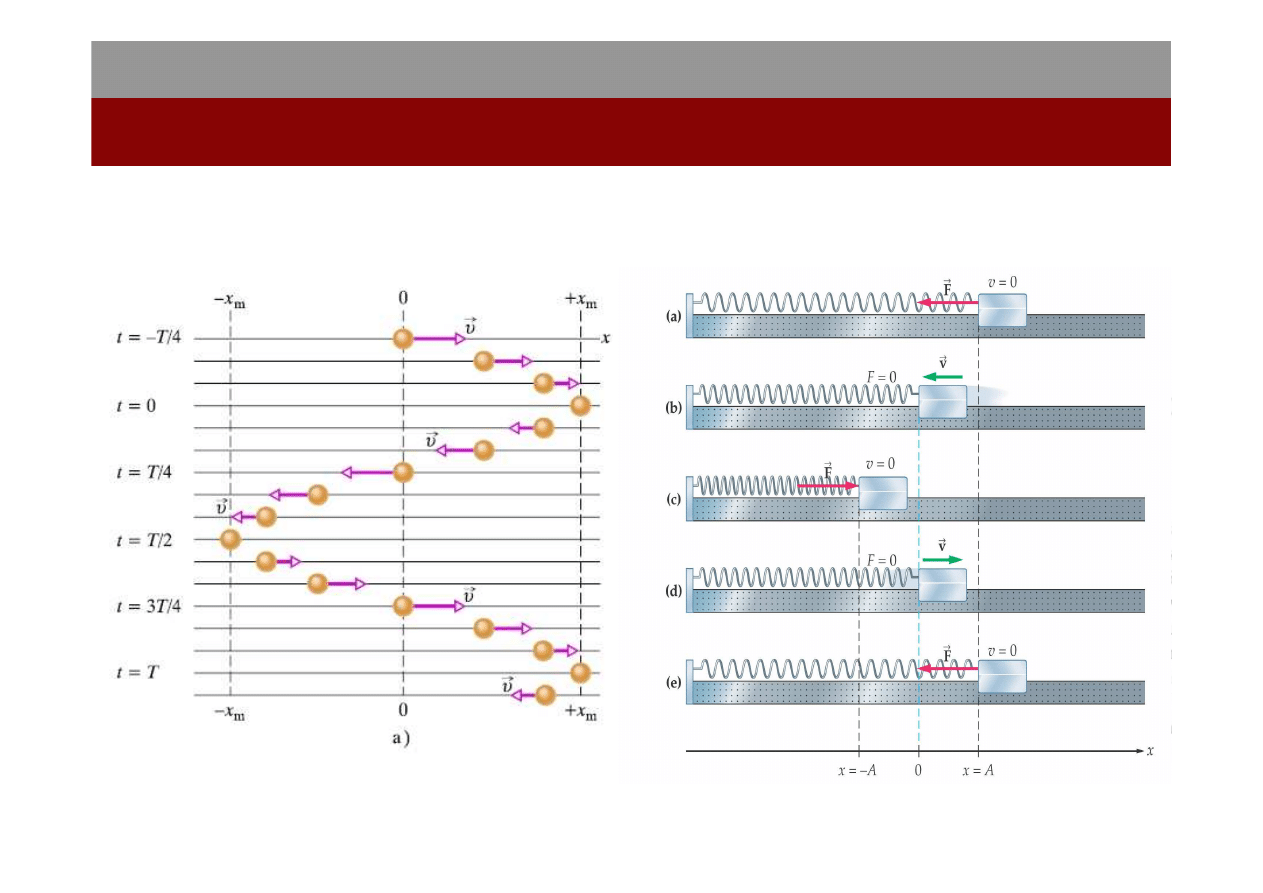
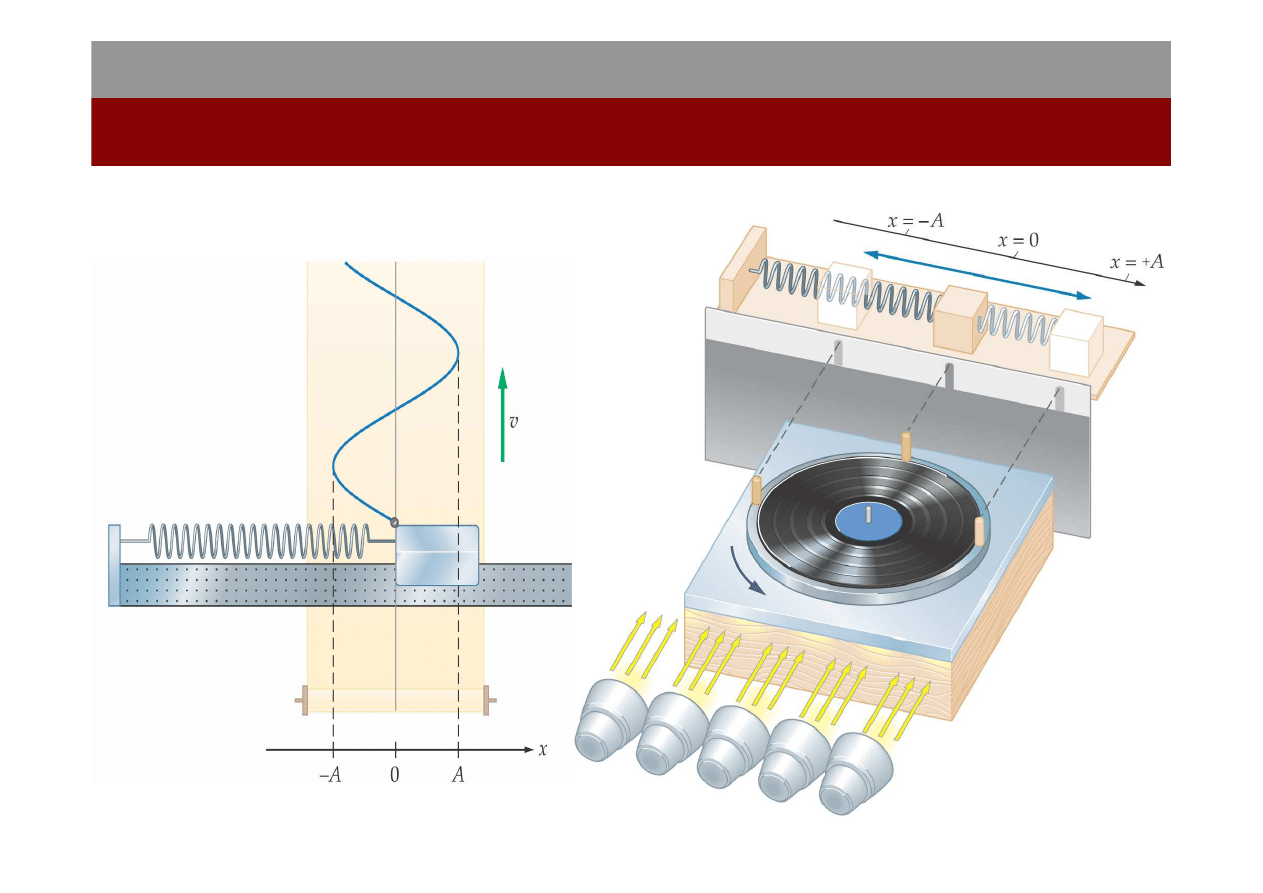
Każdy ruch powtarzający się w regularnych odstępach czasu nazywamy
ruchem okresowym.
6
Ruch harmoniczny
Ruch harmoniczny
07.I.2012
7
Ruch harmoniczny
Ruch harmoniczny
07.I.2012
W ruchu harmonicznym zależność przemieszczenia x ciała względem
początku układu współrzędnych od czasu opisana jest wzorem:
gdzie:
x(t) – przemieszczenie w chwili czasu t,
A – amplituda,
ω
– częstość ko
ł
owa,
t – czas,
Φ – faza początkowa.
(
)
Φ
+
=
t
A
t
x
ω
cos
)
(
8
Ruch harmoniczny
Ruch harmoniczny
07.I.2012
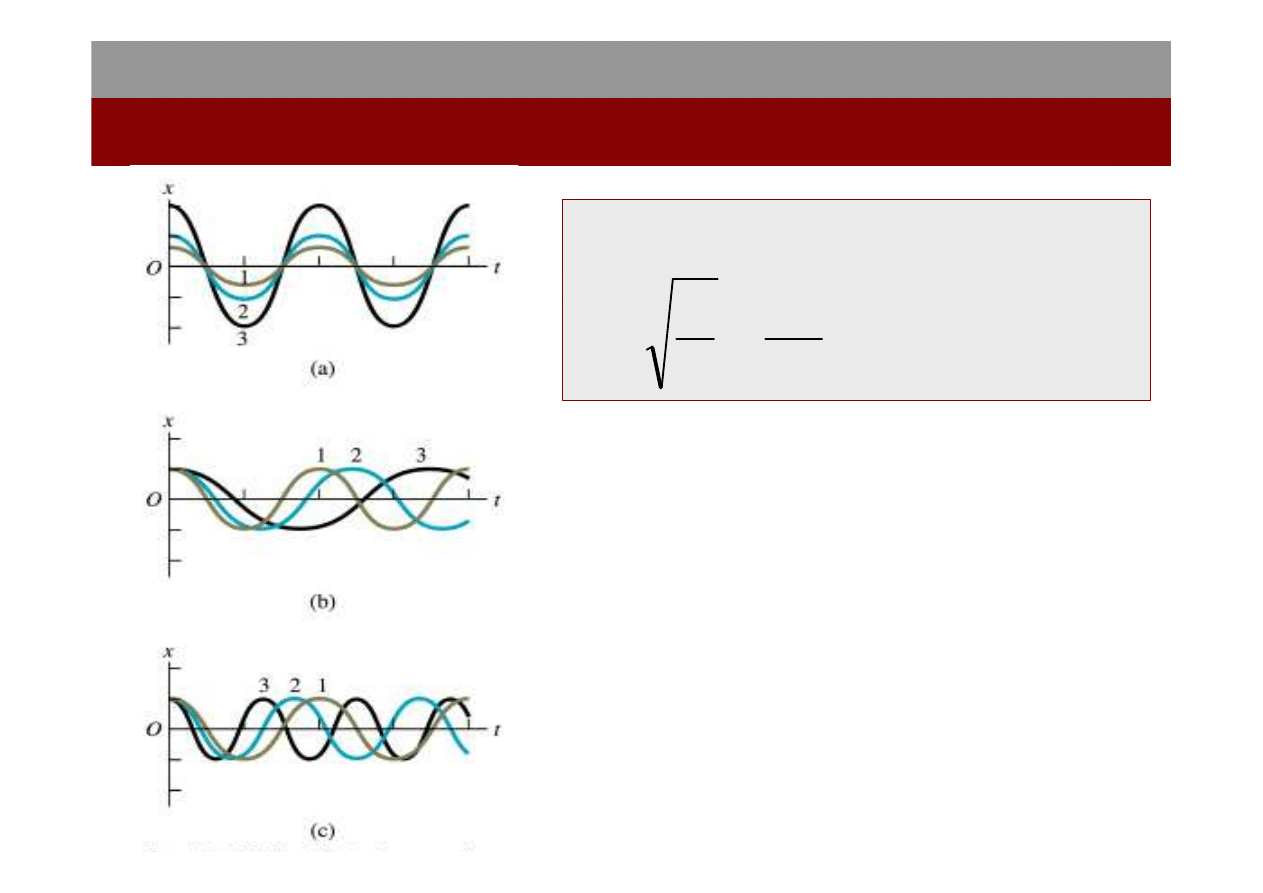
• (a) zmienia się A : stałe T
• (b) większe m : większe T
• (c) większe k : mniejsze T
T
m
k
t
A
t
x
π
ω
ω
2
0
)
cos(
)
(
0
0
=
=
=
Φ
Φ
+
=
9
Ruch harmoniczny
)
cos(
)
(
t
A
t
x
ω
=
)
sin(
)
(
)
(
t
A
dt
t
dx
t
v
ω
ω
−
=
=
Ruch harmoniczny
07.I.2012
)
cos(
)
(
)
(
2
t
A
dt
t
dv
t
a
ω
ω
−
=
=
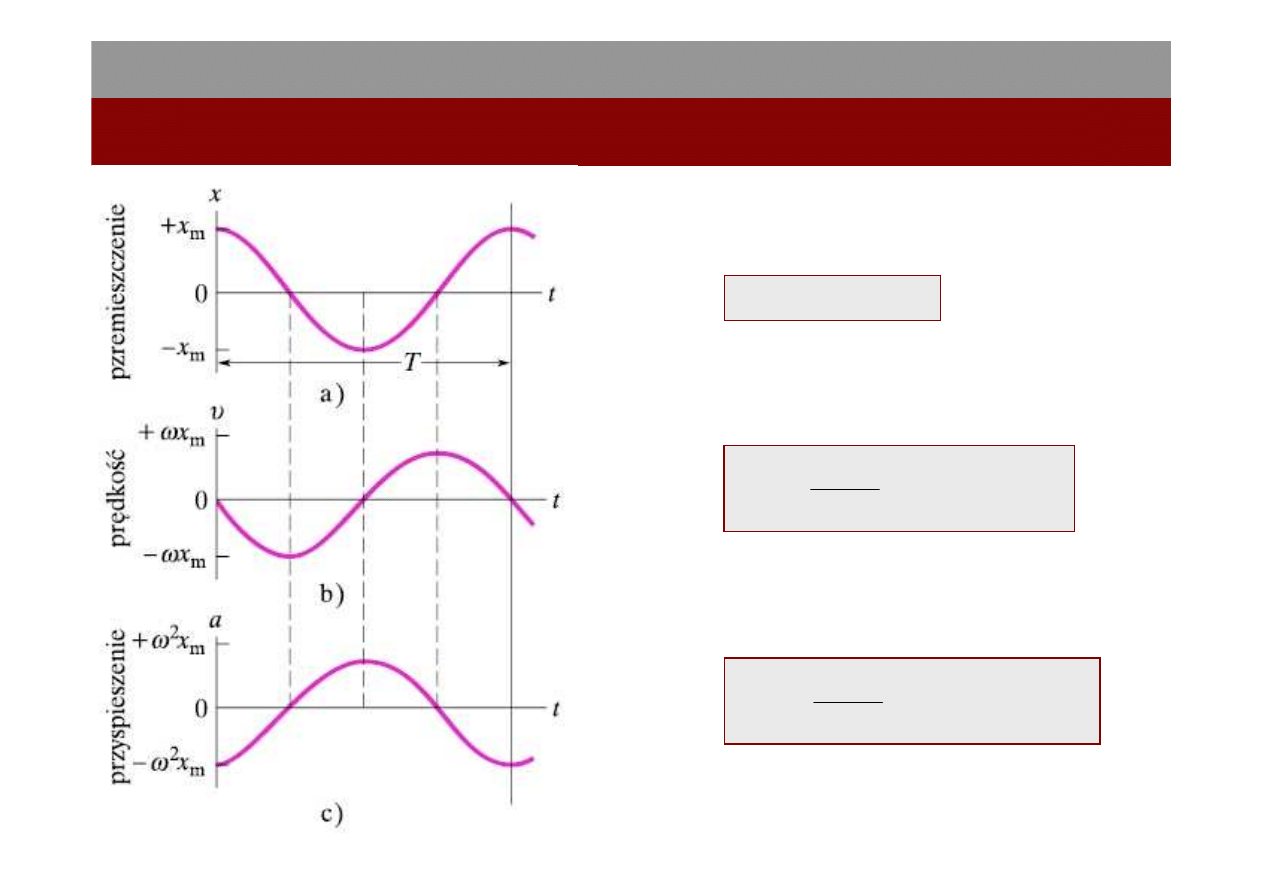
Przemieszczenie
Prędkość
Przyspieszenie
10
Ruch harmoniczny
Ruch harmoniczny
07.I.2012
4
3
42
1
)
(
2
)
cos(
)
(
)
(
t
x
t
A
dt
t
dv
t
a
ω
ω
−
=
=
)
(
)
(
2
t
x
t
a
ω
−
=
W ruchu harmonicznym przyspieszenie jest proporcjonalne do przemieszczenia,
ale ma przeciwny znak, przy czym łączący obie wielkości współczynnik
proporcjonalności równy jest kwadratowi częstości kołowej.

11
Siła w ruchu harmonicznym
Ruch harmoniczny
07.I.2012
Z drugiej zasady dynamiki Newtona
(
)
x
m
ma
F
2
ω
−
=
=
Z drugiej strony wiemy, że
kx
F
−
=
Stąd
x
k
2
ω
=
Ruch harmoniczny jest to ruch, jaki wykonuje ciało o masie m, na które działa
siła proporcjonalna do przemieszczenia, ale o przeciwnym znaku.

12
Ruch harmoniczny
(
)
x
m
ma
2
ω
−
=
Ruch harmoniczny
07.I.2012
x
m
k
dt
x
d
−
=
2
2
(rad/s)
m
k
=
ω
Rozwiązanie
)
cos(
)
(
φ
ω
+
=
t
A
t
x
A
x
x
A
x
0
0
arccos
,
cos
)
0
(
=
=
=
φ
φ
A
f
T
f
,
/
1
,
2
/
=
=
π
ω
Cz
ę
sto
ść
[Hz]
Okres [s]
Amplituda
13
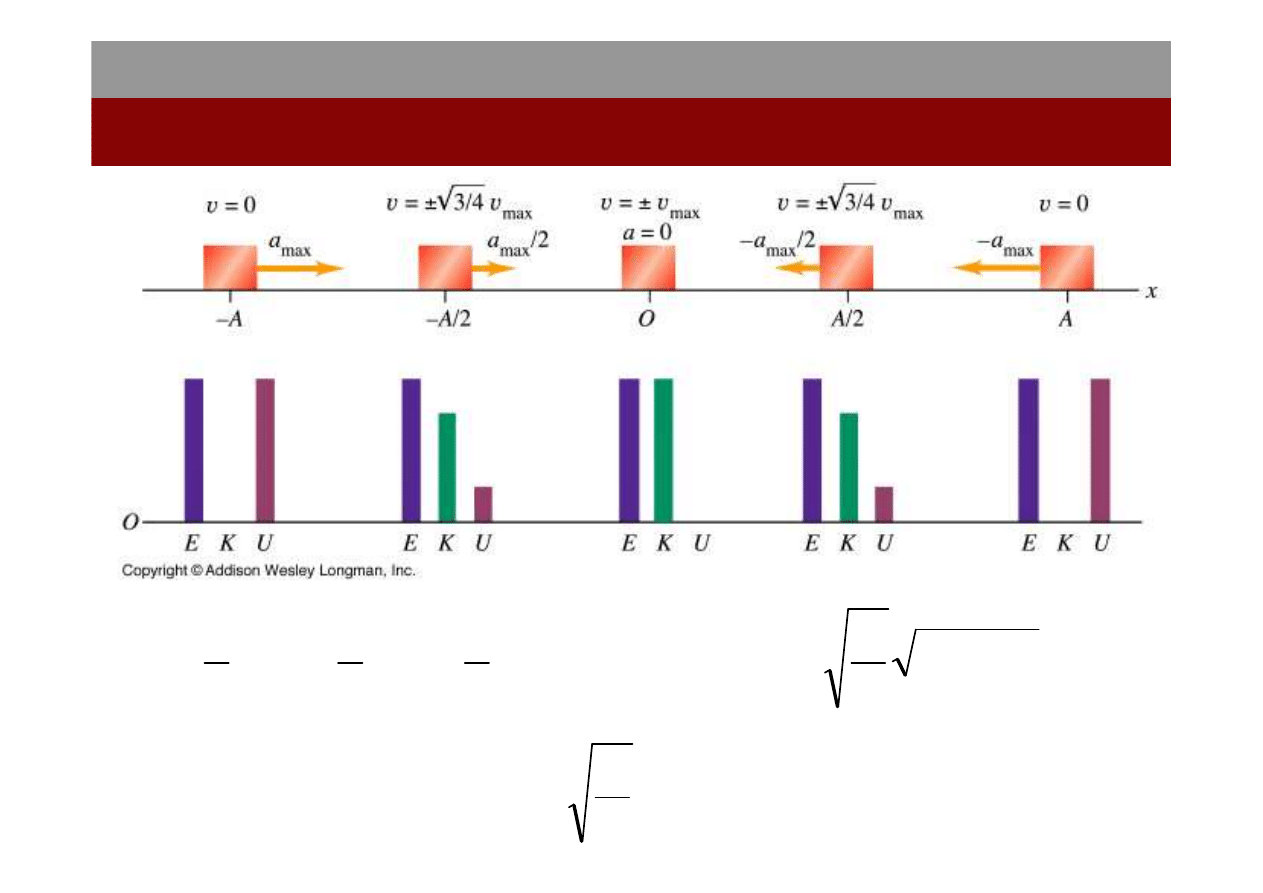
Energia w ruchu harmonicznym
Ruch harmoniczny
07.I.2012
(
)
Φ
+
=
=
t
kA
kx
E
p
ω
2
2
2
cos
2
1
2
1
Energia potencjalna
Energia kinetyczna
(
)
Φ
+
=
=
t
kA
mv
E
k
ω
2
2
2
sin
2
1
2
1
Energia mechaniczna
(
)
(
)
(
)
(
)
(
)
2
2
2
2
2
2
2
2
2
1
sin
cos
2
1
sin
2
1
cos
2
1
kA
t
t
kA
t
kA
t
kA
E
E
k
p
=
Φ
+
+
Φ
+
=
=
Φ
+
+
Φ
+
=
+
ω
ω
ω
ω
14
Energia w ruchu harmonicznym
Ruch harmoniczny
07.I.2012
2
2
2
2
2
2
1
2
1
2
1
x
A
m
k
v
kA
kx
mv
−
±
=
⇒
=
+
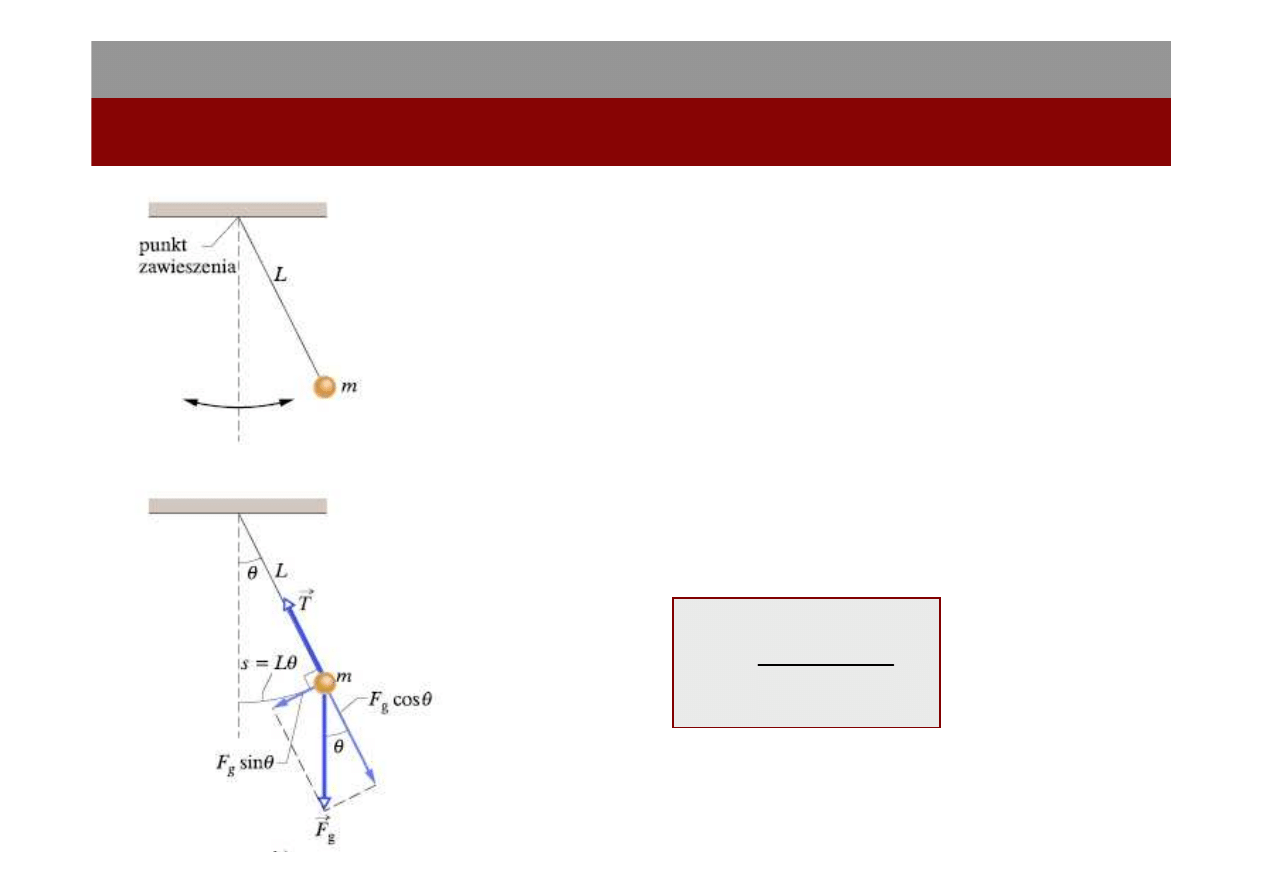
Energia mechaniczna ruchu harmonicznego jest stała, stąd
Prędkość maksymalna występuje dla x = 0 i wynosi:
A
A
m
k
v
ω
=
=
max
15
Wahadło matematyczne
Ruch harmoniczny
07.I.2012
(
)
θ
sin
g
F
L
F
r
M
−
=
×
=
Z drugiej zasady dynamiki Newtona
(
)
ε
θ
I
mg
L
=
−
sin
⇓
θ
ε
I
Lmg
−
=
16
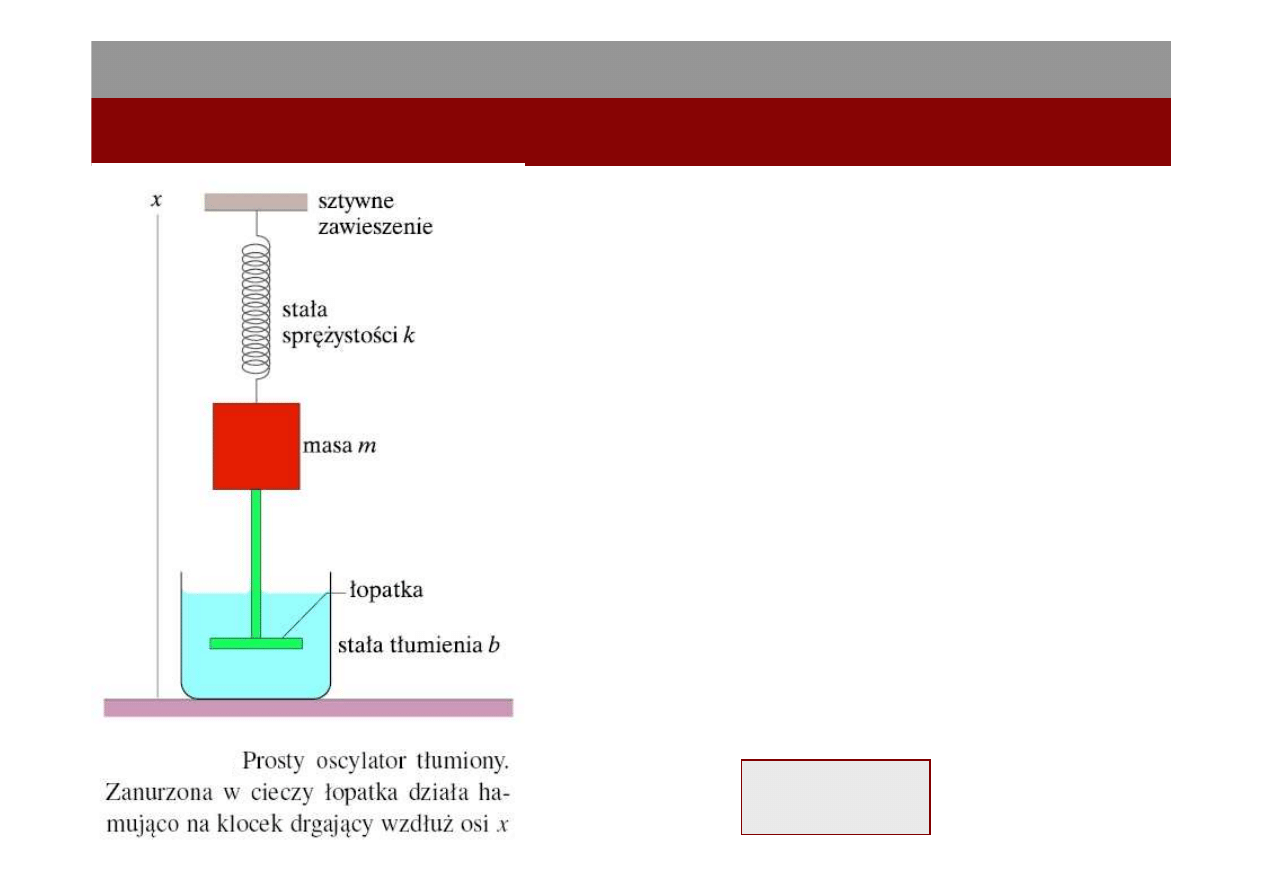
Ruch harmoniczny tłumiony
Ruch harmoniczny
07.I.2012
Prosty oscylator tłumiony - klocek o masie m drga
w pionie zawieszony na sprężynie o stałej
sprężystości k. Do klocka przyczepiony jest pręt
zakończony łopatką (zakładamy, że oba te
elementy mają znikomą masę) zanurzoną w
cieczy. Gdy łopatka porusza się w górę i w dół,
ciecz wywiera na nią (i w konsekwencji na cały
układ drgający) siłę oporu. Z upływem czasu
energia mechaniczna układu klocek-sprężyna
maleje — przekształca się w energię termiczną
cieczy i łopatki.
Siła oporu F
0
, jaką działa ciecz, jest proporcjonalna
do wartości prędkości v łopatki i klocka (takie
założenie jest poprawne, gdy łopatka porusza się
powoli):
bv
F
−
=
0
17
Ruch harmoniczny tłumiony dE/dt<0
Ruch harmoniczny
07.I.2012
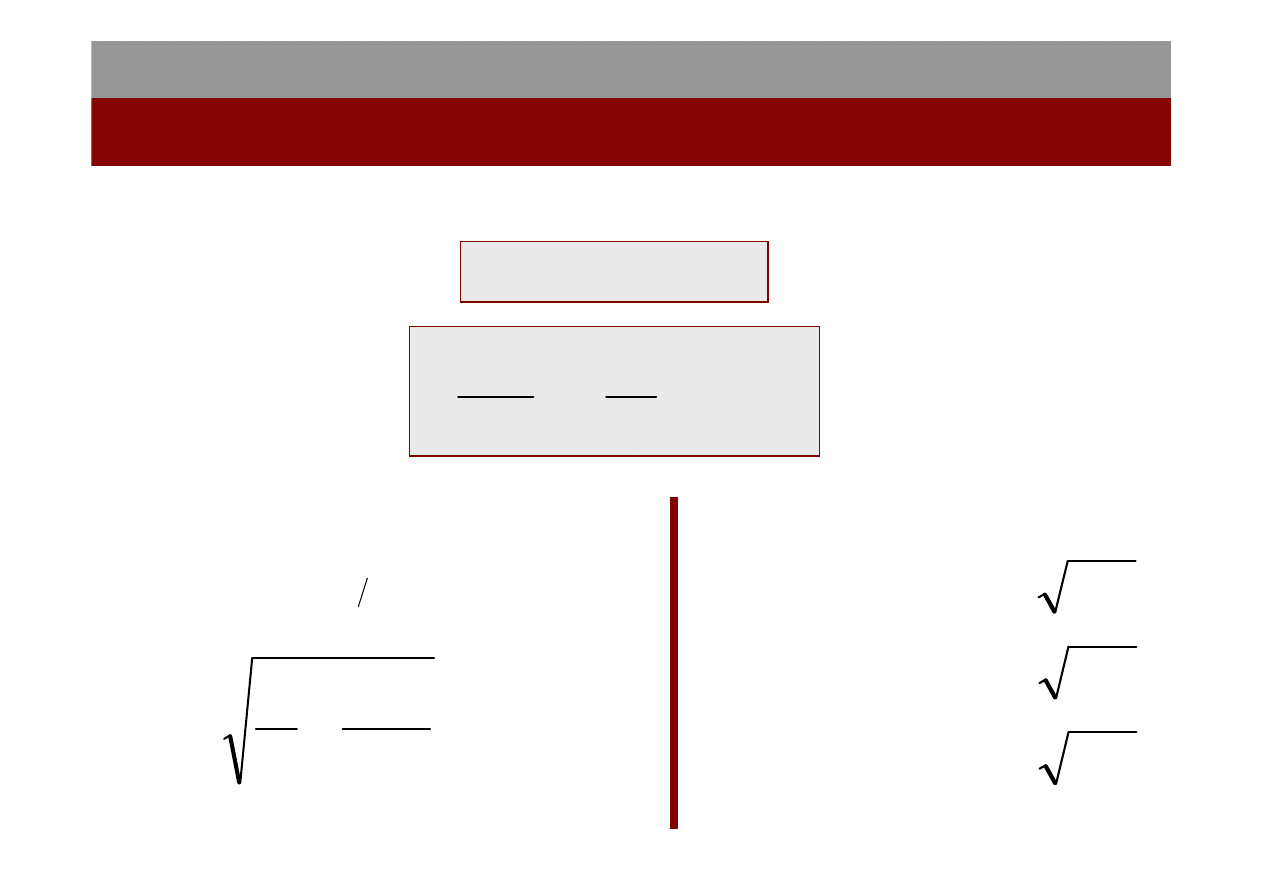
Równanie ruchu harmonicznego tłumionego wynikające z prawa Newtona
przyjmuje postać:
ma
kx
bv
=
−
−
0
2
2
=
+
+
kx
dt
dx
b
dt
x
d
m
Rozwiązanie tego równania ma postać:
(
)
2
2
2
4
'
'
cos
)
(
m
b
m
k
t
Ae
t
x
m
bt
−
=
Φ
+
=
−
ω
ω
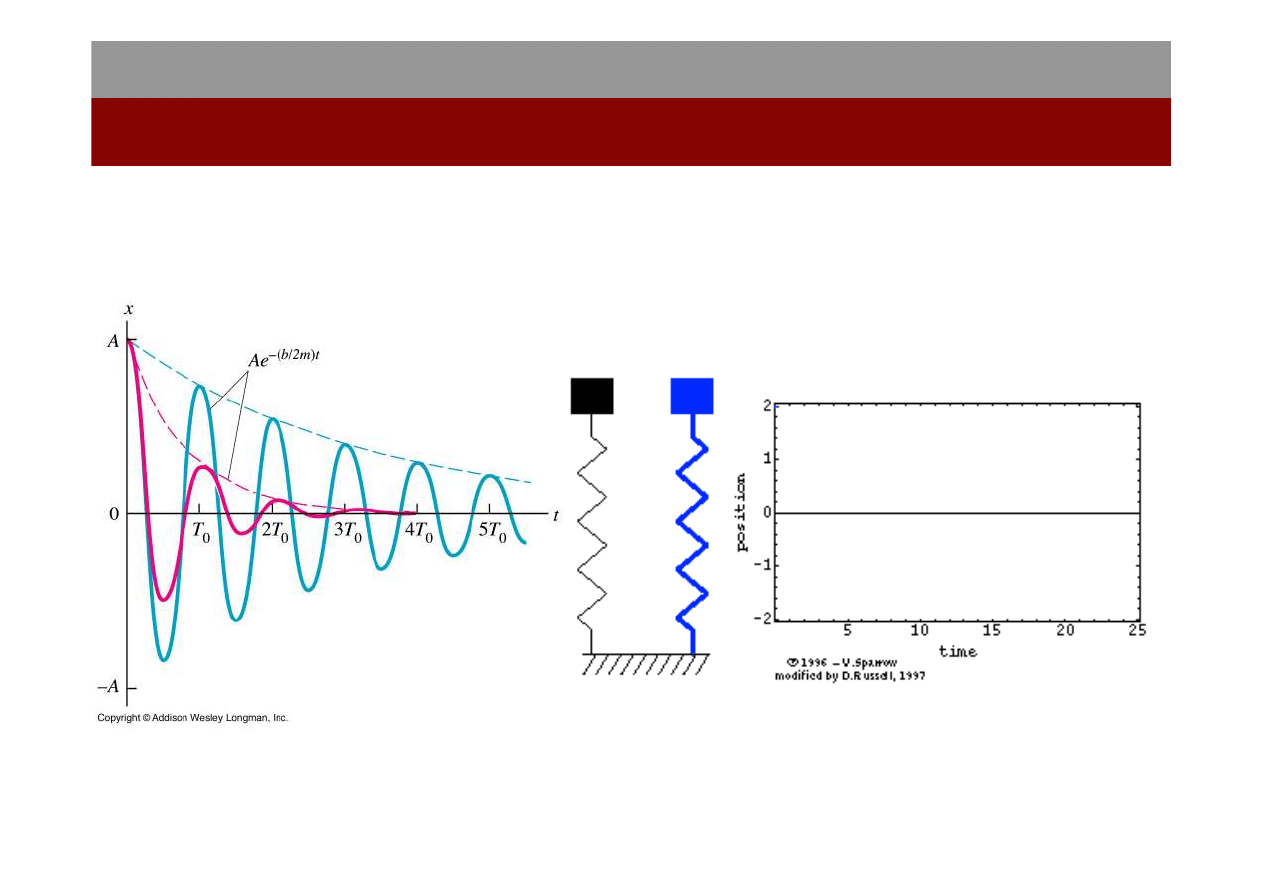
Rodzaje tłumień:
- Małe
(niedotłumienie)
- Średnie
(tłumienie krytyczne)
- Duże
(przetłumienie)
mk
b
mk
b
mk
b
>
=
<
18
Ruch harmoniczny tłumiony
Ruch harmoniczny
07.I.2012
19
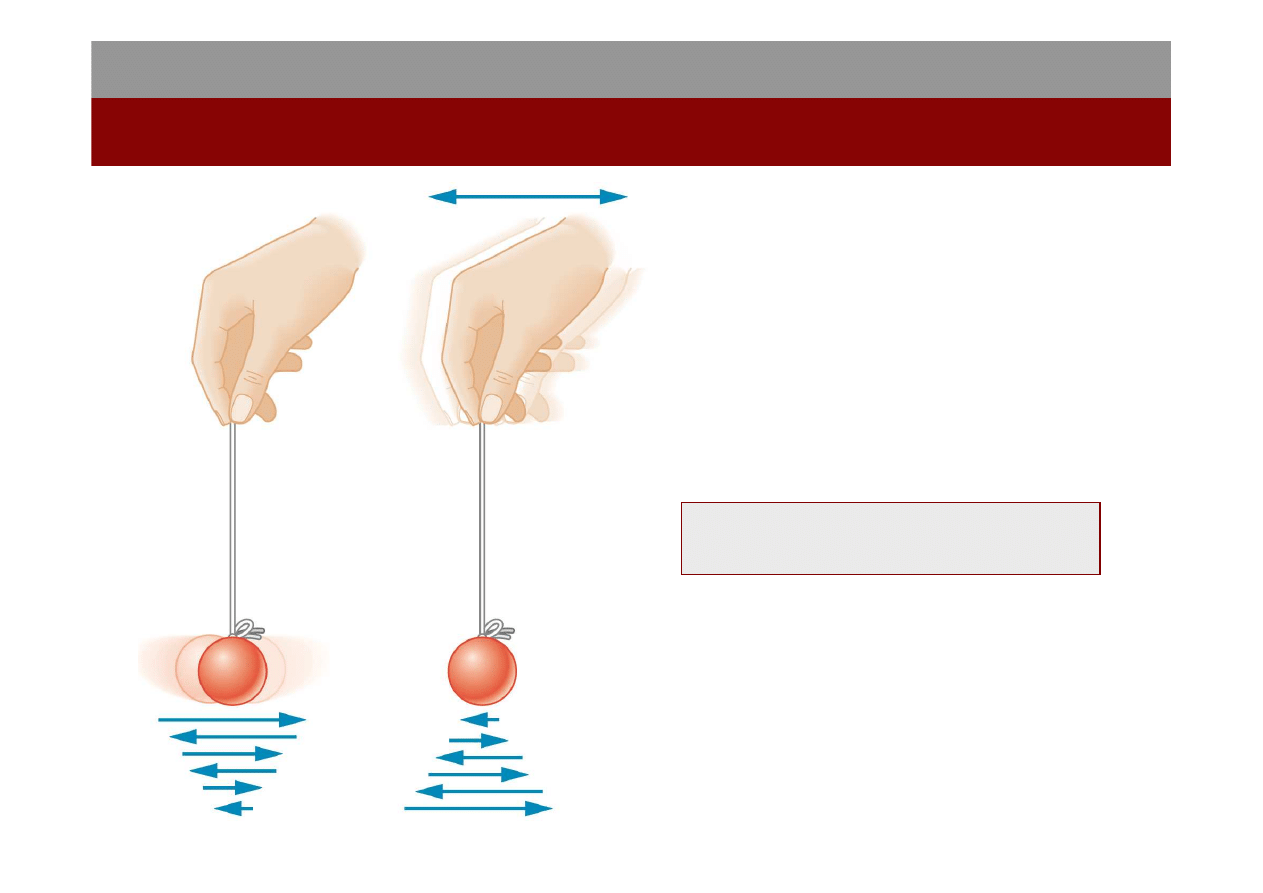
Drgania wymuszone
Ruch harmoniczny
07.I.2012
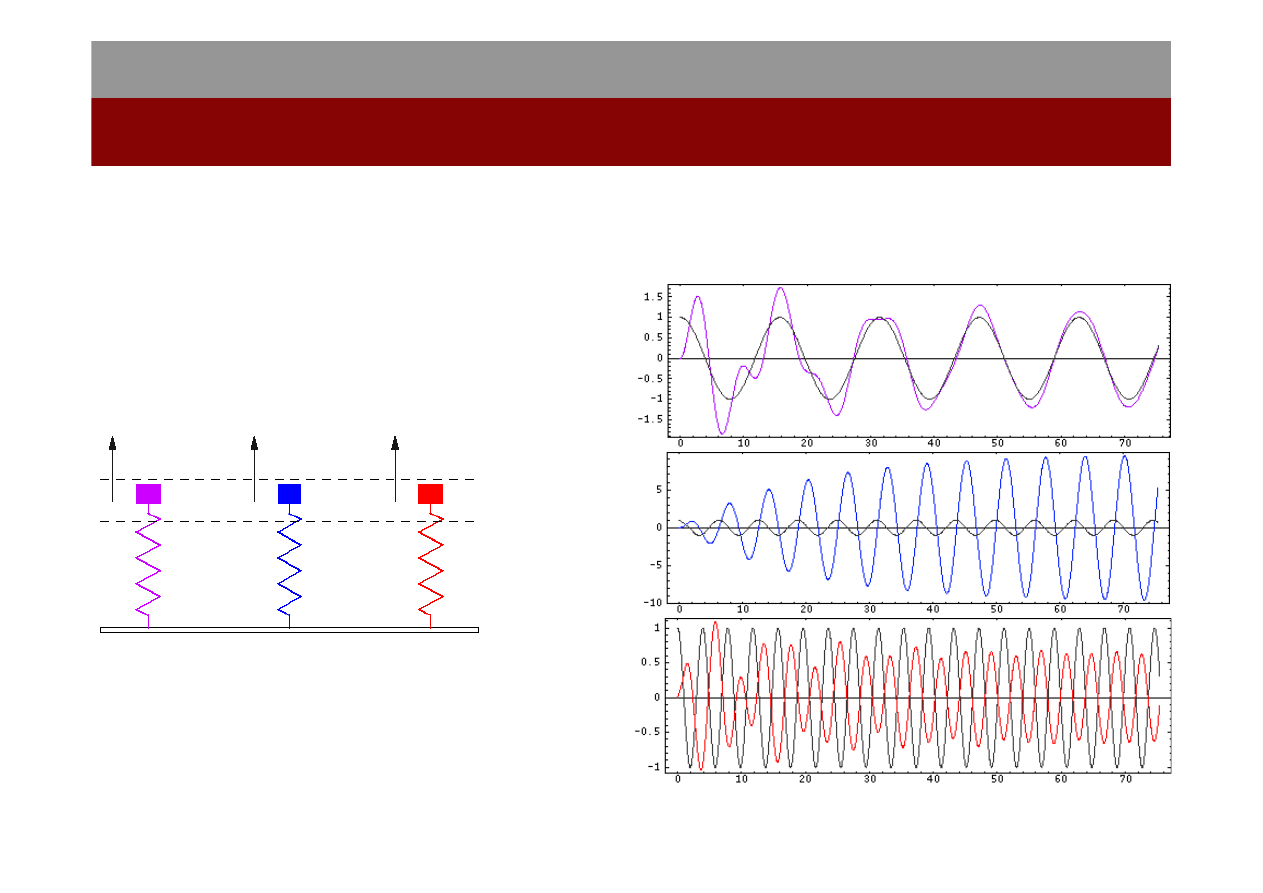
Taki oscylator wymuszony drga
z częstością kołową ω
wym
siły
wymuszającej, a jego
przemieszczenie x(t) dane jest
wzorem:
)
cos(
)
(
Φ
+
=
t
A
t
x
wym
ω
20
Drgania wymuszone
Ruch harmoniczny
07.I.2012
Kiedy periodycznie zmieniająca się siła wymuszająca o częstości kołowej ω
wym
jest przyłożona do harmonicznego oscylatora tłumionego, w rezultacie powstają
drgania wymuszone.
)
cos(
F
F
wym
max
wym
t
ω
=
ω
wym
=
0.4ω
ω
wym
=
1.01ω
ω
wym
=
1.6ω
By Dr. Dan Russell, Kettering University
Siła wymuszająca:
21
Drgania wymuszone
Ruch harmoniczny
07.I.2012
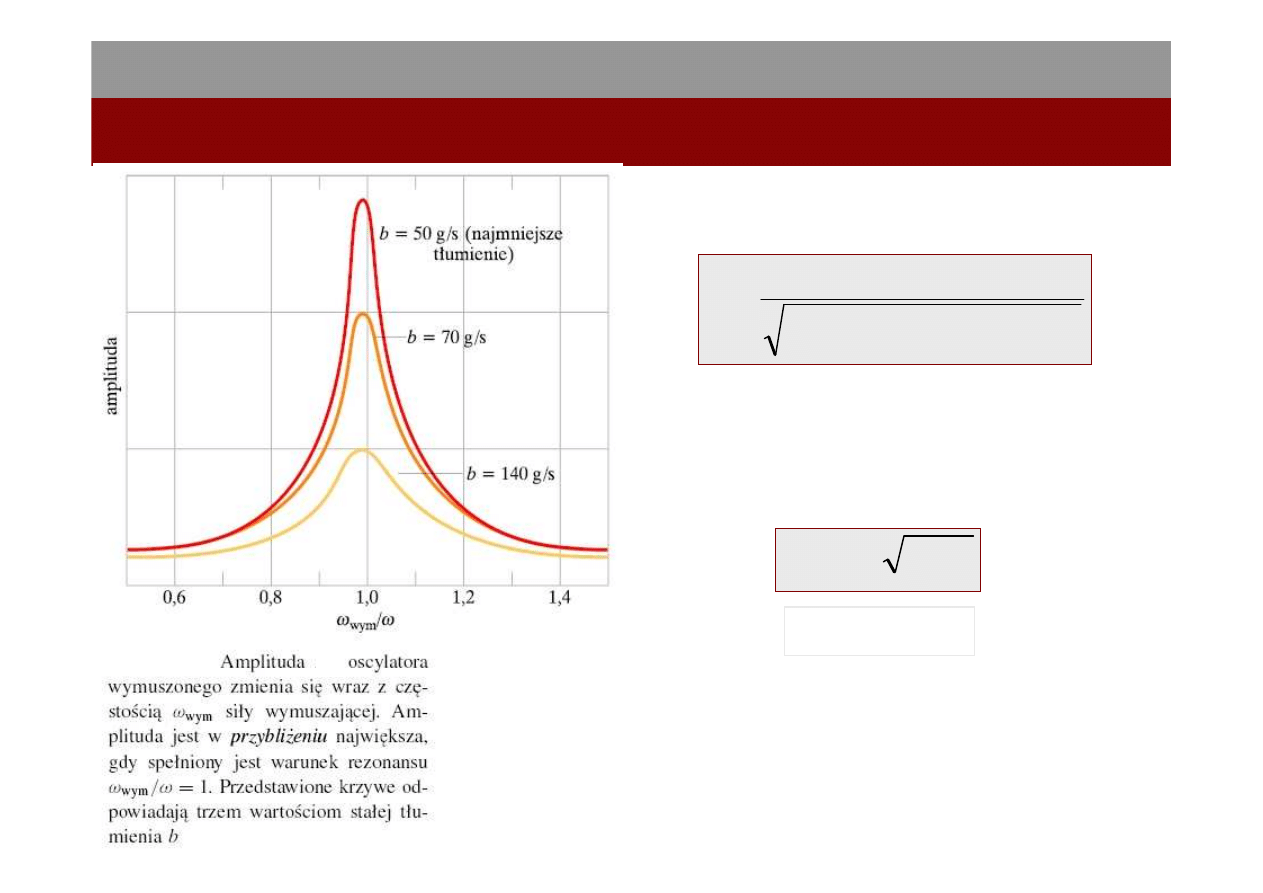
Amplituda drgań wymuszonych:
2
2
2
2
max
)
(
wym
wym
b
m
k
F
A
ω
ω
+
−
=
A
Kiedy
wtedy A przyjmuje maksimum w
2
wym
m
k
ω
=
m
k
wym
/
=
ω
REZONANS
Wyszukiwarka
Podobne podstrony:
K4 L8
L8 kalkulacja współczynnikowa xlsx
L8
pattern, wisisz, wydzial informatyki, studia zaoczne inzynierskie, podstawy programowania, l8
M6 Engine Workshop Manual L8 LF L3 1 (2)
l8 (4)
l8(3)
L8
zpdots, wisisz, wydzial informatyki, studia zaoczne inzynierskie, podstawy programowania, l8
L8, Studia Odlewnictwo inż, Materiały Inżynierskie
ulamki, wisisz, wydzial informatyki, studia zaoczne inzynierskie, podstawy programowania, l8
ponadgim m3 L8
strukt~1, wisisz, wydzial informatyki, studia zaoczne inzynierskie, podstawy programowania, l8
szanow, wisisz, wydzial informatyki, studia zaoczne inzynierskie, podstawy programowania, l8
mod3, wisisz, wydzial informatyki, studia zaoczne inzynierskie, podstawy programowania, l8
zpdop, wisisz, wydzial informatyki, studia zaoczne inzynierskie, podstawy programowania, l8
kwadraty, wisisz, wydzial informatyki, studia zaoczne inzynierskie, podstawy programowania, l8
1 3 m2 L8
Zams Wrzyszcz L8
więcej podobnych podstron