POJĘCIE BAZY DANYCH
Czym jest baza danych?
•
pamięć trwała danych – duży zbiór zawierający istotne dane z punktu widzenia
użytkownika, te same dane mogą znajdować wiele zastosowań, mogą być wykorzystywane
przez wielu użytkowników
•
określona struktura i reguły integralności – zbiór danych jest zorganizowany zgodnie z
pewną strukturą wewnętrzną zgodą z wybranym modelem danych; struktura danych musi
pozwalać na reprezentowanie istotnych dla użytkownika cech charakterystycznych danych
za pomocą wybranych własności (wartości atrybutów); struktura bazy danych musi
zapewniać reprezentowanie powiązań (związków) pomiędzy danymi
(Zbiór danych zorganizowanych zgodnie z pojęciową strukturą opisującą charakterystyki tych
danych oraz związki między ich elementami, stosowany w jednym lub wielu zastosowaniach.)
Struktura bazy danych powinna umożliwiać:
•
niezawodność zapisu danych na zewnętrznym nośniku
•
integralność danych (spójność danych)
•
sprawność zapytań (selektywny dostęp do danych)
System zarządzania bazą danych (SZBD)
Z uwagi na specjalną strukturę zbioru bazy danych konieczny jest SZBD do jej obsługi. System
Zarządzania Bazą Danych to odpowiednio zorganizowane, specjalistyczne oprogramowanie
narzędziowe pozwalające na realizację istotnych dla użytkownika operacji na danych. Podstawowe
operacje na danych obejmują:
•
wprowadzanie danych
•
zapamiętywanie i przechowywanie danych
•
wyszukiwanie i prezentację danych
•
aktualizację danych
•
przetwarzanie arytmetyczne, statystyczne, algebraiczne i logiczne
•
operacje teoriomnogościowe na danych i operacje algebry relacji
•
kodowanie i dekodowanie danych
Do zadań SZBD należy:
•
umożliwienie projektowania i implementacji nowej bazy danych przy użyciu narzędzi i
języka definicji danych (z ang. Data Definition Language – DDL)(CREATE TABLE;
ALTER TABLE; DROP TABLE)
•
umożliwienie selektywnego dostępu do danych za pomocą języka zapytań i tworzonych w
nim kwerend (SELECT)
•
umożliwienie wykonywania określonych operacji na danych przy pomocy języka
operowania na danych ( ang. Data Manipulation Language- DML) (INSERT, UPDATE;
DELETE)
•
obsługa przechowywania dużych zbiorów danych, zapewnienie niezawodności oraz
efektywności
•
zapewnienie integralności ( spójności) danych
•
ochrona dostępu do danych, zapewnienie różnych obszarów i poziomów dostępu
(przypisywanie uprawnień użytkownikom, hasła)
•
zapewnienie dostępu dla wielu użytkowników (wielodostęp) oraz synchronizacja dostępu w
przypadku dostępu współbieżnego
•
zapewnienie możliwości komunikacji z innymi systemami (import, eksport danych)
•
optymalizacja pracy (m.in. wykonywanie zapytań w sposób jak najbardziej efektywny)
•
dostęp przez sieć (klient-serwer)
•
zarządzanie transakcjami
Najbardziej rozpowszechnione SZBD to : ORACLE, MS SQL SERWER , DB2, SYSBASE,
PostgreSQL, MySQL, Firebird, ACCESS.
Przykładowe zastosowania baz danych
•
systemy finansowo-księgowe
•
systemy płacowe
•
systemy kadrowe
•
systemy bankowe
•
systemy magazyn – sprzedaż
•
system ZUS- Płatnik
•
system obsługi bibliotek
•
systemy w firmach ubezpieczeniowych do rejestracji składek
•
systemy rezerwacji (np. lotniczej)
•
systemy wspomagające zarządzanie
•
CAD (Computer Aided Design)
•
GIS (Geographical Information Systems)
•
Ankiety (Firma mająca licznych agentów zbiera od klientów ankiety)
•
Parametry procesu technologicznego (System informatyczny przechowuje parametry
pewnego procesu technologicznego
•
Rozgłośnia radiowa (Rozgłośnia radiowa nadaje audycje na kilku programach. Układanie
programów ma wspomagać system informatyczny)
•
Kontrola zamówień (Firma wprowadza system kontroli obiegu wewnętrznych zamówień)
•
System nadzoru obsługi reklamacji
•
Oczyszczanie miasta
•
Baza dla nauczyciela – dziekanat
•
Firma remontowa- Firma remontowo-budowlana wykonuje typowe usługi składające się z
typowych czynności - system kosztorysujący
•
Rekrutacja -Wyższa uczelnia prowadzi nabór kandydatów na studia
•
Refundacja leków - Apteka musi, co miesiąc raportować do NFZ informację o sprzedaży
leków refundowanych.
•
Rejestracja hospitalizacji - Szpital rejestruje hospitalizacje dla celów rozliczenia z NFZ
•
Zakład opieki zdrowotnej - Zakład opieki zdrowotnej tworzy bazę danych do rejestracji
usług medycznych
Cele, jakie stawiane są bazą danych.
•
Umożliwienie pełnego dostępu do wszystkich danych; centralizacja – skupienie
danych w jednym systemie.
•
Zapewnienie łatwości wyszukiwania danych.
•
Zmniejszenie redundancji – nadmiarowości (powtórzeń)
•
Zachowanie spójności
•
Zapewnienie jednolitego formatu danych; ułatwienie wymiany danych i dostępu do
nich
•
Umożliwienie użytkowania tych samych danych przez wielu użytkowników-
wielodostęp
•
Umożliwienie użytkownikom korzystania z danych w dogodnej dla nich postaci
•
Umożliwienie jednoczesnego operowania na tych samych danych (blokowanie
dostępu; synchronizacja) – dostęp równoległy
Podział zadań w projektowaniu bazy danych
•
użytkownik -- odbiorca systemu (kierownicy, managerowie, dyrektorzy określają
przeznaczenie bazy danych i cele, jakim ma ona służyć)
•
analityk – bada własności danych (ustala charakterystyki danych), wykrywa zależności
między danymi
•
projektant – projektuje schemat bazy danych (tabele, relacje, zapytania, formularze,
raporty)
•
programista - tworzy przyjazny użytkownikowi dostęp do bazy danych
•
administrator bazy danych (zarządza dostępem do bazy danych i przydziela uprawnienia,
dba o bezpieczeństwo danych (replikacja, archiwizacja danych)
MODELE BAZ DANYCH
Model zewnętrzny
•
opisuje świat z punktu widzenia użytkowników bazy danych.
•
może istnieć wiele modeli zewnętrznych tej samej rzeczywistości
•
nie musi być związany z konkretnym modelem danych
Model pojęciowy (konceptualny)
•
tworzony przez analityków
•
opisuje świat w kategoriach konkretnego modelu danych
•
abstrahuje od szczegółów implementacji
•
odpowiada na pytanie "co?" a nie "jak?"
Model logiczny
•
tworzony przez projektantów bazy danych
•
opisuje projekt struktury w kontekście konkretnej implementacji
•
model struktury zgodny z modelem danych, a nie z ich fizyczną reprezentacją
•
może zawierać parametry dotyczące reprezentacji fizycznej
Reprezentacja fizyczna
•
tworzona przez SZBD
•
izolowana od aplikacji przez SZBD
•
zarządzana przez administratora
Modele danych
Model hierarchiczny
Cechy podstawowe
•
struktura danych ma postać drzewa (graf spójny bez cykli; graf, w którym każda krawędź
jest mostem)
•
węzły -- typy opisywanych obiektów
•
łuki -- związki typu ojciec-syn
•
drzewo jest uporządkowane, tj. na każdym poziomie kolejność węzłów jest określona
•
opis obiektu (rekord) zbudowany z pól zawierających dane opisujące obiekt
•
związki zrealizowane jako wskaźniki
Hierarchiczna struktura danych
Języki obsługi
•
o charakterze nawigacyjnym
•
operacje typu: GET LEFTMOST typ WHERE warunek ; GET NEXT typ
Ograniczenia
•
nie ma związków typu n-m (np. oddziały pomieszane w kilku budynkach)
•
tylko jeden rodzaj związku między dwoma typami obiektów
Znaczenie praktyczne
•
system IBM IMS (1978)
o
bardzo wielkie dane zgromadzone
o
poprzednik użyty w programie Apollo
•
nowych projektów nie robi się
Model sieciowy
Cechy podstawowe
•
struktura danych ma postać grafu (sieci)
•
wierzchołki grafu -- typy obiektów
•
łuki w grafie -- powiązania między typami
•
opis obiektu (rekord) zbudowany z pól zawierających dane opisujące obiekt
•
reprezentacja wiązań (wskaźniki):
•
rekordy powiązane stanowią kolekcję (set)
o
jeden rekord nadrzędny
o
wiele rekordów podrzędnych
•
kolekcja realizowana jako lista zamknięta
•
brak bezpośredniej reprezentacji
wiązań n-m
Języki obsługi
•
języki manipulowania -- nawigacyjne
•
CODASYL: język definiowania danych pozwala określić sposób automatycznego włączania
rekordów do kolekcji
Znaczenie praktyczne
•
system IDS (General Electric)
•
obecnie raczej nie używany
Model relacyjny
Cechy podstawowe
•
dane zawarte w tabelach
•
tabele składają się z kolumn
•
liczba kolumn i typy -- stałe
•
liczba wierszy zmienna
•
wiersze nie mają tożsamości innej niż wynikająca z zawartości kolumn
•
związki pomiędzy wierszami tabel -- zdefiniowane poprzez zależności między wartościami
wybranych kolumn, tzw. kluczy (nie ma wskaźników)
•
z punktu widzenia teorii model można opisać algebrą relacji między zbiorami atrybutów
Języki obsługi
•
nieproceduralne: SQL, Sequel, QUEL, QBE
•
proceduralne: xBase
Znaczenie praktyczne
•
model dominujący w zastosowaniach komercyjnych
•
przykłady SZBD: Oracle, Informix, Sybase, DB2, Progress, SQL Server, Firebird, Access,
dBase,
Realizacja relacyjna
Ograniczenia
•
brak bezpośredniej reprezentacji związków n-m
•
dla trudniejszych problemów -- bardzo wiele tabel
•
mało naturalna reprezentacja danych
•
ograniczona podatność na zmiany
•
trudne operowanie na złożonych obiektach -- dane rozproszone w wielu tabelach
•
brak złożonych typów danych
Historia:
•
1970 - E.F.Codd - podstawy relacyjnego modelu danych, rozprawa doktorska; „A relational
model for large shared data banks”
•
1968-1979 - opracowanie pierwszej wersji RMD, powstanie algebry relacyjnej
•
1970-… - IBM opracowuje prototyp relacyjnego SZBD o nazwie System/R, który później
przekształcił się w INGRES
•
1979 - Codd wprowadza rozszerzenia do podstawowego modelu relacyjnego RM/T
•
1980…- początek – dBase II firmy Ashton Tate
•
1983 - IBM, pierwsza baza danych DB2
Model obiektowy
Cechy podstawowe
•
obiekt w bazie reprezentuje obiekt w świecie zewnętrznym
•
typ obiektowy (klasa):
o
definicja złożonego typu danych (może zawierać inne typy obiektowe lub ich
kolekcje)
o
procedury (metody) i operatory do manipulowania tymi danymi
•
tożsamość obiektu jest niezależna od zawartości danych
•
dziedziczenie (inheritance):
o
strukturalne: potomek dziedziczy strukturę danych
o
behawioralne: potomek dziedziczy metody i operatory
Cechy dodatkowe
•
enkapsulacja: wnętrze obiektu dostępne jedynie w sposób w nim zdefiniowany
•
polimorfizm: tak samo nazwane metody i operatory działają swoiście w zależności od klasy
obiektu
Model obiektowy -- zawieranie i dziedziczenie
Zalety modelu
•
dość naturalna reprezentacja świata
•
łatwość działania na złożonych obiektach
•
duża podatność na zmiany
Znaczenie praktyczne
•
w zastosowaniach naukowych lub eksperymentalnych
•
przykłady systemów: GemStone, O2
•
przewidywana ewolucja baz relacyjnych w kierunku obiektowo-relacyjnych
RELACYJNE BAZY DANYCH
W relacyjnym modelu danych, do opisu własności obiektów reprezentowanych w bazie danych
wykorzystuje się wybrany zestaw atrybutów (własności). Dla danego problemu dokonuje się
wyboru tych własności oraz stopnia szczegółowości ich opisu. Przykładami atrybutów mogą
być: kolor, waga, wiek, marka, nazwisko, PESEL, nip, wartość towaru. Atrybuty przyjmują
wartości z określonego zbioru zwanego dziedziną atrybutu (domeną, oznaczaną czasami przez
DOM(A) gdzie A jest atrybutem). Dla danego obiektu każdy z atrybutów przyjmuje tylko
pojedynczą wartość dziedziny atrybutu (atrybut jest funkcją). Wymagania, co do atomowego
(atomicznego) charakteru wartości atrybutu stanowi jeden z podstawowych kanonów
relacyjnych baz danych.
Typy dziedzin:
Dziedziny binarne – dziedzina taka zawiera dokładnie dwa elementy np. 0 i 1 (lub Tak i Nie)
Dziedziny trójwartościowe – dziedzina taka zawiera dokładnie trzy elementy np. Tak, Nie,
Brak_danych (lub TRUE, FALSE, NULL)
Dziedziny nominalne – skończone zbiory nazw; zbiory takie można jedynie porządkować
leksykograficznie.
Dziedzin częściowo uporządkowane – skończone zbiory nazw z relacją częściowego porządku
Dziedziny liniowo uporządkowane- zbiory (nazw lub liczb), w których określona jest relacja
liniowego porządku
Dziedziny liczbowe – na danych tego typu można wykonywać operacje obliczeniowe (bajt,
liczba całkowita (krótka, długa), liczba rzeczywista (pojedynczej, podwójnej długości), data,
waluta, procenty
Dane typu tekstowego – zawierają dowolne pliki tekstowe (w polach typu Memo); brak
możliwości wykonywania operacji poza edycją
Dane typu dźwięk – w specjalnych plikach; brak możliwości operacji poza odtwarzaniem
Dane typu obraz – w specjalnych plikach w określonym formacie; ich zastosowanie polega na
prezentacji obrazka (osoba; okładka; widok szczytu górskiego)
Dane typu sekwencja – podobnie jak obraz – do prezentacji
Dane typu hiperłącze – umożliwia uruchomienie usługi sieciowej
Model relacyjny - podstawy teoretyczne
Niech zbiór U:={A
1
, A
2
, …, A
n
} (zwany dalej schematem relacji) będzie zbiorem atrybutów. Z
każdym z atrybutów A
k
∈
∈
∈
∈
U związana jest dziedzina D
k
dla k=1,2, ...,n. Zakładamy, że istnieje
funkcja ρU=(ρA
1
, ρA
2
, ..., ρA
n
) określona na zbiorze rozważanych obiektów o wartościach w
D
1
××××
D
2
××××
...
××××
D
n
Relacja R(U) o schemacie U to podzbiór iloczynu kartezjańskiego dziedzin atrybutów:
R(U)
⊂
⊂
⊂
⊂
D
1
××××
D
2
××××
...
××××
D
n
Relacja jest zbiorem krotek:
R={k
1,
k
2,...,
k
m
}
Krotka to funkcja przyporządkowująca atrybutom wartości atrybutów dla ustalonego obiektu.
K[U]={A
1
→k[A
1
], A
2
→k[A
2
],..., A
n
→k[A
n
],}
Jeżeli kolejność atrybutów jest ustalona to krotkę można traktować jako ciąg wartości atrybutów
dla wybranego obiektu.
Zbiór krotek (relacja) może być reprezentowany jako tabela:
kolumny odpowiadają nazwom atrybutów
wiersze odpowiadają krotkom
Tablice reprezentujące relacje mają następujące własności:
•
Liczba kolumn jest ustalona na etapie projektowania i jest taka sama dla wszystkich wierszy
(krotek)
•
Kolumny etykietowane są atrybutami
•
Liczba wierszy zależy od liczby opisywanych obiektów
•
Kolejność kolumn nie jest istotna
•
Kolejność wierszy nie jest istotna
•
W tabeli będącej zapisem relacji wiersze nie mogą się powtarzać
Relacyjna baza danych
•
schemat relacyjnej bazy danych jest zbiorem schematów relacji
•
relacyjna baza danych jest zbiorem relacji spełniających warunki integralności dla każdej
relacji i między relacjami
Klucze
•
klucz K relacji R(U) jest zbiorem atrybutów, które jednoznacznie wyznaczają krotkę:
])
[
]
[
(
(
:
2
1
2
1
)
(
,
2
1
K
k
K
k
k
k
U
K
U
R
k
k
≠≠≠≠
⇒
⇒
⇒
⇒
≠≠≠≠
∀
∀
∀
∀
⊆
⊆
⊆
⊆
∈
∈
∈
∈
,
gdzie k
i
[K] oznacza podkrotkę zawierającą tylko atrybuty z klucza K
•
klasyfikacja kluczy:
o
klucze właściwe: żaden podzbiór właściwy klucza właściwego nie jest kluczem
o
klucz główny: jeden z kluczy właściwych relacji, wybrany do identyfikowania krotek
•
klucze wykrywa się analizując opisywany świat, a nie dostępne dane!
Zbiór identyfikujący (nadklucz) – to dowolny atrybut lub zestaw atrybutów pozwalających na
identyfikację (jednoznaczną) obiektu w relacji (w bazie danych).
Klucz to każdy minimalny zbiór identyfikujący tzn. że żaden jego właściwy podzbiór nie jest
wystarczający do identyfikacji obiektu (krotki)
Klucz prosty – klucz złożony z pojedynczego atrybutu
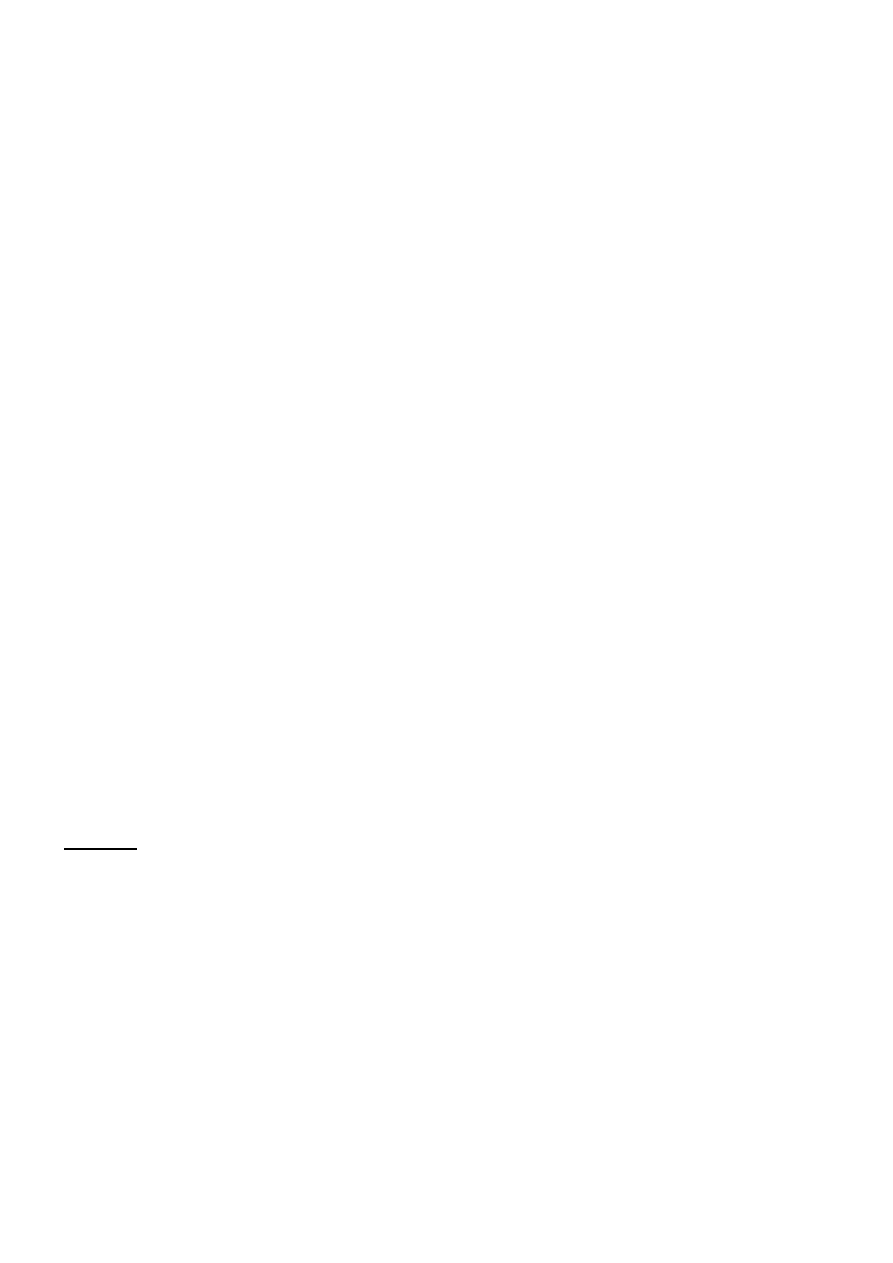
Klucz obcy – atrybut lub ich zestaw występujący w danej tabeli a będący kluczem w innej tabeli
(klucz obcy stosowany jest przy złączaniu schematów relacji (tabel))
Przykład: (czytelnicy)
o
id czytelnika jest kluczem
o
nazwisko nie jest kluczem
o
nazwisko + imię + data urodzenia + imię ojca -- jest kluczem (?)
Operacje na relacjach
Selekcja
•
selekcja to wybór krotek (wierszy) spełniających określony warunek:
)}
(
;
{
)
(
k
w
R
k
R
S
w
∈
∈
∈
∈
====
,
gdzie w jest warunkiem selekcji (warunek selekcji jest po prostu podzbiorem iloczynu
dziedzin atrybutów
•
selekcja jest komutatywna (przemienna):
))
(
(
))
(
(
R
S
S
R
S
S
v
w
w
v
====
,
gdzie w i v są warunkami selekcji
Projekcja (rzut)
•
projekcja relacji R to wybór atrybutów (kolumn):
}
);
'
(
{
)
(
'
R
k
U
k
R
U
∈
∈
∈
∈
====
ππππ
,
gdzie
U' jest podzbiorem schematu U
Operacje teoriomnogościowe
•
dotyczące relacji opartych na identycznych schematach:
o
suma
o
iloczyn
o
różnica
Złączenie
•
operacja na dwóch relacjach -- podzbiór iloczynu kartezjańskiego dwóch relacji:
)}
'
'
,
'
(
'
'
'
'
'
'
;
'
'
'
{
'
'
'
k
k
w
R
k
R
k
k
k
R
R
∧∧∧∧
∈
∈
∈
∈
∧∧∧∧
∈
∈
∈
∈
====
∗∗∗∗
⊳⊲
,
gdzie
w jest warunkiem złączenia.
•
krotki złączenia stanowią sklejenie (konkatenację) krotek relacji złączanych
•
rodzaje złączeń:
o
równościowe -- warunek równościowy (zgodność wartości na wybranych atrybutach)
o
naturalne -- równościowe i nazwy atrybutów zgodne
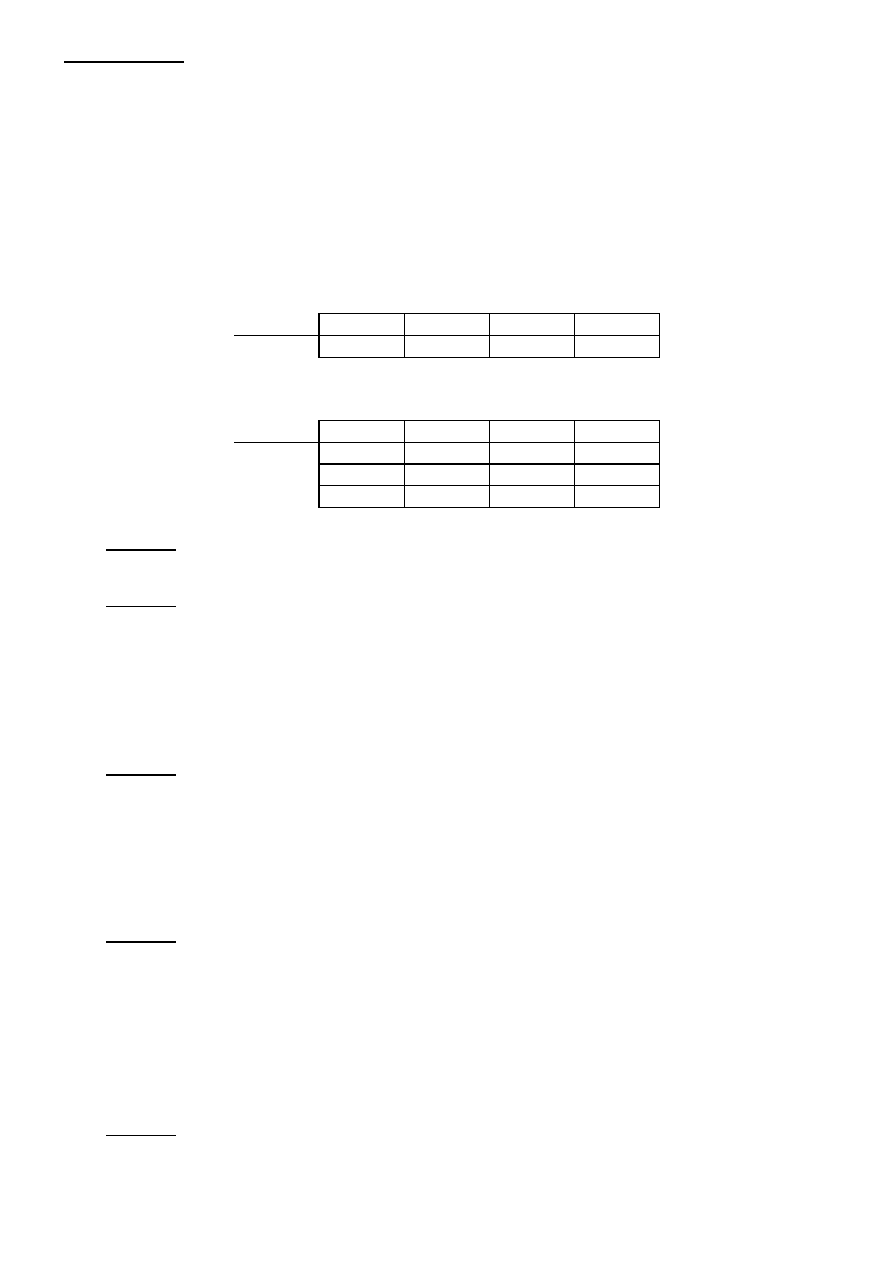
Algebra relacji
Relacje typu U oznaczać będziemy R(U),S(U),T(U),.... Jeżeli z kontekstu wynikać będzie
jednoznacznie o jaki zbiór atrybutów chodzi, pisać będziemy R, S, T, ... .
Krotki typu U oznaczać będziemy r(U),s(U),t(U).... Jeżeli z kontekstu wynikać będzie jednoznacznie
typ krotki, pisać będziemy r,s,t,....
Podzbiory zbioru atrybutów U oznaczać będziemy dużymi literami X,Y,Z,.... Do oznaczenia sumy
dwóch zbiorów X,Y
⊆
⊆
⊆
⊆
U stosować będziemy zapis XY zamiast X
∪
∪
∪
∪
Y.
Ścisłe przedstawienie krotki utożsamianej ze zbiorem jej wartości wymaga zapisu
r = { (A
1
, a
1
), (A
2
, a
2
),..., (A
n
, a
n
) }, gdzie a
i
= r(A
i
), i = 1,2,...,n. Zamiast tego będziemy pisać (a
1
, a
2
, ...
, a
n
).
Dla zbioru atrybutów {A,B} zamiast pisać R({A,B}), stosować będziemy zapis R(A,B).
Uwaga. Niech zbiór U := {A
1
,A
2
,...,A
n
}. Ponieważ krotka r(U) jest funkcją, więc można ją
przedstawić w postaci tabeli:
U
A
1
A
2
...
A
n
r
r(A
1
)
r(A
2
)
...
r(A
n
)
Gdy R(U) := {r
1
, r
2
,..., r
m
} to można tą relację przedstawić w postaci tabeli:
U
A
1
A
2
...
A
n
r
1
(A
1
)
r
1
(A
2
)
...
r
1
(A
n
)
R
...
...
...
...
r
m
(A
1
)
r
m
(A
2
)
...
r
m
(A
n
)
Definicja. Wartość a
∈
∈
∈
∈
DOM(A) nazywamy wartością prostą, gdy nie jest ona zbiorem ani
ciągiem elementów należących do
(((( ))))
{{{{
}}}}
DOM
|
A
A U
∈
∈
∈
∈
∪
.
Definicja. Mówimy, że relacja R(U) jest relacją znormalizowaną
( pierwszej postaci normalnej -1PN ) gdy dziedziny DOM(A) wszystkich atrybutów A
∈
∈
∈
∈
U są
zbiorami wartości prostych.
Przykład:
Baza danych BIBLIOTEKA ; Tabela Wypożyczenia ( pole książki_wypożyczone a w nim
id_k1, id_k2, id_k3 )
Taka baza danych (relacja ) nie jest znormalizowana ( nie jest w 1PN)
Definicja. Dla danej krotki r(U) i X
⊂
⊂
⊂
⊂
U krotkę t typu X nazywamy ograniczeniem krotki r(U)
do zbioru X gdy (
∀
∀
∀
∀
A
∈
∈
∈
∈
X) ( r(A)= t(A)}. Dla krotki będącej ograniczeniem będziemy używać
oznaczenia r(X) lub r[X].
Przykład. Niech U := {A,B,C}, X := {A,C} i r(U) := (a,b,c). Wtedy r[X] = (a,c).
Operacje na relacjach.
Na relacjach definiuje się pewne operacje mnogościowe i relacyjne.
Definicja. Zbiory
(a)
T(U):={t
∈
∈
∈
∈
KROTKA(U)|t
∈
∈
∈
∈
R(U)
∨∨∨∨
t
∈
∈
∈
∈
S(U) };
(b)
T(U) := { t
∈
∈
∈
∈
KROTKA(U) | t
∈
∈
∈
∈
R(U)
∧∧∧∧
t
∉
∉
∉
∉
S(U) };
(c)
T(U) := { t
∈
∈
∈
∈
KROTKA(U) | t
∈
∈
∈
∈
R(U)
∧∧∧∧
t
∈
∈
∈
∈
S(U) };
(d)
T(U):=KROTKA(U)-R(U) , przy czym zbiór KROTKA(U) jest zbiorem
skończonym, gdyż w przeciwnym wypadku byłaby sprzeczność z definicją relacji;
nazywamy odpowiednio sumą, różnicą, przekrojem i dopełnieniem relacji R(U) i oznaczać
będziemy przez R(U)
∪
∪
∪
∪
S(U), R(U)
∩
∩
∩
∩
S(U), R(U)-S(U)
i -R(U). Zauważmy, że definicje te dotyczą relacji tego samego typu.
Definicja. Niech U będzie zbiorem atrybutów, X,Y
⊂
⊂
⊂
⊂
U, r
∈
∈
∈
∈
KROTKA(X), s
∈
∈
∈
∈
KROTKA(Y) i
Z:=X
∪
∪
∪
∪
Y. Krotkę t
∈
∈
∈
∈
KROTKA(Z) nazywamy złączeniem krotki r i s, co oznaczamy t=r
⊳⊲
s, gdy t[X]
= r i t[Y ]= s.
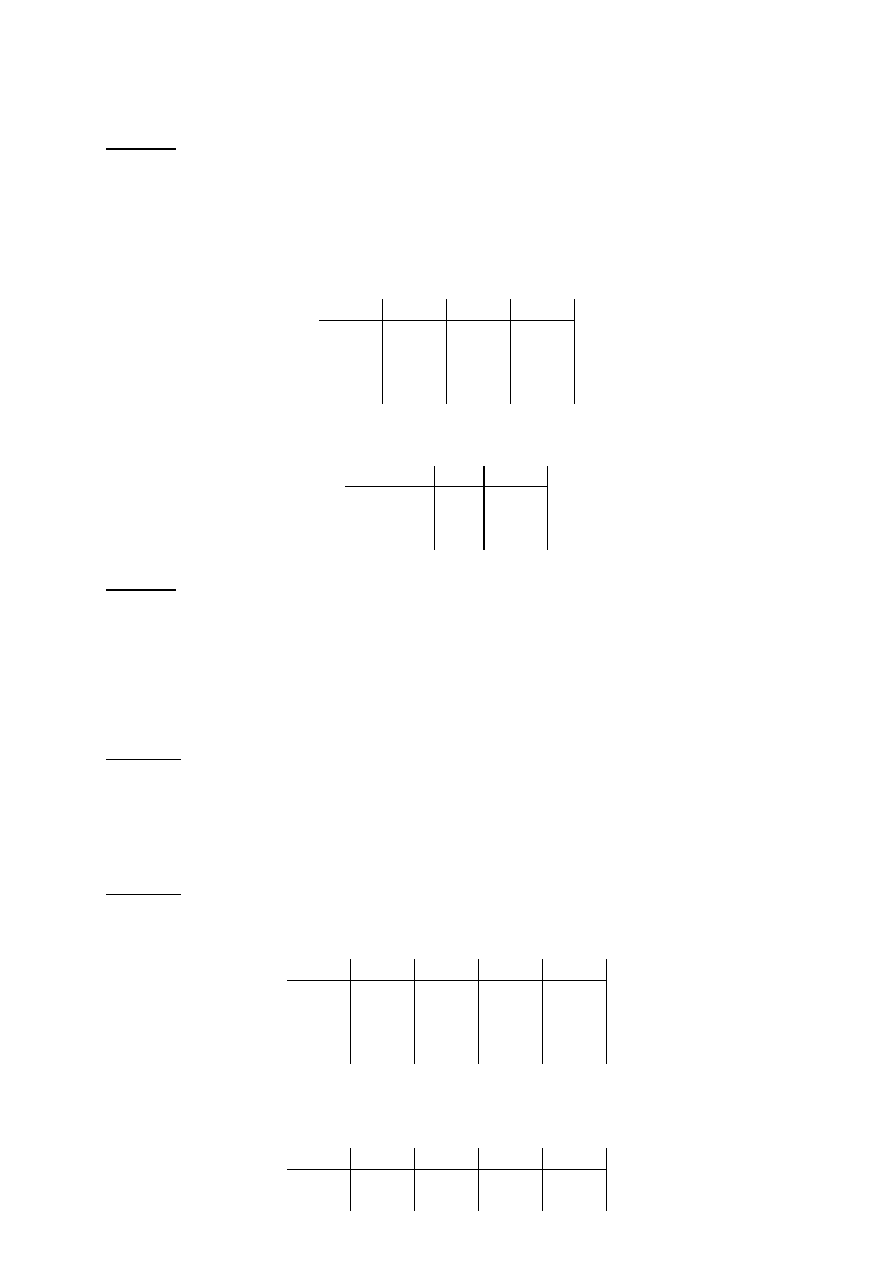
Stwierdzenie. Mają miejsce następujące własności:
(a)
r
⊳⊲
s = s
⊳⊲
r,
(b)
r[
∅
∅
∅
∅
] =
εεεε
gdzie
εεεε
oznacza krotkę pustą,
(c)
r
⊳⊲
εεεε
= r.
Definicja. Dla danej relacji R(U) oraz zbioru X
⊂
⊂
⊂
⊂
U relację T(X) nazywamy projekcją R na X,
gdy
T = { t
∈
∈
∈
∈
KROTKA(X) | (
∃∃∃∃
r
∈
∈
∈
∈
R ) ( t = r[X] ) }.
Dla projekcji używać będziemy oznaczenia T=R[X].
Stwierdzenie. Jeżeli dana jest relacja R(U) i X
⊂
⊂
⊂
⊂
U to
R[X] = { t
∈
∈
∈
∈
KROTKA(X) | (
∃∃∃∃
s
∈
∈
∈
∈
KROTKA(U-X) ) (t
⊳⊲
s
∈
∈
∈
∈
R ) }.
Przykład. Niech U := {A,B,C} i R(U) określona następująco:
R:
A
B
C
a
x
1
b
x
1
a
x
2
c
y
3
Dla X:={B,C} mamy:
R [X]:
B
C
x
1
x
2
y
3
Definicja. Odwzorowanie
(((( ))))
(((( ))))
:REL
REL
,
U
X
U
X
X
U
ππππ
→
⊂
→
⊂
→
⊂
→
⊂
przyporządkowujące relacjom typu U ich projekcję na X nazywamy operacją projekcji.
Stwierdzenie. Jeżeli R
∈
∈
∈
∈
REL(U) to
(((( )))) {{{{ }}}}
,
gdy
,
,
gdy
.
U
R
R
R
ππππ
εεεε
∅
∅
∅
∅
∅
∅
∅
∅
=∅
=∅
=∅
=∅
====
≠∅
≠∅
≠∅
≠∅
Definicja. Niech U := {A
1
,A
2
,...,A
n
},
(((( ))))
{{{{
}}}}
DOM
|
v
A
A U
∈
∈
∈
∈
∈
∈
∈
∈
∪
,
⊗
⊗
⊗
⊗∈
∈
∈
∈
{ =,
≠≠≠≠
, <, >,
≤
,
≥
}.
Elementarnym warunkiem selekcji nazywamy wyrażenia postaci v
⊗
⊗
⊗
⊗
A
i
lub A
i
⊗
⊗
⊗
⊗
A
j
. Warunkiem
selekcji nazywamy:
(a)
elementarny warunek selekcji,
(b)
wyrażenia postaci:
∼∼∼∼
E , E
1
∧∧∧∧
E
2
lub E
1
∨∨∨∨
E
2
gdzie E , E
1
, E
2
są warunkami
selekcji.
Definicja. Relację T(U) nazywamy selekcją relacji R(U) względem warunku selekcji E, co
oznaczamy przez T=R/E/, gdy T = {t
∈
∈
∈
∈
R | E(t)=true }.
Przykład. Dla relacji R(U) postaci
R:
A
B
C
D
a
x
1
3
a
y
4
2
c
x
3
3
b
x
2
1
z warunkiem selekcji E := ( C
≥
D
∧∧∧∧
( A = a
∨∨∨∨
A = b ) ) relacja T=R/E/ jest postaci
T:
A
B
C
D
a
x
4
2
b
x
2
1
Definicja. Odwzorowanie
(((( ))))
(((( ))))
:REL
REL
U
E
U
U
σσσσ
→
→
→
→
przyporządkowujące relacji typu U jej selekcję względem warunku E nazywamy operacją selekcji.
Definicja. Dla danych relacji R(X) i S(Y) relację
T:={ t
∈
∈
∈
∈
KROTKA(X
∪
∪
∪
∪
Y) | ( t[X]
∈
∈
∈
∈
R )
∧∧∧∧
( t[Y]
∈
∈
∈
∈
S ) }
typu X
∪
∪
∪
∪
Y nazywamy złączeniem relacji i oznaczamy przez R
⊳⊲
S.
Stwierdzenie. Jeżeli dane są relacje R(X) i S(Y) to
R
⊳⊲
S ={ t
∈
∈
∈
∈
KROTKA(X
∪
∪
∪
∪
Y) | (
∃∃∃∃
r
∈
∈
∈
∈
R ) (
∃∃∃∃
s
∈
∈
∈
∈
S ) ( t = r
⊳⊲
s ) }.
Przykład. Dla relacji R(X) i S(Y) określonych następująco:
R:
A
B
C
S:
A
B
D
a
x
1
a
x
f
a
x
2
a
y
g
a
y
2
b
x
h
b
y
3
ich złączenie T:=R
⊳⊲
S jest relacją postaci:
T:
A
B
C
D
a
x
1
f
a
x
2
f
a
y
2
g
{ krotki nowej relacji tworzone są tylko z tych krotek relacji R i S, które na wspólnych atrybutach
mają te same wartości }.
Definicja. Odwzorowanie
⊳⊲
X,Y
: REL(X)
××××
REL(Y)
→
→
→
→
REL(X
∪
∪
∪
∪
Y)
przyporządkowujące dwóm relacjom typów, odpowiednio X i Y, relację typu X
∪
∪
∪
∪
Y będącą ich
złączeniem nazywamy operacją złączenia.
Stwierdzenie. Dla danych relacji R ,S ,T i X, Y
⊂
⊂
⊂
⊂
U mamy
(1)
R
⊳⊲
S = S
⊳⊲
R,
(2)
(R
⊳⊲
S )
⊳⊲
T = R
⊳⊲
(S
⊳⊲
T),
(3)
jeżeli X
⊂
⊂
⊂
⊂
U to R[X]
⊳⊲
R = R,
(4)
jeżeli X
∪
∪
∪
∪
Y=U to R
⊂
⊂
⊂
⊂
R[X]
⊳⊲
R[Y],
(5)
jeżeli X=Y to R
⊳⊲
S = R
∩
∩
∩
∩
S,
(6)
jeżeli X
∩
∩
∩
∩
Y=
∅
∅
∅
∅
to R
⊳⊲
S = R
××××
S.
Przykład. Niech a
i
≠≠≠≠
a
j
, b
i
≠≠≠≠
b
j
, c
i
≠≠≠≠
c
j
, dla i
≠≠≠≠
j, Wtedy dla relacji R określonej następująco:
Ad. 3) U := {A,B}, X := {B}, X
∪
∪
∪
∪
U = U,
R: A
B
R[X]
:
B
R[X]
⊳⊲
R
:
A
B
a
1
b
1
b
1
a
1
b
1
a
1
b
2
b
2
a
1
b
2
a
2
b
3
b
3
a
2
b
3
Ad. 5) U := {A,B}, X := {A,B}, Y := {A,B}, X
∪
∪
∪
∪
Y = {A,B},
R:
A
B
S:
A
B
R
⊳⊲
S:
A
B
a
1
b
1
a
2
b
2
a
2
b
2
a
2
b
2
a
3
b
3
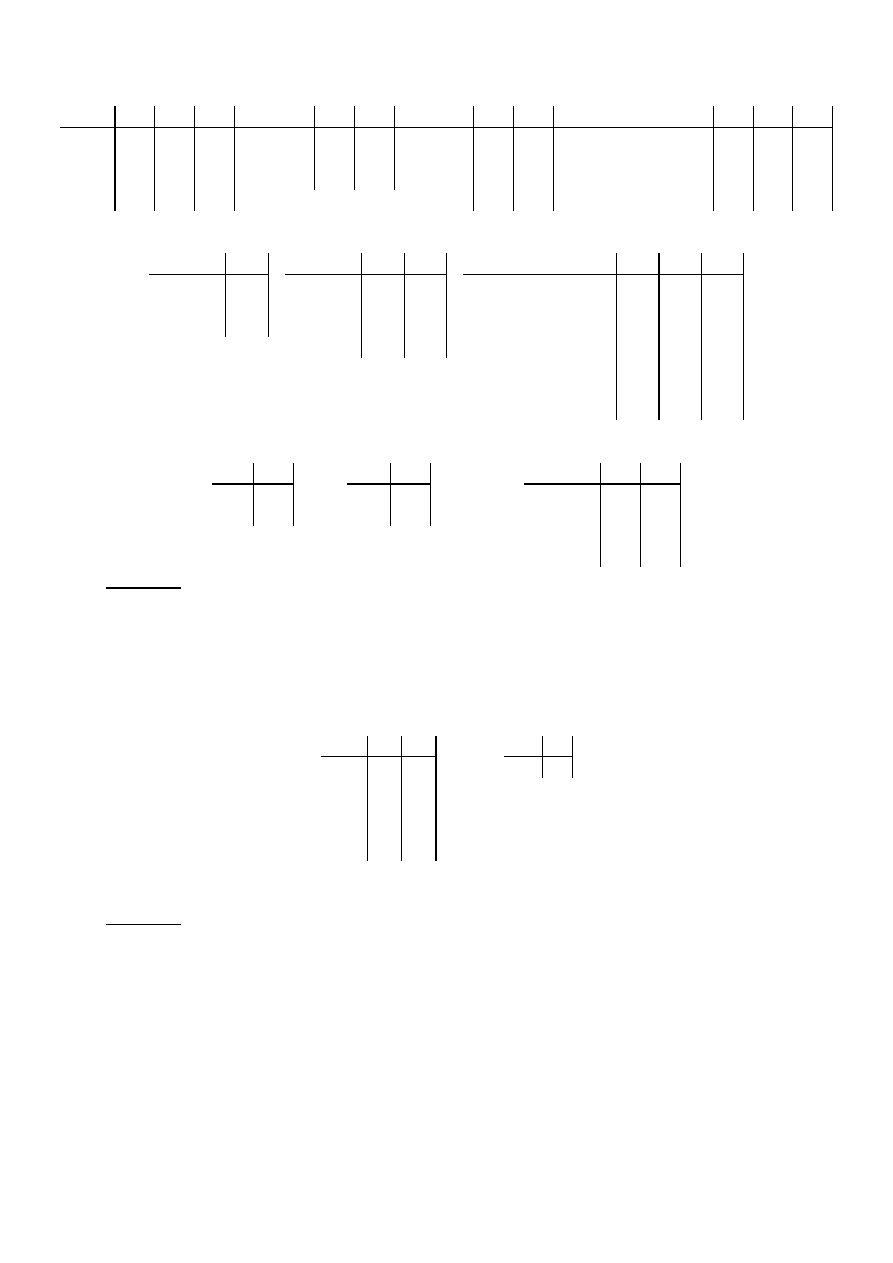
Ad. 4)
a) U := {A,B,C}, X := {A,B}, Y := {B,C}, X
∪
∪
∪
∪
Y = {A,B,C},
R:
A
B
C
R[X]:
A
B
R[Y]:
B
C
R[X]
⊳⊲
R[Y]:
A
B
C
a
1
b
1
c
1
a
1
b
1
b
1
c
1
a
1
b
1
c
1
a
2
b
2
c
2
a
2
b
2
b
2
c
2
a
1
b
1
c
2
a
3
b
3
c
3
a
3
b
3
b
3
c
3
a
2
b
2
c
2
a
1
b
1
c
2
b
1
c
2
a
3
b
3
c
3
U := {A,B,C}, X := {A}, Y := {B,C}, X
∪
∪
∪
∪
Y = {A,B,C},
R[X]:
A
R[Y]:
B
C
R[X]
⊳⊲
R[Y]:
A
B
C
a
1
b
1
c
1
a
1
b
1
c
1
a
2
b
2
c
2
a
1
b
2
c
2
a
3
b
3
c
3
a
1
b
3
c
3
b
1
c
2
a
2
b
1
c
1
a
2
b
2
c
2
...
...
...
a
3
b
3
c
3
Ad. 6) X := {A}, Y := {B}, X
∪
∪
∪
∪
Y = {A,B},
R:
A
S:
B
R
⊳⊲
S:
A
B
a
1
b
2
a
1
b
2
a
2
b
3
a
2
b
2
a
1
b
3
a
2
b
3
Definicja. Dla danej relacji R(U) i zbioru X
⊂
⊂
⊂
⊂
U relację T(U-X) nazywamy podzieleniem relacji
R przez zbiór X, co oznaczamy przez T=R/X, gdy
T={ t
∈
∈
∈
∈
KROTKA(U-X) | (
∀
∀
∀
∀
s
∈
∈
∈
∈
KROTKA(X) ) ( t
⊳⊲
s
∈
∈
∈
∈
R ) },
{ krotka t typu U-X należy do R/X, gdy dla każdej krotki s typu X złączenie krotek t i s jest krotką
należącą do R}.
Przykład. Niech U:={A,B), X:={B}, U-X = {A} zbiory DOM(A):={1,2,3}, DOM(B):={a,b,c}.
Wtedy T:=R/{B} dla relacja R(U) określonej następująco:
R:
A
B
T:
A
1
a
1
2
b
1
b
1
c
3
c
Niech 1,2,3 oznacza numer studenta i a,b,c nazwę przedmiotu. Niech (n,p)
∈
∈
∈
∈
R(U) oznacza, że student
n zdał egzamin z przedmiotu p. Zatem n
∈
∈
∈
∈
T, gdy student n zdał wszystkie egzaminy.
Definicja. Odwzorowanie
(((( ))))
((((
))))
:REL
REL
,
,
U
X
U
U
X
X
U
δδδδ
→
−
⊂
→
−
⊂
→
−
⊂
→
−
⊂
które relacji typu U przyporządkowuje relację będącą wynikiem podzielenia przez zbiór X
nazywamy operacją dzielenia.
R:S = { t
∈
∈
∈
∈
R [U-X] | ( S
⊂
⊂
⊂
⊂
R(t,X) ) },
gdzie
R(t,X) := { s
∈
∈
∈
∈
R[X] | (t
⊳⊲
s
∈
∈
∈
∈
R ) }.
Uwaga. Operacje mnogościowe i relacyjne zdefiniowane powyżej tworzą zbiór operacji algebry
relacji. Operacje te wykorzystuje się do
1.
tworzenia języków manipulowania danymi;
2.
badania zależności między danymi;
3.
projektowania schematu logicznego relacyjnych baz danych.