
1
RELACYJNE BAZY DANYCH cd.
Zależności funkcyjne. Sprowadzanie schematów relacji do postaci normalnej.
Zależności funkcyjne
•
Relacja R(U) o schemacie U:={A1, A2,..., An} spełnia zależność funkcyjną
X
Y
→
→
→
→
(
,
X Y
U
⊂
⊂
⊂
⊂
)
gdy w ramach krotek relacji R(U) wartości atrybutów zbioru X determinują jednoznacznie
wartości atrybutów zbioru Y tzn.
*
1
2
1
2
1
2
,
(
)
(
( [
]
[
]
[ ]
[ ])
k k
R U
X
Y
k X
k X
k Y
k Y
∈
∈
∈
∈
→ ⇔
∀
=
→ ⇔
∀
=
→ ⇔
∀
=
→ ⇔
∀
=
⇒
⇒
⇒
⇒
====
Przykład1 Niech U := {ID_PRACOWNIKA, NAZWISKO_PRACOWNIKA, IMIĘ_PRACOWNIKA}
o
IMIĘ_PRACOWNIKA zależy funkcyjnie od ID_PRACOWNIKA
o
ID_PRACOWNIKA nie zależy funkcyjnie od IMIĘ_PRACOWNIKA
o
IMIĘ_PRACOWNIKA nie zależy funkcyjnie od NAZWISKO_PRACOWNIKA
Przykład2. Niech U := {NR_INDEKSU, NAZWISKO_STUDENTA, NR_PRZEDMIOTU,OCENA} i
relacja R(U) określona następująco:
R:
NR_I
NAZ
NR_P
O
1
a
101
3
1
a
102
4
2
b
101
3
3
c
101
3
W relacji R(U) spełnione są następujące zależności funkcyjne: I
→
→
→
→
N , IP
→
→
→
→
O. Zauważmy, że dla zbiorów
{P} i {O} warunek z (
∗∗∗∗
) jest również spełniony, ale między tymi zbiorami nie istnieje zależność funkcyjna.
Istotnie, po dodaniu krotki (3, c, 102, 3) warunek z (
∗∗∗∗
) nie będzie spełniony.
Z każdym schematem relacji U wiążemy pewien zbiór zależności funkcyjnych F. Mówimy, że
zależność funkcyjna
Y
X
→
→
→
→
wynika logicznie z zależności funkcyjnych F jeżeli w każdej
relacji o schemacie U w której spełnione są zależności ze zbioru F spełniona jest również
zależność
Y
X
→
→
→
→
.
Przez domknięcie zależności funkcyjnych F (zapis F+) rozumiemy zbór wszystkich zależności
funkcyjnych wynikających logicznie z zależności funkcyjnych F.
Aksjomatyka ARMSTRONGA -- pozwala znaleźć nowe zależności funkcyjne na podstawie już
znalezionych:
Aksjomaty Armstronga. Niech U będzie zbiorem atrybutów i niech
F
⊂
⊂
⊂
⊂
{ X
→
→
→
→
Y | ( X
⊂
⊂
⊂
⊂
U )
∧∧∧∧
( Y
⊂
⊂
⊂
⊂
U ) }.
Przez F
+
oznaczmy najmniejszy (ze względu na relację zawierania) zbiór zależności funkcyjnych, który
zawiera zbiór F i dla dowolnych X,Y,Z
⊂
⊂
⊂
⊂
U spełnia następujące aksjomaty:
•
( Y
⊂
⊂
⊂
⊂
X ) ⇒
⇒
⇒
⇒ [ (X
→
→
→
→
Y )
∈
∈
∈
∈
F
+
],
(zwrotność);
•
[ (X
→
→
→
→
Y )
∈
∈
∈
∈
F
+
] ⇒
⇒
⇒
⇒ [ (X
∪
∪
∪
∪
Z
→
→
→
→
Y
∪
∪
∪
∪
Z )
∈
∈
∈
∈
F
+
],
(poszerzalność);
•
[ (X
→
→
→
→
Y )
∈
∈
∈
∈
F
+
∧∧∧∧
(Y
→
→
→
→
Z )
∈
∈
∈
∈
F
+
] ⇒
⇒
⇒
⇒ [ (X
→
→
→
→
Z )
∈
∈
∈
∈
F
+
],
(przechodniość).
Zbiór F
+
nazywamy (najmniejszym) domknięciem zbioru F.
Analizując zależności funkcyjne w schemacie relacyjnym musimy brać pod uwagę wszystkie zależności
funkcyjne obowiązujące w tym schemacie ( a więc te z F
+
a nie tylko z F)

2
W tej terminologii pojęcie klucza relacji R(U) o schemacie U:={A1, A2,..., An} i zbiorze zależności
funkcyjnych F można zdefiniować w następujący sposób
Kluczem (właściwym) nazywamy taki zbiór atrybutów X (
X
U
⊂
⊂
⊂
⊂
), że
•
X
U
F
++++
→ ∈
→ ∈
→ ∈
→ ∈
•
dla żadnego
,
Y
X Y
X
⊂
≠
⊂
≠
⊂
≠
⊂
≠
nie zachodzi
Y
U
F
++++
→ ∈
→ ∈
→ ∈
→ ∈
(każdy atrybut i cały schemat zależą funkcyjnie od klucza )
Normalizacja
Redundancja
•
redundancja polega na powtarzaniu
•
wady redundancji: anomalie, konieczność utrzymania spójności kopii, marnowanie miejsca
Anomalie
•
rodzaje:
o
wstawiania
o
usuwania
o
modyfikacji
Przykład: IMIĘ_PRAC NAZWISKO_PRAC NR_DZIAŁU NAZWA_DZIAŁU
Rozkład relacji i normalizacja
•
redundancję usuwa się przez rozkład relacji
•
rozkład ma być odwracalny: można odwrócić przez naturalne złączenie
•
rozkład relacji powinien doprowadzić do tzw. postaci normalnej
•
rozkład relacji nie powinien powodować utraty danych ani zależności funkcyjnych istniejących w
relacji pierwotnej
Pierwsza postać normalna
•
Schemat relacji (U,F) jest w 1PN gdy wszystkie atrybuty są atomowe -- prostych typów
•
1NF jest wymogiem dla rachunku relacyjnego, a więc i języków zapytań
o
kontrprzykłady:
atrybut tablicowy
zbiór
Uwaga: Dalej będzie mowa jedynie o relacjach spełniających 1PN
Definicje :
•
Zależność funkcyjna
A
X
→
→
→
→
nazywa się zależnością częściową, jeśli X jest właściwym
podzbiorem pewnego klucza.
•
Zależność funkcyjna
A
X
→
→
→
→
nazywa się zależnością przechodnią jeśli X nie jest ani podzbiorem
ani nadzbiorem żadnego klucza (
A
X
K
→
→
→
→
→
→
→
→
)

3
Druga postać normalna
Schemat relacji (U,F) jest w 2PN gdy każdy atrybut niekluczowy (nie należący do klucza właściwego)
jest zależny funkcyjnie od całego klucza właściwego (F
+
nie zawiera żadnej zależności częściowej)
•
przyczyną braku 2PN jest zwykle błędne połączenie danych
•
kontrprzykład: spis przepustek { ID_PRAC. ID_BUDYNKU. NAZWISKO IMIĘ }
o
nazwisko zależy funkcyjnie od id prac., czyli od fragmentu klucza
o
rozkład { ID_PRAC. ID_BUDYNKU.},{ ID_PRAC. NAZWISKO IMIĘ }
doprowadza do 2NF
Trzecia postać normalna
Schemat relacji (U,F) jest w 3PN gdy
o
jest w 2PN i
o
każdy atrybut niekluczowy jest bezpośrednio zależny funkcyjnie od całego klucza
właściwego
Inne sformułowanie 3PN :
Schemat relacji (U,F) jest w 3PN gdy dla każdej zależności
(X
U,A
U)
X
A
F
++++
→ ∈
⊆
∈
→ ∈
⊆
∈
→ ∈
⊆
∈
→ ∈
⊆
∈
zachodzi:
•
X
A
∈
∈
∈
∈
(zależność jest trywialna) albo
•
X jest nadkluczem, albo
•
A jest atrybutem głównym (jest częścią klucza)
•
możliwe przypadki naruszenia 3PN:
o
naruszenie 2PN
o
istnienie zależności tranzytywnej (a więc przechodniej) od klucza właściwego
•
przyczyną braku 3PN jest zwykle błędne połączenie danych
•
3PN jest zazwyczaj wystarczająca dla usunięcia praktycznie ważnych anomalii
•
każdy schemat relacji daje się rozłożyć na sumę schematów relacji w 3PN zachowując:
o
zależności funkcyjne
o
odwracalność rozkładu przez złączenie naturalne (zachowując informacje)
Przykład
ID_PRAC. NAZWISKO STANOWISKO PENSJA
•
jest w 2PN bo klucz jest jednoatrybutowy
•
istnieje zależność tranzytywna:
_
ID PRAC
STANOWISKO
PENSJA
→
→
→
→
→
→
→
→
(pensja zależy funkcyjnie od stanowiska)
•
rozkład { ID_PRAC, NAZWISKO, STANOWISKO}, {STANOWISKO, PENSJA)
doprowadza do 3PN
Własność:
Każdy schemat relacji daje się rozłożyć na sumę schematów relacji w trzeciej postaci normalnej z
zachowaniem zależności funkcyjnych i informacji.

4
Metoda rozkładu schematu na sumę schematów w trzeciej postaci normalnej
1) Wyznaczamy minimalne pokrycie G zbioru zależności funkcyjnych F - minimalne i równoważne F
(tzn takie, że
•
ma miejsce równość G
+
= F
+
(zbiór G jest równoważny F)
•
prawa strona każdej zależności w G składa się z jednego atrybutu
•
usunięcie dowolnej zależności funkcyjnej z G powoduje, że G
+
≠≠≠≠
F
+
•
dla każdej zależności
X
A
→
→
→
→
w G i
,
Y
U Y
X
⊂
≠
⊂
≠
⊂
≠
⊂
≠
, jeśli zastąpimy
X
A
→
→
→
→
przez
Y
A
→
→
→
→
otrzymamy zbiór, który nie jest równoważny F)
2) Dla każdej zależności funkcyjnej w minimalnym pokryciu (włączając do nich klucz podstawowy) z jej
atrybutów tworzymy schemat relacji po czym schematy te odpowiednio grupujemy (wg tego samego
klucza).
Przykłady:
U:={D,A,T,C} (z interpretacją odpowiednio Dostawca, Adres, Towar, Cena)
F:={
,
D
A DT
C
→
→
→
→
→
→
→
→
}
Jedynym kluczem jest DT. Zależność
D
A
→
→
→
→
jest zależnością częściową. Schemat ten nie jest w
drugiej postaci normalnej. Rozkład {D, A}, {D,T,C} jest rozkładem na schematy w 3PN.
U:={S,T,D,K} (z interpretacją odpowiednio Sklep, Towar, Dział, Kierownik}
F:={
,
TS
D SD
K
→
→
→
→
→
→
→
→
}
Jedynym kluczem jest TS,
SD
K
→
→
→
→
jest zależnością przechodnią. Schemat jest w drugiej postaci
normalnej ale nie jest w trzeciej. Rozkład {T,S,D}, {D,S,K} jest rozkładem na schematy w 3PN.
Zadanie. Niech U := { A,B,C,D,E,X,Y } i F := { X
→
→
→
→
C, X
→
→
→
→
D, CD
→
→
→
→
E, CD
→
→
→
→
A, Y
→
→
→
→
B, C
→
→
→
→
A, X
→
→
→
→
A }.
Stosując algorytm dokonać rozkładu U na sumę schematów w 3PN bez utraty danych i utraty zależności
funkcyjnych.
Zbiór G={ X
→
→
→
→
C, X
→
→
→
→
D, CD
→
→
→
→
E, Y
→
→
→
→
B, C
→
→
→
→
A} jest minimalnym pokryciem.
Zbiór K={X,Y} jest kluczem głównym.
Stąd rozkład na schematy {X,Y}, {X,C,D}, {C,D,E}, {C,A} będącej w trzeciej postaci normalnej.
Postać normalna Boyce-Codda
Relacja jest w BCPN gdy każda nie trywialna zależność funkcyjna jest zależnością od klucza
(niekoniecznie właściwego)
Inne sformułowanie BCPN :
Relacja jest w BCPN gdy dla każdej zależności
(X
U,A
U)
X
A
F
++++
→ ∈
⊆
∈
→ ∈
⊆
∈
→ ∈
⊆
∈
→ ∈
⊆
∈
zachodzi:
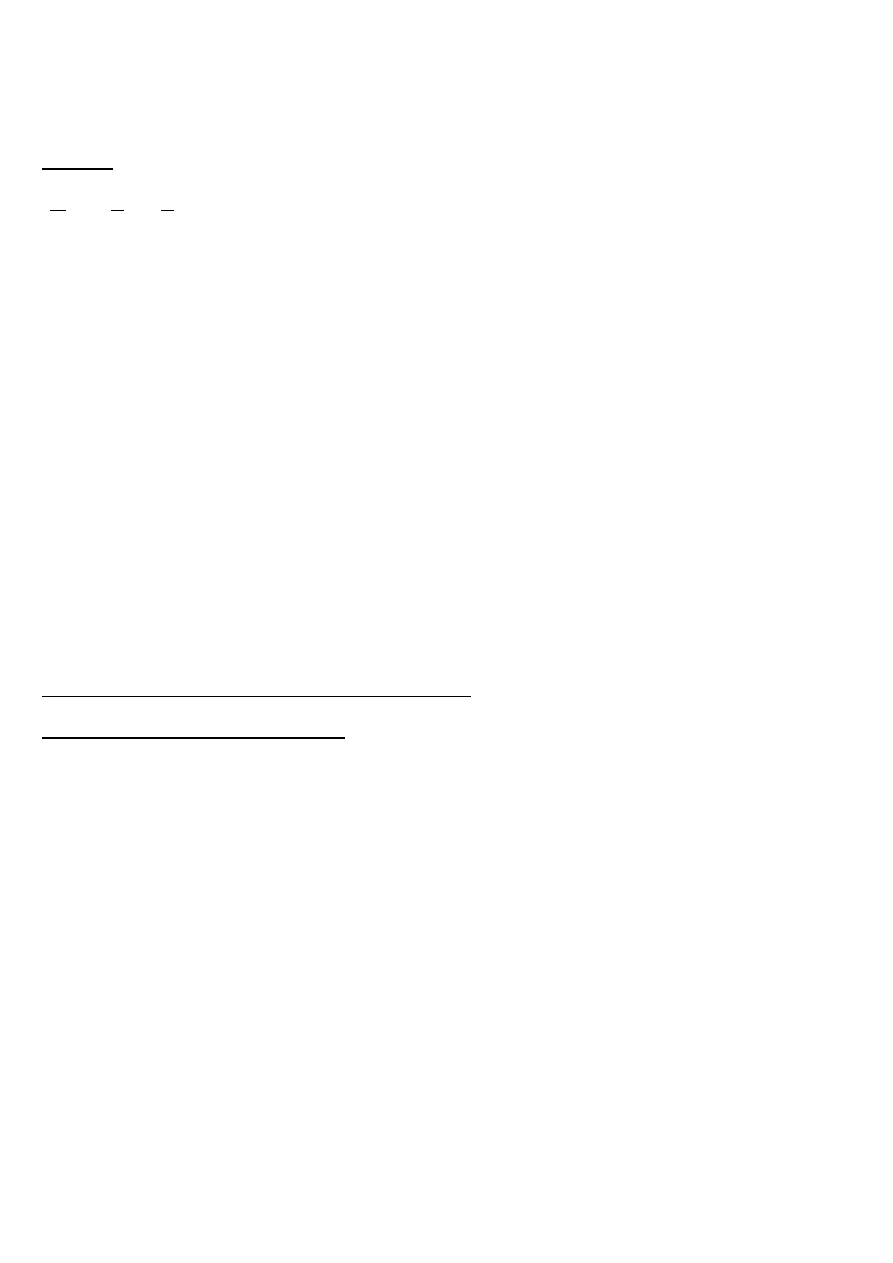
5
X
A
∈
∈
∈
∈
(zależność jest trywialna) albo X jest nadkluczem
Każdy schemat można rozłożyć na schematy w BCNF z zachowaniem informacji (ale niekoniecznie z
zachowaniem zależności funkcyjnych)
Przykład
{Miasto, Ulica, Kod}
relacja ta jest w 3PN z anomaliami:
istnieją tu klucze: {M,U}, {U,K}
(nazwy ulic mogą się powtarzać w różnych miastach, zakładamy że nazwy miast się nie powtarzają)
występują zależności:
,
MU
K K
M
→
→
→
→
→
→
→
→
schemat jest w 3NF
schemat nie jest w BCNF: K nie jest kluczem
schemat jest nierozkładalny do BCNF (np. {K,U}, {K,M}) bez utraty zależności
MU
K
→
→
→
→
Najczęściej zależności prowadzące do braku BCNF nie są istotne z punktu widzenia projektu.
Związki między postaciami normalnymi :
BCPN => 3PN => 2PN => 1PN
Zależności wielowartościowe i czwarta postać normalna
Zależności funkcyjne wielowartościowe.
Zbiór atrybutów Y jest zależny wielowartościowo od zbioru X gdy z każdą konfiguracją wartości
atrybutów z X jest związany zbiór konfiguracji wartości z Y niezależnie od wartości pozostałych
atrybutów:
1
2
3
1
2
,
(
)
3
1
3
1
3
2
(
)
(
( [
]
[
])
( [
]
[
]
[ ]
[ ]
[ ]
[ ]))
k k
R U
k
R U
X
Y
k X
k X
k X
k X
k Y
k Y
k Z
k Z
∈
∈
∈
∈
∈
∈
∈
∈
→> ⇔
∀
=
→> ⇔
∀
=
→> ⇔
∀
=
→> ⇔
∀
=
∃
=
∧
=
∧
=
∃
=
∧
=
∧
=
∃
=
∧
=
∧
=
∃
=
∧
=
∧
=
gdzie Z = U \ (X
∪
∪
∪
∪
Y)
Zauważmy, że zależności między atrybutami możemy interpretować jako reguły:
•
X
Y
→
→
→
→
można interpretować jako regułę:
jeśli
R
z
y
x
∈
∈
∈
∈
〉〉〉〉
〈〈〈〈
,
,
oraz
R
z
y
x
∈
∈
∈
∈
〉〉〉〉
〈〈〈〈
'
,
'
,
, to
'
y
y
====
•
X
Y
→>
→>
→>
→>
można interpretować jako regułę:
jeśli
R
z
y
x
∈
∈
∈
∈
〉〉〉〉
〈〈〈〈
,
,
oraz
R
z
y
x
∈
∈
∈
∈
〉〉〉〉
〈〈〈〈
'
,
'
,
, to
R
z
y
x
∈
∈
∈
∈
〉〉〉〉
〈〈〈〈
'
,
,
oraz
R
z
y
x
∈
∈
∈
∈
〉〉〉〉
〈〈〈〈
,
'
,
najważniejsze własności:
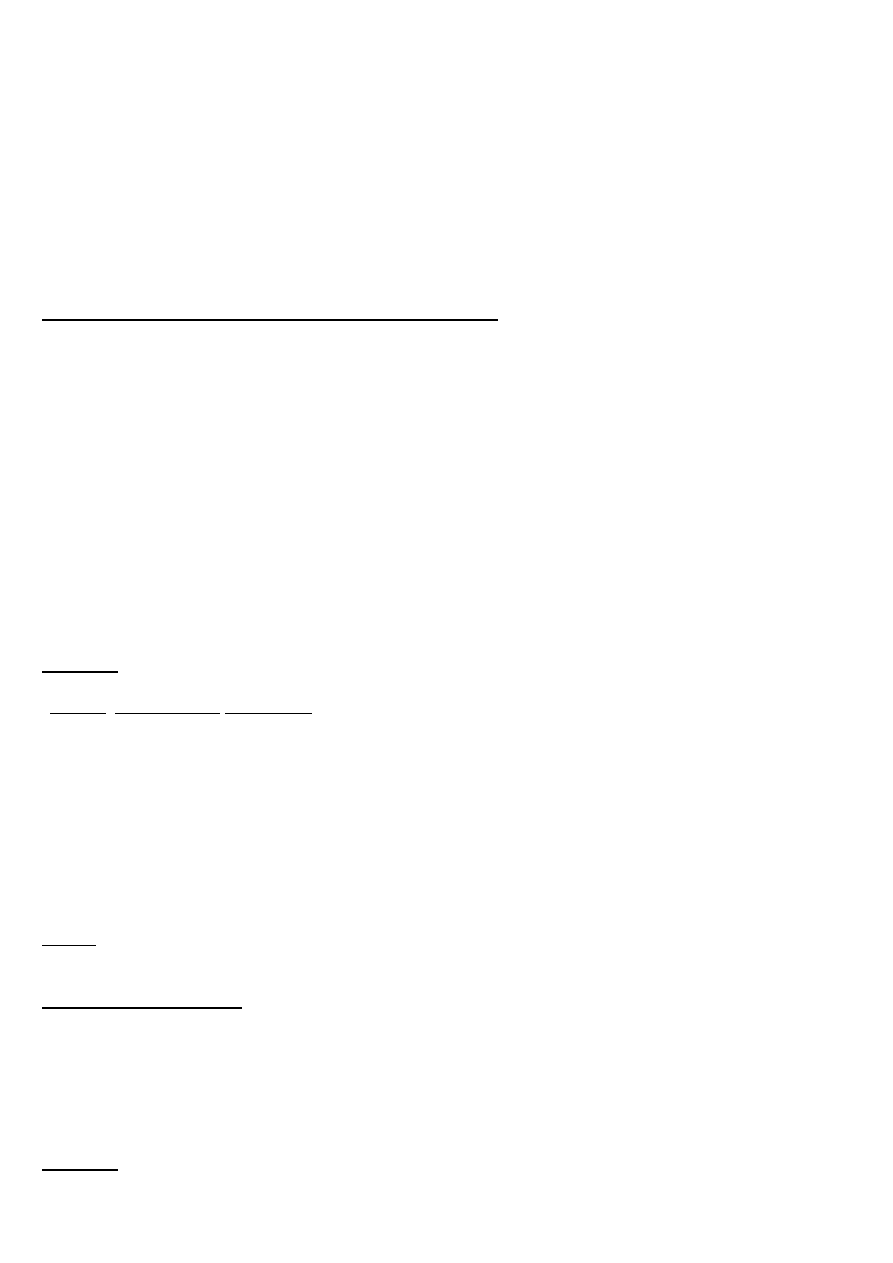
6
X
→
→
→
→>>>>
Y ⇒
⇒
⇒
⇒ X
→
→
→
→>>>>
Z
X
→
→
→
→
Y ⇒
⇒
⇒
⇒ X
→
→
→
→
> Y
Uwagi.
•
Relacja R(U) (w powyższej sytuacji) daje się rozłożyć w sposób odwracalny na dwie: R(X
∪
∪
∪
∪
Y) i
R(X
∪
∪
∪
∪
Z)
•
Istnieje odpowiednik aksjomatów Armstronga dla zależności wielowartościowych
•
Zależności X
→
→
→
→>>>>
U i X
→
→
→
→>>>>
∅
∅
∅
∅
spełnione są w każdej relacji R(U). Nazywamy je trywialnymi
zależnościami wielowartościowymi
Aksjomaty Armstronga dla zależności wielowartościowych.
Niech U będzie zbiorem atrybutów i niech
M
⊂
⊂
⊂
⊂
{ X
→
→
→
→
> Y | ( X
⊂
⊂
⊂
⊂
U )
∧∧∧∧
( Y
⊂
⊂
⊂
⊂
U ) }.
Przez M
+
oznaczmy najmniejszy (ze względu na relację zawierania) zbiór zależności funkcyjnych
wielowartościowych, który zawiera zbiór M i dla dowolnych X,Y,Z
⊂
⊂
⊂
⊂
U spełnia następujące aksjomaty:
((((
)))) ((((
))))
,
Y
X
X
Y
M
++++
⊂
⊂
⊂
⊂
⇒
⇒
⇒
⇒
→>
∈
→>
∈
→>
∈
→>
∈
( zwrotność ),
((((
))))
((((
))))
(
)
,
X
Y
M
X
U
X
Y
M
+
+
+
+
+
+
+
+
→>
∈
→>
∈
→>
∈
→>
∈
⇒
⇒
⇒
⇒
→> −
∪
∈
→> −
∪
∈
→> −
∪
∈
→> −
∪
∈
( dopełnialność ),
((((
))))
((((
))))
,
X
Y
M
X
Z
Y
Z
M
+
+
+
+
+
+
+
+
→>
∈
→>
∈
→>
∈
→>
∈
⇒
⇒
⇒
⇒
∪ →> ∪
∈
∪ →> ∪
∈
∪ →> ∪
∈
∪ →> ∪
∈
( poszerzalność ),
Przykład:
{Zajęcia, Wykładowca, Podręcznik}
podręczniki nie zależą od wykładowców
nie ma zależności funkcyjnych
zachodzą zależności wielowartościowe
Z
→
→
→
→>>>>
P i Z
→
→
→
→>>>>
W (zawsze para!)
można zamienić części krotek ZP i W
Uwaga. Zależności X
→
→
→
→>>>>
U i X
→
→
→
→>>>>
∅
∅
∅
∅
spełnione są w każdej relacji R(U). Nazywamy je trywialnymi
zależnościami wielowartościowymi.
Czwarta postać normalna
Relacja jest w 4NF gdy jeżeli każda nietrywialna zależność wielowartościowa jest zależnością od klucza
(niekoniecznie właściwego)
**
((((
))))
((((
))))
((((
))))
.
X
Y
M
Y
U
X
X
U
F
+
+
+
+
+
+
+
+
→>
∈
∧
⊂ −
→>
∈
∧
⊂ −
→>
∈
∧
⊂ −
→>
∈
∧
⊂ −
⇒
⇒
⇒
⇒
→
∈
→
∈
→
∈
→
∈
Przykład:
{Zajęcia, Wykładowca, Podręcznik }
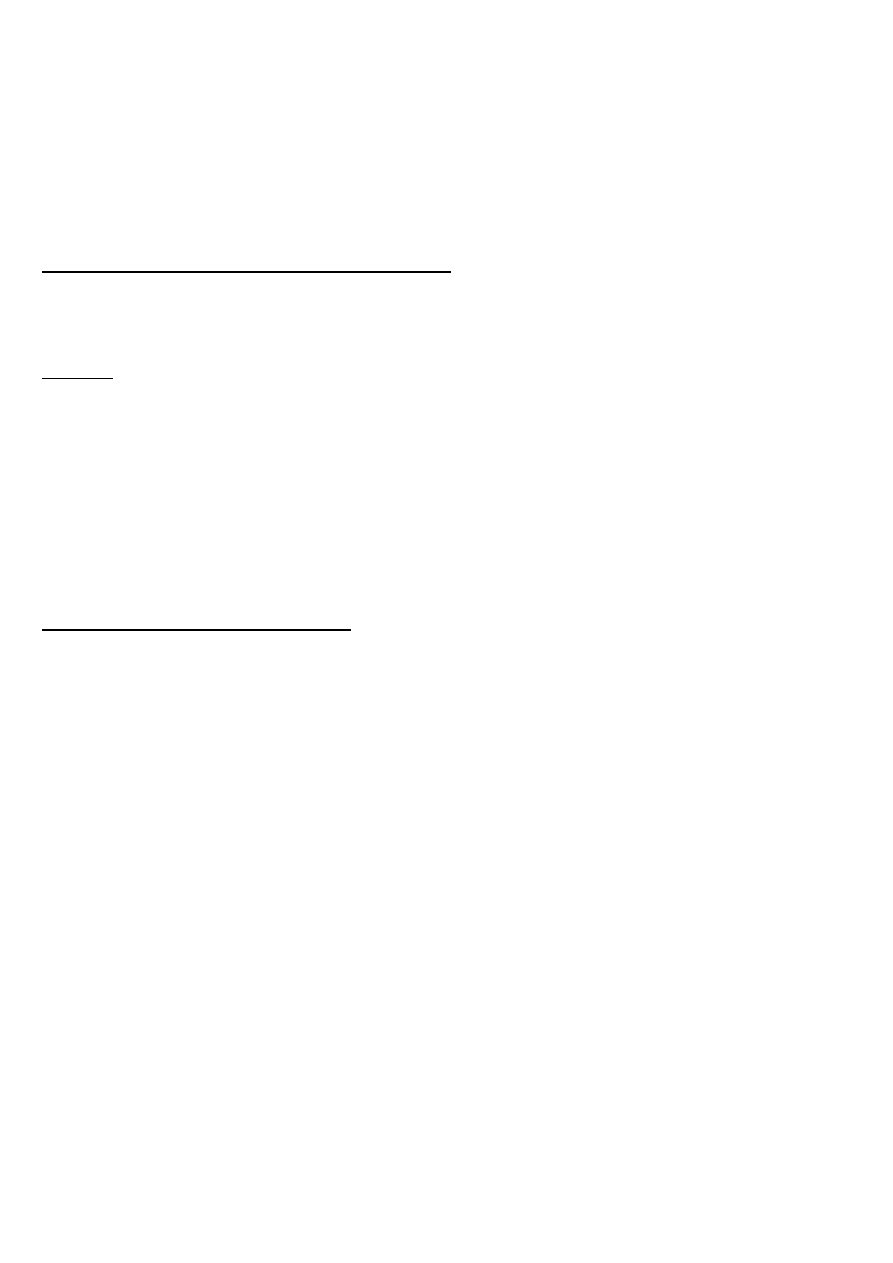
7
istnieją zależności Z
→
→
→
→>>>>
P i Z
→
→
→
→>>>>
W
nie ma zależności funkcyjnych
jest więc BCPN
występuje nadmiar informacji: powtórzone dane podręczników i wykładowców
schemat ten można rozłożyć na schematy {Z,W}, {Z,P}
Reguła rozkładu (dla zależności wielowartościowych)
Dla każdej zależności wielowartościowej X
→
→
→
→>>>>
Y jeśli X
∩
∩
∩
∩
Y=0 oraz X
∪
∪
∪
∪
Y
≠≠≠≠
U oraz X nie jest nadkluczem,
dokonujemy rozkładu U na X
∪
∪
∪
∪
Y oraz U-Y.
Przykład
U:={Nr_studenta, Przedmiot, Sport}
F:={ N
→
→
→
→>>>>
P, N
→
→
→
→>>>>
S}
X={N}, Y={P}
Stąd U rozkładamy na schematy {N,P}, {N,S}
Związki między postaciami normalnymi
4PN => BCPN => 3PN => 2PN => 1PN
Wyszukiwarka
Podobne podstrony:
doWydruku 4 G Bazy danych 2012
Bazy danych2 2012
Bazy danych1 2012
Internetowe bazy danych 2012
kolokwium2 2012, studia wsiz, semestr 4, bazy danych, bazy danych, BD T M
1 Tworzenie bazy danychid 10005 ppt
bazy danych II
Bazy danych
Podstawy Informatyki Wykład XIX Bazy danych
Bazy Danych1
eksploracja lab03, Lista sprawozdaniowych bazy danych
bazy danych druga id 81754 Nieznany (2)
bazy danych odpowiedzi
Bazy danych
więcej podobnych podstron