MudoL nr 1 wprowadzenie do programowania

Materiały uzupełniające na prawach rękopisu do ćwiczeń
Laboratoryjnych (MudoL) „Informatyka – Programowanie”.
Wyłącznie

celów

dydaktycznych,

dla

studentów

Politechniki Świętokrzyskiej

Politechnika Świętokrzyska, Katedra Inżynierii Produkcji

Wersja: 2008-11-19

Mudo

udo

udoL

Nr 1

ROGRAMOWANIE

Wybrane zagadnienia

Sławomir Luściński

Programowanie

Wersja: 2008-11-19

PIS

REŚCI

Informatyka

Informatyka ................................

................................

................................................................

................................

.........................................................

.........................

......................... 2

Przedmiot informatyki ........................................................................ 2

System informacyjny .......................................................................... 2

System informatyczny ........................................................................ 3

Wprowadzenie do algorytmów

Wprowadzenie do algorytmów ................................

................................

.............................................................

.............................

............................. 3

Algorytm .............................................................................................. 3

Procedury ............................................................................................ 5

Modularyzacja algorytmów ................................................................ 7

Język programowania

Język programowania ................................

................................

................................................................

................................

..........................................

..........

.......... 8

Co to jest język programowania? ........................................................ 8

Twierdzenie Boehma- Jacopiniego o strukturach sterujących ......... 9

Podstawowe struktury sterujące .................................................... 9

D-struktury ...................................................................................... 9

Twierdzenie ................................................................................... 10

Proces programowania

Proces programowania ................................

................................

................................................................

................................

......................................

......

...... 11

Typy danych ...................................................................................... 11

Zasady programowania .................................................................... 12

Programy podporządkowane strukturom danych ........................... 13

Niezawodność oprogramowania ....................................................... 13

Bibliografia

Bibliografia ................................

................................

................................................................

................................

........................................................

........................

........................ 16

Programowanie

Wersja: 2008-11-19

IIII

NFORMATYKA

Przedmiot informatyki

Informatyka

jest nauką o przetwarzaniu

informacji

, zwłaszcza przy

użyciu komputerów (Turski, 1989). Informatyka, jako ogół dyscyplin
naukowych i technicznych obejmuje:

• teorie informatyczne,
• budowanie systemów informatycznych (w tym programowanie),
• budowę i działanie sprzętu komputerowego,
• zastosowania metod informatycznych w różnych dziedzinach

działalności ludzkiej i in.

Teorie informatyczne zajmują się badaniem zjawisk związanych z

operowaniem informacją. W oparciu o prawa rządzące tymi zjawiskami
konstruuje się narzędzia informatyki, na które składają się algorytmy,
języki programowania, programy, komputery, systemy przesyłu danych
itp. Teorie informatyki posługują się językiem i metodami matematyki,
logiki matematycznej oraz takich specyficznych dziedzin jak: teoria
języków formalnych i automatów, teoria algorytmów, teoria kolejek.

Informatyka określana współcześnie jako Information Technology

Information Technology

Information Technology (IT)

integruje przede wszystkim dwa obszary wiedzy: techniczny związany z
technologiami

komputerowymi

komunikacyjnymi

oraz

obszar

metodologiczny o zachowaniach środowisk społecznych i przyrodniczych.
Interdyscyplinarne tło wiedzy informatycznej obejmuje nauki techniczne,
przyrodnicze, społeczne, logikę (Bazewicz, 1993).

Programowanie i budowanie systemów informatycznych

Programowanie i budowanie systemów informatycznych obejmuje w

szczególności tworzenie narzędzi ułatwiających programowanie i ogólnie
— posługiwanie się komputerami. Do narzędzi tych należą: języki
programowania, translatory, systemy operacyjne i in.; do działu
informatyki związanego z programowaniem należą też metody
programowania i dowodzenia poprawności programów.

System informacyjny

System

System informacyjny

informacyjny

informacyjny to „wielopoziomowa struktura, która pozwala

użytkownikowi tego systemu na transformowanie określonych informacji
wejścia na pożądane informacje wyjścia za pomocą odpowiednich
procedur i modeli” (Kisielnicki, i inni, 2005). System informacyjny (SI)
dowolnej organizacji jest zbiorem elementów określonym jako:

SI = {P, I, T, O, M, R}

gdzie:

P – zbiór podmiotów, które są użytkownikami systemu,
I – zbiór informacji o sferze realnej, a więc tzw. zasoby

informacyjne,

T – zbiór narzędzi technicznych stosowanych w procesie

pobierania, przesyłania, przetwarzania,
przechowywania i wydawania informacji,

Programowanie

Wersja: 2008-11-19

Algorytm to specyfikacja ciągu

operacji, które w wyniku

działania na wejściowy zbiór

obiektów dają wyjściowy zbiór

obiektów

(Marcotty, i inni, 1991)

O – zbiór rozwiązań systemowych stosowanych w danej

organizacji, czyli stosowana formuła zarządzania
(scentralizowana, rynkowa),

M – zbiór metainformacji, czyli opis systemu informacyjnego

i jego zasobów informacyjnych,

R – relacje pomiędzy poszczególnymi elementami.

System informatycz

System informatyczny

System informatyczny (SI) to „

wyodrębniona część systemu

informacyjnego, która z punktu widzenia przyjętych celów jest
skomputeryzowana”

(Kisielnicki, i inni, 2005). System informatyczny

składa się z następujących elementów:

• sprzętu (hardware),
• oprogramowania komputerów (software),
• baz danych, telekomunikacji,
• ludzi (personelu),
• organizacji.

System informatyczny zarządzania

System informatyczny zarządzania (SIZ) (

Management Information

System - MIS

) to formalny system komputerowy dokonujący wyboru,

udostępniania i integracji pochodzących z różnych źródeł danych po to,
aby w odpowiednim czasie dostarczyć informacji niezbędnych do
podejmowania decyzji

PROWADZENIE DO ALGOR

PROWADZENIE DO ALGORYTMÓW

YTMÓW

Algorytm

Za (Turski, 1979) przez algorytm będziemy rozumieć „

opis obiektów

łącznie z opisem czynności , które należy wykonać z tymi obiektami, aby
osiągnąć określony cel”

przy znanym poziomie szczegółowości

którym

formułuje się dany algorytm. Poziom szczegółowości wyznaczony jest
przez repertuar nazw czynności i klasę obiektów.

Algorytm musi być przedstawiony w formie komunikatywnej co

najmniej dla programisty. W dalszej części tekstu posłużymy się
przykładową koncepcją notacyjną – rodzajem języka – do zapisu
algorytmów przedstawioną w (Turski, 1979).

Opisy obiektów występujących w

algorytmie nazywamy

deklaracjami

, zaś

opisy czynności –

instrukcjami.

algorytmach występują obiekty proste i
obiekty złożone. Do obiektów prostych
zaliczamy obiekty, których wartościami
są liczby całkowite, rzeczywiste, wartości
logiczne, ciągi znakowe. Do obiektów
złożonych

zaliczamy

tablice.

E. Turban za (Kisielnicki, i inni, 2005)

Programowanie

Wersja: 2008-11-19

Jednowymiarowa

tablica

(np.

kolumna

lub

wiersz)

ciąg

ponumerowanych obiektów, których wartości są tego samego typu;
rozmiar takiej tablicy to liczba elementów. Dwuwymiarowa tablica to
ciąg wierszy lub kolumn , z których każdy liczy tyle samo elementów o
wartościach tego samego typu. Rozmiary dwuwymiarowej tablicy to
liczba wierszy (kolumn) i liczba elementów w wierszu (kolumnie).

Tabela 1 poniżej prezentuje podstawowe schematy instrukcji

stosowanych w języku zapisu algorytmów zaproponowanego w (Turski,
1979).

Tabela 1. Schematy instrukcji. Źródło: opracowanie własne na podstawie (Turski, 1979)

Nazwa

schematu

Schemat

Instrukcja
przypisania

jest nazwą obiektu, a

– wyrażeniem.

Wylicza się wartość wyrażenia

, a następnie podstawia się jako

wartość obiektu o nazwie

Wyliczenie wartości wyrażenia

polega

na wykonaniu operacji, których znaki występują w

, na wartościach

obiektów, których nazwy figurują w

Instrukcje z
wyborem
(warunkowe,
(selekcje)

jeśli W to I

jest opisem warunku, a

– opisem instrukcji którą zamierzamy

wykonać, jeśli wartość logiczna warunku = Prawda.

jeśli W to I

w przeciwnym wypadku I

Wyboru uzależnionego od wartości logicznej warunku

można

dokonać pomiędzy dwoma instrukcjami

przypadek N spośród ( I

, I

, …, I

)

Najbardziej ogólna postać selekcji który interpretuje się następująco:
wylicza się wartość wyrażenia

przyjmującego wyłącznie wartości

całkowite z przedziału [1:n], następnie wykonuje się tę instrukcję z
wykazu

, …, I

której numer jest zgodny z otrzymaną wartością

wyrażenia

Iteracja

powtarzaj I aż do W

Instrukcja

jest powtarzana tyle razy, ile trzeba na doprowadzenie do

spełnienia warunku

Uwaga: jeśli warunek

nie zależy od zmian stanu powstających na

skutek wykonania instrukcji

to iteracja taka może być nieskończona

(co świadczy o błędzie logicznym)

dopóki W wykonuj I

Instrukcja

jest powtarzana tyle razy, ile można, nie naruszając

prawdziwości warunku

Instrukcje
wejścia/wyjścia

czytaj(N)

Wykonanie instrukcji wejścia polega na odczytaniu z urządzenia
zewnętrznego (plik, klawiatura) tylu znaków binarnych, ile trzeba , aby
uzyskać ciąg kodowy wartości obiektu należącego do ustalonej klasy.
Klasa obiektu jest znana z deklaracji nazwy

; mówimy też, że nazwa

N stanowi

parametr

instrukcji wejścia .

pisz(W)

Wykonanie instrukcji wyjścia polega na znalezieniu wartości wyrażenia
W i wydaniu jej na zewnątrz w kodzie i postaci obowiązującej dla
konkretnego urządzenia wyjściowego.

Programowanie

Wersja: 2008-11-19

Deklarowanie jako procedury

czynności wykonywanych

wielokrotnie i różniących się

między sobą co najwyżej

wartościami ułatwia i

upraszcza zapis algorytmu.

Stosowanie procedur ułatwia

układanie algorytmów – w

trakcie ich pisania możemy

początkowo jedynie nazywać

pewne czynności i określić ich

parametry, pozostawiając na

później deklarację tychże

procedur.

Przykład zapisu algorytmu wyliczania silni z liczby naturalnej:

początek

całkowite

liczba, silnia, i;

i := 1

silnia := 1

czytaj(liczba)

dopóki

i<=

liczba wykonuj początek

i:=i+1

;

silnia := silnia*i

koniec

pisz (silnia)

koniec

Procedury

Wyodrębnioną (zwykle ze względu na wielokrotne użycie w różnych

miejscach) część algorytmu, posiadającą jednoznaczną nazwę ustalony
sposób wymiany informacji z pozostałymi częściami algorytmu
nazywamy procedurą. Procedurę opisuje się przy pomocy deklaracji,
stosuje zaś przez wywołanie. Raz zdeklarowaną procedurę można
wywoływać w dowolnie wielu miejscach algorytmu.

Deklaracja procedury składa się z nagłówka i treści. Nagłówek

procedury ma postać:

procedura

(

);

;

gdzie:

jest

nazwą

procedury ,

– wykazem

parametrów formalnych

, a

S – specyfikacją

parametrów formalnych. Wykaz parametrów formalnych

jest listą nazw parametrów formalnych, zaś specyfikacja opisem ich
własności.

Parametr

formalny

jest

obiektem, który występuje w treści
procedury; w chwili użycia procedury
każdemu

parametrowi

formalnemu

zostaje

przyporządkowany

parametr

aktualny

- obiekt algorytmu, który

zastępuje odpowiadający mu parametr
formalny w treści procedury. Rodzaj
parametru aktualnego musi być zgodny
ze specyfikacją odpowiadającego mu
parametru formalnego.

Treść procedury ma taką postać, jak

instrukcja

(złożona

lub

prosta).

Występują w niej obiekty dwu rodzajów:
parametry formalne zastępowane w
chwili

wywołania

procedury

przez

parametry aktualne oraz obiekty lokalne
– zadeklarowane w treści procedury.

Programowanie

Wersja: 2008-11-19

Wywołanie procedury w algorytmie ma postać:

(

)

gdzie:

jest

nazwą

procedury ,

– wykazem parametrów aktualnych,

zgodnym co do liczby z wykazem

parametrów formalnych w deklaracji

procedury. Wykonanie wywołanej procedury polega na wykonaniu z
parametrami aktualnymi instrukcji tworzących ich treść.

Przykład użycia procedury w algorytmie wyliczającym sumę silni

trzech liczb naturalnych:

początek całkowite

x; y; z; xs; ys; zs; suma;

procedura

silnia(liczba, wynik);

całkowite

liczba;

całkowite

wynik;

początek

całkowite

i := 1

wynik:= 1

dopóki

i<=

liczba wykonuj początek

i:=i+1

;

wynik:= wynik*i

koniec

czytaj(x); czytaj(y), czytaj (z)

silnia(x, xs)

silnia(y,ys)

silnia(x, zs)

suma := xs+ys+zs

pisz(suma)

koniec

Kolejnym ułatwieniem jest użycie procedur funkcyjnych, w przypadku
których nazwa pełni podwójną rolę: jako nazwa procedury i jako nazwa
obiektu, uzyskującego określoną wartość na skutek wykonania procedury.
Deklarację procedury funkcyjnej poprzedzamy określeniem typu wartości,
które przyjmuje obiekt nazwany tak samo jak procedura. W treści
procedury musi wystąpić co najmniej jedna instrukcja przypisania z
nazwą procedury po lewej stronie znaku :=

Programowanie

Wersja: 2008-11-19

Poniżej przykład użycia procedury funkcyjnej.

początek całkowite

x; y; z; xs; ys; zs; suma;

całkowite procedura

silnia(liczba);

całkowite

liczba;

początek

całkowite

i := 1

silnia := 1

dopóki

i<=

liczba wykonuj początek

i:=i+1

;

silnia := silnia*i

koniec

czytaj(x); czytaj(y), czytaj (z)

suma := silnia(x)+silnia(y)+silnia(z)

pisz(suma)

koniec

Modularyzacja algorytmów

Modularyzacja algorytmów to technika układania algorytmów

polegająca na wyodrębnieniu w algorytmie możliwie niezależnych części –
modułów, z których każdy opisuje dobrze opisane czynności na dobrze
opisanych obiektach przy jednoczesnym ustaleniu zasad łączenia takich
części w spójną całość.

Własności modułów:

Semantyczn

Semantyczna

a nieza

nieza

niezależność

leżność

leżność modułów.

modułów.

modułów. Moduł algorytmu opisuje

dobrze opisane czynności na dobrze opisanych obiektach, co
oznacza że sens modułu możemy zinterpretować niezależnie od
pozostałych części algorytmu. Zatem jeśli w danym algorytmie
wymienimy wskazany moduł na inny ale o identycznym znaczeniu
(interpretacji), całość algorytmu nie zmieni znaczenia.

II.

Syntaktyczna niezależność

Syntaktyczna niezależność modułów.

modułów.

modułów. Moduły algorytmu łączą się w

całość

zgodnie

ustalonymi

regułami

określającymi

współzależności i współdziałanie poszczególnych modułów, zatem
reguły budowy wewnętrznej indywidualnych modułów mogą być
różne, co np. pozwala stosować różne konwencje notacji dla
poszczególnych modułów (przypadek kilku autorów algorytmu).

III.

Zasada abstrakcji danych.

Zasada abstrakcji danych. Ze względu na semantyczną i
syntaktyczną niezależność modułów interpretacja przekazywanych
informacji nie może być zależna od interpretacji obowiązującej
wewnątrz modułów.

Patrząc na moduł z zewnątrz, możemy traktować go jako spójną

całość; nie wnikając w szczegóły poprzestajemy na stwierdzeniu że jest to
opis czynności mających w określonych warunkach określone skutki.

Programowanie

Wersja: 2008-11-19

Języki programowania są

głównym narzędziem

programisty; aby odpowiednio

wykorzystać narzędzie, należy

je najpierw w pełni zrozumieć.

(Marcotty, i inni, 1991)

Można powiedzieć, że modularyzacja
służy do ukrywania zbędnych informacji:
dla obserwatora z zewnątrz modułu będą
to szczegóły realizacji czynności w
module, z punktu widzenia wnętrza
modułu będą to informacje dotyczące
wszystkich innych modułów.

ĘZYK

ĘZYK PROGRAMOWANIA

PROGRAMOWANIA

Co to jest język programowania?

Język programowania

jest zbiorem konwencji umożliwiających

komunikatywność algorytmów zarówno dla programistów jak i dla
komputerów.

Programem

nazywamy algorytm wyrażony w języku

programowania (Marcotty, i inni, 1991).

Implementacją

nazywamy

realizację języka programowania jako systemu komputerowego, która
może przyjąć jedną z dwóch form:

kompilacji

lub

interpretacji.

• Kompilacja

Kompilacja

Kompilacja: program napisany w języku programowania (

program

źródłowy)

jest tłumaczony na równoważny program (

program

wynikowy

) w języku maszynowym tego komputera (maszyny

docelowej), na którym ma być wykonany.

• Interpretacja

Interpretacja

Interpretacja: program źródłowy nie jest tłumaczony, ale jest
wykonywany

bezpośrednio

przez

interpretator

–

program

wykonywany na maszynie docelowej. Interpretacja każdej instrukcji
polega na jej sprawdzeniu i wykonaniu operacji przez nią
specyfikowanych.

W uczeniu się języków programowania należy uwzględnić następujące
podstawowe aspekty języków formalnych, do jakich należą: składnia
(

syntaktyka

) języka, sensowność zdań jakiegoś języka (

semantyka

) oraz

zalecenia dotyczące używania różnych poprawnych form lingwistycznych
o zbliżonym znaczeniu semantycznym (

pragmatyka

• Formalna składnia języka

Formalna składnia języka

Formalna składnia języka to zbiór reguł, które pozwalają generować
syntaktycznie poprawne zdania rozważanego języka. W przypadku
języków programowania znajomość składni umożliwia zapisanie
konstrukcji złożonych z symboli elementarnych danego języka –
łańcuchów symboli – które nazywamy

programami poprawnymi

syntaktycznie

• Tylko niewielka część programów poprawnych syntaktycznie może

być wykonana poprawnie, jako że reguły składniowe nie dotyczą akcji
zachodzących podczas wykonywania programów. Reguły semantyczne

Reguły semantyczne

języka

języka definiują podzbiór programów poprawnych; są podawane na
ogół nieformalnie.

• Pragmatyka języka

Pragmatyka języka

Pragmatyka języka obejmuje zalecenia dotyczące używania różnych
poprawnych

form

lingwistycznych

zbliżonym

znaczeniu

semantycznym: dotyczy wyboru między uformowanymi już zdaniami.

Programowanie

Wersja: 2008-11-19

Przykład zapisu fragmentu programu w języku VBA, który choć
poprawny syntaktycznie to zawiera błąd semantyczny (jest semantycznie
błędny).

K = 0

V = 3 / K

Twierdzenie Boehma

Twierdzenie Boehma---- Jacopiniego o strukturach sterujących

Jacopiniego o strukturach sterujących

Podstawowe struktury sterujące

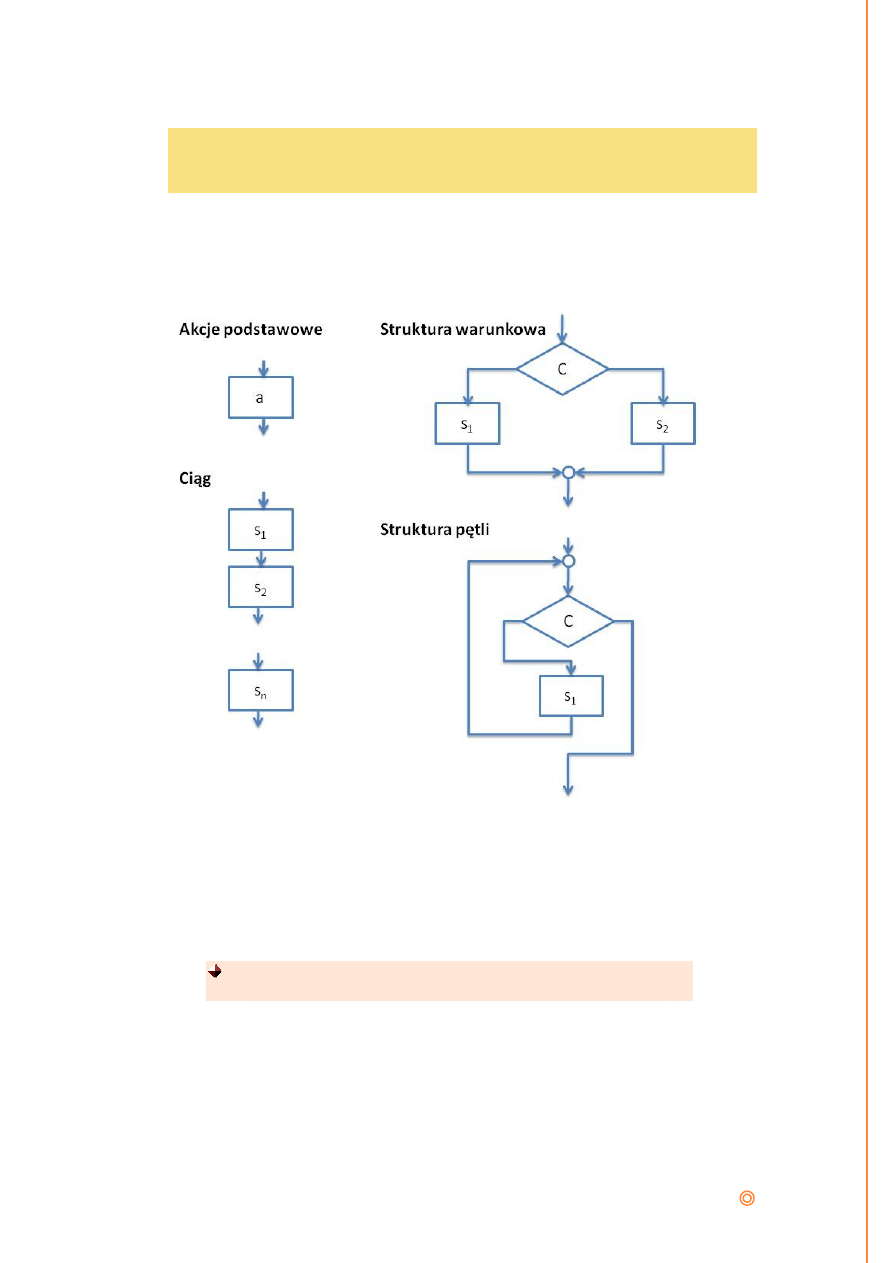
Do definicji ciągu wykonywanych instrukcji służą takie narzędzia

języka programowania jak pętle (iteracje), instrukcje warunkowe,
instrukcje skoku.

W analizie przekazywania sterowania jest wygodnie przedstawić

program w postaci schematu blokowego. Schemat blokowy to zbiór
wierzchołków oznaczających akcje programu połączonych drogami z
zaznaczonym kierunkiem, które pokazują przepływ sterowania. Schemat
blokowy reprezentuje ciąg, w którym wykonywane są akcje programu
(Marcotty, i inni, 1991). Rozróżniamy trzy rodzaje wierzchołków:

•

Akcje podstawowe

– reprezentowane przez prostokąty. Oznaczają

akcje które mogą zmienić wartość zmiennych, ale nie mogą zmienić
sterowania. Mają tylko jedną drogę wyjściową.

•

Warunki

- reprezentowane są przez romby, które mogą zmienić

sterowanie, ale nie mogą zmienić wartości zmiennych. Z warunku
wychodzą dwie drogi ilustrujące binarny wybór sterowania.

•

Połączenia

– odpowiadają im miejsca połączeń dwóch dróg. Nie

oznaczają żadnych akcji, a więc nie mogą zmienić wartości zmiennych
i mają tylko jedną drogę wyjściową.

D----struktury

struktury

Bruno i Steiglitz (1972) zdefiniowali klasę prostych struktur

sterujących, zwanych D-strukturami (D – od nazwiska Dijkistra).

D- strukturą jest:

•

Akcja podstawowa

– instrukcja przypisania, wywołanie procedury,

instrukcja wejścia lub wyjścia lub jeden z następujących elementów, z
których każdy jest kompozycją D-struktur:

•

Ciąg
s

… s

gdzie s

do s

są D-strukturami

•

Struktura warunkowa
if c then
s

else

end if

gdzie c jest warunkiem, a

są

D-strukturami.

Programowanie

Wersja: 2008-11-19

•

Struktura iteracyjna
while c loop
s
end loop

gdzie c jest warunkiem, a

ssss

jest D-strukturą.

Program skonstruowany wyłącznie z D-struktur jest też D-strukturą.
Na rysunku poniżej przedstawiono schematy blokowe D-struktur.

Rysunek 1. Schematy blokowe D-struktur. Źródło: (Marcotty, i inni, 1991)

Twierdzenie

Twierdzenie Boehma

Twierdzenie Boehma ----Jacopiniego

Jacopiniego

Jacopiniego (1966) mówi nam, że D-struktury

wystarczają do konstrukcji dowolnego programu. Dowód tego twierdzenia
przedstawił Mills (1972). Podstawowa konkluzja twierdzenia jest
następująca:

Dla dowolnego programu istnieje ekwiwalentny program,

który jest D-strukturą.

Dowolny program oznacza tutaj program komputerowy spełniający

następujące warunki:

Istnieje dokładnie jedno wejście i jedno wyjście z programu.

Dla każdego wierzchołka w schemacie blokowym programu istnieje co

najmniej jedna droga prowadząca od wejścia do programu przez ten
wierzchołek do wyjścia z programu.

Programowanie

Ekwiwalentnym programem nazywamy

identycznych danych wejściowych daje takie same wyniki jak program
wyjściowy, dla wszystkich możliwych wartości danych wejściowych.
Dowód istnienia ekwiwalentnego programu polega na podaniu k
kroków konstrukcji schematu blokowego D
ekwiwalentny ze schematem blokowym oryginalnego programu, przy
czym może on zawierać akcje, warunki i zmienne, które nie występowały
w oryginalnym programie.

Zatem jeśli w jeżyku progra

jeśli w jeżyku progra

typu D

typu D----struktur lub inne równoważne, to teoretycznie jest to

struktur lub inne równoważne, to teoretycznie jest to

wystarczający zbiór do zaprogramowania dowolnego problemu.

ROCES PROGRAMOWANIA

Typy danych

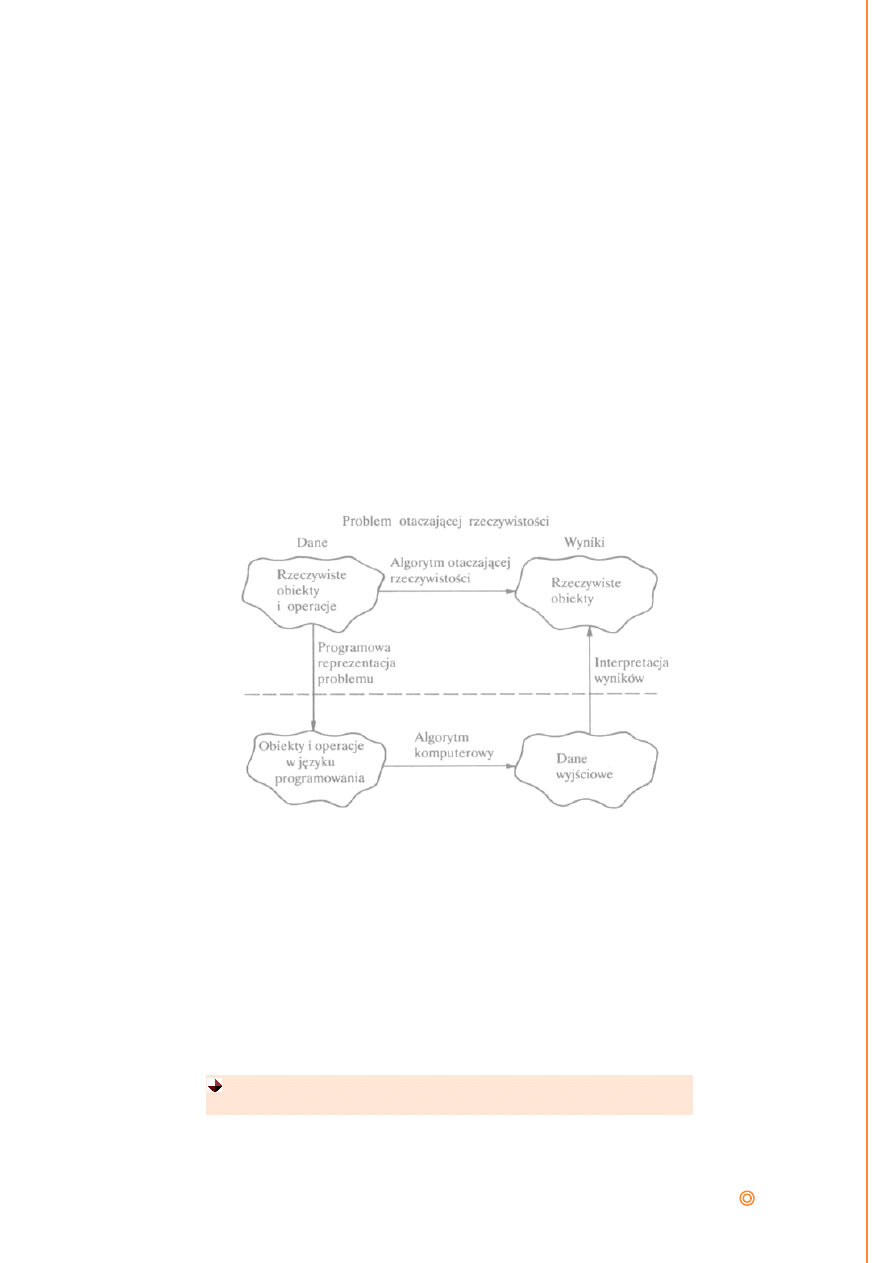
Rysunek poniżej ilustruje proces programowania.

Rysunek 2. Proces programowania.

Problemem do rozwiązania jest algorytm występujący w rzeczywistym

świecie i działający na rzeczywistych obiektach.
na opisaniu w języku programowania komputerowego modelu
rzeczywistego algorytmu. Aby utworzyć model algorytmu, programista
musi wybrać reprezentację obiektów dopuszczalnych w danym języku
programowania; konsekwencją tego wyboru jest zbiór operacji, które może
wykonać na modelu. Wszystkie operacje dopuszczalne na obiektach
modelu w języku programowania powinny mieć sens w świecie
rzeczywistym. Stąd w językach programowania występowanie pojęcia

typu,

które definiuje się w następujący sposób:

Typ jest zbiorem obiek

w sensowny sposób przekształcać te obiekty.

Wersja:

Sławomir Luściński. Politechnika Świętokrzyska 2008

programem nazywamy

taki program, który dla

identycznych danych wejściowych daje takie same wyniki jak program
wyjściowy, dla wszystkich możliwych wartości danych wejściowych.
Dowód istnienia ekwiwalentnego programu polega na podaniu k
kroków konstrukcji schematu blokowego D-struktury, który jest
ekwiwalentny ze schematem blokowym oryginalnego programu, przy
czym może on zawierać akcje, warunki i zmienne, które nie występowały
w oryginalnym programie.

jeśli w jeżyku progra

jeśli w jeżyku programowania dostępne są instrukcje sterujące

mowania dostępne są instrukcje sterujące

struktur lub inne równoważne, to teoretycznie jest to

wystarczający zbiór do zaprogramowania dowolnego problemu.

ROCES PROGRAMOWANIA

Rysunek poniżej ilustruje proces programowania.

Proces programowania. Źródło:

(Marcotty, i inni, 1991)

Problemem do rozwiązania jest algorytm występujący w rzeczywistym

działający na rzeczywistych obiektach. Programowanie polega

saniu w języku programowania komputerowego modelu

rzeczywistego algorytmu. Aby utworzyć model algorytmu, programista
musi wybrać reprezentację obiektów dopuszczalnych w danym języku

; konsekwencją tego wyboru jest zbiór operacji, które może

konać na modelu. Wszystkie operacje dopuszczalne na obiektach

modelu w języku programowania powinny mieć sens w świecie
rzeczywistym. Stąd w językach programowania występowanie pojęcia

definiuje się w następujący sposób:

Typ jest zbiorem obiektów i operacji, którymi można
w sensowny sposób przekształcać te obiekty.

Wersja: 2008-11-19

taki program, który dla

struktury, który jest

ekwiwalentny ze schematem blokowym oryginalnego programu, przy
czym może on zawierać akcje, warunki i zmienne, które nie występowały

mowania dostępne są instrukcje sterujące

struktur lub inne równoważne, to teoretycznie jest to

wystarczający zbiór do zaprogramowania dowolnego problemu.

(Marcotty, i inni, 1991)

Problemem do rozwiązania jest algorytm występujący w rzeczywistym

Programowanie polega

saniu w języku programowania komputerowego modelu

rzeczywistego algorytmu. Aby utworzyć model algorytmu, programista
musi wybrać reprezentację obiektów dopuszczalnych w danym języku

; konsekwencją tego wyboru jest zbiór operacji, które może

konać na modelu. Wszystkie operacje dopuszczalne na obiektach

modelu w języku programowania powinny mieć sens w świecie
rzeczywistym. Stąd w językach programowania występowanie pojęcia

tów i operacji, którymi można

Programowanie

Wersja: 2008-11-19

Paradoks Wynalazcy:

bardziej ogólny problem

może być prostszy.

Polya, 1964

Zasady programowania

Oto wybrane zasady zalecane do stosowania w procesie

programowania (Bentley, 1992)

•

Właściwe zrozumienie

problemu

. Znajomość i zrozumienie kontekstu,

w jakim pojawił się problem.

•

Określ abstrakcyjny problem

. Przejrzyste, lapidarne sformułowanie

problemu pomaga nam ten problem rozwiązać, a następnie to samo
rozwiązanie zastosować do innych
zadań. Napisanie ogólnego programu
dla N przypadków może się okazać
łatwiejsze, niż napisanie programu dla
ograniczonej liczby przypadków. Warto
tu przytoczyć Edwarda de Bono który
zwraca uwagę na fakt, że „poprawnego
określenie problemu możemy dokonać
jedynie z perspektywy znalezionego rozwiązania” (de Bono, 1998).
Ponieważ jest mało prawdopodobne, abyśmy znaleźli najlepszą
definicję, należy szukać określeń alternatywnych.

•

Zbadaj przestrzeń rozwiązań.

Nie należy przystępować do

programowania w oparciu o pierwszy pomysł rozwiązania problemu,
jaki przychodzi nam do głowy. Badając przestrzeń rozwiązań, należy
zadać sobie pytanie: jak moglibyśmy rozwiązać to samo zadanie w
inny sposób.

•

Spojrzenie wstecz.

„Zawsze pozostaje coś do zrobienia, przy

odpowiedniej dozie namysłu i dociekań moglibyśmy poprawić każdy
projekt, a w każdym razie możemy pogłębić nasze zrozumienie
mechanizmów rozwiązania” (Polya, 1964)

rozwiązywaniu

problemów

związanych

zadaniami

programistycznymi

szczególnie

przydatne

może

być

zalecenie

pokonywania blokad koncepcyjnych rozumianych jako „powstałe w
umyśle tamy, które odgradzają rozwiązującego pewien problem od
właściwego postrzegania tego problemu, czy też poszukiwania”.

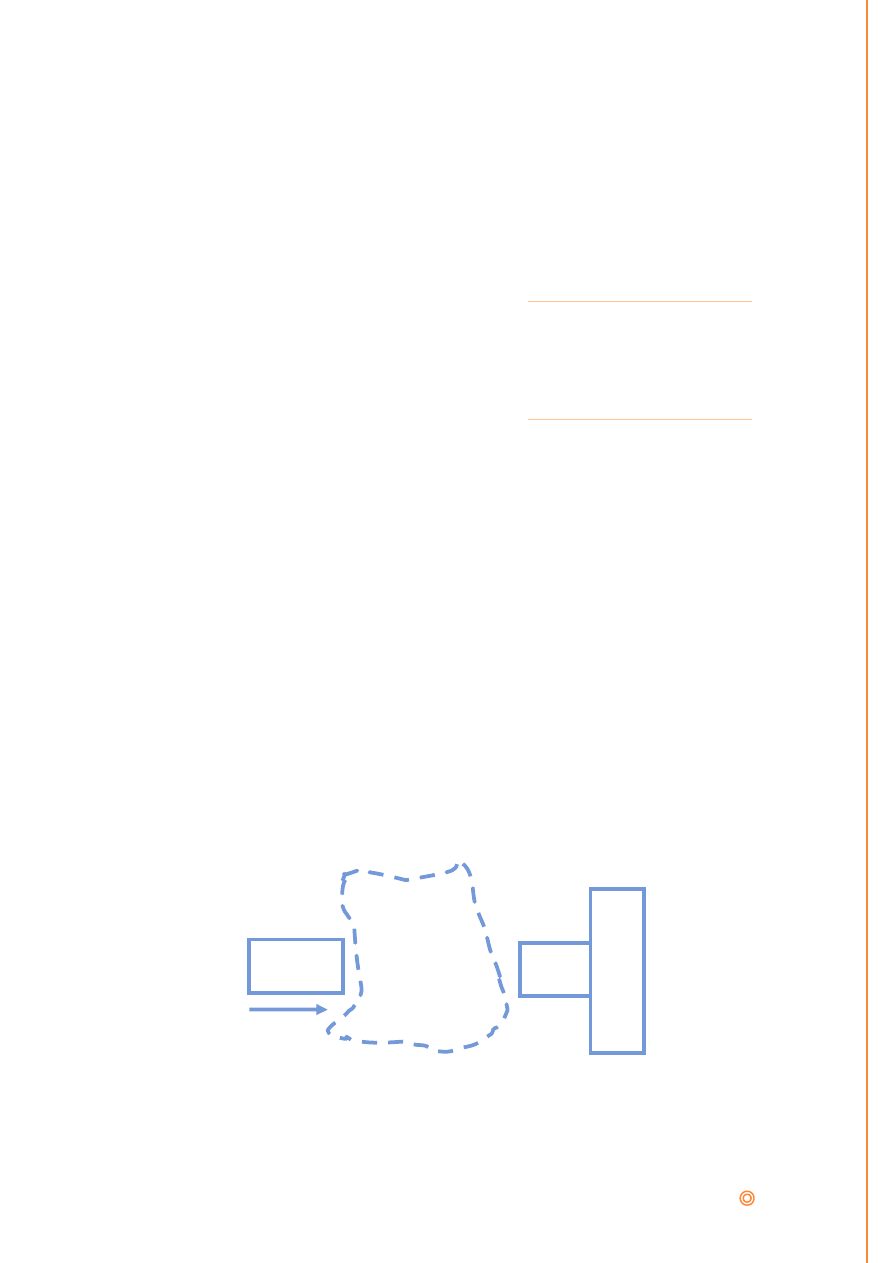
Rysunek 3. Rozwiązanie problemu. Źródło:

(de Bono, 1998)

Rysunek powyżej zaczerpnięty z (de Bono, 1998) przedstawia
rozwiązanie określonego problemu i dokładnie określony punkt wyjścia.

Programowanie

Wersja: 2008-11-19

Wszystko należy robić w

sposób tak prosty, jak to tylko

możliwe i ani trochę prościej

Albert Enstein

Pomiędzy nimi znajduje się obszar nieokreśloności, w którym należy
wytyczyć drogę od punktu wyjścia do rozwiązania.

„Rozwiązanie problemu może wymagać idei w takim samym stopniu jak
informacji… Zajmując się jakimś problemem, dobrze jest zebrać jak
najwięcej danych i stwierdzić, czy rozwiązanie będzie zależeć od
uzyskania większej liczby informacji, czy od nowej idei.”

Programy podpo

Programy podporządkowane strukturom danych

rządkowane strukturom danych

Właściwie dobrane do problemu

struktury

danych

umożliwiają

konsekwencji

uproszczenie

zadania

programistycznego polegającego na
sprowadzeniu dużych programów do
małych (Bentley, 1992) . Zalecenia dla
programisty w odniesieniu do struktur
danych formułuje się następująco:

• Przekształć powtarzający się kod w tablice. Długie ciągi podobnych do

siebie instrukcji często najlepiej jest wyrazić w najprostszej
strukturze danych, tzn. w tablicy.

• Zapoznaj się z bardziej złożonymi strukturami danych.
• Pozwól, by dane określały strukturę programu. Dane mogą narzucić

programowi kształt pozwalający zastąpić skomplikowany kod
odpowiednią strukturą danych.
Przed napisaniem kodu dobrzy programiści starannie analizują

wejście i wyjście oraz pośrednie struktury danych, na których opierają się
ich programy.

Niezawodność

Niezawodność oprogramowania

oprogramowania

Glenford J. Myers w swojej książce poświęconej niezawodności

oprogramowania pisze: „

błędy są wrodzoną własnością programów…

Możemy wykryć pewne błędy , takie jak nieskończona pętla, lecz z racji
pierwotnej natury błędów oprogramowania nigdy nie wykryjemy ich
wszystkich

(Myers, 1980)

Definicja błędu oprogramowania

edług

Myers’a jest następująca:

Błąd

oprogramowania

występuje

wówczas,

gdy

oprogramowanie

nie

spełnia

sensownych

oczekiwań

użytkownika. Awaria oprogramowania jest to wystąpienie
błędu oprogramowania.

Niezawodność oprogramowania jest funkcją wpływu błędów na

użytkowników systemu, przy czym niekoniecznie odzwierciedla wielkość
błędu wewnątrz systemu. Myres podaje przykład fiaska bezzałogowej
wyprawy na Wenus z powodu braku przecinka w instrukcji pętli
programu. Definicja niezawodności oprogramowania jest następująca:

Niezawodność oprogramowania jest prawdopodobieństwem,

że oprogramowanie działa bez awarii w określonym przedziale
czasu, opatrzonym wagą odpowiadającą kosztom poniesionym
przez użytkownika z powodu każdej zaistniałej awarii.

Programowanie

Wersja: 2008-11-19

Niezawodność nie jest wrodzoną cechą programu i zależy przede

wszystkim od sposobu użycia programu. Przez

prawdopodobieństwo

powyższej definicji należy rozumieć prawdopodobieństwo nie wystąpienia
zdarzenia polegającego na wprowadzenia przez użytkownika zestawu
danych wejściowych do programu, który powoduje awarię systemu.

Proces budowy oprogramowania można przedstawić jako ciąg

czynności poczynając od sformułowania problemu, a kończąc na
obszernym zestawie szczegółowych instrukcji sterujących komputerem w
trakcie wykonywania programu. Budowa programu polega na dokonaniu
„

pewnej liczby przekładów informacji,

tłumaczących problem początkowy

na różne rozwiązania pośrednie, aż do otrzymania szczegółowego kodu
maszynowego.”

Zatem:

Główną przyczyną błędów oprogramowania są błędy w

tłumaczeniu informacji.

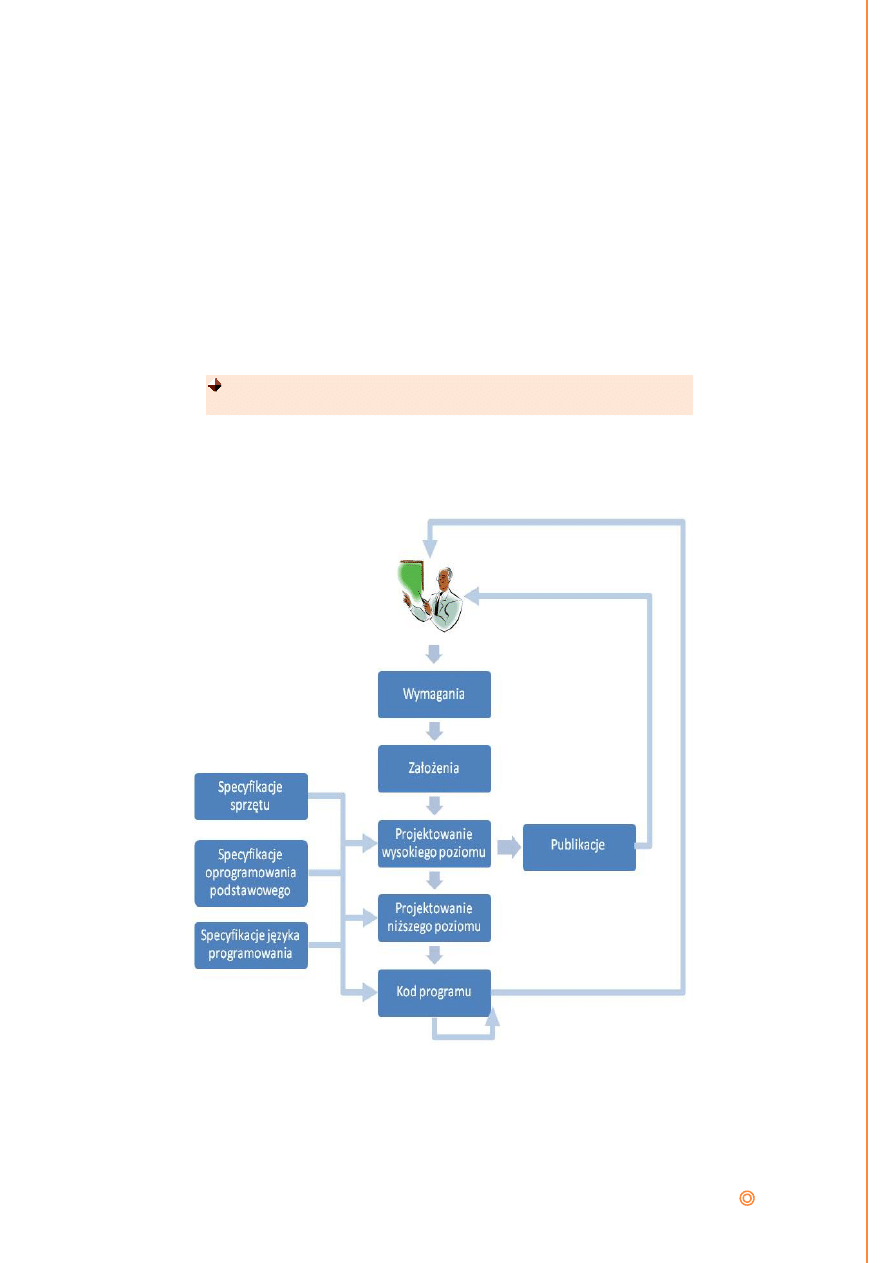
Rysunek poniżej przedstawia makroskopowy model tłumaczenia

występujący w procesie budowy oprogramowania.

Rysunek 4. Model makroskopowy. Źródło: opracowanie własne na podst. (Myers, 1980)

Programowanie

Wersja: 2008-11-19

Etapy programowania:

Wymagania. Opis rozwiązywanego problemu, ma zwykle postać
wymagań użytkownika.

II.

Tłumaczenie wymagań użytkownika na język założeń dla

budowanego programu.

III.

Przekształcenie założeń w specyfikacje zewnętrzne precyzyjnie

opisujące zachowanie całości systemu z punktu widzenia
użytkownika.

IV.

Tłumaczenie opisu zewnętrznego na strukturę składowych

oprogramowania (np. modułów) i przetłumaczenie każdej z tych
składowych na opis kroków proceduralnych (np. schematy blokowe)

Przełożenie logicznej specyfikacji oprogramowania na język
programowania.

Pętle sprzężenia zwrotnego:

VI.

Jako wynik przedsięwzięcia programistycznego uzyskujemy sam

program oraz jego dokumentację. Dokumentacja – określana jako
publikacje – powstaje jako translacja specyfikacji zewnętrznych na
informacje i dyrektywy przeznaczonego dla określonego typu
użytkownika.

VII.

Bezpośrednie współdziałanie użytkownika z programem, które

uwarunkowane jest sposobem zaprojektowania i wykonania
interfejsu użytkownika.

VIII.

Czytanie i rozumienie istniejących już tekstów programów dotyczy

zarówno pielęgnacji oprogramowania (usuwania błędów) jak i jego
modyfikacji (wzbogacania o nowe funkcje)

Programowanie

Wersja: 2008-11-19

IBLIOGRAFIA

Bazewicz, Mieczysław. 1993.

Wstęp do systemów informatycznych i

reprezentacji wiedzy.

Wrocław : Wydawnictwo Politechniki

Wrocławskiej, 1993.

Bentley, Jon. 1992.

Perełki oprogramowania.

Warszawa :

Wydawnictwa Naukowo-Techniczne, 1992.

de Bono,

de Bono, Edward. 1998.

Edward. 1998.

Atlas myślenia dla menadżera.

Warszawa :

Wydawnictwo Medium, 1998.

Kisielnicki, Jerzy i Sroka, Henryk. 2005.

Systemy informatyczne

biznesu.

III uzupełnione i zmienione. Warszawa : Wydawnictwo

PLACET, 2005.

Marcotty, Michael i Ledgard, Henry.

Marcotty, Michael i Ledgard, Henry. 1991.

1991.

W kręgu języków

programowania.

Warszawa : Wydawnictwa Naukowo-Techniczne,

1991.

Myers, Glenford J. 1980.

Myers,

Glenford

1980.

Myers,

Glenford

1980.

Myers,

Glenford

1980.

Projektowanie

niezawodnego

oprogramowania.

Warszawa : Wydawnictwa Naukowo-Techniczne,

1980.

Turski, Władysław M. 1989.

Turski,

Władysław

1989.

Turski,

Władysław

1989.

Turski,

Władysław

1989.

Propedeutyka informatyki.

Warszawa : PWN, 1989.

—

—. 1979.

. 1979.

Propedeutyka informatyki.

Warszawa : Państwowe

Wydawnictwo Naukowe, 1979.